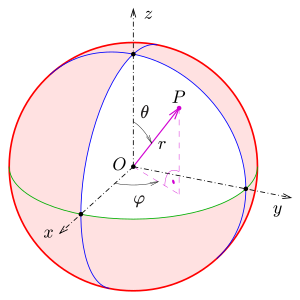
Übliche Darstellung der Kugelkoordinaten mit Radius ρ , Zenitwinkel θ und Azimut φ . Kugelkoordinaten oder räumliche Polarkoordinaten sind orthogonale Koordinaten , in denen ein Punkt im dreidimensionalen Raum durch seinen Abstand vom Ursprung und zwei Winkel angegeben wird.
Bei Punkten auf einer Kugeloberfläche (Sphäre ) um den Koordinatenursprung ist der Abstand vom Kugelmittelpunkt konstant. Dann sind nur noch die beiden Winkel variabel, sie werden dann als sphärische Koordinaten oder Kugelflächenkoordinaten [ 1] [ 2]
Der Begriff „Kugelkoordinaten“ kann als Oberbegriff für den allgemeinen Fall und die sphärischen Koordinaten angesehen werden. Kugelkoordinaten sind wie Zylinderkoordinaten eine Verallgemeinerung der ebenen Polarkoordinaten auf den dreidimensionalen euklidischen Raum . Sie lassen sich auch weiter auf Räume beliebiger endlicher Dimension verallgemeinern.
Ein Kugelkoordinatensystem im dreidimensionalen euklidischen Raum wird festgelegt durch die Wahl
eines Zentrums
O
{\displaystyle O}
einer gerichteten Gerade durch das Zentrum (Polachse), die die Polrichtung (oder Zenitrichtung) angibt, und durch diese festgelegt die Äquatorebene, die orthogonal zur Polrichtung durch das Zentrum verläuft, und
einer Bezugsrichtung in der Äquatorebene . Oft wird gleichzeitig ein kartesisches Koordinatensystem verwendet. Dann wird typischerweise der Ursprung des kartesischen Koordinatensystems als Zentrum gewählt, die z -Achse als Polachse (und damit die x-y -Ebene als Äquatorebene) und die x -Achse als Bezugsrichtung.
In der Version der Kugelkoordinaten, die in der Mathematik und in der Physik üblich ist, wird ein Punkt
P
{\displaystyle P}
Koordinaten festgelegt:
r
{\displaystyle r}
ρ
{\displaystyle \rho }
Radius , ist der Abstand des Punktes
P
{\displaystyle P}
O
{\displaystyle O}
P
{\displaystyle P}
θ
{\displaystyle \theta }
ϑ
{\displaystyle \vartheta }
[ 3] Polarwinkel oder Poldistanzwinkel, [ 4] Vertikalwinkel zwischen der Polrichtung und der Strecke
O
P
{\displaystyle OP}
0
{\displaystyle 0}
π
{\displaystyle \pi }
P
{\displaystyle P}
Kugeloberfläche festgelegt.
φ
{\displaystyle \varphi }
ϕ
{\displaystyle \phi }
[ 3] Azimutalwinkel ,[ 4] Horizontalwinkel zwischen der Bezugsrichtung und der Orthogonalprojektion der Strecke
O
P
{\displaystyle OP}
−
π
{\displaystyle -\pi }
π
{\displaystyle \pi }
0
{\displaystyle 0}
2
π
{\displaystyle 2\pi }
P
{\displaystyle P}
Die nachfolgende Abbildung zeigt einen Punkt
P
{\displaystyle P}
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
θ
{\displaystyle \theta }
φ
{\displaystyle \varphi }
Winkelkoordinaten bezeichnet.
Kugelkoordinaten
r
,
θ
,
φ
{\displaystyle r,\theta ,\varphi }
P
{\displaystyle P}
x
,
y
,
z
{\displaystyle x,y,z}
Jedem Koordinatentripel
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
Gleichungen beschrieben werden:
x
=
r
⋅
sin
θ
⋅
cos
φ
y
=
r
⋅
sin
θ
⋅
sin
φ
z
=
r
⋅
cos
θ
{\displaystyle {\begin{array}{cll}x&=&r\cdot \sin \theta \cdot \cos \varphi \\y&=&r\cdot \sin \theta \cdot \sin \varphi \\z&=&r\cdot \cos \theta \end{array}}}
Bei diesen Gleichungen können für
r
{\displaystyle r}
θ
{\displaystyle \theta }
φ
{\displaystyle \varphi }
r
{\displaystyle r}
θ
{\displaystyle \theta }
Intervall
[
0
,
π
]
{\displaystyle [0,\pi ]}
φ
{\displaystyle \varphi }
(
−
π
,
π
]
{\displaystyle (-\pi ,\pi ]}
[
0
,
2
π
)
{\displaystyle [0,2\pi )}
z -Achse ist der Winkel
φ
{\displaystyle \varphi }
θ
{\displaystyle \theta }
φ
=
0
{\displaystyle \varphi =0}
θ
=
0
{\displaystyle \theta =0}
Für die anderen Punkte lassen sich die Kugelkoordinaten
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
(
x
,
y
,
z
)
{\displaystyle (x,y,z)}
[ 5]
r
=
x
2
+
y
2
+
z
2
{\displaystyle r={\sqrt {x^{2}+y^{2}+z^{2}}}}
θ
=
arccos
(
z
r
)
{\displaystyle \theta =\arccos \left({\frac {z}{r}}\right)}
φ
=
arctan2
(
x
,
y
)
{\displaystyle \varphi =\operatorname {arctan2} (x,y)}
Mit der arctan2 -Funktion wird ein Winkel im Bogenmaß zwischen
−
π
{\displaystyle -\pi }
π
{\displaystyle \pi }
arctan2
(
x
,
y
)
=
{
arctan
(
y
x
)
, wenn
x
>
0
,
π
2
sgn
y
, wenn
x
=
0
,
arctan
(
y
x
)
+
π
, wenn
x
<
0
∧
y
≥
0
,
arctan
(
y
x
)
−
π
, wenn
x
<
0
∧
y
<
0.
{\displaystyle \operatorname {arctan2} (x,y)={\begin{cases}\arctan \left({\frac {y}{x}}\right)&{\text{, wenn }}x>0,\\{\frac {\pi }{2}}\operatorname {sgn} y&{\text{, wenn }}x=0,\\\arctan \left({\frac {y}{x}}\right)+\pi &{\text{, wenn }}x<0\land y\geq 0,\\\arctan \left({\frac {y}{x}}\right)-\pi &{\text{, wenn }}x<0\land y<0.\end{cases}}}
Die obige Koordinatenwahl ist internationaler Konsens in der theoretischen Physik . Manchmal werden die Zeichen
θ
{\displaystyle \theta }
φ
{\displaystyle \varphi }
Der Zenitwinkel
θ
{\displaystyle \theta }
nicht die geographische Breite , sondern lässt sich mit der Kobreite identifizieren. Die geographische Breite ist der Winkel zwischen der Äquatorialebene und dem Ortsvektor und nimmt Werte zwischen
−
90
∘
{\displaystyle -90^{\circ }}
90
∘
{\displaystyle 90^{\circ }}
ϕ
{\displaystyle \phi }
ϕ
=
90
∘
−
θ
,
θ
=
90
∘
−
ϕ
{\displaystyle \phi =90^{\circ }-\theta ,\theta =90^{\circ }-\phi }
φ
{\displaystyle \varphi }
geographischen Länge
λ
{\displaystyle \lambda }
Greenwich gleichsetzen (siehe geographische Koordinaten ).
In der Darstellung mit dem Koordinatentripel
(
r
,
ϕ
,
φ
)
{\displaystyle (r,\phi ,\varphi )}
x
=
r
cos
ϕ
cos
φ
{\displaystyle x=r\cos \phi \,\cos \varphi }
y
=
r
cos
ϕ
sin
φ
{\displaystyle y=r\cos \phi \,\sin \varphi }
z
=
r
sin
ϕ
{\displaystyle z=r\sin \phi \quad }
entspricht
ϕ
{\displaystyle \phi }
Die Umrechnung der kartesischen Koordinaten eines Punktes
P
(
x
,
y
,
z
)
{\displaystyle P(x,y,z)}
r
=
x
2
+
y
2
+
z
2
{\displaystyle r={\sqrt {x^{2}+y^{2}+z^{2}}}}
θ
=
arcsin
(
z
r
)
{\displaystyle \theta =\arcsin \left({\frac {z}{r}}\right)}
φ
=
arctan2
(
x
,
y
)
.
{\displaystyle \varphi =\operatorname {arctan2} (x,y).}
Kugelkoordinaten werden oft bei der Untersuchung von Systemen verwendet, die rotationssymmetrisch bezüglich eines Punktes sind. Beispiele sind: Volumenintegrale über Kugeln, die Beschreibung und Untersuchung rotationssymmetrischer Kraftfelder , wie z. B. das Gravitationsfeld eines kugelförmigen Himmelskörpers, das elektrische Feld einer Punktladung oder einer geladenen Kugel (siehe Beispiele zum Oberflächenintegral) . Die betrachteten Größen hängen dann nicht von den Winkelkoordinaten ab, was viele Formeln vereinfacht. Wichtige partielle Differentialgleichungen wie die Laplace-Gleichung oder die Helmholtzgleichung können in Kugelkoordinaten durch Separation der Variablen gelöst werden.
Aus der Koordinatentransformation als Vektorgleichung mit dem Ortsvektor
r
→
{\displaystyle {\vec {r}}}
r
→
=
(
x
y
z
)
=
(
r
sin
θ
cos
φ
r
sin
θ
sin
φ
r
cos
θ
)
{\displaystyle {\vec {r}}={\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}r\sin \theta \cos \varphi \\r\sin \theta \sin \varphi \\r\cos \theta \end{pmatrix}}}
ergeben sich
die Koordinatenlinien , indem man jeweils zwei der drei Koordinaten
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
die Koordinatenflächen , indem man eine der drei Koordinaten
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
Für Kugelkoordinaten sind die Koordinatenlinien durch den Punkt
(
r
0
∣
θ
0
∣
φ
0
)
{\displaystyle (r_{0}\mid \theta _{0}\mid \varphi _{0})}
für den Parameter
r
{\displaystyle r}
für den Parameter
θ
{\displaystyle \theta }
r
0
{\displaystyle r_{0}}
für den Parameter
φ
{\displaystyle \varphi }
r
0
sin
θ
0
{\displaystyle r_{0}\sin \theta _{0}}
Als Koordinatenfläche durch den Punkt
(
r
0
∣
θ
0
∣
φ
0
)
{\displaystyle (r_{0}\mid \theta _{0}\mid \varphi _{0})}
für konstanten Radius
r
0
{\displaystyle r_{0}}
für festen Winkel
θ
0
{\displaystyle \theta _{0}}
θ
0
=
π
/
2
{\displaystyle \theta _{0}=\pi /2}
θ
0
=
0
{\displaystyle \theta _{0}=0}
θ
0
=
π
{\displaystyle \theta _{0}=\pi }
für konstanten Wert von
φ
0
{\displaystyle \varphi _{0}}
Zwei unterschiedliche Koordinatenflächen durch einen Punkt schneiden sich in einer Koordinatenlinie. Koordinatenlinien und Koordinatenflächen dienen dazu, die lokalen Basisvektoren zu berechnen.
In der Tensorrechnung unterscheidet man wegen ihres unterschiedlichen Verhaltens bei Koordinatentransformationen zwischen kovarianten und kontravarianten Basisvektoren:
die kovarianten Basisvektoren an einem Punkt sind jeweils tangential zu den Koordinatenlinien gerichtet
die kontravarianten Basisvektoren an einem Punkt stehen jeweils senkrecht auf den Koordinatenflächen. Die lokalen Eigenschaften der Koordinatentransformation werden durch die Jacobi-Matrix beschrieben. Für die Transformation von Kugelkoordinaten in kartesische Koordinaten lautet diese
J
=
∂
(
x
,
y
,
z
)
∂
(
r
,
θ
,
φ
)
=
(
sin
θ
cos
φ
r
cos
θ
cos
φ
−
r
sin
θ
sin
φ
sin
θ
sin
φ
r
cos
θ
sin
φ
r
sin
θ
cos
φ
cos
θ
−
r
sin
θ
0
)
.
{\displaystyle J={\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}={\begin{pmatrix}\sin \theta \cos \varphi &r\cos \theta \cos \varphi &-r\sin \theta \sin \varphi \\\sin \theta \sin \varphi &r\cos \theta \sin \varphi &r\sin \theta \cos \varphi \\\cos \theta &-r\sin \theta &0\end{pmatrix}}.}
Die zugehörige Funktionaldeterminante lautet:
det
J
=
r
2
sin
θ
{\displaystyle \det J=r^{2}\sin \theta }
Man berechnet die Jacobi-Matrix der entgegengesetzten Transformation am einfachsten als Inverse von
J
{\displaystyle J}
J
−
1
=
∂
(
r
,
θ
,
φ
)
∂
(
x
,
y
,
z
)
=
(
sin
θ
cos
φ
sin
θ
sin
φ
cos
θ
1
r
cos
θ
cos
φ
1
r
cos
θ
sin
φ
−
1
r
sin
θ
−
1
r
sin
φ
sin
θ
1
r
cos
φ
sin
θ
0
)
.
{\displaystyle J^{-1}={\frac {\partial (r,\theta ,\varphi )}{\partial (x,y,z)}}={\begin{pmatrix}\sin \theta \cos \varphi &\sin \theta \sin \varphi &\cos \theta \\{\frac {1}{r}}\cos \theta \cos \varphi &{\frac {1}{r}}\cos \theta \sin \varphi &-{\frac {1}{r}}\sin \theta \\-{\frac {1}{r}}{\frac {\sin \varphi }{\sin \theta }}&{\frac {1}{r}}{\frac {\cos \varphi }{\sin \theta }}&0\end{pmatrix}}.}
Einige Komponenten dieser Matrix sind Brüche , an deren Nennern man die Uneindeutigkeit der Polarkoordinaten bei
r
=
0
{\displaystyle \textstyle r=0}
sin
θ
=
0
{\displaystyle \textstyle \sin \theta =0}
θ
=
0
{\displaystyle \textstyle \theta =0}
π
{\displaystyle \textstyle \pi }
J
−
1
=
(
x
r
y
r
z
r
x
z
r
2
x
2
+
y
2
y
z
r
2
x
2
+
y
2
−
(
x
2
+
y
2
)
r
2
x
2
+
y
2
−
y
x
2
+
y
2
x
x
2
+
y
2
0
)
.
{\displaystyle J^{-1}={\begin{pmatrix}{\frac {x}{r}}&{\frac {y}{r}}&{\frac {z}{r}}\\\\{\frac {xz}{r^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {yz}{r^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {-(x^{2}+y^{2})}{r^{2}{\sqrt {x^{2}+y^{2}}}}}\\\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\end{pmatrix}}.}
Die Jacobi-Matrix erlaubt es, die Umrechnung von Differentialen übersichtlich als lineare Abbildung zu schreiben:
(
d
x
d
y
d
z
)
=
J
⋅
(
d
r
d
θ
d
φ
)
{\displaystyle {\begin{pmatrix}\mathrm {d} x\\\mathrm {d} y\\\mathrm {d} z\end{pmatrix}}=J\cdot {\begin{pmatrix}\mathrm {d} r\\\mathrm {d} \theta \\\mathrm {d} \varphi \end{pmatrix}}}
beziehungsweise
(
d
r
d
θ
d
φ
)
=
J
−
1
⋅
(
d
x
d
y
d
z
)
.
{\displaystyle {\begin{pmatrix}\mathrm {d} r\\\mathrm {d} \theta \\\mathrm {d} \varphi \end{pmatrix}}=J^{-1}\cdot {\begin{pmatrix}\mathrm {d} x\\\mathrm {d} y\\\mathrm {d} z\end{pmatrix}}.}
Das Volumenelement
d
V
=
d
x
d
y
d
z
{\displaystyle \mathrm {d} V=\mathrm {d} x\,\mathrm {d} y\,\mathrm {d} z}
Funktionaldeterminante
det
J
=
r
2
sin
θ
{\displaystyle \det J=r^{2}\sin \theta }
umrechnen:
d
V
=
r
2
sin
θ
d
φ
d
θ
d
r
.
{\displaystyle \,\mathrm {d} V=r^{2}\sin \theta \,\mathrm {d} \varphi \,\mathrm {d} \theta \,\mathrm {d} r.}
Durch Differentiation
d
V
d
r
{\displaystyle {\frac {\mathrm {d} V}{\mathrm {d} r}}}
d
A
{\displaystyle \mathrm {d} A}
r
{\displaystyle r}
d
A
=
r
2
sin
θ
d
φ
d
θ
.
{\displaystyle \mathrm {d} A=r^{2}\sin \theta \,\mathrm {d} \varphi \,\mathrm {d} \theta .}
Das Linienelement
d
s
{\displaystyle \mathrm {d} s}
d
s
2
=
d
x
2
+
d
y
2
+
d
z
2
=
d
r
2
+
r
2
d
θ
2
+
r
2
sin
2
θ
d
φ
2
{\displaystyle \mathrm {d} s^{2}=\mathrm {d} x^{2}+\mathrm {d} y^{2}+\mathrm {d} z^{2}=\mathrm {d} r^{2}+r^{2}\mathrm {d} \theta ^{2}+r^{2}\sin ^{2}\theta \mathrm {d} \varphi ^{2}}
Im Fehlen gemischter Glieder im Linienelement
d
s
{\displaystyle \mathrm {d} s}
metrische Tensor
g
=
J
T
J
=
(
1
0
0
0
r
2
0
0
0
r
2
sin
2
θ
)
{\displaystyle g=J^{T}J={\begin{pmatrix}1&0&0\\0&r^{2}&0\\0&0&r^{2}\sin ^{2}\theta \end{pmatrix}}}
auch in Kugelkoordinaten keine Außerdiagonalelemente hat.
Der metrische Tensor ist offensichtlich das Quadrat der Diagonalmatrix
h
=
diag
(
1
,
r
,
r
sin
θ
)
.
{\displaystyle h=\operatorname {diag} (1,r,r\sin \theta ).}
Mit Hilfe dieser Matrix lässt sich die Jacobi-Matrix als
J
=
S
h
{\displaystyle J=Sh}
S
{\displaystyle S}
Rotationsmatrix
S
=
(
sin
θ
cos
φ
cos
θ
cos
φ
−
sin
φ
sin
θ
sin
φ
cos
θ
sin
φ
cos
φ
cos
θ
−
sin
θ
0
)
{\displaystyle S={\begin{pmatrix}\sin \theta \cos \varphi &\cos \theta \cos \varphi &-\sin \varphi \\\sin \theta \sin \varphi &\cos \theta \sin \varphi &\cos \varphi \\\cos \theta &-\sin \theta &0\end{pmatrix}}}
ist.
Im Folgenden soll die Transformation von Vektoren und Differentialoperatoren exemplarisch dargestellt werden. Die Ergebnisse werden bevorzugt in kompakter Form unter Benutzung von Transformationsmatrizen geschrieben. Die allermeisten Aussagen und Formeln gelten nur für Punkte außerhalb der z -Achse, für die die Jacobi-Determinante ungleich null ist.
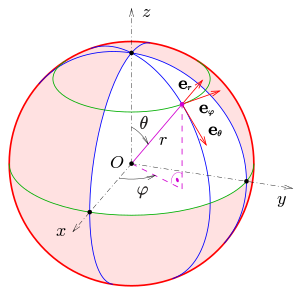
Kugelkoordinaten mit zugehöriger vom Ort abhängigen Orthogonalbasis
e
r
,
e
θ
,
e
φ
{\displaystyle \mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi }}
Der Basisvektor
e
φ
{\displaystyle \mathbf {e} _{\varphi }}
φ
{\displaystyle \varphi }
P
(
r
,
θ
,
φ
)
{\displaystyle P(r,\theta ,\varphi )}
φ
{\displaystyle \varphi }
d
φ
{\displaystyle d\varphi }
e
φ
∼
∂
P
∂
φ
=
∂
x
∂
φ
e
x
+
∂
y
∂
φ
e
y
+
∂
z
∂
φ
e
z
.
{\displaystyle \mathbf {e} _{\varphi }\sim {\frac {\partial \mathrm {P} }{\partial \varphi }}={\frac {\partial x}{\partial \varphi }}\mathbf {e} _{x}+{\frac {\partial y}{\partial \varphi }}\mathbf {e} _{y}+{\frac {\partial z}{\partial \varphi }}\mathbf {e} _{z}.}
Daraus erhält man
e
φ
∼
∂
P
∂
φ
=
−
r
sin
θ
sin
φ
e
x
+
r
sin
θ
cos
φ
e
y
.
{\displaystyle \mathbf {e} _{\varphi }\sim {\frac {\partial \mathrm {P} }{\partial \varphi }}=-r\sin \theta \sin \varphi \mathbf {e} _{x}+r\sin \theta \cos \varphi \mathbf {e} _{y}.}
Um eine orthonormale Basis zu erhalten, muss
e
φ
{\displaystyle e_{\varphi }}
1
{\displaystyle 1}
e
φ
=
−
sin
φ
e
x
+
cos
φ
e
y
.
{\displaystyle \mathbf {e} _{\varphi }=-\sin \varphi \,\mathbf {e} _{x}+\cos \varphi \,\mathbf {e} _{y}.}
Auf gleiche Weise erhält man die Basisvektoren
e
r
{\displaystyle e_{r}}
e
θ
{\displaystyle e_{\theta }}
e
r
=
sin
θ
cos
φ
e
x
+
sin
θ
sin
φ
e
y
+
cos
θ
e
z
{\displaystyle \mathbf {e} _{r}=\sin \theta \cos \varphi \,\mathbf {e} _{x}+\sin \theta \sin \varphi \,\mathbf {e} _{y}+\cos \theta \,\mathbf {e} _{z}}
e
θ
=
cos
θ
cos
φ
e
x
+
cos
θ
sin
φ
e
y
−
sin
θ
e
z
{\displaystyle \mathbf {e} _{\theta }=\cos \theta \cos \varphi \,\mathbf {e} _{x}+\cos \theta \sin \varphi \,\mathbf {e} _{y}-\sin \theta \,\mathbf {e} _{z}}
Als Spaltenvektoren geschrieben:
e
r
=
(
sin
θ
cos
φ
sin
θ
sin
φ
cos
θ
)
,
e
θ
=
(
cos
θ
cos
φ
cos
θ
sin
φ
−
sin
θ
)
,
e
φ
=
(
−
sin
φ
cos
φ
0
)
{\displaystyle \mathbf {e} _{r}={\begin{pmatrix}\sin \theta \cos \varphi \\\sin \theta \sin \varphi \\\cos \theta \end{pmatrix}},\qquad \mathbf {e} _{\theta }={\begin{pmatrix}\cos \theta \cos \varphi \\\cos \theta \sin \varphi \\-\sin \theta \end{pmatrix}},\qquad \mathbf {e} _{\varphi }={\begin{pmatrix}-\sin \varphi \\\cos \varphi \\0\end{pmatrix}}}
Diese Basisvektoren bilden in der Reihenfolge
e
r
,
e
θ
,
e
φ
{\displaystyle \mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi }}
Rechtssystem .
Die zugehörigen Richtungen werden auch radial , meridional und azimutal genannt. Diese Begriffe spielen nicht nur in der Astronomie und den Geowissenschaften (z. B. Geographie , Geologie oder Geophysik ) eine zentrale Rolle, sondern auch in Mathematik , Physik und verschiedenen Ingenieurwissenschaften , etwa bei der Ausstrahlung von elektromagnetischen Wellen („Hertzscher Dipol “) durch eine in z -Richtung aufgespannte Antenne, wo die Ausstrahlung in radialer Richtung erfolgt, während elektrisches bzw. magnetisches Feld in meridionaler bzw. azimutaler Richtung schwingen.
Mithilfe der oben eingeführten Rotationsmatrix
S
{\displaystyle S}
(
e
r
,
e
θ
,
e
φ
)
=
(
e
x
,
e
y
,
e
z
)
⋅
S
{\displaystyle (\mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi })=(\mathbf {e} _{x},\mathbf {e} _{y},\mathbf {e} _{z})\cdot S}
In die Gegenrichtung lauten die Gleichungen dann:
(
e
x
,
e
y
,
e
z
)
=
(
e
r
,
e
θ
,
e
φ
)
⋅
S
T
.
{\displaystyle (\mathbf {e} _{x},\mathbf {e} _{y},\mathbf {e} _{z})=(\mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi })\cdot S^{T}.}
Dabei wird verwendet, dass
S
{\displaystyle S}
S
−
1
=
S
T
{\displaystyle S^{-1}=S^{T}}
Ein Vektor , als ein geometrisches Objekt, muss vom Koordinatensystem unabhängig sein:
A
x
e
x
+
A
y
e
y
+
A
z
e
z
=
A
=
A
r
e
r
+
A
θ
e
θ
+
A
φ
e
φ
.
{\displaystyle A_{x}\mathbf {e} _{x}+A_{y}\mathbf {e} _{y}+A_{z}\mathbf {e} _{z}=\mathbf {A} =A_{r}\mathbf {e} _{r}+A_{\theta }\mathbf {e} _{\theta }+A_{\varphi }\mathbf {e} _{\varphi }.}
Diese Bedingung wird erfüllt durch
(
A
x
A
y
A
z
)
=
S
⋅
(
A
r
A
θ
A
φ
)
{\displaystyle {\begin{pmatrix}A_{x}\\A_{y}\\A_{z}\end{pmatrix}}=S\cdot {\begin{pmatrix}A_{r}\\A_{\theta }\\A_{\varphi }\end{pmatrix}}}
(
A
r
A
θ
A
φ
)
=
S
T
⋅
(
A
x
A
y
A
z
)
.
{\displaystyle {\begin{pmatrix}A_{r}\\A_{\theta }\\A_{\varphi }\end{pmatrix}}=S^{T}\cdot {\begin{pmatrix}A_{x}\\A_{y}\\A_{z}\end{pmatrix}}.}
Die partiellen Ableitungen transformieren sich wie die Basisvektoren, aber ohne Normierung. Man kann genau wie oben rechnen, nur lässt man den Punkt
P
{\displaystyle P}
Differentialgeometrie die Koordinatenbasisvektoren des Tangentialraums und die partiellen Ableitungen gleichgesetzt) und verwendet die Jacobi-Matrix
J
=
S
h
{\displaystyle J=Sh}
S
{\displaystyle S}
(
∂
∂
r
,
∂
∂
θ
,
∂
∂
φ
)
=
(
∂
∂
x
,
∂
∂
y
,
∂
∂
z
)
⋅
J
,
{\displaystyle \left({\frac {\partial }{\partial r}},{\frac {\partial }{\partial \theta }},{\frac {\partial }{\partial \varphi }}\right)=\left({\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}}\right)\cdot J,}
und in die Gegenrichtung
(
∂
∂
x
,
∂
∂
y
,
∂
∂
z
)
=
(
∂
∂
r
,
∂
∂
θ
,
∂
∂
φ
)
⋅
J
−
1
.
{\displaystyle \left({\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}}\right)=\left({\frac {\partial }{\partial r}},{\frac {\partial }{\partial \theta }},{\frac {\partial }{\partial \varphi }}\right)\cdot J^{-1}.}
Der Nabla-Operator
∇
{\displaystyle \nabla }
∇
=
e
x
∂
∂
x
+
e
y
∂
∂
y
+
e
z
∂
∂
z
.
{\displaystyle \mathbf {\nabla } =\mathbf {e} _{x}{\frac {\partial }{\partial x}}+\mathbf {e} _{y}{\frac {\partial }{\partial y}}+\mathbf {e} _{z}{\frac {\partial }{\partial z}}.}
Sowohl die partiellen Ableitungen als auch die Einheitsvektoren muss man in der oben hergeleiteten Weise transformieren. Man findet:
∇
=
e
r
∂
∂
r
+
e
θ
1
r
∂
∂
θ
+
e
φ
1
r
sin
θ
∂
∂
φ
.
{\displaystyle \mathbf {\nabla } =\mathbf {e} _{r}{\frac {\partial }{\partial r}}+\mathbf {e} _{\theta }{\frac {1}{r}}{\frac {\partial }{\partial \theta }}+\mathbf {e} _{\varphi }{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \varphi }}.}
In dieser Form kann der transformierte Nabla-Operator unmittelbar angewandt werden, um den Gradienten eines in Kugelkoordinaten gegebenen Skalarfeldes zu berechnen.
Um die Divergenz eines in Kugelkoordinaten gegebenen Vektorfeldes A zu berechnen, ist hingegen zu berücksichtigen, dass
∇
{\displaystyle \nabla }
A
r
,
A
θ
,
A
φ
{\displaystyle A_{r},A_{\theta },A_{\varphi }}
A implizit enthaltenen Basisvektoren
e
r
,
e
θ
,
e
φ
{\displaystyle \mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi }}
∇
⋅
A
=
1
r
2
∂
∂
r
(
r
2
A
r
)
+
1
r
sin
θ
∂
∂
θ
(
sin
θ
A
θ
)
+
1
r
sin
θ
∂
∂
φ
A
φ
.
{\displaystyle \mathbf {\nabla } \cdot \mathbf {A} ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}(r^{2}A_{r})+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \theta }}(\sin \theta A_{\theta })+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \varphi }}A_{\varphi }.}
Um die Rotation eines in Kugelkoordinaten gegebenen Vektorfeldes A zu berechnen, ist dasselbe zu berücksichtigen:
∇
×
A
=
1
r
sin
θ
(
∂
∂
θ
(
A
φ
sin
θ
)
−
∂
A
θ
∂
φ
)
e
r
+
1
r
(
1
sin
θ
∂
A
r
∂
φ
−
∂
∂
r
(
r
A
φ
)
)
e
θ
+
1
r
(
∂
∂
r
(
r
A
θ
)
−
∂
A
r
∂
θ
)
e
φ
.
{\displaystyle \mathbf {\nabla } \times \mathbf {A} ={1 \over r\sin \theta }\left({\partial \over \partial \theta }(A_{\varphi }\sin \theta )-{\partial A_{\theta } \over \partial \varphi }\right)\mathbf {e} _{r}+{1 \over r}\left({1 \over \sin \theta }{\partial A_{r} \over \partial \varphi }-{\partial \over \partial r}(rA_{\varphi })\right)\mathbf {e} _{\theta }+{1 \over r}\left({\partial \over \partial r}(rA_{\theta })-{\partial A_{r} \over \partial \theta }\right)\mathbf {e} _{\varphi }.}
Wenn man in der Divergenzformel als Vektorfeld A den Gradientenoperator
∇
{\displaystyle \nabla }
Laplace-Operator
Δ
=
∇
2
=
1
r
2
∂
∂
r
(
r
2
∂
∂
r
)
+
1
r
2
sin
θ
∂
∂
θ
(
sin
θ
∂
∂
θ
)
+
1
r
2
sin
2
θ
∂
2
∂
φ
2
{\displaystyle \mathbf {\Delta } =\mathbf {\nabla } ^{2}={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial }{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}}
bzw.
Δ
=
∂
2
∂
r
2
+
2
r
∂
∂
r
+
1
r
2
∂
2
∂
θ
2
+
1
r
2
cos
θ
sin
θ
∂
∂
θ
+
1
r
2
sin
2
θ
∂
2
∂
φ
2
.
{\displaystyle \mathbf {\Delta } ={\frac {\partial ^{2}}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial }{\partial r}}+{\frac {1}{r^{2}}}{\frac {\partial ^{2}}{\partial \theta ^{2}}}+{\frac {1}{r^{2}}}{\frac {\cos \theta }{\sin \theta }}{\frac {\partial }{\partial \theta }}+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}.}
Eine Verallgemeinerung der Kugelkoordinaten auf
n
{\displaystyle n}
x
1
=
r
cos
(
ϕ
1
)
x
2
=
r
sin
(
ϕ
1
)
cos
(
ϕ
2
)
x
3
=
r
sin
(
ϕ
1
)
sin
(
ϕ
2
)
cos
(
ϕ
3
)
⋮
x
n
−
1
=
r
sin
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
cos
(
ϕ
n
−
1
)
x
n
=
r
sin
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
sin
(
ϕ
n
−
1
)
{\displaystyle {\begin{aligned}x_{1}&=r\cos(\phi _{1})\\x_{2}&=r\sin(\phi _{1})\cos(\phi _{2})\\x_{3}&=r\sin(\phi _{1})\sin(\phi _{2})\cos(\phi _{3})\\&{}\,\,\,\vdots \\x_{n-1}&=r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})\\x_{n}&=r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})\end{aligned}}}
Die Winkel entwickeln sich nach:
tan
(
ϕ
n
−
1
)
=
x
n
x
n
−
1
tan
(
ϕ
n
−
2
)
=
x
n
2
+
x
n
−
1
2
x
n
−
2
⋮
tan
(
ϕ
1
)
=
x
n
2
+
x
n
−
1
2
+
⋯
+
x
2
2
x
1
{\displaystyle {\begin{aligned}\tan(\phi _{n-1})&={\frac {x_{n}}{x_{n-1}}}\\\tan(\phi _{n-2})&={\frac {\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}}}{x_{n-2}}}\\&{}\,\,\,\vdots \\\tan(\phi _{1})&={\frac {\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}+\cdots +{x_{2}}^{2}}}{x_{1}}}\end{aligned}}}
Durch Umnummerierung erhält man eine Rekursionsformel für die Winkel:
x
n
=
r
cos
(
ϕ
n
−
1
)
x
n
−
1
=
r
sin
(
ϕ
n
−
1
)
cos
(
ϕ
n
−
2
)
x
n
−
2
=
r
sin
(
ϕ
n
−
1
)
sin
(
ϕ
n
−
2
)
cos
(
ϕ
n
−
3
)
⋮
x
2
=
r
sin
(
ϕ
n
−
1
)
⋯
sin
(
ϕ
2
)
cos
(
ϕ
1
)
x
1
=
r
sin
(
ϕ
n
−
1
)
⋯
sin
(
ϕ
2
)
sin
(
ϕ
1
)
{\displaystyle {\begin{aligned}x_{n}&=r\cos(\phi _{n-1})\\x_{n-1}&=r\sin(\phi _{n-1})\cos(\phi _{n-2})\\x_{n-2}&=r\sin(\phi _{n-1})\sin(\phi _{n-2})\cos(\phi _{n-3})\\&{}\,\,\,\vdots \\x_{2}&=r\sin(\phi _{n-1})\cdots \sin(\phi _{2})\cos(\phi _{1})\\x_{1}&=r\sin(\phi _{n-1})\cdots \sin(\phi _{2})\sin(\phi _{1})\end{aligned}}}
Woraus sich die folgenden Winkel ergeben:
‖
L
→
k
‖
=
sgn
(
x
k
)
x
k
2
+
‖
L
→
k
−
1
‖
2
=
x
k
‖
x
k
‖
x
k
2
+
‖
L
→
k
−
1
‖
2
{\displaystyle \left\Vert {\vec {L}}_{k}\right\Vert =\operatorname {sgn}(x_{k}){\sqrt {x_{k}^{2}+\left\Vert {\vec {L}}_{k-1}\right\Vert ^{2}}}={\frac {x_{k}}{\left\Vert x_{k}\right\Vert }}{\sqrt {x_{k}^{2}+\left\Vert {\vec {L}}_{k-1}\right\Vert ^{2}}}}
mit
‖
L
→
0
‖
=
0
{\displaystyle \left\Vert {\vec {L}}_{0}\right\Vert =0}
tan
(
ϕ
k
)
=
x
k
2
+
‖
L
→
k
−
1
‖
2
x
k
+
1
=
‖
L
→
k
‖
x
k
+
1
{\displaystyle \tan(\phi _{k})={\frac {\sqrt {x_{k}^{2}+\left\Vert {\vec {L}}_{k-1}\right\Vert ^{2}}}{x_{k+1}}}={\frac {\left\Vert {\vec {L}}_{k}\right\Vert }{x_{k+1}}}}
Der Radius ist:
r
=
‖
L
→
n
‖
{\displaystyle r=\left\Vert {\vec {L}}_{n}\right\Vert }
Eine Fallunterscheidung liefert mittels Arkustangens den passenden Winkel zur gegebenen kartesischen Koordinate , wobei
arctan
(
±
∞
)
=
±
π
2
{\displaystyle \arctan(\pm \,\infty )=\pm \,{\tfrac {\pi }{2}}}
ϕ
k
=
{
arctan
(
‖
L
→
k
‖
x
k
+
1
)
+
π
,
(1) wenn:
x
k
+
1
<
0
∧
k
=
n
−
1
arctan
(
‖
L
→
k
‖
x
k
+
1
)
,
(2) wenn:
nicht (1)
∧
nicht (3)
0
,
(3) wenn:
x
k
+
1
=
‖
L
→
k
‖
=
0
{\displaystyle {\begin{aligned}\phi _{k}={\begin{cases}\arctan \left({\frac {\left\Vert {\vec {L}}_{k}\right\Vert }{x_{k+1}}}\right)+\pi ,&{\text{(1) wenn: }}x_{k+1}<0\;\land \;k=n-1\\\arctan \left({\frac {\left\Vert {\vec {L}}_{k}\right\Vert }{x_{k+1}}}\right),&{\text{(2) wenn: }}{\text{nicht (1)}}\land \;{\text{nicht (3)}}\\0,&{\text{(3) wenn: }}x_{k+1}=\left\Vert {\vec {L}}_{k}\right\Vert =0\\\end{cases}}\end{aligned}}}
Dabei fällt auf, dass
L
→
k
{\displaystyle {\begin{aligned}{\vec {L}}_{k}\end{aligned}}}
k
>
0
{\displaystyle {\begin{aligned}k>0\end{aligned}}}
Die Jacobi-Matrix der Kugelkoordinaten lautet bezüglich der als oberes gegebenen Nummerierung:
J
=
(
cos
(
ϕ
1
)
−
r
sin
(
ϕ
1
)
0
0
⋯
0
sin
(
ϕ
1
)
cos
(
ϕ
2
)
r
cos
(
ϕ
1
)
cos
(
ϕ
2
)
−
r
sin
(
ϕ
1
)
sin
(
ϕ
2
)
0
⋯
0
⋮
⋮
⋱
⋱
⋱
⋮
⋮
⋮
⋱
⋱
⋱
0
sin
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
cos
(
ϕ
n
−
1
)
r
cos
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
cos
(
ϕ
n
−
1
)
⋯
⋯
⋯
−
r
sin
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
sin
(
ϕ
n
−
1
)
sin
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
sin
(
ϕ
n
−
1
)
r
cos
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
sin
(
ϕ
n
−
1
)
⋯
⋯
⋯
r
sin
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
cos
(
ϕ
n
−
1
)
)
{\displaystyle J=\left({\begin{matrix}\cos(\phi _{1})&-r\sin(\phi _{1})&0&0&\cdots &0\\\sin(\phi _{1})\cos(\phi _{2})&r\cos(\phi _{1})\cos(\phi _{2})&-r\sin(\phi _{1})\sin(\phi _{2})&0&\cdots &0\\\vdots &\vdots &\ddots &\ddots &\ddots &\vdots \\\vdots &\vdots &\ddots &\ddots &\ddots &0\\\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})&r\cos(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})&\cdots &\cdots &\cdots &-r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})\\\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})&r\cos(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})&\cdots &\cdots &\cdots &r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})\end{matrix}}\right)}
Ihre Determinante beträgt:
det
J
(
n
)
=
r
n
−
1
sin
(
ϕ
1
)
n
−
2
sin
(
ϕ
2
)
n
−
3
⋯
sin
(
ϕ
n
−
2
)
=
r
n
−
1
⋅
∏
k
=
2
n
−
1
(
sin
(
ϕ
n
−
k
)
)
k
−
1
n
≥
2
{\displaystyle \det J_{(n)}=r^{n-1}\sin(\phi _{1})^{n-2}\sin(\phi _{2})^{n-3}\cdots \sin(\phi _{n-2})=\displaystyle r^{n-1}\cdot \prod _{k=2}^{n-1}\left(\sin(\phi _{n-k})\right)^{k-1}\quad n\geq 2}
Das Integral über den Betrag dieser Determinante lässt sich mit der Gammafunktion
Γ
{\displaystyle \Gamma }
∫
0
R
∫
0
2
π
∫
0
π
…
∫
0
π
|
det
J
(
n
)
|
d
ϕ
1
…
d
ϕ
n
−
2
d
ϕ
n
−
1
d
r
=
2
π
R
n
n
⋅
∏
k
=
2
n
−
1
∫
0
π
(
sin
(
ϕ
n
−
k
)
)
k
−
1
d
ϕ
n
−
k
=
2
π
R
n
n
⋅
∏
k
=
2
n
−
1
π
Γ
(
k
2
)
Γ
(
k
+
1
2
)
=
π
n
R
n
Γ
(
n
2
+
1
)
n
≥
2
{\displaystyle \int _{0}^{R}\int _{0}^{2\pi }\int _{0}^{\pi }\dots \int _{0}^{\pi }|\det J_{(n)}|\,{\text{d}}\phi _{1}\dots {\text{d}}\phi _{n-2}{\text{d}}\phi _{n-1}{\text{d}}r={\frac {2\pi R^{n}}{n}}\cdot \prod _{k=2}^{n-1}\int _{0}^{\pi }(\sin(\phi _{n-k}))^{k-1}{\text{d}}\phi _{n-k}={\frac {2\pi R^{n}}{n}}\cdot \prod _{k=2}^{n-1}{\frac {{\sqrt {\pi }}\;\Gamma \left({\frac {k}{2}}\right)}{\Gamma \left({\frac {k+1}{2}}\right)}}={\frac {{\sqrt {\pi }}^{n}R^{n}}{\Gamma \left({\frac {n}{2}}+1\right)}}\quad n\geq 2}
Dies entspricht dem Kugelvolumen einer
n
{\displaystyle n}
Hyperkugel :
V
n
(
R
)
=
π
n
R
n
Γ
(
n
2
+
1
)
{\displaystyle V_{n}(R)={\frac {{\sqrt {\pi }}^{n}R^{n}}{\Gamma \left({\frac {n}{2}}+1\right)}}}
2D:
∫
0
R
∫
0
2
π
r
d
ϕ
1
d
r
=
π
R
2
{\displaystyle \int _{0}^{R}\int _{0}^{2\pi }r\mathrm {d} \phi _{1}\mathrm {d} r=\pi R^{2}}
3D:
∫
0
R
∫
0
2
π
∫
0
π
r
2
sin
(
ϕ
2
)
d
ϕ
2
d
ϕ
1
d
r
=
4
π
R
3
3
{\displaystyle \int _{0}^{R}\int _{0}^{2\pi }\int _{0}^{\pi }r^{2}\sin(\phi _{2}){\text{d}}\phi _{2}{\text{d}}\phi _{1}{\text{d}}r={\frac {4\pi R^{3}}{3}}}
4D:
∫
0
R
∫
0
2
π
∫
0
π
∫
0
π
r
3
sin
2
(
ϕ
1
)
sin
(
ϕ
2
)
d
ϕ
1
d
ϕ
2
d
ϕ
3
d
r
=
π
2
R
4
2
{\displaystyle \int _{0}^{R}\int _{0}^{2\pi }\int _{0}^{\pi }\int _{0}^{\pi }r^{3}\sin ^{2}(\phi _{1})\sin(\phi _{2}){\text{d}}\phi _{1}{\text{d}}\phi _{2}{\text{d}}\phi _{3}{\text{d}}r={\frac {\pi ^{2}R^{4}}{2}}}
Zuordnung am Beispiel
n
=
3
{\displaystyle n=3}
x
,
y
,
z
{\displaystyle x,y,z}
x
3
=
z
=
r
cos
(
ϕ
2
)
x
2
=
x
=
r
sin
(
ϕ
2
)
cos
(
ϕ
1
)
x
1
=
y
=
r
sin
(
ϕ
2
)
sin
(
ϕ
1
)
{\displaystyle {\begin{aligned}x_{3}&=z=r\cos(\phi _{2})\\x_{2}&=x=r\sin(\phi _{2})\cos(\phi _{1})\\x_{1}&=y=r\sin(\phi _{2})\sin(\phi _{1})\\\end{aligned}}}
Die Winkel sind dann:
tan
(
ϕ
2
)
=
‖
L
→
2
‖
x
3
=
x
2
2
+
x
1
2
x
3
=
x
2
+
y
2
z
tan
(
ϕ
1
)
=
‖
L
→
1
‖
x
2
=
x
1
2
x
2
=
y
x
{\displaystyle {\begin{aligned}\tan(\phi _{2})={\frac {\left\Vert {\vec {L}}_{2}\right\Vert }{x_{3}}}&={\frac {\sqrt {x_{2}^{2}+x_{1}^{2}}}{x_{3}}}={\frac {\sqrt {x^{2}+y^{2}}}{z}}\\\tan(\phi _{1})={\frac {\left\Vert {\vec {L}}_{1}\right\Vert }{x_{2}}}&={\frac {\sqrt {x_{1}^{2}}}{x_{2}}}={\frac {y}{x}}\end{aligned}}}
W. Werner: Vektoren und Tensoren als universelle Sprache in Physik und Technik . Band 1 . Springer Vieweg, ISBN 978-3-658-25271-7 .
↑
Richard Doerfling: Mathematik für Ingenieure und Techniker. Oldenbourg Verlag, Seite 169.
↑
F. W. Schäfke: Einführung in die Theorie der speziellen Funktionen der mathematischen Physik. Springer, 1963, ISBN 978-3-642-94867-1 , Seite 129.
↑ a b
Lothar Papula : Mathematik für Ingenieure und Naturwissenschaftler. Band 3: Vektoranalysis, Wahrscheinlichkeitsrechnung, mathematische Statistik, Fehler- und Ausgleichsrechnung. 4. verbesserte Auflage. Vieweg + Teubner, Wiesbaden 2001, ISBN 3-528-34937-9 .
↑ a b
Zylinder- und Kugelkoordinaten. Memento Internet Archive TU München.
↑
Kugelkoordinaten.


















![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)
![{\displaystyle (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)








































































































