Ravigneaux-Satz
Ein Ravigneaux-Satz ist ein spezielles doppeltes Planetengetriebe, das üblicherweise in Automatikgetrieben verwendet wird. Benannt ist es nach dem französischen Erfinder Pol Ravigneaux, der es Mitte der 1930er Jahre in Neuilly-sur-Seine vorstellte.[1]
Bestandteile
[Bearbeiten | Quelltext bearbeiten]Es besteht aus:
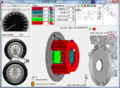
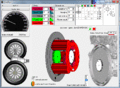
- einem gemeinsamen Hohlrad (im Bild grau), das in vielen Getrieben mit der Abtriebswelle zu den Antriebsrädern verbunden ist
- zwei verschieden großen Sonnenrädern (grün und dunkelgrün)
- einem Planetenradträger (rot), in dem alle Planetenräder gelagert sind
- lange Planetenräder (hellrot), die in das größere Sonnenrad und das Hohlrad eingreifen
- kurze Planetenräder (dunkelrot), die in das kleinere Sonnenrad und die langen Planetenräder eingreifen
Funktion
[Bearbeiten | Quelltext bearbeiten]Der Ravigneaux-Satz ist die Basis für die meisten Vier-Gang-Automatikgetriebe. Ergänzt mit weiteren Planetenradsätzen ist er auch in vielen Automatikgetrieben mit 5, 6, 7 oder 9 Gängen zu finden. Die verschiedenen Übersetzungsstufen werden wie beim einfachen Planetenradsatz durch Antreiben und Festbremsen bestimmter Teile oder durch Beblockung des gesamten Planetenradsatzes erreicht. Der Abtrieb kann entweder über das Hohlrad oder über den Planetenradträger geführt werden. Die Zeichnung zeigt einen Abtrieb über das Hohlrad. Zum Schalten von Gängen müssen über Bremsen die große (grüne) Sonne oder der Planetenradträgerring (rot) festgehalten werden und über Kupplungen die Motorwelle (weißes Zahnrad) mit einem der Sonnenräder oder dem Planetenradträger verbunden werden. Daraus ergeben sich nach der Gangtabelle sechs sinnvolle Kombinationen, die entsprechend vier Vorwärtsgänge, einen Rückwärtsgang und einen Leerlauf ergeben.
| Leerlauf | 1. Gang | 3. Gang |
|---|---|---|
Durch Variation der Zähnezahl der beteiligten Zahnräder können die erreichten Übersetzungen verändert werden. Eine Besonderheit stellt der dritte Gang dar. Dort werden zwei beliebige Kupplungen gleichzeitig geschaltet, so dass das Getriebe verblockt ist und unabhängig von der Zähnezahl immer die Übersetzung eins resultiert.
Üblicherweise werden jeweils drei kurze und drei lange Planetenräder verwendet. Es wären aber auch andere Anzahlen denkbar. Die Anzahl der Planeten hat keinen Einfluss auf die Übersetzung, wohl aber einen Einfluss auf das maximal übertragbare Drehmoment.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Beschreibung mit Abbildung
- Erklärung und Animation zur Funktionsweise eines Ravigneaux-Satzes
- Animation eines Ravigneaux-Satzes in allen Gängen
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Malcolm James Nunney: Light and heavy vehicle technology. 4. Aufl. Butterworth-Heinemann, Oxford 2007, ISBN 978-0-7506-8037-0, Seite 331 [1]