Serpent (Verschlüsselung)

Serpent
Serpent Die lineare Transformation von Serpent
Entwickler	Ross Anderson, Eli Biham, Lars Knudsen
Veröffentlicht	21. August 1998
Abgeleitet von	Square
Zertifizierung	AES Finalist
Schlüssellänge	128, 192 oder 256 Bit
Blockgröße	128 Bit
Struktur	Substitutions-Permutations-Netzwerk
Runden	32

Serpent ist ein symmetrischer Verschlüsselungsalgorithmus, der von den Kryptographen Ross Anderson, Eli Biham und Lars Knudsen entwickelt wurde. Es ist eine Blockchiffre mit einer Blockgröße von 128 Bit und variabler Schlüsselgröße bis 256 Bit.

Serpent war ein Kandidat für den Advanced Encryption Standard (AES) und gehörte mit Twofish, Rijndael, MARS und RC6 zu den fünf Finalisten des AES-Ausscheidungsverfahrens.

Serpent scheint eine sicherere Architektur als Rijndael zu haben. MARS, Twofish und Serpent wurden als hoch-sicher eingestuft, während Rijndael und RC6 „nur“ als hinreichend-sicher eingestuft wurden. Rijndael wurde vor allem wegen seiner mathematischen Struktur, die möglicherweise zu Angriffen führen könnte, kritisiert. Im Gegensatz zu den beiden anderen als hoch-sicher eingestuften Kandidaten der letzten Runde, MARS und Twofish, wurde Serpent bezüglich seiner Sicherheit nicht kritisiert und es wurde angenommen, dass dieser der sicherste der fünf Finalisten sei.

Serpent weist außerdem bei Implementierung in Hardware, die als Pipeline erfolgen kann, die höchste Geschwindigkeit unter den Finalisten auf. Er ist jedoch bei Software-Implementierungen der Langsamste, während Rijndael sowohl in Hardware als auch in Software relativ schnell ist. Vor allem dieser Geschwindigkeitsvorteil dürfte bei der Entscheidung, Rijndael zum AES zu erklären, den Ausschlag gegeben haben.

Funktionsweise

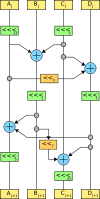
Aus dem Schlüssel werden zunächst 33 Teilschlüssel $K_{\,\!0}$ bis $K_{\,\!32}$ mit je 128 Bit Länge gebildet, und die Daten werden in Blöcke zu je vier 32-Bit-Wörtern eingeteilt. Diese Blöcke werden dann unabhängig voneinander in 32 aufeinanderfolgenden Runden verschlüsselt.

In jeder der Runden $i=0$ bis $i=31$ werden nacheinander folgende Operationen durchgeführt:

1. Der Datenblock wird mit dem Teilschlüssel $K_{\,\!i}$ bitweise XOR-verknüpft.
2. Es werden immer vier Bits, die in den vier Datenwörtern jeweils an der gleichen Position stehen, gemeinsam in einer S-Box substituiert. Es gibt acht verschiedene S-Boxen $S_{\,\!0}$ bis $S_{\,\!7}$, die periodisch durchlaufen werden: in Runde $i$ wird $S_{i\,{\bmod {8}}}$ verwendet.
3. In Runde $i=0$ bis $i=30$ werden die Datenwörter einer linearen Transformation unterzogen, die sich aus Rotationen, Verschiebungen und XOR-Verknüpfungen zusammensetzt. Sie ist in der Abbildung dargestellt. In Runde $i=31$ wird stattdessen mit dem Teilschlüssel $K_{\,\!32}$ XOR-verknüpft.

Diese Implementierung (sog. Bitslice-Technik) hat den Vorteil, dass mit bitweisen Operationen alle 32 Substitutionen in einer Runde parallel ausgeführt werden können. Bei entsprechend optimierter Software-Implementierung geht die Substitution so schneller als durch Tabellenzugriff. Außerdem konnten die Entwickler des Verfahrens hier eine zugleich einfache und effektiv vermischende lineare Transformation darstellen: Wird z. B. ein Datenwort rotiert, werden dadurch alle 32 Substitutionsblöcke geteilt und neu zusammengesetzt.

Eine alternative Implementierung des Verfahrens arbeitet mit der Substitution von immer vier in einem Datenwort aufeinanderfolgenden Bits. Dadurch kann die Substitution einfacher als Tabellenzugriff realisiert werden: Die vier Index-Bits stehen schon beisammen und sie müssen nur ggf. nach rechts geschoben und die höheren Bits ausmaskiert werden. Vor der ersten Runde werden die 128 Datenbits permutiert, so dass die niederwertigsten Bits in den vier Datenwörtern an die Positionen 0 bis 3 des ersten Worts kommen, die nächst-höherwertigen an die Positionen 4 bis 7 usw. Diese Permutation wird nach der letzten Runde rückgängig gemacht. Auch die 33 Teilschlüssel müssen entsprechend permutiert werden. Die lineare Transformation wird bei dieser Implementierung jedoch komplizierter, denn auch hierbei muss die andere Anordnung der Bits berücksichtigt werden.

Lizenz

Serpent ist nicht patentiert und wurde als Public-Domain-Software veröffentlicht. Es steht damit jedem zur Nutzung frei zur Verfügung. Optimierte Versionen des Codes wurden unter der GNU General Public License lizenziert.

Beispielanwendungen

Der Serpent-Algorithmus wird unter anderem von folgenden Open-Source-Softwarepaketen implementiert:

• DiskCryptor – Festplattenverschlüsselung, Verschlüsselung von Partitionen
• VeraCrypt – Festplattenverschlüsselung, Verschlüsselung von Partitionen und von Containerdateien
• dm-crypt – Festplattenverschlüsselung

Angriff

2002 veröffentlichten Courtois und Pieprzyk eine Arbeit, in der eine potentielle Attacke gegen Serpent (und Rijndael) mit Namen XSL vorgestellt wurde. Der Angriff ist lediglich theoretisch und kann aufgrund seiner Komplexität nicht tatsächlich ausprobiert werden. Es ist unbekannt, ob der Angriff praktisch durchgeführt werden könnte.

Die Kryptographen T. Moh und Don Coppersmith sind der Meinung, dass der Angriff auf Serpent derzeit nicht durchgeführt werden kann.

Weblinks

• Serpent (englisch)
• Beschreibung von Markus Repges
• Standard Cryptographic Algorithm Naming zu Serpent (englisch)
• NIST, Report on the Development of the Advanced Encryption Standard (AES), 2. Oktober 2000 (englisch) (PDF; 392,6 kB)