Spidron

Erstes Spidron nach Dániel Erdély

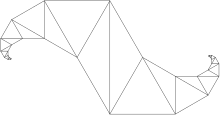
Ein Spidron ist eine komplexe geometrische Figur aus einer Folge gleichschenkliger, gleichseitiger Dreiecke, wobei zwei Dreiecke jeweils ein Hexagon, ein regelmäßiges Sechseck bilden, das mit einem weiteren Sechseck verbunden wird, indem ein Eckpunkt mit dem übernächsten Eckpunkt verbunden wird. Auf diese Weise kann die Form zu einer Vielzahl von Strukturen verschachtelt werden. Diese wurden auch schon mathematisch untersucht. Der Name entstand aus den englischen Bezeichnungen spider (Spinne) und spiral (Spirale), da die Form des Spidrons an ein Spinnennetz erinnert.

Definition

Ein klassisches Spidron im Hexagon

Ausgangspunkt des klassischen Spidrons ist ein regelmäßiges Sechseck mit der Kantenlänge a. Jeder Eckpunkt wird mit dem übernächsten Eckpunkt (d. h. zwei Ecken weiter) durch eine Strecke verbunden. Die Verbindungsstrecken schneiden sich in sechs Schnittpunkten. Aus Symmetriegründen entsteht dabei im Inneren ein kleineres, regelmäßiges Sechseck. Dieses neue Sechseck kann auf die gleiche Weise wie vorher unterteilt werden. Setzt man diese Erzeugung von Sechsecken unendlich fort, so gelangt man zu einer Abfolge von immer kleineren Dreiecken. Die dabei entstehende Figur wird Spidron genannt."

Ursprünge und Entwicklung

Entdeckt wurden Spidrons 1979 durch den ungarischen Designstudenten Dániel Erdély. Die Formen waren Teil einer Hausarbeit von Erdély. Er wurde dazu während seines Studiums an der Moholy-Nagy-Universität für Kunsthandwerk und Gestaltung in Budapest von Ernő Rubik, dem Erfinder des Zauberwürfels animiert.

Spidron Relief nach Stefan Stenzhorn

In seinen ersten Arbeiten ging Erdély bei der Konstruktion von Spidrons noch von einem regelmäßigen Sechseck (Hexagon) aus. Spidrons kann man jedoch aus allen regelmäßigen n-Ecken generieren, deren Eckzahl größer als vier beträgt. Darüber hinaus kann auch die Verbindung um zwei Ecken zu Verbindungslinien um m Ecken erweitert werden. Nach Stenzhorn kommt man daher zur Erkenntnis, dass ein Spidron im Hexagon lediglich ein Spezialfall eines allgemeinen Spidrons ist.

Weiterhin gilt, dass die Eckpunkte eines Spidrons eine logarithmische Spirale bilden. In seinen ersten Arbeiten gab Erdély den gefundenen Figuren unterschiedliche Namen. Eine Spidron-Hälfte bezeichnete er als “Semispidron”. Je nachdem, wie zwei “Semispidrons” aneinander gelegt wurden, definierte Erdély weitere Figurnamen wie “B-Spidron”, “J-Spidron” oder “Hornflake”. Letztlich lassen sich aber alle zusammengesetzten Figuren auf den hier verwendeten Spidronbegriff zurückführen.

Praktische Anwendung

Bekannt ist die Form aus vielen Arbeiten Eschers, der sich bevorzugt solchen Körpern mit hoher Symmetrie widmete. Allgemein ist bekannt, dass mit Hilfe von regelmäßigen Sechsecken eine zweidimensionale Ebene lückenlos parkettieren lässt. Da jedes Hexagon aus sechs Spidronarmen besteht, ist auch mit Spidrons eine lückenlose Parkettierung der Ebene möglich.

In Bezug auf ein dreidimensionales Spidron schreibt Stefan Stenzhorn: "Das Spidron bietet die Möglichkeit dreidimensional verformt zu werden, so dass sich Reliefs daraus herstellen lassen. Ausgangspunkt sind die sechs Spidrons eines Hexagons. Es werden jeweils drei Spidrons so gefaltet, dass jeder Falz ein Bergfalz ist. Die anderen drei Spidrons werden so gefaltet, dass jeder Falz ein Talfalz ist.". Im Hinblick auf Spidron-Reliefs sieht Erdély mögliche Anwendungsgebiete z. B. als Schock-Dämpfer oder Knautschzonen. Auch eine Anwendung in der Raumfahrt sieht er als möglich an. Darüber hinaus könnte ein Spidron-Relief in einem Solarsystem die Sonne leichter einfangen.

Weblinks

Commons: Spidrons – Sammlung von Bildern, Videos und Audiodateien

• http://spidron.hu/
• http://www.gamepuzzles.com/resourc5c.htm Concept Spidron System, geschrieben von Dániel Erdély (PDF-Dokument)
• http://www.szinhaz.hu/edan/SpidroNew/index.html Spidron System
• Erklärung in englischer Sprache (Memento vom 28. November 2010 im Internet Archive)