Wienerprozess

Ein Wienerprozess (nach dem US-amerikanischen Mathematiker Norbert Wiener) oder Wienerscher Prozess ist ein zeitstetiger stochastischer Prozess, der normalverteilte, unabhängige Zuwächse hat. Er stellt ein mathematisches Modell für die brownsche Bewegung dar und wird deswegen selbst häufig als „brownsche Bewegung“ bezeichnet.
Seit der Einführung der stochastischen Analysis durch Itō Kiyoshi in den 1940er Jahren spielt der Wienerprozess die zentrale Rolle im Kalkül der zeitstetigen stochastischen Prozesse und dient in vielen Gebieten der Natur- und Wirtschaftswissenschaften als Grundlage zur Modellierung zufälliger Entwicklungen.
Geschichte
[Bearbeiten | Quelltext bearbeiten]

1827 beobachtete der schottische Botaniker Robert Brown unter dem Mikroskop, wie Pflanzenpollen sich in einem Wassertropfen unregelmäßig hin- und herbewegten (daher der Name brownsche Bewegung).
1880 beschrieb der Statistiker und Astronom Thorvald Nicolai Thiele (1838–1910) in Kopenhagen erstmals einen solchen „Prozess“ (die Theorie der stochastischen Prozesse war damals noch nicht entwickelt), als er wirtschaftliche Zeitreihen und die Verteilung von Residuen bei der Methode der kleinsten Quadrate studierte. 1900 griff der französische Mathematiker Louis Bachelier (1870–1946), ein Schüler Henri Poincarés, Thieles Idee auf, als er versuchte, die Kursbewegungen an der Pariser Börse zu analysieren. Beide Ansätze hatten letztendlich nur geringen Einfluss auf die zukünftige Entwicklung des Prozesses, zum Teil wohl, weil Finanzmathematik damals eine untergeordnete Rolle in der Mathematik spielte; heute jedoch gilt sie als Hauptanwendungsgebiet von Wienerprozessen. Dennoch bevorzugte z. B. der Stochastiker William Feller die Bezeichnung Bachelier-Wiener-Prozess.
Der Durchbruch kam, als Albert Einstein 1905 in seinem annus mirabilis,[1] offenbar ohne Kenntnis von Bacheliers Arbeiten, und unabhängig von ihm Marian Smoluchowski 1906[2] den Wienerprozess in seiner heutigen Gestalt definierte. Einsteins Motivation war es, die Bewegung der brownschen Partikel durch die molekulare Struktur des Wassers zu erklären – ein Ansatz, der damals äußerst kontrovers war, heute aber unbestritten ist – und diese Erklärung mathematisch zu untermauern. Interessanterweise forderte er dabei eine weitere, physikalisch sinnvolle Eigenschaft, die Rektifizierbarkeit der Zufallspfade, nicht für sein Modell. Obwohl dies bedeutet, dass die Partikel in jeder Sekunde eine unendlich lange Strecke zurücklegen können (was das gesamte Modell theoretisch disqualifiziert), bedeutete der einsteinsche Ansatz den Durchbruch sowohl für die molekulare Theorie als auch für den stochastischen Prozess.
Einen Beweis für die wahrscheinlichkeitstheoretische Existenz des Prozesses blieb Einstein allerdings schuldig. Dieser gelang erst 1923 dem US-amerikanischen Mathematiker Norbert Wiener, der dabei neue Hilfsmittel von Lebesgue und Borel auf dem Gebiet der Maßtheorie nutzen konnte. Dennoch war sein Beweis so lang und kompliziert, dass ihn wohl nur eine Handvoll Zeitgenossen verstehen konnten. Von Itō Kiyoshi ist überliefert, dass er einige seiner größten Fortschritte bei der Entwicklung des stochastischen Integrals bei dem Versuch erreichte, Wieners Arbeit nachzuvollziehen.
Letztendlich war es auch Itō, der dem Wienerprozess den Weg von der Physik in andere Wissenschaften ebnete: Durch die von ihm aufgestellten stochastischen Differentialgleichungen konnte man die brownsche Bewegung an mehr statistische Probleme anpassen. So löst die aus einer stochastischen Differentialgleichung abgeleitete geometrische brownsche Bewegung das Problem, dass der Wienerprozess, unabhängig von seinem Startwert, im Laufe der Zeit fast sicher einmal negative Werte erreicht, was für Aktien unmöglich ist; Bacheliers Ansatz war daran letztendlich noch gescheitert. Seit der Entwicklung des berühmten Black-Scholes-Modells gilt die geometrische brownsche Bewegung daher als Standard.
Das von den nicht rektifizierbaren Pfaden des Wienerprozesses aufgeworfene Problem bei der Modellierung brownscher Pfade führt zum Ornstein-Uhlenbeck-Prozess und macht ebenfalls den Bedarf einer Theorie der stochastischen Integration und Differentiation deutlich – hier wird nicht die Bewegung, sondern die Geschwindigkeit des Teilchen als ein nicht rektifizierbarer vom Wienerprozess abgeleiteter Prozess modelliert, aus dem man rektifizierbare Teilchenpfade durch Integration erhält.
Heute werden in praktisch allen Natur- und vielen Sozialwissenschaften brownsche Bewegungen und verwandte Prozesse als Hilfsmittel verwendet.
Definition
[Bearbeiten | Quelltext bearbeiten]Ein Wienerprozess ist ein zeitstetiger stochastischer Prozess, der normalverteilte, unabhängige Zuwächse hat:
Ein stochastischer Prozess auf dem Wahrscheinlichkeitsraum heißt (Standard-)Wienerprozess, wenn folgende vier Bedingungen gelten:
- (P-fast sicher).
- Für gegebene Zeitpunkte sind die Zuwächse stochastisch unabhängig. Der Wienerprozess hat also unabhängige Zuwächse.
- Für alle gilt . Die Zuwächse sind also stationär und normalverteilt mit dem Erwartungswert null und der Varianz .
- Die einzelnen Pfade sind (P-)fast sicher stetig.
Der vierte Punkt kann auch aus der Definition insofern gestrichen werden, als sich mit dem Stetigkeitssatz von Kolmogorow-Tschenzow zeigen lässt, dass es unter den o. g. Voraussetzungen immer eine fast sicher stetige Version des Prozesses gibt.
Alternativ lässt sich ein Wienerprozess nach Paul Lévy durch folgende zwei Eigenschaften charakterisieren:
- ist ein stetiges lokales Martingal mit .
- ist ein Martingal.
Eigenschaften
[Bearbeiten | Quelltext bearbeiten]Aus der Definition folgt sofort .
Einordnung
[Bearbeiten | Quelltext bearbeiten]- Der Wienerprozess zählt zur Familie der Markowprozesse und dort speziell zur Klasse der Lévyprozesse. Außerdem erfüllt er die starke Markoweigenschaft.
- Der Wienerprozess ist ein spezieller Gaußprozess mit der Wahrscheinlichkeitsdichtefunktion , der Erwartungswertfunktion , der Varianz (siehe auch Gleichung von Bienaymé), der Kovarianzfunktion und der Korrelation .
- Der Wienerprozess ist ein Martingal. Ist also die von erzeugte Filtrierung, dann gilt für die bedingte Erwartung für alle .
- Der Wienerprozess ist ein Lévyprozess mit stetigen Pfaden und konstantem Erwartungswert .
Eigenschaften der Pfade
[Bearbeiten | Quelltext bearbeiten]- Die Pfade eines Wienerprozesses sind fast sicher an keiner Stelle differenzierbar (Satz von Paley-Wiener-Zygmund) und fast sicher nicht rektifizierbar. Betrachtet man die Menge der nirgends-differenzierbaren Pfade in , so erhält man eine Menge, von der man nicht weiß, ob sie messbar ist. Allerdings wurde 1961 von Dvoretzky-Erdős-Kakutani eine Beweismöglichkeit der Nirgends-Differenzierbarkeit geliefert, bei der man ein Gitter von über die brownsche Bewegung konstruiert und zeigt, dass die Menge der differenzierbaren Pfade in[3][4]
- enthalten ist. Diese Menge besitzt als äußeres Maß den Wert .
- Die Pfade haben in jedem Intervall fast sicher unendliche Variation.
- Für die quadratische Variation gilt fast sicher .
- Über Asymptotik im Unendlichen und um den Nullpunkt geben die Gesetze des iterierten Logarithmus Auskunft.
- Für einen Wienerprozess gilt das lokale Gesetzt des iterierten Logarithmus:
- Damit sind die Pfade des Wienerprozesses insbesondere hölderstetig zum Exponenten mit , jedoch nicht für .
- Für das Bild einer Menge unter einem Wienerprozess, das heißt für , gelten die Dimensionsverdopplungssätze.
Selbstähnlichkeiten, Reflexionsprinzip
[Bearbeiten | Quelltext bearbeiten]
- Auch das Negative eines Standard-Wienerprozesses, also ist ein Standard-Wienerprozess. Allgemeiner gilt auch das Reflexionsprinzip: Ein an einer beliebigen Stoppzeit gespiegelter Wienerprozess ist wieder ein Wienerprozess. Der gespiegelte Prozess ist dabei wie folgt definiert: , falls , und , falls .
- Der Wienerprozess ist selbstähnlich unter Streckung der Zeitachse, d. h., ist für jedes ein Standard-Wienerprozess.
- Inversion der Zeitachse: Auch ist ein Standard-Wienerprozess
- Verschiebung der Zeitachse: Für jedes deterministische ist der stochastische Prozess ebenfalls ein Wienerprozess; hier werden die Zuwächse vom Zeitpunkt an betrachtet, d. h., erfüllt die schwache Markoweigenschaft.
Wiener-Maß
[Bearbeiten | Quelltext bearbeiten]Eine Funktion nennt man Koordinaten-Abbildung. Der dazugehörige Prozess heißt Koordinaten-Prozess.
Das eindeutige Bildmaß für den Wienerprozess auf dem Wienerraum, einer unendlichdimensionalen Sphäre im Funktionenraum der stetigen Funktionen, nennt man Wiener-Maß, wenn der Koordinaten-Prozess eine -dimensionale Standard-Brownsche-Bewegung ist.[5]
Generator
[Bearbeiten | Quelltext bearbeiten]
Für den Generator eines eindimensionalen Standard-Wienerprozesses gilt
- ,
das heißt, ist ½ Mal der Operator der zweiten Ableitung. Allgemeiner ist der Generator eines mehrdimensionalen Wienerprozesses ½ Mal der Laplaceoperator. Diese Beziehung kann verwendet werden, um Wienerprozesse auch auf anderen Mannigfaltigkeiten wie z. B. auf einer Kugel (siehe Bild) zu definieren, nämlich als Markowprozess mit dem Laplace-Beltrami-Operator als Generator. Für die Konstruktion der brownschen Bewegung auf einer Mannigfaltigkeit braucht man allerdings zusätzliche geometrische Strukturen und Bochners horizontalen Laplace-Operator, welcher in der stochastischen Differentialgeometrie behandelt wird.
Verallgemeinerter Wienerprozess
[Bearbeiten | Quelltext bearbeiten]Ist ein Standard-Wienerprozess, so nennt man den stochastischen Prozess
brownsche Bewegung mit Drift und Volatilität . Damit lassen sich auch stochastische Prozesse darstellen, die tendenziell eher fallen () oder tendenziell eher steigen (). Dabei gilt
- .
Auch allgemeine Wienerprozesse sind Markow- und Lévyprozesse, aber die Martingaleigenschaft gilt nur noch in abgeschwächter Form:
Ist , so ist ein Supermartingal, ist , so ist ein Submartingal. Für ist ein Martingal.
Der mehrdimensionale Fall
[Bearbeiten | Quelltext bearbeiten]
Ein mehrdimensionaler stochastischer Prozess heißt n-dimensionaler (Standard-)Wienerprozess oder n-dimensionale brownsche Bewegung, falls die Koordinaten unabhängige (Standard-)Wienerprozesse sind.
Die Zuwächse sind dann ebenfalls unabhängig und -verteilt (n-dimensionale Normalverteilung), wobei die Einheitsmatrix der Dimension n ist.
Die Lévy-Charakterisierung lässt sich wie folgt verallgemeinern: Seien stetige lokale Martingale mit , dann ist ein -dimensionaler Standard-Wienerprozess.[6]
Der n-dimensionale Wienerprozess hat eine besonders schöne Eigenschaft, die ihn von den meisten anderen mehrdimensionalen Prozessen abhebt und die ihn für die Modellierung des brownschen Partikels prädestiniert: Er ist invariant unter Drehungen der Koordinatenachsen. Das bedeutet, dass für jede orthogonale Matrix der gedrehte (oder gespiegelte) Prozess genau dieselbe Verteilung wie besitzt.
Genau wie die eindimensionale brownsche Bewegung kann man nun auch die n-dimensionale verallgemeinern: Für jeden Vektor und jede Matrix wird durch
eine brownsche Bewegung mit Drift und Varianz definiert. Dementsprechend gilt . Hierbei können die einzelnen Koordinaten also auch miteinander korreliert sein.
Zusammenhang zu anderen stochastischen Prozessen
[Bearbeiten | Quelltext bearbeiten]- Ist eine geometrische brownsche Bewegung, so ist eine brownsche Bewegung (mit Drift). Andererseits kann man aus jedem Wienerprozess mit Drift und Volatilität durch eine geometrische brownsche Bewegung gewinnen.
- Mit Hilfe des stochastischen Integralbegriffes von Itō lässt sich der Wienerprozess zum Itōprozess verallgemeinern.
- Die symmetrische Irrfahrt kann als zeitdiskretes Pendant zum Wienerprozess angesehen werden, denn es gilt der folgende Konvergenzsatz: Ist für die Irrfahrt auf dem diskreten Zeitgitter so definiert, dass gilt und sich in jedem Zeitschritt mit Wahrscheinlichkeit um nach oben und mit Wahrscheinlichkeit um nach unten bewegt, so konvergiert für gegen einen Standard-Wienerprozess (für die Art der Konvergenz siehe Invarianzprinzip von Donsker).
- Ist ein Standard-Wienerprozess und , so ist , , eine brownsche Brücke.
- Ist ein -dimensionaler Standard-Wienerprozess und , so heißt Bessel-Prozess.
Simulation von brownschen Pfaden
[Bearbeiten | Quelltext bearbeiten]Um mit Hilfe von Zufallszahlen Pfade eines Wienerprozesses zu simulieren, stehen verschiedene Methoden zur Verfügung, die allesamt auf verschiedenen Eigenschaften des Prozesses aufbauen:
Einfache Irrfahrt
[Bearbeiten | Quelltext bearbeiten]Die einfachste Möglichkeit besteht darin, die oben erwähnte Konvergenz der einfachen Irrfahrt nach dem Satz von Donsker gegen einen Wienerprozess auszunutzen. Dazu muss man lediglich rademacherverteilte Zufallsvariablen B1, B2, B3, … simulieren, die untereinander unabhängig sind und jeweils mit Wahrscheinlichkeit die Werte 1 und −1 annehmen. Dann kann man zu einer vorgegebenen Schrittweite einen Wienerprozess an den Stellen durch
approximieren. Der Vorteil dieser Methode liegt darin, dass nur sehr einfach herzustellende rademacherverteilte Zufallsvariablen benötigt werden. Allerdings handelt es sich nur um eine Approximation: Das Resultat ist kein Gauß-Prozess, sondern hat quasi binomialverteilte Zustände (genauer gesagt ist binomial(n; 0,5)-verteilt). Um die Normalverteilung hinreichend gut anzunähern, muss deshalb sehr klein gewählt werden. Diese Methode ist deshalb nur zu empfehlen, wenn man den Prozess ohnehin auf einem sehr feinen Zeitgitter simulieren möchte.
Gaußsche Irrfahrt
[Bearbeiten | Quelltext bearbeiten]Die folgende Methode ist der einfachen Irrfahrt überlegen (sofern kein besonders feines Zeitgitter benötigt wird), da sie den Prozess exakt simuliert (d. h., die resultierenden Zustände stimmen in Verteilung mit denen eines Wienerprozesses überein):
- ,
wobei unabhängige, standardnormalverteilte Zufallszahlen sind (beispielsweise erzeugt durch die Polar-Methode von Marsaglia). Diese als gaußsche Irrfahrt bezeichnete Diskretisierung ist nur dann von Nachteil, wenn die vorhandenen normalverteilten Zufallsvariablen nicht von gleichmäßiger „Qualität“ sind. Wenn zum Beispiel Quasi-Zufallszahlen verwendet werden, weisen spät auftretende Zahlen bisweilen Abhängigkeitsstrukturen auf, die das Ergebnis verzerren können. In einem solchen Fall ist eine der nachfolgenden Methoden vorzuziehen.
Brownsche Brücke
[Bearbeiten | Quelltext bearbeiten]
Diese auf Paul Lévy zurückgehende Methode[7] (die nur am Rande etwas mit dem stochastischen Prozess der Brownschen Brücke zu tun hat) nutzt die Kovarianzstruktur des Wienerprozesses aus und legt ein höheres Gewicht auf frühe standardnormalverteilte Zufallsvariablen .
Hier wird zuerst , welches normalverteilt mit Varianz 1 ist, durch simuliert. Nun wird das Intervall schrittweise halbiert und folgender Schritt wiederholt:
ergibt sich als arithmetisches Mittel plus eine weitere Normalverteilte Zufallsvariable, um die Varianz zu korrigieren. Also:
Analog:
und so weiter. Die Faktoren verringern sich dabei in jedem Halbierungsschritt um den Faktor und sorgen dafür, dass die Zustände die richtige Varianz erhalten.
Um einen Wienerprozess statt auf auf ein beliebiges Intervall auszuweiten, kann man nun die oben beschriebene Transformation anwenden; ist dann ein Wienerprozess auf .
Hintergrund dieser nichtkausalen Modellierung ist, dass bedingt auf und wiederum normalverteilt ist.
Spektralzerlegung
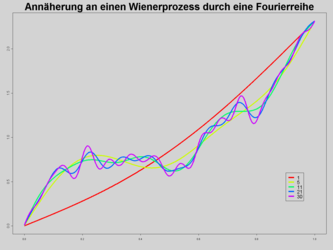
[Bearbeiten | Quelltext bearbeiten]Bei der Spektralzerlegung wird der Wienerprozess in einer Art stochastischer Fourieranalyse als trigonometrische Polynome mit zufälligen Koeffizienten approximiert. Sind unabhängig und standardnormalverteilt, so konvergiert die Reihe
gegen einen Wienerprozess. Diese Methode konvergiert bezüglich der L2-Norm zwar mit maximaler Geschwindigkeit, beinhaltet aber im Gegensatz zur brownschen Brücke viele aufwändige trigonometrische Funktionsauswertungen. Daher findet sie, vor allem in der Monte-Carlo-Simulation, weniger oft Anwendung.
- Annäherung an einen Wienerprozess durch Fourierreihe
Geometrie
[Bearbeiten | Quelltext bearbeiten]Die ein- und zwei-dimensionale brownsche Bewegung ist rekurrent, in allen höheren Dimensionen ist sie transient. (Satz von Pólya (Irrfahrten): „Ein betrunkener Mann findet immer heim, ein betrunkener Vogel nicht.“)
Siehe auch
[Bearbeiten | Quelltext bearbeiten]Literatur
[Bearbeiten | Quelltext bearbeiten]- Andrei N. Borodin, Paavo Salminen: Handbook of Brownian Motion - Facts and Formulae. Birkhäuser, Basel 2002, ISBN 3-7643-6705-9.
- Ioannis Karatzas, Steven E. Shreve: Brownian Motion and Stochastic Calculus (Graduate Texts in Mathematics). Springer, New York 1997, ISBN 0-387-97655-8.
- David Meintrup, Stefan Schäffler: Stochastik. Theorie und Anwendungen. Springer, Berlin/Heidelberg 2005, ISBN 3-540-21676-6, Kap. 12, S. 341–374.
- P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, Wienerscher Prozeß, S. 495–498.
- René L. Schilling, Lothar Partzsch: Brownian Motion. An Introduction to Stochastic Processes. De Gruyter, Berlin/Boston 2012, ISBN 978-3-11-027889-7.
- John Michael Steele: Stochastic Calculus and Financial Applications. Springer, New York 2000, ISBN 0-387-95016-8.
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Einstein, Albert: Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. In: Annalen der Physik. Band 17, 1905, S. 549–560, doi:10.1002/andp.19053220806.
- ↑ Smoluchowski, M.: Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen. In: Annalen der Physik. Band 21, 1906, S. 756–780 (bnf.fr).
- ↑ A. Dvoretzky, P. Erdős, S. Kakutani: Nonincrease Everywhere of the Brownian Motion Process. In: Berkeley Symposium on Mathematical Statistics and Probability. Band 4.2, 1961, S. 103–116 (projecteuclid.org).
- ↑ René L. Schilling und Lothar Partzsch: Brownian Motion: An Introduction to Stochastic Processes. De Gruyter, Berlin, Boston 2012.
- ↑ Daniel Revuz und Marc Yor: Continuous Martingales and Brownian Motion. In: Springer (Hrsg.): Grundlehren der mathematischen Wissenschaften. Band 293, 1999, S. 33–41 (englisch).
- ↑ Philip E. Protter: Stochastic Integration and Differential Equations. 2. Auflage. ISBN 978-3-540-00313-7, S. 87–88.
- ↑ P. Lévy: Processus stochastiques et mouvement brownien. Gauthier-Villars, Paris 1965.
























![{\displaystyle [s,t]\subset \mathbb {R} _{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/531afc6675a6dfcc072275526b8fe5a9dc136340)
![{\displaystyle [W,W]_{t}=\langle W,W\rangle _{t}=t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0164e9d172a7d67f8d98010e6c051d78aa21bd42)












































![{\displaystyle [X^{i},X^{j}]_{t}={\begin{cases}t,\,{\text{ falls }}i=j\\0,{\text{ falls }}i\neq j\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed1de6fced1d7ede750c0d5b8700ac05d987e95e)





































![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)






![{\displaystyle [0,a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63d050b0ffe6cc6f635808b9a013366a60e6d0c0)