Zufallsstichprobe
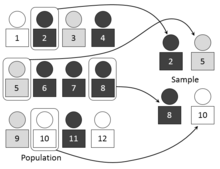
Eine Zufallsstichprobe (auch Wahrscheinlichkeitsauswahl, Zufallsauswahl, Random-Sample) ist eine Stichprobe aus der Grundgesamtheit, die mit Hilfe eines speziellen Auswahlverfahrens gezogen wird. Bei einem solchen Zufallsauswahlverfahren hat jedes Element der Grundgesamtheit eine angebbare Wahrscheinlichkeit (größer null), in die Stichprobe zu gelangen. Nur bei Zufallsstichproben sind, streng genommen, die Methoden der induktiven Statistik anwendbar. Zufallsstichproben spielen in Monte-Carlo-Methoden eine zentrale Rolle. Zufällige Stichprobenwiederholungen können mithilfe der Resampling-Methode generiert werden.
Begriff der Zufallsstichprobe
[Bearbeiten | Quelltext bearbeiten]Eine Stichprobe ist das Ergebnis einer Stichprobenziehung, das ist eine Entnahme von einem oder mehreren Einheiten aus einer Grundgesamtheit. Im einfachsten Fall der gleichzeitigen Entnahme mehrerer Einheiten aus einer endlichen Gesamtheit ist die Stichprobe eine Teilmenge einer Grundgesamtheit. Erfolgen mehrere Entnahmen jeweils einer Einheit, wobei die gezogene Einheit zurückgelegt wird, bevor die nächste Einheit gezogen wird, so können Einheiten der Grundgesamtheit mehrfach in die Stichprobe gelangen. In diesem Fall kann das Ergebnis einer Stichprobenziehung durch einen Vektor dargestellt werden, dessen Komponenten das Ergebnis der ersten Ziehung, zweiten Ziehung usw. angeben. Bei unendlichen Grundgesamtheiten ist diese Unterscheidung irrelevant, bei sehr großen Grundgesamtheiten ist sie vernachlässigbar.
Für eine Zufallsstichprobe werden zusätzliche Bedingungen gestellt:
- Die Elemente werden zufällig aus der Grundgesamtheit gezogen und
- die Wahrscheinlichkeit, mit der ein Element aus der Grundgesamtheit gezogen wird, ist angebbar.
Des Weiteren unterscheidet man zwischen einer uneingeschränkten und einer einfachen Zufallsstichprobe:
- uneingeschränkte Zufallsstichprobe
-
- Jedes Element der Grundgesamtheit hat die gleiche Wahrscheinlichkeit, in die Stichprobe zu gelangen.
- Einfache Zufallsstichprobe
-
- Jedes Element der Grundgesamtheit hat die gleiche Wahrscheinlichkeit, in die Stichprobe zu gelangen, und
- die Ziehungen aus der Grundgesamtheit erfolgen unabhängig voneinander.
Eine uneingeschränkte Zufallsstichprobe erhält man z. B. bei einem Ziehen ohne Zurücklegen und eine einfache Zufallsstichprobe z. B. bei einem Ziehen mit Zurücklegen.
Beispiele
[Bearbeiten | Quelltext bearbeiten]Literary-Digest-Desaster
[Bearbeiten | Quelltext bearbeiten]Das Literary-Digest-Desaster von 1936 zeigt auf, was passieren kann, wenn keine Zufallsstichprobe aus der Grundgesamtheit gezogen wird.[1] Eine verzerrte Stichprobe führte zu einer vollständig falschen Wahlprognose.
Wahlbefragung
[Bearbeiten | Quelltext bearbeiten]Eine Befragung von Wählern, nachdem sie aus der Wahlkabine gekommen sind, bzgl. ihres Wahlverhaltens ist eine uneingeschränkte Zufallsstichprobe (wenn kein Befragter die Antwort verweigert) bzgl. der Wähler. Sie ist jedoch keine (uneingeschränkte) Zufallsstichprobe bzgl. der Wahlberechtigten.
Taschenkontrolle
[Bearbeiten | Quelltext bearbeiten]Der Einzelhandel beklagt immer wieder, dass durch Diebstahl von Waren durch eigene Mitarbeiter große Schäden verursacht werden.[2] Deswegen führen größere Supermärkte unter anderem eine Taschenkontrolle durch, wenn Mitarbeiter den Supermarkt verlassen. Da eine vollständige Taschenkontrolle aller Angestellten zu aufwändig wäre (und dies vermutlich auch als Arbeitszeit bezahlt werden müsste), gehen die Angestellten beim Verlassen des Supermarktes durch den Personalausgang an einer Lampe vorbei. Sie zeigt computergesteuert entweder ein grünes Licht (Angestellter wird nicht kontrolliert) oder ein rotes Licht (Angestellter wird kontrolliert). Diese Auswahl ist dann eine einfache Zufallsauswahl.
Zufallsstichproben in der mathematischen Statistik
[Bearbeiten | Quelltext bearbeiten]In der mathematischen Statistik sind Zufallsstichproben die Grundlage für den Rückschluss von der Stichprobe auf Eigenschaften der Grundgesamtheit. Die Stichprobenwerte werden dann als Realisierungen der Zufallsvariablen betrachtet. Diese Zufallsvariablen werden als Stichprobenvariablen bezeichnet und geben an, mit welcher Wahrscheinlichkeit bei der -ten Ziehung mit einem bestimmten Auswahlverfahren ein bestimmtes Element der Grundgesamtheit gezogen werden kann.
Stochastisch unabhängig und identisch verteilt
[Bearbeiten | Quelltext bearbeiten]Wurde eine einfache Zufallsstichprobe gezogen, so kann man zeigen, dass die Stichprobenvariablen stochastisch unabhängig und identisch verteilt sind (Abkürzung i.i.d., aus dem engl. independent and identically distributed). D. h., der Verteilungstyp und die Verteilungsparameter aller Stichprobenvariablen sind gleich der Verteilung in der Grundgesamtheit (identically distributed), und aufgrund der Unabhängigkeit der Ziehungen sind die Stichprobenvariablen auch unabhängig voneinander (independent).
Bei vielen Problemen in der induktiven Statistik wird vorausgesetzt, dass die Stichprobenvariablen i.i.d. sind. Anderenfalls sind die Stichprobenwerte die Komponenten eines Vektors , der die Realisation eines Zufallsvektors ist, dessen mehrdimensionale Wahrscheinlichkeitsverteilung durch das jeweilige Stichprobendesign bestimmt ist.
Geordnete Stichprobe
[Bearbeiten | Quelltext bearbeiten]Die geordneten Stichprobenwerte entstehen, wenn die Werte einer Stichprobe einen Größenvergleich erlauben und der Größe nach angeordnet werden.[3][4] Meistens erfolgt die Anordnung nichtfallend, so dass gilt. Man nennt den Vektor oft kurz Stichprobe und den Vektor dann geordnete Stichprobe. Beispielsweise führt die Stichprobe zur geordneten Stichprobe . Es sind verschiedenen Notationen für die aufsteigend geordneten Stichprobenwerte üblich, z. B. auch oder .
Es gibt eine entsprechende Verallgemeinerung für einen Vektor unabhängig und identisch verteilter reeller Zufallsvariablen .[3][4] Die -te Komponente der geordneten Stichprobe heißt -te Ordnungsstatistik oder -te Ranggröße.[3] Die geordnete Stichprobe heißt auch Positionsstichprobe oder Variationsreihe.[3] Die -te Ordnungsstatistik heißt auch Positionsstichprobenfunktion -ten Rangs.[3] Die geordnete Stichprobe spielt eine zentrale Rolle in der nichtparametrischen Statistik, da sie eine suffiziente und vollständige Statistik ist.[5]
Abhängige und unabhängige Stichproben
[Bearbeiten | Quelltext bearbeiten]Bei Analysen mit mehr als einer Stichprobe muss zwischen abhängigen und unabhängigen Stichproben unterschieden werden. Statt von einer abhängigen Stichprobe spricht man auch von verbundenen Stichproben[6] oder gepaarten Stichproben[7].
Abhängige Stichproben treten meist bei wiederholten Messungen an dem gleichen Untersuchungsobjekt auf. Zum Beispiel besteht die erste Stichprobe aus Personen vor der Behandlung mit einem bestimmten Medikament, und die zweite Stichprobe aus denselben Personen nach der Behandlung, d. h., die Elemente von zwei (oder mehr) Stichproben können einander jeweils paarweise zugeordnet werden.
Bei unabhängigen Stichproben besteht kein Zusammenhang zwischen den Elementen der Stichproben. Dies ist beispielsweise der Fall, wenn die Elemente der Stichproben jeweils aus unterschiedlicher Population kommen. Die erste Stichprobe besteht beispielsweise aus Frauen, und die zweite Stichprobe aus Männern, oder wenn Personen nach dem Zufallsprinzip in zwei oder mehrere Gruppen aufgeteilt werden.
Formal bedeutet dies für die Stichprobenvariablen (mit das te Untersuchungsobjekt und die te Messung):
- bei unabhängigen Stichproben: Alle Stichprobenvariablen sind unabhängig voneinander.
- bei abhängigen Stichproben: Die Stichprobenvariablen der ersten Stichprobe sind unabhängig voneinander, jedoch gibt es eine Abhängigkeit zwischen den Stichprobenvariablen , da sie am gleichen Untersuchungsobjekt erhoben werden.
Einstufige Zufallsstichproben
[Bearbeiten | Quelltext bearbeiten]Eine reine (auch: einfache) oder uneingeschränkte Zufallsstichprobe kann mittels eines Urnenmodells beschrieben werden. Dazu wird ein fiktives Gefäß mit Kugeln gefüllt, welche anschließend zufällig gezogen werden: Ziehen mit Zurücklegen ergibt eine einfache Zufallsstichprobe, Ziehen ohne Zurücklegen ergibt eine uneingeschränkte Zufallsstichprobe. Durch ein Urnenmodell lassen sich so verschiedene Zufallsexperimente, etwa eine Lottoziehung, simulieren.
Stichprobenumfang
[Bearbeiten | Quelltext bearbeiten]Der Stichprobenumfang (auch Stichprobenlänge[8] oder Stichprobengröße genannt) ist die Anzahl der Einheiten in einer Stichprobe. Der effektive Stichprobenumfang oder die effektive Stichprobenlänge[8] ist die Anzahl verschiedener Einheiten der Grundgesamtheiten in der Stichprobe. Im Falle einer einfachen Zufallsstichprobe ist es in der Regel so, dass die statistischen Kenngrößen umso besser werden, desto größer der Stichprobenumfang ist (siehe z. B. die Tabelle in diesem Abschnitt). Daher kann der Stichprobenumfang häufig so geplant werden, dass bestimmte Genauigkeitsanforderungen erfüllt sind.
Wenn die Ziehungen aus der Grundgesamtheit jedoch nicht unabhängig voneinander erfolgen können (z. B. bei Zeitreihen bzw. bei stochastischen Prozessen), kann es passieren, dass die Erhöhung des Stichprobenumfangs zur Verschlechterung der statistischen Kenngrößen (z. B. der Varianz) führt.
Der Stichprobenumfang wird häufig auch durch Normen bzw. Erfahrungswerte festgelegt. Durch eine geeignete Wahl des Stichprobenumfangs und die Anwendung von Methoden zur Verringerung systematischer Fehler können statistisch belastbare Ergebnisse erzielt werden.
Notwendiger Stichprobenumfang
[Bearbeiten | Quelltext bearbeiten]Der notwendige Stichprobenumfang ist die Anzahl der Stichprobenwerte, z. B. der für eine Prüfung benötigten Proben einer Grundgesamtheit, die notwendig ist, um statistische Kenngrößen mit einer vorgegebenen Genauigkeit mittels Schätzung zu ermitteln. Die notwendige Stichprobengröße ist für Methoden des Maschinellen Lernens durch die Stichprobenkomplexität gegeben.
Wenn der unbekannte Parameter in der Grundgesamtheit ist, dann wird eine Schätzfunktion in Abhängigkeit von den Stichprobenvariablen konstruiert. Der Erwartungswert der Zufallsvariablen ist meist . Es soll der Stichprobenumfang bestimmt werden, der notwendig ist, damit die Genauigkeitsanforderung
erfüllt ist. Dabei ist ein Punktschätzer (oder eine Punktschätzfunktion) des unbekannten Parameters , ist der vorgegebene tolerierte absolute Fehler und die vorgegebene Wahrscheinlichkeit dafür, dass die Schätzfunktion eine Realisierung im zentralen Schwankungsintervall annimmt, also gilt.
Der absolute Fehler ist häufig gleich , wobei ein Quantil der Wahrscheinlichkeitsverteilung von ist und die Standardabweichung der Schätzfunktion ist, die häufig proportional zu ist. Es ist also
- .
Die folgende Tabelle gibt für den unbekannten Mittelwert bzw. den unbekannten Anteilswert eine Abschätzung des notwendigen Stichprobenumfanges an. In allen Fällen ist die Schätzfunktion für .
| Unbekannter Parameter |
Bedingung | e | Abschätzung des notwendigen Stichprobenumfangs | |
|---|---|---|---|---|
| und bekannt | ||||
| und unbekannt | ||||
| und | ||||
| und | ||||
In der Tabelle bezeichnen eine Normalverteilung, eine Bernoulli-Verteilung, das p-Quantil einer Standardnormalverteilung und das p-Quantil einer t-Verteilung mit Freiheitsgraden. Die vorletzte Zeile beruht auf einer asymptotisch (für ) begründeten Approximation der Verteilung von durch eine Normalverteilung. Die letzte Zeile der Tabelle beruht auf einer asymptotisch begründeten Approximation der Binomialverteilung durch eine Normalverteilung und der Oberschranke für die Varianz . Zu beachten ist, dass in der zweiten und dritten Zeile vor der Stichprobenziehung die Größe unbekannt ist und z. B. aus einer Stichprobe vor eigentlichen Stichprobe, einer sogenannten Vorstichprobe, bestimmt werden muss.
Beispiel (Wahl)
[Bearbeiten | Quelltext bearbeiten]
Eine Partei hat in einer Umfrage kurz vor der Wahl 6 % erreicht. Welchen Umfang muss eine Wählerbefragung am Wahltag mit Sicherheit haben, damit der wahre Anteilswert mit einer Genauigkeit von ermittelt werden kann?
bzw. etwas genauer
- .
D. h., bei der etwas genaueren Abschätzung des Stichprobenumfanges für den Anteilswert ergibt sich, dass immer noch 2167 Wähler befragt werden müssen, um mit einer Genauigkeit von 1 % das Wahlergebnis zu erhalten. Die Grafik rechts zeigt, welche Stichprobenumfänge nötig sind für einen bestimmten geschätzten Anteilswert und eine gegebene Sicherheit.
Beispiel (Werkstoffprüfung)
[Bearbeiten | Quelltext bearbeiten]In der Werkstoffprüfung ist ein Stichprobenumfang von 10 pro 1000 produzierten Teilen durchaus üblich. Er ist u. a. von der Sicherheitsrelevanz des Bauteils oder des Werkstoffes abhängig. Bei den zerstörenden Prüfungen wie zum Beispiel beim Zugversuch wird versucht, den Prüfaufwand und damit die Stichprobe möglichst klein zu halten. Bei der zerstörungsfreien Prüfung – z. B. bei Bildverarbeitungssystemen für die Vollständigkeitsprüfung – wird häufig eine 100-%-Kontrolle durchgeführt, um Fehler in der Produktion möglichst schnell zu erkennen.
Mehrstufige Zufallsauswahl (auch komplexe Zufallsauswahl)
[Bearbeiten | Quelltext bearbeiten]Insbesondere sind folgende Auswahlverfahren von Bedeutung, wobei die letzten beiden als Zweistufige Auswahlverfahren bezeichnet werden:
- Geschichtete Zufallsstichprobe (stratified sample): Die Elemente werden nach einem bestimmten Merkmal in Gruppen (Untermengen) eingeordnet. Die Gruppeneinteilung hat zum Ziel möglichst homogene Gruppen zu bilden; in sich homogen bezogen auf das zu untersuchende Merkmal. Innerhalb jeder dieser Gruppen wird dann eine Zufallsstichprobe gezogen. Als Auswahlverfahren kommen sowohl die reine Zufallsstichprobe als auch ein gewichtetes Verfahren in Frage.
- Klumpenstichprobe (cluster sample): Im Gegensatz zu den Gruppen in der geschichteten Stichprobe werden hier Gruppen gebildet, die möglichst heterogen sind (wobei jedoch sich die Gruppen als ganzes alle möglichst ähneln sollten, z. B. Schulklassen einer Schule). Zuerst wird eine (relativ kleine) Zufallsstichprobe unter den Gruppen gezogen. Danach werden alle in den gezogenen Gruppen enthaltenen Elemente in die Stichprobe aufgenommen. Ein klassisches Beispiel ist die Befragung ganzer Häuserblocks oder von Schulklassen. Zuerst werden die zu befragenden Schulklassen per Zufallsauswahl bestimmt. Dann werden alle in den Schulklassen enthaltenen Schüler befragt. Bei der Klumpenstichprobe tritt der sogenannte Klumpeneffekt auf. Er ist umso größer, je homogener die Elemente innerhalb der Gruppen und heterogener die Gruppen untereinander sind.[9]
- Gestufte Zufallsstichprobe (staged sample): Sie wird häufig aus Gründen der Kostensenkung und Zeitersparnis der Schichtung vorgezogen. Ebenfalls empfiehlt sich die Stufung, wenn eine Auflistung aller Fälle (Untersuchungsgegenstände, Merkmale etc.) der Grundgesamtheit nicht existiert und sich deshalb eine einfache Zufallsstichprobe nicht durchführen lässt (z. B. eine Untersuchung anhand von Texten. Da noch nicht alle Texte elektronisch erfasst bzw. verfügbar sind, entstehen durch das Aufsuchen der jeweiligen Archive hohe Kosten. Durch eine Stufung kann dies vermieden werden). Im Wesentlichen orientiert sich das Vorgehen der Stufung an der Schichtung, indem man:
- Stufungskriterien (Merkmale) bestimmt,
- die Grundgesamtheit nach diesen Merkmalen in einander ausschließende Teilgesamtheiten (Primäreinheiten) aufteilt,
- nun eine zufällige Auswahl der Teilgesamtheiten trifft und sich auf eine bestimmte Anzahl von Primäreinheiten begrenzt, die man untersucht. Die restlichen Teilgesamtheiten werden ignoriert.
- Aus den zufällig ausgewählten Primäreinheiten ermittelt man nun die Zufallsstichprobe der Merkmalsträger (Objekte, Individuen, Fälle). Ein Institut will bspw. 500 Personen nach ihrem Konsumverhalten befragen. In Schritt 2 wurde die Grundgesamtheit, z. B. anhand geographischer Merkmale, in Ost-, Nord-, Süd- und Westdeutschland aufgeteilt. In Schritt 3 wurde festgelegt, dass das Konsumverhalten in ost- und süddeutschen Supermärkten (Sekundäreinheiten) im Mittelpunkt der Untersuchung steht, so dass in jeder der beiden Regionen 250 Leute (Tertiäreinheiten) befragt werden.
- Die Teilgesamtheiten (der beiden untersuchten Regionen) werden nun zu einer Gesamtstichprobe zusammengefügt.
- Random-Route-Verfahren
Anwendungsmodelle
- ADM-Design als Kombination von Schichtung und Stufung
Probleme der Zufallsziehung
[Bearbeiten | Quelltext bearbeiten]In der praktischen Forschung (v. a. im Bereich der Sozialwissenschaften) kann nur sehr selten eine „echte“ Zufallsstichprobe ausgewählt werden. Dies hat mehrere Gründe:
- Grundgesamtheiten werden statistisch als Menge im mathematischen Sinn aufgefasst. Dies bedeutet, dass eindeutig definiert ist, welche Merkmalsträger zur Grundgesamtheit gehören und welche nicht, was eine zeitliche, räumliche und auf das Merkmal bezogene eindeutige Abgrenzbarkeit verlangt. Dies gelingt oft nicht, da die Grundgesamtheit gar nicht bekannt ist (z. B. sind nicht alle Personen, die momentan eine Depression in Deutschland haben, bekannt) oder diese sich zeitlich ändert (z. B. durch Geburten und Todesfälle).
- Aufgrund ethisch und datenschutzrechtlicher Bedenken kann nicht auf eine Liste der gesamten Population (z. B. alle Personen in Deutschland oder einer bestimmten Stadt) zugegriffen und Personen daraus ausgewählt werden.
- Nicht alle aus einem Register gezogenen Personen sind bereit, an einer Untersuchung (z. B. Telefonbefragung) teilzunehmen. Zusätzlich ist davon auszugehen, dass teilnehmende Personen sich von nicht teilnehmenden Personen in bestimmten Merkmalen (sozialer Status, Bildungsniveau etc.) unterscheiden.
In der Praxis wird deshalb oft auf eine Ad-hoc-Stichprobe zurückgegriffen, d. h., es werden diejenigen Personen erhoben, die sich freiwillig bereit erklären, an einer Untersuchung teilzunehmen. Deshalb ist zu überprüfen, ob die Erhebungsgrundgesamtheit (frame population; Grundgesamtheit, die faktisch erhoben wird) der angestrebten Grundgesamtheit (target population, Grundgesamtheit, für welche die Aussagen der Untersuchung gelten sollen) entspricht.
Siehe auch
[Bearbeiten | Quelltext bearbeiten]Literatur
[Bearbeiten | Quelltext bearbeiten]- Joachim Behnke, Nina Baur, Nathalie Behnke: Empirische Methoden der Politikwissenschaft (= UTB 2695 Grundkurs Politikwissenschaft). Schöningh u. a., Paderborn u. a. 2006, ISBN 3-506-99002-0.
- Markus Pospeschill: Empirische Methoden in der Psychologie. Band 4010. UTB, München 2013, ISBN 978-3-8252-4010-3.
- Jürgen Bortz, Nicola Dörig: Forschungsmethoden und Evaluation für Human- und Sozialwissenschaftler. 4. Auflage. Springer, Heidelberg 2006, ISBN 3-540-33305-3.
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Literary Digest Desaster. Marktforschungs-Wiki, abgerufen am 12. Februar 2011.
- ↑ Diebstahl kostet Handel Milliarden. Der Tagesspiegel, 14. November 2007, abgerufen am 12. Februar 2011.
- ↑ a b c d e P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 3-05-500608-9, geordnete Stichprobe, S. 141.
- ↑ a b Guido Walz (Hrsg.): Lexikon der Mathematik. 2. Auflage. Band 2. Eig bis Inn. Springer Spektrum, Berlin 2017, ISBN 978-3-662-53503-5, geordnete Stichprobe, S. 277, doi:10.1007/978-3-662-53504-2.
- ↑ P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 3-05-500608-9, geordnete Stichprobe, S. 142.
- ↑ Bernd Rönz, Hans G. Strohe (Hrsg.): Lexikon Statistik. Gabler Wirtschaft, Wiesbaden 1994, ISBN 3-409-19952-7, S. 412.
- ↑ Jürgen Janssen, Wilfried Laatz: Statistische Datenanalyse mit SPSS für Windows. Eine anwendungsorientierte Einführung in das Basissystem und das Modul Exakte Tests. 6., neu bearbeitete und erweiterte Auflage. Springer, Berlin u. a. 2007, ISBN 978-3-540-72977-8, S. 353.
- ↑ a b Fritz Pokropp: Stichproben – Theorie und Verfahren. 2. Auflage. Oldenbourg, München 1996, ISBN 3-486-23856-6, S. 11.
- ↑ Vgl.: Hans-Friedrich Eckey, Reinhold Kosfeld, Matthias Türck: Wahrscheinlichkeitsrechnung und Induktive Statistik. Grundlagen – Methoden – Beispiele. Gabler, Wiesbaden 2005, ISBN 3-8349-0043-5, S. 185.







![{\displaystyle x_{[1]}\leq x_{[2]}\leq \dots \leq x_{[n]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ab74bad3a025bed50e4db863bfd0f0c2c178754)
![{\displaystyle (x_{[1]},\dots ,x_{[n]})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40e4e0248523a151930f3f409331aa07b6cf43bd)

![{\displaystyle (x_{[1]},\dots ,x_{[5]})=(1,2,2,3,4)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/517276d8fc0e23aa05ef0eaf9a03cee98df710c3)



![{\displaystyle (X_{[1]},\dots ,X_{[n]})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96a6a842055306ccb3e307c0b7ba4871e58ecdb4)











![{\displaystyle [\theta -e,\theta +e]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39a0ff50143297eb94d6eb3cb694d534a4f62f26)




































