Tensor
Ein Tensor ist eine multilineare Abbildung, die eine bestimmte Anzahl von Vektoren auf einen Vektor abbildet und eine universelle Eigenschaft erfüllt.[1] Er ist ein mathematisches Objekt aus der linearen Algebra, das in vielen Bereichen, so auch in der Differentialgeometrie, Anwendung findet und den Begriff der linearen Abbildung erweitert. Der Begriff wurde ursprünglich in der Quantenphysik eingeführt und erst später mathematisch präzisiert.
In der Differentialgeometrie und den physikalischen Disziplinen werden meist keine Tensoren im Sinn der linearen Algebra betrachtet, sondern es werden Tensorfelder behandelt, die oft vereinfachend ebenfalls als Tensoren bezeichnet werden. Ein Tensorfeld ist eine Abbildung, die jedem Punkt des Raums einen Tensor zuordnet. Viele physikalische Feldtheorien handeln von Tensorfeldern. Das prominenteste Beispiel ist die allgemeine Relativitätstheorie. Das mathematische Teilgebiet, das sich mit der Untersuchung von Tensorfeldern befasst, heißt Tensoranalysis und ist ein wichtiges Werkzeug in den physikalischen und ingenieurwissenschaftlichen Disziplinen.
Begriffsgeschichte
[Bearbeiten | Quelltext bearbeiten]

Das Wort Tensor (abgeleitet vom Partizip Perfekt von lateinisch tendere ‚spannen‘) wurde in den 1840er Jahren von William Rowan Hamilton in die Mathematik eingeführt; er bezeichnete damit den Absolutbetrag seiner Quaternionen, also keinen Tensor im modernen Sinn. James Clerk Maxwell scheint den Spannungstensor, den er aus der Elastizitätstheorie in die Elektrodynamik übertrug, selbst noch nicht so genannt zu haben.
In seiner modernen Bedeutung, als Verallgemeinerung von Skalar, Vektor, Matrix, wird das Wort Tensor erstmals von Woldemar Voigt in seinem Buch Die fundamentalen physikalischen Eigenschaften der Krystalle in elementarer Darstellung (Leipzig, 1898) eingeführt.[2]
Unter dem Titel absolute Differentialgeometrie entwickelten Gregorio Ricci-Curbastro und dessen Schüler Tullio Levi-Civita um 1890 die Tensorrechnung auf riemannschen Mannigfaltigkeiten.[3] Einem größeren Fachpublikum machten sie ihre Ergebnisse 1900 mit dem Buch Calcolo differenziale assoluto zugänglich, aus dem sich Albert Einstein die mathematischen Grundlagen aneignete, die er zur Formulierung der allgemeinen Relativitätstheorie benötigte. Einstein selbst prägte 1916 den Begriff Tensoranalysis und trug mit seiner Theorie maßgeblich dazu bei, den Tensorkalkül bekannt zu machen; er führte überdies die einsteinsche Summenkonvention ein, nach der über doppelt auftretende Indizes unter Weglassung der Summenzeichen summiert wird.
Arten von Tensoren
[Bearbeiten | Quelltext bearbeiten]
Ausgehend von einem endlichdimensionalen Vektorraum bezeichnet man Skalare als Tensoren vom Typ , Spaltenvektoren als Tensoren vom Typ und Kovektoren (bzw. Zeilenvektoren) als Tensoren vom Typ . Tensoren höherer Stufe definiert man als multilineare Abbildungen mit Tensoren geringerer Stufe als Argumenten und Abbildungswerten. So kann etwa ein Tensor vom Typ als lineare Abbildung zwischen Vektorräumen oder als bilineare Abbildung mit einem Vektor und einem Kovektor als Argumente aufgefasst werden.
Beispielsweise ist der mechanische Spannungstensor in der Physik ein Tensor zweiter Stufe – eine Zahl (Stärke der Spannung) oder ein Vektor (eine Hauptspannungsrichtung) reichen nicht immer zur Beschreibung des Spannungszustandes eines Körpers aus. Als Tensor vom Typ aufgefasst ist er eine lineare Abbildung, die einem Flächenelement (als Vektor) die darauf wirkende Kraft (als Kovektor) zuordnet, oder eine bilineare Abbildung, die einem Flächenelement und einem Verschiebungsvektor die Arbeit zuordnet, die bei der Verschiebung des Flächenstücks unter dem Einfluss der wirkenden Spannung verrichtet wird.
Bezüglich einer fest gewählten Vektorraumbasis erhält man die folgenden Darstellungen der verschiedenen Typen von Tensoren:
- Ein Skalar durch eine einzelne Zahl
- Ein Vektor durch einen Spaltenvektor
- Ein Kovektor durch einen Zeilenvektor
- Ein Tensor zweiter Stufe durch eine Matrix
Die Anwendung des Spannungstensors auf ein Flächenelement ist dann z. B. durch das Produkt einer Matrix mit einem Spaltenvektor gegeben. Die Koordinaten von Tensoren höherer Stufe können entsprechend in ein höherdimensionales Schema angeordnet werden. So können diese Komponenten eines Tensors anders als die eines Spaltenvektors oder einer Matrix mehr als ein oder zwei Indizes haben. Ein Beispiel für einen Tensor dritter Stufe, der drei Vektoren des als Argumente hat, ist die Determinante einer 3×3-Matrix als Funktion der Spalten dieser Matrix. Bezüglich einer Orthonormalbasis wird er durch das Levi-Civita-Symbol repräsentiert.
Ko- und Kontravarianz von Vektoren
[Bearbeiten | Quelltext bearbeiten]Die Begriffe ko- und kontravariant beziehen sich auf die Koordinatendarstellungen von Vektoren, Linearformen und werden auch, wie später im Artikel beschrieben, auf Tensoren angewandt. Sie beschreiben, wie sich solche Koordinatendarstellungen bezüglich eines Basiswechsels im zugrundeliegenden Vektorraum verhalten.
Legt man in einem -dimensionalen Vektorraum eine Basis fest, so kann jeder Vektor dieses Raumes durch ein Zahlentupel – seine Koordinaten – mittels dargestellt werden. Legt man der Koordinatendarstellung eine andere Basis von zugrunde, so werden sich die Koordinaten (ein und desselben Vektors) bezüglich dieser neuen Basis ändern. Der Übergang zu einer anderen Basis bedingt also eine Transformation der Koordinatendarstellung. Dabei gilt: Ist die neue Basis durch in der alten Basis bestimmt, so ergeben sich die neuen Koordinaten durch Vergleich in
also:
Dreht man zum Beispiel eine orthogonale Basis in einem dreidimensionalen euklidischen Raum um um die -Achse, so drehen sich die Koordinatenvektoren im Koordinatenraum ebenfalls um die -Achse, aber in der entgegengesetzten Richtung, also um . Dieses der Basistransformation entgegengesetzte Transformationsverhalten nennt man kontravariant. Oft werden Vektoren zur Abkürzung der Notation mit ihren Koordinatenvektoren identifiziert, sodass Vektoren allgemein als kontravariant bezeichnet werden.
Eine Linearform oder ein Kovektor ist dagegen eine skalarwertige lineare Abbildung auf dem Vektorraum. Man kann ihr als Koordinaten ihre Werte auf den Basisvektoren, , zuordnen. Die Koordinatenvektoren einer Linearform transformieren sich wie das Basistupel als
weshalb man dieses Transformationsverhalten kovariant nennt. Identifiziert man wieder Linearformen mit ihren Koordinatenvektoren, so bezeichnet man auch allgemein Linearformen als kovariant. Hierbei geht, wie bei Vektoren, die zugrundeliegende Basis aus dem Kontext hervor. Man spricht in diesem Kontext auch von Dualvektoren.
Diese Bezeichnungen werden auf Tensoren übertragen. Dies wird im nächsten Abschnitt zur Definition der -Tensoren erklärt.
Definition
[Bearbeiten | Quelltext bearbeiten](r,s)-Tensorraum
[Bearbeiten | Quelltext bearbeiten]Im Folgenden sind alle Vektorräume endlichdimensional über dem Körper . Mit bezeichne man die Menge aller Linearformen aus dem -Vektorraum in den Körper und – allgemeiner – mit die Menge aller -linearen Abbildungen eines -Vektorraums in einen -Vektorraum . Sind Vektorräume über , so werde der Vektorraum der Multilinearformen mit bezeichnet. Entsprechend bezeichne die Menge aller -multilinearen Abbildungen , hier speziell der -fach -linearen Abbildungen. Im Falle von und handelt es sich um Bilinearformen.
Ist ein -Vektorraum, so wird mit sein Dualraum bezeichnet. Dann existieren (gemäß der universellen Eigenschaft) kanonische Isomorphismen
und allgemeiner
Der kanonischen Isomorphie eines Vektorraums mit seinem Bidualraum wegen folgt (durch Ersetzen von durch und mithin von durch ), dass zum Tensorprodukt isomorph ist. (Zur Realisierung des Tensorproduktraums als Raum von Multilinearformen sowie zur kanonischen Identifizierung , die in diesem Abschnitt noch häufiger genutzt wird, siehe die Abschnitte über die universelle Eigenschaft und über Tensorprodukte und Multilinearformen.)
Es gibt natürliche Isomorphismen der folgenden Art:
Diesen natürlichen Isomorphismen liegen die Zurückführung -fach-linearer Abbildungen auf -fach-lineare Abbildungen (vgl. Currying oder Schönfinkeln) einerseits und die universelle Eigenschaft des Tensorprodukts andererseits – mehrfach angewandt – zugrunde:
Speziell für besteht also der oben behauptete natürliche Isomorphismus und für die Linearform die Identifikation vorgenommen wird. Es genügt hierbei, die Abbildungen auf den elementaren Tensoren (siehe auch Abschnitt Tensor als Element des Tensorproduktes) als einem Erzeugendensystem über dem Grundkörper festzulegen. Zu ergänzen ist noch, dass in den Fällen und das leere Tensorprodukt entsteht, das mit dem Grundkörper zu identifizieren ist. Insbesondere besteht also für -Vektorräume und die Identifikation
- .
Definition: Für einen fixierten Vektorraum über einem Körper mit Dualraum sei definiert durch
mit Einträgen von und Einträgen von . Elemente dieser Menge heißen Tensoren, kontravariant der Stufe und kovariant der Stufe . Kurz spricht man von Tensoren vom Typ . Die Summe heißt Stufe oder Rang des Tensors.[4][5]
Mit den obigen Überlegungen (bei und sowie für bzw. für ) ergibt sich insgesamt
Also realisiert der Vektorraum der Tensoren vom Typ das Tensorprodukt , nämlich durch die obige kanonische Identifikation
- .
Diese natürlichen Isomorphismen bedeuten, dass man Tensoren der Stufe auch induktiv als multilineare Abbildungen zwischen Tensorräumen geringerer Stufe definieren kann. Dabei hat man für einen Tensor eines bestimmten Typs mehrere äquivalente Möglichkeiten.
In der Physik sind die Vektorräume in der Regel nicht identisch, z. B. kann man einen Geschwindigkeitsvektor und einen Kraftvektor nicht addieren. Man kann jedoch die Richtungen miteinander vergleichen, d. h., die Vektorräume bis auf einen skalaren Faktor miteinander identifizieren. Daher kann die Definition von Tensoren des Typs entsprechend angewendet werden. Es sei außerdem erwähnt, dass (dimensionsbehaftete) Skalare in der Physik Elemente aus eindimensionalen Vektorräumen sind und dass Vektorräume mit Skalarprodukt mit ihrem Dualraum identifiziert werden können. Man arbeitet z. B. mit Kraftvektoren, obwohl Kräfte ohne die Verwendung des Skalarprodukts als Kovektoren anzusehen sind.
Äußeres Tensorprodukt
[Bearbeiten | Quelltext bearbeiten]Als (äußeres) Tensorprodukt oder Tensormultiplikation bezeichnet man eine Verknüpfung zwischen zwei Tensoren. Sei ein Vektorraum und seien und Tensoren. Das (äußere) Tensorprodukt von und ist der Tensor , der durch
definiert ist. Hierbei sind die und die .
Beispiele von (r,s)-Tensoren
[Bearbeiten | Quelltext bearbeiten]Im Folgenden seien und endlichdimensionale Vektorräume.
- Die Menge der (0,0)-Tensoren ist isomorph mit dem zugrunde liegenden Körper . Sie ordnen keiner Linearform und keinem Vektor ein Körperelement zu. Deshalb die Bezeichnung als (0,0)-Tensoren.
- (0,1)-Tensoren ordnen keiner Linearform und einem Vektor eine Zahl zu, entsprechen somit den Linearformen auf .
- (1,0)-Tensoren ordnen einer Linearform und keinem Vektor eine Zahl zu. Sie sind somit Elemente des bidualen Vektorraums . Sie entsprechen bei endlichdimensionalen Vektorräumen den Ausgangsvektorräumen , da hier gilt (siehe Isomorphismus).
- Eine lineare Abbildung zwischen endlichdimensionalen Vektorräumen kann als Element von aufgefasst werden und ist dann ein (1,1)-Tensor.
- Eine Bilinearform lässt sich als ein Element von auffassen, also als ein (0,2)-Tensor. Insbesondere lassen sich also Skalarprodukte als (0,2)-Tensoren auffassen.
- Das Kronecker-Delta ist wieder ein (0,2)-Tensor. Es ist ein Element von und somit eine multilineare Abbildung . Multilineare Abbildungen sind durch die Wirkung auf die Basisvektoren eindeutig bestimmt. So ist das Kronecker-Delta eindeutig durch
- bestimmt.
- Die Determinante von -Matrizen, aufgefasst als alternierende Multilinearform der Spalten, ist ein (0,n)-Tensor. Bezüglich einer Orthonormalbasis wird er durch das Levi-Civita-Symbol (den „Epsilontensor“) dargestellt. Speziell in drei reellen Dimensionen ist die Determinante ein Tensor dritter Stufe und es gilt für die Elemente einer Orthonormalbasis. Sowohl das Kronecker-Delta als auch das Levi-Civita-Symbol werden häufig verwendet, um Symmetrieeigenschaften von Tensoren zu untersuchen. Das Kronecker-Delta ist symmetrisch bei Vertauschungen der Indizes, das Levi-Civita-Symbol antisymmetrisch, sodass man mit ihrer Hilfe Tensoren in symmetrische und antisymmetrische Anteile zerlegen kann.
- Ein weiteres Beispiel für einen kovarianten Tensor 2. Stufe ist der Trägheitstensor.
- In der Elastizitätstheorie verallgemeinert man die hookesche Gleichung über den Zusammenhang zwischen Kräften und zugehörigen Dehnungen und Verzerrungen in einem elastischen Medium ebenfalls mit Hilfe der Tensorrechnung durch Einführung des Verzerrungstensors, der Verzerrungen, Deformationen beschreibt, und des Spannungstensors, der die die Deformationen verursachenden Kräfte beschreibt. Siehe dazu auch unter Kontinuumsmechanik nach.
- Sei ein Vektorraum mit Skalarprodukt . Wie oben bereits erwähnt, ist das Skalarprodukt linear in beiden Argumenten, also ein (0,2)-Tensor bzw. ein zweifach kovarianter Tensor. Man spricht auch von einem metrischen Tensor oder kurz von einer „Metrik“. Dabei ist zu beachten, dass selbst keine Metrik im Sinne eines metrischen Raums ist, aber eine solche erzeugt. Mit werden die Koordinaten der Metrik bezüglich einer Basis des Vektorraums bezeichnet; und seien die Koordinaten der Vektoren und bezüglich derselben Basis. Für die Abbildung zweier Vektoren und unter der Metrik gilt deshalb
- Der Übergang zwischen ko- und kontravarianten Tensoren lässt sich mittels der Metrik durch
- bewerkstelligen.
- In der Differentialgeometrie auf riemannschen Mannigfaltigkeiten ist diese Metrik zusätzlich eine Funktion des Ortes. Eine tensorwertige Funktion des Ortes wird Tensorfeld genannt, im Fall des metrischen Tensors speziell riemannsche Metrik.
- In der Theorie der pseudo-riemannschen Mannigfaltigkeiten wird der Begriff des metrischen Tensors dahingehend verallgemeinert, dass auf die Definitheit des Skalarprodukts verzichtet wird. Wichtigste Anwendung ist die Relativitätstheorie. In der speziellen Relativitätstheorie verwendet man statt der euklidischen Metrik die uneigentliche Metrik des Minkowskiraumes. In der allgemeinen Relativitätstheorie wird ein Tensorfeld mit derselben Signatur wie die Minkowski-Metrik verwendet.
Basis
[Bearbeiten | Quelltext bearbeiten]Basis und Dimension
[Bearbeiten | Quelltext bearbeiten]Sei wie oben ein Vektorraum, dann sind die Räume ebenfalls Vektorräume. Weiterhin sei nun endlichdimensional mit der Basis . Die duale Basis wird mit bezeichnet. Der Raum der Tensoren ist dann ebenfalls endlichdimensional und
ist eine Basis dieses Raumes. Das heißt, jedes Element kann durch
dargestellt werden. Die Dimension dieses Vektorraums ist . Wie in jedem endlichdimensionalen Vektorraum reicht es auch im Raum der Tensoren zu sagen, wie eine Funktion auf der Basis operiert.
Da die obige Summendarstellung sehr viel Schreibarbeit mit sich bringt, wird oft die einsteinsche Summenkonvention verwendet. In diesem Fall schreibt man also
Die Koeffizienten werden Komponenten des Tensors bezüglich der Basis genannt. Oft identifiziert man die Komponenten des Tensors mit dem Tensor an sich. Siehe dafür unter Tensordarstellungen der Physik nach.
Basiswechsel und Koordinatentransformation
[Bearbeiten | Quelltext bearbeiten]Seien und paarweise verschiedene Basen der Vektorräume . Jeder Vektor, also auch jeder Basisvektor kann als Linearkombination der Basisvektoren dargestellt werden. Der Basisvektor werde dargestellt durch
Die Größen bestimmen also die Basistransformation zwischen den Basen und . Das gilt für alle . Dieses Verfahren wird Basiswechsel genannt.
Ferner seien die Komponenten des Tensors bezüglich der Basis . Dann ergibt sich für das Transformationsverhalten der Tensorkomponenten die Gleichung
Es wird in der Regel zwischen der Koordinatendarstellung des Tensors und der Transformationsmatrix unterschieden. Die Transformationsmatrix ist zwar eine indizierte Größe, aber kein Tensor. Im euklidischen Raum sind das Drehmatrizen und in der speziellen Relativitätstheorie z. B. Lorentz-Transformationen, die sich auch als „Drehungen“ in einem vierdimensionalen Minkowskiraum auffassen lassen. Man spricht in diesem Fall auch von Vierertensoren und Vierervektoren.
Beispiel
[Bearbeiten | Quelltext bearbeiten]Mit Hilfe der Komponenten kann ein Tensor bezüglich einer Basis dargestellt werden. Beispielsweise kann ein Tensor mit Rang 2 in einem gegebenen Basissystem wie folgt als Matrix dargestellt werden:
Dadurch lässt sich der Wert im Rahmen des entsprechenden Basissystems mit Hilfe der Matrixmultiplikation berechnen:
Betrachtet man nun konkret den Trägheitstensor , so kann mit ihm bezüglich eines gewählten Koordinatensystems die Rotationsenergie eines starren Körpers mit der Winkelgeschwindigkeit wie folgt berechnet werden:
Operationen auf Tensoren
[Bearbeiten | Quelltext bearbeiten]Neben dem Tensorprodukt gibt es für (r,s)-Tensoren weitere wichtige Operationen.
Inneres Produkt
[Bearbeiten | Quelltext bearbeiten]Das innere Produkt eines Vektors (bzw. eines (Ko-)Vektors ) mit einem Tensor ist der (bzw. )-Tensor, der durch
bzw. durch
definiert ist. Dies bedeutet, dass der -Tensor an einem festen Vektor bzw. festen Kovektor ausgewertet wird.
Tensorverjüngung
[Bearbeiten | Quelltext bearbeiten]Gegeben sei ein (r,s)-Tensor sowie und . Die Tensorverjüngung bildet den Tensor
auf den Tensor
ab. Dieser Vorgang heißt Tensorverjüngung oder Spurbildung. Im Fall von (1,1)-Tensoren entspricht die Tensorverjüngung
unter der Identifizierung der Spur eines Endomorphismus.
Mit Hilfe der einsteinschen Summenkonvention kann man die Tensorverjüngung sehr kurz darstellen. Seien beispielsweise die Koeffizienten (bzw. Koordinaten) des zweistufigen Tensors bezüglich einer gewählten Basis. Will man diesen (1,1)-Tensor verjüngen, so schreibt man oft anstatt nur die Koeffizienten . Die einsteinsche Summenkonvention besagt nun, dass über alle gleichen Indizes summiert wird und somit ein Skalar ist, der mit der Spur des Endomorphismus übereinstimmt. Der Ausdruck ist hingegen nicht definiert, weil über gleiche Indizes nur dann summiert wird, wenn einer oben und einer unten steht. Hingegen ist also ein Tensor erster Stufe.
Pull-Back (Rücktransport)
[Bearbeiten | Quelltext bearbeiten]Sei eine lineare Abbildung zwischen Vektorräumen, die kein Isomorphismus zu sein braucht. Der Rücktransport von sei eine Abbildung , die durch
definiert ist. Dabei ist und .
Push-Forward
[Bearbeiten | Quelltext bearbeiten]Sei ein Vektorraumisomorphismus. Definiere den Push-Forward von durch mit
Dabei ist , und . Mit wird der Rücktransport der Linearform notiert. Konkret heißt dies Analog zum Rücktransport kann man beim Push-Forward auf die Isomorphie von verzichten und diese Operation nur für -Tensoren definieren.
Tensoralgebra
[Bearbeiten | Quelltext bearbeiten]Sei ein Vektorraum über einem Körper . Dann ist durch
die sogenannte Tensoralgebra definiert. Mit der Multiplikation, die auf den homogenen Bestandteilen durch das Tensorprodukt gegeben ist, wird zu einer unitären assoziativen Algebra.
Tensorproduktraum
[Bearbeiten | Quelltext bearbeiten]In diesem Abschnitt werden Tensorprodukträume definiert, sie werden typischerweise in der Algebra betrachtet. Diese Definition ist allgemeiner als die der (r,s)-Tensoren, da hier die Tensorräume aus unterschiedlichen Vektorräumen konstruiert werden können.
Die universelle Eigenschaft für das Tensorprodukt zweier Faktoren
[Bearbeiten | Quelltext bearbeiten]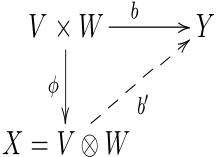
Es seien und Vektorräume über dem Körper . Sind weitere -Vektorräume, eine beliebige bilineare Abbildung und eine lineare Abbildung, dann ist auch die Verknüpfung eine bilineare Abbildung. Ist also eine bilineare Abbildung gegeben, so kann man daraus auch beliebig viele weitere bilineare Abbildungen konstruieren. Es stellt sich die Frage, ob es eine bilineare Abbildung gibt, aus der auf diese Art, durch Verknüpfung mit linearen Abbildungen, alle bilinearen Abbildungen auf (auf eindeutige Weise) konstruiert werden können. Ein solches universelles Objekt, d. h. die bilineare Abbildung samt ihrem Bildraum, wird als Tensorprodukt von und bezeichnet.
Definition: Als Tensorprodukt der Vektorräume und wird jeder -Vektorraum bezeichnet, zu dem es eine bilineare Abbildung gibt, die die folgende universelle Eigenschaft erfüllt:
- Zu jeder bilinearen Abbildung von in einen Vektorraum existiert genau eine lineare Abbildung , sodass für alle gilt:
Gibt es einen solchen Vektorraum , so ist er bis auf Isomorphie eindeutig bestimmt. Ist nämlich bereits mit der Bilinearform (als seinem Tensorprodukt ) ein zweiter derartigen Vektorraum , so gibt es neben der eindeutig bestimmten linearen Abbildung mit der Eigenschaft auch eine eindeutig bestimmte lineare Abbildung mit der Eigenschaft , da ja auch die universelle Eigenschaft hat. Also sind beide, und , Isomorphismen. Man schreibt und . Die universelle Eigenschaft kann also als geschrieben werden. Zur Konstruktion solcher Produkträume sei auf den Artikel Tensorprodukt verwiesen.
Die universelle Eigenschaft des Tensorproduktes gibt also auf die obige Fragestellung eine bejahende Antwort und lässt sich so formulieren: Die Abbildung
ist surjektiv (Existenzaussage) und injektiv (Eindeutigkeitsaussage), mithin bijektiv und somit ein Isomorphismus von Vektorräumen. Für den Fall ergibt sich eine Deutung des Dualraumes des Tensorproduktraumes als Raum der Bilinearformen. Zusammen mit den bereits erwähnten Identifikationen ergibt sich:
Tensor als Element des Tensorproduktes
[Bearbeiten | Quelltext bearbeiten]In der Mathematik sind Tensoren Elemente von Tensorprodukten.
Es sei ein Körper und es seien Vektorräume über dem Körper .
Das Tensorprodukt von ist ein -Vektorraum, dessen Elemente Summen von Symbolen der Form
sind. Dabei gelten für diese Symbole die folgenden Rechenregeln:
Die Tensoren der Form heißen elementar. Jeder Tensor lässt sich als Summe von elementaren Tensoren schreiben, aber diese Darstellung ist außer in trivialen Fällen nicht eindeutig, wie man an der ersten der beiden Rechenregeln sieht.
Ist eine Basis von (für ; ), so ist
eine Basis von Die Dimension von ist also das Produkt der Dimensionen der einzelnen Vektorräume
Erweiterung auf mehrere Faktoren: Universelle Eigenschaft für mehrfache Tensorprodukte und Multilinearformen
[Bearbeiten | Quelltext bearbeiten]Die bisherigen Betrachtungen zur universellen Eigenschaft lassen sich wie folgt auf mehrere Faktoren ausweiten.
Der Dualraum von kann (gemäß der universellen Eigenschaft) mit dem Raum der -Multilinearformen identifiziert werden:
- Ist eine Linearform auf so ist durch eine -Multilinearform gegeben. Es stellt sich die Frage, ob jede -Multilinearform auf diese Weise konstruiert werden kann. Die bejahende Antwort gibt die universelle Eigenschaft des Tensorproduktes:
- Ist nämlich umgekehrt eine -Multilinearform, so ist die mit ihr – gemäß der universellen Eigenschaft – korrespondierende Linearform festgelegt, indem sie für die elementaren Tensoren (im Einklang mit der universellen Eigenschaft) definiert und dann linear auf den ganzen Vektorraum fortgesetzt wird. Für die elementaren Tensoren gilt gemäß der universellen Eigenschaft:
Wie oben (im Abschnitt zur universellen Eigenschaft) für den Fall zweier Vektorräume formuliert, gilt nämlich auch für mehrere Faktoren (bis auf Isomorphie) die universelle Eigenschaft. Und diese lässt sich in folgender Weise formulieren und umfasst zugleich die Aussage der beiden obigen Spiegelpunkte:
- Definition: Es seien sowie und Vektorräume über dem Körper . Dann heißt die multilineare Abbildung das Tensorprodukt der Vektorräume über , wenn sie folgende Eigenschaft hat: Zu jeder multilinearen Abbildung gibt es eine eindeutig bestimmte lineare Abbildung mit der Eigenschaft für alle Tupel Man schreibt dann:
- Wenn es einen solchen Vektorraum mit einer solchen multilinearen Abbildung gibt, dann ist der Vektorraum aufgrund eben dieser universellen Eigenschaft bis auf Isomorphie eindeutig bestimmt. Daher wird häufig nur von dem Vektorraum gesprochen, obwohl genau genommen auch die zugehörige multilineare Abbildung Bestandteil des Tensorproduktes ist.
Tatsächlich lässt sich für die Kategorie der Vektorräume (genauer: in der Kategorie der multilinearen Abbildungen auf vorgegebenen Vektorräumen in einen beliebigen Vektorraum) ein solches Tensorprodukt konstruieren. Es ist durch die universelle Eigenschaft eindeutig bis auf Isomorphie gekennzeichnet.
Wenn also das (bis auf Isomorphie eindeutig bestimmte) Tensorprodukt der Vektorräume bezeichnet, so etabliert die universelle Eigenschaft einen Isomorphismus von Vektorräumen (Beachte: Der Raum der linearen Abbildungen und der Raum der multilinearen Abbildungen sind in natürlicher Weise Vektorräume): Die Surjektivität dieser Abbildung nämlich ist gleichbedeutend mit der Existenzaussage („zu jeder multilinearen Abbildung gibt es“, vgl. zweiten Spiegelpunkt), die Injektivität hingegen mit der Eindeutigkeitsaussage („eine eindeutig bestimmte“). Da die angegebene Abbildung eine lineare Abbildung ist (Homomorphismus von Vektorräumen), ist sie ein Isomorphismus von Vektorräumen.
Sind alle betrachteten Vektorräume endlichdimensional, so kann man demnach für den Fall die beiden Vektorräume
in natürlicher Weise miteinander identifizieren, d. h., Elemente von entsprechen -Multilinearformen auf
Invarianten von Tensoren 1. und 2. Stufe
[Bearbeiten | Quelltext bearbeiten]Als Invarianten eines ein- oder zweistufigen Tensors bezeichnet man Skalare, die sich unter orthogonalen Koordinatentransformationen des Tensors nicht ändern. Für Tensoren erster Stufe führt die Bildung der vom Skalarprodukt induzierten Norm zu einer Invarianten
- ,
wobei hier und im Folgenden wieder die einsteinsche Summenkonvention verwendet wird. Für Tensoren zweiter Stufe im dreidimensionalen euklidischen Raum lassen sich im Allgemeinen sechs irreduzible Invarianten (das heißt Invarianten, die nicht durch andere Invarianten ausgedrückt werden können) finden:
Im Falle von symmetrischen Tensoren 2. Stufe (z. B. dem Verzerrungstensor) fallen die Invarianten und zusammen. Außerdem lässt sich über die anderen 3 Invarianten darstellen (ist also nicht mehr irreduzibel). Die Determinante ist auch eine Invariante, sie lässt sich beispielsweise für -Matrizen über die irreduziblen Invarianten , und darstellen als[6]
Für antisymmetrische Tensoren gilt , , und lässt sich wieder auf zurückführen.[7] Somit haben im dreidimensionalen euklidischen Raum symmetrische Tensoren 2. Stufe drei irreduzible Invarianten und antisymmetrische Tensoren 2. Stufe eine irreduzible Invariante.
Tensorprodukte eines Vektorraums und Symmetrie
[Bearbeiten | Quelltext bearbeiten]Man kann das Tensorprodukt eines Vektorraumes mit sich selbst bilden. Ohne weiteres Wissen über den Vektorraum kann ein Automorphismus des Tensorprodukts definiert werden, der darin besteht, in den reinen Produkten die Faktoren zu vertauschen:
Da das Quadrat dieser Abbildung die Identität ist, folgt, dass für die Eigenwerte nur die Werte in Frage kommen.
- Ein , das erfüllt, heißt symmetrisch. Beispiele sind die Elemente
- .
- Die Menge aller symmetrischen Tensoren der Stufe 2 wird mit bezeichnet.
- Ein , das erfüllt, heißt antisymmetrisch oder alternierend. Beispiele sind die Elemente
- .
- Die Menge aller antisymmetrischen Tensoren der Stufe 2 wird mit bezeichnet.
Mittels können Tensorpotenzen von beliebiger Stufe gebildet werden. Entsprechend können weitere paarweise Vertauschungen definiert werden. Nur sind diese nicht mehr voneinander unabhängig. So lässt sich jede Vertauschung der Stellen und auf Vertauschungen mit der ersten Stelle zurückführen:
Injektives und projektives Tensorprodukt
[Bearbeiten | Quelltext bearbeiten]Falls die Vektorräume, die man miteinander tensorieren will, eine Topologie besitzen, so ist es wünschenswert, dass ihr Tensorprodukt ebenfalls eine Topologie besitzt. Es gibt natürlich viele Möglichkeiten, eine solche Topologie zu definieren. Das injektive beziehungsweise das projektive Tensorprodukt sind dafür jedoch eine natürliche Wahl.
Tensoranalysis
[Bearbeiten | Quelltext bearbeiten]Ursprünglich wurde der Tensorkalkül nicht in dem modernen hier vorgestellten algebraischen Konzept untersucht, sondern entstand aus Überlegungen zur Differentialgeometrie. Insbesondere Gregorio Ricci-Curbastro und sein Schüler Tullio Levi-Civita haben ihn entwickelt. Man nennt den Tensorkalkül daher auch Ricci-Kalkül. Albert Einstein griff den Kalkül in seiner Relativitätstheorie auf, was diesem große Bekanntheit in der Fachwelt einbrachte. Die damaligen Tensoren werden heute als Tensorfelder bezeichnet und spielen in der Differentialgeometrie auch heute noch eine wichtige Rolle. Im Gegensatz zu Tensoren sind Tensorfelder differenzierbare Abbildungen, die jedem Punkt des zugrundeliegenden (oft gekrümmten) Raums einen Tensor zuordnen.
Siehe auch
[Bearbeiten | Quelltext bearbeiten]Literatur
[Bearbeiten | Quelltext bearbeiten]- Adalbert Duschek, August Hochrainer: Grundzüge der Tensorrechnung in analytischer Darstellung: I. Teil: Tensoralgebra. Vierte ergänzte Auflage. Springer-Verlag, Wien 1960 (V, 171 S., Erstausgabe: 1946).
- Adalbert Duschek, August Hochrainer: Grundzüge der Tensorrechnung in analytischer Darstellung: II. Teil: Tensoranalysis. Zweite ergänzte Auflage. Springer-Verlag, Wien 1961 (VI, 334 S., Erstausgabe: 1950).
- Adalbert Duschek, August Hochrainer: Grundzüge der Tensorrechnung in analytischer Darstellung: III. Teil: Anwendungen in Physik und Technik. Erste Auflage. Springer-Verlag, Wien 1955 (VI, 250 S.).
- Adalbert Duschek: Der Tensorbegriff und seine Bedeutung für die Physik. Teil 1, 2, 3, Physikalische Blätter 1954, 1955:
- André Lichnerowicz: Einführung in die Tensoranalysis (= BI Hochschultaschenbuch. 77). Bibliographisches Institut, Mannheim u. a. 1966.
- Horst Teichmann: Physikalische Anwendungen der Vektor- und Tensorrechnung (= BI-Hochschultaschenbücher. 39). 3. Auflage. Bibliographisches Institut, Mannheim u. a. 1973, ISBN 3-411-00039-2.
- Horst Lippmann: Angewandte Tensorrechnung. Springer 1993.
- Karin Reich: Die Entwicklung des Tensorkalküls. Vom absoluten Differentialkalkül zur Relativitätstheorie. Birkhäuser 1994 (zur Geschichte).
- Theodore Frankel: The Geometry of Physics. An Introduction. Cambridge University Press, Cambridge u. a. 1997, ISBN 0-521-38334-X.
- Ralph Abraham, Jerrold E. Marsden, T. Ratiu: Manifolds, tensor analysis, and applications (= Applied mathematical sciences. 75). 2. Auflage. Springer, New York NY u. a. 1998, ISBN 0-387-96790-7.
- Theodor Bröcker: Lineare Algebra und Analytische Geometrie. Birkhäuser, Basel 2004, ISBN 3-7643-2178-4, Kap. VII: Tensorrechnung.
- Mikhail Itskov: Tensor algebra and tensor analysis for engineers. 3. Auflage. Springer, Heidelberg u. a. 2013, ISBN 978-3-642-30878-9.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Georg Bernhardt: Über Tensoren, Matrizen und Pseudovektoren. PDF, deutsch, 340 kB.
- Joseph C. Kolecki: An Introduction to Tensors for Students of Physics and Engineering. Einführung in die Tensorrechnung für Studenten, PDF, englisch, 328 kB, NASA-Publikation.
- Einführung in die Tensorrechnung. (Wikibooks)
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Ein elementarer Tensor (oder einfacher Tensor) bildet auf einen Zahlenwert (Skalar) ab.
- ↑ Woldemar Voigt: Die fundamentalen physikalischen Eigenschaften der Krystalle in elementarer Darstellung. Verlag von Veit & Comp., Leipzig 1898 (VIII, 243 S., eingeschränkte Vorschau in der Google-Buchsuche). Reprint 2021: de Gruyter, Berlin ISBN 978-3-11-243943-2. Voigt schreibt auf S. IV: Ich habe deshalb, ebenso wie es die Bezeichnung „Vector“ thut, an einen speciellen und charakteristischen Vorgang angeknüpft und für jene zweiseitigen gerichteten Grössen den Namen „Tensoren“ in Vorschlag gebracht.
- ↑ M. M. G. Ricci, T. Levi-Civita: Méthodes de calcul différentiel absolu et leurs applications. In: Mathematische Annalen. 54, 1901, ISSN 0025-5831, S. 125–201, online.
- ↑ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, S. 172–179.
- ↑ R. Abraham, Jerrold E. Marsden, T. Ratiu: Manifolds, tensor analysis, and applications (= Applied mathematical sciences 75). 2. Auflage. Springer, New York NY u. a. 1988, ISBN 0-387-96790-7, S. 338–339.
- ↑ Kerstin Weinberg: Vorlesungsskript. Tensoralgebra und -Analysis. (PDF; 235 kB) Universität Siegen, 24. Oktober 2012, abgerufen am 27. November 2020.
- ↑ Heinz Schade, Klaus Neemann: Tensoranalysis. 2. überarbeitete Auflage. de Gruyter, Berlin / New York 2006, ISBN 3-11-018943-7, S. 277 ff.




















































![{\displaystyle {\begin{matrix}L^{k}(E_{1},\dotsc ,E_{k};K)&{\stackrel {\sim }{\longrightarrow }}&L(E_{1}\otimes \dotsc \otimes E_{m};E_{m+1}^{*}\otimes \dotsc \otimes E_{k}^{*})\\\lambda &\longmapsto &\left[\lambda _{(1,\dotsc ,m)}\colon v_{1}\otimes \dotsc \otimes v_{m}\mapsto \lambda _{(v_{1},\dotsc ,v_{m})}\in (E_{m+1}\otimes \dotsc \otimes E_{k})^{*}\right]{\text{ ,}}\\&&{\text{wobei }}\left[\lambda _{(v_{1},\dotsc ,v_{m})}\colon (v_{m+1}\otimes \dotsc \otimes v_{k})\mapsto \lambda (v_{1},\dotsc ,v_{k})\right]\\\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5af0ca5982fcea7f59fe2aa8996dd0c3de44ce0)















































































































































































![{\displaystyle \psi :V_{1}\times \dotsb \times V_{s}\to [??]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/597d0dd2574ad69e6b77499917be8e727960cd06)































