Unberührbare Zahl
Zur Navigation springen
Zur Suche springen
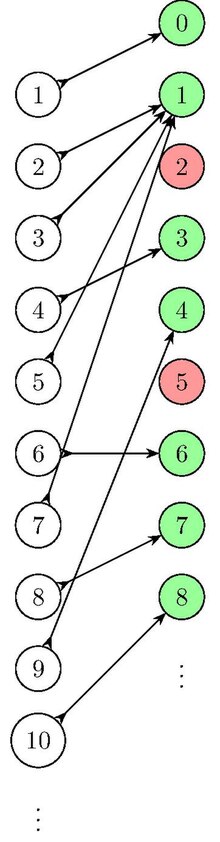
In der Zahlentheorie ist eine unberührbare Zahl (vom englischen untouchable number) eine positive ganze Zahl , die nicht als Summe aller echten Teiler irgendeiner positiven ganzen Zahl dargestellt werden kann (inklusive der unberührbaren Zahl selbst). Diese Zahlen kommen somit in keinen Inhaltsketten vor. Sie wurden erstmals von ʿAbd al-Qāhir al-Baghdādī (etwa im Jahr 1000) untersucht, der bemerkt hat, dass die beiden Zahlen 2 und 5 unberührbar sind.[1]
Beispiele
[Bearbeiten | Quelltext bearbeiten]- Die Zahl ist eine unberührbare Zahl.
- Beweis:
- Man muss zeigen, dass nicht als Summe der echten Teiler irgendeiner Zahl dargestellt werden kann.
- In einer echten Teilersumme kommt kein Teiler mehrmals vor. Es gibt nur zwei Möglichkeiten, die Zahl 5 additiv mit verschiedenen Zahlen darzustellen: . Die zweite Darstellung ist keine Teilersumme, weil die Zahl 1 fehlt, die immer in jeder Teilersumme enthalten sein muss. Die erste Darstellung kommt als Teilersumme auch nicht in Frage, weil wenn eine Zahl die Teiler 1 und 4 hat, sie auch die Zahl 2 als Teiler haben muss und somit ihre Teilersumme mindestens sein muss. Somit bleibt keine Möglichkeit übrig, dass es ein gibt, sodass ist. Die Zahl 5 ist somit eine unberührbare Zahl.
- Beweis:
- Die Zahl ist keine unberührbare Zahl.
- Beweis:
- Man muss zeigen, dass die Summe der echten Teiler irgendeiner Zahl ist.
- Es ist . Es gibt eine Zahl, die nur die Zahlen 1 und 3 als echte Teiler hat, nämlich die Zahl . Somit ist ihre Teilersumme , womit die Zahl 4 keine unberührbare Zahl ist.
- Beweis:
- Die folgenden Zahlen sind die kleinsten unberührbaren Zahlen:
Eigenschaften
[Bearbeiten | Quelltext bearbeiten]- Perfekte Zahlen sind niemals unberührbare Zahlen.
Beweis:- Sei eine perfekte Zahl. Perfekte Zahlen haben die Eigenschaft, dass sie gleich ihrer echten Teilersumme sind. Es gilt also . Somit existiert eine Zahl, deren echte Teilersumme gleich ist. Somit ist keine unberührbare Zahl.
- Befreundete Zahlen sind niemals unberührbare Zahlen.
Beweis:- Seien zwei befreundete Zahlen. Befreundete Zahlen haben die Eigenschaft, dass die eine Zahl gleich der echten Teilersumme der anderen Zahl ist und umgekehrt. Es gilt also und . Somit existiert für jede der beiden Zahlen und eine echte Teilersumme, die gleich bzw. ist. Somit sind und keine unberührbaren Zahlen.
- Gesellige Zahlen sind niemals unberührbare Zahlen.
Beweis:- Seien mit gesellige Zahlen. Gesellige Zahlen haben die Eigenschaft, dass die echte Teilersumme der -ten Zahl gleich ist (mit ). Es gilt also und . Somit existiert für jede der Zahlen eine echte Teilersumme, die gleich ist. Somit sind keine unberührbaren Zahlen.
- Sei eine Primzahl und eine Zahl, die um 1 größer ist als eine Primzahl. Dann gilt:
ist keine unberührbare Zahl.
Beweis:- Weil eine Primzahl ist, hat nur die echten Teiler und . Somit gilt für die echte Teilersumme . Also kann niemals eine unberührbare Zahl sein, weil es eine Zahl gibt, deren echte Teilersumme gleich ist.
- Sei eine ungerade Primzahl und eine Zahl, die um 3 größer ist als eine Primzahl. Dann gilt:
ist keine unberührbare Zahl.
Beweis:- Sei eine ungerade Primzahl. Dann hat nur die echten Teiler und . Somit gilt für die echte Teilersumme . Also kann niemals eine unberührbare Zahl sein, weil es eine Zahl gibt, deren echte Teilersumme gleich ist.
- Es gibt unendlich viele unberührbare Zahlen. Ihre asymptotische Dichte beträgt mindestens
Beweis: von Paul Erdős[2] und von Chen & Zhao[3]
Ungelöste Probleme
[Bearbeiten | Quelltext bearbeiten]- Es wird vermutet, dass die Zahl die einzige ungerade unberührbare Zahl ist.
- Dies würde aus der starken Goldbachschen Vermutung folgen, wenn sie bewiesen wäre:
Eine Zahl (mit Primzahlen , ) hat nur die echten Teiler und . Somit ist die Summe ihrer echten Teiler . Wenn jede gerade Zahl als Summe zweier verschiedener Primzahlen dargestellt werden kann (genau das ist die Aussage der starken Goldbachschen Vermutung), dann ist jede ungerade Zahl keine unberührbare Zahl, weil sie die Teilersumme der Zahl (mit den echten Teilern und ) ist. Weiters ist , und . Somit kann nur eine ungerade unberührbare Zahl sein.[4]
- Dies würde aus der starken Goldbachschen Vermutung folgen, wenn sie bewiesen wäre:
- Es wird vermutet, dass alle unberührbaren Zahlen außer 2 und 5 zusammengesetzte Zahlen sind.
- Dies würde unmittelbar aus der obigen Behauptung folgen, zumal diese aussagt, dass außer der Zahl 5 nur gerade Zahlen unberührbare Zahlen sein können. Gerade Zahlen, die ungleich 2 sind, sind aber immer zusammengesetzt.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Eric W. Weisstein: Untouchable Number. In: MathWorld (englisch).
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ J. Sesiano: Two problems of number theory in Islamic times. In: Archive for History of Exact Sciences. Band 41 (3), 1991, S. 235–238 (springer.com [abgerufen am 24. November 2018]).
- ↑ Paul Erdős: Über die Zahlen der Form und . In: Elemente der Math. Band 28, 1973, S. 83–86 (emis.de [abgerufen am 24. November 2018]).
- ↑ Yong-Gao Chen, Qing-Qing Zhao: Nonaliquot numbers. In: Publicationes Mathematicae. Band 78 (2), Februar 2011, S. 439–442 (researchgate.net [abgerufen am 24. November 2018]).
- ↑ Eric W. Weisstein: Untouchable Number. In: MathWorld (englisch).
























































