WORHP

WORHP
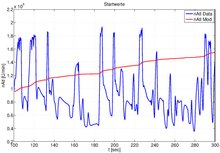Konsolenansicht, Ausgangssituation und Optimale Lösung
Basisdaten
Entwickler	Christof Büskens, Matthias Gerdts et al.
Erscheinungsjahr	2010
Aktuelle Version	1.16 (7. Mai 2024)
Betriebssystem	Linux, Microsoft Windows
Programmier­sprache	ANSI C, FORTRAN 77, Fortran 95 und Fortran 2003
Kategorie	Mathematik, Optimierung
Lizenz	Proprietär, Kostenfrei für akademische Zwecke
deutschsprachig	nein
worhp.de

WORHP [wɔːrp], bei der ESA auch bekannt als „eNLP“ (NLP solver), ist ein mathematisches Programm bzw. eine Bibliothek zur numerischen Lösung stetiger hochdimensionaler nichtlinearer Optimierungsprobleme. Die Abkürzung WORHP bedeutet ausgeschrieben “We Optimize Really Huge Problems” („Wir optimieren richtig große Probleme“), dies stellt das primäre Anwendungsgebiet der Software dar. WORHP ist hybrid in den Sprachen Fortran und C implementiert und bietet zusätzlich die Möglichkeit über verschiedene Schnittstellen in C/C++- und Fortran-Programmen integriert zu werden. Zusätzlich existieren Schnittstellen zur Einbindung in die Modellierungsumgebungen Matlab, CasADi und AMPL.

Formulierung des Problems

WORHP wurde entwickelt, um Probleme der Form

$\min _{x\in \mathbb {R} ^{n}}f(x)$

unter

$L\leq {\begin{pmatrix}x\\g(x)\end{pmatrix}}\leq U$

mit hinreichend glatten Funktionen $f\colon \mathbb {R} ^{n}\to \mathbb {R}$ (Zielfunktion) und $g\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}$ (Nebenbedingungen) zu lösen, die nichtlinear sein dürfen und nicht notwendig konvex sein müssen. Sogar Probleme mit sehr großen Dimensionen $n$ und $m$ können effizient gelöst werden, wenn das Problem hinreichend dünnbesetzt ist; die höchsten bisher erreichten Dimensionen liegen in der Größenordnung $10^{9}$. Problemstellungen, in denen es nicht möglich ist, Zielfunktion und Nebenbedingungen separat auszuwerten, oder in denen es möglich ist, die Nebenbedingungen elementweise auszuwerten, können von WORHP ausgenutzt werden, um die Berechnung effizient zu gestalten.

Ableitungen

WORHP benötigt die erste Ableitung (Gradient) von $f$ und von $g$ (Jacobi-Matrix) und die zweite Ableitung (Hesse-Matrix) der Lagrange-Funktion; in einer Modellierungsumgebung wie AMPL können diese durch automatische Differentiation zur Verfügung gestellt werden, aber in anderen Anwendungen müssen diese durch den Benutzer übergeben werden. Erste und zweite Ableitungen können durch WORHP mit Hilfe von finiten Differenzen ermittelt werden. Um die typischerweise dadurch entstehende sehr hohe Anzahl an Funktionsauswertungen in hochdimensionalen dünnbesetzten Anwendungen zu vermeiden, wird die Graphenfärbungstheorie ausgenutzt, um erste und zweite Ableitungen zu gruppieren. Zweite Ableitungen können außerdem durch Variationen der klassischen BFGS-Verfahren, inklusive block-diagonaler und dünnbesetzter Variante, approximiert werden. WORHP implementiert als erstes NLP-Verfahren ein strukturerhaltendes (ggf. also dünnbesetztes) SBFGS-Verfahren, für das ein Konvergenzbeweis existiert.

Struktur

Auf NLP-Ebene basiert WORHP auf einem klassischen SQP-Algorithmus, wohingegen die quadratischen Teilprobleme mit Hilfe von Innere-Punkte-Verfahren gelöst werden. Dieser Aufbau wurde gewählt um von der Robustheit von SQP-Verfahren und dem zuverlässigen numerischen Aufwand von IP-Verfahren zu profitieren, da klassische Aktive-Mengen-Strategien bei hochdimensionalen Problemen ungeeignet sind.

Entwicklung

Die Entwicklung von WORHP startete 2006 mit einer Finanzierung des deutschen Zentrums für Luft- und Raumfahrt und wurde unter dem Namen „eNLP“ nach 2008 mit Unterstützung der ESA/ESTEC zusammen mit dem Innere-Punkte-Löser ipfilter fortgesetzt. Ziel war die Implementierung eines NLP-Lösers zur Bestimmung optimaler Trajektorien, zur Missionsanalyse und für Raumfahrtanwendungen im Allgemeinen. (Die Benutzung von Ipfilter in WORHP wurde nach 2010 nicht weiter verfolgt.) Das Steinbeis-Forschungszentrum Optimierung, Steuerung und Regelung und Wissenschaftler der Arbeitsgruppe Optimierung und Optimale Steuerung an der Universität Bremen und der Universität der Bundeswehr München arbeiten an der weiteren Entwicklung von WORHP. Die Entwickler von WORHP betonen, dass es trotz seines akademischen Ursprungs von Beginn an als industriell nutzbares Werkzeug entwickelt wurde, statt als reine Forschungsplattform.

Anwendungen

WORHP wurde in Programmen zur Analyse von Trajektorien wie LOTNAV und ASTOS integriert und wird am ESOC und am ESTEC genutzt. Es ist auch möglich WORHP als Optimierer in CasADi (ab Version 1.5.0 beta) einzubinden und es wird als lokaler Optimierer im Programm SVAGO MDO, entwickelt an der Universität Bremen und am Politecnico di Milano, zur multidisziplinären Optimierung im ESA-PRESTIGE-Programm genutzt.

Weblinks

• WORHP-Website (englisch)
• The ESA NLP Solver WORHP – Kapitelzusammenfassung bei SpringerLink (englisch)