Benutzer:Elcap/Kondensator (Elektrotechnik)/ReviewJan2007

Ein Kondensator (von lateinisch condensare ‚verdichten‘) ist ein passives elektrisches Bauelement mit der Fähigkeit, in einem Gleichstromkreis elektrische Ladung und die damit zusammenhängende Energie statisch in einem elektrischen Feld zu speichern. Die gespeicherte Energie wird als elektrische Kapazität bezeichnet und in der Einheit Farad gemessen. In einem Wechselstromkreis wirkt ein Kondensator als Wechselstromwiderstand mit einem frequenzabhängigen Impedanzwert.

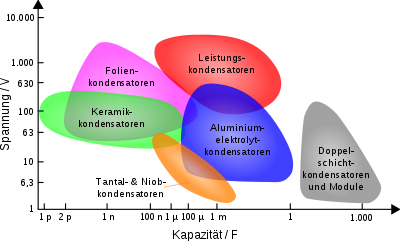
Kondensatoren bestehen im Prinzip aus zwei elektrisch leitfähigen Flächen, den Elektroden, die von einem isolierenden Material, dem Dielektrikum, voneinander getrennt sind. Die Größe der Kapazität wird durch die Größe der Elektroden, dem Material des Dielektrikums und dem Kehrwert des Abstandes der Elektroden zueinander bestimmt. Die Elektroden und das Dielektrikum können aufgerollt oder parallel geschaltet als Stapel angeordnet sein. Industriell hergestellte Kondensatoren werden mit Kapazitätswerten von etwa 1 Picofarad (10^-12 F) bis zu etwa 1 Farad, bei Superkondensatoren sogar bis zu 10.000 Farad geliefert.

Die mit großem Abstand am meisten produzierten Kondensatoren sind integrierte Speicherkondensatoren in digitalen Speicherschaltungen. Die wichtigsten diskreten Kondensatorarten sind Keramikkondensatoren, Kunststoff-Folienkondensatoren, Aluminium- und Tantal- Elektrolytkondensatoren und, obwohl sie auf völlig andere Speicherprinzipien beruhen, die Superkondensatoren. Neben diesen Kondensatoren mit festen Kapazitätswerten gibt es Kondensatoren mit einstellbaren Kapazitätswerten, die variablen Kondensatoren.

Kondensatoren werden in vielen elektrischen Anlagen und in nahezu allen elektrischen und elektronischen Geräten eingesetzt. Sie realisieren beispielsweise elektrische Energiespeicher als Zwischenkreiskondensatoren in Frequenzumrichtern, als Speicherkondensator in Sample-and-Hold-Schaltungen oder als Photo-Flash-Kondensatoren in Blitzlichtgeräten. Sie koppeln Signale in Frequenzweichen von Audiogeräten und bilden als hochstabile Klasse-1-Kondensatoren zusammen mit Spulen Filter und Schwingkreise. Als Glättungskondensatoren in Netzteilen und Stützkondensatoren in Digitalschaltungen sind sie im Bereich der Stromversorgung zu finden. Sie unterdrücken als Entstörkondensatoren elektromagnetische Störsignale und bewirken als Leistungskondensatoren eine erwünschte Phasenkompensation. Spezielle Bauformen von Kondensatoren werden als Sensor verwendet.

Unerwünschte kapazitive Störeinkopplungen aus elektrischen Feldern benachbarter Bauteile in Schaltungen und parasitäre Kapazitäten, sogenannte Streukapazitäten, gehören nicht zu den Kondensatoren. Ebenfalls nicht zu den Kondensatoren gehören Kapazitätsdioden sowie eine Reihe von Aktoren wie piezoelektrische Wandler, elektrostatische Lautsprecher, Ablenkplatten und Bauelemente der Elektrooptik.

Funktionsweise

Ein Kondensator sperrt den Gleichstrom aber leitet den Wechselstrom weiter.

Funktionsweise im Gleichstromkreis

Prinzipielle Darstellung des Stromflusses durch einen Kondensator mit der Bildung eines elektrischen Feldes und der Aufladung der Elektroden, wobei eine Spannung V entsteht

Verlauf von Spannung U und Strom I beim Ladevorgang.

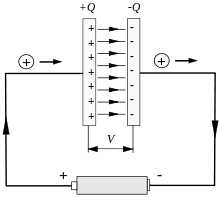
Nach dem Anlegen einer Gleichspannung an einen realen Kondensator in einem Gleichstromkreis beginnt ein elektrischer Strom zu fließen, der die Elektroden gegenpolig auflädt, so dass sich im Kondensator eine Spannung aufbaut. Das sich aufbauende elektrische Potential auf den Elektroden lässt im Raum zwischen den Elektroden ein elektrisches Feld entstehen, dessen Feldstärke der aufgebauten Spannung proportional ist. Die Aufladung folgt einer Exponentialfunktion, solange, bis die Spannung an den Elektroden gleich der anliegenden Spannung ist und der Stromfluss zum Erliegen kommt. Dann sperrt der Kondensator den Gleichstromkreis.

Wird der Kondensator von der Spannungsquelle getrennt, so bleiben Energie und Ladungen erhalten, die Spannung bleibt konstant. Allgemein ausgedrückt, wird dadurch die auf den Elektroden gebildete Ladung vom Kondensator gespeichert. Wird durch Anlegen eines Verbrauchers dem Kondensator Energie entnommen, dann sinkt die Feldstärke des elektrischen Feldes und damit die Kondensatorspannung entsprechend den Bedingungen in der Schaltung.

Da in einem geschlossenen Stromkreis der Strom im ganzen Kreis fließt, fließt er auch durch den Kondensator hindurch. Physikalisch besteht der Strom im Stromkreis jedoch aus zwei Strömen, einem leitungsgebundenem Strom von Ladungsträgern wie Elektronen oder Ionen und einem sogenannten „Verschiebungsstrom“ im Raum zwischen den Elektroden, der als ein Teil der Wirkung des elektrischen Feldes zu verstehen ist und mit einer entsprechenden Änderung der elektrischen Feldstärke einhergeht. Bei realen Kondensatoren ist der Raum zwischen den Elektroden mit einem Dielektrikum ausgefüllt. Der Verschiebungsstrom ergibt sich dann zusätzlich zu dem Anteil durch die Änderung der Feldstärke noch aus der Ladungsverschiebung im Dielektrikum, der Polarisation, die sich aus seiner Dielektrizitätszahl ergibt.

Bei kleinen Feldstärken und linearen dielektrischen Materialien wächst die Polarisation linear mit der Spannung am Kondensator. Proportional zur Spannung wächst die im Kondensator gespeicherte Ladung. Die Proportionalitätskonstante wird als Kapazität bezeichnet; sie ist das wesentliche Merkmal eines Kondensators. Je größer die Kapazität ist, desto mehr Ladung und Energie kann ein Kondensator bei einer bestimmten Spannung speichern. Die Gleichungen

Q=C\cdot U

und

W={\frac {1}{2}}\cdot C\cdot U^{2}

fassen das zusammen. Q ist die Ladung (in Coulomb, C, oder Amperesekunden, As), C die Kapazität (in Farad, F) und U die Spannung (in Volt, V); die Energie (in Joule, J) ist mit W bezeichnet, um sie von der Feldstärke E zu unterscheiden.

Reale Kondensatoren können nur bis zu einer maximal zulässigen Spannung, die sich aus der Durchschlagsfestigkeit des Dielektrikums ergibt, geladen werden.

Die Zeit, die ein realer Kondensator braucht, um sich aufzuladen bzw. um entladen zu werden, kann dem Artikel RC-Glied entnommen werden.

Funktionsweise im Wechselstromkreis

Kondensatoren leiten im Wechselstromkreis Wechselspannungen und Wechselströme weiter, jedoch mit einer Verschiebung der Phasenlage zwischen Spannung und Strom, der Strom eilt der Spannung um 90 ° voraus. Denn aufgrund ihrer Ladungsspeicherfähigkeit beginnt bei Kondensatoren erst ein Strom zu fließen, bevor sich Spannung ändert, während bei einer Spule sich erst die Spannung ändert, bevor ein Strom fließt. Merksatz:

„Kondensator: Strom eilt vor. Induktivitäten: Ströme sich verspäten.“

Ein Kondensator mit der Kapazität $C$ (F) bildet im Wechselstromkreis bei der Frequenz $\omega$ als Quotient der Wechselspannung $u(\omega )$ und dem Wechselstrom $i(\omega )$ einen Wechselstromwiderstand mit der Impedanz ${\underline {Z}}$ (Ω) als komplexe Größe:

Z_{C}={\frac {u(\omega )}{i(\omega )}}={\frac {U_{0}e^{j\omega t}}{CU_{0}j\omega e^{j\omega t}}}={\frac {1}{j\omega C}}={\underline {Z}}

Der Betrag der komplexen Impedanz ${\underline {Z}}$ ist der Scheinwiderstand $Z\ =|{\underline {Z}}|$ .

Der Scheinwiderstand ist umso kleiner, je größer die Kapazität und je höher die Frequenz ist.

Die Eigenschaft von Kondensatoren als Wechselstromwiderstand mit möglichst geringen Scheinwiderstand wird neben der Energiespeicherung in vielen Anwendungen genutzt zur Trennung von Gleich- und Wechselstromanteilen, zur Korrektur von Phasenverschiebungen und zur Erzeugung von Resonanzkreisen.

Funktionsweise (alt)

Kondensatoren besitzen Eigenschaften, die sowohl bei Gleich- als auch bei Wechselstrombetrieb technisch genutzt werden, vielfach, bei überlagerten Spannungen, werden sogar beide Eigenschaften zusammen genutzt.

Wird eine Gleichspannung über eine niederohmige Quelle an einen ungeladenen Kondensator angelegt, so fließt ein zeitlich begrenzter Gleichstrom durch den Kondensator hindurch. Zwischen den beiden Elektroden des Kondensators fließt der Strom als Verschiebungsstrom. Er baut, mit einer entsprechenden Änderung der elektrischen Feldstärke, zwischen den Elektroden ein elektrisches Feld auf, wobei sich eine Elektrode positiv, die andere negativ auflädt. Bei realen Kondensatoren ist der Raum zwischen den Elektroden mit einem Dielektrikum ausgefüllt. Der Verschiebungsstrom ergibt sich dann zusätzlich zu dem Anteil durch die Änderung der Feldstärke noch aus der Ladungsverschiebung im Dielektrikum, der Polarisation, die sich aus seiner Dielektrizitätszahl ergibt.

Bei kleinen Feldstärken und linearen dielektrischen Materialien wächst die Polarisation linear mit der Spannung am Kondensator. Proportional zur Spannung wächst die im Kondensator gespeicherte Ladung. Die Proportionalitätskonstante wird als Kapazität bezeichnet; sie ist das wesentliche Merkmal eines Kondensators. Je größer die Kapazität ist, desto mehr Ladung und Energie kann ein Kondensator bei einer bestimmten Spannung speichern. Die Gleichungen

Q=C\cdot U

und

W={\frac {1}{2}}\cdot C\cdot U^{2}

fassen das zusammen. Q ist die Ladung (in Coulomb, C, oder Amperesekunden, As), C die Kapazität (in Farad, F) und U die Spannung (in Volt, V); die Energie (in Joule, J) ist mit W bezeichnet, um sie von der Feldstärke E zu unterscheiden.

Wird der Kondensator von der Spannungsquelle getrennt, so bleiben Energie und Ladungen erhalten, die Spannung bleibt konstant. Umgangssprachlich ausgedrückt wird hierbei die auf den Elektroden gebildete Ladung vom Kondensator gespeichert. Ist die am Kondensator anliegende Spannung gleich der Kondensatorspannung, dann nehmen die Elektroden keine weitere Ladung mehr auf, der Gleichstromkreis wird unterbrochen. Wird durch Umkehr der Stromrichtung Energie entnommen, sinkt die Spannung wieder.

Das Aufladen und Entladen eines realen Kondensators über einen Widerstand resultiert in einen exponentiell abflachenden Spannungsverlauf, siehe RC-Glied.

Neben seiner Eigenschaft, im Gleichstromkreis elektrischer Energie speichern zu können, hat ein Kondensator im Wechselstromkreis als Wechselstromwiderstand (Impedanz) eine weitere wichtige Funktion, die industriell überaus häufig genutzt wird.

Wird eine Wechselspannung an einen Kondensator gelegt, tritt zwischen Spannung und Strom eine Phasenverschiebung auf, siehe Abschnitt #Phasenverschiebung und Blindwiderstand. Der Strom fließt um 90° versetzt zur Spannung. Die Stromstärke ist proportional zur Frequenz f der angelegten Spannung und zur Kapazität C des Kondensators. Das Verhältnis von Spannungsamplitude zu Stromamplitude wird allgemein Scheinwiderstand oder Impedanz genannt, bei genau 90° Phasenverschiebung heißt er kapazitiver Blindwiderstand X_C

X_{\mathrm {C} }={\frac {U_{\mathrm {S} }}{I_{\mathrm {S} }}}\cdot \sin(\varphi _{\mathrm {z} })={\frac {U_{\mathrm {S} }}{\omega CU_{\mathrm {S} }}}\cdot \sin \left(-{\frac {\pi }{2}}\right)=-{\frac {1}{\omega C}}\,.

Die Formel zeigt, dass der elektrische Blindwiderstand des Kondensators mit zunehmender Frequenz bis zum praktischen Kurzschluss bei Hochfrequenz abnimmt und andererseits bei der Frequenz f = 0, also bei Gleichspannung, unendlich groß wird und praktisch wie eine Leitungsunterbrechung wirkt.

Die Eigenschaft des Kondensators, bei anliegender Wechselspannung eine Impedanz zu bilden, wird genutzt um beispielsweise Wechselströme von Gleichströmen zu trennen (Filteranwendungen), in Zusammenschaltung mit einer Spulen einen Schwingkreise bilden zu können oder um eine Phasenverschiebung eines induktiven Verbrauchers (Energietechnik) zu kompensieren.

Die für den Betrieb diskreter Kondensatoren wichtigen Einsatzgrenzen wie z. B. maximale Spannungsgrenzen, maximale Strombelastungen und maximale Temperaturbereiche werden weiter unten im Abschnitt #Material- und bauartbedingte Merkmale beschrieben.

Geschichte

Leidener Flasche

Die Leidener Flasche war die älteste Bauform eines Kondensators. Sie besteht aus einem Glasgefäß, das innen wie außen mit Metall belegt ist. Das Glas wirkt als Isolator. Das Prinzip der Leidener Flasche wurde unabhängig voneinander 1745 von dem Domdechanten Ewald Jürgen Georg von Kleist in Cammin (Pommern) und ein Jahr später von dem Physiker Pieter van Musschenbroek in Leiden gefunden, als sie bei Laborversuchen mit Anordnungen von Gläsern und Metallteilen elektrische Stromschläge erlitten.

Die Leidener Flasche und ähnliche Laborgeräte wurden in der Folge vornehmlich zur publikumswirksamen Demonstration von Stromschlägen (auch als „Kleist’scher Stoß“ bekannt geworden) eingesetzt, bei später zunehmenden Kenntnissen über das Wesen der Elektrizität auch als Stromquelle für fortgeschrittenere Experimente: Benjamin Franklin verband eine Leidener Flasche über eine Metallschnur mit einem Drachen, den er in den Himmel steigen ließ. Es gelang ihm mit diesem gefährlichen Experiment, Ladung von Gewitterwolken auf die Leidener Flasche zu übertragen. Er prägte den Begriff „electrical condenser“, welcher im angelsächsischem noch häufig synonym zum „capacitor“ gebraucht wird.

Ein verbesserter Kondensator wurde 1775 durch Alessandro Volta (1745-1827) erfunden, welchen er mit „electrophorous“ (Elektrizitätsträger) bezeichnete. Er bestand aus zwei Metallplatten, die durch eine Ebonitschicht gegeneinander isoliert waren. Man kann diese Anordnung bereits als Prototyp moderner Kondensatoren betrachten. Der Einsatz besserer Dielektrika führte später zu einer Reduzierung der Baugröße. Etwa ab 1850 wurde Glimmer, ein natürlich vorkommendes Mineral, in Scheiben geschnitten als Isolator für Kondensatoren verwendet. Papierkondensatoren mit Metallfolienbelägen, sind seit 1876 bzw. 1900 in Gebrauch. Da beide Kondensatorarten als quaderförmige „Blöcke“ hergestellt wurden und in Gleichstromkreisen die überlagerten Wechselspannungen gegen Masse ableiteten, sie quasi „blockierten“, lag es nahe, diese Fähigkeit dieser Blockkondensatoren „abblocken“ zu nennen. Der Begriff „abblocken“ wird auch heute noch für Schaltungen mit Kondensatoren verwendet, die unerwünschte Störungen unterdrücken (sieben). Gewickelte Als Metall-Papier-Kondensatoren (MP-Kondensatoren) sind diese Kondensatoren auch heute noch in der Leistungselektronik zu finden.

Blockkondensator aus dem Jahre 1923 in den Abmessungen 50x45x35 mm, Kapazität 2 µF, aufgebaut aus geschichteten und mit Paraffin getränkten Papierfolien, die mit dünnen Metallfolien (Aluminium) belegt sind.

Elektrische Flüssigkeitskondensatoren mit Aluminiumelektroden, die späteren „Elektrolytkondensatoren“, die mit Hilfe der aus der Chemie stammenden Entdeckung, dass sich bei der Elektrolyse von Salzsäure auf Aluminium-Elektroden eine isolierende Schicht aus Aluminiumoxid auf der Anode bildet, wurden 1896 von Charles Pollak erfunden (Patentschrift Nr. 92564) und waren ab Anfang 1900 als Siebkondensatoren zur Unterdrückung von Brummgeräuschen in Telefonnetzen in Benutzung

Seit etwa 1900 wurde auch Porzellan als Dielektrikum in Kondensatoren verwendet. Erst in den Dreißiger Jahren des 20. Jahrhunderts erfolgte durch die Erforschung keramischer Werkstoffe als Ersatz für Porzellan und Glimmer die Entwicklung der Keramikkondensatoren.

Zum Verändern der Resonanzfrequenz von Sendern und Empfängern in der „drahtlosen Telegrafie“ wurde zu Beginn dieser Technik die Induktivität des Schwingkreises verändert. Ab 1915 kamen dann Drehkondensatoren zum Einsatz, die bereits 1901 von Koespel erfunden wurden

Mit der Entwicklung von Kunststoffen nach dem zweiten Weltkrieg begann die Industrie Papier in den Metall-Papierkondensatoren durch dünnere und spannungsfestere Kunststoff-Folien zu ersetzen, aus denen sich eine breite Palette von unterschiedlichen Kunststoff-Folienkondenstoren entwickelte.

Eine Miniaturisierung militärischer und industrieller Kondensatoren gelang ebenfalls nach dem zweiten Weltkrieg ab 1950 bei der General Electric mit der Entwicklung von Tantal-Elektrolytkondensatoren.

Eine nochmals deutlich Kapazitätsteigerung bei gegebenem Bauvolumen gelang mit dem von General Electric 1957 patentierten „Low voltage electrolytic capacitor“, welcher durch SOHIO und ab 1971 durch NEC zu einem marktreifen Bauelement weiterentwickelt wurde und später die Bezeichnung „Doppelschichtkondensator“ erhielt. Diese Doppelschichtkondensatoren sind keine Elektrolytkondensatoren, auch wenn sie mit einem Elektrolyten versehen sind. Sie nutzen den physikalischen Effekt einer elektrischen Doppelschicht, die z. B. an der Oberfläche von Aktivkohlepartikeln besteht und ermöglichen damit sehr große Kapazitätswerte bis in den Farad-Bereich hinein.

In der letzten Zeit erfolgte bei allen Kondensatorarten eine Entwicklung zu immer kleinerem Bauvolumen bei gleichzeitig verbesserten elektrischen und mechanischen Eigenschaften. Neue Keramiksorten und verbesserte Fertigungstechniken gestatten z. B. die Herstellung von oberflächenmontierbaren (SMD) Vielschicht-Keramikkondensatoren (MLCC) mit Kapazitätswerten über 100 μF hinaus, das sind Kapazitätswerte, die weit in den Bereich der Elektrolytkondensatoren hineinragen.

Als neueste Entwicklung auf dem Gebiet der Kondensatoren sind Silizium-Kondensatoren zu sehen. Diese profitieren von der großen Erfahrung in der Halbleiterindustrie mit Silizium und bieten dem Anwender frequenzstabile Kapazitätswerte bis in den GHz-Bereich hinein.

Die Miniaturisierung in der Elektronik wurde nicht zuletzt auch durch eine teilweise erhebliche Steigerung der Kapazität bei gegebenem Bauvolumen im Bereich der Kondensatoren erreicht

Kondensatoren werden in einer Vielzahl von Geräten eingesetzt, sie hatten 1998 ein Marktvolumen von 9,2 Milliarden Dollar, wobei 38 % Keramikkondensatoren und 28 % Elektrolytkondensatoren einnahmen. Der Rest verteilte sich überwiegend auf Folien- und MP-Kondensatoren bzw. Leistungskondensatoren.^[1]

Physikalische Grundlagen

Physikalische und elektrotechnische Begriffe

Influenz und elektrisches Feld

Das Phänomen der elektrischen Ladungstrennung auf der Oberfläche von vorher elektrisch neutralen Leitern durch ein elektrisches Feld wird Influenz genannt. Wird also eine elektrische Ladung auf eine elektrisch leitende Platte gebracht und steht ihr eine gleichartig elektrisch leitende Platte gegenüber, so wird auf die 2. Platte eine Ladung mit umgekehrter Polarität induziert. In dem Raum zwischen den Platten wird ein elektrisches Feld erzeugt.

Die Darstellung dieses Feldes erfolgt üblicherweise mit Feldlinien. Diese Feldlinien führen stets von der positiven Ladung zur negativen Ladung. Sie treten stets senkrecht ein und aus. Die Feldlinien berühren oder schneiden sich niemals.

Elektrische Felder bei denen die Feldstärke weitgehend gleich ist, wie z. B. bei zwei sich parallel gegenüberstehenden Platten, werden als homogene elektrische Felder bezeichnet. Diese Anordnung ist für Kondensatoren üblich.

Die Feldstärke eines homogenen Feldes wird berechnet mit:

E = U/l

Dabei ist E = die elektrische Feldstärke (V/m), U = die Spannung zwischen den Platten (V) und l = der Abstand der Platten (m) zueinander.

Dielektrische Polarisation

Bringt man in ein elektrisches Feld einen Isolator ein, so reagiert das Material, das in einem Kondensator Dielektrikum genannt wird, infolge der Kraftwirkung des elektrischen Feldes mit einer Verschiebung seiner inneren Ladungen. Die mit den Ladungsverschiebungen verbundene dielektrische Polarisation ist mitverantwortlich für die Kapazität von Kondensatoren. Als Maß für die dielektrische Polarisierbarkeit dient die Dielektrizitätszahl oder Permittivität εr des Dielektrikums. Die Permittivität ergibt sich aus dem Verhältnis einer Kapazität C eines Kondensators ohne das dielektrische Material zu einer Kapazität C0 des gleichen Kondensators mit dem dielektrischen Material.

εr = C / C0

In der Sprache der Maxwellschen Gleichungen gilt

D = εr ε0 E

wobei D die elektrische Verschiebungsdichte (As/m2), E die elektrische Feldstärke (V/m) und ε0 die elektrische Feldkonstante bzw. die Dielektrizitätskonstante ε0 = 8,8543 • 10-12 As/Vm ist.

Kapazität und Ladung

Die Kapazität (C) eines Kondensator ergibt sich aus der wirksamen Elektrodenoberfläche A, dem Kehrwert des Elektrodenabstandes d und der Permittivität ε des Dielektrikums:

C = ε A/d (F) d. h. die Kapazität eines Kondensators ist um so größer, je größer die wirksame Elektrodenfläche. je höher die Permittivität des Dielektrikums und je kleiner der Elektrodenabstand ist.

Ein Kondensator kann elektrische Ladungsträger speichern. Das Maß für das Speichervermögen heißt Kapazität (C) und wird Farad (F), zu Ehren des englischen Physikers Faraday genannt. Nach DIN 1301 besitzt ein Kondensator die Kapazität 1 Farad, wenn bei einem Ladestrom von 1 Ampere (A) innerhalb 1 Sekunde (s) die Spannung am Kondensator auf 1 Volt (V) ansteigt.

1 F = 1 As/1 V

Handelsübliche Kondensatoren besitzen Kapazitätswerte, die meist viele Größenordnungen kleiner als 1 F sind:

- Keramikkondensatoren im Bereich Pico-Farad pF (1pF=10-12 F)

- Kunststofffolien-Kondensatoren im Bereich Nano-Farad nF (1nF=10-9 F)

- Elektrolytkondensatoren im Bereich Mikro-Farad uF (1uF= 10-6 F)

- Doppelschichtkondensatoren im Bereich 1 F

Im Gleichstromkreis ist ein Kondensator ein Ladungsspeicher, mit dem Speichervermögen Q (As) proportional zur Kapazität (C) des Kondensators und der anliegenden Spannung U:

Q = C • U (As)

Je größer die Kapazität ist, umso mehr Ladung kann ein Kondensator bei einer bestimmten Spannung speichern.

Spannungsfestigkeit

Neben der Kapazität ist die Spannungsfestigkeit das weitere wesentlichen Merkmal eines Kondensators. Beide Größen werden durch die verwendeten Materialien und deren Eigenschaften bestimmt. Die Spannungsfestigkeit eines Kondensators wird mit dem Begriff Nennspannung spezifiziert. Die Nennspannung ist die höchste Gleichspannung oder Spitzenwert einer Impulsspannung, die im Dauerbetrieb innerhalb des Nenntemperaturbereiches anliegen darf. Weitere Spannungsbegriffe bei Kondensatoren sind: Kategoriespannung UC ,Temperaturabhängig geminderte Spannung, Umpolspannung (nur bei gepolten Kondensatoren) Urev , Spitzenspannung US , Überlagerte Nenn-Wechselspannung, Transientenspannung.

Feldenergie

Ein geladener Kondensator speichert elektrische Energie in dem elektrischen Feld, das zwischen den geladenen Platten besteht. Ist ein Kondensator der Kapazität C auf die Spannung U geladen, so enthält sein Feld die Energie W gemäß:

W={\frac {1}{2}}C\cdot U^{2}

Um den Kondensator zu laden, muss man elektrische Ladung von der einen Platte zur anderen transportieren. Je weiter der Kondensator während dieses Vorgangs bereits aufgeladen ist, desto stärker ist das bereits zwischen seinen Platten herrschende elektrische Feldstärke E, desto mehr Kraft muss also ausgeübt werden, um die Ladung von einer Platte zur anderen zu bringen. Während des Ladens wird daher (immer mehr) Arbeit an den bewegten elektrischen Ladungen verrichtet. Am Schluss ist die während des Aufladens verrichtete Gesamtarbeit als Feldenergie gespeichert. Diese wird beim Entladen wieder frei.

Davon abgeleitet ist die elektische Leistung P, die ein Kondensator abgeben kann:

$P={\frac {W}{\mathrm {ESR} \cdot C}}={\frac {U^{2}}{2\cdot \mathrm {ESR} }}$

Hierin ist „ESR“ der „Äquivalente Serienwiderstand“ in dem Serien-Ersatzschaltbild eines Kondensators, in dem alle ohmschen Verluste eines realen Kondensators zusammengefasst werden.

Phasenverschiebung

Eine kosinusförmige Wechselspannung mit der Amplitude U_S und der Frequenz f bzw. der Kreisfrequenz ω=2π f, also

U(t)=U_{S}\cos(\omega t)\

an einem Kondensator bewirkt den Stromfluss

$I(t)\,$	$=C\ {\frac {\mathrm {d} U(t)}{\mathrm {d} t}}=CU_{S}\omega \ (-\sin(\omega \ t))$
	$=I_{S}(-\sin(\omega t))\,$ .

Der Strom fließt zeitlich versetzt zur Spannung („Phasenverschiebung“), er eilt dieser um π/2 bzw. 90° voraus.

Die Stromstärke I_S ist proportional zur Frequenz f der angelegten Spannung und zur Kapazität C des Kondensators:

I_{\mathit {S}}\ \;\sim \ f

I_{\mathit {S}}\ \;\sim \ C

Blindwiderstand

Das Verhältnis von Spannungsamplitude zu Stromamplitude wird als Blindwiderstand X_C bezeichnet, somit ist

-X_{C}={\frac {U_{S}}{I_{S}}}={\frac {U_{S}}{CU_{S}\omega }}={\frac {1}{\omega C}}

.

Aufgrund der Phasenverschiebung von 90° wandelt der Blindwiderstand keine Leistung in Wärme um. Gelegentlich wird der Blindwiderstand auch mit einem negativen Vorzeichen versehen, um die Stromrichtung von der entgegengerichteten einer Induktivität zu unterscheiden.

Die Formel zeigt, dass der elektrische Widerstand des Kondensators mit zunehmender Frequenz abnimmt bis zum praktischen Kurzschluss bei Hochfrequenz und andererseits bei der Frequenz f = 0, also bei Gleichstrom, unendlich groß wird und praktisch wie eine Leitungsunterbrechung wirkt.

Wird ein Kondensator von mehreren Strömen durchflossen, insbesondere mit verschiedenen Frequenzen, so lässt sich diese Gesetzmäßigkeit von Strom zu Spannung auf jeden einzeln anwenden: Die resultierende Spannung ist die Summe der einzelnen, so ermittelten Spannungen. Ein Kondensator wird deshalb auch als lineares Bauelement bezeichnet.

Um nicht Phase und Betrag von Signalen getrennt berechnen zu müssen, werden in der komplexen Wechselstromrechnung die Amplituden sinus- und kosinusförmiger Spannungsverläufe in Imaginär- und Realanteil einer komplexen Amplitude der auf die komplexe Ebene erweiterten Kreisfunktion e^jwt zusammengefasst (die nebenstehende Darstellung verdeutlicht dies). Kleine Buchstaben kennzeichnen entsprechende Größen:

u(\omega )=U_{0}e^{j\omega t}\

i(\omega )=CU_{0}j\omega e^{j\omega t}\

.

Der Realanteil davon bestimmt den Momentanwert der Größe. Die imaginäre Einheit ist mit dem in der Elektrotechnik üblichen j bezeichnet.

Impedanz bzw. Scheinwiderstand

Der Zusammenhang zwischen Strom und Spannung, die Impedanz Z_C, lässt sich daraus analog dem ohmschen Widerstand durch Quotientenbildung gewinnen:

Z_{C}={\frac {u(\omega )}{i(\omega )}}={\frac {U_{0}e^{j\omega t}}{CU_{0}j\omega e^{j\omega t}}}={\frac {1}{j\omega C}}

Durch diese Betrachtungsweise werden Differentialgleichungen vermieden. Anstelle der Ableitung tritt eine Multiplikation mit 1/jω.

Für reale Kondensatoren wird der Zusammenhang der Phasenverschiebung vereinfacht in einem statischen Zeigerdiagramm dargestellt. Dann wird daraus:

Der Scheinwiderstand Z ist der Betrag der vektoriellen Summe von Ersatzserienwiderstand ESR und Blindwiderstand XC der Kapazität abzüglich des Blindwiderstandes XL der Induktivität.

Die Impedanz eines Kondensators in einem Wechselstromkreis ist ein Maß für die Fähigkeit eines Kondensators in Siebschaltungen, unerwünschte Frequenzanteile gegen Masse abzuleiten.

Typische Impedanzverläufe verschiedener Kondensatoren mit unterschiedlicher Kapazität. Je kleiner die Kapazität ist, desto höher wird die Frequenz, die der Kondensator ableiten (filtern, sieben) kann. Der Restwiderstand im Bereich des unteren Wendepunktes einer Impedanzkurve ist mit dem ESR gleichzusetzen

.

Verlustfaktor tan δ und Äquivalenter Serienwiderstand ESR

Technische Kondensatoren weisen Verluste auf. Sie setzen einen Teil der in sie hineingesteckten elektrischen Energie in Wärme um. Als Maße für diese Verluste gelten der Tangens des Winkels δ, des sog. Verlustfaktors tan δ.

Erklärung der Impedanz aus dem kapazitiven Blindwiderstand und dem ESR, des Verlustfaktors und des Leistungsfaktors

Der Verlustfaktor tan δ ist das Verhältnis vom Ersatzserienwiderstand ESR zum Blindwiderstand XC der Kapazität in der Ersatzserienschaltung oder das Verhältnis von Wirkleistung zu Blindleistung bei sinusförmiger Spannung. tan δ = ESR / Xc

Die Größenordnung von Verlustfaktoren technischer Kondensatoren beträgt bei

Keramikkondensatoren tan δ = 1..200 • 10-3 Kunststofffolien-Kondensatoren tan δ = 3..20 • 10-3 Elektrolytkondensatoren tan δ = 6..500 • 10-3

Für Kondensatoren, die nicht in frequenzbestimmenden Kreisen zum Einsatz kommen, wird oft anstelle des Verlustfaktors tan δ ohmsche Anteil der Ersatzserienschaltung eines Kondensators, der Ersatzserien¬widerstand ESR angegeben. Die Umrechnung erfolgt mit:

Formel

wobei Cmax. die Kapazität an der oberen Toleranzgrenze der Nennkapazität und f die Frequenz der Messspannung ist.

Zeitverhalten

Eine Beziehung zwischen Strom und Spannung ergibt sich durch zeitliches Ableiten der Gleichung Q=CU:

I=C{\frac {\mathrm {d} U}{\mathrm {d} t}}

,

der Strom ist proportional zu der Spannungsänderung des Kondensators. Legt man einen konstanten Strom an an den Kondensator an, so folgt daraus eine konstante Spannungsänderung, die Spannung steigt linear an. Bedeutung bekommt das Zeitverhalten von Kondensatoren, wenn

a)die Isolierung des Dielektrikums nicht „ideal“ ist und einen ohmschen Widerstand, den „Isolationswiderstand“ aufweist, dann entlädt sich der Kondensator mit der Zeit über seinen Isolationswiderstand und

b)wenn der Kondensator durch eine Spannungsquelle über einen Widerstand geladen wird oder über einem Widerstand entladen wird.

Das Aufladen und Entladen eines Kondensators durch eine Spannungsquelle über einen Widerstand resultiert in einem zeitlich exponentiell abflachenden Spannungsverlauf. Für dieses Verhalten wird allgemein eine Zeitkonstante τ (Tau) definiert.

Die Zeitkonstante gibt die Zeit an, in der die Spannung am Kondensator beim Entladen das (e − 1)-fache (ca. 36,8 %) der Anfangsspannung und beim Laden das (1 − e − 1)-fache (ca. 63,2 %) der Endspannung erreicht hat. Nach 5τ sind 99,3% (Aufladen) bzw. 0,7% (Entladen) erreicht.

Schaltungstechnisch wird die Kombination Widerstand und Kondensator im Gleichstromkreis als RC-Glied behandelt.

Idealisierte physikalische Kondensatoren

Bereits Michael Faraday machte darauf aufmerksam, dass zwischen einem gewöhnlichen Leiter und einer Leidener Flasche kein prinzipieller Unterschied besteht. Wird ein Leiter frei in der Luft gehalten und beispielsweise positiv geladen, so werden an den umgebenden Leitern, etwa den Wänden eines Zimmers, durch Influenz die negativen Ladungen angezogen, die positiven in die Erde abgeleitet. Die Zimmerwände bilden dann gewissermaßen die äußere Belegung der Flasche, die zwischenliegende Luft die isolierende Schicht. Diese Kondensator-Eigenschaft wird jedes Mal sichtbar, wenn jemand beispielsweise beim Berühren einer Türklinke einen elektrischen Schlag erhält.

Aus physikalischer Sicht unterscheiden sich diese Beispiele hinsichtlich der Anordnung der Elektroden und dem dazwischen liegenden Isolator, der auch als Dielektrikum bezeichnet wird. Bei der Leidener Flasche besteht der Isolator aus Glas, bei dem in der Luft befindlichen Körper isoliert die umgebende Luft. Den Einfluss des Isolators erfasst ε, das Produkt aus der materialspezifischen Dielektrizitätszahl ε_r und der Dielektrizitätskonstante ε₀ des Vakuums:

\varepsilon _{0}=8,8542...\cdot 10^{-12}\;\mathrm {F/m}

.

Für eine Reihe von idealisierten Elektrodenanordnungen lässt sich das elektrische Feld und die Kapazität des Kondensators exakt bestimmen. In der folgenden Tabelle sind einige wichtige Anordnungen aufgeführt; die Kapazität wird durch $C$ symbolisiert, die Feldstärke durch $E$ :

Bezeichnung	Kapazität	Elektrisches Feld
Plattenkondensator	$C=\varepsilon _{0}\varepsilon _{r}\cdot {{A} \over {d}}$	$E={\frac {Q}{\varepsilon _{0}\varepsilon _{r}A}}$
Zylinderkondensator	$C=2\pi \varepsilon _{0}\varepsilon _{r}{\frac {l}{\ln({\frac {R_{2}}{R_{1}}})}}$	$E(r)={\frac {Q}{2\pi rl\varepsilon _{0}\varepsilon _{r}}}$
Kugelkondensator	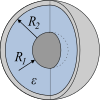$C=4\pi \varepsilon _{0}\varepsilon _{r}\left({\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\right)^{-1}$	$E(r)={\frac {Q}{4\pi r^{2}\varepsilon _{0}\varepsilon _{r}}}$
Kugel	$C=4\pi \varepsilon _{0}\varepsilon _{r}R_{1}$
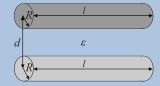
Parallele Zylinder (Lecher-Leitung)	$C=\pi \varepsilon _{0}\varepsilon _{r}{\frac {l}{\ln({\frac {d}{R}})}}$

In den obigen Formeln bezeichnet A die Elektrodenfläche, d deren Abstand voneinander, l deren Länge, $R_{1}$ sowie $R_{2}$ deren Radien. In der Schematischen Darstellung sind die Elektroden hellgrau bzw. dunkelgrau und das Dielektrikum blau gefärbt.

Plattenkondensatoren erlauben in einer modifizierten Ausführung sehr hohe Kapazitäten pro Volumen: Indem man die jeweils mit einem Potential verbundenen Elektroden abwechselnd aufeinander stapelt werden die Einzelkapazitäten parallel geschaltet, sie addieren sich. Die Abbildung des Keramik-Vielschichtkondensators verdeutlicht dies. Sind die Platten als Metallfolie oder -film ausgeführt und durch einem geeigneten Isolator voneinander getrennt wie z. B. bei einem Kunststoff-Folienkondensator, können sie auch aufgewickelt werden.

Zylinderkondensatoren werden meist nur bei speziellen Anwendungen eingesetzt, beispielsweise als Vakuum- oder Durchführungskondensator. Die für die Bauform angegebene Gleichung ist aber auch hilfreich, um den Kapazitätsbelag einer Koaxialleitung zu bestimmen.

Bei Kugelkondensatoren ist insbesondere der Spezialfall, $R_{2}\to \infty$ von Bedeutung, die Kapazität einer freistehenden Kugel. Hier wird die Gegenelektrode durch die Umgebung gebildet, sie liegt deshalb für Gewöhnlich auf Erdpotenzial. Die Kapazitäten dieser Bauform sind sehr gering. Beispielsweise hat eine Kugel mit 30 cm Durchmesser, wie sie in Van-de-Graaff-Generator zur Ladungsspeicherung oder in Tesla-Spulen zur Bildung eines LC-Schwingkreises eingesetzt werden, eine Kapazität von 30 pF. Da auf der Kugeloberfläche das elektrische Feld sehr homogen ist, können diese jedoch auf mehrere Millionen Volt aufgeladen werden, bevor es zu einer Funkenentladung kommt.

Kondensatorarten und Kondensatorbezeichnungen

Aufgrund der sehr langen Historie von Kondensatoren haben sich eine Vielzahl von Namen für die unterschiedlichen Kondensatorfamilien, -Bauformen und -Applikationen ergeben. Die Namen sind teilweise irreführend wie z. B. „Chipkondensator“ oder mehreren Technologien zuzuordnen, z. B. beim Begriff „Wickelkondensator“. Sinnvoll ist es deshalb, die vielen verschiedenen Kondensatorfamilien nach ihrer Herstell-Technologie zu ordnen. So geschieht es auch in den international gültigen Normen in der Gruppe der IEC 60 384-xxx Normen.

In diesem Sinne werden die Kondensatoren, die heute in der Elektrik und der modernen Elektronik Verwendung finden, zunächst in Festkondensatoren und veränderbare Kondensatoren (variable Kondensatoren) unterteilt.

Gliederung der Kondensatoren in die Hauptgruppen Veränderbare Kondensatoren und Festkondensatoren sowie die Haupt-Kondensatorarten unter den Festkondensatoren

Zu den Festkondensatoren, den Kondensatoren, die einen festen Kapazitätswert aufweisen, gehören die Kondensatortechnologien:

Glimmer-Kondensatoren
Keramik-Kondensatoren,
Metall-Papier-Kondensatoren
Kunststoff-Folienkondensatoren
Elektrolytkondensatoren,
Doppelschicht-Kondensatoren
Silicium-Kondensatoren (neuer)

Zu den veränderbaren Kondensatoren gehören

Trimmer-
Drehkondensatoren.

Neben den o. g. Kondensatorbezeichnungen, der sich zumindest bei den Festkondensatoren auf die jeweilige Herstell-Technologie bezieht, gibt es eine Reihe von nicht genormter Kondensatorbezeichnungen, die von der jeweiligen Bauform stammen bzw. die sich auf die Applikation des jeweiligen Kondensators beziehen.

Bauformbezogene Kondensatorbezeichnungen sind u. a.

Chipkondensator
Becherkondensator
Wickelkondensator
Durchführungskondensator

Applikationsbezogene Kondensatorbezeichnungen sind u. a.

Stützkondensator
Siebkondensator
Bedämpfungskondensator
Snubber-Kondensator
Motor-Start- und Motor-Betriebskondensator
Entstörkondensator
Gleich- bzw. Wechselspannungskondensator
Ballast-Kondensator

Die Liste der Bauform- und Applikationsbezogenen Kondensatorbezeichnungen soll hier nicht vollständig wiedergegeben werden, weil es auch teilweise recht kuriose Bezeichnungen wie den „Abklatschkondensator“ (Fa. Jahre) gibt. Es soll lediglich darauf hingewiesen werden, dass Begriffe unter den beiden letztgenannten Kondensator-Bezeichnungen nicht eindeutig einer Kondensator-Technologie zuzuordnen sind.

Festkondensatoren

Festkondensatoren besitzen einen festen Kapazitätswert. Je nach Kondensatortechnologie beginnt dieser Wert bei:

Kondensatortechnologie	Kapazitätsbereich
Silicium-, Glimmer - und Keramikkondensatoren	Picofarad pF (1 pF=10^-12 F)
Kunststofffolien-Kondensatoren	Nanofarad nF (1 nF=10^-9 F)
Elektrolytkondensatoren	Mikrofarad uF (1 uF= 10^-6 F)
Doppelschichtkondensatoren	0,1 Farad und größer

Aufsteigend nach dem Kapazitätsbereich unterscheiden sich die einzelnen Kondensatortechnologien durch folgende Besonderheiten:

Siliciumkondensator

Siliciumkondensatoren gibt es in drei unterschiedlichen Ausführungsformen. - Als Einschichtkondensatoren (single layer) mit Siliciumoxid als keramik-ähnliches Material des Dielektrikums und mit aufgedampften metallischen Elektroden - Als Vielschichtkondensatoren mit ähnlichem Aufbau wie die MLCC-Keramikkondensatoren, jedoch mit Siliciumoxid als Dielektrikum - Als Schichtfolge von Silicium, Siliciumoxid und Aluminium die in einem epitakischen Verfahren ähnlich der integrierten MOS-Schaltungen hergestellt wird und als Kondensator in SMD-Bauform angeboten wird. Siliziumkondensatoren haben bis in den GHz-Bereich gute und stabile elektrische Eigenschaften. Ebenfalls „Siliciumkondensator“ genannt wird die kapazitive Speicherzelle in der Halbleitertechnik auf der Basis von Siliciumoxid oder Siliciumnitrid als Dielektrikum in dynamischen RAM’s (DRAM). Hier wird der Kondensator als Ladungsspeicher benutzt, wobei die Quantität der gespeicherten Ladung pro Zelle einer Information (Bit) entspricht.

Glimmerkondensator

Glimmer ist ein natürlich vorkommendes Mineral mit hoher Spannungsfestigkeit und mit Schichtstruktur. Es bestellt aus Kalium-Aluminium-Silikaten mit chemisch gebundenem Kristallwasser und ist spaltbar in dünne Blättchen bis hinab zu etwa 0,02 mm Dicke. Glimmer wurde schon recht frühzeitig in der Elektronik als Dielektrikum von Kondensatoren verwendet und hat auch heute noch, vor allem in den USA, als MYCA-Capacitor eine gewisse Bedeutung. Eingesetzt werden Glimmerkondensatoren wegen des niedrigen, nahezu frequenzunabhängigen Verlustfaktors und der hohen Spannungsfestigkeit in der Sendertechnik als Hochfrequenzkondensator und wegen der großen zeitlichen Kapazitätskonstanz in Meßnormalen und in Filter- und Schwingkreisanwendungen für hohe Anforderungen.

Keramikkondensator

Siehe Hauptartikel: Keramikkondensator

Keramikvielschicht- Chipkondensatoren unterschiedlicher Größe zwischen Keramik-Scheibenkondensatoren

Keramikkondensatoren haben keramische Dielektrika mit hoher Spannungsfestigkeit bei verschieden hoher Dielektrizitätskonstante (Permittivität). Sie bilden eine große Gruppe von Kondensatoren im unteren Kapazitätsbereich (0,5 pF bis zu 100 µF oder mehr). Die verwendeten Keramikarten gehören einerseits zu den paraelektrischen Materialien mit feldstärkeunabhängiger relativer Dielektrizitätskonstante, beispielsweise Titandioxid (TiO₂), andererseits zu den ferroelektrischen Materialien mit feldstärkeabhängiger relativer Dielektrizitätskonstante, wie z. B. Bariumtitanat (BaTiO₃). Keramikkondensatoren werden aus feingemahlenen Granulaten durch Sinterung im Temperaturbereich zwischen 1200 und 1400 °C hergestellt. Durch geeignete Zusatzstoffe Aluminium-Silikate, Magnesium-Silikate. Aluminiumoxide) kann die relative Dielektrizitätskonstante ε_r eines Keramikkondensators zwischen 6 und 14.000 liegen.

Keramikkondensatoren für elektronische Geräte werden entsprechend ihrer Eigenschaften in Anwendungsklassen eingeteilt.

Klasse I: (NP0) Kondensatoren mit definiertem Temperaturkoeffizienten.; Eigenschaften: Annähernd lineare Abhängigkeit des Kapazitätswertes von der Temperatur mit entweder positivem oder negativem Temperaturkoeffizenten und niedrigen frequenzabhängigen Verlusten.; Anwendungen: Schwingkreise. Filterschaltungen, Temperaturkompensation, Kopplung und Siebung in HF-Kreisen.

Klasse 2: (X7R, YV5) Kondensatoren mit hoher Dielektrizitätskonstante.; Eigenschaften: Größere Kapazitätswerte bei gleichen Abmessungen gegenüber Klasse-1-Kondensatoren, nichtlineare Abhängigkeit der Kapazität von der Temperatur und der Spannung. Alterungserscheinungen des Kapazitätswertes, höhere frequenzabhängige Verluste.; Anwendungen: Kopplung, Entkopplung. Funkentstörung. Siebung.

Klasse 3: Sperrschichtkondensatoren; Eigenschaften: Höchste spezifische Kapazität im Bereich der Keramikkondensatoren, starke nichtlineare Abhängigkeit der Kapazität von der Temperatur und von der Spannung, höhere frequenzabhängige Verluste, kleine Nennspannungen.; Anwendungen: Kopplung. Entkopplung. Funkentstörung. Siebung.

Größte Bedeutung innerhalb der Keramikkondenstoren hat die Bauform für die Oberflächenmontage, die Keramikvielschicht-Chipkondensatoren (MLCC = Multilayer Ceramic Chip Capacitors) als Siebkondensatoren in Digitalschaltungen erlangt. Keramik-Scheibenkondensatoren oder spezielle Keramikkondensatoren wie z. B. Keramik-Hochspannungskondensatoren, Keramik-Funkentstörkondensatoren oder Keramik-Durchführungskondensatoren sind wegen ihre leichten Formbarkeit in spezielle Bauformen jedoch weiterhin auf dem Markt zu finden.

Aufbau eines Keramik-Vielschichtkondensators (MLCC): Das Dielektrikum ist blau, die mit einem Potentialanschluss verbundenen Elektroden sind dunkelgrau, mit dem anderen hellgrau dargestellt.

Folienkondensatoren

In der Industrie kommen überwiegend die folgenden Folien als Dielektrika in Folienkondensatoren zur Anwendung, in Klammern, die chemische Kurzbezeichnung der Folie:

Papier (P), MP-Kondensator
Polyethyleneterephthalate,Polyester (PET), KT- MKT-Kondensator
Polyethylennaphtalat (PEN), KN-, MKN-Kondensator
Polyphenylensulfid (PPS), KI-, MKI-Kondensator
Polypropylen (PP), KP-, MKP-Kondensator

Es können auch Mischformen mehrere Arten auftreten.

Metall-Papierkondensator (MP-Kondensator)

Der Metall-Papierkondensator ist die älteste industriell gefertigte Art Ausführung unter den Kondensatoren. Er besteht aus je zwei Lagen ölgetränktem Papier (Isolierpapier) und daraufliegenden Metallfolien, die die zu einem Wickel aufgewickelt werden, in einen Becher gepackt und verschlossen werden. Man verwendet Metall-Papierkondensatoren auch heute noch in Anlagen der Leistungselektronik.

Metall-Papierkondensatoren werden fast nur noch in elektrischen Anlagen und Geräten als Leistungskondensatoren verwendet.

Kunststoff-Folienkondensator

Kunststoff-Folienkondensatoren sind Kondensatoren mit hochwertigen Isolierstoffen aus dem Bereich der organischen Chemie in Form von Kunststoffolien als Dielektrika. Sie sind meist als Wickelkondensatoren hergestellt, wobei die Kunststofffolie das Dielektrikum des Kondensators bildet. Man unterscheidet zwei Arten von Kunststoff-Folienkondensatoren:

Kunststoff-Folienkondensatoren mit Metallfolien als Elektroden.
Kunststoff-Folienkondensatoren, deren Folien mit einem Metall, meist Aluminium, bedampft ist und wo die bedampfte Metallschicht die Elektrode bildet.

Die gewickelten bzw. gestapelten Kondensatorzellen werden mit einem nach Dr. Schoop genannten Verfahren stirnseitig kontaktiert (schoopiert) und je nach Bauform zu liegenden oder zu stehenden Kondensatoren weiterverarbeitet.

Metallisierte Kunststoff-Folienkondensatoren sind selbstheilend, d. h., bei einem Kurzschluß durch das Dielektrikum verdampfen infolge hoher Lichtbogentemperatur die aufgedampften Metallbelege in der Umgebung der Durchschlagsstelle. Die Kurzschlußursache wird förmlich weggebrannt. Diese Eigenschaft gestattet ein einlagiges Wickeln der metallisierten Folien ohne zusätzlichen Schutz gegen Fehlstellen. Außerdem sind diese Kondensatoren kleiner als Kunststoff-Folienkondensatoren mit Metallbelägen.

In der Industrie kommen überwiegend die folgenden Folien als Dielektrika in Folienkondensatoren zur Anwendung, in Klammern, die chemische Kurzbezeichnung der Folie:

Polyethyleneterephthalate, Polyester (PET), KT- MKT-Kondensator Anwendungen: Kopplung, Entkopplung. Funkentstörung. Siebung.

Polyethylennaphtalat (PEN), MKN-Kondensator Anwendungen: Kopplung, Entkopplung. Funkentstörung. Siebung.

Polyphenylensulfid (PPS), MKI-Kondensator Anwendungen: Schwingkreise. Filterschaltungen, Kopplung und Siebung in HF-Kreisen.

Polypropylen (PP), KP-, MKP-Kondensator Anwendungen: Schwingkreise. Filterschaltungen, Kopplung und Siebung in HF-Kreisen, Schaltungen mit hoher Impuls-Strombelastung (Snubber), Funkentstörung, Blindstromkompensation Es können auch Mischformen mehrerer Dielektrika auftreten.

Kunststoff-Folienkondensatoren werden in vielen Bereichen der Elektronik eingesetzt. Die elektrischen Eigenschaften, das Temperatur- und Frequenzverhalten von Folienkondensatoren werden dabei von der Foliensorte bestimmt, die das Dielektrikum des Kondensators bildet. Hauptvorteile von Kunststoff-Folienkondensatoren sind die selbstheilenden Eigenschaften metallisierter Folien, die geringen Verlustfaktoren und der nahezu lineare Kapazitätsverlauf im mittleren Frequenzbereich von 10 kHz bis 10 MHz der PP und der PPS-Folie und die hohe Strombelastbarkeit der PP-Folie.

typische Bauform von Kunststoff-Folienkondensator

Elektrolytkondensator

Siehe Hauptartikel: Elektrolytkondensator

Elektrolytkondensatoren sind Kondensatoren, in denen auf einem Ventilmetall durch Elektrolyse (anodische Oxidation, Formierung) eine nichtleitende Isolierschicht erzeugt wird, die das Dielektrikum des Kondensators bildet. Die Kathode (Gegenelektrode) kann aus einem flüssigen oder pasteusen Elektrolyten (lonenleiter) oder einem festen Elektrolyten (Elektronenleiter) bestehen. Die Stromzuführung zum Elektrolyten erfolgt über Folien gleichen Metalls wie das der Anode oder über eine geeignete Kontaktierung des Elektrolyten.

Als technisch praktikable Ventilmetalle zum Aufbau von Elektrolytkondensatoren, haben sich

Aluminium mit Al₂O₃ (Aluminiumoxid) als Dielektrikum (Al-Elektrolytkondensator),
Tantal mit Ta₂O₃ (Tantal-Pentoxid) als Dielektrikum (Tantal-Elektrolytkondensator) und neuerdings
Niob mit Ni₂O₃ (Niob-Oxid) als Dielektrikum (Niob-Elektrolytkondensator)

durchgesetzt. Elektrolytkondensatoren mit Titan oder Zirkon als Anode sind bisher aus dem Entwicklungsstadium nicht hinausgekommen.

Elektrolytkondensatoren sind grundsätzlich gepolte Bauelemente. Ein Einsatz in Falschpolrichtung zerstört das Dielektrikum und zerstört somit den Kondensator. Die Zerstörung kann katastrophale Folgen (Explosion, Brand) nach sich ziehen. (Betrieb von Elektolytkondensatoren, VDE 0560).

Durch gegenpolige Serienschaltung zweier Anodenfolien in einem Kondensatorgehäuse können jedoch für spezielle Anwendungen (z. B.Tonfrequenzweichen) auch Bipolar-Elektrolytkondensatoren für Wechselspannungsbetrieb hergestellt werden.

Hauptvorteil von Elektrolytkondensatoren ist die sehr hohe spezifische Kapazität. Das ist eine hohe elektrische Speicherfähigkeit bei kleinem Bauvolumen. Sie resultiert aus der Permittivität ε des Dielektrikums, dem äußerst geringen Elektrodenabstand im Kondensator, der Oxidschicht auf der Anode und der Oberflächenstruktur der Anode. Die Spannungsfestigkeit des jeweiligen Kondensators wird durch eine gezielt hergestellte angepasste Dicke des Dielektrikums bewirkt. Eine aufgerauhte Oberflächenstruktur der Anode wiederum vergrößert die Oberfläche der Elektrode und erhöht somit die Kapazität des Kondensators.

Aluminium-Elektrolytkondensatoren mit flüssigem Elektrolyten

Aluminium-Elektrolytkondensatoren werden als Wickel hergestellt. Er besteht aus der aufgerauhten und schon mit der Oxidschicht versehenen Anodenfolie, einer Papierfolie als Abstandshalter und Speicher des Elektrolyten, einen zweiten Aluminiumfolie als Stromzuführung zum Elektrolyten und einer weiteren Papierfolie. Der Wickel wird mit dem Elektrolyten getränkt, mit einem Becher versehen und fest verschlossen.

Tantal-Elektrolytkondensatoren mit Sinterkörper und festem Elektrolyten Tantal-Elektrolytkondensatoren werden überwiegend aus gesinterten Tantalkügelchen hergestellt. Der Sinterblock behält bei der Sinterung seine offenporige Struktur und hat somit eine sehr hohe Oberfläche. In einem Elektrolysebad wird diese Oberfläche dann oxidiert. In einem speziellen Verfahren wird dann der Elektrolyt in die Poren des Blockes hineingebracht. Anschließend wird der Elektrolyt mit dem negativen Anschluss des Kondensators verbunden. Tantal-Elektrolytkondensatoren mit festem Elektrolyten kommen wegen ihrer sehr hohen Kapazität bei kleinsten Abmessungen insbesondere als sog. Chip-Kondensatoren für die Oberflächenmontage in allen Bereichen der Elektronik zum Einsatz.

Oberflächenmontierbare Tantal-Elektrolytkondensatoren

Doppelschichtkondenstoren

Die neue Familie der Superkondensatoren umfasst Doppelschicht-, Pseudo- und Hybridkondensatoren

Datei:Maxwell MC and BC ultracapacitor cells and modules.jpg

Doppelschichtkondensatoren bis 3000 F

Doppelschichtkondensatoren (englisch electrochemical double layer capacitor, EDLC) sind gemeinsam mit den Pseudokondensatoren und den Hybridkondensatoren ein Teil einer neuen Familie von Kondensatoren, die unter dem Oberbegriff "Superkondensatoren" zusammengefasst werden. Sie haben die größte Energiedichte aller Kondensatoren. Ihre hohe Kapazität, bezogen auf das Bauvolumen, basiert einerseits auf dem physikalischen Phänomen äußerst dünner elektrisch isolierender Helmholtz-Doppelschichten an den Oberflächen spezieller großflächiger Elektrodenmaterialen, in denen die elektrische Energie statisch als Doppelschichtkapazität in elektrischen Feldern gespeichert wird. Andererseits stammt sehr oft ein weiterer Anteil an der hohen Kapazität aus einer sogenannten Pseudokapazität, einer innerhalb enger Grenzen spannungsabhängigen elektrochemischen bzw. faradayschen Speicherung elektrischer Energie, die mit in einer Redoxreaktion und mit einem Ladungsaustausch an den Elektroden verbunden ist, wobei allerdings im Gegensatz zu Akkumulatoren an den Elektroden keine chemische Stoffänderung eintritt. Die Pseudokapazität kann durch spezielle Elektroden bei gleichem Bauvolumen einen erheblich größeren Wert als die Doppelschichtkapazität erreichen.

Der jeweilige Anteil der Doppelschichtkapazität und der Pseudokapazität an der Gesamtkapazität des Kondensators wird in sehr grober Verallgemeinerung durch die Namensgebung solcher Kondensatoren in industriellen Veröffentlichungen erkennbar.

Doppelschichtkondensatoren speichern die elektrische Energie überwiegend in Helmholtz-Doppelschichten ihrer Elektroden und haben keinen oder nur einen nur geringen Anteil (bis etwa 10 %) von Pseudokapazität an der Gesamtkapazität
Superkondensatoren und Ultrakondensatoren weisen aufgrund ihrer Elektrodenkonstruktion mit hoher Redoxkapazität meist einen zum Teil deutlich höheren Anteil an der Pseudokapazität auf, wodurch sie eine höhere spezifische Kapazität als Doppelschichtkondensatoren haben.
Hybridkondensatoren sind Superkondensatoren mit einer statischen Doppelschichtelektrode und einer elektrochemischen Redox-Elektrode, wobei die Redox-Elektrode einer Elektrode aus einer anderen Technologie, beispielsweise aus dem Bereich der Akkumulatoren oder der Elektrolytkondensatoren, ähneln kann.

Allen Doppelschichtkondensatoren, Pseudokondensatoren, Superkondensatoren, Ultrakondensatoren und Hybridkondensatoren gemeinsam ist, dass der Elektrolyt die leitfähige Verbindung zwischen zwei Elektroden bildet. Das unterscheidet sie von Elektrolytkondensatoren, bei denen der Elektrolyt die Kathode bildet, der Elektrolyt also eine Elektrode ist, die mit dem negativen Anschluss des Kondensators verbunden ist.

Doppelschichtkondensatoren sind, wie auch Elektrolytkondensatoren, gepolte Bauelemente. die nur mit korrekter Polarität betrieben werden dürfen.

Doppelschichtkondensatoren, Superkondensatoren, Ultrakondensatoren und Hybridkondensatoren, zu denen die Lithium-Ionen-Kondensatoren zählen, werden unter vielen unterschiedlichen Handelsnamen wie z. B. BestCap, BoostCap, DLCAP, EVerCAP, DynaCap, Faradcap, GreenCap, Goldcap, SuperCap, PAS, PowerStor oder Ultracapacitor sowie die Lithium-Ionen-Kondensatoren unter Premlis, EneCapTen, Ultimo oder LIC angeboten.

Bauformen von Festkondensatoren

Bauformen von Kondensatoren für die Oberflächenmontage, die Leiterplattenmontage und für die Schraub-Befestigung

Festkondensatoren weisen mehrere unterschiedliche Bauformen auf. Dieses resultiert einerseits aus den Anforderungen der Anwender nach einer bestimmten Montagemöglichkeit und andererseits aus den elektrischen Randbedingungen, die aus den Schaltungsanforderungen herrühren:

SMD-Bauform für die Oberflächenmontage auf Leiterplatten oder Substraten
Bauform mit axialen Drahtanschlüssen für eine liegende Einbauweise auf Leiterplatten
Bauform mit radialen (einseitig herausgeführten) Draht- oder Stiftanschlüssen für eine stehende Einbauweise auf Leiterplatten
Bauform mit Flachbandanschlüssen für hohe Impulsbelastbarkeit
Bauform mit Schraubanschlüssen für hohe Strombelastbarkeit
Bauform mit Lötfahnen

Diese Bauformen kombiniert mit den spezifischen Fertigungsmerkmalen der einzelnen Technologien führt zu einer Vielzahl von unterschiedlichen Ausführungsformen und Baugrößen und somit zu einer schier unübersichtlichen Bauformenvielfalt im Bereich der Kondensatoren.

Kondensatoren mit einstellbarer Kapazität

Einstellbare oder Variable Kondensatoren sind elektrische Kondensatoren, deren Kapazität in definierten Grenzen mechanisch stufenlos von Hand oder mit einer geregelten Motorsteuerung einstellbar ist. Sie werden unterschieden in Drehkondensatoren, kurz Drehkos genannt und in Trimmkondensatoren, auch Trimmer genannt. Neben den mechanisch einstellbaren Dreh- und Trimmkondensatoren gibt es Bauelemente mit elektrisch veränderbaren kapazitiven Eigenschaften, wie Kapazitätsdioden (Varicaps) und weitere, die als Sensoren (Winkelgeber, Näherungsschalter, Touchscreen) verwendet werden.

Drehkondensatoren

Mechanisch einstellbare Drehkondensatoren, auch Regel- oder Korrektionskondensatoren genannt, sind für häufige und wiederholende Betätigungen ausgelegt z. B. für die manuelle Sendereinstellung in Rundfunkgeräten. Die Kapazitätsänderung bei Drehkondensatoren erfolgt durch Änderung der kapazitiv wirksamen Fläche, meist indem ein Elektrodenpaket, der Rotor, mit einer Welle mechanisch kammartig in ein zweites, feststehende Elektrodenpaket, den Stator, hineingedreht werden kann. Als Dielektrikum wird Luft, eine Kunststofffolie, ein Vakuum oder ein Schutzgas verwendet.

Drehkondensatoren für Kleinsignalanwendungen (Senderwahl und Schwingkreisabstimmung in Rundfunk- und Fernsehempfängern) sind heute weitgehend entweder durch Kapazitätsdioden abgelöst, deren Sperrschichtkapazität durch eine überlagerte Gleichspannung gesteuert wird oder sind durch VCO-gesteuerte PLL-Schaltungen ersetzt worden. Allerdings sind für Leistungsanwendungen mechanisch einstellbare Vakuum- und Schutzgaskondensatoren in Hochfrequenzsendern auch heutzutage (2009) durchaus noch im Einsatz, wobei die mechanische Betätigung zur Konstanthaltung einer Senderfrequenz meist über eine Motor-gesteuerte automatische Regelung erfolgt.

Vakuum- und Schutzgas-Drehkondensatoren

Vakuum- und Schutzgas-Drehkondensatoren ähneln konstruktiv den unter Variable Kondensatoren beschriebenen „Tauchtrimmern. Umhüllt sind diese einstellbaren Kondensatoren in einem hermetisch abdichtenden Glas- oder Keramikgehäuse.

Als Dielektrikum wird bei den variablen Vakuumkondensatoren ein Vakuum mit einer sehr hohen Spannungsfestigkeit, die im Mittel mit etwa 40 kV/mm angegeben wird. Bei den variablen Schutzgas-Drehkondensatoren wird Schwefelhexafluorid SF₆ als Isoliergas eingesetzt. Es besitzt ebenfalls eine hohe Durchschlagsfestigkeit und darüber hinaus auch noch eine hohe Dielektrizitätszahl. Eingesetzt werden beide Arten dieser variablen Kondensatoren in Hochfrequenz-Sendern. Die größten und leistungsstärksten Kondensatoren dieser Art besitzen eine Vorrichtung zur Wasserkühlung. ^[2]

Trimmer

Trimmerkondensatoren (kurz Trimmer) sind ebenfalls stufenlos einstellbare Variable Kondensatoren, deren Kapazität in definierten Grenzen mechanisch einstellbar sind. Sie sind im Gegensatz zu Drehkondensatoren nicht für häufige Betätigung ausgelegt und werden nur zur Erstinbetriebnahme und ggf. nach Reparaturen betätigt, um einen schaltungstechnisch bedingten Kapazitätsausgleich eines Filters oder eines Schwingkreises in z. B. Rundfunk- oder Fernsehgeräten herbeizuführen (Abgleich). Die Kapazitätsänderung bei einem Trimmer erfolgt durch Veränderung der kapazitiv wirksamen Fläche des Kondensators. Trimmerkondensatoren können oft nur mit einem isolierenden (HF-neutralen) Werkzeug, meist einem Plastik-Schraubendreher, eingestellt werden. Als Dielektrikum in Trimmkondensatoren wird Luft (Luftplatten- und Tauchtrimmer), Kunststofffolie, (Folientrimmer) und Keramik (Draht-, Rohr-, Scheiben- und SMD-Trimmer) verwendet. Trimmer für Kleinsignalanwendungen (Senderwahl und Schwingkreisabstimmung in Rundfunk- und Fernsehempfängern) sind heute weitgehend entweder durch Kapazitätsdioden abgelöst, deren Sperrschichtkapazität durch eine überlagerte Gleichspannung gesteuert wird oder sind durch VCO-gesteuerte PLL-Schaltungen ersetzt worden.

Die moderneren Bauformen von Trimmerkondensatoren sind oberflächenmontierbar. Die Keramik-SMD-Trimmer haben eine keramische Schichtung mit einer halbkreisförmigen Metallisierung in der Stator-Grundplatte und eine Rotorelektrode, die drehbar montiert ist. SMD-Trimmer für Lötwellenlötung sind, um Verschmutzungen während des Lötprozesses zu verhindern, gekapselt. Trimmer für Reflow-Lötung können etwas einfacher geschützt sein. ^[3]

Bei der zweiten Trimmer-SMD-Bauform, den SMD-Abgleichkondensatoren, gibt es keine mechanisch bewegliche Einstellmöglichkeit mehr. Bei ihnen wird der Kapazitätswert durch gezieltes Wegbrennen von Flächenanteilen einer oben liegenden offen zugänglichen Elektrode mit Hilfe eines Laserstrahles eingestellt. Damit lässt sich gezielt gewünschter Kapazitätswert mit einer sehr großen Genauigkeit einstellen. ^[4]

Normung

Im Laufe der letzten Jahre fand auch auf dem Gebiet der Normung von Kondensatoren ein großer Umbruch statt. Aus den deutschen Einzelnormen (DIN…) wurden zunächst im Rahmen der europäischen Einigung europäische Normen (EN…) erstellt. Da aber grade auf dem Gebiet der Kondensatoren die Anzahl der europäischen Hersteller rapide abgenommen hat, diese bis auf wenige Ausnahmen auf dem Weltmarkt keine bedeutende Rolle mehr spielen, versucht man jetzt zu international gültigen „Weltnormen“ (IEC…) zu kommen. Dieser Prozess findet zur Zeit statt. Wird eine solche IEC-Norm, die Normenbehörden schreiben anstatt „Norm“ das Wort „Spezifikation“, ins deutsche übersetzt, dann trägt eine solche Norm den Titel: „DIN IEC…“

In der folgenden Tabelle sind die zur Zeit spezifizierten IEC-Normen zusammengefasst.

Übersicht über die deutschen Normen für industriell gefertigte Kondensatoren

Kennzeichnungen

Die Kennzeichnung von Kondensatoren kennt mittels Farbcodierung, wie z. B. bei Widerständen, wird heutzutage nicht mehr verwendet. Sofern der Platz dazu ausreicht, sollten die Kondensatoren durch entsprechende Aufdrucke gekennzeichnet sein mit:

Polarität (bei Elektrolytkondensatoren)
Nennkapazität
Toleranz
Nennspannung
Nenntemperaturbereich
Herstelldatum
Hersteller
Baureihenbezeichnung

Kapazität, Toleranz, und Herstelldatum können nach DIN EN 60062 mit Kurzkennzeichen gekennzeichnet werden. Für Kunstoff-Folienkondensatoren können Kennbuchstaben für die Art des Dielektrikums verwendet werden.

Beispiele einer Kurz-Kennzeichnung der Nennkapazität:

p47 = 0,47 pF (Picofarad)
4n7 = 4,7 nF (Nanofarad)
47µ = 47 µF (Mikrofarad)

Die Problematik bei der Kennzeichnung liegt in der gegebenen Baugröße des Kondensators. Auf einem MLCC-Chip in der Größe 0,2x0,4 mm passt keine Kennzeichnung mehr drauf. Darüber hinaus gibt es gerade bei Kondensatoren eine Reihe von Herstellern, die sich an keiner Norm orientieren.

Elektrische Kennwerte

Die allgemeinen elektrischen Kennwerte von Kondensatoren werden in der technischen Anwendung im internationalen Bereich harmonisiert durch die Rahmenspezifikation IEC 60384-1, die in Deutschland als DIN EN 60384-1 im Februar 2002 erschienen ist. Kennwerte heißen sie deswegen, weil die Kondensatoren für die Herstellung und die Anwendung „benannt“ werden müssen. Die Kennwerte werden beschrieben durch ein idealisiertes Serien-Ersatzschaltbild eines Kondensators.

Serien-Ersatzschaltbild eines Kondensators

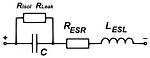
Hierin sind: Kapazität C die ideale Kapazität des Kondensators, der Isolationswiderstand Risol , der den Isolationswiderstand des Dielektrikums bzw. der Widerstand Rleak, der den Reststrom bei Elektrolytkondensatoren repräsentiert, der RESR , der die ohmschen Verluste und die Induktivität LESL , die die Induktivität des Bauelementes zusammengefasst. Die ohmschen Verluste werden allgemein nur „ESR“ (Eqivalent Series Resistance, Äqivalenter Serienwiderstand) und die Induktivität nur „ESL“ (Equivalent Series Inductivity L, Äquivalente Serieninduktivität L) genannt. Die wichtigsten elektrischen Kennwerte für Kondensatoren sind:

Kapazität C

Die Kapazität eines Kondensators ist normalerweise frequenzabhängig. Der Nennwert der Kapazität wird gemessen mit der Frequenz von 100/120 Hz bei Elkos bzw. 1 kHz bei anderen Kondensatoren. Da die Kapazität bei Keramikkondensatoren auch eine Spannungsabhängigkeit besitzt, wird die Messspannung festgelegt mit 0,5 V bei Elkos und 3 % der Nennspannung bei anderen Kondensatoren. Die Kapazität eines Kondensators ist auch temperaturabhängig.

Nennkapazität CR

Die Nennkapazität ist der Kapazitätswert, für den der Kondensator ausgelegt ist und der üblicherweise auf ihn angegeben ist. Die bevorzugten Nennwerte der Kapazität sind der E3-Reihe in IEC 63, sowie deren dezimale Vielfachen zu entnehmen. Werden andere Werte benötigt, müssen diese vorzugsweise aus der E6 oder E12-Reihe ausgewählt werden. Kapazitätstoleranz Die Kapazitätstoleranz gibt an, wie weit der Anlieferwert der Kapazität von der Nennkapazität abweichen darf.

Nennspannung UR

Die Nennspannung ist die höchste Gleichspannung oder Spitzenwert einer Impulsspannung, die im Dauerbetrieb innerhalb des Nenntemperaturbereiches anliegen darf. Vorzugswerte für die Nennspannung sind aus den Reihen R5 (und deren dezimale Vielfache) und R10 der ISO 3 zu wählen. Weitere Spannungsbegriffe bei Kondensatoren sind: Kategoriespannung UC ,Temperaturabhängig geminderte Spannung, Umpolspannung (nur bei gepolten Kondensatoren) Urev , Spitzenspannung US , Überlagerte Nenn-Wechselspannung, Transientenspannung. Die wesentlichen Kennwerte von Kondensatoren sind Kapazität und Spannungsfestigkeit. Beide Größen werden durch die verwendeten Materialien und deren Eigenschaften bestimmt.

Isolationswiderstand

Ein geladener Kondensator entlädt sich mit der Zeit über seinen eigenen Isolationswiderstand Ris.

Die Selbstentladezeitkonstante τ isol ist ein Maß für die Qualität des Dielektrikums in Hinsicht auf seine Isolationsfähigkeit. Sie ist im Allgemeinen größer, je hochwertiger ein Kondensator ist. Üblich sind Werte zwischen 1000 s bis zu 10.000 s (mit s = Einheitenzeichen für Sekunden). Diese Zeitkonstanten sind immer dann relevant, wenn Kondensatoren als zeitbestimmendes Glied (z.B. in Zeitrelais) oder zur Speicherung eines Spannungswertes eingesetzt werden. Bei Elektrolytkondensatoren wird nicht der Isolationswiderstand spezifiziert sondern der Reststrom.

Reststrom, Leckstrom

Der Reststrom eines Kondensators ist der Gleichstrom, der durch den Elektrolytkondensator fließt, wenn eine Gleichspannung an die Anschlüssen des Kondensators gelegt wird. Der Reststrom ist kapazitäts-, spannungs-, zeit- und temperaturabhängig. Bei Aluminium-Elektrolytkondensatoren mit flüssigem Elektrolyten ist der Reststrom auch noch abhängig von der vorangehenden Temperaturbelastung durch Löten. Spezifiziert wird der Reststrom meist durch eine Multiplikation des Kapazitätswertes und der Nennspannung, zu dem noch ein Summand hinzugefügt wird. Zum Beispiel: IR = CN • UN + 0,4 (µA)

Bedingt durch Selbstheilungseffekte in Elektrolytkondensatoren wird der Reststrom normalerweise immer geringer, je länger der Kondenstor an Spannung liegt. Strombelastbarkeit von Kondensatoren

Überlagerter Wechselstrom Ir, Rippelstrom

Ein einer Gleichspannung überlagerter Wechselstrom bewirkt Lade- und Entladevorgänge im Kondensator. Dieser Wechselstrom fließt über den ESR und führt zu Verlusten, die den Kondensator von Innen heraus erwärmen. Die internen Wärmeverluste sind frequenzabhängig, sie werden an die Umwelt abgegeben. Dieses hängt von den Maßen und weiteren Bedingungen, wie z. B. Zwangskühlung ab. Bei Elektrolytkondensatoren dient als Maß für die zulässige Strombelastbarkeit der sog. Überlagerte Wechselstrom (Rippelstrom). Bei den anderen Festkondensatoren wird als Grenze der internen Verluste die Überlagerte Wechselspannung (Rippelspannung) spezifiziert.

Nachladeeffekt (dielektrische Absorbtion)

Waren Kondensatoren einmal geladen und werden sie dann vollständig entladen können sie anschließend ohne äußeren Einfluss eine Spannung aufbauen, die an den Anschlüssen gemessen werden kann. Dieser Nachladeeffekt ist als dielektrische Absorbtion oder als dielektrische Relaxation bekannt. Ein geladener Kondensator hat elektrische Raumladungen (elektrische Dipole) im Dielektrikum. Mit einer Entladung des Kondensators werden nicht alle Raumladungen gelöscht, einige Dipole verbleiben infolge einer Trägheit im geladenen Zustand. Diese Dipole entladen sich nach einiger Zeit spontan, dadurch bildet sich an nicht kurzgeschlossenen Anschlüssen des Kondensators dann im Verlauf des Raumladungsausgleiches eine steigende Spannung aus. Abhängig vom Kondensatortyp können solche Nachladungen bis zu 10 % der vorher angelegten Spannung erreichen. Das kann unter Umständen zu relativ hohen Spannungen (sogar einige -zig Volt) führen, die eine Gefährdung darstellen können: Es können dadurch Schäden an Halbleitern oder Funkenbildung beim Kurzschließen von Anschlüssen verursacht werden. Aber auch in Messschaltungen ist dieser Effekt eher unerwünscht, da er zu falschen Messergebnissen führt.

Kondensatortyp	Dielektrische Absorption
Kunststoff-Folienkondensatoren, Polyesterdielektrikum	0,2 bis 0,25 %,
Kunststoff-Folienkondensatoren, Polypropylendielektrikum	0,01 bis 0,05 %,
Keramikkondensatoren, X7R	0,6 bis 1 %,
Keramikkondensatoren, Z5U	2,0 bis 2,5 %,
Aluminium-Elektrolytkondensatoren	etwa 10 bis 15 %,

Anwendungen

Die 3 wichtigsten Kondensatorfamilien haben entsprechend ihrer speziellen Eigenschaften bestimmte Haupt-Anwendungen. Allerdings können und werden viele Applikationen sowohl mit der Einen als auch mit der anderen Kondensatorgruppe realisiert. Es gibt deshalb Überlappungsbereiche bei den Applikationen, bei denen der Wettbewerb der Technologien deutlich wird.

Die häufigsten Anwendungsgebiete von Kondensatoren oder von Bauelementen oder Strukturen, die das Kondensatorprinzip nutzen, lassen sich grob und etwas unscharf in drei Kategorien unterteilen: Als Kondensatoren: - Energie- oder Ladungsspeicher - Frequenzabhängiger Widerstand - Mischapplikation als Energiespeicher und Siebkondensator - Phasenschieber Weitere Bauelemente: - Sensoren, die Kondensatorprinzipien nutzen - Ladungsspeicher für Informationsspeicherung

Energie- oder Ladungsspeicher

Die elektrische Energie Joule J in Wattsekunden (Ws), die in einem Kondensator gespeichert werden kann, ist proportional zu dem Quadrat der anliegenden Spannung:

Charakteristisch für die Anwendung als Energie- oder Ladungsspeicher ist, dass der Kondensator hierfür eine Mindestkapazität besitzen muss, deren Wert aber prinzipiell überschritten werden kann und es sich um eine reine Gleichspannungsanwendung handelt. Die Anforderungen an Stabilität der elektrischen Kennwerte und an die ohmschen Verluste sind meist nicht sehr hoch. Als Beispiel hierfür dienen die Stütz- oder Bufferkondensatoren zur Stabilisierung der Versorgungsspannung für digitale Schaltungen. Parallel zur Versorgungsspannung geschaltet, liefern Kondensatoren kurzfristig die benötige Energie in Momenten hohen Strom- bzw. Leistungsbedarfs. Kondensatoren können zeitlich begrenzt eine hohe Leistung niederohmig bereitstellen. Auf eine hohe Spannung aufgeladen können sie dann Verbraucher mit hohem kurzzeitigem Leistungsbedarf antreiben. Beispiele hierfür sind die Blitzröhre, Hochspannungs-Kondensatorzündung bei Verbrennungsmotoren, Airbag-Zündschaltungen in der Kfz-Sicherheitselektronik und Zündkondensatoren, wie der exploding-bridgewire detonator in der Waffentechnik. Des Weiteren werden Verschaltungen von mehreren Kondensatoren zum Herauf-, Herabsetzen und zum Invertieren von Versorgungsspannungen genutzt. Hierbei werden Kondensatoren zyklisch auf einem Potential aufgeladen, mit einem anderen Potential verbunden und dort entladen. Gebräuchliche Schaltungen sind die Ladungspumpe und deren spezielle Ausführung als Hochspannungskaskade. Der zeitliche Verlauf der Kondensatorspannung wird zur Festlegung von Schaltzeiten genutzt, zum Beispiel bestimmt er die Schaltzeiten einer astabilen Kippstufe. Hierin wird ein Kondensator über eine Stromquelle geladen; seine Spannung nimmt proportional mit der verstrichenen Zeit zu. Sobald die Spannung einen bestimmten Wert überschreitet, erfolgt ein Zustandswechsel der Schaltung. Früher wurden so die Blinkerschaltungen in der KFZ-Elektronik realisiert. In ähnlicher Weise werden eine Reihe von Wandlerschaltungen realisiert: Integrator: Ein Kondensator kann als Integrator eingesetzt werden. Einzelne Stromimpulse sequenziell dem Kondensator zugeführt lassen die Spannung im Kondensator ansteigen bis eine Schaltschwelle erreicht ist. Pulsweitenmodulation: Diese Schaltung wandelt eine Eingangsspannung in ein Tastverhältnis um. Ein Kondensator wird zyklisch durch eine Stromquelle bis zu einer vorgegebenen Spannung geladen, dann schlagartig entladen. Der Vergleich von Eingangsspannung und dem sägezahnförmigen Spannungsverlauf am Kondensator liefert das Ausgangssignal. Slope-Wandler: Dieser Wandler gleicht dem Pulsweitenmodulator, arbeitet allerdings nicht zwingend zyklisch. Time-Voltage Converter: Hier wird die Stromquelle durch einen Eingangspuls gesteuert, die Spannung des Kondensators ist proportional der Pulsbreite. Der Ladungszustand eines Kondensators kann Information in analoger Form repräsentieren. Analoge Informationsspeicherung mittels eines Kondensator findet beispielsweise in einer Abtast-Halte-Schaltung statt: hier wird während der Abtastphase ein Kondensator mit einer Signalspannung verbunden, von welcher er während der Haltephase getrennt wird. Der Spannungswert steht dann der Weiterverarbeitung, typischerweise einer Analog-Digital-Wandlung, konstant zur Verfügung. Der Ladungszustand eines Kondensators kann auch Information in digitaler Form repräsentieren. Zur Speicherung von großen Informationsmengen können einige Milliarden Kondensatoren in einer integrierten Schaltung zusammengefasst werden. Beispiele hierfür sind dynamisches RAM, Eraseable Programmable Read Only Memory, Flash-Speicher und in ähnlicher Funktionsweise Ferroelectric Random Access Memory.

Kondensatoren in Leistungsanwendungen

Der kapazitive Blindwiderstand Xc bewirkt im Wechselstromkreis eine Phasenverschiebung des Stromes gegenüber der Spannung von 90 °C. Der Strom eilt der Spannung um 90 °C voraus. Damit kann die Phasenlage von Wechselströmen beeinflusst werden. In der Energietechnik können Kondensatoren dazu genutzt werden, die Phasenlage zwischen Strom und Spannung eines Wechselstromes zu ändern: Werden in Industrieanlagen große Elektromotoren betrieben, kommt es aufgrund deren Induktivität zu einem erheblichen Blindstrom. Dieser kann durch die „Phasenverschiebung“ des Kondensators kompensiert werden, der den „funktionalen Gegenpol“ der Induktivität bildet. Für diese Blindstromkompensation müssen Kondensator und Induktivität die gleiche Impedanz haben. Eine weitere Anwendung als Phasenschieber findet der Kondensator in einem Kondensatormotor, bei dem er zusammen mit einer Feldspule des Motors die Phasenlage des Wechselstrom verschiebt, wodurch letztendlich ein magnetisches Drehfeld erzeugt wird. Man unterscheidet hier zwischen Motor-Betriebskondensatoren, die ständig den Motorspulen parallel geschaltet sind und den Motor-Startkondensatoren, die nur während des Anlaufens des Motors durch Erzeugen einer Hilfsphase für das Anlauf-Drehmoment sorgen, anschließend mit einem Fliehkraftschalter aber abgeschaltet werden müssen.

Frequenzabhängiger Widerstand in Wechselstromkreisen

Im Wechselstromkreis bildet der Kondensator einen Blindwiderstand Xc in Ohm (Ω) dessen Wert um so kleiner ist, je größer die Kapazität und je höher die Frequenz ist. Damit können höherfrequente Wechselspannungen gegen Masse niederohmig abgeleitet werden. Für den Einsatz als frequenzabhängiger Widerstand muss der Kondensator eine möglichst genau definierte Kapazität haben und meist auch sehr niedrige ohmsche Verluste (kleiner Verlustfaktor) und ein möglichst lineares Verhalten der Kennwerte haben. Die Frequenzabhängigkeit des Wechselstromwiderstands wird benutzt, um Wechselspannungen frequenzabhängig abzusenken, zu „filtern“. Eine einfache Schaltung ist das RC-Glied, das je nach Schaltung für Wechselströme als Hoch- oder Tiefpass wirkt. Ein Koppelkondensator dient dazu, Gleich- und Wechselstromanteile zu trennen. Das ist u. a. nötig, um den Arbeitspunkt bei Analog-Verstärkern einstellbar zu halten oder um von Lautsprecherspulen die Gleichspannung fernzuhalten. Zusammen mit Spulen (Induktivität), Widerständen und eventuell aktiven Bauelementen werden Kondensatoren auch für Schwingkreise, Bandfilter und Frequenzweichen verwendet. Es ergibt sich eine bestimmte Resonanzfrequenz, ein Hoch- oder Tiefpassverhalten; ein Beispiel hierfür sind die Frequenzweichen in Lautsprechern. Eine zeitdiskrete Variante dieser Filter stellen die Switched-Capacitor-Filter dar.

Mischapplikation als Energiespeicher und Siebkondensator

In vielen Kondensator-Anwendungen kann eine Trennung zwischen Energie- und Ladungsspeicher und frequenzabhängigem Widerstand nicht gemacht werden. Es werden dann beide Funktionen vom Kondensator erfüllt. Einerseits soll eine bestimmte Ladungsänderung eine möglichst geringe Spannungsänderung bewirken, andererseits wird eine überlagerte Wechselspannung möglichst effektiv gegen Masse abgeleitet. Charakteristisch für die Mischapplikation sowohl als Energie- oder Ladungsspeicher als auch als frequenzabhängiger Widerstand ist, dass der Kondensator hierfür ebenfalls eine Mindestkapazität besitzen muss, deren Wert aber prinzipiell überschritten werden kann. Die Anforderungen an Stabilität der elektrischen Kennwerte und an die ohmschen Verluste sind meist nicht sehr hoch. Mischapplikationen bilden die überwiegende Anwendungsform für Kondensatoren. Kondensatoren werden als Energiespeicher in vielfältiger Form verwendet. Eine typische Anwendung in der Leistungselektronik bilden Hierbei übernimmt eine Schaltung (z. B. Gleichrichter, Vierquadrantensteller) die Gleichrichtung von Wechselstrom, dieser Schaltungsteil agiert als Stromquelle. Ein zweiter Schaltungsteil agiert als Senke (z. B. Wechselrichter). Der Zwischenkreiskondensator hat die Aufgabe, den pulsierenden Strom aus dem Gleichrichter aufzunehmen und eine möglichst konstante Spannung dem Wechselrichter zuzuführen. Seine Kapazität ist deshalb so groß, dass der Puls des Ladestrom sowie die Stromentnahme dazwischen nur eine kleine Spannungsänderung bewirken. Die gleiche Funktion haben auch die Kondensatoren in Gleichspannungsnetzteilen, sie halten die der Gleichspannung überlagerte Wechselspannung (Brummspannung, Rippelspannung) möglichst klein. Umgekehrt können Kondensatoren aber auch störende, zeitlich begrenzte Überspannungen in elektronischen Schaltungen aufnehmen und so ihre Ausbreitung und schädliche Wirkung verhindern. Man nennt dies Glätten oder Abblockung und bezeichnet jene Kondensatoren als Glättungs- oder Blockkondensatoren. Eine Sonderstellung solcher Blockkondensatoren stellen die Entstörkondensatoren dar. Die Bezeichnungen X1, X2 sowie Y1 und Y2 dienen der Kennzeichnung von Entstörkondensatoren zur Verwendung in Geräten im Niederspannungsnetz. X-Kondensatoren werden zwischen Phase und Nullleiter eingesetzt. Der X1-Typ hält einem Spannungspuls von 4000 V stand, X2 von 2500 V. Durch eine spezielle Konstruktion geraten sie auch bei Überlastung und Zerstörung nicht in Brand. Die Y-Typen werden eingesetzt, wenn eine Schutzisolierung überbrückt wird und deren Defekt zu einem Stromschlag führen kann; sie halten Spannungspulsen der doppelten Höhe stand.

Bestimmte Applikationen von Kondensatoren können teilweise sowohl von der einen als auch der anderen Kondensator-Familie bedient werden.

Schaltbild

Grundschaltungen mit Kondensatoren

Parallelschaltung

Kondensatoren sind in einer elektrischen Schaltung als Parallelschaltung miteinander verbunden, wenn dieselbe Spannung an allen Bauteilen anliegt. In diesem Fall addieren sich die Kapazitäten der einzelnen Bauteile zur Gesamtkapazität:

C_{\rm {ges}}=C_{1}+C_{2}+\cdots +C_{n}\,\!

Der gesamte Stromfluss I_ges verteilt sich auf den k-ten Kondensator gemäß:

I_{k}={\frac {C_{k}}{C_{\rm {ges}}}}\cdot I_{\rm {ges}}

Neben einer Erhöhung des Kapazität und Strombelastbarkeit der Schaltung, reduzieren sich durch parallelgeschaltete Kondensatoren auch deren unerwünschte Eigenschaften wie parasitäre Induktivität und Reihenwiderstand.

Reihenschaltung

Reihenschaltung von Kondensatoren

Eine Reihenschaltung liegt vor, wenn durch zwei oder mehr Kondensatoren derselbe elektrische Strom fließt. Dann addiert sich der Kehrwert der Kapazität der einzelnen Bauteile zum Kehrwert der Gesamtkapazität:

{\frac {1}{C_{\rm {ges}}}}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}+\cdots +{\frac {1}{C_{n}}}

Diese Schaltung wird beispielsweise angewendet, um eine hohe Spannung auf mehrere Kondensatoren mit geringerer Spannungsfestigkeit zu verteilen, wenn kein Einzel-Bauteil für diese Spannung verfügbar ist.

Tiefpass

Datei:Tiefpass.PNG

Einfacher RC-Tiefpass (Tiefpass 1.Ordnung)

Siehe Hauptartikel: Tiefpass

Als Tiefpass bezeichnet man in der Elektronik Filter, die Signalanteile mit Frequenzen unterhalb der Grenzfrequenz annähernd ungeschwächt passieren lassen und Anteile hoher Frequenzen abschwächen.

Hochpass

Datei:Hochpass.PNG

Einfacher RC-Hochpass (Hochpass 1.Ordnung)

Siehe Hauptartikel: Hochpass

Als Hochpass bezeichnet man Filter, die nur Frequenzen oberhalb der Grenzfrequenz ungeschwächt passieren lassen, die also tiefe Frequenzen im Frequenzgang eingreifend wegnehmen.

Schwingkreis

Siehe Hauptartikel: Schwingkreis

Ein elektrischer Schwingkreis ist eine Baugruppe aus einer Spule und einem Kondensator, die elektrische Schwingungen ausführen kann. Hierbei wird die Energie zwischen Spule und Kondensator periodisch ausgetauscht, wodurch abwechselnd hoher Strom oder hohe Spannung vorliegen.

RC-Glied

Siehe Hauptartikel: RC-Glied

Unter RC-Gliedern versteht man in der Elektronik Schaltungen, die aus einem ohmschen Widerstand (R) und einem Kondensator (C) aufgebaut sind. Es ist ein lineares, zeitinvariantes System. In der Elektronik wurden früher RC-Glieder zur Erzeugung von Zeitintervallen (Blinker) häufig eingesetzt.

der nachfolgende Text wird noch nachbearbeitet

Material- und bauartbedingte Merkmale

Spannungsfestigkeit

Reale Kondensatoren können nicht bis zu einer beliebigen Spannung aufgeladen werden. Überschreitet man die zulässige Spannung bis zur „Durchschlagsspannung“, so schlägt der Kondensator durch, das heißt, es fließt plötzlich ein erheblich größerer Strom über eine Funkenstrecke oder auf eine ähnliche Art ab. Meist führt das zur Zerstörung des Kondensators (z. B. durch Explosion oder Hitzewirkung) und zu weitergehenden Zerstörungen an den Geräten. Manche Kondensatoren besitzen in gewissen Grenzen die Fähigkeit zur Selbstheilung, wenn der Schaden nicht allzu groß ist. Die zulässige Höchstspannung kann im allgemeinen berechnet werden.

Nichtlineares Verhalten

Besonders Elektrolyt-, Tantal- und bestimmte Keramikkondensatoren zeigen im Wechselstromwiderstand ein spannungsabhängiges, nichtlineares Verhalten. Das Maß für den Anteil durch nichtlineares Verhalten erzeugter Signale wird als Klirrfaktor bezeichnet. Die Bezeichnung resultiert aus Anwendungen im Audiobereich, wo die genannten Störungen als „Klirren“ wahrgenommen werden. Dort werden deshalb für höhere Qualität andere Typen wie Folienkondensatoren eingesetzt.

Formal lässt sich ein nichtlinearer Kondensator durch eine von der Momentanspannung u abhängige Dielektrizitätszahl beschreiben: $\varepsilon _{r}(u)$ . D.h. die relative Dielektrizitätszahl ist nicht konstant sondern eine Funktion von der am Kondensator anliegenden Spannung u. Beispielsweise ist bei einem nichtlinearen Plattenkondensator die spannungsabhängige Kapazität gegeben als:

C(u)=\varepsilon _{r}(u)\cdot \varepsilon _{0}\cdot {A \over d}

Die Funktion $\varepsilon _{r}(u)$ ist werkstoffabhängig.

Frequenzabhängigkeit

Neben der Frequenzabhängigkeit von Kondensatoren durch bauartbedingte Induktivität sind auch die Isolationsmaterialien frequenzabhängig. Ist bei einer Anwendung eine geringe Impedanz in einem weiten Frequenzbereich gewünscht, kann man hierfür Kondensatoren verschiedener Bauarten parallelschalten.

Temperaturabhängigkeit

Die Kapazität eines Kondensators ist temperaturabhängig. Für Keramikkondensatoren gibt es Dielektrika mit positivem, negativem und nahe null betragendem Temperaturkoeffizienten. Bei hohen Stabilitätsanforderungen bei Schwingkreisen können auf diese Weise Temperatureinflüsse auf andere Bauteile ausgeglichen werden. Kondensatoren aus sogenannten ferroelektrischer Keramik haben günstigerweise eine sehr hohe Dielektrizitätskonstante, jedoch auch einen hohen Temperaturkoeffizienten und eignen sich bei hohen Stabilitätsanforderungen nicht.

Temperaturstabilität einiger Dielektrika:

Keramik NP0: ±0,3 % bzw. ± 30 ppm/K,
Keramik X7R: ±15 %
Keramik Y5V: +22 % / -82 %
Polypropylen (PP): +0,5 % / -1,5 % bzw. -200 ppm/K
Polyester (PET): +3 % / -4 %
Polyphenylensulfid (PPS): ±1 %
Papier (MP): ±10 % bzw. 700..1200ppm/K

Bei Temperaturen von 20 °C - 40 °C weisen die Dielektrika (mit Ausnahme von Polypropylen) einen Bereich geringerer Temperaturabhängigkeit auf.

Verlustfaktor und Erwärmung

(Anmerkung Elcap: Nach DIN EN IEC 60384.1 heißt der englische Begriff "dissipation factor" im deutschen Sprachraum "Verlustfaktor")

Kondensatoren setzen einen Teil der in sie hineingesteckten elektrischen Energie in Wärme um; dieser Prozess wird durch den Verlustfaktor beschrieben. Der Verlustfaktor wird anhand des Tangens des Phasenwinkels zwischen idealem und realem Stromverlauf einer sinusförmigen Spannung angegeben. In Schwingkreisen ist der Kehrwert des Verlustfaktors ein Kennzeichen für die Güte Q.

Die folgende Tabelle gibt einen Überblick über die Verlustfaktorenfaktoren verschiedener Dielektrika:

Verlustfaktor (tan d) in 10^-3
Material	100 Hz	1 kHz	10 kHz	100 kHz
Keramik NP0				< 1
Keramik X7R		> 10
Polypropylen (PP)	0,2	0,2	0,2	0,3
Polyester (PET)	1,5	4	10	20
Polyphenylensulfid (PPS)	1	1	1,5	3,5
(Metall)papier		8	12	30

Die Verlustfaktoren von X7R sind spannungs- und temperaturabhängig. Beträgt die Spannung beispielsweise 10 % der Nennspannung des Kondensators, so hat sie einen Wert von 80·10^-3.

Die absorbierte Leistung kann aus dem Verlustfaktor Tan d durch folgende Beziehung berechnet werden:

(Bitte Formel auf "Verlustfaktor" korrigieren)

P_{Verlust}=2\pi fCU^{2}\tan {\delta }

f bezeichnet die Frequenz und U die Spannungsamplitude.

Durch die ohmschen Verluste, die mit dem Verlustfaktor gekoppelt sind, kann bei entsprechneder Belastung die zulässige Betriebstemperatur eins Kondensators überschritten werden. Dies kann zur Explosion des Bauteils und der Verursachung von Bränden führen.

Induktivität (ESL) & Reihenwiderstand (ESR)

(Anmerkung Elcap: Hier gehört das Serien-Ersatzschaltbild des Kondensators hinein. Ich habe ein eigenes Bild dazu, dass ich gern zur Verfügung stelle, wenn man mir sagt, wie ich es in den Artikel hineinbekomme. Mit dem Serien-Ersatzschaltbild lässt sich dann der unten stehende Text um 80 % kürzen)

Jeder Kondensator hat wegen seiner Zuleitungen und der teilweise gewickelten Anordnung der Kondensatorplatten zwangsläufig eine parasitäre Induktivität, die im Ersatzschaltbild in Reihe zur Kapazität liegt. Diese Induktivität wird als ESL (engl. equivalent series inductance; L als allgemeines Formelzeichen für Induktivität) bezeichnet. Diese Induktivität macht sich bei höheren Frequenzen störend bemerkbar. Elektrolytkondensatoren haben eine relativ hohe Induktivität und werden deshalb häufig mit einem parallelgeschalteten Keramik- oder Folienkondensator überbrückt. Kondensatoren in SMD-Bauweise haben dagegen eine äußerst kleine Induktivität, was sie bis in den GHz-Bereich anwendbar macht.

Ebenfalls im Ersatzschaltbild in Reihe zur Kapazität liegt im Kondensator ein parasitärer ohmscher Widerstand. Dieser wird als ESR (engl. equivalent series resistance) bezeichnet. Er entsteht durch die inneren Verbindungsstrukturen des Kondensators und vor allem durch die begrenzte Leitfähigkeit der Elektrolyte in Elkos. Jeder Strom, der in den Kondensator hinein- oder herausfließt, erzeugt an diesem Widerstand eine Verlustleistung, die den Kondensator erwärmt. Hitze schadet vor allem dem Elektrolyt und kann bis zur Zerstörung des Kondensators führen. Bei Temperaturen unter dem Nullpunkt steigt der ESR von Elektrolytkondensatoren an und kann die Funktion des Kondensators beeinträchtigen.

Der äquivalente induktive Blindwiderstand (ESL) wirkt dem kapazitiven Blindwiderstand des Kondensators entgegen und verringert den Scheinwiderstand des Kondensators hin zu höherer Frequenz zunächst bis zur Serienresonanz, um danach wieder anzusteigen. Schließlich überwiegt der induktive Anteil und der Kondensator ist als solcher unwirksam. Der ohmsche Anteil (ESR) addiert sich ebenfalls vektoriell zum Blindanteil und muss bei Hochfrequenzanwendungen berücksichtigt werden. Für Standardanwendungen spezifizierte Elkos haben ihre Serienresonanz oft unterhalb von 100 kHz und sind auch aufgrund des hohen ESR nicht für höherfrequente Anwendung geeignet. Für solche Fälle (z. B. Schaltnetzteile) gibt es Low-ESR (< 1 Ω), ultra-Low-ESR (< 100 mΩ) und Low-ESL-Elektrolytkondensatoren.

Der ESR eines Kondensators lässt sich bei einer bestimmten Frequenz mit Hilfe des frequenzabhängigen Verlustfaktors tanδ und der Kapazität C wie folgt berechnen:

$ESR={\frac {\tan {\delta }}{\omega \cdot C}}$

Isolationswiderstand und Selbstentladung

Ein geladener Kondensator entlädt sich mit der Zeit auch über seinen eigenen Isolationswiderstand R_is.

\tau _{s}=R_{is}\cdot C

Die Selbstentladezeitkonstante $\tau _{s}$ ist im Allgemeinen größer, je hochwertiger ein Kondensator ist. Üblich sind Werte zwischen 1000 s bis zu 10.000 s (mit s = Einheitenzeichen für Sekunden).

Diese Zeitkonstanten sind immer dann relevant, wenn Kondensatoren als zeitbestimmendes Glied (z.B. in Zeitrelais) oder zur Speicherung eines Spannungswertes eingesetzt werden.

Der Isolationswiderstand von Elektrolytkondensatoren sinkt ab, wenn der Kondensator gealtert ist oder überlastet wurde. Das verändert die Eigenschaften, erhöht dessen Verlustleistung und führt oft zu dessen vollständiger Zerstörung.

Dielektrische Absorption

Die Dielektrische Absorption ist eine unerwünschte Ladungsspeicherung des Dielektrikums. Wird ein Kondensator kurz entladen, entsteht an den Elektroden nach einigen Sekunden bis Minuten wieder ein Teil der vorher angelegten Spannung. Das Dielektrikum hatte einen Teil der Ladung absorbiert und gibt ihn nun nach und nach wieder frei. Die Größe der Absorption wird im Verhältnis zur ursprünglich angelegten Spannung angegeben und hängt von dem verwendeten Dielektrikum ab. Polypropylen hat einen sehr geringen Wert von 0,05 %, bestimmte Keramiken (Z5U) erreichen 2 %.

Kondensatortyp	Dielektrische Absorption
Kunststoff-Folienkondensatoren, Polyesterdielektrikum	0,2 bis 0,25 %,
Kunststoff-Folienkondensatoren, Polypropylendielektrikum	0,01 bis 0,05 %,
Keramikkondensatoren, X7R	0,6 bis 1 %,
Keramikkondensatoren, Z5U	2,0 bis 2,5 %,
Aluminium-Elektrolytkondensatoren	etwa 10 bis 15 %,

Streu- bzw. Parasitärkapazität

Aus physikalischen Gründen hat jedes reale elektrische Bauelement mehr oder weniger stark eine kapazitive Kopplung mit der Umgebung (Streukapazität) oder parallel zu seinem gewünschten Verhalten (Parasitärkapazität). Dieses kapazitive Verhalten kann vor allem bei hohen Frequenzen eine spürbare Auswirkung haben.

Schaltungen, die an sich einen Kondensator benötigten, können aufgrund dieser schon vorhandenen Streukapazität zuweilen ohne einen Kondensator als separates Bauteil ausgeführt werden. Insbesondere können Kondensatoren im Picofaradbereich durch eine entsprechende Ausformung von Leiterzügen auf einer Leiterplatte ersetzt werden: Zwei gegenüberliegende Kupferflächen von 1 cm² haben bei einem Abstand von 0,2 mm beispielsweise bei Verwendung von FR4-Material (ε_r=3,4) eine Kapazität von 15 pF.

Auch bei einem Kondensator können unerwünschte kapazitive Kopplungen entstehen. Insbesondere gewickelte Kondensatoren sind unsymmetrisch in Bezug auf die Außenfläche. An diese Schicht wird gewöhnlich, wenn zutreffend, die Masse angeschlossen, um eine Kopplung des Kondensators mit dem Umfeld zu verringern. Ähnlich verhält es sich mit Trimmkondensatoren, hier wird der Trimmanschluss mit Masse verbunden.

Kapazität im CGS- und im SI-Einheitensystem

Die heutzutage übliche Einheit für die Kapazität eines Kondensators, das Farad, wurde erst Mitte des 20ten Jahrhunderts eingeführt. Bis dahin wurde die Kapazität im sog. CGS-Einheitensystem in „cm“ angegeben. Diese Angabe ist nicht mit einer Längenangabe zu verwechseln, sondern rührt daher, dass die Kapazität im heute praktisch kaum noch gebrauchten elektrostatischen CGS-Einheitensystem in der Längendimension ausgedrückt wird

Die nebenstehende Abbildung zeigt einen Papierkondensator der Firma SATOR aus dem Jahr 1950 mit einer Kapazität laut Aufdruck von „5000 cm“ bei einer Prüfspannung von „2000 V“. Dies wäre eine Kapazität von ca. 5,6 nF im heute üblichen SI-Einheitensystem. Eine Kapazität von 1 cm im CGS-Einheitensystem entspricht 1,1 pF im SI-Einheitensystem, der Umrechnungsfaktor ist 4πε0.

Heute wird die Kapazität gemäß dem international geltenden SI-Einheitensystem angegeben, das in DIN 1301 festgeschrieben wurde und seit 1970 in der Bundesrepublik auch gesetzlich vorgeschrieben ist. Danach besitzt ein Kondensator die Kapazität 1 Farad, wenn bei einem Ladestrom von 1 Ampere (A) innerhalb 1 Sekunde (s) die Spannung am Kondensator auf 1 Volt (V) ansteigt. 1 F = 1 As / 1 V

Siehe auch

Commons: Bilder von Kondensatoren – Sammlung von Bildern, Videos und Audiodateien

Verlustfaktor, Güte und Serienwiderstand

Reale Kondensatoren weisen parasitäre ohmsche Verluste auf. Sie bewirken, dass die Phasenverschiebung zwischen Strom und Spannung an den Klemmen eines realen Kondensators nicht mehr genau 90° beträgt, sondern um den sogenannten Verlustwinkel δ reduziert ist. Dieser Winkel wird als Tangens ausgedrückt und heißt dann Verlustfaktor tan δ (engl.: dissipation factor, abgekürzt DF). Er ergibt sich aus dem Tangens des Phasenwinkels δ zwischen der geometrischen Summe der Blindwiderstände X_C und X_L und dem Ersatzreihenwiderstand ESR. Unter Vernachlässigung der Induktivität ESL sind der Verlustfaktors tan δ, der ESR und die Kapazität C eines Kondensators bei einer bestimmten Frequenz f mit folgender Formel miteinander verbunden: ^[5]

\tan \delta ={\mbox{ESR}}\cdot \omega C

Für kleine Werte von δ (ausgedrückt im Bogenmaß) gilt:

\tan \delta \approx \delta

Bei verlustarmen Klasse-1-Keramikkondensatoren wird anstelle des Verlustfaktors häufig sein Kehrwert, die Güte Q oder der Gütefaktor spezifiziert.

Q={\frac {1}{tan\delta }}={\frac {1}{ESR\cdot \omega C}}\,

,

Dieser Wert bezieht sich auf die Bandbreite B bei der Resonanzfrequenz f₀ und berechnet sich nach der Gleichung:

Q={\frac {f_{0}}{B}}\,

,

wobei sich die Bandbreite, definiert als der Frequenzbereich, an dessen Grenzen sich der Spannungspegel um 3 dB gegenüber dem Mittenwert geändert hat, ergibt aus:

B={f_{2}}-{f_{1}}\,

.

mit f₂ als obere und f₁ als untere Grenzfrequenz. Da der Verlauf der Impedanzkurve im Resonanzbereich um so steiler ist, je kleiner der ESR ist, kann auch mit der Spezifikation der Güte bzw. des Gütefaktors eine Aussage über die ohmschen Verluste gemacht werden

Die oben beschriebene Definition der Spezifikation der ohmschen Verluste in einem Kondensator geht von dem allgemein üblichen und in der Fachgrundspezifikation DIN EN (IEC) 60384-1 spezifizierten Serien-Ersatzschaltbild aus, in dem die dielektrischen und die Leitungsverluste zum ESR bzw. Verlustfaktor zusammengefasst werden. Einige Fachbücher benutzen zur Erklärung des Verlustfaktors aber ein anderes Ersatzschaltbild, in dem die ohmschen Verluste durch einen Widerstand Rp modelliert werden, der (zusätzlich zum Isolationswiderstand) zu einem idealen Kondensator mit der Kapazität C parallelgeschaltet ist. (Wenn in diesen Beschreibungen dann die ohmschen Verluste mit den dielektrischen Verlusten gleichgesetzt werden, dann erfolgt das aus dem Wissen heraus, dass die Leitungsverluste in diesen Kondensatoren vernachlässigbar sind.) Die Verlustleistung P_V ergibt sich damit beim Betrieb des Kondensators an einer Wechselspannung mit dem Effektivwert U zu

P_{\mathrm {v} }={\frac {U^{2}}{R_{\mathrm {p} }}}\,.

Der Kehrwert dieses Widerstands ist der Leitwert G (wird auch als Ableitung bezeichnet). Der Tangens des Verlustwinkels δ kann in der Form

\tan \delta ={\frac {I_{\mathrm {R} }}{I_{\mathrm {C} }}}={\frac {G}{B_{\mathrm {C} }}}={\frac {1}{2\pi fCR_{\mathrm {p} }}}

^[6]

dargestellt werden.

Ohmsche Verluste

Ohmschen Verluste in diskreten, handelsüblichen Kondensatoren für die Elektronik entstehen durch dielektrische Umpolarisierungsverluste im Wechselfeld und durch den ohmschen Widerstand der Zuleitungen und der Elektroden des Kondensators. Bei Aluminium-Elektrolytkondensatoren trägt besonders die begrenzte Leitfähigkeit flüssiger Elektrolyte zu diesen Verlusten bei. Die verschiedenen Verlustwiderstände werden, da sie bei industriell gefertigten Kondensatoren messtechnisch nicht voneinander getrennt gemessen werden können, zu einem gemeinsamen Wert zusammengefasst. Sie können in den jeweiligen Datenblättern als Verlustfaktor tan δ, als Güte Q und als Ersatzreihenwiderstand ESR dargestellt werden Der Zahlenwert des Verlustfaktors und der Güte ist, bei gleicher Messfrequenz, innerhalb eines spezifizierten Bereiches unabhängig von dem Kapazitätswert des Kondensators. Der ESR dagegen ist unabhängig von den Blindwiderständen und ist eine Größe, die jeden Kondensator einzeln kennzeichnet. Über ihn kann mit Hilfe der Gleichung

P=\ I^{2}\cdot \ ESR

leicht die im Kondensator entstehende Verlustwärme P bei Strombelastung mit dem Strom I errechnet werden.

Bei Leistungskondensatoren wie z. B. Vakuumkondensatoren, große Keramik- und Polypropylen-Folienkondensatoren werden die ohmschen Verluste anders definiert. Anstatt Verlustfaktor, Güte oder ESR wird hier oft die maximale Strom- oder Impulsbelastung spezifiziert. Auch diese Angabe ist letztendlich ein Ausdruck der ohmschen Verluste des Kondensators und ermittelt sich aus der zulässigen Verlustwärme, die über die ohmschen Verluste bei der Strombelastung entsteht.

Die ohmschen Verluste von Kondensatoren hängen von der Bauart ab, sind also spezifisch für eine bestimmte Herstelltechnologie. Innerhalb einer Bauart sinken die ohmschen Verluste mit steigender Kapazität. Dies scheint zunächst paradox, weil mit steigender Kapazität die dielektrischen Verluste größer werden müssten. Das dies nicht der Fall ist liegt am technischen Aufbau der Kondensatorarten. Anschaulich wird es am Beispiel der Keramik-Vielschichtkondensatoren. Die vielen Einzelkondensatoren im Schichtverbund sind parallel geschaltet, so dass auch ihre einzelnen Verlustwiderstände parallel geschaltet sind. Dadurch reduziert sich der Gesamtwiderstand entsprechend der Anzahl parallel geschalteter Einzelkondensatoren. Bei Folienkondensatoren bewirkt die Stirnflächenkontaktierung des Wickels ähnliches. Die Art der Kontaktierung kann als eine Vielzahl parallel geschalteter Einzelkondensatoren beschrieben werden. Bei Elektrolytkondensatoren, bei denen die Zuleitungsverluste über den Elektrolyten die ohmschen Verluste maßgeblich bestimmen, kann bei größer werdenden Elektrodenflächen die steigende Anzahl der Zuleitungspfade als Parallelschaltung vieler Einzelwiderstände verstanden werden, wodurch sich die gesamten ohmschen Verluste verringern. Bei sehr großen Aluminium-Elektrolytkondensatoren reduziert außerdem häufig eine Mehrfachkontaktierung der Anoden- und Kathodenfolien die ohmschen Verluste. Aus demselben Grund werden Tantal-Elektrolytkondensatoren in einigen Ausführungsformen mit Mehrfach-Anoden gefertigt.

Die ohmschen Verluste sind Wechselstromverluste, Gleichstromverluste (Isolationswiderstand, Reststrom) bei Kondensatoren sind meist vernachlässigbar. Die Messfrequenz zum Messen der Verluste muss eindeutig festgelegt sein. Da aber handelsübliche Kondensatoren mit Kapazitätswerten von pF (Pikofarad, 10-12 F) bis einigen 100 F bei Doppelschichtkondensatoren mit etwa 14 Zehnerpotenzen einen außerordentlich großen Kapazitätsbereich abdecken, ist es nicht möglich, mit nur einer Messfrequenz den gesamten Bereich zu erfassen. Nach der Fachgrundspezifikation für Kondensatoren, der DIN EN (IEC) 60384-1, sollen die ohmschen Verluste mit derselben Frequenz gemessen werden, die auch zur Messung der Kapazität verwendet wird, mit:

100 (120) Hz für Elektrolytkondensatoren und andere Kondensatoren mit C > 10 µF
100 kHz, 1 MHz (Bezugsfrequenz) oder 10 MHz für andere Kondensatoren mit C ≤ 1 nF,
1 kHz (Bezugsfrequenz) oder 10 kHz für andere Kondensatoren mit C = > 1 nF bis ≤ 10 µF:

Die ohmschen Verluste von Kondensatoren sind frequenz-, temperatur- und zum Teil auch zeitabhängig (Alterung). Eine Umrechnung der Einheit tan δ in ESR und umgekehrt ist möglich, erfordert aber einige Erfahrung. Sie kann nur erfolgen, wenn die Messfrequenz hinreichend weit entfernt von der Resonanzfrequenz ist. Denn bei der Resonanz ändert sich der Kondensator von einem kapazitiven in ein induktives Bauelement, dabei ändert sich der Verlustwinkel dramatisch und ist deshalb zur Umrechnung nicht mehr geeignet.

Ohmsche Verluste unterschiedlicher Klasse-1-Kondensatorarten

Die Güte und der Verlustfaktor sind charakteristische Größen der ohmschen Verluste im Dielektrikum bestimmter Kondensatoren, bei denen die Leitungsverluste vernachlässigbar sind. Diese Kondensatoren, bei den Keramikkondensatoren "Klasse-1" genannt, werden überwiegend in Frequenz bestimmenden Schaltungen oder in Hochleistungsanwendungen als Leistungskondensatoren eingesetzt. Als Messfrequenz für den in der Elektronik üblichen Kapazitätsbereich von 30 pF bis ≤ 1 nF wird von großen Herstellern meist 1 MHz genommen. Mit dieser hohen Frequenz wird auch Bezug auf die Anwendung solcher Kondensatoren genommen, die überwiegend im höheren Frequenzbereich liegt. Die betroffenen kleinen Kapazitätswerte mit den dazu vorhandenen niedrigen ESL-Werten stellen außerdem sicher, dass der Messwert noch weit genug von der Resonanzfrequenz entfernt ist.

Die folgende Tabelle, in der die ESR-Werte rechnerisch ermittelt wurden, gibt einen Überblick über die ohmschen Verluste (Maximalwerte) unterschiedlicher Kondensatorarten (ohne Leistungskondensatoren) bei 1 MHz in für Frequenz bestimmende Anwendungen in der Elektronik:

Ohmsche Verluste unterschiedlicher Kondensatorarten
für frequenzbestimmende Schaltungen (Bezugsfrequenz 1 MHz)
Kondensatorart	Kapazität (pF)	ESR 100 pF (mΩ)	ESR 1000 pF (mΩ)	tan δ (10^-4)	Güte Q
Siliziumkondensator ^[7]	560	400	-	2,5	4000
Glimmerkondensator ^[8]	1000	650	65	4	2500
Klasse-1-Keramikkondensator (NP0) ^[9]	1000	1600	160	10	1000

Ohmsche Verluste unterschiedlicher Kondensatorarten im mittleren Kapazitätsbereich

Der Kapazitätsbereich von > 1 nF bis ≤ 10 µF wird überwiegend von Klasse-1- und Klasse-2-Keramikkondensatoren und von Kunststoff-Folienkondensatoren abgedeckt. Elektrolytkondensatoren werden in diesem Kapazitätsbereich weniger häufig eingesetzt. Dieser Kapazitätsbereich ist durch eine Vielzahl unterschiedlicher Anwendungen mit stark unterschiedlichen Anforderungen gekennzeichnet. Die ohmschen Verluste dieser Kondensatoren in den Datenblättern der Hersteller werden überwiegend über den Verlustfaktor spezifiziert. Allerdings sind in diesem Bereich auch Wechselspannungs- und Impulskondensatoren angesiedelt, die sich über eine Strombelastung spezifizieren.

In der folgenden Tabelle sind als allgemeines Beispiel die Verlustfaktoren (Maximalwerte) bei 1 kHz, 10 kHz und 100 kHz sowie die daraus abgeleiteten ESR-Werte für einen 100 nF Kapazitätswert gelistet.

Ohmsche Verluste unterschiedlicher Kondensatorarten
mit C > 1 nF bis ≤ 10 µF (Bezugswert 100 nF)
Kondensatorart	ESR 1 kHz (mΩ)	ESR 10 kHz (mΩ)	ESR 100 kHz (mΩ)	tan δ (10^-3)	tan δ (10^-3)	tan δ (10^-3)
Klasse-1- Keramikkondensator (NP0, N750) ^[10]	1600	160	16	1	1	1
Klasse-2- Keramikkondensator (X7R, Y5V) ^[11]	4000	400	40	2,5	2,5	2,5
PP-Folienkondensator (Polypropylen) ^[12]	6400	800	160	4	5	10
PET-Folienkondensator (Polyester)	12700	2400	480	8	15	30
PEN-Folienkondensator (Polyethylennaphthalat)	12700	2400	480	8	15	30
PPS-Folienkondensator (Polyphenylensulfid)	24000	3200	800	15	20	50

Ohmsche Verluste unterschiedlicher Kondensatorarten im höheren Kapazitätsbereich

Kondensatoren mit Kapazitätswerten > 10 µF werden überwiegend in Anwendungen im Bereich der Stromversorgungen, der Sieb- und der Stützschaltungen eingesetzt. Es ist der typische Kapazitätsbereich, in dem Elektrolytkondensatoren und hochkapazitive Keramik-Vielschichtkondensatoren eingesetzt werden. Nach der Fachgrundspezifikation für Kondensatoren, der DIN EN (IEC) 60384-1 sollen die ohmschen Verluste solcher Kondensatoren mit 100 (120) Hz gemessen werden. Da in der Elektronik die Arbeitsfrequenzen in den letzten Jahrzehnten aber deutlich gestiegen sind und auch im Bereich der Schaltnetzteile mit sehr viel höheren Frequenzen gearbeitet wird, finden sich in den Datenblättern, speziell denen von Elektrolytkondensatoren, auch häufig die 100 kHz-ESR-Werte.

Die folgende Tabelle gibt einen Überblick über die ohmschen Verluste (Maximalwerte) verschiedener Kondensatorarten für Sieb- oder Stützanwendungen im Niedervoltbereich. Zur Vergleichbarkeit der Kondensatorarten miteinander ist jeweils die Kapazität von etwa 100 µF und eine Spannungsfestigkeit von 10 bis 16 V gewählt worden. Da für diesen Anwendungsbereich in der Elektronik das Bauvolumen eine große Rolle spielt, sind in der Tabelle die Abmessungen mit aufgeführt worden. Die Zeile mit der Kapazität 2200 µF ist als Beispiel dafür aufgeführt, dass mit größerer Kapazität und Baugröße auch bei der preiswertesten Kondensatorart, den "Elkos", niedrige ESR-Werte zu erreichen sind. Im Übrigen ist der höhere ESR bei den "Elkos" mitunter schaltungstechnisch sogar erwünscht, weil die Dämpfung über diese Verluste unerwünschte Resonanzen auf Leiterplatten verhindern kann.

Ohmsche Verluste unterschiedlicher Kondensatorarten
für Sieb- und Stützanwendungen im Niedervoltbereich
Kondensatorart	Kap./Spg (µF/V)	LxBxH DxL (mm)	ESR 100 Hz (mΩ)	tan δ 100 Hz (%)	ESR 100 kHz (mΩ)
Klasse-2-Keramikkondensator (X5R) ^[13]	100/6,3	3,2x1,6x1,6	2400	15	typ. 2
Klasse-2-Keramikkondensator (YV5)	100/6,3	3,2x1,6x1,6	3180	20	-
Tantal-Elektrolytkondensator mit Polymer-Elektrolyten ^[14]	100/10	7,3x4,3x2,8	1600	10	18
Tantal-Elektrolytkondensator mit Braunstein-Elektrolyten	100/10	7,3x4,3x2,8	1275	8	150
Aluminium-Elektrolytkondensator mit Polymer-Elektrolyten	100/10	7,3x4,3x1,6	960	6	15
Aluminium-Elektrolytkondensator mit TCNQ-Elektrolyten ^[15]	120/10	8x6,9x8,3	1600	12	35
Aluminium-Elektrolytkondensator mit flüssigem Elektrolyten ^[16]	150/10	6,3x5,8	2020	19	260
Aluminium-Elektrolytkondensator mit flüssigem Elektrolyten ^[17]	2200/10	12,5x20	130	18	90

Literatur

O. Zinke, H. Seither: Widerstände, Kondensatoren, Spulen und ihre Werkstoffe. Springer Verlag, Heidelberg (1982), ISBN 3-540-11334-7
P. Volkmann, P. (Hrsg.): Aufgaben Elektrotechnik und Elektronik 2 – Elektrisches Feld und Kondensator. 1999, ISBN 3-8007-2018-3
W. Just, W. Hofmann: Blindstromkompensation in der Betriebspraxis 2003, ISBN 3-8007-2651-3
Bohler, Kähler, Weigt: Bauelemente der Elektronik und ihre Grundschaltungen. Stam-Verlag, ISBN 3-8237-0214-9

Aktuelle (2009) Forschungen beschäftigen sich unter anderem mit neuen Oberflächenstrukturierungen der Elektroden. Beispielsweise lässt sich durch eine Nanostruktur in Form von Milliarden nebeneinander liegender kleiner Löcher die Leistungsdichte eines Kondensators, gemessen in W/kg, um mehr als das Zehnfache gegenüber konventionellen Kondensatoren vergrößern, siehe ^[18], oder auch ^[19] , und ^[20]

Quellen

↑ Capacitors: A Story of Dielectrics
↑ WVS-Technology, Vakuum-Kondensatoren: [1]
↑ Murata: [2]
↑ Johanson, LASERtrim® tuning capacitors, [3]
↑ Film Capacitors. General technical information. EPCOS, Mai 2009, Abgerufen am 11. August 2009 (PDF, 1,8 MB).
↑ Wolf-Ewald Büttner: Grundlagen der Elektrotechnik 2. Oldenbourg, 2004, ISBN 3-486-27296-9, S. 102.
↑ Siliziumkondensator, Vishay, HPC0603A, [4]
↑ Simic Electronics, Chip Mica Capacitors, [5]
↑ AVX, NP0, 1000 pF 100 V, 0805, Q >= 1000 (1 MHz), [6]
↑ Murata, C0G, 100 nF 50 V, 1206, Q > 1000/1 kHz, [7]
↑ Holystone, HCC, X7R, Y5V, 0805, 100 nF 25 V, [8]
↑ Wima,, FKP3, 100 nF 63 V, MKS4, 100 nF 50 V, SMD-PEN, 100 nF 63 V, , MKI2, 100 nF 63 V, [9]
↑ Murata, X5R, 100 µF 6,3 V, 1206, Tan d 0,15/120Hz, Y5V, 100 µF 6,3 V, 1206, Tan d 0,2/100Hz, http://search.murata.co.jp/Ceramy/image/img/A18X/E0000026.pdf
↑ Kemet, Produktsuche, T491, T510, T520, T530, A700, 100/10 http://www.kemet.com/kemet/web/homepage/kechome.nsf/weben/products
↑ Sanyo, Os-Con, SMD-SVP, 120/10, http://www.edc.sanyo.com/pdf/e046.pdf
↑ Panasonic, SMD-FP, 150/10, http://www.panasonic.com/industrial/components/capacitive/cap_smtelec.htm
↑ Jianghai, CD 263 BK, 1000/10, 10x16 mm, http://xcnet.de/projekte/xnetcreate.de_v2/pics/kunden/dateimanager/5221/JE8_CD_263_BK.pdf
↑ Katherine Bourzac: Winzige Sandwiches für den großen Energiehunger. In: Telepolis. 20. April 2009, abgerufen am 20. April 2009.
↑ Nanotechnology Now, NanoCenter Improves Energy Storage Options, Maryland NanoCenter, College Park, MD | Posted on March 23rd, 2009, <
↑ Green Car Congress, New Electrostatic Nanocapacitors Offer High Power and High Energy Density, 17 March 2009, [10]

Weblinks

Grundlagen und Funktionsweise
Elektrisches Feld im Plattenkondensatoren (Animation)
CapSite Technische Details zu industriell relevanten Kondensatoren (Englisch)
Eigenbau von Kondensatoren: Make your own High-Voltage Capacitor, Tony van Roon (Englisch)
Technische Daten und weiterführende Informationen finden sich auf den Seiten der Hersteller, insbesondere: AVX, epcos, Europe Chemi-Con, KEMET, Panasonic, RUBYCON, VISHAY, WIMA

Versuche

P=\ I^{2}\cdot \ ESR

[1] Capacitors: A Story of Dielectrics

[2] WVS-Technology, Vakuum-Kondensatoren: [1]

[3] Murata: [2]

[4] Johanson, LASERtrim® tuning capacitors, [3]

[5] Film Capacitors. General technical information. EPCOS, Mai 2009, Abgerufen am 11. August 2009 (PDF, 1,8 MB).

[6] Wolf-Ewald Büttner: Grundlagen der Elektrotechnik 2. Oldenbourg, 2004, ISBN 3-486-27296-9, S. 102.

[7] Siliziumkondensator, Vishay, HPC0603A, [4]

[8] Simic Electronics, Chip Mica Capacitors, [5]

[9] AVX, NP0, 1000 pF 100 V, 0805, Q >= 1000 (1 MHz), [6]

[10] Murata, C0G, 100 nF 50 V, 1206, Q > 1000/1 kHz, [7]

[11] Holystone, HCC, X7R, Y5V, 0805, 100 nF 25 V, [8]

[12] Wima,, FKP3, 100 nF 63 V, MKS4, 100 nF 50 V, SMD-PEN, 100 nF 63 V, , MKI2, 100 nF 63 V, [9]

[13] Murata, X5R, 100 µF 6,3 V, 1206, Tan d 0,15/120Hz, Y5V, 100 µF 6,3 V, 1206, Tan d 0,2/100Hz, http://search.murata.co.jp/Ceramy/image/img/A18X/E0000026.pdf

[14] Kemet, Produktsuche, T491, T510, T520, T530, A700, 100/10 http://www.kemet.com/kemet/web/homepage/kechome.nsf/weben/products

[15] Sanyo, Os-Con, SMD-SVP, 120/10, http://www.edc.sanyo.com/pdf/e046.pdf

[16] Panasonic, SMD-FP, 150/10, http://www.panasonic.com/industrial/components/capacitive/cap_smtelec.htm

[17] Jianghai, CD 263 BK, 1000/10, 10x16 mm, http://xcnet.de/projekte/xnetcreate.de_v2/pics/kunden/dateimanager/5221/JE8_CD_263_BK.pdf

[18] Katherine Bourzac: Winzige Sandwiches für den großen Energiehunger. In: Telepolis. 20. April 2009, abgerufen am 20. April 2009.

[19] Nanotechnology Now, NanoCenter Improves Energy Storage Options, Maryland NanoCenter, College Park, MD | Posted on March 23rd, 2009, <

[20] Green Car Congress, New Electrostatic Nanocapacitors Offer High Power and High Energy Density, 17 March 2009, [10]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

Benutzer:Elcap/Kondensator (Elektrotechnik)/ReviewJan2007

Funktionsweise

Funktionsweise im Gleichstromkreis

Funktionsweise im Wechselstromkreis

Funktionsweise (alt)

Geschichte

Leidener Flasche

Physikalische Grundlagen

Physikalische und elektrotechnische Begriffe

Influenz und elektrisches Feld

Dielektrische Polarisation

Kapazität und Ladung

Spannungsfestigkeit

Feldenergie

Phasenverschiebung

Blindwiderstand

Impedanz bzw. Scheinwiderstand

Verlustfaktor tan δ und Äquivalenter Serienwiderstand ESR

Zeitverhalten

Idealisierte physikalische Kondensatoren

Kondensatorarten und Kondensatorbezeichnungen

Festkondensatoren

Siliciumkondensator

Glimmerkondensator

Keramikkondensator

Folienkondensatoren

Metall-Papierkondensator (MP-Kondensator)

Kunststoff-Folienkondensator

Elektrolytkondensator

Doppelschichtkondenstoren

Bauformen von Festkondensatoren

Kondensatoren mit einstellbarer Kapazität

Drehkondensatoren

Vakuum- und Schutzgas-Drehkondensatoren

Trimmer

Normung

Kennzeichnungen

Elektrische Kennwerte

Kapazität C

Nennkapazität CR

Nennspannung UR

Isolationswiderstand

Reststrom, Leckstrom

Überlagerter Wechselstrom Ir, Rippelstrom

Nachladeeffekt (dielektrische Absorbtion)

Anwendungen

Energie- oder Ladungsspeicher

Kondensatoren in Leistungsanwendungen

Frequenzabhängiger Widerstand in Wechselstromkreisen

Mischapplikation als Energiespeicher und Siebkondensator

Schaltbild

Grundschaltungen mit Kondensatoren

Parallelschaltung

Reihenschaltung

Tiefpass

Hochpass

Schwingkreis

RC-Glied

Material- und bauartbedingte Merkmale

Spannungsfestigkeit

Nichtlineares Verhalten

Frequenzabhängigkeit

Temperaturabhängigkeit

Verlustfaktor und Erwärmung

Induktivität (ESL) & Reihenwiderstand (ESR)

Isolationswiderstand und Selbstentladung

Dielektrische Absorption

Streu- bzw. Parasitärkapazität

Kapazität im CGS- und im SI-Einheitensystem

Siehe auch

Verlustfaktor, Güte und Serienwiderstand

Ohmsche Verluste

Literatur

Quellen

Weblinks

Versuche

Navigationsmenü

Suche