Benutzer:Mbasti01/Konzept 01
Hinweis: Von 2005 bis 2015 existierte ein eigenes WikiProjekt Farbe. Dieses kann jederzeit reaktiviert werden.
Farbe
[Bearbeiten | Quelltext bearbeiten]| Formelzeichen | |
|---|---|
| ,, | CIE-Normalbeobachter, Spektralwertfunktionen: Tabellarische Werte abhängig von der Wellenlänge zur Bewertung von Lichtspektren. Charakterisiert die Farbwahrnehmung eines normalsichtigen Beobachters. |
| Wertetripel der Spektralwertfunktionen an einer bestimmten Wellenlänge | |
| Normiertes Wertetripel der Spektralwertfunktionen an einer bestimmten Wellenlänge, bezogen auf die Gesamtsumme X+Y+Z. Durch die Normierung ergibt sich: | |
| Normiertes Wertepaar der Spektralwertfunktionen an einer bestimmten Wellenlänge, das zur Kennzeichnung eines Farbortes in der Normfarbtafel dient. (z könnte bei Bedarf aus x und y berechnet werden.) | |
| ,, | Farbabgleichsfunktionen: Ergebnis der Farbabgleichs-Versuche, Tabellarische Werte abhängig von der Wellenlänge. Ausgangspunkt zur Berechnung von ,, |
| Wertetripel der Farbabgleichsfunktionen an einer bestimmten Wellenlänge | |
| Normiertes Wertetripel der Farbabgleichsfunktionen an einer bestimmten Wellenlänge, bezogen auf die Gesamtsumme R+G+B. Durch die Normierung ergibt sich: | |
... und bei Körperfarben durch subtraktive Farbmischung. Die Farbvalenz (Farbe) Grün der Vegetation beruht darauf, dass das Chlorophyll den purpurnen Lichtanteil photochemisch absorbiert.
Das gewöhnliche Bild von Wahrnehmung – Reize aus der Außenwelt treffen auf die Sinnesorgane, diese leiten Informationen an das Gehirn weiter, das daraus ein Weltbild erstellt–, ist demnach veraltet. In seinem beeindruckend klaren Buch „Wie unser Gehirn die Welt erschafft“ (Spektrum-Verlag, 312 Seiten, 24,95 Euro) bringt Frith es auf eine einfache Formel: Was wir wahrnehmen, ist ein Fantasiebild, das sich mit der Realität deckt. „Meine Wahrnehmung ist eine Vorhersage dessen, was in der Außenwelt sein sollte“, sagt Frith.
https://www.amazon.de/Das-Buch-Farben-Max-Kobbert/dp/3896787691
Panpsychismus
https://www.nzz.ch/wissenschaft/die-seltsame-wiederkehr-der-weltseele-ld.1379451
##########################
Das schwärzeste Schwarz
https://www.spiegel.de/auto/aktuell/vanta-schwarz-das-schwaerzeste-schwarz-der-welt-a-1287643.html
Das röteste Rot
https://www.scinexx.de/news/physik/forscher-erzeugen-das-roeteste-rot/
Das blaueste Blau
Prototypentheorie
https://www.anglistik.uni-muenchen.de/personen/professoren/schmid/schmid_publ/prototypentheorie.pdf
https://books.google.de/books/about/Empiristische_Theorie_der_Gef%C3%BChlswirkun.html?id=CpJumAEACAAJ&redir_esc=y ... wird im Artikel Farbe erwähnt
https://de.wikipedia.org/wiki/Kognitionswissenschaft#Kognitive_Architekturen
https://www.duden.de/rechtschreibung/Farbe
https://en.m.wikipedia.org/wiki/Rg_chromaticity
https://fr.wikiversity.org/wiki/Colorimétrie/CIE_RGB_1931
https://www.kennerblick.net/farbmetrik.html
https://www.kennerblick.net/grassmannsche-gesetze.html
https://www.kennerblick.net/kubelka-munk-theorie.html
https://www.kennerblick.net/delta-e.html. Gleichabständigkeit von Farben !! Farbensehen der Tiere
https://www.annualreviews.org/doi/full/10.1146/annurev-vision-091517-034231#_i2 Farbwahrnehmung, ausführlich, gut
Farbensehen der Tiere
https://link.springer.com/content/pdf/10.1007/s00347-017-0543-6.pdf?pdf=button%20sticky
Tabelle mit Wellenlängen und Farbbereichen und Wellenlängenbereich von Licht:
Umrechung cmyk nach rgb: Buntaufbau, Unbuntaufbau etc
http://www.spectrumcolors.de/cor_separation.php. Demo-Rechner mit unterschiedlichen Verfahrenhttps://www.farbtabelle.at/farben-umrechnen/. Rechner
https://www.rapidtables.org/de/convert/color/rgb-to-cmyk.html. Rechner mit Formeln
https://www.101computing.net/cmyk-to-rgb-conversion-algorithm/ Formeln, Programm
https://stackoverflow.com/questions/14088375/how-can-i-convert-rgb-to-cmyk-and-vice-versa-in-python Programm
https://www.teamnext.de/blog/was-ist-rgb-und-cmyk/ Textuell
Philosophie des Geistes. Karl Popper#Drei-Welten-Theorie Qualia ...
Farbwahrnehmung ( Farbempfindung )
Additive FarbmischungGraßmannsche Gesetze
Farbmerkmal. >> Bezug zur Farbmetrik ??
Fotodrucker ... schlecht. https://previous.publisher.ch/dynpg/ftp/FineArtPrinting.pdf.
Farbdruck ... schlecht
Farbmetrik >> Verbessern
Liste der Farben im Farbkreis >> Textbaustein
Strukturfarben. http://www.naklar.at/content/features/strukturfarben/

Farben im Farbkreis - Benennungen
[Bearbeiten | Quelltext bearbeiten]Itten Küppers
Gelbgrün Lind
Blaugrün Türkis
Blau Cyan
Blauviolett Blau
Rotviolett Lila
Rot Magenta
Rotorange Rot
Gelborange Dotter
Farbmetrik Sammlung
[Bearbeiten | Quelltext bearbeiten]| Formelzeichen | |
|---|---|
| ,, | CIE-Normalbeobachter, Spektralwertfunktionen: Tabellarische Werte abhängig von der Wellenlänge zur Bewertung von Lichtspektren. Charakterisiert die Farbwahrnehmung eines normalsichtigen Beobachters. |
| Wertetripel der Spektralwertfunktionen an einer bestimmten Wellenlänge | |
| Normiertes Wertetripel der Spektralwertfunktionen an einer bestimmten Wellenlänge, bezogen auf die Gesamtsumme X+Y+Z. Durch die Normierung ergibt sich: | |
| Normiertes Wertepaar der Spektralwertfunktionen an einer bestimmten Wellenlänge, das zur Kennzeichnung eines Farbortes in der Normfarbtafel dient. (z könnte bei Bedarf aus x und y berechnet werden.) | |
| ,, | Farbabgleichsfunktionen: Ergebnis der Farbabgleichs-Versuche, Tabellarische Werte abhängig von der Wellenlänge. Ausgangspunkt zur Berechnung von ,, |
| Wertetripel der Farbabgleichsfunktionen an einer bestimmten Wellenlänge | |
| Normiertes Wertetripel der Farbabgleichsfunktionen an einer bestimmten Wellenlänge, bezogen auf die Gesamtsumme R+G+B. Durch die Normierung ergibt sich: | |
https://www.itp.uni-hannover.de/de/institut/personen/dietrich-zawischa/
https://www.itp.uni-hannover.de/fileadmin/itp/emeritus/zawischa/static_html/fmetr.html. >>> zitierte Quelle
Das von einem Gegenstand reflektierte, durchgelassene oder von ihm selbst ausgesandte Licht, das ins Auge eintritt und eine Farbempfindung hervorruft, ist der Farbreiz. Zwar nehmen wir außer der Farbe auch noch wahr, ob der Gegenstand selbst leuchtet oder beleuchtet ist, ob er transparent oder lichtundurchlässig ist; wir bemerken, ob die Oberfläche matt oder glänzend ist, und dabei können verschiedene Arten Glanz unterschieden werden (Glasglanz, Metallglanz), aber man kann sich leicht überzeugen, dass all diese Attribute außer Farbe und Helligkeit nur durch das Zusammenwirken der Eindrücke von benachbarten Stellen des Gegenstandes und seiner Umgebung bestimmt werden: Betrachtet man eine Stelle, die so klein ist, dass sie völlig einheitlich erscheint, durch eine Blende, so bleiben nur die Merkmale Farbe und Helligkeit übrig.
Das Licht, also der Farbreiz, kann mit physikalischen Mitteln untersucht werden: Es kann durch ein Prisma in Anteile verschiedener Wellenlängen aufgespalten werden, und man kann messen, welche Energie pro Zeiteinheit in einem bestimmten Wellenlängenbereich transportiert wird. Man unterteilt die Wellenlängenskala in kleine Abschnitte. Die Leistung (Energie/Zeiteinheit), die von der Strahlung in so einem kleinen Wellenlängenbereich in dem Intervall von λ − Δλ/2 bis λ + Δλ/2 in einen bestimmten Raumwinkelbereich hinein (z. B. in die Pupille) transportiert wird, nennen wir
φλΔλ(1)
(Diese Leistung ist natürlich umso größer, je größer Δλ gewählt wird, daher schreiben wir Δλ als Faktor dazu.) Kennen wir φλ für alle Wellenlängen des sichtbaren Bereiches, also für jeden Abschnitt der Wellenlängenskala, so haben wir eine Funktion der Wellenlänge vorliegen, die spektrale Leistungsverteilung, die von der Physik her den Farbreiz vollständig bestimmt. Man nennt φλ auch Farbreizfunktion. Wir stellen fest, dass z. B. eine Verdopplung der Werte φλ für alle Wellenlängen zwar die Helligkeit, nicht aber die Farbe einer Strahlungsquelle ändert; daher ist es üblich, diese Funktion willkürlich zu normieren, d.h. mit einem beliebigen Zahlenfaktor zu multiplizieren, so dass man die Funktionen für Lichtquellen verschiedener Strahlungsleistung bequem in einem Diagramm unterbringen kann. (Noch größere Bequemlichkeit bedeutet dies für die Messung, da man sich auf eine Relativmessung beschränken kann, die viel einfacher ist als eine Absolutmessung).
Stimmen zwei Farbreize in ihren spektralen Verteilungen überein, also φ1,λ = φ2,λ, so erscheinen sie unbedingt gleich, man spricht in diesem Fall von Isomerie. Die Farbreize können aber auch gleich erscheinen, wenn die Verteilungsfunktionen verschieden sind. Diese Übereinstimmung nennt man Metamerie oder bedingte Gleichheit.
Wertigkeit einer Farbvalenz
Um diesem Sachverhalt Rechnung zu tragen, führen wir die Wertigkeit V eines Farbreizes in Hinblick auf den Farbsinn des Beobachters ein. Erscheinen einem Beobachter zwei Farbreize gleich, so schreiben wir
V1 = V2(2)
d.h. die Wertigkeiten, Farbvalenzen oder kurz Valenzen der beiden Farbreize sind gleich, und über die Farbreizfunktion selbst sagt diese Gleichung nichts aus.
... Wir schreiben die Übereinstimmung der Bildhälften als Gleichung für die Farbvalenzen:
V = RR + GG + BB(3)
Die fett gedruckten Großbuchstaben stehen für Farbvalenzen, die Buchstaben R, G, B (Farbmaßzahlen) für die in zunächst noch beliebigen Einheiten gemessenen Mengen der Grundvalenzen R, G, B.
Dies ist das 1. Graßmannsche Gesetz, das man so formulieren kann: Von vier Farben lässt sich immer eine als Überlagerung der anderen darstellen.
Hat man eine metamere Übereinstimmung, so bleibt diese Übereinstimmung erhalten, wenn die Helligkeit von beiden im gleichen Maße erhöht oder verringert wird, es gilt also
V1 = V2 ⇒ aV1 = aV2(6)
zumindest innerhalb gewisser Grenzen.
Die Gleichheit zweier Farben bleibt auch bestehen, wenn beiden die gleiche Farbe additiv überlagert wird:
V1 = V2 ⇒ V1 + U = V2 + U(7)
oder auch
U1 = U2, V1 = V2 ⇒ U1 + V1 = U2 + V2(8)
(3. Graßmannsches Gesetz, H. Graßmann 1853)
...haben wir für V1, V2 die Maßzahlen R1, G1, B1 bzw. R2, G2, B2 ermittelt,
V1 = R1R + G1G + B1B
V2 = R2R + G2G + B2B(9)
dann gilt auch
V1 + V2 = (R1 + R2) R + (G1 + G2) G + (B1 + B2) B.(10)
Es besteht also ein linearer Zusammenhang zwischen den Farbreizen und den Farbmaßzahlen, und es gelten für die Addition von metameren Farbvalenzen die gleichen Gesetze wie für die Addition von Vektoren. Daher kann man jeden Farbwert als Vektor in einem Farbenraum darstellen,
Vektoraddition zur Berechnung der additiven Farbmischung nur im CIE-XYZ-Raum möglich ist. Aufgrund der nichtlinearen Transformationsformeln gibt es im L*u'v'-, L*u*v*und L*a*b*-Raum keine so einfachen Zusammenhänge.
Bild 2: Darstellung eines Farbvektors F als Summe dreier Komponenten. R, G, B sind Einheitsvektoren, RR etc. dann Vektoren in Richtung der Einheitsvektoren, aber mit veränderter Länge. F ist die vektorielle Summe von RR, GG und BB. Dies ist in der Abbildung rechts noch einmal hervorgehoben. In diesen Skizzen sind R, G, B die Beträge der Komponenten, RR, GG und BB die Komponentenvektoren
(Ausgangspunkt der Vektoren ist E)
Aus der Konstruktion folgt, dass die Überlagerung zweier Farben im Farbdreieck durch einen Punkt auf der Verbindungslinie der beiden Ausgangsfarbarten dargestellt wird, und die Abstände verhalten sich umgekehrt wie die Mengen (in trichromatischen Einheiten) der Komponenten (Hebelgesetz), Abb. 4.
Bild 4: Für die additive Mischung von Farben gilt im Farbdreieck der Hebel- oder Schwerpunktssatz: Denkt man sich an den Farborten Gewichte angebracht, die durch die Einheitenzahlen der Farben F1, F2, … gegeben sind, so befindet sich der Farbartpunkt der Mischfarbe genau im gemeinsamen Schwerpunkt dieser Gewichte.
... dieser Farbenraum ist dreidimensional, d. h. es gibt nur drei linear unabhängige Basisvektoren, genau wie in dem physikalischen Raum unserer Anschauung. Damit haben wir die Dreidimensionalität des Farb-Empfindungs-Raumes in der Dreidimensionalität des Raumes der Farbwerte wiedergefunden.
In der Darstellung durch Vektoren unterscheiden sich Farben, die durch Vektoren in der gleichen Richtung gegeben sind, nur durch ihre Helligkeit; die Farbart ist allein durch die Richtung des Vektors gegeben.
Bis jetzt ist nichts über die Einheiten gesagt worden, in denen die Farbvalenzen gemessen werden; man kann sie willkürlich festlegen. Es ist üblich, diese Festlegung wie folgt zu treffen: Je eine drittel Einheit der Primärvalenzen Rot, Grün und Blau (Blauviolett) addiert sollen eine Einheit Weiß ergeben, wobei als Weiß die Farbvalenz des energiegleichen Spektrums φλ = const gewählt wird. Die absolute Größe der Einheiten ist wegen Gl. (6) unerheblich, es wird auf diese Weise nur die relative Größe fixiert.
1/3 (R + G + B) = E(11)
Die in diesen Einheiten gemessenen Größen R, G, B nennt man die trichromatischen Maßzahlen.
.... Dabei hat aber die Länge der Valenzvektoren selbst keine tiefere Bedeutung, sondern als Maß für das Gewicht der Valenzen bei Farbmischungen dient die Summe ihrer Komponenten, eine Größe, der sonst bei Vektoren keine Bedeutung zukommt. Im Farbraum liegen die Spitzen aller Vektoren einer bestimmten Einheitenzahl m in der Ebene R + G + B = m.
... da auch die Winkel zwischen den Achsen in Abb. 3 keine Bedeutung haben, kann man das Farbdreieck rechtwinklig oder gleichseitig zeichnen, ohne an den obigen Beziehungen etwas zu ändern.
Bemerkenswert ist der Helligkeitsunterschied der Primärvalenzen R, G, B. Bei Verwendung von spektralreinem Licht der Wellenlängen λR = 700 nm, λG = 546,1 nm, λB = 435,8 nm für die primären Farbreize erscheint eine Einheit Rot etwa 15 bis 20 mal so hell wie eine Einheit Blau, eine Einheit Grün noch vier bis fünf mal so hell wie Rot, d. h. etwa viereinhalb Einheiten R erscheinen erst so hell wie G.
Allerdings ist der Vergleich der Helligkeiten von verschiedenen Farben problematisch, und so sind die den genormten Lichtquellen zugeordneten Helligkeitsbeiwerte (Leuchtdichtebeiwerte) als aus der Helligkeitsempfindungskurve Vλ entnommene Zahlen und nicht als mit derart exzessiver Genauigkeit gemessene Werte zu verstehen. Die Helligkeitsempfindungskurve Vλ ist aus Messreihen an einer größeren Zahl von farbnormalsichtigen Versuchspersonen gewonnen worden und kann als repräsentativ gelten ( "Normalbeobachter"). Für die oben angegebenen Wellenlängen sind die Leuchtdichtebeiwerte
lR = 1, lG = 4,5907; lB = 0,0601(13)
damit errechnet man die Helligkeit (Leuchtdichte) eines farbigen Lichtes zu
cL = lRR + lGG + lBB(14)
Dabei ist c ein Proportionalitätsfaktor, über den wir noch so verfügen können, dass sich L in den gewünschten Einheiten ergibt, z. B. in cd/m2, Candela pro Quadratmeter.
Bemerkenswert ist im übrigen, dass die Energien, die die drei Lichtquellen je Zeiteinheit aussenden, wieder in einem anderen Verhältnis stehen: Es ist, für je eine trichromatische Einheit
SR : SG : SB = 72,0962 : 1,3791 : 1(15)
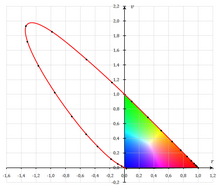
Es liegt auf der Hand, dass bei der Mischung von Spektralfarben aus vorgegebenen Primärvalenzen nur die verallgemeinerte Form der Gleichung (3) mit einem oder auch zwei negativen Koeffzienten möglich ist, denn Spektralfarben sind die sattesten Farben überhaupt. Daher liegt der Kurvenzug der Spektralfarben außerhalb des Dreiecks unserer Primärvalenzen. Die Kurve ist nicht geschlossen. Beim Mischen der Valenzen von den beiden Endpunkten bewegen wir uns auf der Purpurlinie, der Verbindungslinie der Endpunkte. Alle überhaupt möglichen Farbvalenzen befinden sich in der Farbtafel innerhalb des durch die Purpurlinie geschlossenen Spektralfarbenzuges.
Der in die Farbtafel eingezeichnete Spektralfarbenzug ermöglicht die Angabe einer anderen Charakterisierung der Farbvalenz Q, die auf Helmholtz zurückgeht und den psychologischen Begriffen Farbton und Sättigung entspricht (Abb. 8): Man legt eine unbunte Farbe U fest, und zeichnet eine Gerade durch die Punkte (Q) und (U), die bis zum Spektralfarbzug zu ziehen ist. Zwei Fälle lassen sich unterscheiden: Liegt (Q) zwischen (U) und (S), so lässt sich Q aus U und spektralreinem Licht der Wellenlänge λS mischen, man nennt λf = λS die farbtongleiche Wellenlänge. Oder aber es liegt (U) zwischen (Q) und (S), dann kann die unbunte Farbe U (Weiß) durch Q und spektralreines Licht der Wellenlänge λS' gemischt werden. Man nennt λk = λS die kompensative Wellenlänge. Als Sättigung bezeichnet man im ersten Fall den Anteil an der Spektralfarbe, der für die Mischung nötig wäre und der durch das Streckenverhältnis
pQ = (QU)/(SU)(19)
gegeben ist, im zweiten Fall bezeichnet Sättigung den Anteil, der von einem auf der Purpurlinie gelegenem Farbreiz benötigt würde, um Q aus U und P zu mischen, und der ist durch das Streckenverhältnis
pQ = (QU)/(PU)(20)
gegeben.
Die DIN-Norm (DIN 5033) zieht statt des Ausdruckes Sättigung die Bezeichnung spektraler Farbanteil bzw. bei Selbstleuchtern spektraler Leuchtdichteanteil vor.
https://www.hs-aalen.de/uploads/publication/file/9373/0805_Nolting.pdf
Im Vektordiagramm ergeben sich also
– die Farbwerte aus den Achsenabschnitten,
– die Farbart aus der Richtung des Vektors zu den drei Bezugsachsen
– die Helligkeit (Leuchtdichte) aus der Länge des Vektors,
– die Farbvalenz die Farbvalenz aus dem Punkt im Vektorraum, auf den der Vektor zeigt.
Es liegt zunächst nahe, monochromatische Primärvalenzen zu wählen, d.h. Primärvalenzen, die im Spektrum nur aus einer einzigen Linie bestehen.
Ein sinnvolle Wahl ist z.B. gegeben durch Wellenlängen, die im roten, grünen und blauen Spektralbereichs liegen, z.B. 700 nm für rot, 546 nm für grün und 436 nm für blau.
Jede Farbvalenz lässt sich dann als Linearkombination aus diesen Primärvalenzen bilden, die Vorfaktoren der Primärvalenzen sind die Farbwerte.
Der Querstrich über den Farbwerten symbolisiert, dass sich die Rechnung auf Primärvalenzen gleicher Strahlungsleistung beziehen.
Zeichnet man alle spektral reinen, monochromatischen Farben in einem Farbdreieck auf, so ergibt sich ein nach außen gekrümmter, konvexer Kurvenzug, der Spektrallinienzug. Alle aus den Primärvalenzen ermischbaren Farben bilden das innere eines Dreiecks, das von den Farbörtern der Primärvalenzen aufgespannt wird. Daraus folgt aber unmittelbar, dass es unmöglich ist, alle Farbörter des Spektralfarbenzuges zu erreichen, wenn man als Primärvalenzen monochromatische Lichter annimmt. Anders ausgedrückt: Es sind nicht alle Farbempfindungen des Spektrallinienzuges dadurch erzeugbar, dass man drei Spektralfarben additiv mischt. Das ändert sich auch nicht, wenn man andere Primärvalenzen wählt, deren Farbörter im Inneren des Farbdreiecks liegen. Rechnerisch kann man bei der Wahl der monochromatischen, spektral reinen Primärvalenzen dennoch zu jeder Farbvalenz gelangen, wenn man negative Farbwertanteile zulässt. Dies ist dann allerdings nur noch rechnerisch möglich, eine Realisierung per additiver Farbmischung gibt es nicht. Nun ist das Ziel der Farbmetrik ja nicht, eine Handlungsanweisung für additive Farbmischung zu geben, sondern ein Verfahren zu finden, nach dem jede Farbvalenz eindeutig durch ein System von Farbwertanteilen definiert ist, um die Basis zu einer messtechnischen Charakterisierung zu schaffen. In diesem Sinne sind negative Farbwertanteile also nicht schädlich, allenfalls unanschaulich.
Die CIE hat ein Normvalenzsystem definiert, in dem nur positive Normspektralwerte vorkommen. Man erhält sie aus den Spektralwerten des 2°-Normalbeobachters durch folgende Transformation: In diesem System sind alle drei Normvalenzen X, Y und Z virtuell. Abbildung 9 zeigt die Spektralwertkurven des CIENormvalenzsystems, das in DIN 5033 festgelegt ist.
DATACOLOR
Zur eindeutigen Klassifizierung von Farbe benötigten wir:
- Die Strahlungsverteilung der Lichtart (E)
- Die wellenlängenabhängige physikalische Remission / den Reflexionsgrad des Objektes (R)
- Die Valenzen des Beobachters / die Spektralwertfunk- tion des Normalbeobachters x
Für die Berechnung einer Farbvalenz von einem bunten Objekt setzt man die Strahlung S () dem Produkt E ()
• R () bei jeder Wellenlänge gleich, d. h. die Strahlung der Lichtquelle E (), die ein Objekt beleuchtet, wird um den Prozentsatz des Reflexionsgrades dieses Objektes reduziert, und zwar für jede Wellenlängenschrittweite ( ).
Literatur
[Bearbeiten | Quelltext bearbeiten]Weitere Bilder
[Bearbeiten | Quelltext bearbeiten]