Benutzer Diskussion:Hennimaniac

Herzlich Willkommen!

Willkommen in der 'Wikipedia-Diskussions-Ecke' der Hennimaniacs.

Hier kann nach Herzenslust gelobt, gedankt, kritisiert, inspiriert, ... usw. werden.

Wikipedia Werkverzeichnis

Hier die Artikel, die von mir entweder neu erstellt oder editiert wurden:

• Erich Jantsch
• Kenneth G. Wilson
• Wilson-Loop
• Spin-Netzwerk
• Spin-Schaum
• Quantenschaum
• Schleifenquantengravitation
• Big Rip
• Klaus Mainzer
• George R. Price
• Robert Axelrod
• Spieltheorie
• Evolutionäre Spieltheorie
• Selbstreplikation
• Strukturwissenschaft

Vielen Dank

Schön, dass du einen Artikel über die Evolutionäre Spieltheorie geschrieben hast. Daumen hoch !Fibonacci

Gern geschehen! Danke auch für die Einordnung des Artikels in die Kategorie 'Theoretische Biologie'. Eine überaus interessante Kategorie, wie ich finde. Zum Thema Evolutionäre Spieltheorie vielleicht noch folgendes: sind wir nicht alle ... ähm ... irgendwie das Ergebnis eines evolutionären 'Spiels' (im Sinne der Spieltheorie)? ;-) __Hennimaniac 16:09, 20. Okt. 2007 (CEST)

Spin-Schaum

Hallo Hennimaniac. Von der Physik-QS hat man mich wegen dieses Artikels zu dir verwiesen, weil du dort Ahnung haben könntest. Leider ist der Artikel für Oma unverständlich und bedarf daher einer Überarbeitung. Könntest du dich darum kümmern? Vielen Dank --BuecHerwuermLeIn DISK+/- 10:23, 3. Nov. 2007 (CET)

Hallo Bücherwürmlein,

schön das Du und Oma sich für Spin-Schaum interessieren. Falls es mir möglich ist, werde ich selbstverständlich gerne die Verständlichkeit des Wikipedia-Eintrages noch weiter verbessern. Ich werde am Besten wohl mal ein neues Bildchen dort einfügen. Zum Begriff selber vielleicht noch soviel: Die Bezeichnung 'Spin-Schaum' ist ein Fachbegriff aus der Loop-Quantengravitation. Die Loop-Quantengravitation ist eine der zwei großen 'Baustellen' der theoretischen Physik (die andere Baustelle ist die String-Theorie), welche zunünftig eine Erklärung der Gravitationskraft ermöglichen sollen, die sich im Einklang sowohl mit der Relativitätstheorie, als auch der Quantenphysik befinden soll.

In der theoretischen Physik suchen die Physiker zunächst einmal nach mathematisch beschreibbaren Mustern, um daraus abstrakte Formeln abzuleiten. Mit dem Begriff 'Spin-Schaum' versuchen die Physiker dabei das zu beschreibende Muster mehr oder weniger anschaulich zu benennen. Dieser 'Schaum' hat daher zunächst keinerlei Beziehung zum Schaum im Sinne der Chemie (also einem thermodynamisch instabilen Zweiphasensystem, bei dem gasgefüllte Blasen in einer Flüssigkeit oder einem Feststoff feinst verteilt sind), sondern die entstehenden Strukturen und Muster der Formelergebnisse ähneln lediglich dem allseits bekannten Schaum. __Hennimaniac 19:33, 4. Nov. 2007 (CET)

Spieltheorie - Extensivform

Hallo Hennimaniac,

ich habe gesehen, dass Du die Abbildung zur Extensivform im gleichnamigen Wikipediaartikel erstellt hast. Kannst Du mir verraten, welches Programm Du dazu verwendet hast? Ich bräuchte dringend vergleichbare Abbildungen und verzweifle schier daran.

Würde mich super freuen, wenn Du mir helfen könntest!

Ganz liebe Grüße, Tami

[Kontakt: fallacy[a]bin-wieder-da.de]

--77.13.73.238 08:44, 22. Mai 2012 (CEST)

Hallo Tami,

mein Wikipedia-Bildchen zur Extensivform habe ich damals noch ganz klassisch mit Paint Shop Pro „gemalt“, also jedes Bildelement einzeln angeordnet. Für eine einfache Prinzipdarstellung ist der Aufwand vertretbar. Wenn es etwas komplexer wird, böte sich auch Excel ab der Version 2007 zum strukturierten zeichnen auf einem Raster an. Wenn Du jedoch für mehrere komplexe Spielbäume eine etwas professionellere und einfachere Art suchst, diese per Programm automatisch zeichnen zu lassen, dann kannst Du das Freeware-Programm "Gambit" http://www.gambit-project.org/doc/index.html verwenden, wie es hier beispielsweise auch schon für Wikipedia eingesetzt wurde:

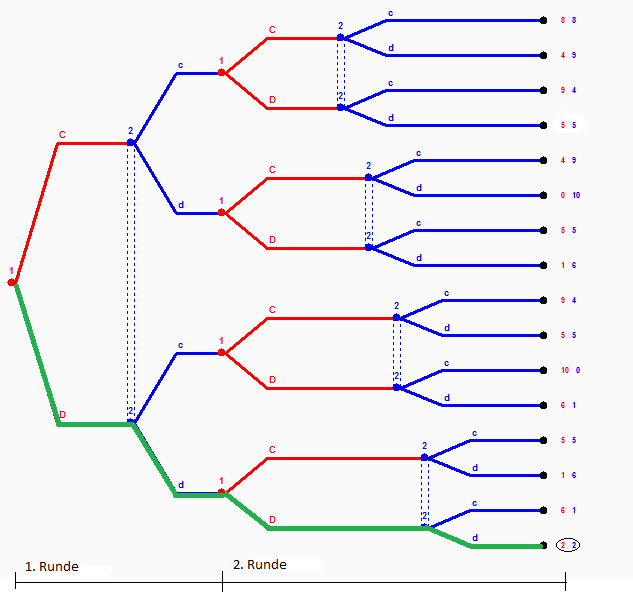
2 x wiederholtes Gefangenendilemma in Extensivform von Benutzer:STHD6/Sandbox

-- Hennimaniac (Diskussion) 21:58, 24. Mai 2012 (CEST)

Strukturwissenschaft

Hallo hennimaniac, vielen Dank zu deinen Verbesserungen im Artikel, du hast dort schon viel gutes getan. Könntest Du, da Du dich ganz gut auszukennen scheinst, auch die Belegsituation des Artikels verbessern? Besonders Sekundärliteratur, die Einordnungen und externe Bewertungen zum Ausdruck bringt, würde den Artikel hoch aufwerten. Schau doch auch mal auf der Disk vorbei. Leibe Grüße und Vielen Dank -- Leif Czerny 09:04, 17. Aug. 2012 (CEST)

Hallo Leif Czerny,

zunächst einmal vielen Dank für das nette Kompliment, mit dem ich als strukturwissenschaftlich Interessierter im Grunde genommen ja auch ganz rational umgehen kann und … oh nein … nun bin ich doch glatt schon wieder bei sowas ganz rot geworden … och menno! ;-)

Die Sache mit der Sekundärliteratur mache ich natürlich gerne, denn da gibt es durchaus eine ganze Menge an Literatur, die in diesem Zusammenhang erwähnenswert ist. Vielleicht dazu noch eine kleine strukturwissenschaftliche Frage: Wie viele Belege soll ich denn anschleppen, bevor ich die Warnhinweise im Artikel löschen kann? Reichen zehn?--Hennimaniac (Diskussion) 21:04, 17. Aug. 2012 (CEST)

Huch, das habe ich als Frage glatt übersehen: Was fehlt, sind externe und vergleichende Bewertungen der Strukturwissenschaft durch Sekundärliteratur. Bisher gibt es die dicken Blockzitate, aber die stammen ja von Protagonisten selbst und sind z.T. erläuterungsbedürftig. M.E.W. es fehlen Belegte Meinungen, Kommentare und begründete Bewertungen, was Strukturwissenschaft ist, kann, wie relevant der Gedanke ist, ob er Opponenten hat etc. Zudem gibt es ganze Abschnitte, die völlig unbelegt sind. Liebe Grüße, und bitte weiter so. -- Leif Czerny 23:21, 22. Aug. 2012 (CEST)

Hallo Hennimaniac, ich glaube, ich bin nicht der einzige, der gerade nicht mehr nachvollziehen kann, in welche Richtung der Artikel da jetzt gehen soll und auf Grundlage welcher Informationsquellen, während auf der Diskussion noch zahlreiche Fragen (zumindest die letzten fünf Abschnitte, jeweils das Ende) offen sind. Schaust du da nochmal vorbei? Liebe Grüße --Chricho ¹ ² ³ 18:33, 24. Aug. 2012 (CEST)

Hallo Chricho,

nur keine Panik! Der Grundgedanke, die Mathematik als Strukturwissenschaft zu interpretieren, ist eigentlich ganz einfach: eine mathematische Struktur = generalisierte Mengen + generalisierte Beziehungen aller Art. Fertig! :-)

Parallel versuche ich gerade, den Kerngedanken der Struktur für den Artikel Strukturwissenschaft etwas präziser herauszuarbeiten und Sekundärliteratur zu finden. Auf die Fragen der Diskussionsseite gehe ich selbstverständlich auch noch ein.

--Hennimaniac (Diskussion) 14:52, 26. Aug. 2012 (CEST)

Hallo! Dass die Mathematik eine Strukturwissenschaft ist, steht wohl so oder so außer Frage. Was mir dagegen fraglich erscheint, ist, das Wesen einer Strukturwissenschaft in mathematischen Strukturbegriffen (das, das oder das) zu suchen. Ich habe da ernsthafte Zweifel, dass das mit dem Präfix „Struktur“ in „Strukturwissenschaft“ gemeint ist, weshalb mir die Betonung dessen als TF erscheint. Ich sehe auch nicht, was an diesen Begriffen so basal sein soll (siehe Disk), wirklich grundlegend für die Mathematik ist, dass sie in formalen Systemen arbeitet, insbesondere der Prädikatenlogik mit der Mengenlehre, und von denen sagt man auch, sie haben eine „Struktur“, auch wenn sie nicht als das definiert sind, was etwa eine algebraische Struktur ist. Grüße --Chricho ¹ ² ³ 15:01, 26. Aug. 2012 (CEST)

Hallo Chricho,

die Frage, was es eigentlich bedeutet, die Mathematik als Strukturwissenschaft darzustellen, beinhaltet in der Tat die äußerst grundsätzliche Frage, was Mathematik eigentlich ist, bzw. sein sollte. Mathematik-Philosophisch gesehen gibt es dazu sicherlich viele unterschiedliche Auffassungen. Folgt man jedoch ganz konkret dem Ansatz von Bourbaki (und damit dem Mainstream der Mathematiker), dann referieren alle (!) Objekte und Inhalte der Mathematik auf Strukturen. Diese spezielle Ontologie sieht dann so aus: Mathematik = axiomatische Mengenlehre + Strukturen aller Art. Die Logik ist als Sprache der Mathematik dann sicherlich ein spezielles „Problem“. Man könnte sie zwar ebenfalls als ein Konstrukt aus einer Menge an Axiomen plus einer Struktur sehen, doch es ist durchaus ein wenig kurios, Mathematik als Strukturwissenschaft zu benennen, und dann in einer Sprache zu beschreiben, die selbst wiederum eine Struktur ist. Solche Selbstbezüglichkeiten haben ja immer ein wenig den Beigeschmack einer Tautologie. Wie man dieses Problem löst, ist mir jedoch nicht bekannt. Deine Aussage, dass die Mathematik basal mit formalen Systemen arbeitet, führt dann jedoch meiner Meinung nach lediglich zur Begriffswelt der Formalwissenschaft, und dort sind dann die Prädikatenlogik und die Mengenlehre ebenfalls grundlegend, aber nicht, weil sie für Strukturen stehen, sondern weil sie formalisierbar sind, und formalisiert wurden. Der Begriff „Struktur“ in den Strukturwissenschaften verweist meinem Wissen nach jedoch im Gegensatz dazu direkt auf die fundamentale Bedeutung von Beziehungs- und Relationengebilde. Wenn ich mich da irre, bitte ich um entsprechende Literatur-Hinweise, denn dann würde der Wikipedia-Eintrag ja am eigentlichen Thema vorbeigehen. Wie lautet in diesem Zusammenhang eigentlich deine eigene Definition einer Struktur?

--Hennimaniac (Diskussion) 16:04, 26. Aug. 2012 (CEST)

Das ist in der Darstellung Bourbakis aber nicht der Fall, dass Strukturen im deinem Sinne basal wären, er baut alles auf dem formalen System der axiomatischen Mengenlehre auf. Aus dem allgemeinen Kapitel zu Strukturen (das auch erst recht weit hinten ist):

„Le but de ce chapitre est de décrire une fois pour toutes un certain nombre deconstructions formatives et de démonstrations (cf. I, p. 17 et p. 22) qui inter-interviennent très fréquemment en mathématique.“

Es geht nicht darum, damit die Mathematik zu begründen oder zu erklären, was Mathematik ist, sondern einfach häufig auftretende Konzepte in allgemeiner Form darzustellen. Wobei ich allerdings nicht ganz verstehe, wieso er dabei auf so metamathematische Weise verfährt, vielleicht um auf mathematische Logik verzichten zu können. Ich habe keine persönliche Definition einer Struktur, im mathematischen Kontext kenne ich die ein oder andere, die ich benutzen kann, ansonsten gibt es noch einen alltäglichen Gebrauch, dieses oder jenes hat Struktur, das was man so sieht oder ein formales System etc. Vom Begriff der Strukturwissenschaft weiß ich so gut wie nichts, es wäre aber an dir, vorzulegen, wo das steht, dass sich das auf Strukturen in jenem mathematischen Sinne bezieht. Ich kann mir eben sehr gut vorstellen, dass sich das nicht auf einen mathematischen Begriff bezieht. Die Wörter „Geist“ in „Geisteswissenschaft“ und „Natur“ in „Naturwissenschaft“ beziehen sich auch nicht auf mathematisch definierte Konzepte. Wir müssen uns jedenfalls daran halten, wie die einschlägigen Vertreter des Konzepts den Begriff verstehen, und nicht daran, wie wir gerade mal das Wort „Struktur“ verstehen. Grüße --Chricho ¹ ² ³ 16:35, 26. Aug. 2012 (CEST)

Problem mit deinen Dateien (09.10.2012)

Hallo Hennimaniac,

bei den folgenden von dir hochgeladenen Dateien gibt es noch ein Problem:

1. Datei:Mathematische Grundstrukturen 01.jpg - Problem: Lizenz
2. Datei:Mathematische Grundstrukturen 04.jpg - Problem: Lizenz

• Lizenz: Eine Lizenz ist die Erlaubnis, eine Datei unter bestimmten Bedingungen zu nutzen. In der deutschsprachigen Wikipedia werden nur solche Dateien akzeptiert, die unter den hier gelisteten Lizenzen stehen. Wenn du der Urheber der Datei bist, solltest du eine solche Vorlage deiner Wahl in die Dateibeschreibungsseite einfügen.

Durch Klicken auf „Bearbeiten“ oben auf den Dateibeschreibungsseiten kannst du die fehlenden Angaben nachtragen. Wenn das Problem nicht innerhalb von 14 Tagen behoben werden, müssen die Dateien leider gelöscht werden.

Fragen beantwortet dir möglicherweise die Bilder-FAQ. Du kannst aber auch gern hier antworten, damit dir individuell geholfen wird.

Vielen Dank für deine Unterstützung, Xqbot (Diskussion) 00:59, 9. Okt. 2012 (CEST)

Hallo Xqbot, danke für den Hinweis. Ich habe die selbsterstellten Bilder nun freigegeben (als Public domain). --Hennimaniac (Diskussion) 19:36, 10. Okt. 2012 (CEST)