Diskussion:Horizont

Diese Diskussionsseite dient dazu, Verbesserungen am Artikel „Horizont“ zu besprechen. Persönliche Betrachtungen zum Thema gehören nicht hierher. Für allgemeine Wissensfragen gibt es die Auskunft.

Füge neue Diskussionsthemen unten an:

Klicke auf Abschnitt hinzufügen, um ein neues Diskussionsthema zu beginnen.

• Diskussionsregeln
• Hilfe zu Diskussionsseiten
• Sei sachlich und freundlich!
• Greife niemanden persönlich an!
• Geh von guten Absichten aus.

Zum Archiv

Wie wird ein Archiv angelegt?

Automatische Archivierung

Auf dieser Seite werden Abschnitte ab Überschriftenebene 2 automatisch archiviert, die seit 7 Tagen mit dem Baustein {{Erledigt|1=--~~~~}} versehen sind.

Vorlage:Autoarchiv-Erledigt/Wartung/Festes_Ziel

Artikel für horizontal/waagerecht?

Das deutsche Adjektiv waagerecht findet bisher nicht hierher. Bitte vervollständigen. Es ist ein wichtiger Begriff, den man sollte verlinkten können in WP. PS: Leider existier noch kein Artikel zu horizontal/waagerecht. thx--178.197.232.81 21:43, 31. Jan. 2013 (CET)

Ehrlich gesagt bin ich mir nicht sicher, ob eine Weiterleitung hierher sinnvoll ist. Dasselbe gilt auch für Waagrechte. --Digamma (Diskussion) 21:55, 31. Jan. 2013 (CET)

Wie weit denn nun? Zahlen, Daten, Fakten

Warum haben die werten Autoren denn nicht verraten, wie weit man denn nun auf der Erde sehen kann? Also vielleicht mit einer kleinen Tabelle für die Betrachtung auf Erdbodenhöhe mit menschlicher Größe und auf dem Wasser in 2m Höhe, so dass man das auch versteht wie sich der Horizont optisch verschiebt wenn man z.B. auf 100 m Höhe geht und vielleicht auf 1000 m. Dann müsste man doch weiter sehen können. Diese ganzen Erklärungen sind doch nur irgendwo abgeschrieben. Oder traut sich niemand sowas selbst zu berechnen, weil es dann dafür keine Quelle gibt? Wenn ich in einer Enzyklopädie nachschlagen will, wie weit denn der Horizont auf der Erde entfert ist, taugt der Artikel gar nichts. Interessant wäre auch zu wissen, wie weit der Horizont auf dem Mond auf auf der Sonne z.B. entfernt wäre... 94.223.116.46 11:34, 9. Mär. 2015 (CET)

Die Formel steht doch da:

$d={\sqrt {2rh+h^{2}}}\approx {\sqrt {12\,800\ \mathrm {km} \cdot h+h^{2}}},$

Meinst du, es ist nötig, noch für einige typischen Werte von h das Ergebnis anzugeben? --Digamma (Diskussion) 17:22, 9. Mär. 2015 (CET)

"Nötig" nicht, aber sehr sinnvoll. 92.106.241.80 16:02, 7. Jul. 2015 (CEST)

Es ist noch etwas schlimmer - für die Praktikabilität einer Enzyklopädie - als es 92.xyz und Digamma vermuten. Es gibt diese Tabelle mit Beispielen nämlich bereits - in Sichtweite. --888344 (Diskussion) 17:57, 7. Jul. 2015 (CEST)

Horizont in der Nautik, Kimmlinie

R*elation

• Erstens: Du hast mich auf der Seite Meer belehren wollen, wie man rechnet. Ich teile Dir aber hier ganz freundlich mit, dass Deine mathematischen Berechnungen hier auf der Seite Horizont einen Fehler enthalten! Es tut mir so leid, aber sie sind falsch! ... und sie sind viel zu komplizert dargestellt!
• Zweitens: Ich schlage Dir vor, das numerische Beispiel mit der Höhe=400m erst nach der Herleitung der Näherung aufzuführen. Es würde alles sehr vereinfachen! (Und Dein Rechenfehler verschwände automatisch!) Also etwa so:

---

...

$d={\sqrt {2rh+h^{2}}}$

Für Höhen $h$, die sehr viel kleiner als der Erdradius $r$ sind $(h\ll r)$, kann der Term $h^{2}$ gegenüber $2rh$ vernachlässigt werden; damit erhält man vereinfacht die folgende Näherungsformel $d\approx {\sqrt {2rh}}$

Setzt man hier den angegebenen Erdradius für $r$ ein, so erhält man die Horizontdistanz in Kilometern, bei Angabe der Höhe $h$ in Metern, mit der Faustformel: $d\ (km)\approx 3{,}57\cdot {\sqrt {h}}.$

Für zum Beipiel eine Höhe $h=400m$ folgt:
$d\ (km)\approx 3{,}57\cdot {\sqrt {400}}=3{,}57*20=71.4\,km$

...

---

Was meinst Du dazu?--Hp.Baumeler (Diskussion) 07:44, 18. Aug. 2018 (CEST)

Hallo, Hp. Baumeler, falls Du mit Rechenfehler die Angabe des (korrekt) gerundeten anstatt eines präziseren Wertes meintest – das ist inzwischen geändert, und ich danke Dir für den Hinweis. Mit der angebenen Formel lässt sich die geometrische Distanz exakt berechnen. Das der Abbildung entsprechende Rechenbeispiel finde ich sinnvoll, da es den dargestellten geometrischen Zusammenhang aufnimmt.

Deinem Vorschlag entnehme ich die Anregung, auch für die Näherungsformel ein Rechenbeispiel zu geben. Dies halte ich ebenfalls für sinnvoll, die bei den unterschiedlichen Berechnungsverfahren gewonnenen Ergebnisse können so gut verglichen werden. Als Ergänzung schlage ich vor:

Damit ergibt sich zum Beispiel für eine Beobachtungshöhe $h$ von 400 m: $d\ (km)\approx 3{,}57\cdot {\sqrt {400}}=3{,}57\cdot 20=71,4\ \mathrm {km} .$ 

Wenn dies Dein Einverständnis findet, füge es ein. Freundliche Grüße, --nanu _*diskuss 20:23, 18. Aug. 2018 (CEST)

Das Rechenbeispiel habe ich nun eingefügt.

Vielleicht kannst Du die Anmerkung (siehe unten) im Artikel noch ergänzen um die Angabe, bis zu welcher Flughöhe diese Näherung gilt, gerne mit Beleg. --nanu _*diskuss 11:45, 20. Aug. 2018 (CEST)

Hallo Nanu / R*elation

Ich sehe, Du interessierst Dich für Mathematik und Du gibst Dir grosse Mühe. Unten habe ich aufgeführt, wie ich den Abschnitt schreiben würde. Weisst Du, es sieht nicht professionell aus, wenn man in den Wurzeln die Zahlen der Höhe und des Erdradius einsetzt, weil der Leser das in Gedanken ja selber tut! Du hattest unter der Wurzel die Höhe h ausgeklammert, das braucht es nicht, es führt nur zur Unübersichtlichkeit!

Es wäre mir eine Freude, Dir in diesen mathematischen Angelegenheiten helfen zu dürfen. Leider musste ich aber wiederholt feststellen, dass Du Dir gar nichts erklären lässt, weil Du wohl schon alles verstehst. Es wäre für Dich sehr förderlich, wenn Du etwas bescheidener würdest und Dir mal von den Spezialisten, die es mit Dir ja gut meinen, etwas erklären lassen würdest. Deine Fähigkeiten würden rasant besser! Es ist nämlich so, dass z.B. ein Mathematiker sofort erkennt, dass Du Mathematik nicht studiert hast, aber hohes Interesse an Mathematik zeigst. Ich bin daher so freundlich und schreibe Dir die Zusammenhänge hier auf der Diskussionsseite und ich habe auf der Wikipediaseite nichts abgeändert. Du hast nun die Möglichkeit, mit meiner Unterstützung, die ich Dir gerne gebe, die Seite selber zu optimieren. Ich offeriere Dir darüber hinaus, mich anzuschreiben, wenn Du in mathematischen Sachen etwas veröffentlichen möchtest. Ich bin gerne bereit, Dich im Entwurf zu unterstützen, damit DU dann das Erarbeitete veröffentlichen kannst. Darüberhinaus weiss ich, und dies ist ja gerade das Schöne an Wikipedia, dass es jenste Biologen, Mediziner, Physiker und Astronomen gibt, die Dich in Deinen Entwürfen gerne unterstützen würden! Versuche doch, das Angebot dieser Wissenschafter anzunehmen, bevor Du etwas heikles veröffentlichst! Du wirst in diesen Entwurfsphasen viel lernen und jeder wird sich darob freuen, dass Du den Abschnitt schlussendlich selber veröffentlichst!

Wir werden sehr bald sehen, ob Du in der Lage bist, meine Offerte und die Offerte all dieser Biologen und Ärzte anzunehmen .... oder ob Du alles besser weisst. Machs gut! Freundliche Grüsse, Hanspeter. --Hp.Baumeler (Diskussion) 13:23, 20. Aug. 2018 (CEST)

Nach meinen bisherigen Erfahrungen – auf der Disk:Meer behauptetest Du, dass $=3{,}8$ und $\approx 3{,}9$ dasselbe seien; hier, dass die Berechnung falsch sei, da ein Zwischenwert gerundet angegeben war – bin ich doch wohl eher in der Lage anzunehmen, dass es, ohne Dir nun auf die Füße treten zu wollen, für mich nicht sonderlich fruchtbar wäre, Dein Angebot anzunehmen. Doch mag es durchaus sinnvoll sein, wenn Du Deine freundliche Mithilfe jemand anderem anbieten würdest. Jenste? sorry

Dass die Ausklammerung der Umformung der Terme gilt, ist doch offensichtlich; vergleiche den dritten mit der Näherungsformel. Ansonsten kommt es mir überhaupt nicht darauf an, dass ich es wäre, der hier etwas veröffentlicht. Ich hab nur was gegen falsche, unklare und unbelegte Behauptungen. Dazu gehört beispielsweise der im Folgenden von Dir unbelegt angegebene Bereich 3,6 ... 3,9. In Bodennähe wirst Du noch ganz andere Werte finden. Schon das übliche Mittel liegt über 3,9. (mit r = 7,680 Mm). Mach's besser!

---

...

Die Kimm ist die auf offenem Meer sichtbare Grenzlinie zwischen Wasser und Himmel. Auf sie beziehen sich Messungen von Höhenwinkeln, zum Beispiel mit einem Sextanten.

Wegen der Erdkrümmung – der mittlere Erdradius beträgt 6371 km, der Krümmungsradius der Erde liegt zwischen minimal 6334 km und 6400 km maximal – erscheint die Kimm umso tiefer unter dem mathematischen Horizont, je höher sich der Beobachter über dem Meeresspiegel befindet.

Daher müssen die Höhenwinkel um die Kimmtiefe $\kappa$ verkleinert werden. Diese sogenannte Höhenbeschickung beträgt

$\kappa =1{,}75\cdot {\sqrt {h}}$

(Kimmtiefe $\kappa$ in Bogenminuten; Höhe $h$ des Beobachters in Metern).

Distanz d des Horizonts von einem Punkt in Höhe h bei Krümmungsradius r = 6400 (Angaben in km)

Nach der DIN 13312 („Navigation; Begriffe, Abkürzungen …“) soll für die Kimmtiefe in der Seefahrt die Abkürzung „Kt“, im Englischen die Abkürzung „D“ (von dip of horizon), in der Luftfahrt die Abkürzung „Dip“ verwendet werden; als Formelzeichen wird für die Seefahrt k empfohlen.

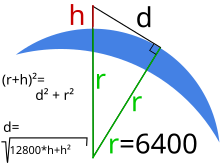
Die Distanz $d$ des Horizonts von einem Punkt mit der Höhe $h$ über dem Meer ist:

$d={\sqrt {2rh+h^{2}}}$

Für Höhen $h$, die sehr viel kleiner als der Erdradius $r$ sind $(h\ll r)$, kann der Term $h^{2}$ gegenüber $2rh$ vernachlässigt werden; damit wird

$d\approx {\sqrt {2rh}}$

Mit dem mittleren Erdradius von $r=6371\,km$ wird die Distanz zum Horizont

$d\ (km)\approx 3{,}57\cdot {\sqrt {h}}.$

Ein Beobachter auf einer Höhe von 400 Metern sieht den Horizont in einer Entfernung von 71 Kilometern.

Die geometrisch berechnete Distanz zum nautischen Horizont entspricht wegen der Lichtbrechung in der Erdatmosphäre nicht genau der Entfernung zum optischen Horizont. Abhängig von den Druck- und Temperaturbedingungen in der unteren Lufthülle kann die terrestrische Refraktion erheblich schwanken.

Die Sichtweite zum optischen Horizont liegt in einem Bereich:

$s_{\mathrm {opt} }\ (km)\approx 3{,}6\,...\,3{,}9\cdot {\sqrt {h}}$.

Im Beispiel mit einer Beobachtungshöhe von 400 Metern kann die Sichweite bis 78 Kilometer betragen.

Für Details und zusätzliche Beispiele siehe auch geodätische Sichtweite.

---

--Hp.Baumeler (Diskussion) 13:23, 20. Aug. 2018 (CEST)

Beide Demonstrationen des Rechenweges sind durchaus sinnvoll; siehe auch den älteren Diskussionsabschnitt weiter oben. Und der Vergleich der Ergebnisse aus den beiden verschiedenen Formeln erst recht (der motiviert doch deine Anmerkung). Wie gesagt, in geringer Höhe stimmt bis 78 nicht (siehe etwa hier); wohl ist der Krümmungsradius als maximal angenommen, doch nur ein mittlerer Refraktionswert. Für eine exakte Berechnung ist der Krümmungsradius nötig. Gruß, --nanu _*diskuss 16:28, 20. Aug. 2018 (CEST)

p.s.: Es ging mir eher um den Beleg (WP:Q) als um die Doppelung der Anmerkung (unten).

Letzte Änderungen am Abschnitt Horizont in der Nautik, Kimmlinie

Im Abschnitt Horizont in der Nautik, Kimmlinie wird die Distanz zum Horizont berechnet.

$d={\sqrt {2rh+h^{2}}}\approx 3{,}6\,km\cdot {\sqrt {h(m)}}$

In Bezug auf die heutige Version des Abschnittes:

• Es ist nicht nötig, die Höhe $h$ unter dem Wurzelzeichen auszuklammern. Es bringt nichts, eine Kette von Wurzeln, die alle dasselbe aussagen, hinzuschreiben.

• Das Einsetzen der numerischen Werte in der Kette der Wurzelzeichen macht den Abschnitt unübersichtlich.

• Es bringt nichts, verschiedene Krümmungsradien in die Formel einzustzen, weil diese verschiedenen Radien in der Konstante vor der Wurzel ${\sqrt {h}}$ nur Unterschiede in der zweiten Stelle hinter dem Komma bringen.

• Die exakte Formel numerisch durchzurechnen bringt nichts, weil die Näherung mit $2rh\ll h^{2}$ eine sehr gute Näherung ist. Die durch die Lichtbrechung erzeugte Unsicherheit ist grösser, als der durch die Näherung erzeugte Fehler.

--Hp.Baumeler (Diskussion) 07:58, 21. Aug. 2018 (CEST)

Wenn ich mich einmischen darf:

Ersteinmal: Warum machst du einen neuen Thread auf? Das ist doch immer noch das gleiche Thema wie darüber.

Inhaltlich: Ich sehe es auch so, dass man hier keine langen Termumformungen ausführen sollte. Ich würde aber durchaus das konkrete Beispiel "vorrechnen", das heißt den Term mit eingesetzten Zahlen hinschreiben. Es geht ja bei dem Beispiel nicht um den Wert, sondern um ein Beispiel für das Anwenden der Formel.

Grundsätzlich: Eigentlich sollte das meiner Meinung nach in diesem Artikel nicht so ausführlich stehen. Der richtige Artikel, das ausführlich darzustellen ist Sichtweite. Hier würde ich mir eher wünschen, dass die Formel für die Kimmtiefe erklärt wird. --Digamma (Diskussion) 18:04, 21. Aug. 2018 (CEST)

PS: Dein erster Vorschlag gefällt mir eigentlich ganz gut. --Digamma (Diskussion) 18:08, 21. Aug. 2018 (CEST)

@Digamma: Du hast recht, vielleicht hättes es keinen neuen Abschnittes gebraucht. Aber oben war Hickhack und ich wollte davon losgelöst die sachlichen Zusammenhänge einzeln nochmals aufzeigen. Ja, ein Rechenbeispiel ist sicherlich angepasst, dies aber nur für die Näherungsformel und nicht für die "exakte" Formel, weil man ja Näherungen macht, um eben auf einfachere Art auf (quasi) dasselbe Resultat zu kommen! Ob man dann die Höhe numerisch wirklich noch unter das Wurzelzeichen zu setzten hat ist nicht sicher. Wir wollen den Leser doch nicht schulmeistern. Und etwas ab der 6-7-ten Primar weiss jeder, dass ${\sqrt {h}}$ mit $h=400$ gleich 20 ist. :-) Danke für Deine Mitarbeit Digamma! ... und lässig, was Du da machst! Gruss, Hp. --Hp.Baumeler (Diskussion) 10:36, 22. Aug. 2018 (CEST)

Es wäre schön, wenn ich da tatsächlich etwas machen würde. Leider ist das eine seit langem brachliegende Baustelle --Digamma (Diskussion) 21:35, 22. Aug. 2018 (CEST)

Quelle

Ich habe ein paar Abschnitte aus diesem Artikel [1] in den DeepL-Übersetzer getan:

"Bei dem Versuch, die Wahrnehmung eines gekrümmten Horizonts zu verstehen, müssen zwei Dinge beachtet werden. Erstens: Ein großer Teil der Menschen trägt eine Brille. Brillen erzeugen eine Vielzahl von Verzerrungen, wenn der Beobachter nicht durch den Mittelteil des Glases schaut. Zweitens kann oberhalb der Höhe des Mt. Everest kein Beobachter direkt auf den Horizont schauen - er muss durch ein Fenster oder ein Vordach schauen. Planparallele Fenster wie in den meisten Flugzeugen geben einen flachen Horizont nicht gekrümmt, aber ein gekrümmtes Fenster oder ein Vordach schon. Was verstehen wir unter "Horizont"? Normalerweise meinen wir damit die scheinbare Grenze zwischen dem Meer und dem Himmel, oder der entfernten Landschaft und dem Himmel. Bohren und Fraser haben jedoch gezeigt, dass ein Beobachter in einer Höhe von mehr als etwa einer Meile den harten Erdhorizont, d.h. den Tangentenpunkt der Sichtlinie, nicht sehen kann. Rayleigh-Streuung und Streuung durch Aerosole reduzieren die Höhe normalerweise auf weniger als eine Meile. Der scheinbare Horizont aus der Höhe von Verkehrsflugzeugen ist nicht als harte Linie, sondern als kontrastarmer Übergang vom hellen Himmel oben zum leicht dunkleren "Himmel" unten zu erkennen. Die Lage dieser Grenze ist schwer zu definieren (Abb.1). Der Vergleich der beiden Bilder in Abb.1 zeigt eine merkwürdige Kontrastumkehr. Der Himmel ist im Allgemeinen über dem Horizont auf Meereshöhe heller, aber über dem Horizont in großer Höhe dunkler. Vom Meeresspiegel aus befindet sich der größte Teil der Atmosphäre über uns, und so sehen wir viel Streulicht. Aus großer Höhe befindet sich der größte Teil der Atmosphäre unter uns, und der Himmel ist dunkler. Die Kontrastumkehr wird noch dadurch verstärkt, dass das Meer relativ dunkel ist, während aus großer Höhe die Luft und die Wolken unterhalb des Horizonts relativ hell sind. Abb. 2 zeigt vertikale Scans durch die beiden Bilder. Die Helligkeitsunterschiede sind offensichtlich, ebenso wie die Amplitude der Helligkeitsänderungen an den beiden Horizonten. Die Helligkeitsänderung für den hochgelegenen Horizont beträgt weniger als 10 % derjenigen des Horizonts auf Meereshöhe. Was der Beobachter als Horizont wahrnimmt, ist in Wirklichkeit ein Übergang von einer optisch dichten Sichtlinie durch die Atmosphäre unterhalb des "Horizonts" zu einer optisch dünnen Sichtlinie oberhalb des "Horizonts". "Dieser scheinbare Horizont wird vollständig in der Atmosphäre erzeugt, und die harte Erde spielt bei seiner Entstehung wenig oder gar keine Rolle. Die tatsächliche Position entspricht wahrscheinlich einer Sichtlinie mit einer optischen Tiefe nahe der Einheit, die mehrere Kilometer über der Erdoberfläche verläuft."

Vielleicht kann man ja etwas davon verwenden. Sciencia58 (Diskussion) 23:15, 8. Apr. 2021 (CEST)

Schnitt Körper - Ebene

"Mathematischer Horizont oder astronomischer Horizont: die Schnittlinie der Himmelskugel mit jener Ebene, die im Beobachtungsort rechtwinklig zur Lotrichtung steht." - Echt? Beim Schnitt einer Kugel mit einer Ebene erhalte ich eine Linie?! Eben mit einer Orange ausprobiert - es sind nur Scheiben reisgekommen, keine Nudeln. So ein Saft(laden hier)! --217.149.170.251 16:44, 10. Aug. 2022 (CEST)

Probiers mal mit einer Glaskugel vom Weihnachtsmann, oder heißt die Christbaumsphäre? Na, egal – muss aber ganz ganz ganz dünn sein, sonst gibts nämlich Scherben. --2003:E4:D707:6E01:A191:E271:D65D:ECED 22:19, 10. Aug. 2022 (CEST)

Mit anderen Worten: Die Himmelskugel ist keine 3-dimensionale Vollkugel, sondern eine 2-dimensionale Kugeloberfläche (Sphäre) --Digamma (Diskussion) 10:43, 12. Aug. 2022 (CEST)

Abschnitt Horizont in der Nautik, Kimmlinie

Auf dieser Diskussionsseite war ja schon eine lange Diskussion zum Abschnitt Horizont#Horizont_in_der_Nautik,_Kimmlinie zugange.Ich finde die Herleitung verständlich und habe keine Fehler entdeckt, jedoch finde ich die Einheiten etwas befremdlich. Ich beziehe mich auf die Formel

$d\approx 3{,}57\cdot {\sqrt {\frac {h}{\text{m}}}}\,{\text{km}}.$

Die hier verwendeten Einheiten ergeben meiner Einschätzung nach keinen Sinn. Wenn man das ausklamüsert, ist die Einheit für die Distanz "${\frac {\text{km}}{\sqrt {m}}}$". Was soll das für eine Einheit sein? Oder wenn man die Einheit unter der Wurzel separat betrachtet, dann hat man "${\frac {1}{\text{m}}}$", wenn man davon ausgeht, dass ${\frac {h}{\text{m}}}=h{\frac {1}{\text{m}}}$ bedeutet. (Was sollte es sonst bedeuten?). Lange Rede kurzer Sinn: Aus meiner Sicht stört das "${\text{m}}$" im Nenner der Formel. Meine Herleitung sieht wie folgt aus:

Ausgangsformel:

$d\approx {\sqrt {2\cdot r\cdot h}}$

Der mittlere Erdradius beträgt $r=6371\ {\text{km}}$. Ist $h$ in Metern gegeben, so beträgt die Höhe ${\frac {h}{1000}}\ {\text{km}}$. Einsetzen in die Formel liefert

${\begin{aligned}d&\approx {\sqrt {2\cdot 6371\ {\text{km}}\cdot {\frac {h}{1000}}\ {\text{km}}}}\\&={\sqrt {{\frac {2\cdot 6371}{1000}}\cdot h\ {\text{km}}^{2}}}\\&={\sqrt {\frac {2\cdot 6371}{1000}}}\cdot {\sqrt {h}}\ {\text{km}}\\&\approx 3{,}57\cdot {\sqrt {h}}\ {\text{km}}\\\end{aligned}}$

Wenn jemand einen Fehler findet, bitte melden. Ansonsten würde ich die Einheiten in der jetzigen Form anpassen. --Mathze (Diskussion) 23:09, 22. Aug. 2024 (CEST)

Ich habe das jetzt geändert. --Mathze (Diskussion) 19:31, 10. Dez. 2024 (CET)

Wenn $h$ eine Größe mit Einheit ist, dann ergibt ${\sqrt {h}}$ keinen Sinn. Vielmehr muss man die Einheit Meter erst entfernen, bevor man die Wurzel ziehen kann. Das geschieht dadurch, dass durch Meter geteilt wird, dann bleibt eine reine Zahl übrig, aus der man die Wurzel ziehen kann. Insofern war die alte Fassung m.E. schon korrekt, wenn auch ungewöhnlich formuliert. --Digamma (Diskussion) 19:52, 15. Dez. 2024 (CET)

Danke für die Klarstellung, ich habe die alte Version wiederhergestellt. Viele Grüße --Mathze (Diskussion) 23:54, 15. Dez. 2024 (CET)

Hallo @Digamma, ich habe nochmal über die Formulierung nachgedacht und bin nicht so ganz zufrieden mit dem, was dort zunächst stand und nach meiner Rückgängigmachung nun dort wieder steht. Ich habe Deine Erklärung nachvollziehen können, aber ich habe noch zwei Punkte, die ich gerne hier klären würde.

• Ich habe bisher noch keine Formel gesehen, in die Einheiten mit als Teil der Formel aufgenommen werden. Was ich kenne, sind Formeln, in denen die Variablen für physikalische Größen stehen. Beispiel: $F=m\cdot a$, und für $m$ wird eine Größe mit Einheit kg eingesetzt in für $a$ eine Größe mit Einheit m/s^2. Deshalb wäre die Frage, ob das Vorgehen bei der Formel $3{,}57\cdot {\sqrt {h/\mathrm {m} }}\,\mathrm {km}$ überhaupt einem Vorbild in der Fachliteratur folgt oder eine Eigenkreation ist. Da hast Du, @Digamma, mehr Erfahrung und einen besseren Überblick über die Literatur als ich.
• Aus Verständlichkeitsgründen finde ich die Darstellung unbefriedigend. Man muss diese Formel gewissermaßen entschlüsseln. Du hast ja selbst davon gesprochen, dass es ungewöhnlich formuliert ist.
• In dem Artikel steht, dass das die richtige Formel ist, wenn $h$ in Metern angegeben wird. So wie ich Dich verstanden habe, passt alles zusammen, wenn man in der Formel für $h$ bspw. "400 m" einsetzt. Das widerspricht aber dem sonstigen Sprachgebrauch von "Größe in Einheit". Wenn ich z. B. eine Tabelle mit der Überschrift "Gewicht in kg" lese, dann erwarte ich in der entsprechenden Spalte einfach nur Zahlen und denke mir dazu, dass das eine Angabe in Metern ist. Noch prominenter das Beispiel mit Porzent: Bei einer Überschrift "Angaben in Prozent" stehen in der entsprechenden Spalte typischerweise nur die Prozentfüße, also z. B. "13, 42, 45" und eben nicht 13 %, 42 %, 45%. Um auf den Artikel zurückzukommen. "Bei Angabe der Höhe h in Metern" würde ich gerade so verstehen, dass man für $h$ eine Zahl einsetzt (z. B. "400") und eben nicht "400 m". Dann kann man sich aber auch die Meter in der Formel sparen, da keine Meter mehr durch Kürzen eliminiert werden müssen.

Mein Vorschlag wäre, in der Formel einfach jegliche Einheiten wegzulassen. Es ist unmissverständlich und richtig formuliert, wenn man sagt:

"Setzt man hier den mittleren Erdradius (6371 km) für $r$ ein, so erhält man die Horizontdistanz in Kilometern, bei Angabe der Höhe $h$ in Metern, mit der Faustformel:

$d\approx 3{,}57\cdot {\sqrt {h}}.$"

--Mathze (Diskussion) 17:10, 16. Dez. 2024 (CET)

Ja, das sehe ich auch so. --Digamma (Diskussion) 17:33, 16. Dez. 2024 (CET)

Ich habe das im Artikel entsprechend geändert. Um die obere Formel ("Höhenbeschickung") würde ich mich auch gerne kümmern, jedoch fehlt mir hier ein Ansatzpunkt, wie man sie überhaupt herleitet. (Im Artikel fällt sie leider vom Himmel und es ist auch kein Beleg genannt.) --Mathze (Diskussion) 20:42, 16. Dez. 2024 (CET)

Kimmlinie

Die Formel für die "Höhenbeschickung" ist für mich leider nicht nachvollziehbar und ich habe sie auch in der Literatur nicht gefunden. Die Formel wurde 2011 von @Geof eingefügt. Vielleicht kann er ja etwas Licht ins Dunkel bringen und/oder eine Quelle nennen? --Mathze (Diskussion) 21:16, 16. Dez. 2024 (CET)

In dem Buch Quetz, Völker: Zum Nachdenken - Unser Sonnensystem habe ich folgende Formel für die Kimmtiefe gefunden: $k'=1,93'{\sqrt {h/\mathrm {m} }}$ --Mathze (Diskussion) 21:25, 16. Dez. 2024 (CET)