Diskussion:Pfeil-Paradoxon

keine kleinsten Einheiten

"In der Quantenphysik mit kleinsten Einheiten für Masse, Energie, Raum und Zeit stellt sich Zenons Pfeil-Paradoxon neu." wieder raus. Es gibt auch in der Quantenphysik keine kleinsten Einheiten dieser Größen. --Nopherox 10:38, 29. Mär 2005 (CEST)

Planck-Einheiten ??? bin kein quantenphysiker, aber wie ist denn das sonst zu verstehen? da kann man schon sagen, dass sich das paradoxon neu stellt.--MiBü 07:01, 30. Mär 2005 (CEST)

Mir fiel zu dem Thema keine gescheite Formulierung ein. Ich kann leider auch nichts Erhellendes über die Physik in der Gegend der Planckgrößen beitragen. Mein Einwand war lediglich, dass es sich bei den Planckgrößen nicht um die kleinsten Einheiten handelt. Dort entsteht, soviel ich weiß, nach heutigem Verständnis keine Diskontinuität, obwohl mir die Aussagen der Loop-Gravitationstheorie an der Stelle nicht klar sind. Worauf du vielleicht angespielt hast, ist das Problem, dass unterhalb der Plancklänge eigentlich alles innerhalb des eigenen Schwarzschildradius liegt und daher in ein schwarzes Loch fallen müsste. Trotzdem tut es das nicht. In diesem Sinn war Zenons Paradox sehr weitblickend. Aber ich glaube, an der Stelle werden die Physiker nicht so schnell arbeitslos. Gruß Nopherox 10:16, 30. Mär 2005 (CEST)

wir kommen der sache näher. interessanter diskurs. (noch was: "reminiszenz erhalten" hat mir nicht gefallen. ich glaub (rein sprachlich) nicht, dass man "reminiszenz erhalten" kann.) --MiBü 19:48, 30. Mär 2005 (CEST)

Mein erstes Mal in der Wikipedia-Diskussionsecke: Das Paradoxon ist kein Paradoxon mehr, wenn man eine Größe namens "Impuls" definiert. Und die ist halt wie Masse, Farbe, Länge etc. auch in Standbildern vorhanden. Ein fliegender Pfeil auf einem Foto hat halt keine Geschwindigkeit (da keine Zeit vorhanden) wohl aber einen Impuls (der sich nur zeigt, wenn man Zeit verstreichen lässt) Das hat nix mit Quantenmechanik und schon gar nix mit Unschärfrelation zu tun!!! (nicht signierter Beitrag von 80.184.131.149 (Diskussion) 18:01, 4. Nov 2005)

genau, und in Worten von Zenon: Für Ruhe muss der Pfeil länger als einen Zeitpunkt lang an einem Ort sein. --androl 19:17, 16. Jul 2006 (CEST)

das paradoxon soll ja kontinuitaet widerlegen, aber das schafft es nur dadurch, dass es das system "fliegender pfeil" (auf eine anreihung von orten) diskretisiert und die zeit wird einfach abgeschaltet --> ich sag nur ex falso quodlibet --Kunobert 00:04, 1. Aug 2006 (CEST)

Die Frage ist nur: Was ist Impuls? Gerade in einem "Standbild"? Eine intrinsische Groesse, die sich jedes Elementarteilchen quasi "merken" muss? Wohl kaum, denn Geschwindigkeit und damit Impuls ist ja nur relativ zu einem Bezugssystem definiert. Der Ansatz zu sagen, es gebe keine Standbilder, ist da irgendwie schon befriedigender, auch wenn es natuerlich nach feiger Ausrede klingt ;) --Mudd1 16:14, 16. Mär. 2007 (CET)

Heisenberg muss hier nicht bemüht werden

Der Autor des Artikels bemüht die Quantenphysik, was in dem Makroskopischen Experiment nicht angemessen ist. Die Ausführung von Zenon, daß der Pfeil an einem Ort in Ruhe sei und sich nicht bewege, ist eher ein deuticher Hinweis darauf, daß das Konzept des infinitesimal kleinen oder - anders gesagt - der Grenzwertbegriff in der damaligen Zeit nicht geläufig war. Ausformuliert wurde dieses Konzept erst Jahunderte später von Newton und Leibnitz (unabhängig voneinander). Zu jedem Zeitpunkt t befindet sich der Pfeil genau an einem Ort s(t), und zum nächsten Zeitpunkt t'>t bereits an einem anderen Ort s(t'). Die Geschwindigkeit v = (s(t') - s(t)) / (t' - t) bleibt einem Inertialsystem (also ohne Beschleunigungen oder Abbremsungen) dabei für alle t' gleich, also auch im Grenzfall lim v für {t' -> t}. Wenn Zenon also von einem Pfeilort s(t') zu einem ZeitPUNKT t' redet, haben wir auch in diesem Fall die konstante Geschwindigkeit v vorliegen.

Ich glaube die ganze Angelegenheit ist viel komplizierter, denn mit der Infinitesimalrechnung wird genau das umgangen, von dem Zenon spricht: Die Unmöglichkeit von einem Wert 0 oder unendlich eine Entwickung zu starten, sei es eine Geschwindigkeit, Beschleunigung, Trägheit etc. In der Infinitesimalrechnung wird durch ein Kunstgriff ein Zustand erschaffen, der fast null oder unendlich ist, der gegen null oder unendlich strebt. Somit umgeht man mit den beiden Werten zu rechnen. Betrachten wir uns beispielsweise das Aufladen eines Kondensators. Hier wird niemals eine Formel angegeben wonach man berechnen kann wann den der Kondensator vollständig aufgeladen ist. Theoretisch ist das nämlich nicht möglich. Es fehlt immer ein infinitessimal kleiner Rest damit der Kondensator ganz aufgeladen wird (Zenon lässt grüssen). Es ist uns in der Praxis egal, ob ein winzig kleiner Rest fehlt, da Temperaturrauschen, Induktionen etc. eine so genaue Betrachtungsweise überhaupt nicht zulassen. Die unglaublich klaren Gedankengänge Zenon's haben heute noch Bestand, selbst, wenn man es mit dem gesunden Menschenverstand nicht erklären kann. Ich bin dafür das der Hinweis der Auflösung des Paradoxons durch die Infinitessimalrechnung nicht gelungen ist, sondern dass dadurch eine Möglichkeit gefunden wurde trotz des Paradoxons Lösungen zu finden. --Stefanobasta 11:49, 3. Jun. 2007 (CEST)--Stefanobasta 11:49, 3. Jun. 2007 (CEST)

Ergänung zur Disskussion: Das mathematische Modell der Grenzwertbildung ist eben das - ein Modell. Passend aber nicht erschöpfend erklärend. Hier noch ein Ansatz, das Paradoxon aufzulösen:

Die Betrachtung des Pfeils in unserer Anschauungswelt kann man auf eine Bewegung im Raum - oder noch einfacher: Strecke - unter Ablauf der eindimensionalen Zeit reduzieren. Der Begriff der Geschwindigkeit bzw. der Bewegung geht nun auf die Relation der Zeit mit der Position iauf der Strecke zurück. Strecke je Zeit definiert die Geschwindigkeit. Mehr Strecke je Zeit bedeutet eine höhere Geschwindigkeit.

Jetzt Betrachtet Zenon aber einen einzigen Zeitpunkt. Er verlässt also das Modell einer eindimensional ablaufenden Zeit zu Gunsten einer nulldimensionalen Punktbetrachtung. Damit gibt er implizit aber auch das Konzept der Bewegung auf. Die Frage nach der Bewegung kann jetzt gar nicht mehr beantwortet werden (etwa so wenig wie die Frage nach dem Druck der Farbe Rot, denn für das Konzept Farbe existiert der Begriff Druck nicht).

Bemerkung zur Ergänzung: Natürlich ist es so, wenn man eine Dimension weglässt kann man sie nicht mehr sehen. Doch geht Zenon genau davon aus eine Bewegung in zwei Teilabschnitte aufzuteilen und das unendlich oft. Die Zeit ist in der Betrachtung, wir sind wieder bei der Infinitessimalrechnung und können abstrakt betrachtet keinen Ausweg aus dem Paradoxon finden. Der Begriff "Zeitpunkt" ist grenzwertig gewählt. Der gesunde Menschenverstand sagt uns, dass der Pfeil fliegt, mathematisch brauchen wir einen Trick um zur gleichen Erkenntnis zu kommen -> ein Paradoxon.

Heisenberg muss hier doch bemüht werden

Es geht nicht darum, dass es in der Quantenmechanik (QM) kleinste Einheiten von etwas gibt. Der Punkt ist, dass nach heutiger Erkenntnis Zenon zumindest prizipiell recht hatte. Der Grund ist die Bedeutung des Messprozesses in der QM. Einfach gesagt: Ein Zustand wird in der QM durch eine Wellenfunktion beschrieben und nach einer Messung geht diese Wellenfunktion in den zum Messwert gehoerenden Eigenzustand ueber. Wenn man also ein Atom immer wieder misst, wobei die Wahrscheinlichkeit fuer einen bestimmten Messwert sehr gross ist, dann wird das System sehr lange in diesem Zustand bleiben, im Grenzfall unendlich haeufiger Messungen sogar fuer immer (siehe [Quanten-Zeno-Effekt]). Uebertragen auf den Pfeil bedeutet dies in etwa: Wenn ich mir permanent den Pfeil anschaue und damit seinen Ort messe und annehme das die Wahrscheinlichkeit das er am selben Ort ist sehr hoch ist, so kann ich durch unendlich haeufige Messungen erreichen, dass sich der Pfeil nicht bewegt (Der Vergleich hinkt etwas, aber prinzipiell). Ich finde das gehoert auf jeden Fall in den Artikel... (nicht signierter Beitrag von 138.246.7.155 (Diskussion | Beiträge) 13:30, 27. Nov. 2009 (CET))

Kritik an dem Wiki-Artikel

Dieser Wikipedia-Artikel wird der gedanklichen Tiefe des Zenonschen Paradoxons in keiner Weise gerecht. Das Pfeil-Paradoxon spricht den tatsächlich widersprüchlichen Charakter der klassischen Bewegung an. Eine klassische Bewegung bedeutet das durchschreiten von unendlich vielen Punkten in jedem beliebig kleinen Zeitintervall. Mathematisch gesehen ist das nicht verwerflich, da es dort nur potentielle Unendlichkeiten gibt: d.h. zwischen zwei unterschiedlichen Punkten auf einer Linie gibt es potentiell überabzählbar unendlich viele andere Punkte. Der Widerspruch kommt dadurch zustande, das wir mathematischen Objekten (Punkt, Linie, etc.) eine physikalische Realität zuordnen. Klassische Bewegung ist deshalb das umwandeln von potenieller Unendlichkeit in aktuale Unendlichkeit (den nach unserem Modell hat der Pfeil Tatsächlich unendlich viele Punkte durchschritten). Die klassische Bewegung kann deshalb physikalisch nur als idealisierte Modellvorstellung gelten. Die Vorstellung eines Punktes selbst hat physikalisch keine Relevanz, da man Abstände nicht beliebig klein werden lassen kann ohne das Kausalitätsprinzip über Bord zu werfen (Stichwort Planck-Länge).

Es wäre schön, wenn diese Kritikpunkte im Artikel selbst auch erwähnt werden. Wenn ich Zeit finde werde ich darüber mal ein bisschen recherchieren und gegebenenfalls selbst ein/zwei Absätze beisteuern ;-) -- Liberty of knowledge 13:43, 17. Mär. 2010 (CET)

aktuelle Version

Ich habe mal einige Kritikpunkte hinzugefügt und versucht mehr Informationen zu dem Thema einzutragen. Wäre schön, wenn da noch jemand drüberlesen würde und Verbesserungen vornimmt. Evtl. ist das ein oder andere nicht direkt verständlich. Ich habe hier versucht meine unten genannten Kritikpunkte aufzugreifen. Vielleicht kommt ja damit ein bisschen Schwung in das Thema ;-) -- Liberty of knowledge 19:04, 30. Sep. 2010 (CEST)

Abschnitt Kritik an der klassischen Beschreibung

Der Abschnitt wurde entfernt:

Die Infinitesimalrechnung selbst ist Widerspruchsfrei, jedoch bedeutet ihre Anwendung auf die klassischen Konzepte der Zeit und des Raumes die Umwandlung von potentieller Unendlichkeit in aktuale Unendlichkeit.

Zeitpunkte können, nach dem klassischen Modell, nicht nacheinander vergehen (Die Punkte einer Linie können nicht wohlgeordnet sein). Spricht man infinitesimal kleinen Zeitpunkten eine Realität zu, so kann auf einen Zeitpunkt kein zweiter direkt folgen, da dieser Zwangsläufig mit ersterem zusammenfällt. Es gibt keinen nächsten Zeitpunkt, in dem Sinne, dass dieser von ersterem unterschieden werden könnte. (Zwischen zwei beliebig nahen unterscheidbaren Punkten gibt es immer überabzählbar unendlich viele andere Punkte).

Die moderne Physik zeigt auch, dass die oben behauptete Art der Bewegung nicht auftritt. Die Heisenbergsche Unschärferelation verbietet es jedem Objekt zugleich einen exakten Ort und Impuls zu haben. Zudem gibt es Indizien dafür, dass Zeit"punkte" nicht beliebig klein gewählt werden können. In einem extrem kurzen Zeitintervall (Planck-Zeit) kann man nicht mehr von kausalen zusammenhängen Reden. In diesem Sinne vergeht dann auch keine Zeit (Es gibt innerhalb der Planck-Zeit kein vorher und kein nachher).

Unabhängig von sachlichen Fragen entspricht Formulierung und Gedankengang nicht den Anforderungen an Klarheit. Außerdem können solche Aussagen ohne hinreichende Belege keinesfalls stehen bleiben. --WolfgangRieger 09:46, 2. Okt. 2010 (CEST)

Hallo alle zusammen,

WolfgangRieger schreibt:

»Unabhängig von sachlichen Fragen entspricht Formulierung und Gedankengang nicht den Anforderungen an Klarheit. Außerdem können solche Aussagen ohne hinreichende Belege keinesfalls stehen bleiben.«

Die Behauptung, der gelöschte Abschnitt sei nicht klar genug, verstehe ich überhaupt nicht. Ich bin zwar kein Pysiker und kann auf diesem Gebiet allenfalls den Status eines interessierten Laien für mich beanspruchen, aber im Zusammenhang mit Zenons Pfeilproblem habe ich mich immer mal wieder mit der Unschärferelation befasst. Beides gehört meiner Ansicht nach eng zusammen. Insbesondere trifft der folgende Satz den Kern des Problems:

»Die Heisenbergsche Unschärferelation verbietet es jedem Objekt zugleich einen exakten Ort und Impuls zu haben.«

Was Zenon von Elea macht, ist, die Strecke, die der Pfeil zurücklegt, in im Prinzip überabzählbar unendlich viele Orte und die Zeit, in der der Pfeil diese Strecke zurücklegt, in überabzählbar unendlich viele Zeitpunkte zu zerlegen. Zenon sagt (nach dem Wikipedia-Text), der Ort, an dem sich der Pfeil zu einem exakt bestimmbaren Zeitpunkt befindet, könne immer exakt bestimmt werden. Wenn ich den Ort mit p und den Zeitpunkt mit t abkürze, dann ist die Frage, wie der Pfeil von Ort p₁ zum Zeitpunkt t₁ zum Ort p₂ zum Zeitpunkt t₂ kommt. Er kann dies nur, wenn er (bei konstanter Geschwindigkeit) nach der Hälfte der Zeit die Hälfte der Strecke zurückgelegt hat, sich also zum Zeitpunkt t_1,5 am Ort p_1,5 befindet. Wie kommt der Pfeil aber nun dorthin? Offensichtlich muss er zuvor in einem Viertel der Zeit ein Viertel der Strecke zurückgelegt haben usw. Der Punkt ist, dass das theoretisch immer weiter getrieben werden kann. Bei jedem beliebig kleinen Bruch, der größer als Null ist, gibt es immer überabzählbar unendlich viele Brüche, die kleiner sind und trotzdem gößer als Null. Deshalb bleibt theoretisch immer eine unerklärte Lücke, die zwar beliebig klein werden kann, aber nicht verschwindet. Unter diesen Voraussetzungen könnte sich der Pfeil tatsächlich nicht bewegen.

Dass er es doch tut, liegt daran, dass diese Art des überabzählbar Unendlichen zwar in der Mathematik existiert, aber nicht in den physikalischen Gegebenheiten der realen Welt. Physikalisch ausgedrückt: Ort und Impuls des Pfeils können nicht gleichzeitig beliebig genau bestimmt werden. Das ist kein Erkenntnisproblem, sondern liegt in den Eigenschaften der realen Welt selbst. Unphysikalisch [1] gesagt: Wenn der Zeitpunkt exakt feststeht, zu dem der Ort, an dem sich ein sich bewegendes Objekt befindet, festgestellt werden soll, dann »schwimmt« dieser Ort. Das Teilchen befindet sich in sehr engen Grenzen, die vom Planckschen Wirkungsquantum bestimmt werden, an mehreren Orten gleichzeiteig, und zwar real. Wenn der Ort exakt feststeht, dann »schwimmt« der Zeitpunkt, zu dem sich das Objekt an diesem Ort befindet. Das heißt, das Objekt befindet sich in sehr engen Grenzen zu verschiedenen Zeitpunkten an diesem Ort.

Die Konsequenz ist, dass im Grunde Hegel recht hatte. Bewegung bedeutet tatsächlich, dass etwas zu einem bestimmten Zeitpunkt an einem bestimmten Ort ist und zugleich nicht ist. Formal:

A: Das Objekt P befindet sich zum Zeitpunkt t an Ort p.

A ∧ ¬A

Anders gesagt: Bewegung existiert, weil sie in sich widersprüchlich ist. Die Möglichkeit, den Widerspruch aufzuheben, liegt in der Bewegung selbst.

Viele Grüße

--Jake2042 (Diskussion) 13:54, 28. Okt. 2022 (CEST)

[1]

Unphysikalisch, weil ich im Folgenden nicht mit den in der Physik üblichen Variablen Zeit und Impuls arbeite, sondern stattdessen mit den Variablen Zeit und Ort. Im Grunde ist das aber eine meiner Ansicht nach zulässige ›Übersetzung‹ dessen, was die Unschärferelation meint.

Der Artikel braucht einen Kritik-Abschnitt, da sonst zu einseitig ... bitte um Beteiligung von Physikern / Philosophen und Mathematikern

Ok, vielleicht wird nicht direkt klar, was gemeint ist, allerdings finde ich nicht, dass hier Belege fehlen. Das es keine klassische Bewegung gibt, ist jedem Physiker klar. Ein Teilchen ist in einem klassischen Sinne nur dann an einem bestimmten Ort, wenn es gemessen wird, bzw. mit der Welt in der Art interagiert dass seine Wellenfunktion kollabiert. Ebenso ist doch offensichtlich, dass die Mathematik hier keinen Ausweg bietet, da sie nur Aussagen über mathematische Objekte macht, also nichts mit der physikalischen Realität gemein hat. Oder um es mit David Hilbert zu sagen: Punkt, Gerade und Ebene sind nur Namen es kommt nur auf die Axiome an. Hegel bspw. war ja auch Mathematikprofessor und kannte mit Sicherheit die Infinitesimalrechnung (sie wurde 130Jahre vor dem im Artikel genannten Hegel-Zitat veröffentlicht). Trotz dieses Wissens hat er den Widerspruch immanent in der Bewegung gesehen.

Es ist ein Irrglaube, dass die Paradoxien die mit der Annahme eines Kontinuums auftreten, gelöst sind. Deshalb wäre es schön, wenn das zumindest in dem Artikel erwähnt werden würde. Wenn man jetzt den Artikel liest denkt man, dass das Thema unter Philosophen und Physikern erledigt wäre, in dem Sinne, dass man auf dem Stand der klassischen Physik verbleibt.

-- Liberty of knowledge 14:05, 2. Okt. 2010 (CEST)

Wäre das Konzept der Emergenz hier nicht der bessere Ansatz zur Auflösung des Paradoxons? Bewegung kann nämlich durchaus als ein emergentes Merkmal, das erst über einen Zeitraum auftritt, aber noch nicht in Zeitpunkten angelegt ist, verstanden werden. Siehe hierzu auch: https://ad.hominem.info/de/logik/begriffe/emergenz. --Sascha (Diskussion) 15:48, 24. Dez. 2021 (CET)

Habe einen Hinweis auf die Unbestimmtheitsrelation wieder eingefügt, weil das essenziell für die Würdigung der Pfeilparadoxie ist. Das Zitat von Aurelius Augustinus scheint mir eher unpasend zu sein und gehört wohl nicht hierher.

--mer 14:56, 9. Jun. 2011 (CEST)

Heisenberg muss hier nicht bemüht werden

Die Unschärferelation ist zwar immer gültig, aber nicht immer relevant. Sie in diesem Fall anzuwenden ist ungefähr so, als würde man einen Ball, der durch einen Türrahmen rollt, als Beugung einer Materiewelle am Einzelspalt auffassen. (nicht signierter Beitrag von 88.65.2.181 (Diskussion) 19:40, 3. Apr. 2012 (CEST))

Heisenberg muss hier doch bemüht werden

Hallo alle zusammen,

der oben stehende Beitrag von 88.65.2.181 ist zwar schon in die Jahre gekommen, sollte aber nicht unbeantwortet bleiben. Die Unschärferelation bekommt gerade im argumentativen Zusammenhang des Pfeil-Paradoxons eine zentrale Bedeutung. Zenon von Elea argumentiert folgendermaßen: Der Pfeil legt in einer bestimmten Zeit eine bestimmte Strecke zurück. Damit er das kann, muss der Pfeil zunächst in einem Teil der Zeit eine kleinere Teilstrecke zurücklegen. Damit er diese Teilstrecke zurücklegen kann, muss er in einer noch kürzeren Zeit eine noch kürzere Teilstrecke zurücklegen usw. Das kann jetzt beliebig oft wiederholt werden, mit dem Ergebnis, dass es immer eine noch nicht erklärte Teilstrecke gibt. Die wird zwar immer kleiner, verschwidet aber nicht. Das ist deshalb so, weil es zu jedem beliebig kleinen Bruch, der größer als Null ist, überabzählbar unendlich viele Brüche gibt, die kleiner als dieser Bruch, aber ebenfalls größer als Null sind. Weil die nicht erklärte Lücke zwar immer kleiner wird, aber nie verschwindet, kann sich der Pfeil in der Konsequenz gar nicht bewegen.

Wenn es in der physikalischen Realität überabzählbar Unendliches wie in der Mathematik gäbe, dann wäre die Argumentation von Zenon von Elea stimmig und kein Pfeil der Welt könnte sich überhaupt irgendwie bewegen. Nur ist das eben nicht so. An dieser Stelle kommt die Unschärferelation ins Spiel, die erklärt, warum der Pfeil sich dennoch durch die Luft bewegt. Ohne die Unschärferelation ist das schlicht nicht erklärbar.

Viele Grüße

--Jake2042 (Diskussion) 18:32, 28. Okt. 2022 (CEST)

Stringtheorie - Theorie-Findung (TF) auf dem Gipfel der Unlogik

Hat hier nicht die Stringtheorie ebenso eine Lösung parat? (nicht signierter Beitrag von 178.115.250.210 (Diskussion) 18:52, 22. Dez. 2012 (CET))

Exakt der richtige Beitrag für die Nonsense-Diskussion hier. Das ganze Problem kann nach dem hiesigen Physik-"Verständnis" womöglich nur in einem 10-, 11- oder 26-dimensionalen Universum geklärt werden - das ist nämlich die die Stringtheorie. Geht's noch?!?! Seht euch doch bitte nur mal die Argumentation von Zenon an. Der Typ startet mit einer Trivialität, nämlich:

"dass ein fliegender Pfeil in jedem Moment seiner Flugbahn einen bestimmten, exakt umrissenen Ort einnimmt".

Damit gibt er zu, dass es eine Vielzahl von "Momenten" und Orten gibt. Wenn er "in jedem Moment seiner Flugbahn einen bestimmten, exakt umrissenen Ort einnimmt", dann befindet er sich nacheinander verschiedenen Orten. Dann folgt fogendes "Argument":

"An einem exakt umrissenen Ort befindet sich der Pfeil in Ruhe, denn an einem Ort kann er sich nicht bewegen."

Das ist aber schon gelogen. Richtig ist zwar: "an einem Ort kann er sich nicht bewegen". Bloß: er tut nun so, als gäbe es nur einen Ort. Er hat die Ortsveränderung weg gelogen. Falsch ist seine Zusammenfassung:

"Da sich der Pfeil in jedem Moment also in Ruhe befindet, müsste er sich insgesamt in Ruhe befinden."

Die "Ruhe" hat er dem Pfeil bloß angedichtet, indem er ihn an einen "exakt umrissenen Ort" festgenagelt hat. --Asw-hamburg (Diskussion) 00:45, 3. Aug. 2015 (CEST)

Überarbeitung notwendig

Wenn ich den Artikel und die Diskussion zum Pfeil-Paradoxon im Zusammenhang lese, dann finde ich, dass der Artikel überarbeitet werden sollte, und zwar so, dass die Geschichte der Behandlung dieses Problems deutlich wird. Das heißt in etwa so:

1. Zenon von Elea. Stellung des Problems
2. Antwort der klassischen Physik (Newton, Leibniz)
3. Antwort durch Hegel
4. Antwort der modernen Physik (Planck, Heisenberg)

Das würde natürlich dazu führen, dass der Artikel erheblich länger wird. Er ist dann aber auch wesentlich informativer und wird dem behandelten Problem dann auch eher gerecht. Die folgende Abbildung würde ich zur Verfügung stellen:

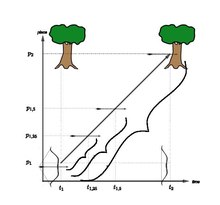
Viele Grüße

--Jake2042 (Diskussion) 19:16, 28. Okt. 2022 (CEST)