Fuhrmann-Dreieck

Fuhrmann-Dreieck (rot): $\triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }$
Kreisbogenmittelpunkte: $M_{a},M_{b},M_{c}$

Fuhrmann-Dreieck (rot): $\triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }$
$\triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }\sim \triangle M_{a}M_{b}M_{c}$

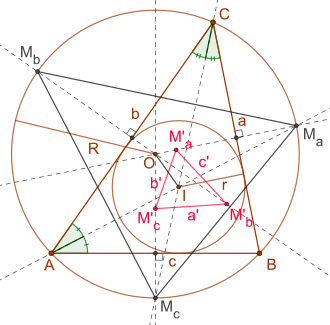
Das Fuhrmann-Dreieck, benannt nach Wilhelm Fuhrmann (1833–1904), ist ein spezielles Dreieck, das über ein gegebenes Ausgangsdreieck definiert ist.

Zu einem gegebenen Ausgangsdreieck $\triangle ABC$ sind $M_{a},M_{b},M_{c}$ die Mittelpunkte der Kreisbögen des Umkreises über den Dreiecksseiten $a,b,c$. Diese Mittelpunkte werden an den zugehörigen Dreiecksseiten gespiegelt und die Spiegelpunkte $M_{a}^{\prime },M_{b}^{\prime },M_{c}^{\prime }$ sind die Eckpunkte des Fuhrmann-Dreiecks. Ist das gegebene Dreieck gleichseitig, so fallen diese drei Punkte zusammen.

Der Umkreis des Fuhrmann-Dreiecks wird auch als Fuhrmann-Kreis bezeichnet. Des Weiteren ist das Fuhrmann-Dreieck ähnlich zu dem von den Mittelpunkten der Kreisbögen gebildeten Dreieck, also $\triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }\sim \triangle M_{a}M_{b}M_{c}$ und für seine Fläche gilt:

$|\triangle M_{c}^{\prime }M_{b}^{\prime }M_{a}^{\prime }|={\frac {(a+b+c)|OI|^{2}}{4R}}={\frac {(a+b+c)(R-2r)}{4}}$

Hierbei bezeichnet $O$ den Mittelpunkt des Umkreises des Ausgangsdreiecks $\triangle ABC$ und $R$ seinen Radius, sowie $I$ den Mittelpunkt des Inkreises und $r$ dessen Radius. Aufgrund des Satzes von Euler gilt zudem für den Abstand der beiden Mittelpunkte $|OI|^{2}=R(R-2r)$. Für die Seitenlängen des Fuhrmann-Dreiecks existieren die folgenden Gleichungen:

$a^{\prime }={\sqrt {\frac {(-a+b+c)(a+b+c)}{bc}}}|OI|$

$b^{\prime }={\sqrt {\frac {(a-b+c)(a+b+c)}{ac}}}|OI|$

$c^{\prime }={\sqrt {\frac {(a+b-c)(a+b+c)}{ab}}}|OI|$

Literatur

• Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, S. 228–229, 300 (Erstveröffentlichung 1929 bei der Houghton Mifflin Company (Boston) unter dem Titel Modern Geometry).
• Ross Honsberger: Episodes in Nineteenth and Twentieth Century Euclidean Geometry. MAA, 1995, S. 49-52

Weblinks

• Eric W. Weisstein: Fuhrmann triangle. In: MathWorld (englisch).