Gitter (Geometrie)
Ein Gitter in der Geometrie ist eine lückenlose und überlappungsfreie Partition eines Raumes durch eine Menge von Gitterzellen. Die Gitterzellen werden definiert durch eine Menge von Gitterpunkten, die untereinander durch eine Menge von Gitterlinien verbunden sind.
Gitter werden in der Naturwissenschaft und Technik zur Vermessung, Modellierung und für numerische Berechnungen verwendet (siehe Gittermodell).
Einteilung
[Bearbeiten | Quelltext bearbeiten]Anhand ihrer Topologie und Geometrie werden Gitter in unterschiedliche Kategorien eingeteilt. Man unterscheidet grundlegend zwischen strukturierten und unstrukturierten Gittern.
Strukturierte Gitter
[Bearbeiten | Quelltext bearbeiten]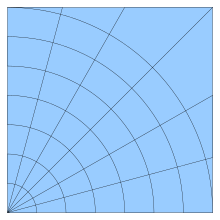



Strukturierte Gitter haben eine regelmäßige Topologie, jedoch nicht notwendigerweise eine regelmäßige Zellgeometrie. Bei strukturierten Gittern liegen die Zellen in einem regelmäßigen Raster vor, so dass sich die Zellen eindeutig durch ganzzahlige Zahlen indizieren lassen. Eindimensionale Gitter (Liniengitter) sind immer strukturiert, die Zellen lassen sich durch i=1..N (N = Anzahl der Elemente) durchzählen. Für zweidimensionale Gitter ist ein Element durch die Indizes (i,j), bei dreidimensionalen durch die Indizes (i,j,k) eindeutig bestimmt. Vorteil der Verwendung strukturierter Gitter gegenüber den nachfolgend beschriebenen unstrukturierten Gitter ist, dass sich durch diese eindeutige Indizierung Nachbarzellen ohne rechnerischen Aufwand ermitteln lassen. Strukturierte Gitter bestehen immer aus einem Elementtyp. Im Zweidimensionalen werden meistens Rechteckelemente und nur selten Dreieckselemente verwendet. Dreidimensionale Gitter sind fast immer Hexaeder und nur manchmal Tetraeder. Die Verwendung von Dreieckselementen oder Tetraeder hat den Nachteil, dass sie den Raum nur schlecht ausfüllen und mehr Elemente notwendig sind. So hat ein Tetraeder mit einer Kantenlänge von 1 nur ein Raumvolumen von 1/6, während ein Kubus ein Volumen von 1 besitzt. Daher müssen etwa für die Strömungssimulation Tetraedergitter sehr viele Zellen verwenden, um eine ausreichende Auflösung zu erreichen.
Bei den strukturierten Gittern sind auch komplexe Strukturen möglich, bei denen das Gittersystem zwar regelmäßig ist, insgesamt aber gekrümmt oder an eine komplexe Geometrie angepasst. Ebenso werden Multiblockstrukturen verwendet, bei denen das Gitter aus mehreren strukturierten Blöcken unterschiedlicher Größe gebildet wird. Solche strukturierten Gitter lassen sich nur teilautomatisch erstellen.
Bei gekrümmten Gittern (englisch curvilinear grids) sind die Gitterlinien durch parametrisierte Kurven gegeben. Der Begriff ist jedoch eher ungebräuchlich. Man spricht dann einfach von strukturierten Gittern.
Rechtwinklige Gitter (englisch rectilinear grids) unterteilen den Raum vollständig in achsenparallele Bereiche, die nicht gleich groß sein müssen. Im dreidimensionalen Raum entstehen so Quader verschiedener oder gleicher Größe.
Ein gleichmäßiges Gitter (englisch regular grid) unterteilt den Raum vollständig in achsenparallele rechtwinklige Bereiche, wobei Kanten entlang einer Achse immer die gleiche Länge haben.
Der einfachste Fall ist ein kartesisches Gitter (englisch cartesian grid), bei denen alle Kantenlängen gleich sind. Im zweidimensionalen Raum entsteht eine Quadratfläche und im dreidimensionalen ein Volumen aus Würfeln.
Unstrukturierte Gitter
[Bearbeiten | Quelltext bearbeiten]
Unstrukturierte Gitter (englisch unstructured grids) haben keine festgelegte Topologie und keine gleichmäßige Gitterzellgeometrie. Unstrukturierte Gitter sind meist das Ergebnis eines Adaptionsprozesses. Bekannt sind auch Gitter aus komplexen Zellen, sogenannte Polyedergitter. Die Zellstruktur ähnelt hier der von Seifenschaum.
Unstrukturierte Gitter sind sehr flexibel einzusetzen und können zudem einfach automatisch erzeugt werden. Die Datenverwaltung ist allerdings aufwändiger als bei strukturierten Gittern. Einerseits sind die Gitterpunkte nicht wie bei strukturierten Gittern in einem regelmäßigen Muster angeordnet, sondern müssen einzeln abgespeichert werden. Andererseits ist auch nicht von vorneherein klar, welches die Nachbarzellen zu einer bestimmten Gitterzelle sind. Auch diese Nachbarschaftsinformationen müssen entweder bei der Gittererzeugung explizit abgespeichert werden oder aber zur Laufzeit aufwendig berechnet werden. Unstrukturierte Gitter benötigen daher im Allgemeinen ein Mehrfaches des Speicherbedarfs von strukturierten Gittern und verursachen in der Regel einen höheren Rechenaufwand.
Gittererzeugung
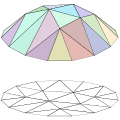
[Bearbeiten | Quelltext bearbeiten]Als Gittererzeugung oder Meshing bezeichnet man eine Gruppe von Verfahren in der Computergrafik sowie der Simulation der physikalischen Eigenschaften von Festkörpern und Fluiden; bei diesen Verfahren wird eine gegebene Oberfläche oder ein gegebenes Raumvolumen durch eine Menge kleinerer, meist sehr einfacher Elemente angenähert (approximiert). Das so entstehende Gitter ist eine vereinfachte Beschreibung der Fläche oder des Körpers, welches dann z. B. für weitergehende Berechnungen genutzt werden kann, etwa mittels der Finite-Elemente-Methode (FEM).
Bei zweidimensionalen Flächen kommen bei der Gittererzeugung am häufigsten Dreiecks- oder Viereckselemente zur Anwendung, bei dreidimensionalen Körpern in der Regel Tetraeder oder Quader.
Die Erzeugung eines Gitters aus Dreieckselementen wird auch als Triangulierung (oder Triangulation) bezeichnet (genau wie das entstehende Dreiecksgitter), die Erzeugung eines Gitters aus Viereckselementen heißt auch Paving. Ist die Anzahl der Außenkanten einer Fläche fest vorgegeben und von ungerader Anzahl, so ist kein reines Vierecks-Paving möglich (es bleibt mindestens ein Element mit ungerader Eckenzahl, z. B. ein Dreieck).
Dreiecksgitter
[Bearbeiten | Quelltext bearbeiten]Als Dreiecksgitter, Dreiecksnetz oder Triangulierung bezeichnet man in der Trigonometrie und elementaren Geometrie die Teilung einer Fläche in Dreiecke. Graphentheoretisch gesehen sind Dreiecksgitter vom Typus „ungerichteter Graphen ohne Mehrfachkanten“, deren Teilgraphen „Kreise mit drei Knoten“ (und entsprechend drei Kanten) sind. Die Verallgemeinerung von Dreiecksnetzen sind Polygonnetze.
Eine Triangulation einer Menge von Punkten in der Ebene bezeichnet eine Zerlegung der konvexen Hülle der Punktmenge in Dreiecke, wobei die Eckpunkte der Dreiecke genau die Punkte aus sind. Somit ist die Triangulation ein ebener Dreiecksgraph. Ist die Menge in konvexer Lage, so ist die Anzahl der möglichen Triangulationen genau die -te Catalan-Zahl, wobei die Anzahl der Punkte in bezeichnet.
Oft ist man daran interessiert, eine Triangulation mit besonderen Eigenschaften zu berechnen. Zum Beispiel gibt es die Delaunay-Triangulation, welche den kleinsten Innenwinkel der Dreiecke maximiert, oder die Minimum-Weight-Triangulation, welche die Gesamtlänge aller Kanten minimiert.
Eine technische Anwendung von Dreiecksgittern in der Ebene und im Raum ist der Fachwerkträger.
Adaptive Gitter
[Bearbeiten | Quelltext bearbeiten]
Es wird weiterhin zwischen adaptiven und nichtadaptiven Diskretisierungen unterschieden.
Nichtadaptive Gitter haben überall im Volumen dieselbe Auflösung. Bei kleinen geometrischen Strukturen oder Bereichen mit starken Rundungen, spitzen Winkeln oder unterschiedlich definierten Materialparametern reicht ein grobes Gitternetz mit großen Gitterzellen nicht mehr aus, um auch solche Problembereiche hinreichend genau zu diskretisieren. Eine globale Verfeinerung des Gitternetzes ist zumeist aufgrund des damit verbundenen erhöhten Speicher- und Rechenzeitaufwands nicht sinnvoll.
Hier greift das Verfahren der adaptiven Gittererzeugung (englisch adaptive meshing), das dort, wo ansonsten große Ergebnis-Fehler zu erwarten wären, das Gitter feiner wählt. Dies geschieht entweder durch A-priori-Wissen über das betrachtete Problem, beispielsweise kleinere Elemente an Bauteiloberflächen oder an stark gekrümmten oder dünnen Stellen, oder durch Verfahren, die anhand gegebener Fehlerabschätzungen dynamisch dort verfeinern, wo der Fehler gerade groß ist. Letzteres ist insbesondere bei instationären Problemen wichtig, wenn also die problematischen Stellen im Laufe der Zeit ihre Position verändern.
Ein anderes Verfahren zur Diskretisierung kritischer Bereiche ist die Sub-Grid-Technologie.
Anwendungen
[Bearbeiten | Quelltext bearbeiten]Technik
[Bearbeiten | Quelltext bearbeiten]- In der technischen Konstruktionslehre zur Modellierung gekrümmter Flächen, insbesondere im Zusammenhang mit CAD (CAD)
- In der Robotik zur Bestimmung von Gelenkstellungen; hierbei ergeben sich hochdynamische Dreiecksnetze, die die Bewegung wiedergeben
- Im Bauwesen für die Ausmessung eines Bauwerks mit Dreiecken: Hier waren Dreiecksnetze – vor allem rechtwinklige (3:4:5) und gleichseitige – schon in den Bauhütten in der Gotik üblich. Moderne Anwendungen sind CAM-Verfahren
Vermessungswesen
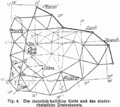
[Bearbeiten | Quelltext bearbeiten]- In der Geodäsie als Vermessungsnetz zur Punktbestimmung, siehe Triangulation (Geodäsie): Mittels des Netzes werden trigonometrischer Punkte (TP) als Vermessungspunkte eingemessen
- Für die Photogrammetrie zur Erfassung der Daten – bei zeilenweisem Abtasten sind hier Vierecksnetze verbreiteter (die sich aber problemlos in Dreiecksnetze umwandeln lassen, um sie den spezifischen Algorithmen zugänglich zu machen)
- In der GIS-Technologie und anderen satellitengestützten Messmethoden zur Umrechnung der meist linearen Messserien auf ein Erdmodell
Numerische Mathematik
[Bearbeiten | Quelltext bearbeiten]Als Rechengitter bezeichnet man in der numerischen Mathematik eine diskrete Zerlegung des Raumes, auf dem eine partielle Differentialgleichung gelöst werden soll. Für eine zeitliche Diskretisierung ist der Begriff weniger gebräuchlich. Die Schnittpunkte zweier Gitterlinien werden als Knoten bezeichnet, die Zellen entweder als Zellen, in Finite-Elemente-Verfahren auch als Elemente und in Finite-Volumen-Verfahren als Volumen. Das Gitter kann räumlich feststehend sein oder sich mit der Zeit bewegen oder im Laufe der Rechnung adaptiert werden.
An den Rändern des Gebiets werden gegebenenfalls Randbedingungen vorgeschrieben.
Rechengitter müssen nicht eindimensional sein. Bei dreidimensionalen Gittern werden schnell sehr große Zellenzahlen erreicht. Ein einfaches rechtwinkliges Gitter, das auf einer Kante nur 100 Zellen auflöst, besitzt in der dritten Dimension bereits 1 Million Zellen.
Auf modernen PC mit 2 GB Hauptspeicher können je nach Softwaresystem heute ca. 1,5–5 Millionen Zellen berechnet werden. Werden größere Auflösungen benötigt, dann muss die Berechnung auf Großrechnern oder Rechnernetzwerken erfolgen.
Beispiele
[Bearbeiten | Quelltext bearbeiten]-
Geodätisches Vermessungsnetz
-
Gittererzeugung in der Computergraphik
-
Ebenes Dreiecksnetz für eine FEM-Modellierung
-
Adaptives ebenes Dreiecksnetz für eine FEM-Modellierung
Literatur
[Bearbeiten | Quelltext bearbeiten]- Michael Bender, Manfred Brill: Computergrafik – Ein anwendungsorientiertes Lehrbuch. 2. Auflage. Hanser, 2006, ISBN 3-446-40434-1.
- Hansen und Johnson: The Visualization Handbook. Elsevier, Burlington 2005, ISBN 0-12-387582-X.
- Jonathan Richard Shewchuk: Delaunay Refinement Mesh Generation, 1997 (PDF (2,635k, 207 Seiten))