Finite-Elemente-Methode

Visualisierung einer FEM-Simulation der Verformung eines Autos bei asymmetrischem Frontalaufprall

Darstellung der Wärmeverteilung in einem Pumpengehäuse mit Hilfe der Wärmeleitungsgleichung. Die „finiten Elemente“ sind mit den Elementkanten als schwarze Linien zu sehen.

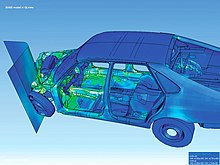
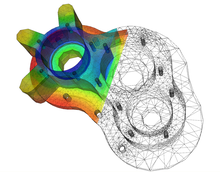
Die Finite-Elemente-Methode (FEM), auch Methode der finiten Elemente und Finite Element Analysen (FEA) genannt, ist ein allgemeines, bei unterschiedlichen physikalischen Aufgabenstellungen angewendetes numerisches Verfahren. Am bekanntesten ist die Anwendung der FEM bei der Festigkeits- und Verformungsuntersuchung von Festkörpern mit geometrisch komplexer Form, weil sich hier der Gebrauch der klassischen Methoden (z. B. die Balkentheorie) als zu aufwändig oder nicht möglich erweist. Logisch basiert die FEM auf dem numerischen Lösen eines komplexen Systems aus Differentialgleichungen.

Das Berechnungsgebiet (z. B. der Festkörper) wird in endlich viele Teilgebiete (z. B. Teilkörper) einfacher Form aufgeteilt, z. B. in viele kleine Quader oder Tetraeder. Sie sind die „finiten Elemente“. Ihr physikalisches Verhalten kann aufgrund ihrer einfachen Geometrie mit bekannten Ansatzfunktionen gut berechnet werden. Das physikalische Verhalten des Gesamtkörpers wird dadurch nachgebildet, wie diese Elemente auf die Kräfte, Lasten und Randbedingungen reagieren und wie sich Lasten und Reaktionen beim Übergang von einem Element ins benachbarte fortpflanzen durch ganz bestimmte problemabhängige Stetigkeitsbedingungen, die die Ansatzfunktionen erfüllen müssen.

Die Ansatzfunktionen enthalten Parameter, die in der Regel eine physikalische Bedeutung besitzen, wie z. B. die Verschiebung eines bestimmten Punkts im Bauteil zu einem bestimmten Zeitpunkt. Die Suche nach der Bewegungsfunktion ist auf diese Weise auf die Suche nach den Werten der Parameter der Funktionen zurückgeführt. Indem immer mehr Parameter (z. B. immer mehr, kleinere Elemente) oder immer höherwertige Ansatzfunktionen benutzt werden, kann die Genauigkeit der Näherungslösung verbessert werden.

Die Entwicklung der FEM war in wesentlichen Etappen nur mittels der Entwicklung leistungsfähiger Computer möglich, da sie erhebliche Rechenleistung benötigt. Daher wurde diese Methode von vornherein computergerecht formuliert. Sie brachte einen wesentlichen Fortschritt bei der Behandlung von Berechnungsgebieten beliebiger Form.

Einführung

Generiertes Strukturmodell eines Hubkolbens (Dieselmotor) als Komponente eines Verbrennungsmotors zum Zwecke der Spannungsanalyse

Mit der FEM können Probleme aus verschiedenen physikalischen Disziplinen (statische, dynamische und nichtlinear thermo-physikalische Probleme) berechnet werden, da es sich grundsätzlich um ein numerisches Verfahren zur Lösung von Differentialgleichungen handelt. Zunächst wird das Berechnungsgebiet („Bauteil“) in eine große Anzahl von Elementen unterteilt – ausreichend fein. Diese Elemente sind endlich klein (finit), ihre tatsächliche Größe bleibt jedoch mathematisch relevant – sie sind nicht „unendlich klein“ (infinit). Das Aufteilen des Gebiets/Bauteils in eine bestimmte Anzahl Elemente finiter Größe, die sich mit einer endlichen Zahl von Parametern beschreiben lassen, gab der Methode den Namen „Finite-Elemente-Methode“.

Für diese Elemente gibt es Ansatzfunktionen (z. B. lokale Ritz-Ansätze je Element), die beschreiben, wie ein Element auf äußere Einflüsse und Randbedingungen reagiert. Setzt man diese Ansatzfunktionen für alle Elemente in die schwache Formulierung des zu lösenden Differentialgleichungsproblems ein, das die physikalischen Gesetze beschreibt, erhält man zusammen mit den Anfangs-, Rand- und Übergangsbedingungen ein meist sehr großes Gleichungssystem. Es (zumindest näherungsweise) zu lösen ist die Aufgabe des FE-Gleichungslösers. Die Größe des zu lösenden Gleichungssystems hängt maßgeblich von der Anzahl der finiten Elemente ab. Seine Lösung stellt letztlich die numerische Lösung des betrachteten Differentialgleichungsproblems dar.

Finit, Infinit

Mathematisch bleibt die Größe jedes Elements relevant und muss auch in seine Berechnung einfließen, es ist nur 'finit' klein. Bei 'infinit' kleinen Elementen wäre ihre Größe vernachlässigbar und würde in den Gleichungen nicht mehr berücksichtigt. Diesbezüglich bleibt die Elementgröße also relevant.

Eine „ausreichend feine“ Aufteilung des Bauteils in Elemente liegt vor, wenn eine weitere Verfeinerung keinen signifikanten Einfluss auf das Rechenergebnis mehr hat. D. h. das Gesamtergebnis wird diesbezüglich unabhängig von der Elementgröße, die (aus dieser Sichtweise) dann nicht mehr relevant ist. Hat die Elementgröße noch nennenswerten Einfluss auf das Gesamtergebnis, dann gilt i. A. die Vernetzung als nicht fein genug.

Geschichte

Der Einsatz der FEM in der Praxis begann in den 1950er Jahren bei einer Strukturberechnung von Flugzeugflügeln in der Luft- und Raumfahrtindustrie (Turner, Clough 1956) und sehr bald auch im Fahrzeugbau. Die Methode basiert hier auf den Arbeiten bei der Daimler AG in Stuttgart, die das selbst entwickelte FEM-Programm ESEM (Elastostatik-Element-Methode) einsetzte, lange bevor die computerunterstützte Konstruktion (CAD) Anfang der 1980er Jahre ihren Einzug hielt. Der Ausdruck Finite-Elemente-Methode wurde erstmals 1960 von R. W. Clough vorgeschlagen und wird seit den 1970er Jahren überall verwendet. Die gängigste deutschsprachige Bezeichnung für industrielle Anwender ist Berechnungsingenieur.

Die Geschichte der Finite-Elemente-Methode erschließt sich aus den Forschungen und Veröffentlichungen der folgenden Autoren (Auswahl):

• Karl Heinrich Schellbach: Variationsrechnung; Lösung eines Minimalflächenproblems (1851/52)
• Ernst Gustav Kirsch: Die Fundamentalgleichungen der Theorie der Elastizität fester Körper, hergeleitet aus der Betrachtung eines Systems von Punkten, welche durch elastische Streben verbunden sind (1868)
• John William Strutt, 3. Baron Rayleigh (1842–1919): On the theory of resonance. 1870
• Walter Ritz (1878–1909): neue Methode zur Lösung von Variationsproblemen, Ritz’sches Verfahren (1908/09)
• Boris G. Galerkin (1871–1945): Verfahren der gewichteten Residuen (1915)
• Erich Trefftz (1926): lokal begrenzte Ansatzfunktionen; Gegenstück zum Ritz’schen Verfahren
• Hans Ebner (1929): Schubblech als ebenes Element im Flugzeugbau
• Alexander Hrennikoff (1896–1984): Stabmodelle, Ersetzen von Scheiben durch Fachwerke, Platten durch Trägerroste 1940/41
• Richard Courant (1888–1972): Variational methods for the solution of problems of equilibrium and vibration(s). 1943 (Ansatzfunktionen mit lokalem Träger, elementweise Ansätze für Schwingungsprobleme)
• William Prager (1903–1980), John Lighton Synge (1897–1995): Approximation in Elasticity based on the concept of function space. 1947
• John Argyris (1913–2004): Kraft- und Verschiebungsmethode für Stabtragwerke, Matrizenformulierung (1954/55)
• M. J. Turner, Ray W. Clough, H. C. Martin, L. J. Topp: Stiffness and deflection analysis of complex structures. 1956 (erste Strukturberechnung von Flugzeugflügeln bei Boeing, erste Anwendung der FEM mit Computerprogramm, erste Anwendung von Flächenelementen)
• Ray W. Clough (1920–2016): The finite element method in plane stress analysis. 1960 (wahrscheinlich erste Verwendung des Begriffs Finite Elemente)
• Spierig (1963): Entwicklung von Dreieckelementen, Übertragung auf Schalen
• Olgierd Cecil Zienkiewicz (1921–2009), Pionier der FEM und erstes Standardwerk (Lehrbuch): The Finite Element Method in Structural and Continuum Mechanics, 1967 (mit Y. K. Cheung)
• Alfred Zimmer (* 1920) und Peter Groth (* 1938), Pioniere der FEM, erstes deutsches FEM-Lehrbuch: Elementmethode der Elastostatik, 1969 Oldenbourg Verlag München, Wien
• Olga Alexandrowna Ladyschenskaja (1922–2004), Ivo Babuška (* 1926) und Franco Brezzi (* 1945) – Ladyschenskaja-Babuška-Brezzi-Bedingung für die Stabilität eines gemischten Finite-Elemente-Problems mit Sattelpunktstruktur
• Ivo Babuška (1926–2023) – adaptive Finite-Elemente-Algorithmen

Anwendung

Die erste Anwendung der FEM war die lineare Behandlung von Festkörpern und Strukturen in Form der Verschiebungsmethode, wobei die Bezeichnung „Finite Elemente“ erst später eingeführt wurde. Im weiteren Verlauf der Forschung wurde die Finite-Elemente-Methode immer weiter verallgemeinert und kann nunmehr auf viele physikalische Problemstellungen angewendet werden, welche bei verschiedensten technischen Fragestellungen in den Ingenieurwissenschaften oder auch bei Wettervorhersagen auftreten. Dementsprechend findet die Methode insbesondere in den Branchen Bauingenieurwesen, Fahrzeugbau, Maschinenbau, Medizintechnik sowie Luft- und Raumfahrttechnik weitverbreitete Anwendung. Von zentraler Bedeutung ist die Methode in der Produktentwicklung, wobei durch Simulation am Computer viele Prototypen, Messungen und Tests eingespart werden können. Beispielsweise kann durch mechanische Festigkeitsberechnung kompletter Fahrwerks- und Karosseriestrukturen die Zahl an notwendigen Crashtests erheblich reduziert werden.

Vorgehen bei einer mechanischen Berechnung (exemplarisch)

Programme, welche die Finite-Elemente-Methode verwenden, arbeiten nach dem EVA-Prinzip: Der Anwender erstellt in einem CAD-Programm eine (Bauteil-)Geometrie. Anschließend gibt er im sogenannten FE-Präprozessor weitere Eingaben vor. Ein FEM-Gleichungslöser führt die eigentliche Rechnung durch, und der Benutzer erhält die berechneten Ergebnisse, welche er dann im sogenannten FE-Postprozessor in Form grafischer Anzeigen betrachten kann. Oft sind Prä- und Postprozessor in einem Programm kombiniert oder sogar Bestandteil des CAD-Programms.

Prozesskette lineare Festigkeitsrechnung

Eingabe: Präprozessor

Im CAD-Programm wird das Bauteil konstruiert und mittels einer Direktschnittstelle oder mit einem neutralen Austauschformat wie STEP in den FE-Präprozessor übertragen. Durch die Anwahl von Netzparametern wie Elementgröße und Elementart (z. B. Tetraeder oder Quader im dreidimensionalen Fall) im Vernetzungsmodul des Programms werden mit Hilfe eines Vernetzungsalgorithmus die Finiten-Elemente erzeugt. Für die mechanische Festigkeitsanalyse ist das Materialverhalten einzugeben, denn je nach Werkstoff ist der Zusammenhang zwischen Spannung und Dehnung unterschiedlich und es ergeben sich verschiedene Verformungen. Im einfachsten Fall, der linearen Isotropie, werden für die FE-Berechnung lediglich der Elastizitätsmodul und die Poissonzahl benötigt. Weitere Randbedingungen sind die einwirkenden Belastungen auf das Bauteil (Kräfte, Druck, Temperatur etc.). Schließlich werden die Auflager des Bauteils sowie ggf. vorgegebene Verschiebungen im Modell eingeführt.

Verarbeitung: Gleichungslöser

Je nach Programm kommt nun ein separater (eigenständiges Programm) oder ein integrierter Gleichungslöser zum Einsatz. Er berechnet, wie sich die Lasten, Kräfte und Randbedingungen auf die Einzelelemente des Bauteils auswirken, und wie sich die Kräfte sowie die Auswirkungen im Bauteil fortpflanzen und auf benachbarte Elemente auswirken. Die Rechenzeit hierfür wird maßgeblich durch die Anzahl der Finiten Elemente bestimmt, wobei auch die Art der Elemente eine Rolle spielt. Der Aufwand steigt außerdem, wenn die Berechnung im Zuge eines iterativen Verfahrens mehrmals durchgeführt wird, wie im Falle einer nichtlinearen FE-Analyse.

Ausgabe: Postprozessor

Im Falle der mechanischen Festigkeitsberechnung erhält der Benutzer als Ergebnis des FEM-Gleichungslösers insbesondere Spannungs-, Deformations- und Dehnungswerte. Diese kann der Postprozessor zum Beispiel in einem Falschfarbenbild darstellen. Die Vergleichsspannungswerte werden beispielsweise zum Festigkeitsnachweis eines Bauteils verwendet.

Allgemeine Funktionsweise

Diskretisierung

Die Finite-Elemente-Methode ist ein Diskretisierungsverfahren. Das bedeutet, dass für ein unendlichdimensionales Problem eine endlichdimensionale Näherung berechnet wird.

Hierzu wird das Grundgebiet in einfache Teilgebiete, die so genannten finiten Elemente zerlegt (Vernetzung, Vermeshen). Die Bezeichnung „finit“ hebt den Unterschied zur analytischen Betrachtung auf infinitesimalen Elementen hervor. Die Ecken der finiten Elemente heißen Knoten. Diese Knoten bilden die diskrete Untermenge für das numerische Verfahren. Auf den Elementen werden endlichdimensionale Approximationen eingeführt, welche die unbekannten Knotengrößen als Parameter enthalten. Die lokalen Approximationen werden dann in die schwache Formulierung des Randwertproblems eingeführt. Die dabei entstehenden Elementintegrale werden i. a. mit numerischer Quadratur berechnet. Dabei werden die Approximationsansätze „herausintegriert“, so dass auf den Elementen nach der Integration nur noch die Knotenwerte als Unbekannte verbleiben. Auf diese Weise werden Randwertprobleme für lineare partielle Differentialgleichungen in ein lineares Gleichungssystem überführt. Für nichtlineare Differentialgleichungen verläuft der Algorithmus analog mit dem Unterschied, dass die nichtlinearen Abhängigkeiten mit geeigneten Methoden (z. B. Newton-Verfahren) iterativ linearisiert werden und das lineare Gleichungssystem in jedem Teilschritt für inkrementelle Größen aufgestellt wird.

Beispiel für die Anwendung eines adaptiven Gitters zur Berechnung der Luftströmung um einen Flugzeugflügel.

Bei gewissen Aufgabenstellungen ist die Unterteilung in Elemente durch das Problem bereits weitgehend vorgegeben, zum Beispiel bei räumlichen Fachwerken, bei denen die einzelnen Stäbe die Elemente der Konstruktion bilden. Das gilt auch bei Rahmenkonstruktionen, wo die einzelnen Balken oder unterteilte Balkenstücke die Elemente der Aufgabe darstellen. Bei zweidimensionalen Problemen wird das Grundgebiet in Dreiecke oder Vierecke eingeteilt. Selbst wenn nur geradlinige Elemente verwendet werden, erreicht man mit einer entsprechend feinen Diskretisierung eine recht gute Approximation (Annäherung) des Grundgebietes. Krummlinige Elemente erhöhen die Güte der Annäherung. Jedenfalls erlaubt diese Diskretisierung eine flexible und auch dem Problem angepasste Erfassung des Grundgebietes. Allerdings muss darauf geachtet werden, dass sehr spitze oder überstumpfe Winkel an den Element-Eckknoten vermieden werden, um numerische Schwierigkeiten auszuschließen. Dann wird das gegebene Gebiet durch die Fläche der approximierenden Elemente ersetzt. Mit dem Patch-Test kann man später überprüfen, ob das gut gelungen ist.

Räumliche Probleme werden mit einer Unterteilung des dreidimensionalen Gebietes in Tetraederelemente, Quaderelemente oder andere dem Problem angepasste, möglicherweise auch krummflächig berandete Elemente, dies sind i. d. R. Serendipity- oder Lagrange-Elemente, bearbeitet.

Die Feinheit der Unterteilung, d. h. die Dichte des Netzes, hat maßgeblichen Einfluss auf die Genauigkeit der Resultate der Näherungsrechnung. Da gleichzeitig der Rechenaufwand bei der Verwendung feinerer und dichterer Netze steigt, gilt es, möglichst intelligente Vernetzungslösungen zu entwickeln.

Element-Ansatz

In jedem der Elemente wird für die gesuchte Funktion, bzw. allgemeiner für die das Problem beschreibenden Funktionen, ein problemgerechter Ansatz gewählt. Im Besonderen eignen sich dazu ganze rationale Funktionen in den unabhängigen Raumkoordinaten. Für eindimensionale Elemente (Stäbe, Balken) kommen Polynome ersten, zweiten, dritten und gelegentlich sogar höheren Grades in Frage. Bei zweidimensionalen Problemen finden lineare, quadratische oder höhergradige Polynome Verwendung. Die Art des Ansatzes hängt dabei einerseits von der Form des Elementes ab, und andererseits kann auch das zu behandelnde Problem den zu wählenden Ansatz beeinflussen. Denn die Ansatzfunktionen müssen beim Übergang von einem Element ins benachbarte ganz bestimmte problemabhängige Stetigkeitsbedingungen erfüllen. Die Stetigkeitsanforderungen sind häufig aus physikalischen Gründen offensichtlich und aus mathematischen Gründen auch erforderlich. Zum Beispiel muss die Verschiebung eines zusammenhängenden Körpers in einer Richtung beim Übergang von einem Element zum anderen stetig sein, um die Kontinuität des Materials zu gewährleisten. Im Fall der Balken- oder Plattenbiegung sind die Stetigkeitsanforderungen höher, da dort aus analogen physikalischen Gründen sogar die Stetigkeit der ersten Ableitung bzw. der beiden ersten partiellen Ableitungen gefordert werden muss.

Um nun die Stetigkeitsanforderungen tatsächlich zu erfüllen, muss der Funktionsverlauf im Element durch Funktionswerte und auch durch Werte von (partiellen) Ableitungen (den Knotenpunktverschiebungen) in bestimmten Punkten des Elementes, den Knotenpunkten, ausgedrückt werden. Die in den Knotenpunkten benutzten Funktionswerte und Werte von Ableitungen nennt man die Knotenvariablen des Elements. Mit Hilfe dieser Knotenvariablen stellt sich die Ansatzfunktion als Linearkombination von sogenannten Formfunktionen mit den Knotenvariablen als Koeffizienten dar.

Es ist zweckmäßig, für die Knotenpunktkoordinaten neben einem elementbezogenen lokalen ein globales Koordinatensystem zu verwenden. Beide werden durch Transformationsfunktionen miteinander verknüpft. Werden für diese Transformation dieselben Formfunktionen wie für den Verformungsansatz benutzt, so sind es isoparametrische Elemente, bei Funktionen niedrigeren bzw. höheren Grades sub- bzw. superparametrische Elemente.

Randbedingungen

Problemstellung	Dirichlet-Randbedingung/Funktionswert	Neumann-Randbedingung
statisches Problem	Auflagerbedingung/Verschiebung	Kraft
Sickerströmung	Standrohrspiegelhöhe	Quelle oder Senke
Wärmeleitung	Temperatur	Wärmestrom bzw. Wärmestromdichte
elektrischer Strom	elektrische Spannung	Stromstärke
Elektrostatik	elektrische Spannung	elektrische Ladung
Magnetostatik	magnetisches Potenzial	magnetischer Fluss

Die häufigsten Randbedingungen für partielle Differentialgleichungen sind Randbedingungen erster Art (Dirichlet-Bedingungen), zweiter Art (Neumann-Bedingungen) und dritter Art (Robin-Bedingungen). Bei Dirichlet-Bedingungen werden am Rand Funktionswerte vorgeschrieben, bei Neumann-Bedingungen Normalableitungen und bei Robin-Bedingungen Linearkombinationen davon.

Je nach Art des physikalischen Problems kann es sich um verschiedene physikalische Größen handeln, wie in der Tabelle beispielhaft dargestellt.

Weitere Arten von Randbedingungen sind periodische Randbedingungen, bei denen die Werte an einem Rand als Daten für einen anderen Rand genommen werden und so ein periodisch unendlich fortgesetztes Gebiet simuliert wird. Für rotationssymmetrische Probleme werden sogenannte zyklische Randbedingungen definiert.

Nur bei Dirichlet-Bedingungen ist die Diskretisierung einfach, hier werden in den Knoten auf dem Rand die gegebenen Randwerte einfach übernommen. Bei homogenen Neumann-Bedingungen hat man gar nichts zu tun, dies sind sogenannte natürliche Randbedingungen. Bei inhomogenen Randbedingungen zweiter Art oder Randbedingungen dritter Art hingegen beeinflussen die Randbedingungen die schwachen Formulierungen des Problems!

Grundgleichungen der Verschiebungsmethode

Die Verschiebungsmethode ist die Standardformulierung der Finite-Elemente-Methode, bei der die Verschiebungen die primären Unbekannten sind, die die Translation, Rotation und Verformung eines Festkörpers beschreiben. Die Verschiebungsmethode ist in allen gängigen Finite-Elemente-Programmen verfügbar, mit denen Probleme der Festkörpermechanik berechnet werden können. Für die Lösung von Festkörper-Problemen liegen mehrere Grundgleichungen vor.

Prinzip von d'Alembert in der Lagrangeschen Fassung

Eine der Verschiebungsmethode zugrunde liegende Gleichung, mit der allgemeine Probleme der Festkörpermechanik behandelt werden können, ist das Prinzip von d’Alembert, wie es die Kontinuumsmechanik in der Lagrangeschen Beschreibung formuliert. Mit diesem Prinzip können sowohl lineare Probleme, wie die Frage nach Eigenschwingungen, als auch hoch nichtlineare Probleme, wie Crashtests, analysiert werden. Hier wird die Methode der gewichteten Residuen nach Galerkin, auch Galerkin-Methode oder Galerkin-Ansatz genannt, verwendet.

Prinzip vom Minimum der potenziellen Energie

In konservativen Systemen können bei einem statischen Problem die Knotenpunktverschiebungen aus der Bedingung ermittelt werden, dass im gesuchten Gleichgewichtszustand die potenzielle Energie ein Minimum hat. Mit dem Prinzip vom Minimum der potenziellen Energie können die Steifigkeitsgleichungen finiter Elemente direkt bestimmt werden. Die potenzielle Energie einer Konstruktion ist die Summe aus der inneren Verzerrungsenergie (der elastischen Formänderungsenergie) und dem Potenzial der aufgebrachten Lasten (der von äußeren Kräften geleisteten Arbeit).

Bogenlängenverfahren (arc-length method)

Das Bogenlängenverfahren ist eine Methode, bei der man kraftgesteuert bis über das Maximum der Traglast hinaus rechnen kann. Die Notwendigkeit von kraftgesteuerten Methoden liegt darin, dass man im Gegensatz zu verschiebungsgesteuerten Methoden mehrere Lasten direkt proportional steigern kann. Beim Bogenlängenverfahren wird die Last wie vorgegeben gesteigert; würde diese Belastungssteigerung zu einer zu großen Deformation führen, so wird die Last mit einem Faktor kleiner als 1 multipliziert, nach Erreichen der Traglast sogar mit negativen Werten.

Stochastische Finite-Elemente-Methode

Bei der Variante der stochastischen Finiten-Elemente-Methode (SFEM) werden Eingangsgrößen des Modells, welche mit einer Unsicherheit behaftet sind, zum Beispiel Materialfestigkeiten oder Belastungen, durch stochastische Größen modelliert. Dies kann mithilfe gewöhnlicher Zufallsvariablen erreicht werden. Oft werden auch Zufallsfelder verwendet, wobei es sich um zufällig variierende, stetige mathematische Funktionen handelt. Eine geläufige Berechnungsmethode ist dabei die Monte-Carlo-Simulation. Dabei wird die FE-Berechnung für viele zufällige Realisierungen (samples) der Eingangsgrößen wiederholt, bis man einen gewissen, im Vorfeld definierten, stochastischen Fehler unterschreitet. Anschließend werden aus allen Ergebnissen die Momente, also Mittelwert und Varianz, berechnet. Je nach Streuung der Eingangsgrößen sind oftmals sehr viele Wiederholungen der FE-Berechnung nötig, was viel Rechenzeit in Anspruch nehmen kann.

Implizite und explizite FE-Löser

Strukturmechanische FEM-Systeme werden durch lineare Gleichungssysteme 2. Ordnung dargestellt:

$M{\ddot {u}}(t)+D{\dot {u}}(t)+Ku(t)=P(t)$

$M,D$ und $K$ sind Massen-, Dämpfungs- und Steifigkeitsmatrix des Systems; $P(t)$ ist der Vektor der externen Kräfte, die auf das Modell wirken. $u$ ist der Vektor der Freiheitsgrade.

Oft bestehen komplexe Bauteilmodelle aus mehreren Millionen Knoten, und jeder Knoten kann bis zu 6 Freiheitsgrade besitzen. Somit müssen FEM-Solver (Gleichungssystemlöser) gewisse Anforderungen in Bezug auf effektives Speichermanagement und ggf. Nutzung mehrerer CPUs erfüllen. Es gibt zwei grundsätzlich verschiedene Arten von FEM-Solvern: implizite und explizite.

Implizite FEM-Solver gehen von bestimmten Annahmen aus, unter denen der berechnete Lösungsvektor $u$ gültig ist. Wirkt z. B. eine zeitlich unveränderliche Last $P(t)=P={\text{const}}.$ auf ein System mit Dämpfung, dann wird sich nach ausreichend langer Zeit auch ein konstanter Verschiebungsvektor $u(t)=u={\text{const}}.$ einstellen. Für $t\to \infty$ ist dann ${\ddot {u}}(t)={\dot {u}}(t)=0$, und das Gleichungssystem vereinfacht sich zu $Ku=P$ mit der Lösung $u=K^{-1}P$

Für einen gegebenen Lastvektor $P$ kann der Verschiebungsvektor $u$ mit Hilfe des Gauß-Algorithmus oder durch QR-Zerlegung von $K$ berechnet werden.

Ist ein mechanisches System einer harmonischen Anregung $P(t)={\hat {P}}\sin(\Omega t)$ ausgesetzt, dann kann es erforderlich sein, die Eigenfrequenzen des Systems zu ermitteln, um Resonanzen im Betrieb zu vermeiden.

Eigenfrequenzen sind alle Frequenzen $\omega _{i}$, für die ein Verschiebungsvektor $u(t)={\hat {u}}_{i}\sin(\omega _{i}t)$ eine Lösung des unbelasteten ($P(t)=0$) und ungedämpften ($D=0$) Gleichungssystems darstellt. Für den Geschwindigkeits- und Beschleunigungsvektor gilt dann

${\dot {u}}_{i}={\hat {u}}_{i}\ \omega _{i}\cos(\omega _{i}t),\ {\ddot {u}}_{i}=-{\hat {u}}_{i}\omega _{i}^{2}\sin(\omega _{i}t)$

und das Gleichungssystem lautet damit

$(-M\omega _{i}^{2}+K){\hat {u}}_{i}\sin(\omega _{i}t)=0$

Um die Eigenfrequenzen $\omega _{i}$ und die dazugehörigen Eigenformen ${\hat {u}}_{i}$ zu berechnen, muss der implizite Solver also das Eigenwertproblem

$-M\omega _{i}^{2}+K=0$

lösen.

Explizite FEM-Solver

Explizite Solver berechnen die Verschiebungsvektoren $u_{i}$ zu bestimmten diskreten Zeitpunkten $t_{i}$ innerhalb eines vorgegebenen Zeitintervalls. Knotengeschwindigkeiten und -beschleunigungen werden durch Differenzenquotienten aus den Verschiebungen $u_{i+1},u_{i},u_{i-1}$ zu aufeinanderfolgenden Zeitpunkten $t_{i+1},t_{i},t_{i-1}$ angenähert. Mit konstanter Zeitschrittweite $t_{i+1}-t_{i}=\Delta \ t$ gilt

${\dot {u}}={\frac {u_{i}-u_{i-1}}{\Delta \ t}}$

${\ddot {u}}={\frac {{\frac {u_{i+1}-u_{i}}{\Delta \ t}}-{\frac {u_{i}-u_{i-1}}{\Delta \ t}}}{\Delta \ t}}={\frac {u_{i+1}-2u_{i}+u_{i-1}}{(\Delta t)^{2}}}$

hat das diskretisierte Gleichungssystem die Form

$M{\frac {u_{i+1}-2u_{i}+u_{i-1}}{(\Delta t)^{2}}}+D{\frac {u_{i}-u_{i-1}}{\Delta \ t}}+Ku_{i}=P_{i}$

Durch Auflösen dieser Gleichung erhält man eine Beziehung, mit der der Verschiebungsvektor $u_{i+1}$ aus den vorher berechneten Vektoren $u_{i}$ und $u_{i-1}$ ermittelt werden kann:

$u_{i+1}=M^{-1}((\Delta t)^{2}(P_{i}-Ku_{i})-D\Delta \ t(u_{i}-u_{i-1}))+2u_{i}-u_{i-1}$

Die Berechnung der Inversen $M^{-1}$ wird in der Praxis nicht durchgeführt, da explizite Solver in der Regel $M$ als Diagonalmatrix annehmen und daher jede Zeile des Gleichungssystems nur durch den Diagonaleintrag in der entsprechenden Zeile von $M$ geteilt werden muss.

Explizite Solver werden u. a. im Fahrzeugbau für die Berechnung von Crash-Lastfällen verwendet.

Der Vorteil direkter Gleichungslöser nach dem Gauß-Verfahren liegt für die praktische Anwendung in der numerischen Stabilität und dem Erhalt eines exakten Ergebnisses. Nachteilig sind die schlechte Konditionierung der üblicherweise dünn besetzten Steifigkeitsmatrizen und der hohe Speicherbedarf, wie oben erwähnt. Iterative Gleichungslöser sind unempfindlicher bei schlechter Konditionierung und benötigen weniger Speicher, wenn die Nicht-Null-Elemente-Speicherung verwendet wird. Allerdings verwenden iterative Solver ein Abbruchkriterium für die Berechnung der Ergebnisse. Wenn dieses erreicht wird, bevor eine annähernd exakte Lösung gefunden wurde, kann das Ergebnis, beispielsweise ein Spannungsverlauf, leicht fehlinterpretiert werden.

In manchen Implementierungen werden für die häufig auftretenden dünn besetzten Matrizen lediglich die Positionen und Werte der Einträge, die von Null abweichen, gespeichert. Damit kann man die Gleichungssysteme weiterhin direkt lösen, spart aber erheblich Speicherplatz.

Isogeometrische Analyse

→ Hauptartikel: Isogeometrische Analysis

Damit bei einer (kleineren) Änderung der (CAD-)Bauteil-Geometrie nicht aufwendig neu in finite Elemente unterteilt werden muss, können manche Programme ein bereits vorhandenes FE-Netz einer (sehr ähnlichen, neuen) CAD-Geometrie anpassen, was meist deutlich weniger Rechenzeit benötigt.

Programme

Finite-Elemente-Software und ihre Anwendung ist mittlerweile eine Industrie mit mehreren Milliarden US-Dollar Jahresumsatz.

• In der Praxis sind viele verschiedene Standalone-Großprogramme mit ähnlichem Anwendungsspektrum im Einsatz; die Auswahl, welches Programm zum Einsatz kommt, ist nicht nur von der Verwendung, sondern auch von Faktoren wie Verfügbarkeit, Zertifizierungsstandard im Unternehmen oder Lizenzkosten abhängig.
• Mit den in kommerziellen CAD-Systemen integrierten Finite-Elemente-Paketen können einfachere (i. d. R. lineare) Problemstellungen berechnet und mithilfe des CAD-Systems anschließend direkt ausgewertet werden. Die einzelnen Schritte, z. B. der Vernetzungs-Prozess (meshing) laufen automatisch im Hintergrund ab.
• Da mitunter sehr viel Rechenleistung nötig ist, um die Berechnung durchzuführen, stellen die ersten Unternehmen ihren Nutzern Rechenleistung in Form von Cloud-Diensten zur Verfügung.
• Es gibt Prä-/Postprozessoren mit graphischer Oberfläche und getrennten FE-Lösern.
• Es gibt Programmframeworks ohne graphische Oberfläche, meist als Präprozessor mit integriertem Gleichungslöser, die per Programmiersprache bedient werden, um beispielsweise mit selbst angefertigten Zusatzroutinen den FE-Solver zu steuern.

Der mathematische Zugang zur Finite-Elemente-Methode

Die schwache Formulierung einer Randwertaufgabe und das Galerkin-Verfahren

Betrachtet wird eine elliptische Randwertaufgabe zweiter Ordnung, als Beispiel die erste Randwertaufgabe für eine Poisson-Gleichung in einem zweidimensionalen Gebiet $\Omega$ mit Rand $\partial \Omega$:

$-\triangle u+cu=f\quad {\text{in}}\,\,\Omega ,\,\,u=0\,\,{\text{auf}}\,\,\partial \Omega =\Gamma .$

Besitzt $\Omega$ Ecken, so sagt die Lösungstheorie elliptischer Gleichungen entgegen der Erwartung, dass dieses Problem gar keine zweimal differenzierbare Lösung besitzt! Deshalb ist die Nutzung einer schwachen Formulierung wichtig, extrem wichtig auch hinsichtlich von Näherungsverfahren zur Berechnung von Lösungen wie der Finiten-Element-Methode (FEM), die nur stetige, aber keine differenzierbaren Ansatzfunktionen nutzen (nur für Probleme höherer, z. B. vierter Ordnung, werden hin und wieder differenzierbare Ansatzfunktionen verwendet).

Zur Herleitung der schwachen Formulierung multipliziert man die gegebene Gleichung mit einer Funktion $v$, integriert über $\Omega$ und beseitigt dann die zweiten Ableitungen durch partielle Integration (bzw. der Anwendung eines Integralsatzes). Das ergibt

$\int _{\Omega }\nabla u\nabla v-\int _{\Gamma }{\frac {\partial u}{\partial n}}v+\int _{\Omega }cuv=\int _{\Omega }fv.$

Nun muss man sich fragen, für welche $u,v$ diese Gleichung Sinn macht. Wichtig ist offenbar, dass $u$ und $v$ und deren Ableitungen quadratisch integrierbar sind, denn dann existieren alle vorkommenden Integrale. Präzise sagt man: $u$ und $v$ seien aus dem Sobolev-Raum $H^{1}(\Omega )$. Die Menge der Funktionen aus dem $H^{1}(\Omega )$, die zudem auf dem Rand von $\Omega$ gleich Null sind, nennt man $H_{0}^{1}(\Omega )$.

Damit ergibt sich folgende schwache Formulierung: $u\in H_{0}^{1}(\Omega )$ genügt

$\int _{\Omega }\nabla u\nabla v+\int _{\Omega }cuv=\int _{\Omega }fv\quad \forall v\in H_{0}^{1}(\Omega ).$

Solch eine Gleichung nennt man auch Variationsgleichung. Fundamental ist, dass sich bei anderen Randbedingungen die schwache Formulierung ändert. Hat man etwa die Randbedingung 2. Art ${\frac {\partial u}{\partial n}}=0$ auf $\Gamma$, so entsteht mit $u\in H^{1}(\Omega )$ die schwache Formulierung

$\int _{\Omega }\nabla u\nabla v+\int _{\Omega }cuv=\int _{\Omega }fv\quad \forall v\in H^{1}(\Omega ).$

Ist aber die Randbedingung 3. Art ${\frac {\partial u}{\partial n}}+pu=0$ gegeben, so bleibt es bei $u\in H^{1}(\Omega )$, aber es entsteht

$\int _{\Omega }\nabla u\nabla v+\int _{\Gamma }puv+\int _{\Omega }cuv=\int _{\Omega }fv\quad \forall v\in H^{1}(\Omega ).$

Das bedeutet später für die Finite-Elemente-Methode: Randbedingungen 1. Art sind unmittelbar zu berücksichtigen, Randbedingungen 2. oder 3. Art sind natürliche Randbedingungen und werden über die adäquate schwache Formulierung indirekt eingebaut.

Jede dieser drei schwachen Formulierungen bzw. Variationsgleichungen besitzt folgende allgemeine Form: Gesucht ist $u\in V$, einem Teilraum vom Raum $H^{1}(\Omega )$ mit

$a(u,v)=(f,v)$ für alle $v\in V$.

Hierbei ist $(f,v)=\int _{\Omega }fv$ eine Linearform, $a(\cdot ,\cdot )$ nennt man Bilinearform.

Da Randwertaufgaben für partielle Differentialgleichungen nur in Spezialfällen exakt lösbar sind, sucht man nun Näherungsverfahren. Ein wichtiges solches Verfahren ist das Galerkin-Verfahren für Variationsgleichungen.

Dazu wählt man einen endlichdimensionalen Teilraum $V_{h}\subset V$ von $V$ und nennt $u_{h}\in V_{h}$ Galerkin-Näherung, wenn gilt

$a(u_{h},v_{h})=(f,v_{h})$ für alle $v_{h}\in V_{h}$.

Dies ist äquivalent zu einem linearen Gleichungssystem mit endlich vielen Unbekannten, und damit ist die Näherungslösung $u_{h}$ berechenbar. Dies sieht man folgendermaßen: Ein linearer endlichdimensionaler Raum besitzt eine endliche Basis, diese Basis von $V_{h}$ sei $\phi _{i}$ für $i=1,\cdots ,N$. Dann gibt es Konstanten $c_{j}$ mit

$u_{h}=\sum _{j=1}^{N}c_{j}\phi _{j}\,\,.$

Setzt man dies in die Diskretisierung ein sowie $v_{h}:=\phi _{i}$ für $i=1,\cdots ,N$, so erhält man das lineare Gleichungssystem

$\sum _{j=1}^{N}a(\phi _{j},\phi _{i})c_{j}=(f,\phi _{i})$ für $i=1,\cdots ,N$

zur Berechnung der unbekannten Koefficienten $c_{j}$ der Näherungslösung. Aus den gegebenen Daten und den gewählten Basisfunktionen des endlichdimensionalen Raumes sind die Elemente der Koeffizientenmatrix und die ,rechte' Seite des Gleichungssystems berechenbar, gegebenenfalls durch numerische Berechnung der auftretenden Integrale. Im Fall einer symmetrischen Bilinearform ist die Koeffizientenmatrix symmetrisch. Unter gewissen Voraussetzungen an die Bilinearform besitzen sowohl das Variationsproblem als auch das diskrete Problem (das erzeugte Gleichungssystem) eine eindeutige Lösung.

Hingewiesen sei noch darauf, dass im Fall einer symmetrischen Bilinearform man das Variationsproblem

$\min _{v\in V}\left[{\frac {1}{2}}a(v,v)-(f,v)\right]$

mit dem Ritz-Verfahren

$\min _{v_{h}\in V_{h}}\left[{\frac {1}{2}}a(v,v)-(f,v)\right]$

näherungsweise lösen kann, die notwendige Optimalitätsbedingung für dieses Optimierungsproblem aber wieder zu der Galerkin-Formulierung $u_{h}\in V_{h}$ mit

$a(u_{h},v_{h})=(f,v_{h})$ für alle $v_{h}\in V_{h}$

führt. Während im symmetrischen Fall also egal ist, ob man mit dem Ritz- oder dem Galerkin-Verfahren diskretisiert, steht im nichsymmetrischen Fall nur der Galerkin-Zugang zur Verfügung.

Entscheidend für die Realisierung einer Galerkin-Diskretisierung (oder auch Ritz) ist die Wahl des endlichdimensionalen Teilraumes $V_{h}$ von $V$. Bei der spektralen Galerkin-Methode wählt man Polynome und speziell orthogonale Polynome als Basisfunktionen. Bei der Finite-Elemente Methode sind die Basisfunktionen Splines, d. h., stückweise polynomiale Funktionen. Da man die finiten Elemente lokal definiert, muss man sorgfältig darauf achten, ob der sich global ergebene Finite-Elemente-Raum $V_{h}$ die Eigenschaft $V_{h}\subset V$ besitzt. Wenn ja, so heißt die resultierende Finite-Elemente-Methode konform.

Finite Elemente und Finite-Elemente-Räume

Ausgangspunkt ist die Zerlegung des Grundgebietes $\Omega$ in endlich viele einfache Teilgebiete. Das sind im zweidimensionalen Fall Dreiecke und Vierecke, im dreidimensionalen Tetraeder und Parallelepipede. Der Einfachheit halber sei hier $\Omega$ zweidimensional und ein polygonales Gebiet. Zerlegt wird in Dreiecke.

Ein Dreieck bzw. Element der Zerlegung sei $K_{i}$, einschließlich des Randes ${\overline {K}}_{i}$. Die Zerlegung sei grundsätzlich zulässig, d. h., für $i\not =j$ sei ${\overline {K}}_{i}\cap {\overline {K}}_{j}$ leer oder ein Eckpunkt (Knoten) oder eine gemeinsame Kante der beiden Dreiecke. Ausgeschlossen wird also bei zwei benachbarten Dreiecken, dass eine Ecke eines Dreiecks auf einer Kante des Nachbardreiecks liegt, aber keine Ecke desselben ist.

Ein finites Element besteht nun aus einem Dreieck $K$, einer linearen Menge $P$ von Polynomen auf $K$ und einer Menge von Vorgaben (oder linearen Funktionalen), die ein Polynom aus $P$ eindeutig festlegen. Die Anzahl dieser Vorgaben ist also gleich der Dimension von $P$. Diese Vorgaben sind oft Werte in Punkten von ${\overline {K}}$ (nicht nur in den Knoten bzw. Eckpunkten), aber auch Integrale über Kanten von $K$ oder Integrale über $K$. Sind nur Funktionswerte vorgegeben, spricht man von Lagrange-Elementen. Strebt man (für Probleme vierter Ordnung) global stetig differenzierbare Elemente an, sind Vorgaben auch Werte von Ableitungen in gewissen Punkten. Solche Elemente heißen Hermite-Elemente.

Da ein finites Element also zunächst nur lokal definiert ist, erhält man ein Element des Finiten-Elemente-Raumes $V_{h}$ nun einfach durch stückweises Zusammensetzen. Für die Galerkin-Diskretisierung von Randwertaufgaben zweiter Ordnung ist nun extrem wichtig, wann $H^{1}$-Konformität vorliegt. Zentral ist folgende Aussage:

Ist $v_{h}\in V_{h}$ stückweise polynomial und global stetig, so gilt $v_{h}\in H^{1}(\Omega )$.

Das bedeutet also, dass man bei der zunächst lokalen Konstruktion nur einen stetigen Übergang von Element zu Element sichern muss, die Vorgaben sind dahingehend zu überprüfen. Benötigt man $v_{h}\in H_{0}^{1}(\Omega )$, so ist zusätzlich dafür zu sorgen, dass $v_{h}$ auf dem Rand des Gebietes gleich Null ist. Bei Randbedingungen 2. oder 3. Art ist die korrekte schwache Formulierung für das Einarbeiten der Randbedingungen zuständig.

Ein grundlegendes Beispiel sind zwei Elemente, für die $K$ ein Dreieck ist und $P$ die Menge aller Polynome ersten Grades auf $K$, also die Menge aller Funktionen der Form $\alpha x+\beta y+\gamma$. Die Werte in drei nicht auf einer Geraden liegenden Punkte bestimmen eine Funktion aus $P$ eindeutig. Wählt man die drei Funktionswerte in den Ecken, so erhält man globale Stetigkeit, denn die Werte in den zwei Ecken einer Kante definieren eine lineare Funktion einer Variablen eindeutig. Wählt man jedoch die drei Funktionswerte in den Seitenmitten, so erhält man ein unstetiges Element. Das erste beschriebene Element heißt konformes $P_{1}$-Element, das zweite ist das nichtkonforme $P_{1}$-Element.

Es sei nun $P$ die Menge aller Polynome vom Grad $k$. Die Dimension von $P$ ist $(k+2)(k+1)/2$. Man benötigt also Werte in $(k+2)(k+1)/2$ Punkten, um das konforme $P_{k}$-Element definieren. Dazu und für die Beschreibung von lokalen Basisfunktionen von $P_{k}$ sind baryzentrische Koordinaten nützlich.

Ist $K$ ein Dreieck mit den Ecken $p^{1},p^{2},p^{3}$, dann sind die baryzentrischen Koordinaten $\lambda _{1},\lambda _{2},\lambda _{3}$ eindeutig durch die beiden Gleichungen $\lambda _{1}+\lambda _{2}+\lambda _{3}=1$ und

$x=\sum _{i=1}^{3}\lambda _{i}p^{i}$

den Punkten $x\in {\overline {K}}$ zugeordnet. Die Ecke $p^{1}$ z. B. besitzt die baryzentrischen Koordinaten $(1,0,0)$, der Schwerpunkt des Dreiecks die Koordinaten $(1/3,1/3,1/3)$.

Für das konforme $P_{1}$-Element sind nun lokale Basisfunktionen leicht angebbar, diese sind $\lambda _{1},\lambda _{2},\lambda _{3}$ und es gilt mit der Kronecker-Delta Funktion $\delta$

$\lambda _{i}(p^{j})=\delta _{ij}$.

Als Nächstes wird die Frage beantwortet, in welchen Punkten eines Dreiecks man die Funktionswerte für das $P_{2}$-Element und das $P_{3}$-Element vorschreibt. Die Menge der quadratischen Funktionen besitzt die Dimension 6. Deshalb wählt man die drei Eckpunkte und die drei Seitenmitten, diese besitzen die baryzentrischen Koordinaten $(1/2,0,0)$, $(0,1/2,0)$ und $(0,0,1/2)$. Die Menge der kubischen Polynome besitzt die Dimension 10. Die Menge der Vorgabepunkte für die Funktionswerte für das $P_{3}$-Element sind die drei Ecken, die zwei Punkte auf jeder Kante, die die Kante in drei gleiche Teile zerlegen und der Schwerpunkt des Dreiecks.

Die lokalen Basisfunktionen für das $P_{2}$-Element sind

$\lambda _{1}(2\lambda _{1}-1),\lambda _{2}(2\lambda _{2}-1),\lambda _{3}(2\lambda _{3}-1),\lambda _{1}\lambda _{2},\lambda _{1}\lambda _{3},\lambda _{2}\lambda _{3}.$

Jede der lokalen Basisfunktionen besitzt folgende Eigenschaft: sie ist gleich Eins in genau einem der 6 Vorgabepunkte und gleich Null in den anderen fünf. Analog konstruiert man eine lokale Basis für $P_{3}$-Elemente.

Sei $q$ einer der Vorgabepunkte bei einem $P_{k}$- Finite-Elemente-Raum. Dann besitzt eine globale Ansatzfunktion die folgende Eigenschaft: sie ist gleich Eins im Punkt $q$ und gleich Null in allen anderen Vorgabepunkten. Dies impliziert, dass der Träger einer globalen Ansatzfunktion (der Bereich, in dem die Ansatzfunktion ungleich Null ist) nur aus wenigen Dreiecken der Zerlegung besteht! Damit entstehen in der Koeffizientenmatrix des Gleichungssystems, das mittels der FEM erzeugt wird, viele Nullen, die Matrix ist schwach besetzt. Dies ist ein Vorteil von Splines als Ansatzfunktionen beim Galerkin-Verfahren.

Bei sogenannten affinen Familien von finiten Elementen, und dazu gehören die $P_{k}$-Elemente, werden die globalen Ansatzfunktionen zur Erzeugung des diskreten Problems (Gleichungssystem) dadurch nicht benötigt, dass man jedes Element durch eine lineare Abbildung auf ein Referenzelement abbildet (dadurch werden auch die Ansatzfunktionen und Vorgabewerte auf $K$ auf ebensolche auf dem Referenzelement abgebildet). Dies wird im Folgenden für lineare Elemente demonstriert.

Die Erzeugung des diskreten Problems durch elementweises Herangehen und Transformation

Betrachtet wird exemplarisch das obige Poissonproblem mit $c=0$ und ihre FEM-Diskretisierung mit linearen finiten Elementen. Es sei

$u_{h}=\sum _{j=1}^{N}c_{j}\phi _{j}$

mit den globalen nodalen Ansatzfunktionen, die genau in einem der inneren Eckpunkte der Triangulation gleich Eins sind, in allen anderen Eckpunkten, insbesondere in denen auf dem Rand des Gebietes, gleich Null. Damit erfüllt der Ansatz die homogenen Randbedingungen. Ist $p^{r}$ der $r$-te der $N$ inneren Eckpunkt der Triangulation, so gilt $c_{r}=u_{h}(p^{r})$.

Die unbekannten $c_{j}$ berechnet man aus dem Gleichungssystem

$A_{h}c=f^{h}.$

Dabei ist $A_{h}$ die sogenannte Steifigkeitsmatrix mit den Elementen

$a_{ik}=\int _{\Omega }\nabla \phi _{i}\nabla \phi _{k}$

und der rechten Seite mit $f^{h}=(f_{i}^{h})$ und $f_{i}^{h}=\int _{\Omega }f\phi _{i}$.

Der entscheidende Trick ist nun, dass man die Integrale über die einzelnen Dreiecke $K_{j}$ der Triangulation berechnet und dann über alle Beiträge der Elemente summiert, zudem nicht wirklich über $K_{j}$ integriert, sondern durch Transformation die Integration über ein Referenzelement realisiert.

Dazu erklärt man zu einem Dreieck bzw. Element $K_{j}$ gehörende Elementsteifigkeitsmatrizen durch

$A_{h}^{j}=(a_{ik}^{j})_{i,k\in I_{j}}$

mit

$a_{ik}^{j}=\int _{K_{j}}\nabla \phi _{i}\nabla \phi _{k}\quad {\text{und }}I_{j}=\{i:\operatorname {supp} \phi _{i}\cap K_{j}\not =\emptyset \}.$

Analog wird durch

$f^{j}=(f_{i}^{j})_{i\in I_{j}}\quad {\text{mit }}f_{i}^{j}=\int _{K_{j}}f\,\phi _{i}.$

eine elementweise rechte Seite erklärt. Durch Summation über alle $K_{j}$ entsteht das final zu lösende Gleichungssystem.

In dem betrachteten Spezialfall kann man die Elementsteifigkeitsmatrizen exakt berechnen, andernfalls ist eine numerische Integration erforderlich. Es sei $K$ ein Element mit den Ecken $p^{i},p^{k},p^{l}$ und z. B. $p^{i}=(x_{1},y_{1})$. Dann kann man $K$ durch die Transformation

$x=x_{1}+(x_{2}-x_{1})\xi +(x_{3}-x_{1})\eta ,\quad y=y_{1}+(y_{2}-y_{1})\xi +(y_{3}-y_{1})\eta$

auf das Referenzelement mit den Ecken $(0,0),(1,0),(0,1)$ in der $(\xi ,\eta )$-Ebene abbilden. Die Integrale zur Berechnung der Elementsteifigkeitsmatrix werden durch diese Transformation auf dem Referenzelement berechnet. Bei der Transformation werden aus den drei nodalen lokalen Basisfunktionen auf $K$ in der $(\xi ,\eta )$-Ebene die Basisfunktionen

$1-\xi -\eta ,\,\,\xi {\text{ und }}\eta .$

Die Berechnung deren Ableitung nach $\xi$ und $\eta$ ist trivial. Die Funktionaldeterminante $D$ der Transformation ist

$D=(x_{2}-x_{1})(y_{3}-y_{1})-(x_{3}-x_{1})(y_{2}-y_{1}),$

der Betrag von $D$ ist gleich dem doppelten Flächeninhalt von $K$. Letztlich muss man noch die Ableitungen nach $x$ und $y$ in Ableitungen nach $\xi$ und $\eta$ umrechnen. Es gilt

$D\,{\frac {\partial }{\partial x}}=(y_{3}-y_{1}){\frac {\partial }{\partial \xi }}+(y_{1}-y_{2}){\frac {\partial }{\partial \eta }}\quad {\text{und }}D\,{\frac {\partial }{\partial y}}=(x_{1}-x_{3}){\frac {\partial }{\partial \xi }}+(x_{1}-x_{2}){\frac {\partial }{\partial \eta }}.$

Insgesamt erhält man dann z. B. für die erste Zeile der Elementsteifigkeitsmatrix

$a_{11}={\frac {1}{2|D|}}[(y_{2}-y_{3})^{2}+(x_{3}-x_{2})^{2}],\,\,a_{12}={\frac {1}{2|D|}}[(y_{2}-y_{3})(y_{3}-y_{1})+(x_{3}-x_{2})(x_{1}-x_{3})]\,\,a_{13}={\frac {1}{2|D|}}[(y_{2}-y_{3})(y_{1}-y_{2})+(x_{3}-x_{2})(x_{2}-x_{1})].$

Zurückkehrend zu der Bezeichnung $K_{j}$ mit den Ecken $p^{i}=(x_{i},y_{i})$, $p^{k}=(x_{k},y_{k})$ und $p^{l}=(x_{l},y_{l})$ ergibt sich für die Elementsteifigkeitsmatrix mit $i\not =k$

$a_{ik}^{j}={\frac {1}{2|D_{j}|}}[(y_{l}-y_{k})(y_{i}-y_{l})+(x_{l}-x_{k})(x_{i}-x_{l})]$

und für die Diagonalelemente

$a_{ii}^{j}={\frac {1}{2|D_{j}|}}[(y_{k}-y_{l})^{2}+(x_{k}-x_{l})^{2}].$

Zur Lösung des diskreten Problems

Die Diskretisierung eines linearen Randwertproblems mit der FEM führt auf ein lineares Gleichungssystem großer Dimension.

Bei nicht zu großer Dimension löst man lineare Gleichungssysteme mit einem direkten Verfahren, Standard ist ein Gaußsches Eliminationsverfahren und seine Varianten. Bei extrem großer Dimension greift man zu einem iterativen Verfahren. Zu den sogenannten Krylow-Unterraum-Verfahren gehören das bekannte konjugierte Gradientenverfahren für symmetrische Probleme und GMRES für nichtsymmetrische Systeme, beide Verfahren werden oft mit Vorkonditionierung genutzt. Da bei der Methode der finiten Elemente durch die notwendige Gitterverfeinerung zur Erreichung der gewünschten Genauigkeit ohnehin mehrere Gitter verwendet werden, bieten sich Mehrgitterverfahren zur Lösung der diskreten Probleme an.

Fehlerabschätzung

Üblich sind Fehlerabschätzungen für die Finite-Element-Methode im Fall elliptischer Randwertaufgaben zweiter Ordnung in der $H^{1}$-Norm, dabei werden Methoden der Funktionalanalysis angewandt.

Ein typisches Ergebnis wird nun skizziert. Die verwendete $H^{1}$-Norm ist definiert durch

$||v||_{H^{1}(\Omega )}:=\left(\int _{\Omega }(\nabla v)^{2}+\int _{\Omega }v^{2}\right)^{1/2}.$

Betrachtet werden lineare finite Elemente, ein polygonales Gebiet $\Omega$ und eine zulässige Zerlegung in Dreiecke. Es sei $h_{K}$ die längste Seite eines Dreiecks $K$ und $h=\max _{K}h_{K}$. Dann erhält man unter gewissen Voraussetzungen an die der elliptischen Randwertaufgabe zugeordneten Bilinearform und für $u\in H^{2}(\Omega )$ die Fehlerabschätzung

$||u-u_{h}||_{H^{1}(\Omega )}\leq C\,h\,,$

wenn zudem die Dreieckszerlegung z. B. der Minimalwinkelbedingung genügt. Das bedeutet: der minimale Innenwinkel aller Dreiecke auf der Familie der betrachteten Zerlegungen ist (auch bei Verfeinerung der Zerlegung) nach unten beschränkt, zu spitz dürfen also Dreiecke bei der Minimalwinkelbedingung nicht werden. Hingewiesen sei darauf, dass für konvexe Gebiete die Voraussetzung $u\in H^{2}(\Omega )$ realistisch ist, für Gebiete mit einspringenden Ecken dagegen nicht.

Für $P_{k}$-Elemente hofft man auf eine höhere Fehlerordnung, d. h.

$||u-u_{h}||_{H^{1}(\Omega )}\leq C\,h^{k}\,.$

Dies ist aber nur zu erwarten, wenn die Lösung der gegebenen Randwertaufgabe zusätzliche Glattheit aufweist.

Erweiterungen der Finite-Elemente-Methode

Gemischte finite Elemente nutzt man vorwiegend bei Problemen mit Nebenbedingungen, z. B. bei der Divergenzfreiheit im Stokes-Problem. Nichtkonforme finite Elemente spielen z. B. bei Problemen 4. Ordnung wie der Plattengleichung eine Rolle, wenn man dieselben Elemente wie für Gleichungen 2. Ordnung verwenden will. Die diskontinuierliche Galerkin-Methode ist ein sehr variables Werkzeug zur Anwendung unstetiger Elemente.

Stabilisierte Finite-Element-Methoden wie die Stromliniendiffusion-Finite-Element-Methode benötigt man für Probleme mit dominanter Konvektion. Besitzt man Informationen über existierende Grenzschichten (s. auch Singuläre Störungen), kann man zudem Grenzschichtangepasste Gitter einsetzen.

Literatur

• Martin Mayr/Ulrich Thalhofer: Numerische Lösungsverfahren in der Praxis: FEM-BEM-FDM. Hanser, 1993, ISBN 3-446-17061-8, S. 312. 
• J.N. Reddy: Energy Principles And Variational Methods In Applied Mechanics. 2. Auflage. John Wiley & Sons, 2002, ISBN 0-471-17985-X. 
• D. Braess: Finite Elemente – Theorie, schnelle Löser und Anwendungen in der Elastizitätstheorie. 4. Auflage. Springer, 2007, ISBN 978-3-540-72449-0. 
• Günter Müller (Hrsg.): FEM für Praktiker. 4 Bände. Expert Verlag, Renningen. 
  • Band 1: Grundlagen: Basiswissen und Arbeitsbeispiele zu FEMAnwendungen. 2007, ISBN 978-3-8169-2685-6.
  • Band 2: Strukturdynamik. 2008, ISBN 978-3-8169-2842-3.
  • Band 3: Temperaturfelder. 2007, ISBN 978-3-8169-2714-3.
  • Band 4: Elektrotechnik. 2009, ISBN 978-3-8169-2841-6.
• Klaus-Jürgen Bathe: Finite-Elemente-Methoden. 2. Auflage. Springer-Verlag, 2002, ISBN 3-540-66806-3. 
• W.E. Gawehn: Finite Elemente Methode. BOD Book on Demand, 2009, ISBN 978-3-8370-2497-5 (FEM-Grundlagen zur Statik und Dynamik). 
• H. Goering/Hans-G. Roos/L. Tobiska: Die Finite-Elemente-Methode für Anfänger. Wiley, 2010, ISBN 978-3-527-40964-8. 
• C. Großmann/Hans-G. Roos: Numerische Behandlung partieller Differentialgleichungen. Teubner, 2005, ISBN 3-519-22089-X. 
• Manfred Hahn/Michael Reck: Kompaktkurs Finite Elemente für Einsteiger, Theorie und Beispiele zur Approximation linearer Feldprobleme. Springer Vieweg, 2021, ISBN 978-3-658-33411-6, S. 325. 
• Frank Rieg, Reinhard Hackenschmidt, Bettina Alber-Laukant: Finite Elemente Analyse für Ingenieure: Eine leicht verständliche Einführung. Hanser Fachbuchverlag, 2012, ISBN 978-3-446-42776-1 (Anwendung der FEM in den Ingenieurwissenschaften). 
• René de Borst, Mike Crisfield, Joris Remmers, Clemens Verhoosel: Nichtlineare Finite-Elemente-Analyse von Festkörpern und Strukturen, Wiley-VCH 2014
• Karl-Eugen Kurrer: The History of the Theory of Structures. Searching for Equilibrium, Ernst und Sohn 2018, S. 881–914, ISBN 978-3-433-03229-9

Weblinks

Commons: Finite-Elemente-Methode – Sammlung von Bildern, Videos und Audiodateien

• Dr.-Ing. Ulrich Simon: Numerische Methoden in der Biomechanik
• Numerische Methoden (Vorlesung und Praktikum, Skript) (Memento vom 20. Oktober 2018 im Internet Archive)
• F.U. Mathiak: Die Methode der finiten Elemente (FEM). (Memento vom 26. November 2019 im Internet Archive) [PDF; 3,86 MB].