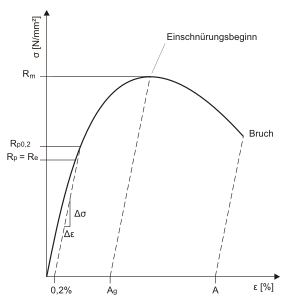
Spannungs-Dehnungs-Diagramm
In der Technik ist es häufig von großer Bedeutung, die Eigenschaften eines verwendeten Materials hinsichtlich seiner Festigkeit, seiner Plastizität bzw. seiner Sprödigkeit, seiner Elastizität und einiger anderer Eigenschaften genau zu kennen.
Zu diesem Zweck werden Materialproben im Zugversuch getestet, indem die Probe mit bekanntem Ausgangsquerschnitt in eine Zugprüfmaschine eingespannt und mit einer Zugkraft F belastet wird.
Unter Erhöhung der Kraft wird diese dann über der verursachten Längenänderung ΔL grafisch dargestellt. Diese Kurve bezeichnet man als Kraft-Verlängerungs-Diagramm.
Um eine Messkurve zu erhalten, die nur von der Art und Struktur des geprüften Materials, also nicht von den geometrischen Abmessungen der Probe abhängt, verwendet man reduzierte Einheiten, das heißt die Längenänderung ΔL wird auf die Anfangslänge L0 und die Kraft F auf den senkrechten Querschnitt S0 des Körpers im undeformierten Zustand bezogen.
Diese jetzt von der Probenform unabhängige Kurve nennt man Spannungs-Dehnungs-Diagramm.
(Nenn-)Spannung:
Die Dehnung ist eine Größe der Dimension Zahl. Häufig wird sie in Prozent oder in Promille angegeben (z. B. „0,2-%-Dehngrenze“).
Die Einheit der Spannung ist N/m² (= 1 Pa). Im Maschinenbau und der Werkstoffkunde wird oft mit der Einheit 1 N/mm² (= 1 MPa) gearbeitet.
Je nachdem, ob man den Versuch spannungsgeregelt oder dehnungsgeregelt fährt, ist die Spannung bzw. die Dehnung die unabhängige Variable. Es hat sich jedoch eingebürgert, immer die Spannung über der Dehnung aufzutragen.
Die (technische) Spannung bezieht sich immer auf den Ausgangsquerschnitt . Die wahre Spannung steigt jedoch im Zugversuch ab weiter an, da sich die Querschnittsfläche aufgrund von Einschnürung verringert. Die wahre Spannung kann allerdings nicht direkt mit dem Zugversuch ermittelt werden, daher verwendet man fast immer die technische Spannung . Eine Möglichkeit, die wahre Spannung zu ermitteln, ist die gleichzeitige optische Auswertung. Die technische Spannung und Dehnung können bei Orthotropie und einachsigem Spannungszustand in die wahre Spannung und Dehnung umgerechnet werden:[1][2]
Wahre Spannung:
Bei Inkompressibilität, z. B. bei plastischem Verhalten, gilt mit :
Wahre Dehnung:
Man unterscheidet verschiedene Bereiche im Spannungs-Dehnungs-Diagramm:
- den linear-elastischen Bereich (Proportionalbereich, „Hookesche Gerade“), in welchem die Dehnung der Spannung proportional ist und somit das Hookesche Gesetz gilt
- den nichtlinear-elastischen Bereich, in welchem die Verformung noch reversibel ist (elastisch) aber nicht mehr der Spannung proportional ist.
- den elastisch-plastischen Bereich, in welchem die Verformung teilweise plastisch – das heißt irreversibel – ist. Wenn die Elastizitätsgrenze überschritten wird, entstehen im Bauteil bleibende Deformationen aufgrund von Versetzungsbewegungen, die temperatur- und dehnratenabhängig sind (Thermisch aktiviertes Fließen).
Baustähle zeigen einen ausgeprägten Streckgrenzeneffekt, der durch interstitiell eingelagerte Fremdatome, beispielsweise Kohlen- und Stickstoff hervorgerufen wird.
-
Abb. 1 schematisches Spannungs-Dehnungs-Diagramm mit ausgeprägter Streckgrenze
-
Abb. 2 schematisches Spannungs-Dehnungs-Diagramm mit kontinuierlichem Fließbeginn und eingetragener 0,2-%-Dehngrenze
-
Abb. 3 schematisches Feindehnungsdiagramm
In den Diagrammen sind folgende Abkürzungen verwendet worden:
- = Zugfestigkeit
- = obere Streckgrenze
- = untere Streckgrenze
- = Dehngrenze mit 0,2 % plastischer Verformung
- = Elastizitätsmodul
- = Bruchdehnung
- = Gleichmaßdehnung
- = Lüdersdehnung
Siehe auch
[Bearbeiten | Quelltext bearbeiten]Literatur
[Bearbeiten | Quelltext bearbeiten]- Eckard Macherauch: Praktikum in Werkstoffkunde. 10., verb. Aufl., Vieweg, Braunschweig 1992, ISBN 3-528-93306-2
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Günter Gottstein: Materialwissenschaft und Werkstofftechnik Physikalische Grundlagen. 4., neu bearb. Aufl. 2014. Berlin, Heidelberg, ISBN 978-3-642-36603-1, S. 215.
- ↑ Wahre Spannung und Dehnung – Baustofftechnik 1. In: Ingenieukurse.de. examio GmbH, abgerufen am 21. November 2020.