Hypozykloide

Die rote Kurve ist eine Hypozykloide, die durch Abrollen des kleinen Kreises in dem großen Kreis erzeugt wird. (Die Parameter sind $R=4,$ $r=1,$ es ist eine Astroide).

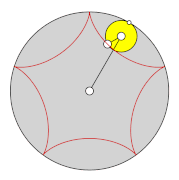
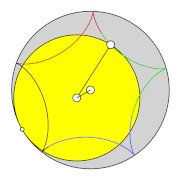
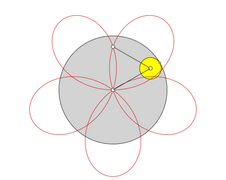
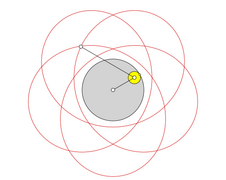
Eine Hypozykloide (von altgriechisch ὑπό hypó = unter und lateinisch cyclus bzw. altgr. κύκλος kýklos = Kreis) ist eine Rollkurve, die sich folgendermaßen beschreiben lässt: Auf der Innenseite eines gegebenen Kreises (Rastkreis) mit Radius $R$ rollt ein kleinerer Kreis (Gangkreis) mit Radius $r$, ohne zu gleiten. Die Bahn, die ein mitrotierender Punkt auf dem Umfang des Gangkreises beschreibt, wird als Hypozykloide bezeichnet. Die Hypozykloide ist das Gegenstück zur Epizykloide und ein Spezialfall der Hypotrochoide. Ein verwandter Begriff ist die Zykloide, bei der ein Kreis auf einer Geraden rollt.

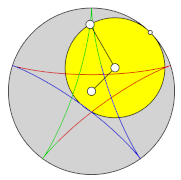
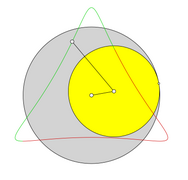
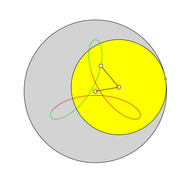
Zweifache Erzeugung von Hypozykloiden

In einem festen Kreis mit Radius $R$ erzeugen zwei kleinere Kreise mit Radius $r$ bzw. $R-r$ beim Abrollen auf der Innenseite kongruente Hypozykloiden.

Geschlossenheit

Eine Hypozykloide ist genau dann eine geschlossene Kurve, wenn das Längenverhältnis $q$ = ${\tfrac {R}{r}}$ der Radien rational ist und sich durch Kürzen als gekürzter Bruch ${\tfrac {i_{R}}{i_{r}}}$ aus den zwei ganzen Zahlen $i_{R}$ und $i_{r}$ schreiben lässt. Mathematisch ausgedrückt bedeutet das: $i_{R}={\tfrac {R}{\operatorname {ggT} (i_{R},i_{r})}}$ und $i_{r}={\tfrac {r}{\operatorname {ggT} (i_{R},i_{r})}}$. Dabei bezeichnet $\operatorname {ggT} (i_{R},i_{r})$ den größten gemeinsamen Teiler von $i_{R}$ und $i_{r}$. $R$ ist in diesem Bruch der Radius des stehenden „Rades“, und $r$ ist der Radius des laufenden „Rades“. Bei der technischen Umsetzung in Form von Zahnrädern ist die Anzahl der „Zähne“ maßgeblich, sodass sich stets geschlossene Kurven ergeben.

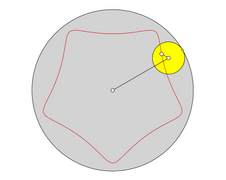
Anzahl der Spitzen

Die Anzahl der Spitzen einer geschlossenen Hypozykloide ist gleich der ganzen Zahl $i_{R}$.

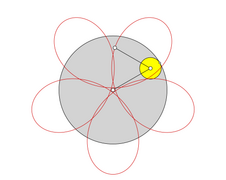
Anzahl der Umläufe

Die Anzahl an Umläufen des sich bewegenden „Rades“ während einer Periode ist $i_{r}$. In den Bildern wird für jeden Teil der Hypozykloide, der während eines Umlaufs des bewegten „Rades“ entsteht, eine andere Farbe verwendet.

• Umläufe und Spitzen von Hypozykloiden
• 
  Hypozykloide q = 5/1
• 
  Hypozykloide q = 5/2
• 
  Hypozykloide q = 5/3
• 
  Hypozykloide q = 5/4

Parametergleichung

Die kartesischen Koordinaten eines Kurvenpunktes $P$ lassen sich berechnen durch

$x=(R-r)\cos \alpha +r\cos(({\frac {R}{r}}-1)\alpha ),$

$y=(R-r)\sin \alpha -r\sin(({\frac {R}{r}}-1)\alpha ).$

Dabei wird vorausgesetzt, dass der Mittelpunkt des festen Kreises mit dem Ursprung übereinstimmt. Die Startposition des erzeugenden Punktes ist $(R,0)$. Als Parameter wird der Winkel $\alpha$ verwendet, den die Verbindungsstrecke zwischen dem Ursprung und dem Mittelpunkt des bewegten Kreises mit der x-Achse einschließt. Die Gleichungen lassen sich dadurch begründen, dass man in der Parameterdarstellung der Epizykloide den Radius $r$ des bewegten Kreises durch $-r$ ersetzt. Mit der Abkürzung $m={\frac {R}{r}}-1$ können die Gleichungen noch einfacher formuliert werden:

$x=mr\cos \alpha +r\cos(m\alpha ),$

$y=mr\sin \alpha -r\sin(m\alpha ).$

Spezielle Hypozykloiden

Für ganzzahlige Längenverhältnisse $q$ ergeben sich spezielle Hypozykloiden:

• Für $q=2$ (Cardanische Kreise) ergibt sich eine geradlinige Hypozykloide, deren sämtliche Punkte auf einem Durchmesser liegen.
• Für $q=3$ ergibt sich eine Deltoide (Hypozykloide mit 3 Spitzen)
• Für $q=4$ ergibt sich eine Astroide (Hypozykloide mit 4 Spitzen): das Karo, wie man es von Spielkarten kennt.

• Spezielle Hypozykloiden
• 
  Hypozykloide q = 2/1 (Cardanische Kreise)
• 
  Hypozykloide q = 3/1 (Deltoide)
• 
  Hypozykloide q = 4/1 (Astroide)

Hypotrochoide

Die rot gezeichnete Hypotrochoide entsteht durch Abrollen des kleineren schwarzen Kreises auf der Innenseite des größeren blauen Kreises (Parameterwerte R = 5, r = 3, d = 5).

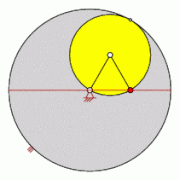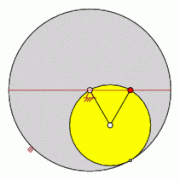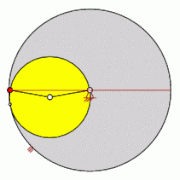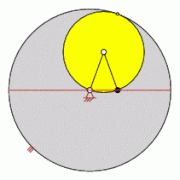
Die Hypotrochoide ist eine nahe liegende Verallgemeinerung der Hypozykloide. Ein kleinerer Kreis mit Radius $r$ rollt auf der Innenseite eines größeren Kreises mit Radius $R$. Der erzeugende Punkt hat zum Mittelpunkt des bewegten Kreises einen Abstand $d>0$.

Folgende Typen werden unterschieden:

• Verkürzte oder gestreckte Hypozykloide ($d<r$)
• Verlängerte oder verschlungene Hypozykloide ($d>r$)
• Hypozykloide ($d=r$), auch als gespitzte Hypozykloide bezeichnet

• Hypotrochoiden mit q = 3/1 bzw. q = 3/2
• 
  Verkürzte Hypozykloide q = 3/1
• 
  Gespitzte Hypozykloide q = 3/1
• 
  Verlängerte Hypozykloide q = 3/1
• 
  Verkürzte Hypotrochoide q = 3/2
• 
  Gespitzte Hypozykloide q = 3/2
• 
  Verlängerte Hypozykloide q = 3/2

Parametergleichung

Für den allgemeinen Fall (Hypotrochoide) muss in der Parameterdarstellung der Hypozykloide der Faktor $r$ (Radius) durch den Abstand $d$ ersetzt werden.

$x=(R-r)\cos \alpha +d\cos(({\frac {R}{r}}-1)\alpha ),$

$y=(R-r)\sin \alpha -d\sin(({\frac {R}{r}}-1)\alpha ).$

Mit $m={\frac {R}{r}}-1$ lauten die Gleichungen

$x=mr\cos \alpha +d\cos(m\alpha ),$

$y=mr\sin \alpha -d\sin(m\alpha ).$

Beispiele

• 
  $R=30,r=10,d=r$
• 
  $R=30,r=10,d=5$
• 
  $R=30,r=10,d=15$
• 
  Doppelte Erzeugung von Hypotrochoiden mit q = 3/1 bzw. q = 3/2
• 
  Zwei Hypotrochoiden (Animation)

Verkürzte Hypozykloide

Alle verkürzten Hypozykloiden weisen die gleiche Anzahl an Schnittpunkten auf wie die gespitzten, also $i_{R}\cdot (i_{r}-1)$.

Die verkürzten Hypozykloiden lassen sich unterscheiden in solche mit und ohne Wendepunkte. Wendepunkte sind dadurch gekennzeichnet, dass der Krümmungsmittelpunkt von einer Seite der Kurve auf die andere wechselt, entsprechen also einem Wechsel zwischen Links- und Rechtskrümmung. Die Anzahl der Kurvenabschnitte mit Links- bzw. Rechtskrümmung ist jeweils gleich $i_{R}$ und damit gleich der Anzahl der Spitzen. Die Anzahl der Wendepunkte beträgt somit $2\cdot i_{R}$. Eine verkürzte Hypozykloide besitzt nur dann Wendepunkte, wenn der erzeugende Punkt nahe genug am Rand des umlaufenden Kreises liegt. Präziser: Wendepunkte existieren, falls $d>r/(i_{R}/i_{r}-1)$ gilt. Im Grenzfall $d=r/(i_{R}/i_{r}-1)$ hat die verkürzte Hypozykloide $i_{R}$ Abschnitte, die annähernd geradlinig verlaufen.

• Gespitzte und verkürzte Hypozykloiden
• 
  Gespitzte Hypozykloide
• 
  Verkürzte Hypozykloide mit Wendepunkten
• 
  Verkürzte Hypozykloide mit genäherten Geraden
• 
  Verkürzte Hypozykloide ohne Wendepunkte

Der Spirograph, ein Spielzeug, mit dem sich reizvolle Ornamente gestalten lassen, ermöglicht unter anderem das Zeichnen von verkürzten Hypozykloiden.

Verlängerte Hypozykloide

Die Anzahl an Schleifen während einer Periode ist identisch mit der Zahl $i_{R}$ und somit identisch mit der Anzahl an Spitzen der Hypozykloide.

Verlängerte Hypozykloiden weisen mindestens $i_{R}$ Schnittpunkte mehr als die (gespitzte) Hypozykloide auf. Die genaue Anzahl an Schnittpunkten lässt sich nur ermitteln mit Hilfe von Übergangskurvenpunkten. Ein Übergangskurvenpunkt erzeugt eine Hypotrochoide mit Berührungspunkten. Die Anzahl an Übergangskurvenpunkten und somit an Hypotrochoiden mit Berührungspunkten ist gleich dem Integerwert von ${\tfrac {i_{R}}{2}}$. Somit treten keine Berührungspunkte auf, wenn $i_{R}$ gleich 1 ist.

Übergangskurvenpunkte lassen sich nicht analytisch berechnen. Die Ermittlung mit Hilfe von Näherungsverfahren ist nicht kompliziert, würde aber den Rahmen dieses Artikels sprengen. Daher sollen hier nur die Phänomene zur Erzeugung der Formenvielfalt der verlängerten Hypozykloiden erläutert werden.

Dass durch geringe Variation des Abstandes des erzeugenden Punkts zum Mittelpunkt des umlaufenden „Rades“ immer wieder anders anmutende Hypotrochoiden entstehen, lässt sich anhand der Sonderfälle erläutern, bei denen Hypotrochoiden mit Berührungspunkten entstehen.

• Hypotrochoiden mit q = 5/1
• 
  Gespitzte Hypozykloide
• 
  Verschlungene Hypozykloide mit 5 Schnittpunkten
• 
  Verschlungene Hypozykloide mit 5 Berührungspunkten
• 
  Verschlungene Hypozykloide mit 15 Schnittpunkten
• 
  Verschlungene Hypozykloide mit 10fach-Schnittpunkt und 5 Schnittpunkten
• 
  Verschlungene Hypozykloide mit 15 Schnittpunkten

Verlängerte Hypozykloiden mit der Mindestanzahl an Schnittpunkten werden durch Punkte erzeugt, die in der Nähe des Außenrandes des umlaufenden Rades liegen. Die Anzahl der Schnittpunkte ist gleich der Anzahl an Spitzen plus $i_{R}$.

Der Integerwert von ${\tfrac {i_{R}}{2}}$ ergibt die Anzahl $n_{b}$ an Hypotrochoiden mit Berührungspunkten. Ist $n_{b}$ größer null, so wird irgendwann einmal eine verschlungene Hypozykloide mit Berührungspunkten erzeugt, wenn der erzeugende Punkt vom Kreisumfang weg verschoben wird. Die Hypotrochoide mit Berührungspunkten selbst weist noch eine unveränderte Anzahl an Selbstschnittpunkten auf. Aber wenn der erzeugende Punkt noch weiter weg verschoben wird, entsteht eine Hypotrochoide ohne Berührungspunkt, deren Anzahl an Schnittpunkten sich um $2\cdot i_{R}$ erhöht hat. Erzeugt das zugrunde liegende „Räderpaar“ mehr als eine Hypotrochoide mit Berührungspunkten, wiederholt sich das gleiche (mehrmals), wenn der erzeugende Punkt weiter vom Kreisumfang entfernt wird und dadurch wieder zu einer Stelle gelangt, in der eine Hypotrochoide mit Berührungspunkten erzeugt wird.

• Alle Punkte, die Hypotrochoiden mit Berührungspunkten erzeugen, liegen zwischen dem Außenrand des umlaufenden „Rades“ und einem konzentrischen Kreis durch den Mittelpunkt des stehenden Rades. Wird der erzeugende Punkt weiter weg vom Rand des umlaufenden Rades über den Mittelpunkt des stehenden Rades hinweg verschoben, ändert sich an der Anzahl der Schnittpunkte nichts mehr und es treten auch keine weiteren Sonderfälle auf.

Punkte, die vom Mittelpunkt des umlaufenden „Rades“ weiter entfernt sind als der Abstand der Mittelpunkte beider „Räder“, erzeugen Hypotrochoiden mit der maximalen Anzahl an Schnittpunkten $n_{\text{max}}$.

• Wenn $i_{R}$ eine gerade Zahl ist, ist die maximale Anzahl an Schnittpunkten $n_{\text{max}}=n_{s0}+2\cdot n_{b}\cdot i_{R}.$
• In allen anderen Fällen, nämlich wenn $i_{R}$ eine ungerade Zahl ist, gilt $n_{\text{max}}=n_{s0}+(1+2\cdot n_{b})\cdot i_{R}.$

Eine Hypotrochoide, die durch den Mittelpunkt des feststehenden „Rades“ verläuft und mehr als einen Schnittpunkt aufweist, stellt immer einen Sonderfall dar:

• Ist $i_{R}$ eine gerade Zahl, dann weist diese verlängerte Hypozykloide mindestens einen Berührungspunkt auf. Gibt es mehrere Berührungspunkte, so liegen Berührungs- und Selbstschnittpunkte übereinander.
• Ist $i_{R}$ eine ungerade Zahl, dann liegen mehrere Schnittpunkte der verlängerten Hypozykloide übereinander.

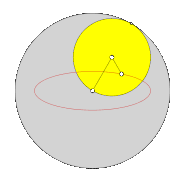
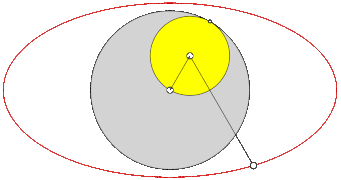
Spezielle Hypotrochoiden

Ein interessanter Spezialfall liegt vor, wenn der rollende Kreis halb so groß ist wie der feste Kreis ($R=2r,q=2,m=1$).

• Falls der erzeugende Punkt am Rand des rollenden Kreises liegt ($d=r$, Hypozykloide oder gespitzte Hypotrochoide), entsteht ein Durchmesser des festen Kreises (zweifach durchlaufen, auf der $x$-Achse, siehe oben).
• Falls der erzeugende Punkt innerhalb des rollenden Kreises ($d<r$) oder außerhalb des rollenden Kreises liegt ($d>r$), entsteht die Ellipse ${\big (}(r+d)\cos \alpha ,(r-d)\sin \alpha {\big )}$.

• Spezielle Hypotrochoiden mit q = 2
• 
  Ellipse als spezielle Hypotrochoide bei q = 2
• 
  Hypotrochoide: Ellipse
• 
  Hypozykloide: Gerade
• 
  Hypotrochoide: Ellipse

Für $d>0$ liegt die große Achse der Ellipse auf der $x$-Achse, für $d<0$ (unüblich) würde sie auf der $y$-Achse liegen. Für $d=0$ ergibt sich ein Kreis.

Eine Ellipse $(a\cos \alpha ,b\sin \alpha )$ lässt sich also auch immer durch eine Hypotrochoide mit den Parametern $\;r={\tfrac {a+b}{2}},\;d={\tfrac {a-b}{2}},\;R=2r=a+b\;$ erzeugen.

• 
  $R=30,r=15,d=r$ (Strecke)
• 
  $R=30,r=15,d=-5,8,25$ (Ellipsen)
• 
  Ellipsen (rot, cyan) mit cardanischen Kreisen

Weblinks

Commons: Hypotrochoide – Sammlung von Bildern, Videos und Audiodateien

• Animation zu Epi-, Hypo- und Peritrochoide mit Schiebereglern (Volker Jäkel)
• Herleitung der Formenvielfalt von Hypotrochoiden einschließlich interaktiver Berechnung von Punkten auf Übergangskurven und BALLscher Kurve
• Interaktives Applet zur Erzeugung von Hypozykloiden (automatisch)
• Interaktives Applet zur Erzeugung von Hypozykloiden (von Hand)