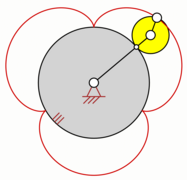
Epizykloide

Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion! (Artikel eintragen)

Die rote Kurve ist eine Epizykloide. Sie entsteht durch Abrollen des kleinen Kreises auf dem großen Kreis durch Verfolgung des anfänglichen Berührpunktes beider Kreise.

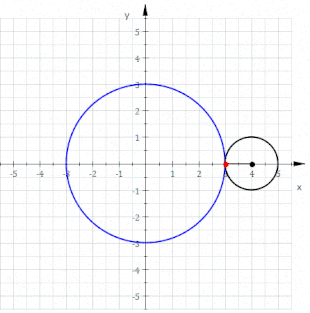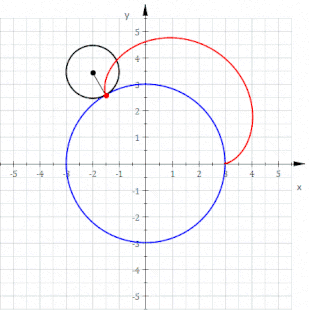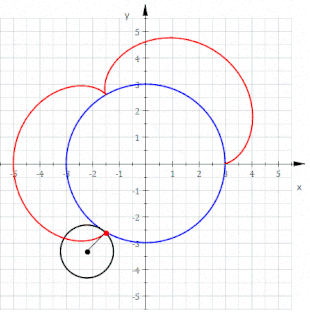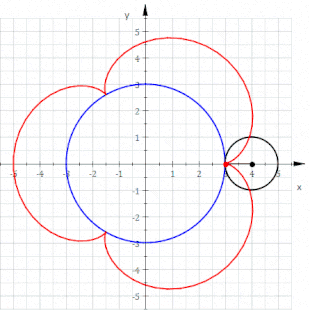
Eine Epizykloide (von altgriechisch ἐπί epí = auf und lateinisch cyclus bzw. altgr. κύκλος kýklos = Kreis) ist eine Rollkurve, die sich folgendermaßen beschreiben lässt: Auf der Außenseite eines gegebenen Kreises (Rastkreis) mit Radius $R$ rollt ein weiterer Kreis (Gangkreis) mit Radius $r$, ohne zu gleiten. Die Bahn, die ein mitrotierender Punkt auf dem Umfang des Gangkreises beschreibt, wird als Epizykloide bezeichnet. Die Epizykloide ist das Gegenstück zur Hypozykloide und ein Spezialfall der Epitrochoide. Ein verwandter Begriff ist die Zykloide, bei der ein Kreis auf einer Geraden rollt.

Epizykloiden sind blumenähnliche Kurven, die an Mandalas erinnern. Historisch spielten Epizykloiden eine wichtige Rolle in der Epizykeltheorie. Mit dieser Theorie versuchte man, die beobachteten Planeten-Bahnen mit teilweise eigentümlich anmutenden Schleifen zu erklären.

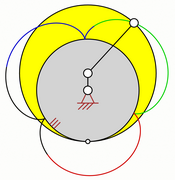
Zweifache Erzeugung von Epizykloiden

Bei einer Epizykloide, die durch Abrollen eines Kreises mit Radius $r$ um einen festen Kreis mit Radius $R$ entsteht, schwankt der Abstand der Kurvenpunkte vom Mittelpunkt des festen Kreises zwischen $R$ und $R+2r$ (Summe aus dem Radius des Leitkreises und dem Durchmesser des bewegten Kreises). Diese Epizykloide lässt sich auch als Perizykloide auffassen: Ein Kreis mit Radius $R+r$ rollt mit seiner Innenseite um einen festen Kreis mit Radius $R$. Getriebetechnisch lässt sich das erzeugende Getriebe einer Perizykloide durch das Abrollen eines Hohlrades um ein stillstehendes kleineres Rad verwirklichen.

• Zweifache Erzeugung von Epizykloiden
• 
  Epizykloide q = 3/1
• 
  Perizykloide q = 3/4

Geschlossenheit

Sowohl Epizykloiden als auch Hypozykloiden sind genau dann geschlossene Kurven, wenn das Längenverhältnis $q$ = ${\tfrac {R}{r}}$ der Radien rational ist und sich durch Kürzen als gekürzter Bruch ${\tfrac {i_{R}}{i_{r}}}$ aus den zwei ganzen Zahlen $i_{R}$ und $i_{r}$ schreiben lässt. Mathematisch ausgedrückt bedeutet das: $i_{R}={\tfrac {R}{\operatorname {ggT} (i_{R},i_{r})}}$ und $i_{r}={\tfrac {r}{\operatorname {ggT} (i_{R},i_{r})}}$. Dabei bezeichnet $\operatorname {ggT} (i_{R},i_{r})$ den größten gemeinsamen Teiler von $i_{R}$ und $i_{r}$. $R$ ist in diesem Bruch der Radius des stehenden „Rades“, und $r$ ist der Radius des umlaufenden „Rades“. Bei der technischen Umsetzung in Form von Zahnrädern ist die Anzahl der „Zähne“ maßgeblich, sodass sich stets geschlossene Kurven ergeben.

Anzahl der Spitzen

Die Anzahl der Spitzen der geschlossenen Epizykloide ist identisch mit der ganzen Zahl $i_{R}$.

Anzahl an Umläufen

Die Anzahl an Umläufen des sich bewegenden „Rades“ während einer Periode ist $i_{r}$.

Parameterdarstellung

Zur Herleitung der Parameterdarstellung

Die kartesischen Koordinaten eines Kurvenpunktes $P$ lassen sich berechnen durch

$x=(R+r)\cos \alpha -r\cos(\alpha +\beta ),$

$y=(R+r)\sin \alpha -r\sin(\alpha +\beta ).$

Dabei wird vorausgesetzt, dass der feste Kreis den Mittelpunkt $O(0,0)$ hat. Die Startposition des erzeugenden Punktes ist $(R,0)$. Als Parameter wird der Winkel $\alpha$ verwendet, den die Verbindungsstrecke zwischen dem Ursprung $O$ und dem Mittelpunkt $M$ des bewegten Kreises mit der x-Achse einschließt.

Zur Begründung betrachtet man die beiden Kreisbögen (in der Skizze rot), die der bisherigen Rollbewegung entsprechen. Der zugehörige Mittelpunktswinkel im bewegten Kreis (grün) sei mit $\beta$ bezeichnet. Nun lassen sich die Gleichungen trigonometrisch begründen. Der Ortsvektor von $M$ ist wegen $|{\overrightarrow {OM}}|=R+r$ gegeben durch

${\overrightarrow {OM}}={\begin{pmatrix}(R+r)\cos \alpha \\(R+r)\sin \alpha \end{pmatrix}}.$

Ähnlich ist

${\overrightarrow {MP}}={\begin{pmatrix}r\cos(\alpha +\beta -180^{\circ })\\r\sin(\alpha +\beta -180^{\circ })\end{pmatrix}}={\begin{pmatrix}-r\cos(\alpha +\beta )\\-r\sin(\alpha +\beta )\end{pmatrix}}$

zu begründen ($\alpha +\beta -180^{\circ }$ ist der Winkel gegenüber der x-Richtung). Insgesamt erhält man für den Ortsvektor von $P$:

${\overrightarrow {OP}}={\overrightarrow {OM}}+{\overrightarrow {PM}}={\begin{pmatrix}(R+r)\cos \alpha -r\cos(\alpha +\beta )\\(R+r)\sin \alpha -r\sin(\alpha +\beta )\end{pmatrix}}$

Da die Kreisbögen gleich groß sein müssen, gilt $R\alpha =r\beta$. Man kann also man den Winkel $\beta$ durch $\alpha$ ausdrücken ($\beta ={\frac {R}{r}}\alpha$). Es folgt:

$x=(R+r)\cos \alpha -r\cos \left(\left(1+{\frac {R}{r}}\right)\alpha \right),$

$y=(R+r)\sin \alpha -r\sin \left(\left(1+{\frac {R}{r}}\right)\alpha \right).$

Mithilfe der Abkürzung $m=1+{\frac {R}{r}}$ lassen sich die Gleichungen noch einfacher schreiben:

$x=mr\cos \alpha -r\cos(m\alpha ),$

$y=mr\sin \alpha -r\sin(m\alpha ).$

Wenn das Verhältnis $k={\frac {R}{r}}$ eine rationale Zahl ist, schließt sich die Kurve nach einer oder mehreren Umdrehungen. Ist es irrational, schließt sie sich nie.

Es ist auch möglich, die Epizykloide mit Polarkoordinaten darzustellen.

Alternativer Startpunkt

Alternative Definition und Parameterdarstellung

Verwendet man $(R+2r,0)$ als Startposition des erzeugenden Punktes, so entsteht eine zur obigen Definition um den Winkel ${\tfrac {\pi }{m-1}}$ gedrehte Kurve. Ihre Parameterdarstellung ist:

$x=mr\cos \alpha {\color {red}+}r\cos(m\alpha ),$

$y=mr\sin \alpha {\color {red}+}r\sin(m\alpha ).$

Weitere Beispiele

In dem folgenden Schaubild ist links ${\tfrac {R}{r}}$ eine ganze Zahl, deswegen überlappen sich die „Blütenblätter“ links nicht und die Kurve ist geschlossen. Rechts überlappen sich aber die „Blütenblätter“, d. h., die Kurve ist nicht geschlossen, da ${\tfrac {R}{r}}=2{,}5$. ${\tfrac {R}{r}}$ wird auch Ordnung der Epizykloide genannt.

Epizykloiden

Länge, Fläche, Evolute

Die ersten Ableitungen der letzten Parameterdarstellung sind

$x'=-mr\;(\sin \alpha -\sin(m\alpha ))\ ,$

$y'=mr\;(\cos \alpha -\cos(m\alpha ))$

und

$x'^{2}+y'^{2}=2m^{2}r^{2}(1-\cos(m-1)\alpha )=4m^{2}r^{2}\;\sin ^{2}({\tfrac {m-1}{2}}\alpha )\ .$

(Es wurden die Formeln $\cos(u+v)=\dots ,\sin ^{2}u={\tfrac {1}{2}}(1-\cos(2u))$ verwendet.)

Länge

Eine sich schließende Epizykloide besitzt $\;m-1\;$ Bögen. Die Länge eines Bogens der Zykloide ist

$s_{0}=\int _{0}^{\frac {2\pi }{m-1}}{\sqrt {x'^{2}+y'^{2}}}\;\mathrm {d} \alpha =2mr\int _{0}^{\frac {2\pi }{m-1}}\sin({\tfrac {m-1}{2}}\alpha )\;\mathrm {d} \alpha ={\frac {8mr}{m-1}}$

und die Gesamtlänge ist

$s=(m-1)s_{0}=8mr\ .$

Epizykloide: Sektor

Flächeninhalt

Mit der Sektorformel von Leibniz

$F={\frac {1}{2}}\int _{a}^{b}{\big (}x(t)y^{\prime }(t)-y(t)x^{\prime }(t){\big )}\mathrm {d} t$

und

${\begin{matrix}xy'-yx'&=&(mr\cos \alpha -r\cos m\alpha )\cdot mr(\cos \alpha -\cos m\alpha )\\&&-(mr\sin \alpha -r\sin m\alpha )\cdot (-mr(\sin \alpha -\sin m\alpha ))\\&=&m(m+1)r^{2}(1-\cos((m-1)\alpha ))\end{matrix}}$

ergibt sich für den Sektor-Flächeninhalt zu einem Bogen

$A_{0}={\frac {1}{2}}m(m+1)r^{2}\int _{0}^{\frac {2\pi }{m-1}}(1-\cos((m-1)\alpha )\;d\alpha ={\frac {\pi m(m+1)r^{2}}{m-1}}$

und für die ganze Kurve ($m-1$ Bögen)

$A=(m-1)A_{0}=m(m+1)\;\pi r^{2}\ .$

Epizykloide: Evolute (rot)

Evolute

Wegen

$x'y''-x''y'=\cdots =m^{2}r^{2}(m+1){\big (}1-\cos(m-1)\alpha {\big )}$ ist

${\tfrac {x'^{2}+y'^{2}}{x'y''-x''y'}}={\tfrac {2}{m+1}}\$ (siehe oben)

und die Parameterdarstellung der Evolute ist

$X=x-y'{\tfrac {x'^{2}+y'^{2}}{x'y''-x''y'}}={\tfrac {m-1}{m+1}}{\Big (}mr\cos \alpha +r\cos m\alpha {\Big )}$

$Y=y+x'{\tfrac {x'^{2}+y'^{2}}{x'y''-x''y'}}={\tfrac {m-1}{m+1}}{\Big (}mr\sin \alpha +r\sin m\alpha {\Big )}\ .$

Das ist die Gleichung einer Epizykloide, die aus der gegebenen Epizykloide durch Skalierung mit dem Faktor ${\tfrac {m-1}{m+1}}$ verkleinert und um ${\tfrac {\pi }{m-1}}$ (im Bild $60^{\circ }$) gedreht ist (siehe nächsten Abschnitt).

Das nächste Bild zeigt ein weiteres Beispiel einer Zykloide mit $R=40,r=10$ und ihre Evolute. Im zweiten Beispiel ist $R=35,r=10$. In diesem Fall schließt sich die Epizykloide erst nach zwei Durchgängen, da $R/r$ keine ganze Zahl ist.

• 
  $R=40,r=10$
• 
  $R=35,r=10$
• 
  $R=30,r=8$

Spezielle Epizykloiden

Kardioide

→ Hauptartikel: Kardioide

Kardioide, Konstruktionsskizze als Animation, Pause zu Beginn 15 s sowie Pause am Ende 10 s; die Spitze der Kardioide liegt auf der Koordinate (-2,0)

Kardioide als Kreis-Konchoide

Für $R=r\ (m=2)$ ergibt sich eine Kardioide (Herzkurve). Für Umfang und Fläche erhält man:

$s=16r,\ A=6r^{2}\pi$

Wenn die Spitze der Kardioide im Koordinatenursprung liegt, lautet die Gleichung in Polar- bzw. kartesischen Koordinaten:

${\begin{matrix}r&=&2r\cdot (1+\cos(\varphi ))\\(x^{2}+y^{2}-2rx)^{2}&=&4r^{2}\cdot (x^{2}+y^{2})\end{matrix}}$

Es sei ein innerer Kreis mit Radius $R=2$, dessen Mittelpunkt der Koordinatenursprung eines kartesischen Koordinatensystems und der darauf abrollende Kreis mit Radius $r=2.$ Um den Punkt $P$ auf dem Radius $r$ innerhalb eines Quadranten – vorteilhaft zwischen den Koordinatenachsen – zu bestimmen, bedarf es nur einer Verbindung der Kreismittelpunkte und der Übertragung des Mittelpunktswinkels $\alpha$ (siehe Bild) vom inneren Kreis (blau) auf das Zentrum des abrollenden Kreises (grün). Der Winkelschenkel des Winkels $\alpha '$ erzeugt mit $P$ (rot) den Punkt, der die Kardioide als Ortskurve liefert.

Diese Kurve kann man auch anders erhalten, und zwar als Kreiskonchoide (Pascalsche Schnecke): Man zeichnet von einem Punkt auf dem Kreisumfang eine Sehne und verlängert sie um den Kreisdurchmesser. Wenn die Sehne sich dreht, beschreibt der Endpunkt der Verlängerung eine Kardioide.

Nephroide

→ Hauptartikel: Nephroide

Nephroide, Konstruktionsskizze als Animation, Pause zu Beginn 25 s sowie Pause am Ende 10 s

Ist $R=2r\ (m=3),$ sprich ${\frac {R}{r}}=2,$ so erhält man, wie im Folgenden beschrieben, eine Nephroide. Sie hat die Maße

${\begin{matrix}s&=&24r&=&12R\\A&=&12r^{2}\pi &=&3R^{2}\pi \end{matrix}}$

Es sei ein innerer Kreis mit Radius $R=4$, dessen Mittelpunkt der Koordinatenursprung eines kartesischen Koordinatensystems und der darauf abrollende Kreis mit Radius $r=2.$ Um den Punkt $P$ auf dem Radius $r$ innerhalb eines Quadranten – vorteilhaft zwischen den Koordinatenachsen – zu bestimmen, verbindet man zuerst die Mittelpunkte der beiden Kreise. Der dabei im Winkelscheitel $O$ des inneren Kreises entstandene Mittelpunktswinkel $\alpha$ (siehe Bild) wird nun mit der Winkelweite $2\alpha$ in das Zentrum des abrollenden Kreises (grün) mit positivem Drehsinn eingearbeitet. Der Winkelschenkel des Winkels $2\alpha$ erzeugt mit $P$ (rot) den Punkt, der die Nephroide als Ortskurve liefert.

Für die dargestellte Nephroide gilt die Gleichung

$(x^{2}+y^{2}-4r^{2})^{3}=108r^{4}y^{2},$

mit dem eingesetzten Wert $r=2$

$(x^{2}+y^{2}-4\cdot 2^{2})^{3}=108\cdot 2^{4}y^{2}$

ergibt sich schließlich

$(x^{2}+y^{2}-16)^{3}=1728y^{2}.$

Schnittpunkte und Teilbarkeit

Für die Anzahl der Schnittpunkte der Epizykloiden bzw. Epitrochoiden gibt es interessante Betrachtungen, die unter anderem den größten gemeinsamen Teiler des Längenverhältnisses der beiden Kreisradien verwenden.

Epitrochoide

Die Epitrochoide ist eine nahe liegende Verallgemeinerung der Epizykloide. Ein Kreis mit Radius $r$ rollt auf der Außenseite eines festen Kreises mit Radius $R$. Der erzeugende Punkt hat zum Mittelpunkt des bewegten Kreises einen Abstand $d>0$.

Folgende Typen werden unterschieden:

• Verkürzte oder gestreckte Epitrochoide/Epizykloide ($d<r$)
• Verlängerte oder verschlungene Epitrochoide/Epizykloide ($d>r$)
• Epizykloide ($d=r$, siehe oben), auch als gespitzte Epitrochoide/Epizykloide bezeichnet

Parametergleichung

Epitrochoide mit $R=3,$ $r=1$ und $d=1/2$

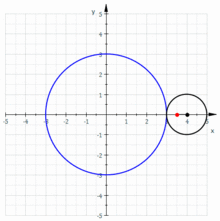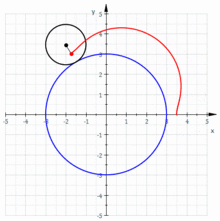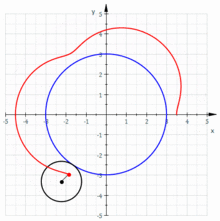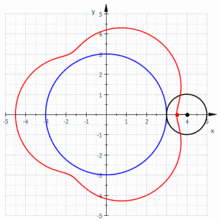
Geht man bei der Herleitung der Parameterdarstellung (s. o.) einer Epizykloide von einem Punkt $P_{0}=(-d,0),\ d>0$ aus, erhält man die Parameterdarstellung einer Epitrochoide:

$x=(R+r)\cos \alpha -{\color {red}d}\cos((1+{\tfrac {R}{r}})\alpha )\ ,$

$y=(R+r)\sin \alpha -{\color {red}d}\sin((1+{\tfrac {R}{r}})\alpha )\ .$

Mit $m=1+{\tfrac {R}{r}}$ ist:

$x=mr\cos \alpha -{\color {red}d}\cos(m\alpha )\ ,$

$y=mr\sin \alpha -{\color {red}d}\sin(m\alpha )\ .$

$d$ ist der Abstand des Startpunktes ($\alpha =0$) zum Mittelpunkt des kleinen Startkreises.

• 
  $R=30,r=10,d=7$
• 
  $R=30,r=10,d=20$

Verkürzte Epitrochoide

Alle verkürzten Epizykloiden, Perizykloiden und Hypozykloiden weisen die gleiche Anzahl an Schnittpunkten auf wie die gespitzten, also $s_{0}$.

Die verkürzten Zykloiden lassen sich unterscheiden in Zykloiden mit Wendepunkten und ohne.

Der Krümmungsmittelpunkt von Zykloiden mit Wendepunkten wechselt in jedem Wendepunkt von einer Seite der Kurve auf die andere. Somit weisen diese Zykloiden Links- und Rechtskurven auf. Die Anzahl der Links- wie auch der Rechtskurven ist $i_{R}$ und damit gleich der Anzahl der Spitzen. Die Anzahl der Wendepunkte ist somit $2\cdot i_{R}$. Punkte, die verkürzte Zykloiden mit Wendepunkten erzeugen, liegen in der Nähe des Randes des umlaufenden „Rades“.

Punkte, die verkürzte Zykloiden ohne Wendepunkte erzeugen, liegen weiter entfernt vom Rand des umlaufenden „Rades“.

Getrennt werden beide Bereiche durch den Sonderfall, dass die verkürzten Zykloiden eine genäherte Gerade durchlaufen. Dies ist der Fall, wenn der erzeugende Punkt auf der Ballschen Kurve liegt und somit folgenden Abstand $d_{r}$ zum Mittelpunkt des umlaufenden Rades aufweist: $d_{r}=r_{r}/(1+i_{R}/i_{r})$. Die Anzahl der genäherten Geraden ist gleich $i_{R}$ und damit gleich der Anzahl an Spitzen.

Verlängerte Epitrochoide

Die Anzahl an Schleifen während einer Periode ist identisch mit der Zahl $i_{R}$ und somit identisch mit der Anzahl an Spitzen der Zykloide.

Verlängerte Zykloiden weisen mindestens $i_{R}$ Schnittpunkte mehr als die (gespitzte) Zykloide auf. Die genaue Anzahl an Schnittpunkten lässt sich nur ermitteln mit Hilfe von Übergangskurvenpunkten. Ein Übergangskurvenpunkt erzeugt eine Zykloide mit Berührungspunkten. Die Anzahl an Übergangskurvenpunkten und somit an Zykloiden mit Berührungspunkten ist gleich dem Integerwert von ${\tfrac {i_{R}}{2}}$. Somit treten keine Berührungspunkte auf, wenn $i_{R}$ gleich 1 ist.

Übergangskurvenpunkte lassen sich nicht analytisch berechnen. Die Ermittlung mit Hilfe von Näherungsverfahren ist nicht kompliziert, würde aber den Rahmen dieses Artikels sprengen. Daher sollen hier nur die Phänomene zur Erzeugung der Formenvielfalt der verlängerte Zykloiden erläutert werden. Die Formen und deren Vielfalt ist so faszinierend, dass diese Faszination von einem speziellen Spielzeug genutzt wird, nämlich dem Spirograph. Mit einem Spirograph können manuell verschiedene blumig anmutende verschlungene Hypozykloiden mit Hilfe eines Zeichenstiftes erzeugt werden. Der Stift wird durch ein Loch eines in einem Hohlrad umlaufen Zahnrades gesteckt und so lange über ein Papier geführt, bis sich eine geschlossene Kurve ergibt.

Dass durch geringe Variation des Abstandes des Loches zum Mittelpunkt des umlaufenden „Rades“ immer wieder anders anmutende Hypozykloiden entstehen, lässt sich anhand der Sonderfälle erläutern, bei denen Zykloiden mit Berührungspunkten entstehen.

Verlängerte Zykloiden mit der Mindestanzahl an Schnittpunkten werden durch Punkte erzeugt, die in der Nähe des Außenrandes des umlaufenden Rades liegen. Die Anzahl der Schnittpunkte ist gleich der Anzahl an Spitzen plus $i_{R}$.

Der Integerwert von ${\tfrac {i_{R}}{2}}$ ergibt die Anzahl $n_{b}$ an Zykloiden mit Berührungspunkten. Ist $n_{b}$ größer null, so wird irgendwann einmal eine verschlungene Zykloide mit Berührungspunkten erzeugt, wenn der erzeugende Punkt vom Kreisumfang weg verschoben wird. Die Zykloide mit Berührungspunkten selbst weist noch eine unveränderte Anzahl an Selbstschnittpunkten auf. Aber wenn der erzeugende Punkt noch weiter weg verschoben wird, entsteht eine Zykloide ohne Berührungspunkt, deren Anzahl an Schnittpunkten sich um $2\cdot i_{R}$ erhöht hat. Erzeugt das zugrunde liegende „Räderpaar“ mehr als eine Zykloide mit Berührungspunkten, wiederholt sich das gleiche (mehrmals), wenn der erzeugende Punkt weiter vom Kreisumfang entfernt wird und dadurch wieder zu einer Stelle gelangt, in der eine Zykloide mit Berührungspunkten erzeugt wird.

• Alle Punkte, die Zykloiden mit Berührungspunkten erzeugen, liegen zwischen dem Außenrand des umlaufenden „Rades“ und einem konzentrischen Kreis durch den Mittelpunkt des stehenden Rades. Wird der erzeugende Punkt weiter weg vom Rand des umlaufenden Rades über den Mittelpunkt des stehenden Rades hinweg verschoben, ändert sich an der Anzahl der Schnittpunkte nichts mehr und es treten auch keine weiteren Sonderfälle auf.

Punkte, die vom Mittelpunkt des umlaufenden „Rades“ weiter entfernt sind als der Abstand der Mittelpunkte beider „Räder“, erzeugenden Zykloiden mit der maximalen Anzahl an Schnittpunkten $n_{\text{max}}$.

• Wenn $i_{R}$ eine gerade Zahl ist, ist die maximale Anzahl an Schnittpunkten $n_{\text{max}}=n_{s0}+2\cdot n_{b}\cdot i_{R}$
• In allen anderen Fällen, nämlich wenn $i_{R}$ eine ungerade Zahl ist, gilt: $n_{\text{max}}=n_{s0}+(1+2\cdot n_{b})\cdot i_{R}$

Eine Zykloide, die durch den Mittelpunkt des feststehenden „Rades“ verläuft und mehr als einen Schnittpunkt aufweist, stellt immer einen Sonderfall dar:

• Ist $i_{R}$ eine gerade Zahl, dann weist diese verlängerte Zykloide mindestens einen Berührungspunkt auf. Gibt es mehrere Berührungspunkte, so liegen Berührungs- und Selbstschnittpunkte übereinander
• Ist $i_{R}$ eine ungerade Zahl, dann liegen mehrere Schnittpunkte der verlängerte Zykloide übereinander.

Spezielle Epitrochoiden

• Für $q=2$ einer Epitrochoide ergibt sich aus einem speziellen Punkt im Innern des rollenden Kreises die Hüllkurve im Gehäuse des Wankelmotors.

Literatur

• Klemens Burg, Herbert Haf, Friedrich Wille, Andreas Meister: Vektoranalysis: Höhere Mathematik für Ingenieure, Naturwissenschaftler und Mathematiker. 2. Auflage, Springer, Vieweg-Teubner, Wiesbaden 2012, ISBN 978-3-8348-8346-9, S. 56–63.
• Mark J. Wygodski: Höhere Mathematik griffbereit: Definitionen, Theoreme, Beispiele. 2. Auflage, Vieweg, Braunschweig 1977, ISBN 3-528-18309-8, S. 755–764.
• Matthias Richter: Grundwissen Mathematik für Ingenieure. Vieweg+Teubner, Wiesbaden 2009, ISBN 978-3-663-05772-7, S. 171–172.

Weblinks

Commons: Epitrochoid – Sammlung von Bildern und Videos

• MacTutor, Famous Curves Index