Weltraumlift

Ein Weltraumlift, auch Weltraumaufzug (engl. space elevator), ist ein hypothetischer Transporter in den Weltraum ohne Raketenantrieb entlang eines gespannten Führungsseils zwischen einer Basisstation am Äquator und einer Raumstation hinter dem geostationären Orbit in 35.786 Kilometern Höhe. Die konkurrierenden Kräfte der auf der Erde stärkeren Gravitation und der am oberen Ende stärkeren Fliehkraft sollen das Seil spannen. Teile der Anlage müssten oberhalb der geostationären Umlaufbahn errichtet werden, um durch die dort größere Fliehkraft die Gravitationskraft tiefer gelegener Teile auszugleichen. Ein selbst- oder fremdangetriebener Lift könnte Personen oder Nutzlasten entlang des Seils in beide Richtungen befördern.
Geschichte
[Bearbeiten | Quelltext bearbeiten]1895 erdachte der vom Eiffelturm inspirierte russische Weltraumpionier Konstantin Ziolkowski einen (35.786 Kilometer hohen) Turm in den Weltraum.[1]
1959 schlug der sowjetische Wissenschaftler Juri Arzutanow vor, ein Seil von einem geostationären Satelliten herabzulassen. Das Seil sollte am geostationären Orbit am dicksten sein und zu den Enden hin dünner. Es sollte zwischen dem Erdboden und einem großen Gegengewicht hinter dem geostationären Orbit straff gespannt sein. Ein russischsprachiges Interview erschien 1960, im Ausland waren seine Arbeiten dazu jedoch lange unbekannt.
1966 berechneten amerikanische Ingenieure die erforderliche Zugfestigkeit für ein Seil konstanter Dicke und stellten fest, dass die damals bekannten Materialien ungeeignet waren.
1975 schlug der US-Amerikaner Jerome Pearson, ähnlich wie zuvor Arzutanow, einen Lift mit ungleichmäßigem Seilquerschnitt vor. Das Seil sollte am Ort des Baubeginns im geostationären Orbit am dicksten sein und sich zu den Enden hin verjüngen. Der Materialtransport hätte tausende Weltraumflüge mit einem Space Shuttle erfordert.
2000 veröffentlichte David Smitherman von der US-Weltraumbehörde NASA einen Bericht, der auf den Ergebnissen einer 1999 im Marshall Space Flight Center abgehaltenen Konferenz beruhte.[2] Er schlug vor, Kohlenstoffnanoröhren zu verwenden.
2004 stellte eine Gruppe von Wissenschaftlern um Alan Windle an der Universität Cambridge einen etwa 100 Meter langen Faden aus Kohlenstoffnanoröhren her. Das Verhältnis von Zugfestigkeit zu Gewicht übertraf das von Stahl bis um das 100-fache. Da Kohlenstoff in der Atmosphäre oxidiert, müsste das Material beschichtet werden.
Ende Juni 2004 teilte der Leiter des Weltraumfahrstuhlprojekts Bradley Edwards in Fairmont, West Virginia mit, dass ein Prototyp bereits in 15 Jahren fertig sein könnte. Die NASA unterstützt das Forschungsprojekt durch ihr Institute for Advanced Concepts (NIAC) mit 500.000 US-Dollar. Laut Edwards verhielte sich ein Seil bis 100.000 Kilometer wie beim Hammerwurf und er schlug vor, es aus einem Verbundmaterial aus Kohlenstoffnanoröhren zu fertigen.
Von 2005 bis 2009 organisierten die NASA und die Spaceward Stiftung mit Geld dotierte Elevator:2010-Wettbewerbe.
Transportkosten
[Bearbeiten | Quelltext bearbeiten]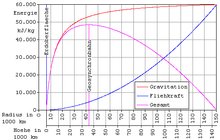

Es wird geschätzt, dass mittels eines Weltraumlifts die herkömmlichen Transportkosten ins All von gegenwärtig 12.000[3] bis 80.000 US-Dollar auf 200 US-Dollar pro Kilogramm gesenkt werden könnten.[4]
Um ein Kilogramm Masse vom Erdäquator bis in die Höhe einer geostationären Umlaufbahn von 35.786 km über dem Äquator hochzuheben, wird eine physikalische Arbeit von 48,4 Megajoule (ca. 13,5 kWh) benötigt.[5] Beim Heben von Massen über die Höhe der geostationären Umlaufbahn hinaus könnte Energie wieder zurückgewonnen werden. Mit zunehmender Höhe nimmt die Gravitationskraft ab und die Zentrifugalkraft zu. Oberhalb der geostationären Umlaufbahn ist die nach oben wirkende Zentrifugalkraft stärker als die nach unten wirkende Gravitationskraft. Eine Masse, die über diese Höhe hinaus gehoben werden würde, „fiele“ von alleine weiter nach oben. Unter Idealbedingungen wäre eine ausgeglichene Energiebilanz denkbar, bei der in der Summe keine physikalische Arbeit aufgewandt werden müsste. Hierzu wäre es notwendig, das Bauwerk um ein Vielfaches höher als die geostationäre Umlaufbahn zu errichten. Die Massen müssten in diesem Fall auf eine Höhe von 143.785 km gehoben werden.[6]
Durch eine Abkopplung vom Weltraumlift in unterschiedlichen Höhen könnten Raumflugkörper ohne weiteren Antrieb auf zahlreiche unterschiedliche Flug- und Umlaufbahnen gebracht werden.
Technik
[Bearbeiten | Quelltext bearbeiten]An den Lift, das Seil und die Basisstation werden enorme technische Ansprüche gestellt. Die NASA hat Wettbewerbe mit hohen Preisgeldern zu diesem Thema ausgeschrieben. Man unterscheidet zwischen den folgenden fünf Problembereichen, zu denen es mehrere Lösungsansätze gibt.
Material für das Seil
[Bearbeiten | Quelltext bearbeiten]
Jedes Segment des Seils muss mindestens das Gewicht der darunterliegenden Seilsegmente zuzüglich der Nutzlastkapazität halten können. Je höher das betrachtete Seilsegment liegt, desto mehr Seilsegmente muss es halten. Ein optimiertes Seil besitzt also mit zunehmender Höhe einen größeren Querschnitt, bis sich dieser Trend auf geostationärem Orbit umkehrt, da ab dort die resultierende Kraft der Seilsegmente erdabgewandt wirkt.
Bei einer gegebenen spezifischen Zugfestigkeit eines Materials wird also der minimale Querschnitt an der Basisstation allein durch die Nutzlastkapazität festgelegt. Weiter ist dann auch die optimale weitere Querschnittsentwicklung festgelegt. Das Verhältnis vom größten Seilquerschnitt zum kleinsten wird taper ratio genannt. Sie und die Nutzlastkapazität legen letztlich die Gesamtmasse des Seils fest.
Grundsätzlich lässt sich bei optimiertem Seildurchschnitt mit jedem Material ein Weltraumlift errichten, indem der Querschnittszuwachs entsprechend rapide gewählt wird bzw. eine große taper ratio verwendet wird. Die Ökonomie diktiert hierbei schlussendlich das Limit der noch sinnvollen Werte in dieser Größe.
Ein gewöhnliches Stahlseil konstanten Querschnittes würde bereits ab einer Länge von vier bis fünf Kilometern unter seinem eigenen Gewicht reißen (materialspezifische Reißlänge), Hochleistungsstahlseile für Seilbahnen, deren Reißfestigkeit mit Kevlar vergleichbar ist, kämen auf rund 30 km. Neue Werkstoffe, deren Reißfestigkeit weit jenseits der von Kevlar liegt, sind deswegen ein entscheidender Faktor für eine zukünftige Realisierung dieses Unternehmens. Nach den bisherigen Forschungen kommen drei Möglichkeiten in Frage:
- Kohlenstoffnanoröhren scheinen die Reißlänge von Kevlar noch einmal um den Faktor fünf zu übertreffen, Berechnungen von Nicola Pugno des Polytechnikums in Turin ergaben jedoch, dass bei der Verwebung von Kohlenstoffnanoröhren zu längeren Seilen die Reißfestigkeit des Seils gegenüber der Reißfestigkeit einzelner Nanoröhren um ca. 70 % abnimmt. Grund dafür sind unvermeidliche Kristallbaufehler, die gemäß Pugnos Modell die Belastbarkeit des Seils auf ca. 30 Gigapascal reduziert. Berechnungen der NASA zufolge wäre jedoch ein Material mit einer Belastbarkeit von etwa 62 Gigapascal notwendig, um den auftretenden Kräften zu widerstehen. Außerdem ist es bisher keinem Labor gelungen, ein zusammenhängendes Seil zu erschaffen, das länger als 100 Meter ist. Einen zusätzlichen Kosten- und Gewichtsfaktor stellt die Beschichtung des Seils dar, denn Kohlenstoffnanoröhren oxidieren und erodieren in der Atmosphäre.
- Vielversprechend ist auch die UHMW-Polyethylen-Faser Dyneema, die bei vertikaler Aufhängung eine Reißlänge von 400 km erreicht und somit alle konventionellen Werkstoffe um ein Vielfaches und sogar Spinnenseide um den Faktor zwei übertrifft. Gegen die Verwendung von Dyneema spricht allerdings, dass der Schmelzpunkt von Dyneema zwischen 144 °C und 152 °C liegt und dass die Festigkeit von Dyneema zwischen 80 °C und 100 °C deutlich nachlässt. Außerdem wird Dyneema unter −150 °C brüchig. Alle diese genannten Temperaturen treten im Weltraum häufig auf.


- Ein neues, noch wenig erforschtes Material ist Graphen. Der Elastizitätsmodul entspricht mit ca. 1020 GPa dem von normalem Graphit entlang der Basalebenen und ist fast so groß wie der des Diamants. Wissenschaftler der New Yorker Columbia University veröffentlichten 2008 weitergehende Messergebnisse, in denen sie hervorhoben, dass Graphen die höchste Reißfestigkeit aufweise, die je ermittelt wurde. Seine Zugfestigkeit von 1,25×105 N/mm² oder 125 Gigapascal ist die höchste, die je ermittelt wurde, und rund 125 mal so hoch wie die von Stahl.[7] Stahl hat mit 7874 kg/m³ eine rund 3,5 mal höhere Dichte als Graphen mit 2260 kg/m³, so dass die Reißlänge von Graphen rund 436 mal so groß ist wie die von Stahl. In einem als homogen angenommenen Gravitationsfeld von 9,81 m/s² hätte Graphen eine Reißlänge von rund 5655 km. Tatsächlich wird aber die Schwerebeschleunigung mit zunehmender Höhe deutlich geringer, was die Reißlänge erhöht. Ein Band aus Graphen mit konstanter Querschnittsfläche (taper ratio = 1) würde in der Höhe der geostationären Umlaufbahn von 35.786 km über dem Erdäquator erst zu 87 % seiner Reißfestigkeit belastet werden (siehe das Bild). In noch größerer Höhe würde die Zugbelastung dann wieder absinken. Wenn das Graphen-Seil bei konstanter Querschnittsfläche 143.780 km lang wäre, dann würde es in völligem Gleichgewicht mit der Gravitationsbeschleunigung der Erde und der Zentrifugalbeschleunigung durch die Rotation der Erde sein. In der Höhe von 143.780 km über dem Erdäquator würde eine Nettobeschleunigung von 0,78 m/s² nach oben wirken, und eine Tangentialgeschwindigkeit von 10.950 m/s vorhanden sein, was den Start von Raumsonden begünstigen würde. Graphen und Graphit haben einen Schmelzpunkt von rund 3700 °C. 76 cm breite, endlose Bänder aus Graphen stellt man dadurch her, dass man eine monoatomare Schicht aus Kohlenstoff auf eine Folie aus inertem Trägermaterial, wie zum Beispiel Kupfer, durch chemische Gasphasenabscheidung (CVD) aufbringt, und dann das Trägermaterial auflöst.[8] Auch für Graphen ist vermutlich eine Schutzbeschichtung notwendig.
Errichtung des Seils
[Bearbeiten | Quelltext bearbeiten]Bisher ist nur denkbar, das Seil von einem geostationären Satelliten herunterzulassen. Das Verhalten von langen Seilen im Weltall ist Gegenstand aktueller Forschung. Es ist denkbar, dass initial nur ein minimal tragfähiges Seil gestartet wird, das danach sukzessive verstärkt wird, bis die finale Nutzlastdicke erreicht ist.
Errichtung des Turms als Basisstation
[Bearbeiten | Quelltext bearbeiten]Auch die Basisstation muss starke Belastungen aushalten, denn auf der Verbindung zwischen Seil und Basisstation lasten laut NASA bis zu 62 Gigapascal. Dadurch wird eine ausreichend tiefe, komplex zu errichtende und teure Verankerung der Basisstation im Erdreich nötig. Das liegt daran, dass beim Weltraumlift in vertikaler Richtung ein Überschuss an Zentrifugalkraft gegenüber der Gravitationskraft herrschen muss, um das Seil zu spannen, und daran, dass beim Weltraumlift in horizontaler Richtung die Corioliskraft der hinauf- oder hinabfahrenden Lasten auf die Erde übertragen wird. Ein Weltraumlift, der sich in völligem Gleichgewicht zwischen der Zentrifugalkraft und der Gravitationskraft befände, würde schon durch minimale Lasten in seiner Stabilität gestört werden, und könnte daher kein Drehmoment durch die Corioliskraft zwischen der Erde und der Last übertragen. Beim straff gespannten Weltraumlift kostet nur die Überwindung des Gewichtes der Last entlang des Höhenunterschiedes Energie, denn die Corioliskraft steht immer quer zur Bewegung der Last. Jener Teil der Energie, der zur Überwindung der Corioliskraft benötigt wird, stammt aus der Abbremsung der Erdrotation.
Antrieb des Satelliten
[Bearbeiten | Quelltext bearbeiten]Ein Raketenantrieb wird für den Satelliten nicht benötigt, denn sobald die Corioliskraft einer nach oben transportierten Last den Satelliten nach hinten zieht, bildet das Seil einen kleinen Winkel zur Senkrechten, und beschleunigt dadurch den Satelliten unter Bremsung der Erdrotation. Zu diesem Zweck ist es günstig, wenn der Satellit etwas höher über der Erdoberfläche kreist als 40.000 km, so dass er zwar geosynchron ist, aber das Seil durch seine Zentrifugalkraft spannt. Dieses Funktionsprinzip lässt sich durch den Hammerwurf veranschaulichen. So lange der Hammerwerfer mit konstanter Geschwindigkeit rotiert, zeigt das Seil des Hammers radial von der Rotationsachse weg. Wenn der Hammerwerfer seine Rotationsgeschwindigkeit erhöht, dann hinkt der Hammer hinter der radialen Ausrichtung hinterher, und kinetische Energie wird vom Hammerwerfer auf den Hammer übertragen. Der Transport der Last wird durch die Corioliskraft kaum behindert, da sie praktisch quer zur Bewegung der Last steht.
Ausbau der allgemeinen Weltrauminfrastruktur und der Raumfahrtindustrie
[Bearbeiten | Quelltext bearbeiten]Es wird vermutet, dass sich durch einen Weltraumlift die Transportkosten ins Weltall drastisch senken ließen. Bei typischen Nutzlasten für Einzeltransporte in der Größenordnung von Tonnen sowie Transportdauern in der Größenordnung von einzelnen Wochen würde ein Weltraumlift über ein Jahr gesehen eine beträchtliche Transportkapazität erreichen. Da die endgültigen Parameter des Liftes wie Geschwindigkeit, Zugfestigkeit und Kosten noch nicht feststehen, ist derzeit eine Abschätzung der Auswirkungen noch schwierig. Es herrscht allerdings Einigkeit darüber, dass wegen der gegenüber einem Raketenstart geringeren auftretenden Beschleunigungskräfte sich die Möglichkeit eröffnet, mechanisch empfindlichere Werkstücke wie Teleskopspiegel ins Weltall zu transportieren.
Weltraumlift auf dem Mond
[Bearbeiten | Quelltext bearbeiten]Technisch bereits im Bereich der Möglichkeiten ist der Vorschlag von Jerome Pearson: Er möchte einen Weltraumlift auf dem Mond installieren. Wegen der im Vergleich mit der Erde geringeren Schwerkraft wäre das benötigte Seil niedrigeren Belastungen ausgesetzt. Aufgrund der langsamen Rotation des Mondes wäre ein Seil bis zum luna-stationären Orbit allerdings mit knapp 100.000 km wesentlich länger als bei einem Erd-Weltraumlift. Der Pearson-Weltraumlift würde jedoch am Lagrange-Punkt L1 oder L2 im Erde-Mond-System anknüpfen. L1 befindet sich in einem Abstand von ca. 58.000 km vom Mondmittelpunkt in Richtung Erde, der der Erde abgewandte Punkt L2 ist ca. 64.500 km vom Mondmittelpunkt entfernt. Mit heutzutage erhältlichen Seilmaterialien reicht eine Verjüngung um den Faktor 2,66.[9]
Das nötige Seil mit einer geschätzten Masse von sieben Tonnen könnte mit einer einzigen Rakete in den Weltraum befördert werden. Jerome Pearson ist Geschäftsführer des Unternehmens Star Technology and Research, das auf seiner Website auch über den Mondlift informiert.[10] Die Forschungen von Pearson an dem Projekt werden von der NASA derzeit mit 75.000 Dollar unterstützt.
Weltraumlift als Motiv in Literatur, Film und Fernsehen
[Bearbeiten | Quelltext bearbeiten]Einen Fahrstuhl, der frei um die Welt und (versehentlich) auch in den Weltraum reicht, beschreibt Roald Dahl in seinem Kinderbuch Charlie und der große gläserne Fahrstuhl (1972), einem Nachfolger des Klassikers Charlie und die Schokoladenfabrik (1964), in dem der Fahrstuhl ebenfalls bereits Erwähnung fand.
Bekannt wurde die Idee des Weltraumlifts in der Öffentlichkeit, als Arthur C. Clarke und Charles Sheffield sie 1978/79 unabhängig voneinander zum zentralen Thema ihrer Romane The Fountains of Paradise (dt.: Fahrstuhl zu den Sternen) und The Web between the Worlds (dt.: Ein Netz aus tausend Sternen) verarbeiteten.
Auch im Manga-Klassiker Battle Angel Alita (ab 1991) von Yukito Kishiro dreht sich der Haupthandlungsstrang um einen Weltraumlift mit Ende im Orbit und Zwischenstation in Art einer Stadt in den Wolken.
Kim Stanley Robinson stellt in seiner Mars-Trilogie (Red Mars (1992), Green Mars (1993), Blue Mars (1995)) den Weltraumlift als Schlüsseltechnologie zur Besiedelung des Mars dar. In den Romanen verfügen Erde und Mars über Weltraumlifte, der Lift auf dem Mars wird allerdings von Separatisten des Planeten durch Sprengung des Ankerpunktes zerstört, um eine weitere Zuwanderung von Bewohnern der Erde zu verhindern.
In der Folge Die Asteroiden (englisch Rise, Staffel 3, Episode 19, 1997) der TV-Serie Star Trek: Raumschiff Voyager trifft die Besatzung der Voyager auf einen Planeten, auf dem ein Weltraumlift existiert.
Die Autoren Terry Pratchett, Ian Stewart und Jack Cohen greifen in ihrem Buch Die Gelehrten der Scheibenwelt (2000)[11] das Konzept des Weltraumliftes sowohl als Metapher als auch als physikalisch realisierbare Einrichtung auf.
Alastair Reynolds stellt in seinem 2001 erschienenen Roman Chasm City dar, was passiert, wenn das Seil eines Weltraumliftes zerreißt.
In Liu Cixins Roman Die drei Sonnen aus dem Jahr 2006 wird die Nanotechnologie, an der der Protagonist Wang Miao forscht, als Schlüssel für den Bau eines Weltraumlifts erkannt.
Im dritten Band der Airborn-Serie, Sternenjäger (2008), von Kenneth Oppel verwenden die Protagonisten einen Weltraumlift um als erste Menschen ins All zu gelangen.
Frank Schätzing verarbeitete die Thematik um den Weltraumlift in seinem 2009 erschienenen Roman Limit.
Felix Reda schlug 2014 im Europawahlkampf für die Piratenpartei den Bau eines Weltraumlifts vor.[12]
Auf einigen Planeten der Spieleserie Halo werden Weltraumlifte verwendet.
Im Aufbauspiel Anno 2205 von Ubisoft aus dem Jahr 2015 wird der Weltraumlift als zentrales Spielelement thematisiert.
In der Fernsehserie Foundation (2021), welche auf der gleichnamigen Buchreihe von Isaac Asimov basiert, besitzt der Planet Trantor einen Weltraumlift, welcher in der 1. Episode zerstört wird.
Kritik
[Bearbeiten | Quelltext bearbeiten]Neben den hohen Anforderungen an das heute noch nicht verfügbare Material für die erforderlichen Seile ergeben sich zwei zentrale Schwachstellen der Idee. Zum einen würde das Seil eines Weltraumfahrstuhls ein fixes Hindernis quer durch alle orbitalen Satellitenbahnen darstellen, weil jede Umlaufbahn zwei Durchgangspunkte durch die Äquatorebene der Erde haben muss. Das Seil wäre somit konstant von Treffern durch Satelliten und Weltraummüll bedroht, die mit mehreren Kilometern pro Sekunde wie Geschosse einschlagen würden. Zum anderen würden auf das mehrere zehntausend Kilometer lange Seil so viele verschiedene Kräfte wirken, dass die Beherrschbarkeit des entstehenden komplexen Schwingungssystems fraglich ist.[13]
Literatur
[Bearbeiten | Quelltext bearbeiten]- Kapitel: Der Weltraumfahrstuhl. In: Eugen Reichl: Typenkompass: Zukunftsprojekte der Raumfahrt, Motorbuch Verlag, Stuttgart 2012, ISBN 978-3-613-03462-4, S. 105–111
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Wissenschaftliche Arbeitsgemeinschaft für Raketentechnik und Raumfahrt (WARR Space Elevator)
- Space Elevator Website von SpaceRef mit aktuellen News zum Projekt, Präsentationen, Fachvorträgen und Links
- German Space Elevator (Max-Born-Team 2006) Weltraumfahrstuhl-Konstruktion(Schüler/Jungstudierenden Projekt)
- ESA-Portal
- Fahrstuhl in den Weltraum. Die achtmillionste Etage. Artikel über Weltraumfahrstühle in der Online-Ausgabe der FAZ (Frankfurter Allgemeine). Ulf von Rauchhaupt, 2. Oktober 2014.
- Der Weltraumaufzug - der einfachste Weg ins All? Terra X, vom 10. Juli 2019
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Mit dem Fahrstuhl ins All? ESA, abgerufen am 14. März 2024.
- ↑ National Space Society: Space Elevators: An Advanced Earth-Space Infrastructure for the New Millennium (pdf, englisch)
- ↑ Erfolgsstory Raumtransport: Wie Phoenix aus der Asche.
- ↑ Peter Odrich: Japaner wollen bis 2050 einen Weltraumlift bauen. In: Ingenieur.de. 1. Oktober 2014, abgerufen am 7. Oktober 2014.
- ↑ Berechnung der physikalischen Arbeit zum Anheben einer Masse in eine geostationäre Umlaufbahn (Höhe: 35.786 km über dem Äquator) ≈ 48,4 MJ ≈ 13,5 kWh:
Differenz der potentiellen Energie im Gravitationsfeld Differenz der potentiellen Energie im Zentrifugalfeldfür die Entfernung vom Erdmittelpunkt: (Äquator) und (Umlaufbahn)
mit:; ; ; ⊕;
und:; ⊕; ; ;
Anm.: 1. Bei und handelt es sich um vektorielle Größen. Unter der Annahme, dass in diesem Rechenbeispiel die Vektoren senkrecht zueinander stehen, wurden nur die jeweiligen Beträge verwendet.
- 2. Bei der Berechnung wurden Energieverluste (z. B. aufgrund des Wirkungsgrads der Anlage) sowie gravitative Einflüsse anderer Himmelskörper als der Erde (z. B. durch Sonne und Mond) nicht berücksichtigt.
- ↑ Berechnung der Höhe bis zur ausgeglichenen Energie-Bilanz (Höhe: 143.785 km über dem Äquator):
Gravitations-Potential und Zentrifugal-Potential auf Höhe des Äquators () auf null setzen und andere Nullstell(en) ermitteln.
mit:; ⊕;
und:; ⊕;
; ; ①;
①mit mathematischem Verfahren zur Lösung von Gleichungen dritten Grades ermittelt oder iterativ bestimmt - ↑ Changgu Lee, Xiaoding Wei, Jeffrey W. Kysar, James Hone: Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. In: Science. Band 321, Nr. 5887, 2008, S. 385–388, doi:10.1126/science.1157996.
- ↑ Sukang Bae, Hyeongkeun Kim, Youngbin Lee, Xiangfan Xu, Jae-Sung Park, Yi Zheng, Jayakumar Balakrishnan, Tian Lei, Hye Ri Kim, Young Il Song, Young-Jin Kim, Kwang S. Kim, Barbaros Ozyilmaz, Jong-Hyun Ahn, Byung Hee Hong, Sumio Iijima: Roll-to-roll production of 30-inch graphene films for transparent electrodes. In: Nat Nano. Band 5, Nr. 8, 2010, S. 574–578, doi:10.1038/nnano.2010.132. PDF ( vom 10. Juli 2012 im Internet Archive)
- ↑ Jerome Pearson, Eugene Levin, John Oldson, and Harry Wykes: The Lunar Space Elevator (PDF; 365 kB), STAR Inc., Mount Pleasant, SC USA, 55th International Astronautical Congress, Vancouver, Canada, 4-8 October 2004.
- ↑ Space Elevator History. In: star-tech-inc.com. Abgerufen am 14. September 2021.
- ↑ Originalausgabe The Science of Discworld, 1999
- ↑ Jolinde Hüchtker, Cyrill Callenius, David Fresen, Max Deibert, Simon Grothe, Xenia Heuss, Antonia Bretschkow: Ein Weltraumaufzug und krumme Gurken. In: tagesspiegel.de. 24. Mai 2014, abgerufen am 30. September 2015.
- ↑ Karl Urban: Was macht eigentlich ... der Weltraumaufzug? In: Spektrum.de. 21. September 2018, abgerufen am 3. Juni 2021.

































