Giuseppe Peano

Giuseppe Peano (* 27. August 1858 in Spinetta, heute Teil von Cuneo, Piemont; † 20. April 1932 in Turin) war ein italienischer Mathematiker. Er arbeitete in Turin und befasste sich mit mathematischer Logik, mit der Axiomatik der natürlichen Zahlen (Entwicklung der Peano-Axiome) und mit Differentialgleichungen erster Ordnung.
Leben
[Bearbeiten | Quelltext bearbeiten]
Peano war der Sohn von Bauern. Er besuchte die Schule in Cuneo und, als sein Talent erkannt wurde, ab 1870 das Gymnasium (Liceo) in Turin, wo ein Onkel Priester und Anwalt war. Ab 1876 studierte er Mathematik an der Universität Turin unter anderem bei Enrico D’Ovidio, Angelo Genocchi, Francesco Faà di Bruno und Francesco Siacci. 1880 promovierte er und wurde Assistent von D'Ovidio und danach bei Genocchi. Gleichzeitig erschien 1880 seine erste mathematische Arbeit. Er hielt die Analysis-Vorlesungen von Genocchi (die 1884 als Buch herauskamen, herausgegeben, geschrieben und mit Zusätzen versehen von Peano). 1884 habilitierte er sich. Außer an der Universität hielt er auch Vorlesungen an der Militärakademie in Turin. 1890 wurde er Nachfolger von Genocchi als Professor an der Universität.
1891 gründete er die Zeitschrift Rivista di matematica, die sich vor allem den Grundlagen der Mathematik und der Logik widmete. 1892 begann er ein Projekt, die bekannten Sätze der Mathematik in logischer Strenge zu formulieren, das Formulario Matematico (beendet 1908), das er später auch für seine Vorlesungen benutzte, was ein pädagogischer Misserfolg wurde. 1901 wurde deshalb seine Lehrtätigkeit an der Militärakademie beendet. An der Universität konnte man ihm dagegen nicht hineinreden. 1900 fand Peano Anerkennung auf dem Internationalen Kongress für Philosophie in Paris.
Peano als Mathematiker
[Bearbeiten | Quelltext bearbeiten]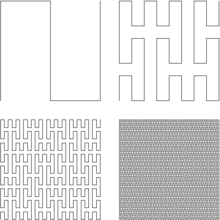
Peanos mathematisches Werk ist durch große logische Rigorosität geprägt. So hat er wiederholt Ausnahmefälle in veröffentlichten Theoremen gefunden (beispielsweise Arbeiten von Corrado Segre und Hermann Laurent). Auch die nach ihm benannte Peano-Kurve ist ein Beispiel hierfür. Sie ist eine stetige, surjektive Abbildung des Einheitsintervalls in das Einheitsquadrat, also eine raumfüllende Kurve, die definiert ist als der Grenzwert einer Folge von Kurven, die schrittweise konstruiert werden können. Vor Peano hatte man nicht mit der Möglichkeit der Existenz einer solchen Kurve gerechnet. Peano fand die Kurven 1890, wenig später gab David Hilbert weitere Beispiele. Er war auch mit Camille Jordan (und mit einem ähnlichen Konzept wie Jordan) ein Pionier der Maßtheorie mit seinem Buch von 1887 über geometrische Anwendungen der Infinitesimalrechnung, einen befriedigenden Maßbegriff fand aber erst Émile Borel.[1]
Auch auf dem Gebiet der Analysis und der Differentialgleichungen hat Peano Wichtiges geleistet. Er fand das Restglied der Simpsonregel für die näherungsweise Berechnung von Integralen und bewies den Existenzsatz von Peano für gewöhnliche Differentialgleichungen (1886). Er fand auch unabhängig von Émile Picard dessen Näherungsverfahren zur Lösung von Systemen gewöhnlicher Differentialgleichungen (1887).
Peano hatte einen prägenden Einfluss auf die moderne Logik, Mengenlehre und Mathematik durch einige Werke, in denen er eine konsequente Formalisierung mathematischer Sachverhalte verfolgte. Peano erstellte in seinem Buch Calcolo Geometrico von 1888 erstmals ein Axiomensystem für den Vektorraum (wobei er unbeachtete Ideen von Hermann Grassmann aufgriff) und formulierte dort auch das moderne Axiomensystem für die boolesche Algebra, wobei er die Symbole und einführte. In seiner Arithmetik von 1889 stellte er – unabhängig von Dedekinds Arithmetik[2] – die ersten formalen Axiome für die natürlichen Zahlen auf, die als Peano-Axiome berühmt wurden. Als Fundament für seine Arithmetik schuf er die erste formalisierte Klassenlogik, in der er unter anderem auch das Elementzeichen und geordnete Paare (a, b) einführte. Die Formalisierung wichtiger logischer und mathematischer Gebiete baute er später in Formelsammlungen weiter aus; aus ihnen stammt unter anderem das Existenzquantorsymbol .
Er gab 1906 einen neuen Beweis des Satzes von Cantor-Bernstein, wobei es zu einem Disput mit Ernst Zermelo kam, der einen ähnlichen Beweis veröffentlichte (publiziert erst 1908). Beiden zuvorgekommen war Richard Dedekind (1899 in einem Brief), der diesen aber nicht veröffentlichte.[3]
1897 hielt er einen Plenarvortrag auf dem ersten Internationalen Mathematikerkongress in Zürich (Logica Matematica).
1899 gab Peano ein Gegenbeispiel, die peanosche Fläche, zu einer Vermutung über die Existenz eines lokalen Extremums einer Funktion von zwei Variablen an.

Peano als Linguist
[Bearbeiten | Quelltext bearbeiten]Auf dem Gebiet der Linguistik machte sich Peano einen Namen, als er die Plansprache Latino sine flexione (= Latein ohne Beugung) schuf. Dies war ein Versuch, die ehemalige Weltsprache Latein wiederzubeleben, indem der weitgehend bekannte Wortschatz gewahrt wurde, die Schwierigkeiten der lateinischen Sprache aber weitgehend getilgt wurden. Dieses Latino sine flexione ging später in Interlingua auf.
Den Formulario Mathematico V (1905/1908) schrieb Peano in Latino sine flexione.
Werke (Auswahl)
[Bearbeiten | Quelltext bearbeiten]- Sulla integrabilità delle funzione, Atti Accad. Sci. Torino, Band 18, 1882/83, S. 439–446 (englische Übersetzung in Kennedy, Peano, Selected Works, 1973, S. 37–43)
- mit Angelo Genocchi: Calcolo differenziale e principii di calcolo integrale, Turin 1884, Archive
- Deutsche Übersetzung (von G. Bohlmann, A. Schepp): Angelo Genocchi: Differentialrechnung und Grundzüge der Integralrechnung, Teubner 1899, im Anhang mit der Übersetzung der Arbeiten von Peano von Sulla definizione di integrale, Ann. mat. pura appl., Band 23, 1895, S. 153–157, von Studii di logica matematica, Atti Accad. Sci. Torino, Band 32, 1897, S. 565–583 und Sulla formula di Taylor, Atti Accad. Sci. Torino, Band 27, 1891, S. 40–46, Archive
- Sull´integrabilità delle equazioni differenziali del primo ordine, Atti Accad. Sci. Torino, Band 21, 1886, S. 677–685 (englische Übersetzung: On the integrability of first order differential equations, in Kennedy, Peano, Selected Works, 1973, S. 51–57)
- Applicazioni geometriche del calcolo infinitesimale, Turin 1887, Archive
- Integration par séries des équations differentielles linéaires, Mathematische Annalen, Band 32, 1888, S. 450–456, SUB Göttingen
- Calcolo geometrico secondo l´Ausdehnungslehre di H. Grassmann, preceduto dalle operazioni della logica deduttiva, Turin 1888, Digitalisat
- Englische Übersetzung: Geometric Calculus, übersetzt von L. C. Kannenberg, Boston 2000.
- Arithmetices principia: nova methodo, Turin: Bocca 1889, Archive (auch in Opera Scelte, Band 2, 1958, S. 20–55)
- Englische Übersetzung: The principles of arithmetic, presented by a new method, in Jan van Heijenoort, From Frege to Goedel, Harvard University Press 1967, S. 83–97, eine weitere englische Übersetzung ist in Kennedy, Peano, Selected Works, 1973, S. 101–134.
- I principii di geometria logicamente esposti, Turin 1889, Digitalisat, Archive
- Démonstration de l´intégrabilité des equations differentielles ordinaires, Mathematische Annalen, Band 37, 1890, S. 182–228, SUB Göttingen
- Sur une courbe qui remplit tout une aire plane, Mathematische Annalen, Band 36, 1890, S. 157–160, SUB Göttingen
- Sopra alcune curvi singolari, Atti della Reale Accademia delle Scienze di Torino, Classe di Scienze Fisiche, Matematiche e Naturali, Band 26, 1890/91, S. 221–224, Biodiversity Heritage Library (Englische Übersetzung: On some singular curves in Kennedy, Peano, Selected Works 1973)
- Principii di logica matematica, Rivista di Matematica, Band 1, 1891, S. 1–10 (englische Übersetzung in Kennedy, Peano, Selected Works 1973, S. 153–161)
- Sul concetto di numero, Rivista di Matematica, Band 1, 1891, S. 87–102, 256–267.
- Gli elementi di calcolo geometrico, Turin 1891, Archive
- Deutsche Übersetzung: Die Grundzüge des geometrischen Calculus, Teubner 1891, Archive
- Generallizazione della formula de Simpson, Atti Accad. Sci. Torino, Band 27, 1892, S. 68–612 (englische Übersetzung in Kennedy, Peano, Selected Works 1973)
- Lezioni di analisi infintesimale, 2 Bände, Turin 1893, Archive, Band 1
- Sur la définition de la limite d´une fonction, exercise de logique mathèmatique, American J. Math., Band 17, 1894, S. 27–68.
- Notations de logique mathèmatique, Turin 1894, Digitalisat
- Saggio di calcolo geometrico, Atti Accad. Sci. Torino, Band 31, 1895/96, S. 852–957 (englische Übersetzung: Essay on geometrical calculus in Kennedy, Peano, Selected Works 1973)
- Studii in logica matematica, Atti Accad. Sci. Torino, Band 32, 1896/97, S. 565–583 (englische Übersetzung in Kennedy, Peano, Selected Works 1973)
- Formules de logique mathématique, Rivista di Matematica, Band 7, 1900, S. 1–41, Archive
- Les définitions mathématiques, Congrès Int. de Philosophie, Paris 1900, Band 3, S. 279–288.
- Aritmetica generale e algebra elementare, Turin 1902, Archive
- De Latino Sine Flexione. Lingua Auxiliare Internationale, Rivista di Matematica, Band 8, Turin, 1903, S. 74–83, Nachgedruckt in: G. Peano, Opere scelte II, Rom 1958, S. 439–447, Project Gutenberg
- Vocabulario de Latino internationale comparato cum Anglo, Franco, Germano, Hispano, Italo, Russo, Græco et Sanscrito, Turin 1904
- Super Theorema de Cantor-Bernstein, Rendiconti del Circolo Mat. di Palermo, Band 21, 1906, S. 360–366 (Nachgedruckt in Rivista di Mathematica, Band 8, 1906, S. 136–157 mit Zusatz)
- Super teorema de Cantor-Bernstein et additione, Rivista di Matematica, Band 8, 1902–1906, S. 136–157 (englische Übersetzung: Supplement to On the Cantor-Bernstein theorem, in Kennedy, Peano, Selected Works, 1973)
- Vocabulario Commune ad linguas de Europa, Turin 1909
- Formulaire des mathématiques, 5 Bände, Turin 1895, 1897, 1901, 1903, 1908 (Band 5 in Peanos vereinfachtem Latein als Formulario matematico), Band 1, Digitalisat, Gallica, Archive, Band 1, Band 2, Band 3, Band 4, Band 5
- Sui fondamenti dell´analisi, Bolletino Mathesis Societa Italiana di Mat., Band 2, 1910, S. 31–37 (englische Übersetzung: On the foundations of analysis, in Kennedy, Peano, Selected Works 1937)
- L´importanze dei simboli in matematica, Scientio, Band 18, 1915, S. 165–173 (englische Übersetzung in Kennedy, Peano, Selected Works 1973)
- La definizioni in matematica, Periodico di matematiche, Band 1, 1921, S. 175–189 (englische Übersetzung in Kennedy, Peano, Selected Works 1973)
- Giochi di aritmetica e problemi interessanti, Turin 1925
Ausgaben
[Bearbeiten | Quelltext bearbeiten]- Peano: Opere Scelte, 3 Bände, Rom: Cremonese 1957 bis 1959 (Herausgeber Ugo Cassina)
- Hubert C. Kennedy (Hrsg.): Selected Works of Giuseppe Peano, Allen and Unwin und University of Toronto Press 1973
- G. Peano: Arbeiten zur Analysis und zur mathematischen Logik. Hrsg. von G. Asser, Leipzig (Teubner) 1990.
Literatur
[Bearbeiten | Quelltext bearbeiten]- Hubert C. Kennedy: Life and Works of Giuseppe Peano. Reidel, Dordrecht u. a. 1980, ISBN 90-277-1068-6 (Studies in the History of Modern Science 4).
- Hubert Kennedy: Giuseppe Peano. Biographie in deutscher Übersetzung von Ruth Amsler. Peremptory Publications, San Francisco CA 2002.
- Hubert C. Kennedy: Giuseppe Peano. Birkhäuser, Basel u. a. 1974, ISBN 3-7643-0697-1 (Elemente der Mathematik. Beiheft 14).
- Hubert Kennedy: Twelve Articles on Giuseppe Peano, Peremptory Publications, San Francisco CA 2002.
- Willard van Orman Quine: Peano as Logician. In: History and Philosophy of Logic 8, 1987, S. 15–24.
- Michael Segre: “Peano's Axioms in their Historical Context”, Archive for History of Exact Sciences 48, 1994, S. 201–342.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Literatur von und über Giuseppe Peano im Katalog der Deutschen Nationalbibliothek
- John J. O’Connor, Edmund F. Robertson: Giuseppe Peano. In: MacTutor History of Mathematics archive (englisch).
- Online-Kopien verschiedener Schriften von Peano
- Spektrum.de: Erfinder einer universellen Sprache – die nur er versteht 1. August 2018
- Giuseppe Peano in der Datenbank zbMATH
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Pierre Dugac, Grundlagen der Analysis, in J. Dieudonné, Geschichte der Mathematik, Vieweg 1985, S. 409.
- ↑ Hubert Kennedy: The origins of modern Axiomatics. In: American Mathematical monthly, 79 (1972), 133–136. Auch in: Kennedy: Giuseppe Peano, San Francisco, 2002, S. 15.
- ↑ Hubert Kennedy, Peano, 2006, S. 164. Das wird auch in Hinkis, Proofs of the Cantor-Bernstein theorem, a mathematical excursion, Birkhäuser 2013, analysiert und in historischem Zusammenhang dargestellt.
| Personendaten | |
|---|---|
| NAME | Peano, Giuseppe |
| KURZBESCHREIBUNG | italienischer Mathematiker |
| GEBURTSDATUM | 27. August 1858 |
| GEBURTSORT | Spinetta, Piemont |
| STERBEDATUM | 20. April 1932 |
| STERBEORT | Turin |



