Rösselsprung-Quadrat
Ein Rösselsprung-Quadrat ist ein achtreihiges Zahlenquadrat, das aus den natürlichen Zahlen 1 bis 64 besteht und folgende Besonderheit aufweist:
Ein Springer auf dem Ausgangsfeld mit der 1 kann regelkonform so gezogen werden, dass er der Reihe nach alle Zahlen bis 64 genau einmal erreicht. Eine solche Abfolge von Springerbewegungen wird in der Schach-Sprache auch Springertour genannt. Von einer geschlossenen Springertour spricht man, wenn mit einem zusätzlichen Sprung vom letzten Feld der Springertour das Anfangsfeld wieder erreicht werden kann.
Veröffentlichungen
[Bearbeiten | Quelltext bearbeiten]Bereits im Mittelalter wurden die Existenz und die Art von Springertouren exemplarisch erörtert. Der Schweizer Mathematiker und Physiker Leonhard Euler analysierte von 1757 bis 1759 Springertouren erstmals detailliert.[1]
1838 beschrieb der Nürnberger Mathematiklehrer Christoph Wilhelm Zuckermandel Regeln zur Bildung von Zauberquadraten, zusammen mit einer Anweisung über den Rösselsprung.[2]
Der ehemalige russische Schachmeister Carl Ferdinand Jänisch veröffentlichte 1859 einen Beitrag über die symmetrische magische Springertour im New Yorker Schachmagazin The Chess Monthly.[3]
Magische und semimagische Rösselsprung-Quadrate
[Bearbeiten | Quelltext bearbeiten]Ist das Rösselsprung-Quadrat ein magisches Quadrat, bzw. semimagisches Quadrat, so handelt es sich um eine sogenannte magische Springertour, bzw. semimagische Springertour.[4]
Beispiel
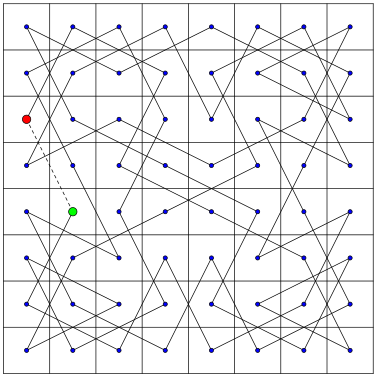
[Bearbeiten | Quelltext bearbeiten]Das folgende semimagische Rösselsprung-Quadrat mit der magischen Zahl 260, bei dem zwar die Zeilen- und Spaltensummen gleich sind, aber nicht mit den beiden Diagonalensummen übereinstimmen, stellt eine geschlossene semimagische Springertour dar. Vom Anfangsfeld 1 (grün) startend kann ein Springer der Reihe nach alle Zahlen bis 64 genau einmal und mit einem Folgesprung vom letzten Feld (rot) wieder das Anfangsfeld erreichen.
-
Semimagisches Rösselsprung-Quadrat
-
Geschlossene semimagische Springertour
Siehe auch
[Bearbeiten | Quelltext bearbeiten]Weblinks
[Bearbeiten | Quelltext bearbeiten]- Klaus Pommerening: Kryptologie - Rösselsprung, Johannes Gutenberg-Universität Mainz, abgerufen am 11. September 2022
- W. Ahrens: Mathematische Unterhaltungen und Spiele, B. G. Teubner Verlag, Leipzig 1901
- Eric Weisstein: There are no Magic Knight’s Tour on the Chessboard, Wolfram MathWorld
- Andreas Kühne, Christina Reiher: Rösselsprung aus magischesquadrat.de, abgerufen am 11. September 2022
- Springerproblem, Rösselsprung, Rösselsprungrätsel aus schach-chess.com, abgerufen am 11. September 2022
- Magische Quadrate im Schach Knowledgebase von Gerald Allerstorfer, veröffentlicht am 18. März 2018, abgerufen am 15. September 2022
- Andreas Stiller: Magisches Springer-Problem gelöst heise online vom 6. September 2003, abgerufen am 15. September 2022
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Leonhard Euler: Solution d'une Question Curieuse qui ne Paroit Soumise a Aucune Analyse. Mémoires de l'Académie des Sciences de Berlin, pages 310–337, 1759
- ↑ Christoph Wilhelm Zuckermandel: Regeln, nach denen alle Zauberquadrate gebildet werden können, Nürnberg 1838
- ↑ Carl Friedrich Andreyevich Jänisch: La solution la plus parfaite du Problème du Cavalier, The Chess Monthly, Band 3, April/Mai/Juni 1859, Seiten 110–115, 146–151 und 176–179
- ↑ Torsten Bosse, Andreas Griewank, Lutz Lehmann, Daniel Schlagk: Die magische Quadratur des Superhirns aus researchgate.net, abgerufen am 11. September 2022