Reguläre Präzession

Abb. 1: Reguläre Präzession eines symmetrischen Kreisels

Bei der regulären Präzession rotiert ein Kreisel mit jeweils konstanter Winkelgeschwindigkeit um eine raumfeste Präzessionsachse und eine körperfeste Achse, die einen gleichbleibenden Winkel einschließen; siehe Animation in Abb. 1.

Die körperfeste Achse ist bei symmetrischen Kreiseln wie in der Animation sowie bei der Grioliʹschen Präzession in Abb. 8 orthogonal zu einer Kreisschnittebene des Trägheitsellipsoids des Kreisels. Bei den Staude-Drehungen fallen die raumfeste und die körperfeste Achse zusammen und sind lotrecht. Die reguläre Präzession des symmetrischen Kreisels ist das kreiseltheoretische Analogon zur Kreisbewegung eines Massenpunkts infolge einer Zentralkraft, siehe #Mechanische Interpretation.

Dissipative Reibeffekte und gleichmäßige Rotationen um die senkrechte Figurenachse symmetrischer Kreisel sind beim Euler-Kreisel und Lagrange-Kreisel nachzuschlagen.

Die reguläre Präzession ist ein wichtiger Punkt in der Kreiseltheorie, nicht zuletzt weil die Erdrotation einer regulären Präzession gleicht, wobei Abweichungen von der Theorie aufgrund der Verformbarkeit und schwankenden Massenverteilung des Erdkörpers auftreten.

Reguläre Präzession symmetrischer Kreisel

Jeder ansonsten kräftefreie Kreisel kann durch geeignete Drehmomente zu beliebigen regulären Präzessionen gezwungen werden. Der Widerstand des Kreisels äußert sich dabei als Kreiselwirkung, die beim symmetrischen schweren Kreisel im dynamischen Gleichgewicht mit dem Moment der Gewichtskraft sein kann, wenn die Eigendrehung um die Figurenachse, die Präzessionsgeschwindigkeit μ und die Neigung des Kreisels gemäß

$F_{g}s=\mu L_{f}$

auf seine Massenverteilung abgestimmt sind. Darin ist

• F_g die Gewichtskraft,
• s der Abstand des Massenmittelpunkts vom Aufstandspunkt und
• L_f die axiale Komponente des Drehimpulses.

Erzwungene reguläre Präzession symmetrischer Kreisel

Ein symmetrischer Kreisel soll mit konstanter Winkelgeschwindigkeit $\mu :={\dot {\psi }}$ um die lotrechte raumfeste Präzessionsachse ê_z und mit konstanter Winkelgeschwindigkeit ν := ${\dot {\varphi }}$ um die körperfeste Figurenachse ê₃ drehen, die dabei den gleichbleibenden Neigungswinkel ϑ mit ê_z einschließt (Bezeichnungen siehe Kreiseltheorie#Bezugssysteme und Euler-Winkel.) Bei einem Kreisel mit axialem Trägheitsmoment C und äquatorialem A wird dementsprechend

${\begin{aligned}{\vec {\omega }}=&\mu {\hat {e}}_{z}+\nu {\hat {e}}_{3}=\mu ({\hat {e}}_{z}-u{\hat {e}}_{3})+(\mu u+\nu ){\hat {e}}_{3}\\{\vec {L}}=&A\mu ({\hat {e}}_{z}-u{\hat {e}}_{3})+C(\mu u+\nu ){\hat {e}}_{3}=L_{\textsf {v}}{\hat {e}}_{z}+L_{f}{\hat {e}}_{3}\\L_{\textsf {v}}=&A\mu \\L_{f}=&(C-A)\mu u+C\nu \end{aligned}}$

mit u := cos(ϑ) = ê_z ‧ ê₃ vorgegeben. Wie bei der Nutation eines kräftefreien Euler-Kreisels liegen die Winkelgeschwindigkeit, der Drehimpuls, die Präzessionsachse und die Figurenachse in einer Ebene, der Präzessionsebene, nur fallen bei der erzwungenen Präzession Drehimpuls und Präzessionsachse nicht zusammen.

Bedingung an den Drehimpuls

Abb. 2:Kräftepaar aus Gewichtskraft F_g und entgegengesetzt gleich großer Aufstandskraft -F_g beim regulär präzedierenden Kreisel.

Aus der Drehung des Drehimpulses resultiert eine Kreiselwirkung, die nur unter Auflagen vom Drehmoment der Gewichtskraft dynamisch ausgeglichen werden kann.

Die Kreiselwirkung ist unmittelbar aus der erzwungenen regulären Präzession eines Kugelkreisels mit A = C und identischem Drehimpuls ersichtlich. Da die Drehimpulse übereinstimmen, nicht so aber die Trägheitsmomente, präzediert der Kugelkreisel mit anderen Winkelgeschwindigkeiten μ_k, ν_k:

${\begin{aligned}{\vec {L}}=&A\mu _{k}{\hat {e}}_{z}+[(A-A)\mu _{k}u+A\nu _{k}]{\hat {e}}_{3}\\=&A\mu _{k}{\hat {e}}_{z}+A\nu _{k}{\hat {e}}_{3}\;{\stackrel {!}{=}}\;L_{\textsf {v}}{\hat {e}}_{z}+L_{f}{\hat {e}}_{3}\end{aligned}}$

Hieraus ist Aμ_k = Aμ = L_v und Aν_k = L_f ablesbar. Die Kreiselwirkung ist umgekehrt gleich der Geschwindigkeit des Drehimpulses, die gleich der des axialen Drehimpulses L_f ist, der beim Kugelkreisel mit μ_k = μ um ê_z kreist:

${\vec {K}}=-{\dot {\vec {L}}}=-(\mu {\hat {e}}_{z})\times (L_{f}{\hat {e}}_{3})=-\mu L_{f}{\hat {e}}_{z}\times {\hat {e}}_{3}$

Das ist analog zu ${\vec {v}}={\vec {\omega }}\times {\vec {r}}$, wo sich die Geschwindigkeit ${\vec {v}}$ bei einer reinen Rotation mit Winkelgeschwindigkeit ${\vec {\omega }}$ aus dem Kreuzprodukt „ד mit dem Abstand ${\vec {r}}$ zu einem Fixpunkt auf der Drehachse ergibt. Die Kreiselwirkung hängt nur vom Drehimpuls und seiner Zeitableitung ab und ist daher beim symmetrischen Kreisel mit A ≠ C gleich der beim Kugelkreisel.

Die Gewichtskraft F_g und die entgegengesetzt gleich große Aufstandskraft bilden, wie in Abb. 2 dargestellt, ein Kräftepaar, das dem Schweremoment ${\vec {M}}:={\vec {s}}\times (-F_{g}{\hat {e}}_{z})$ entspricht. Es ist nur dann parallel zur Kreiselwirkung, wenn der Massenmittelpunkt gemäß ${\vec {s}}=\rho {\hat {e}}_{z}+s{\hat {e}}_{3}$ in der Präzessionsebene liegt, aber die erste Komponente ρê_z keine Eigendrehung um die Figurenachse mitmacht, was beim Spielkreisel in Abb. 3 und bei den #Staude-Drehungen symmetrischer Kreisel der Fall ist. Das Schweremoment lautet dann:

${\vec {M}}:=(\rho {\hat {e}}_{z}+s{\hat {e}}_{3})\times (-F_{g}{\hat {e}}_{z})=F_{g}s{\hat {e}}_{z}\times {\hat {e}}_{3}$

Dem Drallsatz zufolge vermag dieses Moment eine reguläre Präzession zu unterhalten, wenn sich Moment und Kreiselwirkung im dynamischen Gleichgewicht ${\vec {M}}+{\vec {K}}={\vec {0}}$ befinden, das bei

$F_{g}s=\mu L_{f}$

eintritt. Dieses Ergebnis betrifft

Abb. 3: Spielkreisel mit kugelförmiger Kreiselspitze mit Radius ρ um dem Mittelpunkt K im Abstand s vom Massenmittelpunkt G

Lagrange-Kreisel

Hier ist der Stützpunkt der Bezugspunkt für das Gewichtsmoment, die Massenträgheitsmomente und den Drehimpuls. Falls die untere Kreiselspitze mit beachtlichem Radius ρ kugelförmig ist, liegt der Bezugspunkt im Mittelpunkt K der Kugel, siehe Abb. 3.

Symmetrische Spielkreisel

Das Stützmoment F_gs ist dasselbe wie beim Lagrange-Kreisel, nur ist hier der Massenmittelpunkt der Bezugspunkt. Unter Einfluss von Gleitreibung nimmt der Kreisel mit der Zeit eine lotrechte Position ein oder verfällt in eine reguläre Präzession, bei der die runde untere Kreiselspitze ohne Schlupf auf dem Untergrund abrollt.

Symmetrische Euler-Kreisel

Hier ist der Drehimpuls konstant und es tritt weder eine Gewichtskraft noch eine Kreiselwirkung auf. Entsprechend ist F_gs = L_f = 0 und der konstante Drehimpuls weist in Richtung der Präzessionsachse ê_z, was weniger eine Einschränkung für den Drehimpuls darstellt, als vielmehr die Voraussetzung dafür ist, dass der kräftefreie Kreisel hier als Spezialfall auftritt. Die Komponente L_v ist gleich dem Betrag L des Drehimpulses, der die Hypotenuse eines rechtwinkligen Dreiecks ist und der axiale Drehimpuls L₃ = L cos(ϑ) bildet in dem Dreieck die Ankathete zum Neigungswinkel ϑ der Figurenachse.

Konstanten der Bewegung

Im Drehimpuls und der Winkelgeschwindigkeit ist nur die Figurenachse ê₃ zeitabhängig: Die Figurenachse rotiert mit gleichbleibender Neigung um die Präzessionsachse ê_z. Unveränderlich sind dabei neben den vorgegebenen μ und ν die Winkelgeschwindigkeiten

${\begin{aligned}r:=&{\vec {\omega }}\cdot {\hat {e}}_{3}\!\!\!\!\!\!\!\!\!\!\!\!&=&\mu u+\nu \\\omega _{z}:=&{\vec {\omega }}\cdot {\hat {e}}_{z}\!\!\!\!\!\!\!\!\!\!\!\!&=&\mu +\nu u\\\omega :=&|{\vec {\omega }}|\!\!\!\!\!\!\!\!\!\!\!\!&=&{\sqrt {\mu ^{2}+2\mu \nu u+\nu ^{2}}}\end{aligned}}$

die schon oben angegebenen Drehimpulse

${\begin{aligned}L_{\textsf {v}}=&A\mu \\L_{f}=&C(\mu u+\nu )-A\mu u\end{aligned}}$

sowie

${\begin{aligned}L_{3}:=&{\vec {L}}\cdot {\hat {e}}_{3}\!\!\!\!\!\!\!\!\!\!\!\!&=&L_{\textsf {v}}u+L_{f}=C(\mu u+\nu )\\L_{z}:=&{\vec {L}}\cdot {\hat {e}}_{z}\!\!\!\!\!\!\!\!\!\!\!\!&=&L_{\textsf {v}}+L_{f}u=A\mu (1-u^{2})+L_{3}u\\L:=&|{\vec {L}}|\!\!\!\!\!\!\!\!\!\!\!\!&=&{\sqrt {L_{\textsf {v}}^{2}+2L_{\textsf {v}}L_{f}u+L_{f}^{2}}}\end{aligned}}$

und die Rotations-, Lage- und Gesamtenergie

${\begin{aligned}E_{\text{rot}}:=&{\frac {1}{2}}{\vec {\omega }}\cdot {\vec {L}}\!\!\!\!\!\!\!\!\!\!\!\!&=&{\frac {1}{2}}{\big (}A\mu ^{2}(1-u^{2})+C(\mu u+\nu )^{2}{\big )}\\E_{\text{pot}}:=&(\rho {\hat {e}}_{z}+s{\hat {e}}_{3})\cdot (F_{g}{\hat {e}}_{z})\!\!\!\!\!\!\!\!\!\!\!\!&=&(\rho +su)F_{g}\\E_{\text{ges}}:=&E_{\text{rot}}+E_{\text{pot}}\!\!\!\!\end{aligned}}$

denn sie lassen sich mit angesetzten Konstanten μ, ν sowie u = cos(ϑ) ausdrücken. Die Lageenergie ist gleich der Arbeit der Gewichtskraft F_g entlang des lotrechten Weges ρ + su, und „·“ bildet das Skalarprodukt.

Mechanische Interpretation

Beim schweren Kreisel erscheint paradox, dass er der Gewichtskraft nicht nachgibt und den Neigungswinkel ϑ vergrößert, wie er es im Ruhezustand täte, sondern senkrecht zur Kraft ausweicht. Das erklärt sich aus der Regel vom gleichsinnigen Parallelismus, nach der der Kreisel versucht, seinen Drehimpuls dem Drehsinn des Moments gleichsinnig parallel auszurichten. Das Moment wirkt aber waagerecht, was dieses Paradoxon aufklärt. Die Figurenachse beginnt sich eher gegen die Knotenachse ê_z × ê₃ zu neigen und kommt ihr nur deshalb nicht näher, weil sich das Schweremoment im gleichen Sinn weiterdreht.

Dieses Verhalten ähnelt der von einer Zentripetalkraft unterhaltenen Kreisbewegung eines Massenpunkts um ein Zentrum:

• Ebenso wenig, wie die Figurenachse des Kreisels der Knotenachse näher kommt, die gleich der Richtung des Schweremoments ist, kommt der umlaufende Massenpunkt dem Kraftzentrum näher.
• Die Zentripetalkraft muss, so wie das Schweremoment beim Kreisel, eine auf die Geschwindigkeit abgestimmte Größe haben.
• Sowenig wie die Zentripetalkraft Arbeit leistet und die Energie des Massenpunkts erhöht, so leistet auch das Schweremoment beim Kreisel keine Arbeit und bleibt der Energiegehalt des Kreisels erhalten.
• Die Zentripetalkraft allein vermag die Kreisbewegung nicht einzuleiten; dazu bedarf es eines dem Abstand vom Zentrum entsprechenden tangentialen Stoßes auf den ruhenden Massenpunkt. Ebenso muss der um seine Figurenachse gleichförmig rotierende Kreisel einen zur Figurenachse senkrechten wohldosierten Drehstoß erhalten, damit eine reguläre Präzession einsetzt.

Präzessionsgeschwindigkeiten

Weil L_f = (C - A)μu + Cν von μ abhängt, resultiert aus der #Bedingung an den Drehimpuls μL_f  = F_gs eine quadratische Gleichung

$(C-A)u\mu ^{2}+C\nu \mu -F_{g}s=0$

mit den Lösungen:

${\begin{aligned}(C-A)u=0:&\quad \mu ={\frac {F_{g}s}{C\nu }}\\(C-A)u\neq 0:&\quad \mu _{1,2}={\frac {-C\nu }{2(C-A)u}}\left(1\pm {\sqrt {1+{\frac {4(C-A)F_{g}su}{C^{2}\nu ^{2}}}}}\right)\end{aligned}}$

Allgemeiner Fall

• Reguläre Präzessionen eines aufrechten gestreckten Kreisels
• 
  Abb. 4: Schnelle reguläre Präzession
• 
  Abb. 5: Langsame reguläre Präzession

Beim gestreckten Kreisel (C < A) sind folgende Fälle zu unterscheiden:

• 0° < ϑ < 90°, 1 > u = cos(ϑ) > 0: Aufrechter gestreckter Kreisel, dessen Präzession von oben gesehen gleichsinnig zur Eigendrehung ist:
  • C² ν² < |4 (C - A) F_gs u|: Eine reguläre Präzession ist nicht möglich.
  • C² ν² = |4 (C - A) F_gs u|: Es gibt eine Präzessionsgeschwindigkeit.
  • C² ν² > |4 (C - A) F_gs u|: Es gibt zwei Präzessionsgeschwindigkeiten, siehe Abb. 4 und 5.
• ϑ = 90°, u = 0: Horizontale Figurenachse, es gibt eine zur Eigendrehung gleichsinnige Präzession, die der Bedingung C μ ν = F_gs gehorcht.
• 90° < ϑ < 180°, 0 > u > -1: Hängender gestreckter Kreisel, der zwei Präzessionsgeschwindigkeiten mit unterschiedlichem Vorzeichen annehmen kann. Bei der schnelleren sind Präzession und Eigendrehung von oben gesehen gleichsinnig, bei der langsameren gegensinnig.

In der Formel für die Präzessionsgeschwindigkeit kommen C - A und u nur als Produkt (C - A) u vor, weswegen sich der hängende gestreckte Kreisel mit u, C - A < 0 vergleichbar verhält wie der aufrechte abgeplattete mit u, C - A > 0 und der hängende abgeplattete ebenso wie der aufrechte gestreckte:

„Die regulären Präzessionen des gestreckten gehobenen Kreisels erfolgen also von oben gesehen im gleichen Sinne wie die Kreiseldrehung, diejenigen des abgeplatteten gesenkten im entgegengesetzten Sinne, und sie sind bei beiden Kreiseln überhaupt nur dann möglich, wenn die Eigendrehgeschwindigket ν hinreichend groß ist.

Beim gestreckten gesenkten Kreisel geschieht die schnellere der beiden regulären Präzessionen von oben gesehen im Sinne der Kreiseldrehung, die langsamere im entgegengesetzten, und beim abgeplatteten gehobenen ist es gerade umgekehrt, doch ist bei beiden Kreiseln kein Mindestwert der Eigendrehgeschwindkeit ν erforderlich.“

– R. Grammel

Die folgenden Spezialfälle sind bemerkenswert.

Schneller Kreisel

Beim schnellen Kreisel, bei dem C² ν² ≫ 4 |(C - A) F_gs u| ist, gilt mit u = cos(ϑ) die Näherung

${\begin{aligned}(C-A)u=0:&\quad \mu ={\frac {F_{g}s}{C\nu }}\\(C-A)u\neq 0:&\quad \mu _{1,2}\approx {\begin{cases}{\frac {-C\nu }{(C-A)u}}&(1)\\{\frac {F_{g}s}{C\nu }}&(2)\end{cases}}\end{aligned}}$

Bei der langsamen Präzession (2) ist die Präzessionsgeschwindigkeit gleichsinnig und umgekehrt proportional zur Eigendrehung ν und außerdem vom Neigungswinkel unabhängig. Die schnelle Präzession (1) entspricht der Nutation des kräftefreien Euler-Kreisels. Dieses die Schwerkraft vernachlässigende Verhalten begründet sich damit, dass beim schnellen Kreisel die potentielle Energie gegenüber der Rotationsenergie eine untergeordnete Rolle spielt.

Die Präzessionsfrequenz entspricht derjenigen bei der pseudoregulären Präzession des schnellen Lagrange-Kreisels. Durch sekundäre Effekte wie Reibung und Verformung geht die pseudoreguläre Präzession rasch in die reguläre über.

Nutation des Euler-Kreisels

Beim Euler-Kreisel ist F_gs = 0 und die quadratische Gleichung reduziert sich auf

$[(C-A)u\mu +C\nu ]\mu =0$

Bei μ = 0 dreht sich der Kreisel nur um die Figurenachse oder ruht gänzlich. Die Nutation des Euler-Kreisels erfolgt mit (C - A) u μ = -C ν in Abhängigkeit von u = cos(ϑ) wie im Fall (1) beim schnellen Kreisel.

Sphärisches Pendel

Abb. 6: Kreisel als aufrechtes sphärisches Pendel

Der Kreisel ohne Eigendrehung (ν = 0) entspricht einem sphärischen Pendel, dessen reguläre Präzession darin besteht, dass der Pendelkörper auf einem Kreiskegel umläuft. Hier lautet die quadratische Gleichung

$(C-A)u\mu ^{2}=F_{g}s$

Bei kleinem axialem Trägheitsmoment (C < A) ist eine Präzession nur in hängender Position möglich (mit u = cos(ϑ) < 0). Bemerkenswert ist der andere Fall mit axialer Massenträgheit C > A, wo das sphärische Pendel wie in Abb. 6 nur eine reguläre Präzession mit einem Massenmittelpunkt oberhalb des Aufstandspunkts ausführen kann (mit u > 0).

Staude-Drehungen symmetrischer Kreisel

Abb. 7: Karussell-Bewegung eines Kowalewskaja-Kreisels

→ Hauptartikel: Staude-Drehung

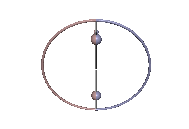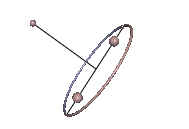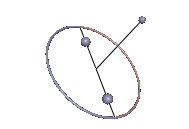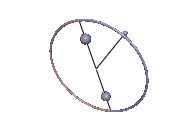
Wenn der Massenmittelpunkt nicht auf der Figurenachse ist, kann der symmetrische Kreisel dann eine reguläre Präzession ausführen, wenn der Massenmittelpunkt immer noch in der Präzessionsebene liegt. Das ist bei den Karussell-Bewegungen des Kowalewskaja-Kreisels wie in Abb. 7 der Fall. Der Kreisel rotiert gleichförmig um eine vertikale, raum- und körperfeste Achse, was als Staude-Drehung bezeichnet wird.

Stabilität

Die Stabilität der Präzessionsbewegungen ist von vielen Faktoren abhängig. Allgemein lässt sich sagen, dass beim Lagrange-Kreisel die reguläre Präzession immer stabil ist. Beim Spielzeugkreisel ist die Stabilität vom Drehimpuls, von der Geometrie der unteren Kreiselspitze und dem Verhältnis der Hauptträgheitsmomente A und C abhängig. Die Stabilität der Nutation des symmetrischen Euler-Kreisels und der Staude-Drehungen ist nicht einfach zu charakterisieren und in den Artikeln nachzuschlagen.

Reguläre Präzession unsymmetrischer Kreisel

Erzwungene reguläre Präzession unsymmetrischer Kreisel

Ein unsymmetrischer ansonsten kräftefreier Kreisel kann wie der symmetrische durch passende Drehmomente zu jeder regulären Präzession gezwungen werden. Von besonderem Interesse ist der Fall, wo die körperfeste Drehachse eine Hauptachse, beispielsweise die 3-Achse, ist. Die Benennungen vom symmetrischen Fall sollen der Einfachheit halber hier übernommen werden: Die z-Achse stellt die Präzessionsachse, die 3-Achse wird als Figurenachse und die Drehung um sie als Eigendrehung bezeichnet. Die beiden Achsen spannen die Präzessionsebene auf, zu der die Knotenachse senkrecht ist. Dann ist

${\begin{aligned}{\vec {\omega }}=&\mu {\hat {e}}_{z}+\nu {\hat {e}}_{3}\\{\dot {\vec {\omega }}}=&{\dot {\nu }}{\hat {e}}_{3}+\nu {\dot {\hat {e}}}_{3}={\dot {\nu }}{\hat {e}}_{3}+\nu {\vec {\omega }}\times {\hat {e}}_{3}\\=&\mu \nu \sin(\vartheta )\cos(\varphi ){\hat {e}}_{1}-\mu \nu \sin(\vartheta )\sin(\varphi ){\hat {e}}_{2}+{\dot {\nu }}{\hat {e}}_{3}\end{aligned}}$

vorgegeben, wo eine Veränderlichkeit der Eigendrehung ν zugelassen wurde. Hier wurde ausgenutzt, dass die körperfeste 3-Achse ê₃ keine Zeitableitung relativ zum Kreisel besitzt. Einsetzen dieser Winkelgeschwindigkeiten und -beschleunigungen in die Eulerʹschen Kreiselgleichungen liefert die Kreiselwirkung

${\begin{aligned}{\vec {K}}=&-K_{a}{\hat {e}}_{N}-K_{b}{\hat {e}}_{N}\cos(2\varphi )+(K_{c}{\hat {e}}_{3}-K_{b}{\hat {e}}_{q})\sin(2\varphi )-C{\dot {\nu }}{\hat {e}}_{3}\\K_{a}=&\left[C\nu +\left(C-{\frac {A+B}{2}}\right)\mu \cos(\vartheta )\right]\mu \sin(\vartheta )\\K_{b}=&{\frac {A-B}{2}}[\mu \cos(\vartheta )+2\nu ]\mu \sin(\vartheta )\\K_{c}=&{\frac {A-B}{2}}\mu ^{2}\sin ^{2}(\vartheta )\end{aligned}}$

Die Vektoren

${\hat {e}}_{N}:={\frac {{\hat {e}}_{z}\times {\hat {e}}_{3}}{\sin(\vartheta )}}$ und ${\hat {e}}_{q}:={\hat {e}}_{3}\times {\hat {e}}_{N}$

bilden mit der 3-Achse eine Orthonormalbasis.

Bei konstantem ν$:={\dot {\varphi }}$ läuft die Kreiselwirkung demnach mit der doppelten Eigendrehgeschwindigkeit 2ν auf einer Ellipse um, deren Ebene die Knotenachse ê_N enthält, und das Zentrum dieser Ellipse ist entlang dieser Achse um -K_a verschoben. Beim schnellen Kreisel mit konstantem ν ≫ μ kann K_c gegenüber den anderen Kreiselwirkungen K_a,b vernachlässigt werden, wonach die Kreiselwirkung in der Äquatorebene kreisförmig mit Radius K_b um -K_aê_N rotiert.

Wenn keine Eigendrehung festgelegt wird, ν also variabel ist, dann ergibt sich in 3-Richtung aus $K_{c}\sin(2\varphi )-C{\dot {\nu }}=0$ die Schwingungsgleichung

${\ddot {\alpha }}+{\frac {g}{l}}\sin(\alpha )=0$

mit $\alpha =2\varphi ,\;{\ddot {\alpha }}=2{\dot {\nu }}$  und  $l={\tfrac {Cg}{(B-A)\mu ^{2}\sin ^{2}(\vartheta )}}$, wo ohne Einschränkung B > A voraus gesetzt werden darf und g die Schwerebeschleunigung ist.

„Der unsymmetrische Kreisel schwingt um die antriebfreie Figurenachse wie ein mathematisches Pendel von der Länge l, jedoch immer mit halb so großem Ausschlag und halb so großer Geschwindigkeit, aber mit gleicher Schwingungsdauer.“

– R. Grammel: Der Kreisel (1920), S. 80.

Ist die Eigendrehung anfänglich groß genug vorgegeben, dann gehen die Schwingungen in ganze Drehungen über, entsprechend einem sich überschlagenden Pendel. Die schnellste Eigendrehung tritt bei sin(α) = 0 auf, wenn die 1-Achse mit dem kleineren Trägheitsmoment A die Knotenachse passiert, und sie ist am langsamsten, wenn sin(α) = ±1 und die 2-Achse mit dem größeren Trägheitsmoment B das tut.

Bei unterdrückter Eigendrehung (ν = 0) wird der Kreisel zu einer Drehung um eine beliebige Körperfeste Achse gezwungen. Angenommen C > B > A. Dann ist die in Knotenrichtung liegende Kreiselwirkung bei spitzem Neigungswinkel ϑ negativ und bei stumpfem positiv. Jedenfalls versucht die Kreiselwirkung die Figurenachse, also die Achse mit dem größten Trägheitsmoment, in die Drehachse hinein zu ziehen.

Staude-Drehungen unsymmetrischer Kreisel

→ Hauptartikel: Staude-Drehung

Die Staude-Drehungen sind allen Kreiseln mögliche, reguläre Präzessionen in Form permanenter Drehungen um eine lotrechte und körperfeste Präzessionsachse. Die Schwereachse vom Aufstandspunkt zum Massenmittelpunkt, die Winkelgeschwindigkeit und der Drehimpuls liegen mit konstanten Komponenten in der Präzessionsebene, die gleichmäßig mit dem Kreisel um die Präzessionsachse umläuft, die auf dem Staude-Kegel des Kreisels liegt. In Abb. 7 ist die Staude-Drehung eines symmetrischen Kreisels zu sehen.

Griolische Präzession

Abb. 8: Grioli’sche Präzession

→ Hauptartikel: Griolische Präzession

Die Grioliʹsche Präzession ist die einzige, dynamisch mögliche, reguläre Präzession schwerer unsymmetrischer Kreisel. Bei ihnen ist die Präzessionsachse nicht vertikal, siehe Abb. 8. Die Komponenten des Drehimpulses in der Präzessionsebene sind nicht konstant und der Drehimpuls liegt zumeist auch nicht in ihr, sondern passiert sie periodisch. Die Grioliʹsche Präzession können Kreisel ausführen, bei denen eine Kreisschnittebene ihres Trägheitsellipsoids senkrecht zur Schwereachse vom Aufstandspunkt zum Massenmittelpunkt gelegen ist.

Weblinks

Commons: Präzession – Sammlung von Bildern, Videos und Audiodateien

• K. Lüders, R. O. Pohl, G. Beuermann, K. Samwer: Präzession eines rotierenden Rades. (MP4) Institut für den wissenschaftlichen Film (IWF), 2003, abgerufen am 13. April 2018 (Film über ein regulär präzedierendes Rad mit horizontaler Drehachse.). 
• K. Lüders, R. O. Pohl, G. Beuermann, K. Samwer: Rotation um freie Achsen. (MP4) Institut für den wissenschaftlichen Film (IWF), 2004, abgerufen am 5. Februar 2020 (Mit drei Körpern verschiedener Form wird gezeigt, um welche freien Achsen sie stabil rotieren können. Als stabilste freie Achse erweist sich die mit dem größten Trägheitsmoment.). 

Literatur

• K. Magnus: Kreisel: Theorie und Anwendungen. Springer, 1971, ISBN 978-3-642-52163-8, S. 77, 117 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 20. Februar 2018]). 
• R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. Vieweg Verlag, Braunschweig 1920, DNB 451641280, S. 40, 89, 112 (archive.org – "Schwung" bedeutet Drehimpuls, „Drehstoß“ etwa Drehmoment und „Drehwucht“ Rotationsenergie, siehe S. VII.). 
• R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. 2. überarb. Auflage. Band 1. Springer, Berlin, Göttingen, Heidelberg 1950, S. 51, 69, 79. 
• Giuseppe Grioli: Existenz und Bestimmung von dynamisch möglichen regulären Präzessionen eines schweren asymmetrischen Körpers. In: Annali di Matematica Pura ed Applicata. Band 26, Nr. 1. Swets & Zeitlinger, 1947, ISSN 0373-3114, S. 271–281, doi:10.1007/BF02415381 (italienisch, Originaltitel: Esistenza e determinazione delle precessioni regolari dinamicamente possibili per un solido pesante asimmetrico.). 
• S. Rauch-Wojciechowski, M. Sköldstam, T. Glad: Mathematische Analyse des Stehaufkreisels. In: Regular and Chaotic Dynamics. Band 10, Nr. 4. Springer Nature, 2005, ISSN 1468-4845, S. 333–362, doi:10.1070/RD2005v010n04ABEH000319 (turpion.org [abgerufen am 15. Dezember 2018] Originaltitel: Mathematical analysis of the tippe top.). 
• Eugene Leimanis: Das allgemeine Problem der Bewegung von gekoppelten starren Körpern um einen festen Punkt. Springer Verlag, Berlin, Heidelberg 1965, ISBN 978-3-642-88414-6, S. 108 ff., doi:10.1007/978-3-642-88412-2 (englisch, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 21. März 2018] Originaltitel: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point.). 
• F. Klein, A. Sommerfeld: The Theory of the Top. Development of the Theory in the Case of the Heavy Symmetric Top. Volume II. Birkhäuser, Boston 2010, ISBN 978-0-8176-4824-4, S. 279 ff., doi:10.1007/978-0-8176-4827-5 (englisch, Formelzeichen werden auf S. 197 ff. insbesondere S. 200 erklärt.). 
  oder das deutsche Original von 1897
  F. Klein, A. Sommerfeld: Über die Theorie des Kreisels. Heft I-III. Teubner, Leipzig 1897 (archive.org [abgerufen am 17. Januar 2020]).