Toroidales Polyeder

Ein polyedrischer Torus kann zur Annäherung an eine Torusoberfläche aus einem Netz viereckiger Flächen konstruiert werden, wie in diesem 6x4-Beispiel.

In der Geometrie ist ein Toroidales Polyeder ein Polyeder, welches auch ein Toroid ist (ein g-gelochter Torus), während es einen topologischen Genus (Fläche) (g) von 1 oder mehr hat. Erwähnenswerte Beispiele sind das Császár- und das Szilassi-Polyeder.

Variationen in der Definition

Toroidale Polyeder werden definiert als Sammlungen von Polygonen, die sich an ihren Kanten und Scheitelpunkten treffen, wobei sie eine Mannigfaltigkeit erstellen. Das heißt, jede Kante sollte von genau zwei Polygonen gemeinsam genutzt werden und an jedem Scheitelpunkt sollten die Kanten und Flächen, die sich am Scheitelpunkt treffen, in einem einzigen Zyklus abwechselnder Kanten und Flächen miteinander verbunden sein; die Verbindung (einfacher Komplex) des Scheitelpunkts. Für toroidale Polyeder ist diese Mannigfaltigkeit eine orientierbare Oberfläche. Einige Autoren beschränken den Ausdruck „toroidale Polyeder“ auf die spezifischere Bezeichnung von Polyedern, die dem (genus 1) Torus topologisch äquivalent sind.

In diesem Bereich ist es wichtig, eingebettete toroidale Polyeder, deren Flächen flache Polygone im dreidimensionalen Euklidischen Raum sind, die sich selbst oder einander nicht kreuzen, von abstrakten Polyedern, topologischen Flächen ohne festgelegte geometrische Realisierung, zu unterscheiden. Zwischen diesen beiden Extremen liegen Polyeder, die aus geometrischen Polygonen oder Sternpolygonen im euklidischen Raum bestehen und sich kreuzen dürfen.

In all diesen Fällen kann die toroidale Natur eines Polyeders durch seine Orientierungsfähigkeit und die Tatsache, dass seine Euler-Charakteristik nicht positiv ist, überprüft werden. Die Euler-Charakteristik verallgemeinert sich zu V − E + F = 2 − 2N, wobei N die Anzahl der Löcher ist.

Császár und Szilassi-Polyeder

Interaktives Császár-Polyeder Modell – In der SVG kann das Model gedreht werden.

Interaktives Szilassi-Polyeder Modell – In der SVG kann das Model gedreht werden.

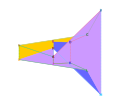Zwei der einfachsten eingebetteten toroidalen Polyeder sind die Császár- und Szilassi-Polyeder.

Das Császár-Polyeder ist ein toroidales Polyeder mit sieben Ecken, 21 Kanten und 14 dreieckigen Flächen. Es und das Tetraeder sind die einzigen bekannten Polyeder, bei denen jedes mögliche Liniensegment, das zwei Eckpunkte verbindet, eine Kante des Polyeders bildet. Sein Dual, das Szilassi-Polyeder, hat sieben sechseckige Flächen, die alle aneinander angrenzend sind, und liefert damit die Existenzhälfte des Theorems, dass die maximale Anzahl von Farben, die für eine Karte auf einem Torus (Genus 1) benötigt werden, sieben beträgt.

Das Császár-Polyeder hat die wenigsten möglichen Eckpunkte aller eingebetteten toroidalen Polyeder, und das Szilassi-Polyeder hat die wenigsten möglichen Flächen aller eingebetteten toroidalen Polyeder

Stewart-Toroiden

Eine besondere Kategorie toroidaler Polyeder besteht ausschließlich aus regelmäßigen Polygonflächen ohne Kreuzungen und mit der weiteren Einschränkung, dass benachbarte Flächen nicht in derselben Ebene liegen dürfen. Diese werden Stewart-Toroide genannt, benannt nach Bonnie Stewart, die sie intensiv untersucht hat. Sie sind analog zu den Johnson-Körpern im Fall konvexer Polyeder; Im Gegensatz zu den Johnson-Körpern gibt es jedoch unendlich viele Stewart-Toroide. Dazu gehören auch toroidale Deltaeder, Polyeder, deren Flächen alle gleichseitige Dreiecke sind.

Eine eingeschränkte Klasse von Stewart-Toroiden, die ebenfalls von Stewart definiert wurden, sind die quasikonvexen toroidalen Polyeder. Dies sind Stewart-Toroide, die alle Kanten ihrer konvexen Hülle umfassen. Bei einem solchen Polyeder liegt jede Fläche der konvexen Hülle entweder auf der Oberfläche des Toroids oder es handelt sich um ein Polygon, dessen Kanten alle auf der Oberfläche des Toroids liegen.

Stewart toroids by augmentation of a single polyhedron

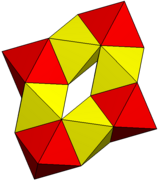
Genus	1	1
Bild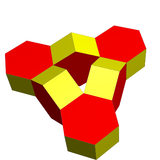
Polyeder	6 Sechseckige Prismen	8 Oktaeder
Eckpunkte	48	24
Kanten	84	72
Flächen	36	48

Quasi-convex Stewart toroids

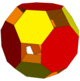
Genus	1		3	11	3	5	7	11
Bild
Polyeder	4 Quadratische Kuppeln 8 tetrahedra	6 Dreieckskuppeln 6 Quadratische Pyramiden	4 Dreieckskuppeln 6 Quadratische Pyramiden	24 Dreieckige Prismen 6 Quadratische Pyramiden 8 Tetraeder	6 Quadratische Kuppeln 4 Dreieckskuppeln 12 Würfel	8 Dreieckskuppeln 12 Würfel	6 Quadratische Kuppeln 12 Würfel	6 Quadratische Kuppeln 8 Dreieckskuppeln
Konvexe Hülle	Hexaeder Strumpf	Oktaederstumpf	Oktaederstumpf	Erweiterter Kuboktaeder	Großes Rhombenkuboktaeder	Großes Rhombenkuboktaeder	Großes Rhombenkuboktaeder	Großes Rhombenkuboktaeder
Eckpunkte	32	30	30	62	72	72	72	72
Kanten	64	60	72	168	144	168	168	168
Flächen	32	30	38	86	68	88	84	76

Selbstkreuzende Polyeder

Oktahemioktaeder

Kleines Kububoktaeder

Großes Dodekaeder

Ein Polyeder, das durch ein System sich kreuzender Polygone gebildet wird, entspricht einer abstrakten topologischen Mannigfaltigkeit, die aus seinen Polygonen und ihrem System gemeinsamer Kanten und Eckpunkte besteht, wodurch die Gattung des Polyeders aus dieser abstrakten Mannigfaltigkeit bestimmt werden kann. Beispiele hierfür sind das Oktahemioktaeder der Gattung 1, das kleine Kubikuboktaeder der Gattung 3 und das große Dodekaeder der Gattung 4.

Kronen-Polyeder

Fünfeckiges Stephanoid. Dieses Stephanoid weist eine fünfeckige Diedersymmetrie auf und hat die gleichen Eckpunkte wie das gleichmäßige fünfeckige Prisma.

Ein Kronenpolyeder oder Stephanoid ist ein toroidales Polyeder, das ebenfalls edel ist und sowohl isogonal (gleiche Eckpunkte) als auch isoedrisch (gleiche Flächen) ist. Kronenpolyeder überschneiden sich selbst und sind topologisch selbst-dual.

Siehe auch

• Projektives Polyeder
• Sphärisches Polyeder
• Toroidaler Graph

Weblinks

• Eric W. Weisstein: Toroidal polyhedron. In: MathWorld (englisch).
• Stewart Toroids (Toroidal Solids with Regular Polygon Faces) (englisch)
• Stewart's polyhedra (englisch)
• Toroidal Polyhedra (englisch)
• Stewart toroids (englisch)