Diskussion:Fluchtgeschwindigkeit (Raumfahrt)
Füge neue Diskussionsthemen unten an:
Klicke auf , um ein neues Diskussionsthema zu beginnen.| Auf dieser Seite werden Abschnitte ab Überschriftenebene 2 automatisch archiviert, die seit 30 Tagen mit dem Baustein {{Erledigt|1=--~~~~}} versehen sind. |
| Archiv |
| Wie wird ein Archiv angelegt? |
|
Dieser Artikel wurde ab November 2015 in der Qualitätssicherung Physik unter dem Titel „Fluchtgeschwindigkeit (Raumfahrt)“ diskutiert. Die Diskussion kann im Archiv nachgelesen werden. |
Erste kosmische Geschwindigkeit
[Quelltext bearbeiten]Ich hätte eine Frage zur 1. kosm. Geschwindigkeit.
Da steht, das ist die Geschwindigkeit, die man braucht, um entweder eine Kreisbahn zu erreichen, oder dem Gravitationsfeld zu entkommen.
Ist des die Geschwindigkeit, die man vom Boden aus braucht? Diese Geschwindigkeit erreicht man nähmlich schon mit einer Hohlladung.
Im Artikel "Satellitenorbit" steht auserdem, dass Spionagesatteliten 7km/s schnell sind, also müsste man mit den restlichen 0,9km/s schon auf die nötige Höhe kommen. Dann könnte man die ja theoretisch schon mit einer normalen Sniper runterschießen!?
- Hallo IP! Vielleicht hilft Dir dieses Bild:
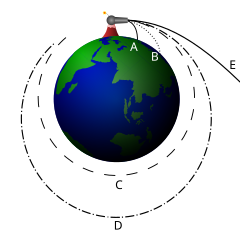 ?
?- Der Satellit braucht in einer Höhe, in der er nicht mehr (oder kaum mehr) der Atmosphärenreibung ausgesetzt ist, die erste kosmischen Geschwindigkeit C. Kann man so etwas mit einer Hohlladung erreichen? Die Angabe im Artikel Satellitenorbit ist abgerundet, da gibt es keine "restlichen 0.9 km/s". Und eine Sniper? Ist das die Waffe eines Snipers? Hat die eine Reichweite von über 100 km? Oder rechnest Du nur mit der Mündungsgeschwindigkeit? Und vergiss den Luftwiderstand nicht. --Asdert 13:35, 11. Feb. 2008 (CET)
OK dann ist das also die Geschwindigkeit die die in der Umlaufbahn haben, und nicht die sie zum starten brauchen. Mich hatte da nämlich der Artikel über Gerald Bull verwirrt, wo steht, dass er 7,9km/s gebraucht hätte um mit seinen Kanonen den Orbit zu erreichen.
- Geschwindigkeit zum Starten? Jeder Raketenstart beginnt mit v=0. Die Flugbahn führt erst senkrecht nach oben, dann schräg und schließlich waagrecht. Wenn die erste kosmische Geschwindigkeit erreicht ist, dann ist auch die Umlaufbahn erreicht. Du gehst wohl von einem Abschuss aus, bei dem die Endgeschwindigkeit sofort nach dem Start erreicht wird. Das geht theoretisch auch, siehe obiges Bild. Nur ist die Flughöhe dann sehr, sehr gering. --Asdert 15:31, 11. Feb. 2008 (CET)
- Also ich habe es mit dem momentanen Artikel auch nicht verstanden und dann nochmal die englische Wiki gelesen in der es einen extra Abschnitt für Missverständnisse gibt. Und wenn der stimmt dann bedeutet das - Fluchtgeschwindigkeit heisst, dass sobald die Fluchtgeschwindkeit erreicht ist (und der Luftwiderstand vernachlässigt wird) das Objekt ausreichend schnell ist um nicht zurückzufallen ohne dass es weiteren Schub benötigt. Also wie in einer Kanone. Wenn man dagegen konstanten Schub hat kann man den Orbit mit jeder beliebigen Geschwindigkeit verlassen. Das war ehrlich gesagt auch die Frage die mich interessiert hatte als ich den Artikel hier gelesen hatte und ich würde das auch gerne deutlicher erklärt sehen. Allerdings ist meine einzige Quelle die englische Wiki und ich weiss nicht sicher genug ob das jetzt auch so stimmt als dass ich mir zutrauen würde den Artikel hier zu überarbeiten. --Michael Zeilfelder 00:36, 30. Mär. 2010 (CEST)
- Ich halte den englischen Abschnitt en:Escape_velocity#Misconception eher für verwirrend als dass er wirklich Missverständnisse ausräumt. Ich bin mir auch nicht sicher, was wirklich Deine Frage ist. Einerseits sprichst Du von "um nicht zurückzufallen", was auf die 1. Kosmische Geschwindigkeit (KG) hinweist, andererseits sprichst Du von "Orbit verlassen", was auf die 2. KG hinweist. Vielleicht bleiben wir bei der 1. KG. Die Formel lautet:
- Für R=6370 km (Erdoberfläche) kommen wir auf 7911 m/s. Wenn man aber eine Kreisbahn in 200 km Höhe betrachtet, dann reichen dort (6570 km einsetzen) schon 7790 m/s (3% mehr Radius = 1,5% weniger Geschwindigkeit, wegen der Wurzel). Allerdings muss der Flugkörper erst einmal in diese Höhe kommen, wozu er ja Energie (Schub) braucht, er muss aber tatsächlich nie schneller als 7790 m/s werden. Mit konstantem Schub (und sei er noch so klein, er muss nur größer als das Gewicht des Flugkörpers sein) kommst Du theoretisch irgendwann in eine Höhe, in dem die Fluchtgeschwindigkeit gering genug für Langsamflieger ist. Wenn die Steiggeschwindkigkeit allerdings klein ist, dann braucht man auch länger, um auf die notwendige Höhe zu kommen. Es hat schon seinen Grund, weshalb Raketen die dichten Schichte der Atmosphäre möglichst schnell durchqueren wollen. Ich bin mir nicht sicher, wo der Dein Knackpunkt genau liegt. Kannst Du uns genauer beschreiben, was Du verstehst oder nicht verstehst? Im Artikel steht übrigens "Wegen des Luftwiderstands haben Satelliten eine Bahnhöhe von mindestens 150 km über der Erdoberfläche. Die dazu notwendige Bahngeschwindigkeit ist entsprechend kleiner". Sollte man diesen Satz etwas detaillieren (z.B. mit einer Rechnung)? --Asdert 01:38, 30. Mär. 2010 (CEST)
- Ich glaube du denkst zu kompliziert. Du weisst schon _was_ eine kosmische Fluchtgeschwindigkeit ist. Ich kam her um das erst herauszufinden. Ich wusste nicht ob das eine Geschwindigkeit ist die Raketen irgenwann mal überschreiten müssen aus irgendeinem Grund um die Erde verlassen zu können oder ob das eine Geschwindigkeit ist die wenn sie einmal erreicht ist genügend um die Erde zu verlassen (bzw. um eine der anderen kosmischen Schwellen zu überschreiten). Also wenn ich z.B. vor dir davonlaufe - dann brauche ich eine Geschwindigkeit die garantiert höher ist als deine. Wenn ich dagegen einfach nur aus deiner Reichweite kommen will während du dich nicht bewegst dann genügt mir ein Sprung der mich weit genug trägt. Was genau eine kosmische Geschwindigkeit ist hatte ich aus dem deutschen Artikel jetzt nicht herauslesen können. Der misconception Abschnitt in der Englischen sagt dagegen ziemlich deutlich dass es hier nicht um eine Geschwindigkeit geht die Raketen je erreichen müssen - was genau meine ursprüngliche Frage war.--Michael Zeilfelder 14:36, 30. Mär. 2010 (CEST)
- Es steht zwar geschrieben, dass die 1. KG für die Oberfläche gilt, und dass die notwendige Bahngeschwindigkeit in üblichen Höhen geringer ist, aber das war wohl nicht deutlich genug. Ich habe das jetzt etwas geändert. Ist es beim Lesen jetzt klarer, worum es geht? Woran könnte ein Leser noch stolpern? Den englischen Absatz halte ich trotzdem für verwirrend bis falsch. Hast Du verstanden, warum da plötzlich vom Baryzentrum die Rede ist? Das macht die Sache doch erst recht kompliziert. (Und Du meinst, _ich_ denke kompliziert? ;-) --Asdert 16:42, 30. Mär. 2010 (CEST)
- Nein - mit dem Baryzentrum konnte ich auch nichts anfangen. Der entscheidende Teil in der englischen Wiki war für mich: "Planetary or lunar escape velocity is sometimes misunderstood to be the speed a powered vehicle (such as a rocket) must reach to leave orbit; however, this is not the case ... <snip>... In fact a vehicle can leave the Earth's gravity at any speed.". Sobald ich das gelesen hatte wusste ich dass es bei einer Fluchtgeschwindigkeit nicht darum geht, dass ein Objekt (ein Raumschiff...) eine bestimmte Mindestgeschwindigkeit erlangen muss um von der Erde flüchten zu können. Das baryocentric Zeug konnte ich ignorieren. Und der Grund für dieses Missverständnis ist ganz einfach, dass ich genau dieses Missverständnis in einer Diskussion gesehen hatte und ich konnte mir das zwar nicht erklären, aber vielleicht gab es ja einen Grund dafür (Astrophysik hat viele Überraschungen). Daher dann in der Wiki hier nachgeschaut und danach wusste ich eben erstmal immner noch nicht ob das bei der Geschwindigkeit jetzt um eine Geschwindigkeit geht die minimal erreicht werden muss von jedem Objekt das die Erde verlassen will oder nicht (jedenfalls wenn die englische Wiki da recht hat - sicher bin ich mir immer noch nicht). Und ja - es geht mir wohl so wie ich es inzwischen verstehe wohl eher um die 2.KG, nicht um die erste, bin also im falschen Diskussionsabschnitt und hätte das alles unter Fluchtgeschwindigkeit posten sollen, 'tschuldige :-( --Michael Zeilfelder 22:56, 30. Mär. 2010 (CEST)
- Es steht zwar geschrieben, dass die 1. KG für die Oberfläche gilt, und dass die notwendige Bahngeschwindigkeit in üblichen Höhen geringer ist, aber das war wohl nicht deutlich genug. Ich habe das jetzt etwas geändert. Ist es beim Lesen jetzt klarer, worum es geht? Woran könnte ein Leser noch stolpern? Den englischen Absatz halte ich trotzdem für verwirrend bis falsch. Hast Du verstanden, warum da plötzlich vom Baryzentrum die Rede ist? Das macht die Sache doch erst recht kompliziert. (Und Du meinst, _ich_ denke kompliziert? ;-) --Asdert 16:42, 30. Mär. 2010 (CEST)
- Ich glaube du denkst zu kompliziert. Du weisst schon _was_ eine kosmische Fluchtgeschwindigkeit ist. Ich kam her um das erst herauszufinden. Ich wusste nicht ob das eine Geschwindigkeit ist die Raketen irgenwann mal überschreiten müssen aus irgendeinem Grund um die Erde verlassen zu können oder ob das eine Geschwindigkeit ist die wenn sie einmal erreicht ist genügend um die Erde zu verlassen (bzw. um eine der anderen kosmischen Schwellen zu überschreiten). Also wenn ich z.B. vor dir davonlaufe - dann brauche ich eine Geschwindigkeit die garantiert höher ist als deine. Wenn ich dagegen einfach nur aus deiner Reichweite kommen will während du dich nicht bewegst dann genügt mir ein Sprung der mich weit genug trägt. Was genau eine kosmische Geschwindigkeit ist hatte ich aus dem deutschen Artikel jetzt nicht herauslesen können. Der misconception Abschnitt in der Englischen sagt dagegen ziemlich deutlich dass es hier nicht um eine Geschwindigkeit geht die Raketen je erreichen müssen - was genau meine ursprüngliche Frage war.--Michael Zeilfelder 14:36, 30. Mär. 2010 (CEST)
- Ich halte den englischen Abschnitt en:Escape_velocity#Misconception eher für verwirrend als dass er wirklich Missverständnisse ausräumt. Ich bin mir auch nicht sicher, was wirklich Deine Frage ist. Einerseits sprichst Du von "um nicht zurückzufallen", was auf die 1. Kosmische Geschwindigkeit (KG) hinweist, andererseits sprichst Du von "Orbit verlassen", was auf die 2. KG hinweist. Vielleicht bleiben wir bei der 1. KG. Die Formel lautet:
- Also ich habe es mit dem momentanen Artikel auch nicht verstanden und dann nochmal die englische Wiki gelesen in der es einen extra Abschnitt für Missverständnisse gibt. Und wenn der stimmt dann bedeutet das - Fluchtgeschwindigkeit heisst, dass sobald die Fluchtgeschwindkeit erreicht ist (und der Luftwiderstand vernachlässigt wird) das Objekt ausreichend schnell ist um nicht zurückzufallen ohne dass es weiteren Schub benötigt. Also wie in einer Kanone. Wenn man dagegen konstanten Schub hat kann man den Orbit mit jeder beliebigen Geschwindigkeit verlassen. Das war ehrlich gesagt auch die Frage die mich interessiert hatte als ich den Artikel hier gelesen hatte und ich würde das auch gerne deutlicher erklärt sehen. Allerdings ist meine einzige Quelle die englische Wiki und ich weiss nicht sicher genug ob das jetzt auch so stimmt als dass ich mir zutrauen würde den Artikel hier zu überarbeiten. --Michael Zeilfelder 00:36, 30. Mär. 2010 (CEST)
die 2.KG heißt auch entweich- oder fluchtgeschwindigkeit. mit 11,2km/s müsste eine kanonenkugel von der nicht rotierenden, athmosphärenfreien erdoberfläche abgeschossen werden, um das schwerefeld der erde zu überwinden. diese 11,2km/s vermindern sich freilich ständig durch den erreichten höhengewinn der kanonenkugel. beim start einer rakete wird 11,2km/s auch für planetenmissionen nie erreicht, der sofortige "langsame" höhengewinn bewirkt ein ständige verringerung der örtlichen fluchtgeschwindigkeit (in einer höhe von 236km beträgt sie z.b. noch 11km/s).raketenantriebe deffiniert man auch über ihr antriebsvermögen in km/s; also jene geschw. die sie außerhalb jedes schwerefeldes im vakuum erreichen würden.
- die fluchtgeschw. der erde bewirkt wohl auch, daß jeder aus den weiten des sonnensystems kommende meteor die erdathmosphäre mit mindestens 11km/s trifft.--Dermauser 20:47, 1. Jan. 2011 (CET)
Fluchtgeschwindigkeit
[Quelltext bearbeiten]ETWAS WICHTIGES - meiner bescheidenen Meinung nach - noch zum Begriff "Fluchtgeschwindigkeit": diese Bezeichnung gilt nur für einen "ballistischen Flug" ins All, also - wie bei den Apollo-Flügen - mit anfangs starkem Beschleunigen und danach - von Kurskorrekturen abgesehen - antriebslosem Weiterflug bis zum Abbremsen oder Einschwenken in eine Mondumlaufbahn. Man könnte theoretisch auch auf einer Strickleiter auf den Mond klettern, so es eine Strickleiter gäbe, man muss also nicht unbedingt 40.000 km/h erreichen. Leider hat noch niemand ein Raketentriebwerk erfunden welches über längere Zeit ausreichend Schub entwickeln kann, sobald es sowas gibt kann man gemächlicher zum Mond reisen (z.B. ständig mit 800 km/h wie ein Verkehrsflugzeug) und - was noch besser wäre - auch gemächlicher zurückfliegen ohne durch die Luftreibung beim Wiedereintritt großen temperaturbedingten Gefahren ausgesetzt zu sein...
Mit freundlichen Grüßen A.M. (nicht signierter Beitrag von 84.115.79.189 (Diskussion | Beiträge) 10:32, 20. Jul 2009 (CEST))
- Hallo A.M.! Diesen Beitrag hast Du auch in Diskussion:Apollo-Programm gemacht. Ich antworte nur hier (und zwar immer unten an der Seite). Ja, Du hast Recht, die Fluchtgeschwindigkeit geht davon aus, dass die Geschwindigkeit plötzlich "da" ist. Das ist eine Vereinfachung, die in der Physik oft gilt, z.B. beim senkrechten oder schiefen Wurf. Es geht dabei immer um eine antriebslose Bewegung. Deiner Meinung, dass noch niemand ein "Raketentriebwerk erfunden welches über längere Zeit ausreichend Schub entwickeln kann" muss ich widersprechen. Den Ionenantrieb gibt es bereits, und mit sieben Wochen Reisedauer zum Mond war SMART-1 auch ziemlich gemächlich. Da die Sonde dabei weiterhin angetrieben wird, gelten die Formeln für die Fluchtgeschwindigkeit nicht (gilt strenggenommen für Mondflüge sowieso nicht, wegen Dreikörperproblem). Den Ionenantrieb kann man aber nicht zum Start verwenden, erst außerhalb der Atmosphäre. --Asdert 11:05, 20. Jul. 2009 (CEST)
- Vielen Dank für deine Erläuterungen! Hab schon mal gelesen vom Ionenantrieb, aber funktioniert dieser wirklich gleich außerhalb der Athmosphäre in ausreichender Stärke (die Gravitation nimmt schließlich nur alle Erdradien um die Hälfte ab)? LG - A.M. P.S.: bist du zufällig via E-Mail erreichbar?*** (nicht signierter Beitrag von 84.115.79.189 (Diskussion | Beiträge) 21:03, 20. Jul 2009 (CEST))
- A.M., erst einmal ein paar technische Tipps zur Wikipedia. Signieren und datieren kannst Du Deine Beiträge mit zwei Bindestrichen und vier Tilden
--~~~~. Dann muss das der Bot nicht nachtragen („nicht signierter Beitrag ...“). Noch besser ist, wenn Du Dich mit einem Benutzername anmeldest. Das bleibt aber Dir überlassen. Und Beiträge einrücken, das geht mit Doppelpunkten am Zeilenanfang, ich habe Deinem Beitrag zwei Doppelpunkte verpasst (da waren drei Sterne, das gab unschöne Klötzchen), mein jetziger hat drei Doppelpunkte, damit ist er weiter eingedrückt, und man kann besser lesen, was nun von wem stammt. E-Mail-Empfang hab ich üblicherweise aus, man kann mir gerne auf die Diskussionsseite schreiben. Ausnahmsweise habe ich den Mailempfang gerade aktiviert, falls Dir der Kontakt per Mail lieber ist. Und der Ionenantrieb funktioniert tatsächlich. Man muss aber mit konventionellem Antrieb in eine Erdumlaufbahn kommen. Anschließend kann man den Ionenantrieb verwenden, um die Bahn zu korrigieren oder aber um sie ganz langsam anzuheben. Auf die Weise kann man sich bis zum Mond hochschrauben. Zwei Links habe ich ja angegeben. Viele Grüße --Asdert 21:54, 20. Jul. 2009 (CEST)
- A.M., erst einmal ein paar technische Tipps zur Wikipedia. Signieren und datieren kannst Du Deine Beiträge mit zwei Bindestrichen und vier Tilden
- Vielen Dank für deine Erläuterungen! Hab schon mal gelesen vom Ionenantrieb, aber funktioniert dieser wirklich gleich außerhalb der Athmosphäre in ausreichender Stärke (die Gravitation nimmt schließlich nur alle Erdradien um die Hälfte ab)? LG - A.M. P.S.: bist du zufällig via E-Mail erreichbar?*** (nicht signierter Beitrag von 84.115.79.189 (Diskussion | Beiträge) 21:03, 20. Jul 2009 (CEST))
- Wie ist das dann bei einem Schwarzen Loch? Da heißt es ja immer, dies sei so definiert, dass die Fluchtgeschwindigkeit c beträgt. Aber wenn das nur für antriebslosen Flug gilt, könnte man dann auch mit geringerer Geschwindigkeit, aber stetigem Antrieb einem schwarzen Loch auch wieder entkommen, obwohl der Ereignishorizont schon überschritten wurde? --79.203.64.98 22:10, 14. Dez. 2018 (CET)
Anmerkung: KU
Bei der Fluchtgeschwindigkeit geht es darum die kinetische Energie und damit die Geschwindigkeit zu ermitteln die notwendig ist um einen Körper aus dem Gravitationsfeld eines anderen (zum Beispiel Rakete von der Erde) zu befördern.
Die Kraft ist gegeben durch
Die Beschleunigung ist hier eine Funktion von . Für die potentielle Energie ergibt sich daher (Energie ist Kraft mal Weg)
Gleichsetzen der Energien führt dann auf die angegebenen Formel und es erübrigt sich zu erörten auf welche Antriebsweise die Rakete aus dem Schwerefeld der Erde entkommen ist.
Wer hat's erfunden (berechnet)
[Quelltext bearbeiten]Es wäre informatif, wenn bei den allen 4 Kosmischen Geschwindigkeiten der jeweilige Erfinder/Endecket stehen würde. Ich kenne nur den Ary Abramovich Sternfeld, er hat die erste Kosmische Geschwindigkeit berechnet.
Fast jeder kennt die Formel E=mc² und weiß wer die endeckt hat oder wie auch immer man es nennen kann. Aber hier und auch in anderen Wikipedia-Artikeln steht nichts. Es gibt doch immer jemanden der die Formel als erstet berechent hat. 87.171.37.104 22:09, 3. Dez. 2014 (CET)
Herleitung der 3. kosmischen Geschwindigkeit
[Quelltext bearbeiten]In dem Abschnitt wird prinzipiell erklärt, wie man vorgeht, um auf diesen Wert zu kommen. Dann steht dort: "Dann braucht der Körper zusätzlich noch die Fluchtgeschwindigkeit der Erde." Der Leser geht wohl davon aus, dass man jetzt rechnen würde 12,3 km/s + 11,2 km/s. Allerdings werden ohne weitere Begründung die Quadrate der Geschwindigkeiten addiert und dann die Wurzel gezogen und niemand weiß warum... die erste Assoziation wird meist der Satz von Pytagroas sein.
In wirklichkeit kommt das wohl daher, dass in der Formel für die kinetische Energie das v quadratisch vorkommt und man kinetische Energie addiert und dann wieder auf v zurückrechnet. Meines Erachtens sollte man das anmerken, allerdings habe ich halt keine Quelle dafür.
(Außerdem habe im Absatz ein v3 durch ein v3' ersetzt, weil die Bennenung sonst inkonsistent ist.) --Myon12 (Diskussion) 18:43, 4. Mai 2015 (CEST)
- Wenn man erst aus dem Feld der Erde 'flieht' (auf einen Near-Earth-Orbit um die Sonne) und dann erneut zündet, dann addieren sich die Geschwindigkeiten linear. Wendet man dagegen alle Energie in der Nähe der Erdoberfläche auf, dann quadratisch. Die Herleitung ist so simpel, dass es keinen Beleg braucht (Superposition der Gravitationspotentiale von Erde und Sonne, dann E_kin = E_pot). --Rainald62 (Diskussion) 20:16, 4. Mai 2015 (CEST)
- Die Herleitung ist mir persönlich schon klar, es ist nur fraglich, ob der durchschnittliche Leser der Seite "Fluchtgeschwindigkeit" das auch so sieht. Wenn man eine Unfrage unter den Lesern dieses Abschnitts machen würde, wie groß wäre der Anteil der Leute, die meinen hier wurde der Satz des Pytagoras verwendet? Selbst wenn ich optimistisch bin, würde ich tippen, dass sich 30% gar nichts denken, 50% an Pytagoras denken und nur 20% an das korrekte. Das war mein Punkt. Daher die Frage ob und wie man das erwähnen sollte. --Myon12 (Diskussion) 20:47, 4. Mai 2015 (CEST)
- Na ja, die Beweisidee ist nicht nur angedeutet, sondern steht explizit da ("das gemeinsame Gravitationsfeld von Erde und Sonne", Betonung im Original). Zusammen mit "Bindungsenergie im Gravitationsfeld" über der Herleitung von v_2 sollte das für den durchschnittlichen Leser reichen. --Rainald62 (Diskussion) 21:18, 4. Mai 2015 (CEST)
- Ich finde halt, dass der Satz "Dann braucht der Körper zusätzlich noch die Fluchtgeschwindigkeit der Erde." eine normale Addition suggeriert. Wenn man dann die Formel mit der Wurzel sieht, könnte man verwirrt sein oder an eine vektorielle Addition (und somit an orthogonale Vektoren und Pytagoras) denken. Außerdem werden ja eigentlich nicht die Fluchtgeschwindigkeiten, sondern die Energien addiert. (Natürlich hat die E_kin einen Zusammenhang mit der Geschwindigkeit - aber dieser ist 1. nicht linear und somit komplizierter und 2. nicht direkt das, was man bei der Herleitung tut, wo man ja die Gravitationspotenzial addiert, welche doch "enger" mit der Energie zusammen hengen als mit der Gewindigkeit). Lange (und hoffentlich nicht allzu unterverständlich formulierte) Rede, kurzer Sinn: Soll man in einem Satz erwähnen, dass die Addition der Geschwindigkeitsquadrate und das anschließende Wurzelziehen daher kommt, dass man die kinetischen Energien addiert, die porportional zum Quadrat der Geschwindigkeit sind? --Myon12 (Diskussion) 21:57, 4. Mai 2015 (CEST)
- Ja, was sonst noch da stand, war verwirrend. Ich habe es samt sonstiger Theoriefindung gelöscht. Die Überarbeitung war ja eh nötig, s.o. --Rainald62 (Diskussion) 14:31, 5. Mai 2015 (CEST)
- Die Änderung an der 3. kosm Geschw. find ich gut, weil jetzt die Beweisidee unmissverständlich dahsteht und jeder der kann und will kann es nach v3=... umformen.
- Bezüglich der ehemals 4. kosmischen Geschwindigkeit hab ich einiges anzumerken.
- Das braucht eine extra Unterübschrift, sonst steht es unter 3. kosmischer Geschw, zB Fluchtgeschwindigkeit aus unserer Galaxie
- Die Formel muss ausgebessert werden, weil das immernoch v4 steht
Der letzt Satz ist falsch, weil . Das ist eben genau deshalb der Fall, weil es sich nicht um ein Zentralfeld handelt.Hab mich wiederholt verlesen und das "deutlich mehr als" überlesen. Tut mir leid! --Myon12 (Diskussion) 21:00, 5. Mai 2015 (CEST)- mE sollte die die Rechnung 533 km/s - 220 km/s wieder rein. Immerhin führt das zu einem öfters genannten Wert (zB: da und da -zwar nicht die renomiertesten Quellen, aber der Leser könnte fragen, warum steht das was anderes als in Wikipedia und die Erklärung ist recht einfach; bei der 3. kosm Geschw wurde entsprechend auch die Rotationsgeschwindigkeit der Erde um die Sonne abgezogen)
- Ich persönlich finde es gut, dass es nicht mehr unter der Überschrift 4. kosm Geschw steht, es ist vlt überlegenswert, ob man hinschreiben sollte, dass es zeitweise so bezeichnet wird (siehe dieses hässliche Preview des Tipler)
- Bezüglich der ehemals 4. kosmischen Geschwindigkeit hab ich einiges anzumerken.
- Ich erledige mal die Punkte 1. und 2. Für den Recht warte ich mal eine Antwort ab --Myon12 (Diskussion) 17:49, 5. Mai 2015 (CEST)
- Warum hast du eigentlich meine vorherige Änderung teilrevertiert? In der Zusammenfassungszeile steht ein Verweis auf die Diskussionsseite, hier steht aber nichts dazu. --Myon12 (Diskussion) 00:01, 6. Mai 2015 (CEST)
- Sorry für die späte Antwort, das RL kam dazwischen.
- Zu 1.) Es steht schon mit Bedacht ohne eigene Überschrift, denn es geht um eine Einschränkung der Anwendung der im gleichen Kapitel hergeleiteten Formel (vgl. Apollo weiter oben).
- Zu 2.) Danke
- Zu 4.) Der Vergleich mit v_3 hinkt: Raumsonden ohne Swing-By aus dem Sonnensystem zu schießen ist eine realistische Option; Raumsonden aus der Galaxis zu schießen ist völlig sinnlos. v_4 ist nicht relevanter als v_Esc von jeder anderen Stelle aus und mit jeder anderen Startgeschwindigkeit. Daher findet man v_4 auch nicht in seriösen Quellen.
- Zu 5.) Tipler gibt, soweit man das hässliche Preview lesen kann, nicht die Differenz an (und ist bezgl. der Physik an dieser Stelle nicht seriöser als das berühmte Milchmädchen). --Rainald62 (Diskussion) 00:30, 6. Mai 2015 (CEST)
- Zu 1) Meine Unterüberschrift war gleichrangig mit "=== Dritte kosmische Geschwindigkeit ===" um es von diesem Absatz zu trennen. Es ist hierachisch eins unter der Überschrift "== Fluchtgeschwindigkeit ==" und war damit dem Abschnitt, wo die Formel hergeleietet wurde, immernoch untergeordnet. Wäre meine Überschrift "== Fluchtgeschwindigkeit aus unserer Galaxie ==" gewesen und nicht "=== Fluchtgeschwindigkeit aus unserer Galaxie ===" , würde ich den Einwand teilen.
- Zu 4) macht Sinn, man muss nicht auf alles eingehen, was an utopischen Überlegungen herumgeistert.
- Zu 5) Ja, stimmt solange man nichteinmal seriös weiß, ob v4 jetzt mit oder ohne Swing-by angeben wird, ist nicht einmal ein Hinweis im Nebensatz sinnvoll. --Myon12 (Diskussion) 15:13, 6. Mai 2015 (CEST)
- Zu 1.) Die Überschrift ist zweitrangig, mir fehlt das Motiv für eine Abtrennung (ohne nennenswerten Inhalt keine Überschrift). Nennenswert wäre, die Fluchtgeschwindigkeit für eine allgemeine Massenverteilung (Dichte gegen null für r gegen unendlich) hinzuschreiben, aber das ist i.W. das Gravitationspotential und gehört imho unter Gravitationspotential. --Rainald62 (Diskussion) 17:01, 6. Mai 2015 (CEST)
- ja, aber es gehört eben nicht zur Unterüberschrift "3. kosmische Geschwindigkeit". Das ist imho das Problem. Ohne Unterüberschrift wird suggeriert, dass es irgendetwas mit der 3. kosmischen Geschwindigkeit zu tun hat, was es aber nicht hat (zumindest nicht mehr als mit jeder beliebigen anderen Fluchtgeschwindigkeit) Soll heißen: Wenn keine anderen Unterüberschriften dazwischen wären, hätte ich dem nie eine Unterüberschrift gegeben, aber so ist eine Abtrennung notwendig (oder ein Verschieben vor die anderen Unterüberschriften, was ich aber wg der vergleichsweise geringen Wichtigkeit eher nicht tun würde) --Myon12 (Diskussion) 17:28, 6. Mai 2015 (CEST)
- Erstmaliges Vorkommen bei der 3. kosmischen Geschwindigkeit: Gravitationspotential ist eine Summe, Bahnradius als Startabstand. So fremd sind die zwei Zeilen also nicht in diesem Kapitel. --Rainald62 (Diskussion) 21:15, 7. Mai 2015 (CEST)
- ja, aber es gehört eben nicht zur Unterüberschrift "3. kosmische Geschwindigkeit". Das ist imho das Problem. Ohne Unterüberschrift wird suggeriert, dass es irgendetwas mit der 3. kosmischen Geschwindigkeit zu tun hat, was es aber nicht hat (zumindest nicht mehr als mit jeder beliebigen anderen Fluchtgeschwindigkeit) Soll heißen: Wenn keine anderen Unterüberschriften dazwischen wären, hätte ich dem nie eine Unterüberschrift gegeben, aber so ist eine Abtrennung notwendig (oder ein Verschieben vor die anderen Unterüberschriften, was ich aber wg der vergleichsweise geringen Wichtigkeit eher nicht tun würde) --Myon12 (Diskussion) 17:28, 6. Mai 2015 (CEST)
- Mit der neuen Überleitung ist es besser. Davor hat man sich gefragt, warum das da steht, und es hat irgendwie unter dieser Überschrift verloren gewirkt. Durch die Umformulierung ist es besser, weil auf den Gegensatz mehr eingegangen wird und dieser ist ja die Rechtfertigung, warum es überhaupt unter der selben Überschrift stehen kann. Dennoch wäre ich eher für eine eigene Unterüberschrift, weil der Gegensatz (kein Zentralfeld mehr) eigentlich für alle bisherigen Berechnungen in diesem Artikel gilt, weil sie alle ein Zentralfeld vorraussetzen. Aber ich kann damit leben. --Myon12 (Diskussion) 23:41, 7. Mai 2015 (CEST)
- Das gemeinsame Feld von Erde und Sonne ist kein Zentralfeld. --Rainald62 (Diskussion) 11:41, 8. Mai 2015 (CEST)
- ja, das ist natürlich völliger Schwachsinn. Das ist in einer unkonzentrierten, überschießenden Einkürzungaktion beim Verfassen dieser Antwort der Plural verloren gegangen. Worauf ich hinaus wollte: Im Fall von Erde und Sonne ist es eine Summe aus Zentralfeldern (idF 2). Man rechnet also mit 2 Punktmassen. Im Fall der Galaxie ist das nicht möglich, weil man 1. etwa 1011 (geschätzte Anzahl der Sterne) Zentralfelder überlagern müsste (viele Spaß beim Rechnen....) und 2. die Daten (Position, Masse aller Sterne in der Galaxie) nicht bekannt sind. Daher wird nich mehr mit einer endlichen Anzahl an Punktmassen, sondern mit einer Massenverteilung gerechnet. --Myon12 (Diskussion) 12:11, 8. Mai 2015 (CEST)
- ...ganz abgesehen von der Dunklen Materie, die den größten Anteil hat und deren Verteilung aller Wahrscheinlichkeit nach auf deutlich kleineren Skalen glatt ist als die von Sternen, Staub und Gas. Aber der Übergang von 1 auf 2 ist im Verständnis sicher ebenso schwierig, siehe oben, wie von 2 auf einige 1000 als Punktmassen angesetzte Volumenelemente (mehr sind angesichts der Unsicherheit der Masseverteilung nicht nötig). Den Übergang von Summe auf Integral muss man dem Leser nicht in jedem Artikel erläutern, wo das tangiert wird, imho. Leser, die damit etwas anfangen können, sind womöglich schon im ersten Satz der Einleitung dem Link auf das Potential gefolgt. --Rainald62 (Diskussion) 13:11, 8. Mai 2015 (CEST)
- Ich bin auch nicht der Meinung, dass es erwähnt werden soll, ich habe nur einen Grund genannt, warum ich gemeint habe, dass es eine Unterüberschrift braucht. Eben weil die beiden Tatsachen (kein Feld, das ein Zentralfeld ist oder durch Überlagerung einer geringen Anzahl dieser entstht; Dunkle Materie) Gegensätze zu allen vorherigen Berechnungen sind und nicht nur zur Berechnung von v3, weshalb ich dem halt eine eigene Unterüberschrift gegeben hätte. Aber wie ich vorher erwähnt habe, ich kann mit der jetztigen Lösung wegen der Umformulierung, die das etwas stimmiger macht, durchaus leben. --Myon12 (Diskussion) 18:21, 8. Mai 2015 (CEST)
Dann können wir uns ja jetzt eine geeignete Überschrift suchen (das war zweitrangig). --Rainald62 (Diskussion) 22:33, 8. Mai 2015 (CEST)
- Eine Möglichkeit wäre "Fluchtgeschwindigkeit aus unserer Galaxie" oder für den Fall, dass man es weniger an der Zahl selbst festmachen will, könnte man in die Richtug "Grenzen dieser Berechnungen" gehen. --Myon12 (Diskussion) 22:53, 8. Mai 2015 (CEST)
- Ich dachte an eine Überschrift anstelle der 3.kG --Rainald62 (Diskussion) 22:57, 8. Mai 2015 (CEST)
- Achso, ich hatte mich eh gewundert, warum doch eine Überschrift, weil wir uns zuerst darauf geeinigt hatten, keine zu setzen. Ich habe mir jetzt nocheinmal die TOC des Artikels angesehen. Das einzige, was noch der Nominklatur v1, v2, v3, (v4) folgt ist dieser Abschnitt. Folglich: Er braucht eine neue Überschrift, das wirkt sonst komisch. Vorschlag: "Fluchtgeschwindigkeit aus unseren Sonnensystem", wobei das uU aufgrund des in v3 eingerechten Swing-By-Effektes (der ja in der bloßen Fluchtgeschwindigkeit nicht dabei ist) problematisch sein könnte.
- Jetzt, wo die kosmischen Geschwindigkeiten so in den Hintergrund treten (was mich persönlich ehrlich gesagt nicht sehr stört, weil es mich nervt, dass man für alles und jedes einen Begriff dazu lernen muss, wo man keinen weiteren braucht) sollte man wegen der hohen Präsenz (zB im Schulunterricht) in Betracht ziehen, Seiten mit entsprechen Redirects einzurichten. --Myon12 (Diskussion) 23:15, 8. Mai 2015 (CEST)
- Swing-by ist etwas anderes (ich hatte mich oben schon gewundert, wie du v4 damit in Verbindung bringst).
- Für die Überschrift dachte ich an etwas wie die Multiple sources im engl. Artikel.
- Apropos "TOC des Artikels": Die Überschrift "Geometrische Bedeutung" ist auch verzichtbar (der Inhalt gehört stark gekürzt und mit Link auf Kepler-Bahn vor die Formeln). --Rainald62 (Diskussion) 00:02, 9. Mai 2015 (CEST)
- Was Swing-by ist, ist mir eigentlich klar, warum ich begonnen habe, diesen Begriff hier über lange Zeit hinweg konsquent falsch zu verwenden und das nicht zu bermerken, allerdings nicht. Danke für den Hinweis! Das ist schon ziemlich peinlich, wie oft ich diesen Begriff falsch verwendet habe. Aber beides nutzt halt die Bahngeschwindigkeit des Planeten, daher kommt die Assoziation vermutlich.
- Für die Überschrift denk ich mal nach, da fällt mir spontan nichts wirklich gutes ein. Vielleicht: "Fluchtgeschwindigkeit von verschiedenen Objekten"
- Bei der geometrischen Bedeutung stimme ich zu.
- Wenn wir schon bei Überschriften, Titeln usw. sind: Der Titel "Fluchtgeschwindigkeit (Raumfahrt)" passt mit fortschreitender Entfernung der kosmischen Geschwindigkeiten immer weniger; auch wenn mir bewusst ist, dass es wegen der Begriffserklärung nötig ist. Aber ich würde mal anmerken, dass diese BKS eher unnötig ist. Natürlich spricht man von "Galaxienflucht", aber warum das unter Fluchtgeschwindigkeit stehen muss (zumal es auch keine Geschwindigkeit im Raum, sondern eine Ausdehnung des Raumes ist, die die kosmische Rotverschiebung verursacht) ist mir nicht ganz klar. --Myon12 (Diskussion) 00:28, 9. Mai 2015 (CEST)
- da diese Diskussion "eingeschlafen" scheint, melde ich mich mal wieder. Damit auch was inhaltiches dabei ist: bzgl der Überschrift könnte man auch "Fluchtgeschwindigkeit aus verschiedenen Gravitationsfeldern", "Fluchtgeschwindigkeit aus den Gravitationsfeldern verschiedener Objekte" oder "weitere Fluchtgeschwindigkeiten" nehmen. Oder die sehr sperrige sperrige Version aus der ne-Wiki, die auf Deutsch heißt: "Fluchtgeschwindigkeit von einem nicht-kugelsymmetrischen Himmelskörper oder einer Kombination von Himmelskörpern" (leicht verändert, weil "statisch" für den Absatz nicht passt). --Myon12 (Diskussion) 16:31, 13. Mai 2015 (CEST)
- Wenn du nichts dagegen sagst, würde ich die Überschrift jetzt auf "Fluchtgeschwindigkeiten von weiteren Objekten" ändern. --Myon12 (Diskussion) 20:15, 14. Mai 2015 (CEST)
- "Objekte" ist kaum besser als "Dings". Wie wäre es mit "...von verteilten Massen"? --Rainald62 (Diskussion) 02:24, 15. Mai 2015 (CEST)
- Deshalb Objekt: Astronomisches Objekt. (ist halt der beste Überbegriff, den ich gefunden habe) Verteilte Masse passt zwar für die Galaxie, aber für v3 klingst mE schon komisch, weil das ist nicht sehr viel verteilt (fast die gesammte Masse entfällt auf ein Objekt, die Sonne; ein kleiner -fast vernachlässigbarer- Bruchteil auf die Planten, nur sind wir halt einen dieser Planeten, der Erde, so nahe, dass man dessen Einfluss nicht vernachlässigen kann) --Myon12 (Diskussion) 10:43, 15. Mai 2015 (CEST)
- Ich habe jetzt 2 Argumente gebracht, warum "Fluchtgeschwindigkeiten von weiteren Objekten" mE besser ist. Wenn kein weiteres Gegenargument kommt, nenn ich das so. --Myon12 (Diskussion) 00:08, 17. Mai 2015 (CEST)
- Ist mir nicht so wichtig. --Rainald62 (Diskussion) 00:45, 17. Mai 2015 (CEST)
- Ich habe jetzt 2 Argumente gebracht, warum "Fluchtgeschwindigkeiten von weiteren Objekten" mE besser ist. Wenn kein weiteres Gegenargument kommt, nenn ich das so. --Myon12 (Diskussion) 00:08, 17. Mai 2015 (CEST)
Dann hab ich das mal gemacht.--Myon12 (Diskussion) 01:09, 17. Mai 2015 (CEST)
BKS
[Quelltext bearbeiten]Was hälst du von der Begriffserklärungsseite Fluchtgeschwindigkeit bzgl meiner oben genannten Einwände? Und hällst du einen Redirekt von kosmische Geschwindigkeit auf Fluchtgeschwindigkeit für sinnvoll? (Ich glaube nähmlich, dass man bei der Suche "kosmische Geschwindigkeit" in Google (und anderen SM), nachdem sich das Entfernen der letzten Überschrift, wo "kosmische Geschwindigkeit" vorkommt, bis ins Google-Index "herumgesprochen" hat, diese WP-Seite kaum noch finden wird) --Myon12 (Diskussion) 01:09, 17. Mai 2015 (CEST)
- Ich habe mal eine neue Überschrift spendiert. Nur eine, denn die Weiterleitung Kosmische Geschwindigkeit existiert ja seit der Verschiebung (mit dem passenden Linkziel – oder habe ich dich falsch verstanden?).
- Die Regel bezüglich BKS oder BKH lautet, dass ein BKH nur angemessen ist, wenn es eine klar dominierende Hauptbedeutung gibt. Meine Literaturrecherche vor der Verschiebungsaktion ergab unerwartet viele Treffer für die Galaxienflucht, > 10 %, sonst hätte ich das gleich in deinem Sinne gemacht. --Rainald62 (Diskussion) 01:51, 17. Mai 2015 (CEST)
- Ok. Einverstanden. Das ein Redirekt seiter der Verschiebung eh schon existiert, wusste ich nicht. Es ist also schon so wie ich es gemacht hätte. (komischerweise wird der Redirekt halt nicht von Suchmaschienen gefunden...aber das soll nicht unser Problem sein, vielleicht wird er auch gefunden, die Überschrift 3 kosm Geschwindigkeit nichtmehr dafür sorgt, dass diese Seite in SM ganz oben ist). Wenn eine Recherche deinerseits ergeben hat, dass eine BKS nötig, dann bleibt sie natürlich. (auch wenn ich den Begriff Fluchtgeschwindigkeit im Kontext von Galaxien nicht sehr schätze, aber ein WP-Artikel ist nicht der Ort diese Vorliebe "durchzustetzen")--Myon12 (Diskussion) 15:51, 17. Mai 2015 (CEST)
3. kosmische Geschwindigkeit (noch einmal)
[Quelltext bearbeiten]Der im Artikel stehende Ausdruck für v3 wird zwar scheinbar einleuchtend begründet, ich halte ihn aber dennoch für falsch. Und er liefert auch nicht "16,7 km/s", sondern 13,8 km/s. Der Fehler scheint mir darin zu liegen, dass einfach die potentiellen Energien im Gravitationsfeld der Erde bzw. der Sonne addiert werden. Der Nullpunkt dieser Energien ist aber "Körper ruht in sehr großer Entfernung von der Erde" bzw. "… von der Sonne", was gleichzeitig natürlich nicht möglich ist. Die korrekte Herleitung findet sich z. B. in Messerschmid & Fasoulas, Raumfahrtsysteme. Die Grundidee dabei ist, dass der Körper nach Verlassen des Schwerefeldes der Erde noch eine genügend große hyperbolische Exzessgeschwindigkeit besitzt, um auch das Schwerefeld der Sonne zu verlassen. Das Ergebnis ist dann, bei Ausnutzung der Bahngeschwindigkeit der Ede, 16,6 km/s. Wenn sich keine ernsthaften Gegenargumente finden, werde ich das entsprechend in den nächsten Tagen in den Artikel einarbeiten. --PaulSch (Diskussion) 17:42, 11. Dez. 2015 (CET)
- Im Wesentlichen richtig. Bloß hast Du meinen Fehler an der falschen Stelle vermutet. Nicht nicht, sondern nur gleichzeitig kann der Körper sehr weit von Erde und Sonne entfernt sein (und Gravitationspotentiale sind additiv). Die Formel im Artikel und deren zu kleines Ergebnis stimmen für den ziemlich ungesunden Fall, dass die Erde unmittelbar nach dem Abschuss der Testmasse ihre Bahnbewegung einstellt. Mit ihrer Bewegung hinter der Testmasse her, bremst sie diese länger. --Rainald62 (Diskussion) 23:55, 11. Dez. 2015 (CET)
- Meine Begründung für den Fehler war: Der Körper kann nicht gleichzeitig bzgl. Erde und Sonne ruhen kann. Deine Formulierung "… bremst sie diese länger" finde ich aber besser.--PaulSch (Diskussion) 08:25, 12. Dez. 2015 (CET)
Revert eine Linkfix'
[Quelltext bearbeiten]Hallo, Rainald62. Du hast meine Korrektur eines Links auf die LEIFI-Website revertiert, Begründung: "keine Verbesserung". Der originale und nun wieder aktuelle Link zeigt auf einen Anker "#Kosmische%20Geschwindigkeiten" auf der Seite "Gravitationsgesetz und -feld". Diesen Anker gibt es nicht mehr, der Nutzer landet am Anfang der Gravitationsseite. Der relevante Unterpunkt zu kosmischen Geschwindigkeiten findet sich nun auf der Unterseite "/kosmische-geschwindigkeiten". Meine Korrektur hat diese Änderung auf der Website nachvollzogen. Sicher keine große Sache, aber doch nichts, was revertiert gehört, oder? Ich fände es schön, wenn Du Dein Revert revertiertest.--PaulSch (Diskussion) 08:35, 12. Dez. 2015 (CET)
- Hallo PaulSch. Ich lande mit deinem Link ebenfalls oben auf der Seite (mit aktuellem Firefox, aber ich denke nicht, dass das vom Browser abhängig ist). --Rainald62 (Diskussion) 02:10, 13. Dez. 2015 (CET)
- Hallo, Rainald62. Wenn ich keinen Unterschied sehen würde, hätte ich (Firefox 42) nichts geändert.
- Originaler/aktueller Link:
- Fenstertitel und in Tab-Leiste "Gravitationsgesetz und -feld …", Scrollbalken kurz;
- Seitenaufbau dauert eine Ewigkeit ("Typesetting math: 37%", …), ich habe ältere Hardware;
- Seitenkopf, Inhaltsverzeichnis;
- Inhalt zu "Das Gravitationsgesetz von NEWTON", "Das 1 durch r-Quadrat-Gesetz", … "Kosmische Geschwindigkeiten", …
- Mein Vorschlag als Link (ich habe ihn aus dem Inhaltsverzeichnis):
- Fenstertitel und in Tab-Leiste "Kosmische Geschwindigkeiten …", Scrollbalken lang;
- Seitenaufbau akzeptabel;
- Seitenkopf, Inhaltsverzeichnis (wie oben);
- Inhalt zu "Kosmische Geschwindigkeiten".
- Ich halte die Unterschiede weiter für markant. Jedenfalls ist meine Änderung doch wohl kein offensichtlicher Vandalismus, der ein revert rechtfertigen würde.--PaulSch (Diskussion) 11:48, 13. Dez. 2015 (CET)
Kreisbahngeschwindigkeit in der allgemeinen Relativitätstheorie
[Quelltext bearbeiten]Guten Abend liebes Forum,
ich habe für die Formel zur Berechnung der Kreisbahngeschwindigkeit in der allgemeinen Relativitätstheorie eine Vereinfachung gefunden, die man eventuell in den Artikel einfügen könnte, da man die Berechnung schneller durchführen kann. Die Herleitung habe ich durch Zufall gefunden als ich die gültige Formel nach umgestellt habe und dann anschließend wieder nach umformte.
Gültige Formel
[Quelltext bearbeiten]Umstellung nach
[Quelltext bearbeiten]Zunächst quadrieren, um die Wurzeln weg zu bekommen:
Anschließend mit multiplizieren:
Ausmultiplizieren:
Mit multiplizieren, um die Brüche weg zu bekommen:
Nun addiert man :
Division durch , Umgestellte Formel nach :
Anschließende Umstellung nach
[Quelltext bearbeiten]Mit multiplizieren:
Mit subtrahieren:
Ausklammern von :
Durch dividieren:
Wurzel ziehen, Umgestellte Formel nach :
Falls jemand einen Fehler bei der Umstellung entdeckt, dann möge er mich bitte korrigieren. Jedoch habe ich durch Rechnung herausgefunden, dass die beiden Formeln auf dieselbe Kreisbahngeschwindigkeit kommen. Theoretisch nimmt man auch meistens die vereinfachte Formel, da sie schneller zu handhaben ist. Außer die Wissenschaft mag die längere Variante. Oder es gibt hier gewisse Formalitäten, die ich als "einfacher" Hobby-Mathematiker nicht kenne ;)
Mit freundlichen Grüßen --79.249.119.254 21:30, 28. Jul. 2016 (CEST)
Sonne im Erdabstand
[Quelltext bearbeiten]In der Tabelle "Fluchtgeschwindigkeiten an der Oberfläche" ist eine Zeile mit "Sonne im Erdabstand" und Wert 42.0 - da ist mir nicht klar wie das gemeint ist bzw. warum der Wert über V3=16.6 km/s (zum Verlassen von Sonne UND Erde) liegt. Ich denke dass wir das entweder genauer erläutern sollten oder die Zeile rausnehmen. -- Gerd Fahrenhorst (Diskussion) 10:29, 10. Mai 2020 (CEST)
- Die mittlere Orbitalgeschwindigkeit der Erde beträgt 29,78 Kilometer pro Sekunde. Multipliziert mit 1,4142, der Wurzel von 2, ergibt sich eine Fluchtgeschwindigkeit, bei Stillstand im leeren Weltraum, im Abstand des mittleren Erdbahnradius von der Sonne, von 42,1152 Kilometern pro Sekunde. -- Karl Bednarik (Diskussion) 08:50, 11. Mai 2020 (CEST).
- Wenn man sich bereits, mit der mittleren Orbitalgeschwindigkeit der Erde, im leeren Weltraum, im Abstand des mittleren Erdbahnradius von der Sonne, bewegt, dann genügen noch zusätzlich 12,335 Kilometer pro Sekunde. Andererseits benötigt man noch die Fluchtgeschwindigkeit der Erde zusätzlich, um von ihr weg zu kommen. -- Karl Bednarik (Diskussion) 09:25, 11. Mai 2020 (CEST).
- Danke für die Erläuterungen! Die Tabellenüberschrift ist "Fluchtgeschwindigkeiten an der Oberfläche", da passt das m.E. nicht rein, und dass das im Stillstand gemeint ist wird auch nicht klar (ich gehe davon aus dass in den anderen Zeilen die Eigenrotation eingerechnet ist?). Vielleicht doch besser diese Zeile rausnehmen? -- Gerd Fahrenhorst (Diskussion) 14:38, 14. Mai 2020 (CEST)
- Ich habe versuchsweise Sonne, im Erdabstand ruhend eingefügt. Die Rotationen der Objekte und die Unterschiede zwischen den Polarradien und den Äquatorradien der Objekte werden oftmals nicht berücksichtigt. -- Karl Bednarik (Diskussion) 09:10, 15. Mai 2020 (CEST).
- Ja danke, das ist schon besser. -- 12:53, 15. Mai 2020 (CEST) (unvollständig signierter Beitrag von Gerd Fahrenhorst (Diskussion | Beiträge) )
- @Karl Bednarik: Von der Intention her ist das richtig, aber: das steht unter der Spaltenüberschrift "Himmelskörper", und das "ruhend" klingt jetzt so, als handele es sich um eine "im Erdabstand ruhende Sonne" (was auch immer das sein soll...). Auch ist "ruhend" eine merkwürdige Bezeichnung, für einen Satelliten, der dann mit 24 km/s weiterfliegen soll
 . Das verwirrt daher m.E. mehr, als das es hilft.
. Das verwirrt daher m.E. mehr, als das es hilft. - Ich würde daher das "ruhend" durch eine Anmerkung ersetzen, die auf den entsprechenden Abschnitt Fluchtgeschwindigkeit (Raumfahrt)#Fluchtgeschwindigkeiten von weiteren Objekten verweist, wo das ja eigentlich bereits erklärt wird.
- Darüberhinaus korrigiere ich die beiden Rundungsfehler in der Tabelle (617,388 ist 617,4; und auch bei einem gerundeten Wert von 150 Mio km für den Erdabstand ergibt sich ein Wert von 42,065, was zu 42,1 gerundet werden sollte, wie auch im zitierten Abschnitt). --Dogbert66 (Diskussion) 14:07, 15. Mai 2020 (CEST)
- @Karl Bednarik: Von der Intention her ist das richtig, aber: das steht unter der Spaltenüberschrift "Himmelskörper", und das "ruhend" klingt jetzt so, als handele es sich um eine "im Erdabstand ruhende Sonne" (was auch immer das sein soll...). Auch ist "ruhend" eine merkwürdige Bezeichnung, für einen Satelliten, der dann mit 24 km/s weiterfliegen soll
- Ja danke, das ist schon besser. -- 12:53, 15. Mai 2020 (CEST) (unvollständig signierter Beitrag von Gerd Fahrenhorst (Diskussion | Beiträge) )
- Ich habe versuchsweise Sonne, im Erdabstand ruhend eingefügt. Die Rotationen der Objekte und die Unterschiede zwischen den Polarradien und den Äquatorradien der Objekte werden oftmals nicht berücksichtigt. -- Karl Bednarik (Diskussion) 09:10, 15. Mai 2020 (CEST).
- Danke für die Erläuterungen! Die Tabellenüberschrift ist "Fluchtgeschwindigkeiten an der Oberfläche", da passt das m.E. nicht rein, und dass das im Stillstand gemeint ist wird auch nicht klar (ich gehe davon aus dass in den anderen Zeilen die Eigenrotation eingerechnet ist?). Vielleicht doch besser diese Zeile rausnehmen? -- Gerd Fahrenhorst (Diskussion) 14:38, 14. Mai 2020 (CEST)























