Diskussion:Ziegenproblem (Geometrie)
| Der Artikel „Ziegenproblem (Geometrie)“ wurde im April 2016 für die Präsentation auf der Wikipedia-Hauptseite in der Rubrik „Schon gewusst?“ vorgeschlagen. Die Diskussion ist hier archiviert. So lautete der Teaser auf der damaligen Hauptseite vom 30.04.2016; die Abrufstatistik zeigt die täglichen Abrufzahlen dieses Artikels. |
Symmetriefrage
[Quelltext bearbeiten]Hallo, im Artikel wird geschrieben: Die vom Tier erreichbare Fläche hat die Form einer asymmetrische Linse. Nun sehe ich eine verlängerte Linie Q-P, an der man die Linse spiegeln kann, gilt das nicht als symmetrisch? Oder auf was bezieht sich die Asymmetrie? --Elrond (Diskussion) 21:02, 6. Apr. 2016 (CEST)
- Asymmetrisch bzgl. der horizontalen Achse. Die Symmetrie bzgl. der vertikalen Achse wird beim Integrieren ausgenutzt, indem man nur die rechte Hälfte der Fläche bestimmt (darum Pi/4). --Mnchnstnr (Diskussion) 21:05, 6. Apr. 2016 (CEST)
- rein interessehalber: dann gibt es also keine symmetrischen Konkav-Konvexlinsen? --Elrond (Diskussion) 21:24, 6. Apr. 2016 (CEST)
- Ich bin aber kein Optiker, fragen Sie Ihren Augenarzt oder Apotheker... --Mnchnstnr (Diskussion) 21:30, 6. Apr. 2016 (CEST)
- Alnilam hat heute mein "asymmetrisch" auf "einfach achsensymmetrisch" geändert, womit sie natürlich recht hat. --Mnchnstnr (Diskussion) 21:08, 8. Apr. 2016 (CEST)
- rein interessehalber: dann gibt es also keine symmetrischen Konkav-Konvexlinsen? --Elrond (Diskussion) 21:24, 6. Apr. 2016 (CEST)
Kritik
[Quelltext bearbeiten]Hallo! Kann es sein, daß hier bei all den Formeln der Charakter der Wikipedia als Enzyklopädie für Jedermann vergessen wurde? Ich erwarte als Leser schon eine Erklärung. Der Satz:
- "Diese Gleichung kann nur iterativ gelöst werden und ergibt r = 1{,}1587 \ldots"
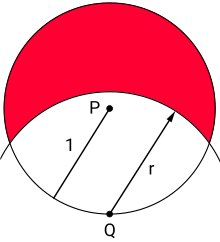
ist unverständlich, wenn man nicht erklärt, daß damit das Vielfache des anderen Radius gemeint ist als Wert 1 gemeint ist. Zu meiner Schulzeit schrieb man dann einfach von r1 und r2. Genauso ist unverständlich, warum für die Punkte nicht A und B sondern P und Q gewählt wurden, ist das heute so Standard? Und zuguterletzt ist per Augenschein die Grafik schlicht falsch. Die beiden Radien haben bei meinem Ausdruck ein Längenverhältnis von 2,9 zu 3,8 - was ein Verhältnis von 1 : 1,31 für r ergibt. Und das sollte man auch einem Laien als Leser zutrauen.Oliver S.Y. (Diskussion) 21:31, 7. Apr. 2016 (CEST)
- Man muss nicht r1 und r2 schreiben, weil es ein Einheitskreis bzw. -kugel ist. Es gibt nur einen variablen Radius. P und Q sind in Ordnung. --Mnchnstnr (Diskussion) 22:14, 7. Apr. 2016 (CEST)
- Siehe Hilberts Axiomensystem der euklidischen Geometrie. 1.1. verwendet P und Q als Begrenzung der Geraden g, welche bei dem Problem hier mit 1 gemeint ist. Nur wäre es dann nicht verständlicher, wenn hier sowas wie "r = 1,15 x g" stehen würde? 1.2./1.3./1.5. verwenden ja ABCD als Bezeichnungen für Punkte in der Geometrie.Oliver S.Y. (Diskussion) 22:57, 7. Apr. 2016 (CEST)
- Also wenn der Herr Hilbert P und Q verwendet hat für Punkte, dann dürfen wir das auch. Allerdings tun zwei Punkte nicht eine Gerade begrenzen, sondern definieren. Eine Gerade hat keinen Anfang und kein Ende. Mit 1 (Eins) ist auf der Grafik im Artikel keine Gerade gemeint, sondern die Länge des Kreisradius, der bei P anfängt und am Kreisrand aufhört. Und nein, ich werde P und Q nicht durch A und B ersetzen. Auch nicht durch V und L. --Mnchnstnr (Diskussion) 23:03, 7. Apr. 2016 (CEST)
- Falls es bei dem Bild wirklich mit den nicht ganz stimmigen Längenverhältnissen ein Problem geben sollte, kann ich das gern heute nachmittag noch einmal neu bauen, ist simpel. Die Bezeichnungen sind jedenfalls völlig in Ordnung. --Alnilam (Diskussion) Heute schon gelobt? 12:20, 8. Apr. 2016 (CEST)
- Nicht nötig, es wird nirgends behauptet, dass auf dem Bild schon die Lösung dargestellt würde. Für die Fragestellung ist das Bild völlig korrekt. Aber wenn du es schaffen würdest, in das zweite Bild mehr 3D hineinzukriegen... --Mnchnstnr (Diskussion) 12:39, 8. Apr. 2016 (CEST)
- Kriege ich hin bis heute abend hin. Und um die sinnose Streiterei zu beenden, werde ich auch für die ebene Variante eine Grafik erstellen, die die Lösung darstellt. Wegen solchem Pillepalle muss doch kein Editwar betrieben werden. *kopfschüttelnd* --Alnilam (Diskussion) Heute schon gelobt? 16:43, 8. Apr. 2016 (CEST)
- Nicht nötig, es wird nirgends behauptet, dass auf dem Bild schon die Lösung dargestellt würde. Für die Fragestellung ist das Bild völlig korrekt. Aber wenn du es schaffen würdest, in das zweite Bild mehr 3D hineinzukriegen... --Mnchnstnr (Diskussion) 12:39, 8. Apr. 2016 (CEST)
- Falls es bei dem Bild wirklich mit den nicht ganz stimmigen Längenverhältnissen ein Problem geben sollte, kann ich das gern heute nachmittag noch einmal neu bauen, ist simpel. Die Bezeichnungen sind jedenfalls völlig in Ordnung. --Alnilam (Diskussion) Heute schon gelobt? 12:20, 8. Apr. 2016 (CEST)
- Also wenn der Herr Hilbert P und Q verwendet hat für Punkte, dann dürfen wir das auch. Allerdings tun zwei Punkte nicht eine Gerade begrenzen, sondern definieren. Eine Gerade hat keinen Anfang und kein Ende. Mit 1 (Eins) ist auf der Grafik im Artikel keine Gerade gemeint, sondern die Länge des Kreisradius, der bei P anfängt und am Kreisrand aufhört. Und nein, ich werde P und Q nicht durch A und B ersetzen. Auch nicht durch V und L. --Mnchnstnr (Diskussion) 23:03, 7. Apr. 2016 (CEST)
- Siehe Hilberts Axiomensystem der euklidischen Geometrie. 1.1. verwendet P und Q als Begrenzung der Geraden g, welche bei dem Problem hier mit 1 gemeint ist. Nur wäre es dann nicht verständlicher, wenn hier sowas wie "r = 1,15 x g" stehen würde? 1.2./1.3./1.5. verwenden ja ABCD als Bezeichnungen für Punkte in der Geometrie.Oliver S.Y. (Diskussion) 22:57, 7. Apr. 2016 (CEST)
- Hallo! Ich verfolge seit meiner Kindheit solche Probleme von "Unterhaltungsmathematik", meist aus Werken der Unterhaltungsliteratur. Nun sind wir aber nicht solche, sondern eine Enzyklopädie. Wenn hier ein wissenschaftlicher Anspruch erhoben wird, gilt der natürlich auch für eine solche Grafik. Du hast nichtmal angegeben, welche Quelle Du für Deine Zeichnung verwendet hast. Es geht hier auch nicht um irgendeine grafische Ungenauigkeit, sondern die Abweichung beträgt das Doppelte, womit das gesamte Problem falsch dargestellt wird. Oder anders ausgedrück 1:1 1/6 oder 1: 1 1/3el ist nicht nur in der Mathematikwissenschaft wesentlich.Oliver S.Y. (Diskussion) 16:49, 8. Apr. 2016 (CEST)
- Zunächst ist die aktuelle Zeichnung/Illustration vom matematischen Standpunkt durchaus in Ordnung. Solche mathematischen Skizzen müssen die wesentlichen Informationen korrekt illustrieren ohne dabei exakt oder maßstabgetreu sein zu müssen. Die aktuelle Zeichnung erfüllt das und es gab daher keinen Grund sie aus dem artikel zu entfernen.
- Allerdings ist es schon richtig, das wenn eine exakte, maßstabgetreue Illustration möglich einfach ist bzw. zur Verfügung steht, man diese im Normalfall vorziehen sollte. Um den Streit hier zu beenden habe ich eine solche mal erstellt (siehe rechts), die dann in den artikel eingebunden werden kann.--Kmhkmh (Diskussion) 17:40, 8. Apr. 2016 (CEST)
- Ui, das hatte ich ja gar nicht gesehen, danke. Geogebra ist natürlich auch schick für so etwas. --Alnilam (Diskussion) Heute schon gelobt? 19:01, 8. Apr. 2016 (CEST)
- Allerdings ist es schon richtig, das wenn eine exakte, maßstabgetreue Illustration möglich einfach ist bzw. zur Verfügung steht, man diese im Normalfall vorziehen sollte. Um den Streit hier zu beenden habe ich eine solche mal erstellt (siehe rechts), die dann in den artikel eingebunden werden kann.--Kmhkmh (Diskussion) 17:40, 8. Apr. 2016 (CEST)
Entfernung unter Literatur & Weblinks
[Quelltext bearbeiten]Ich habe keine Lust darum zu streiten, aber einen Sinn oder Vorteil für Leser oder Editoren kann ich in denen meisten Fällen nicht sehen.
- Die Angaben von JSTOR-Links sind zwar nicht nötig, aber durchaus üblich und von Vorteil, da zum einen ein beträchter Teil der WP-AUtoren über JSTOR-Zugänge verfügt (und jeder Autor sich einen JSTOR-ASrtikel über WP:BIBA besorgen kann). Zudem bieten verfügen viele Bibliotheken und Institute über JSTOR-Zugänge. Für alle diese Fälle ist angenehm bzw. vereinfachend wen ein Direktlink bereits verfügbar ist und man nicht erst separat suchen muss. In diesem Sinne ist JSTOR (and ähnliche Literarurdataenbanken) eine Ausnahme von den üblichen Bezahllinks um die es in der referenzierten Richtlinie geht, zudem sind die beiden Artikel hier sogar online frei für jeden einsehbar (wenn man sich frei registriert).
- Wenn Frasers zweiter Artikel einen fehlerhaften Beweisschritt enthält, macht es in der Tat Sinn ihn aus der Literaturliste zu entfernen. Allerdings wäre es hier naheliegend bzw. besser ihn durch durch eine korrigierte Literatur. d. h. Meyerson zu ersetzen, anstatt ihn nur zu löschen.
- Mathworld wird gerne standardmäßig verlinkt (obwohl das natürlich nur optional ist), er enthält streng genommen auch weitere Informationen und ist zudem belegfähig bzw. auch als Beleg zulässig.
- Der Matheplanet-Artikel (16 Seiten(!)) bietet sowohl weiterführende Informationen und behandelt auch genau die Problemstellung des WP-Lemmas (unter Variante 2)
- Der zweite Ziegenproblemlink bietet in der Tat nur eine alternative Darstellung ohne weiterführende Inhalte, aber er enthält eine detalliertere (alternative) Herleitung und liefert wie auch der vorherige Link immerhin ein Hinweis darauf, dass die Bezeichnung "Ziegenproblem" im Deutschen bzw. im schulischen Umfeld tatsächlich verwendet wird (darüber wurde in der Qualitätssicherung ja diskutiert). Zudem muss man bei wenigen Weblinks auch nicht unbedingt eine päpstlicher als der Papst sein, d. h. eine gute Alternativdarstellung mag man im Einzelfall schon verlinken, auch wenn sie keine weiterführenden Informationen enthält.
--Kmhkmh (Diskussion) 13:10, 8. Apr. 2016 (CEST)
- Es ist ja schon ein Artikel angegeben, in dem es bewiesen wird (Monsieur Jacquelin). Der Durchschnittsleser hat keinen Zugang zu JSTOR und wird ihn auch nicht kostenlos bekommen. --Mnchnstnr (Diskussion) 13:16, 8. Apr. 2016 (CEST)
- Ich habe den Link zu Mathworld wunschgemäss wieder eingefügt. Dort steht auch etwas zur "Ziege außerhalb des Zauns". --Mnchnstnr (Diskussion) 15:38, 8. Apr. 2016 (CEST)
Vorschläge zur Bebilderung
[Quelltext bearbeiten]ch hab da mal was gebastelt, ihr könnt ja würfeln, was davon brauchbar ist oder mir mitteilen, was noch geändert werden soll. Die Maße stimmen auf drei Nachkommastellen, und wenn jemand so richtig gut ist, ergänzt derjenige noch ein paar Kategorien - mein Englisch ist bekanntlich nicht so toll.
--Alnilam (Diskussion) Heute schon gelobt? 18:38, 8. Apr. 2016 (CEST)
- Welche Software hast du für die verwendet?--Kmhkmh (Diskussion) 18:48, 8. Apr. 2016 (CEST)
- Inkscape. Da muss ich zwar immer ein bissl fummeln, weil ich ansonsten Corel benutze, sieht auch nicht ganz so schön aus wie ich wollte, aber hoffentlich passt es trotzdem. --Alnilam (Diskussion) Heute schon gelobt? 18:58, 8. Apr. 2016 (CEST)

Herzlichen Dank. Mir fallen folgende Punkte auf:
- An einem Ort sind vier Nachkommastellen, am anderen drei. Die Werte für 2D, 3D und 4D lauten 1,158728..., 1,228544... und 1,268079... (das Erstellen der Grafik für den Fall 4D überlassen wir anderen Benutzern).
- Für die Einleitung hätte ich schon gerne weiterhin eine Grafik (meinetwegen maßstabgetreu die Lösung zeigend), die mit 1 und r angeschrieben ist, denn das ist die Fragestellung.
- Wäre es für die 3D-Grafiken vielleicht möglich, Mesh zu verwenden? Dann sieht man das 3D besser. Bei den jetzigen beiden 3D-Versionen ist für mich nicht klar erkennbar, was "innen" (die Linse) ist.
- Hier habe ich dazu etwas gefunden, ich versuche auch nochmals. --Mnchnstnr (Diskussion) 19:42, 8. Apr. 2016 (CEST)
- Es gibt Leute, die sagen die "grasende" Ziege. Das Problem fußt aber nicht darauf, dass sie grast, sondern darauf, dass sie angebunden ist ("tethered goat").
--Mnchnstnr (Diskussion) 19:07, 8. Apr. 2016 (CEST)
- Das neue 3D-Bild ist grafisch ja ganz nett, aber mit dem eingezeichneten Gradnetz fallen die Unstimmigkeiten erst richtig auf. Der Mittelpunkt der Ziegenkugel liegt nicht auf der Oberfläche der Einheitskugel, die Größenverhältnisse stimmen wieder nicht. Da würde ich noch einmal eine Nachbearbeitung empfehlen. --Alnilam (Diskussion) Heute schon gelobt? 20:30, 8. Apr. 2016 (CEST)
- Das scheint mit der Perspektive zu tun zu haben, im Modell ist der Mittelpunkt der grauen Kugel auf der Oberfläche der roten Kugel. --Mnchnstnr (Diskussion) 20:37, 8. Apr. 2016 (CEST)
- Keine Ahnung, mit welchem Programm du arbeitest, aber egal in welcher Perspektive muss der untere Pol der roten Kugel im Mittelpunkt des Großkreises der grauen sitzen. Was benutzt du? Vielleicht kann ich da ja was dran basteln. --Alnilam (Diskussion) Heute schon gelobt? 20:49, 8. Apr. 2016 (CEST)
- Mathematica, wenn du möchtest maile ich dir den Code. --Mnchnstnr (Diskussion) 20:58, 8. Apr. 2016 (CEST)
- Das wird wohl nichts, kostet leider. Versuche mal, den Radius einer der Kugeln entsprechend der Lösungsverhältnisse besser anzupassen, dann sieht es evtl. nicht mehr ganz so schräg aus. Ich spiele mal ein bissl mit meinen Bordmitteln, vielleicht kriege ich etwas hin, was deiner Optik entspricht. Wäre doch gelacht, wenn man dieses simple Problem nicht auch in schön darstellen kann. --Alnilam (Diskussion) Heute schon gelobt? 21:11, 8. Apr. 2016 (CEST)
- Es gibt eine hochoffizielle Gratisversion für den Raspberry Pi... OK ich versuche weiter. --Mnchnstnr (Diskussion) 21:13, 8. Apr. 2016 (CEST) Besser jetzt? --Mnchnstnr (Diskussion) 21:22, 8. Apr. 2016 (CEST)
- Erheblich. Der Pol der roten Kugel liegt zwar immer noch nicht in der Äquatorebene der grauen (warum auch immer), aber es fällt nicht mehr so auf, und die Radienverhältnisse sehen brauchbar aus. Danke. --Alnilam (Diskussion) Heute schon gelobt? 21:52, 8. Apr. 2016 (CEST)
- Es gibt eine hochoffizielle Gratisversion für den Raspberry Pi... OK ich versuche weiter. --Mnchnstnr (Diskussion) 21:13, 8. Apr. 2016 (CEST) Besser jetzt? --Mnchnstnr (Diskussion) 21:22, 8. Apr. 2016 (CEST)
- Das wird wohl nichts, kostet leider. Versuche mal, den Radius einer der Kugeln entsprechend der Lösungsverhältnisse besser anzupassen, dann sieht es evtl. nicht mehr ganz so schräg aus. Ich spiele mal ein bissl mit meinen Bordmitteln, vielleicht kriege ich etwas hin, was deiner Optik entspricht. Wäre doch gelacht, wenn man dieses simple Problem nicht auch in schön darstellen kann. --Alnilam (Diskussion) Heute schon gelobt? 21:11, 8. Apr. 2016 (CEST)
- Mathematica, wenn du möchtest maile ich dir den Code. --Mnchnstnr (Diskussion) 20:58, 8. Apr. 2016 (CEST)
- Keine Ahnung, mit welchem Programm du arbeitest, aber egal in welcher Perspektive muss der untere Pol der roten Kugel im Mittelpunkt des Großkreises der grauen sitzen. Was benutzt du? Vielleicht kann ich da ja was dran basteln. --Alnilam (Diskussion) Heute schon gelobt? 20:49, 8. Apr. 2016 (CEST)
- Das scheint mit der Perspektive zu tun zu haben, im Modell ist der Mittelpunkt der grauen Kugel auf der Oberfläche der roten Kugel. --Mnchnstnr (Diskussion) 20:37, 8. Apr. 2016 (CEST)
- Was die Nachkommastellen anbetrifft: Ich habe das 3D-Bild angepasst, da habe ich nicht aufgepasst, danke für den Hinweis. --Alnilam (Diskussion) Heute schon gelobt? 20:35, 8. Apr. 2016 (CEST)
Da könnt Ihr das Bild drehen und wenden wie ihr wollt, es wird als Projektion eines nicht konvexen Gebildes (beide Kugeln) immer unübersichtlich sein. Das einfachste für den unbedarften Leser ist, die Zeichnung des ebenen Problems als Längsschnitt des räumlichen, rotationssymmetrischen Problems zu deklarieren, eine Rotationsachse einzufügen und den fraglichen 3d-Bereich durch Rotation entstehen lassen. Für ein 3d-Bild würde eine Reduzierung auf die Linse übersichtlicher ausfallen.--Ag2gaeh (Diskussion) 08:23, 9. Apr. 2016 (CEST)
- Oder wie hier bei einer Zyklide nur eine "Hälfte" zeigen
 --Ag2gaeh (Diskussion) 08:40, 9. Apr. 2016 (CEST)
--Ag2gaeh (Diskussion) 08:40, 9. Apr. 2016 (CEST)
- Oder wie hier bei einer Zyklide nur eine "Hälfte" zeigen
Unterhaltungsmathematik
[Quelltext bearbeiten]Wenn das Problem als Problem der Unterhaltungsmathematik vorgestellt wird (und nicht nur als geometrisches Problem), dann sollte es auch in der Form eines Problems der Unterhaltungsmathematik vorgestellt werden, das heißt eingekleidet: Der erste Kreis ist eine kreisförmige Wiese; der zweite ist der Bereich, den eine im Punkt Q angebundene Ziege erreichen kann; gefragt ist danach, wie lange das Seil sein muss, damit die Ziege genau die Hälfte der Wiese abgrasen kann. Man sollte es dann auch nicht so formulieren, dass nach der roten Fläche (diejenige, die von der Ziege nicht erreicht wird) gefragt wird, sondern nach der Schnittmenge der beiden Kreise. Der vorgegebene Kreis sollte dann auch kein Einheitskreis sein, denn solche gibt es in der Natur nicht, sondern nur in der Mathematik, sondern entweder variablen Radius haben, oder einen für die Einkleidung realistischen Wert haben (z.B. 10 m). Dafür müsste man aber natürlich schauen, in welcher Form das Problem tatsächlich in der Literatur auftaucht.
Zur Zeichnung: Ich finde es verwirrend, wenn die beiden Strecken (bzw. Pfeile), die die beiden Radien darstellen, (gegensinnig) parallel sind. --Digamma (Diskussion) 19:49, 8. Apr. 2016 (CEST)
- Vermutlich wäre es am besten die (bewegliche) Ziegenleine durch einen Pfeil zu kennzeichen, währed der Radius des (statischen) (Einheits)kreises nur als Strecke dargestellt werden sollte.--Kmhkmh (Diskussion) 19:57, 8. Apr. 2016 (CEST)
- Ich habe für den 2D-Fall nun dein Bild genommen, Kmhkmh. Welches maßstabgetreu die Lösung darstellt, und den Radius des Einheitskreises nicht als Pfeil. Dafür sieht jetzt nicht mehr jeder auf den ersten Blick, dass die Wölbungen unterschiedlich sind. --Mnchnstnr (Diskussion) 22:35, 8. Apr. 2016 (CEST)
- Die Lösungen basieren darauf, dass es ein Einheitskreis / eine Einheitskugel ist. Die Einstufung als Unterhaltungsmathematik stammt von mir, ich werde nicht darauf insistieren. Die älteste Publikation die ich dazu gefunden habe stammt aus einer Damenzeitschrift aus dem 18. Jahrhundert. Trotzdem (trotz vermeintlicher Unterhaltungsmathematik, nicht trotz Damen) habe ich auf allzu idyllische Blümchen-auf-der-Wiese-Sprache verzichtet, denn das Problem ist in der hier dargestellten Fassung nicht einfach, ich habe mehr als einen Mathematiker damit zum Husten gebracht, Ingenieure lustigerweise eher weniger. Es wird auch der Fall mit >3 Dimensionen angetönt (bei unendlich vielen Dimensionen passiert übrigens seltsames: Der Radius wird mit 21/2 einfacher, doch ist er kürzer, ist der überschnittene Anteil des Einheitskörpers gleich Null, ist er höher, ist der Anteil gleich Eins. --Mnchnstnr (Diskussion) 20:34, 8. Apr. 2016 (CEST)
- Das ist aber ein Charakteristikum des Lösungswegs, nicht des Problems. Ist x eine Lösung des Problems mit Radius 1, so ist xr eine Lösung des Problems mit Radius r. Die Annahme, dass der erste Kreis Radius 1 hat, dient nur der Vereinfachung der Formulierung der Lösung. --Digamma (Diskussion) 20:30, 8. Apr. 2016 (CEST)
Varianten
[Quelltext bearbeiten]Es liegen sechs Varianten des Problems auf der Hand: Die Ziege kann innerhalb und außerhalb des Zauns in der Ebene, auf der Kugeloberfläche oder im R3 angebunden sein. Um Theoriefindung zu vermeiden, habe ich im Artikel nur die drei üblicherweise gefragten Fälle behandelt. Auch noch nicht in den Sinn gekommen zu sein scheint den Mathematiklehrern dieser Welt, dass es mehr als eine Ziege gibt. --Mnchnstnr (Diskussion) 06:00, 10. Apr. 2016 (CEST)
Vorschläge
[Quelltext bearbeiten]- Die leicht nachvollziehbare Standardisierung (Einheitskreis mit ) ist erstaunlicherweise im Web nur bei einem kleinereren Teil der Seiten zu finden. Diesen Schritt sollte man in der Einleitung, denn das gilt für alle Versionen, erwähnen.
- 2D-Modell mit der Ziege außerhalb
- Das Thema ist Teil der Populärmathematik. Eine etwas "natürlichere Grafik" mit angedeutetem Seil macht das Ganze für deren Freunde leichter.
- Verwendung etwas passenderer Bezeichner für die "natürliche Grafik"
- Im Web findet man folgende Seillängen:
- Seillänge gleich halbem Kreisumfang (). Die Ziege erreicht also gerade noch den hinteren Punkt. Das findet man am häufigsten. Diese Version würde ich auf die erwähnte natürliche Darstellung bringen.
- Seillänge gleich halbem Kreisumfang ().
- Seillänge gleich Kreisradius ().
- Seillänge derart, dass die abgegraste fläche der Kreisfläche entspricht. ().
- Gruß von ÅñŧóñŜûŝî (Ð) 11:54, 10. Apr. 2016 (CEST)
- Ich glaube nicht, dass die Leser, die diese Aufgabe lösen können, auf "populäre" Bilder angewiesen sind. Es braucht doch etwas fortgeschrittene Kenntnisse der Integralrechnung, um die Fläche der dunkelblau eingezeichneten Bereiche ausrechnen zu können. Versuche es. --Mnchnstnr (Diskussion) 12:25, 10. Apr. 2016 (CEST)
Was ist mit d gemeint?
[Quelltext bearbeiten]Hallo,
in der Version vor meinem Edit stand, dass d der Mittelpunktabstand sei. Das ist doch das gleiche wie r, da der Mittelpunkt des zweiten Kreises ja auf dem Kreisrand des anderen liegt. Irgendwas stimmt hier nicht.--Christian1985 (Disk) 19:53, 10. Apr. 2016 (CEST)
- Hallo Christian, in der Version stand, dass die allgemeine Formel für die Schnittfläche zweier Kreise abhängig sei von d und den beiden Radii der Kreise, dass sich die ganze Gesichichte aber erheblich vereinfacht weil im genannten Problem d=R=1. --Mnchnstnr (Diskussion) 20:36, 10. Apr. 2016 (CEST)
Leinenlänge und Co.
[Quelltext bearbeiten]Hallo! Wer von Euch hat schonmal ein Stück Vieh angebunden, egal welches, für das Thema egal ^^. Eine Leine wird sowohl am Hals des Tieres als auch am Pflock befestigt. Darum gehts hier um das Teilstück der Leine zwischen diesen beiden Punkten. Dazu kommt die Dicke der Leine, welche bei einer Berechnung, die bis auf 4 Stellen nach dem Komma genau sein soll wichtig ist. Und ganz ehrlich, wenn hier über 3D gesprochen wird, da der Knoten sich häufig am Boden befindet, und vor dem Hals noch der Kopf des Tieres bis zur Maulspitze kommt, sollten vieleicht für den Normaluser auch alle Aspekte erklärt werden, welche hier unbeachtet bleiben. Denn auch wenn Geometrie im Lemma steht, die Praxisnähe ist dann doch sehr weitgehend. Und vieleicht gehört dann auch hierzu, daß die Lösung 7/6 lautet, genauso wie 22/7 = Pi im Alltag sind.Oliver S.Y. (Diskussion) 19:59, 10. Apr. 2016 (CEST)
- Ich glaube nicht, dass die Dicke der Leine für die zu bestimmende Fläche / das zu bestimmende Volumen relevant ist, weil deren Durchmesser tangential zum abgegrasten Kreis / zur durchgegrasten Kugel ist. Zumindest an deren Rand, weil dann ist die Leine voll gestreckt. --Mnchnstnr (Diskussion) 20:38, 10. Apr. 2016 (CEST)
- Mal kalkulieren, eine solche Leine hat 2cm im Umfang. selbst wenn Du sie an Ösen festmachst, brauchst Du 15 bis 20cm für einen Knoten. wenn man also nen Weideradius von 5 Metern nimmt, sind das 40cm, also 8%. Selbst bei dem aufeinanderlegen von Enden hast Du etwa 8cm, mal 2, als 16cm, was 3 Prozent ausmacht. Nun kannst Du der Ziege auch 10 oder 50 Meter Luft lassen, nur wird das Beispiel dadurch unrealistisch. Das Problem ist ja eben für mich, auf der einen Seiten höchstmögliche Exaktheit bis zur Kommastelle, aber alle anderen Faktoren werden ausgeblendet. Oliver S.Y. (Diskussion) 21:00, 10. Apr. 2016 (CEST)
- Es dürfen auch keine österreichischen Ziegen sein, denn dort gilt laut Verordnung der Bundesministerin für Gesundheit und Frauen über die Mindestanforderungen für die Haltung von Pferden und Pferdeartigen, Schweinen, Rindern, Schafen, Ziegen, Schalenwild, Lamas, Kaninchen, Hausgeflügel, Straußen und Nutzfischen (1. Tierhaltungsverordnung) klipp und klar: "Die Anbindehaltung ist verboten." Bist du Österreicher? --Mnchnstnr (Diskussion) 21:06, 10. Apr. 2016 (CEST)
- Mal kalkulieren, eine solche Leine hat 2cm im Umfang. selbst wenn Du sie an Ösen festmachst, brauchst Du 15 bis 20cm für einen Knoten. wenn man also nen Weideradius von 5 Metern nimmt, sind das 40cm, also 8%. Selbst bei dem aufeinanderlegen von Enden hast Du etwa 8cm, mal 2, als 16cm, was 3 Prozent ausmacht. Nun kannst Du der Ziege auch 10 oder 50 Meter Luft lassen, nur wird das Beispiel dadurch unrealistisch. Das Problem ist ja eben für mich, auf der einen Seiten höchstmögliche Exaktheit bis zur Kommastelle, aber alle anderen Faktoren werden ausgeblendet. Oliver S.Y. (Diskussion) 21:00, 10. Apr. 2016 (CEST)
- Nein, aber habe einige verreckte Tiere mit entsorgt, weshalb ich persönlich auch gegen diese Form der Haltung bin. Also es wäre hier schon hilfreich, daß nach dem "Teilstück einer Leine" gefragt wird. Die Knoten sind ja immer gleich, also unabhängig von den Radien.Oliver S.Y. (Diskussion) 21:11, 10. Apr. 2016 (CEST)
- Dann solltest du als Fachmann besagter Bundesministerin vermitteln, dass man Nutzfische gar nicht anbinden kann. Für die Ziege im Ziegenproblem reicht es, wenn du annimmst sie sei dimensionslos. Das löst dir dann auch gleich das Problem der Gravitation im drei- und höherdimensionalen Fall des Ziegenproblems. --Mnchnstnr (Diskussion) 21:13, 10. Apr. 2016 (CEST)
- Nein, aber habe einige verreckte Tiere mit entsorgt, weshalb ich persönlich auch gegen diese Form der Haltung bin. Also es wäre hier schon hilfreich, daß nach dem "Teilstück einer Leine" gefragt wird. Die Knoten sind ja immer gleich, also unabhängig von den Radien.Oliver S.Y. (Diskussion) 21:11, 10. Apr. 2016 (CEST)
- @Oliver S.Y.: Dies ist ein Problem der Unterhaltungsmathemtik, kein reales Problem. Es geht nicht wirklich um angeleinte Ziegen, sondern die Geschichte mit der Ziege dient nur dazu, das mathematische Problem zu verpacken. --Digamma (Diskussion) 06:50, 11. Apr. 2016 (CEST)
- Nur ist die Wikipedia eine allgemeine Enzyklopädie, und man sollte das dem Leser hier direkt mitteilen. Wenn ich zB. die Rätsel bei SPON lese, auch Unterhaltungsmathematik, wird sowas bis ins letzte Detail erläutert. Für Mathematiklehrer und Mathematiker vieleicht selbstverständlich, für einen Leser nicht, wenn er solche Problemschilderung bekommt. Oliver S.Y. (Diskussion) 08:55, 11. Apr. 2016 (CEST)
- Darum steht im Artikel (mittlerweile der dritte Satz), was das Problem ist: Es geht um r, nicht um Leinen oder irgendwelche Abschnitte davon. Und um eine rote Fläche, nicht um eine grüne Wiese. --Mnchnstnr (Diskussion) 09:01, 11. Apr. 2016 (CEST)
- Nur ist die Wikipedia eine allgemeine Enzyklopädie, und man sollte das dem Leser hier direkt mitteilen. Wenn ich zB. die Rätsel bei SPON lese, auch Unterhaltungsmathematik, wird sowas bis ins letzte Detail erläutert. Für Mathematiklehrer und Mathematiker vieleicht selbstverständlich, für einen Leser nicht, wenn er solche Problemschilderung bekommt. Oliver S.Y. (Diskussion) 08:55, 11. Apr. 2016 (CEST)
- Nur nochmal zur Klarstellung des Problems: "Wie lang muss die Leine sein, damit das Tier auf genau der Hälfte der Kreisfläche grasen kann? Es geht hier also gar nicht um Merkmale des Tieres, wenn jedoch bis auf 4 Kommastellen genau gerechnet wird, sollte man das in der Problemstellung auch klar formulieren. Denn nicht jeder Leser weiß was Unterhaltungsmathematik ist, und klickt erst auf den Artikel zu lesen dessen. Und wenn er es gelesen hat, findet er "Unter Unterhaltungsmathematik versteht man die Beschäftigung mit mathematischen Fragestellungen, welche vorrangig unter dem Aspekt des Zeitvertreibs betrieben wird.", ich kann in diesem Artikel wirklich gar nicht von diesem vorrangigen Aspekt des Zeitvertreibs finden, sondern nur eine knochentrockene Matheaufgabe.Oliver S.Y. (Diskussion) 09:11, 11. Apr. 2016 (CEST)
- Das hat Unterhaltungsmathematik so an sich. Man vertreibt sich die Zeit mit knochentrockenen Matheaufgaben. Was die Problemstellung ist, steht im dritten Satz. --Mnchnstnr (Diskussion) 09:12, 11. Apr. 2016 (CEST)
- Nur nochmal zur Klarstellung des Problems: "Wie lang muss die Leine sein, damit das Tier auf genau der Hälfte der Kreisfläche grasen kann? Es geht hier also gar nicht um Merkmale des Tieres, wenn jedoch bis auf 4 Kommastellen genau gerechnet wird, sollte man das in der Problemstellung auch klar formulieren. Denn nicht jeder Leser weiß was Unterhaltungsmathematik ist, und klickt erst auf den Artikel zu lesen dessen. Und wenn er es gelesen hat, findet er "Unter Unterhaltungsmathematik versteht man die Beschäftigung mit mathematischen Fragestellungen, welche vorrangig unter dem Aspekt des Zeitvertreibs betrieben wird.", ich kann in diesem Artikel wirklich gar nicht von diesem vorrangigen Aspekt des Zeitvertreibs finden, sondern nur eine knochentrockene Matheaufgabe.Oliver S.Y. (Diskussion) 09:11, 11. Apr. 2016 (CEST)
Man sollte im Artikel den Unterschied des praktische Problems (angebundene Ziege ...) von dem mathematischen Modell des Problems mehr betonen. Der größte Teil des Artikels handelt ausschließlich vom mathematischen Modell. Und nur da machen Kommastellen auch Sinn. Und da es ein mathematisches Prinzip ist, nach Verallgemeinerungsmöglichkeiten Ausschau zu halten, macht auch die Diskussion des höher dimensionalen mathematischen Problems Sinn, das mit einem realen Problem (n-dimensionale Heuhaufen ?) aber nichts mehr zu tun hat. Eigentlich ist das Ziegenproblem doch nur der Aufhänger für das mathematische Problem "Schnitt zweier Kreisflächen" in vorgegebener Art.--Ag2gaeh (Diskussion) 10:26, 11. Apr. 2016 (CEST)
- ... und kugelförmige Silos, um die herum die von der österreichischen Frauenministerin (sie unterrichtete auch Russisch und Leibesübungen) legiferierten Nutzfische in Anbindehaltung (siehe oben) schwimmen? --Mnchnstnr (Diskussion) 10:39, 11. Apr. 2016 (CEST)
Abschnitt "Lösung mit Integration" - zu lösende Gleichung
[Quelltext bearbeiten]Als Ergebnis der Integration wird als zu lösende Gleichung
angegeben. In der ursrünglichen Form steht aber auf der linken Seite . Welchen Sinn macht es, die Gleichung so umzuformen, dass links "r = " steht? Man hat ja nicht nach r aufgelöst, da r auf der rechten Seite noch vorkommt. --Digamma (Diskussion) 19:53, 12. Apr. 2016 (CEST)
- Die Frage ist ja, wie groß muss r sein. Darum wird versucht, nach r aufzulösen. Und dann festgestellt, dass sich eine transzendente Gleichung ergibt. In der ursprünglichen Form steht pi/4, weil nur die rechte Hälfte der Linse integriert wird. Die ganze Linse hat den halben Flächeninhalt des Einheitskreises, die rechte Hälfte einen Viertel. --Mnchnstnr (Diskussion) 20:18, 12. Apr. 2016 (CEST)
- Aber das ist doch kein Auflösen nach r, wenn r auf der rechten Seite noch 3-mal vorkommt. Möglicherweise soll hier die Gleichung in eine Fixpunktgleichung umgeformt werden, um sie so iterativ zu lösen. Es ist aber für die Aufgabenstellung völlig unerheblich, auf welchem Weg die transzendente Gleichung numerisch gelöst wird. Deshalb wäre es wohl besser, sie z.B. in der Form
- anzugeben. Am besten in der Form, wie sie beim Berechnen des Integrals herauskommt. --Digamma (Diskussion) 20:56, 12. Apr. 2016 (CEST)
- Ich habe nicht behauptet, es sei ein Auflösen der Gleichung. --Mnchnstnr (Diskussion) 21:00, 12. Apr. 2016 (CEST)
- Aber das ist doch kein Auflösen nach r, wenn r auf der rechten Seite noch 3-mal vorkommt. Möglicherweise soll hier die Gleichung in eine Fixpunktgleichung umgeformt werden, um sie so iterativ zu lösen. Es ist aber für die Aufgabenstellung völlig unerheblich, auf welchem Weg die transzendente Gleichung numerisch gelöst wird. Deshalb wäre es wohl besser, sie z.B. in der Form
Wie das Problem genannt wird
[Quelltext bearbeiten]Ich versuche, deutschsprachige Belege für das Problem zu sammeln. Du darfst gerne das, was du nützlich findest, in den Artikel einbauen. Ergänzungen sind willkommen.
- Das Ziegenproblem: Die folgenden Links habe ich alle vonKmhkmh:
- Das Ziegenproblem. bigbandi.de, abgerufen am 16. April 2016.
- Das Ziegenproblem. Matroids Matheplanet, 31. Mai 2013, abgerufen am 15. April 2016.
- Das Ziegenproblem. khloebel.de, 25. Januar 2014, abgerufen am 15. April 2016.
- Die grasende Ziege
- Bereits im Artikel: Seiten 32 in Heinrich Hemme: Die Hölle der Zahlen. 92 mathematische Rätsel mit ausführlichen Lösungen. Vandenhoeck & Ruprecht, Göttingen 2007, ISBN 978-3-525-40841-4 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 10. April 2016]).
- VonGeodel: Rätsel. hans-henschel.de, abgerufen am 15. April 2016.
- Das Bauer-Ziege-Wiese-Problem
- S. 37 in Michael Knorrenberger: Numerische Mathematik. Eine beispielorientierte Einführung. Fachbuchverlag Leipzig im Carl Hanser Verlag, München 2013, ISBN 978-3-446-43233-8 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 15. April 2016]).
- Die weidende Ziege
- S. 53 in Rüdeger Baumann: Analysis 2: Integralrechnung, Kurven und Flächen, Differenzialgleichungen. Ein Arbeitsbuch mit Derive. Ernst Klett Verlag, Stuttgart 2002, ISBN 978-3-12-739514-3.
- D. Treiber: Zum Problem der „Weidenden Ziege“. Sekundarstufen 1 und 2. In: Praxis der Mathematik. Nr. 3. Aulis Verlag, Köln 1991, S. 97–100.
Als Engländer lehne ich (als Begriffsetablierung!) das Argument ab, wonach das Goat Problem auf Deutsch automatisch Ziegenproblem heißen müsste. Sei das Feld der reellen Zahlen ….
Eigene Einschätzung: Es gibt keinen klar etablierten Namen in der deutschen Sprache. Ziegenproblem ist tatsächlich einer der vier Namen im Umlauf. Bevorzugt man die Quellen, die bei WP als zuverlässig gelten, dann könnte sich das Bild ändern. Da könnten alle vier Webseiten rausfliegen – allerdings habe selbst ich von Matheplanet gehört, und ich habe normalerweise mit Schul- und Unterhaltungsmathematik wenig zu tun. Danach wäre die weidende Ziege sogar leicht vorn. Andererseits hatMnchnstnr den Namen Ziegenproblem (Geometrie) gewählt, und immerhin hat er einen großen Teil des Inhalts beigesteuert. Derzeit sehe ich kein zwingendes Argument für eine Umbenennung.
Andere deutschsprachigen Quellen: Zitierfähig, aber für die Benennung irrelevant.
- S. 52 in Bernard Ksiazek: Mathe an Stationen. Figuren und Körper Klasse 8–10. Auer Verlag, Donauwörth 2013, ISBN 978-3-403-36887-8 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 15. April 2016]).
- Der Fall einer L-förmigen Wiese: S. 939 in Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 3. Auflage. Springer Spektrum, Berlin 2015, ISBN 978-3-642-44918-5, doi:10.1007/978-3-642-44919-2 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 15. April 2016]).
Übrigens: Solltest du finden, dass einige Informationen aus diesen Quellenangaben entfernt werden sollten, dann bitte ich darum, dass du vorher deine Gründe hier diskutierst. --GroupCohomologist (Diskussion) 19:11, 15. Apr. 2016 (CEST)
- Danke für deine Mühe. Ich sehe es ähnlich: Keinen klar etablierten Namen in der deutschen Sprache. Darum nannte ich das Problem mit der Ziege ... eben "Ziegenproblem". Ich hänge nicht daran, aber ich kann mir nicht ohne weiteres eine bessere Lösung vorstellen, weil eben ... kein klar etablierter Name in der deutschen Sprache, wie auch deine Recherche zeigt. Es ist ein Problem mit einer Ziege. Wenn man den Faktor 1.158728473 in eine Suchmaschine eingibt, findet man in für mich exotischen Sprachen auch "una vaca" (Spanisch für Kuh), "en ged" (Dänisch für Ziege), "kecskés" (Ungarisch für Ziege), "um cavalo" (Portugiesisch für Pferd), "pässi" (Finnisch für Schaf, wen ich das richtig verstehe). Aber eben, nichts Etabliertes auf Deutsch. --Mnchnstnr (Diskussion) 19:44, 15. Apr. 2016 (CEST)
Falscher Wert beim Silo?
[Quelltext bearbeiten]Überschneiden sich bei der Variante mit dem Silo die dunkelblauen Flächen nicht bei r > 1/2Pi? --Wikilaser (Diskussion) 21:07, 30. Apr. 2016 (CEST)
- Nein, denn der Umfang eines Kreises ist 2 Pi r. --Mnchnstnr (Diskussion) 22:14, 30. Apr. 2016 (CEST)
- In diesem Fall ist aber r = 1/2, da ja vom Einheitskreis mit Durchmesser = 1 ausgegangen wird. Und da bei einer Leinenlänge > 1/2 Pi eine Überschneidung der rechten mit der linken dunkelblauen Fläche entstünde, müßte mein Einwand stimmen.--Wikilaser (Diskussion) 12:01, 2. Mai 2016 (CEST)
- Der Einheitskreis hat einen Radius von 1, sein Durchmesser ist 2. --schulhofpassage 12:25, 2. Mai 2016 (CEST)
- Mein Fehler war, daß Pi der Umfang eines Kreises mit Durchmesser 1 ist und ich diesen Kreis für den Einheitskreis hielt. Also hat der Umfang des Einheitskreises 2 Pi, folglich darf der Radius des gesuchten Kreises nicht größer als Pi sein. Vielen Dank für die Erklärung.--Wikilaser (Diskussion) 12:31, 2. Mai 2016 (CEST)
- Gegen diese Verwirrungen (und um 2er-Faktoren zu vermeiden), gibt es den Vorschlag der alternative Kreiszahl τ. Hat aber bislang keinen großen Anklang gefunden. --schulhofpassage 12:39, 2. Mai 2016 (CEST)
- Mein Fehler war, daß Pi der Umfang eines Kreises mit Durchmesser 1 ist und ich diesen Kreis für den Einheitskreis hielt. Also hat der Umfang des Einheitskreises 2 Pi, folglich darf der Radius des gesuchten Kreises nicht größer als Pi sein. Vielen Dank für die Erklärung.--Wikilaser (Diskussion) 12:31, 2. Mai 2016 (CEST)
- Der Einheitskreis hat einen Radius von 1, sein Durchmesser ist 2. --schulhofpassage 12:25, 2. Mai 2016 (CEST)
- In diesem Fall ist aber r = 1/2, da ja vom Einheitskreis mit Durchmesser = 1 ausgegangen wird. Und da bei einer Leinenlänge > 1/2 Pi eine Überschneidung der rechten mit der linken dunkelblauen Fläche entstünde, müßte mein Einwand stimmen.--Wikilaser (Diskussion) 12:01, 2. Mai 2016 (CEST)
Silo, irgendwas ist da falsch
[Quelltext bearbeiten]Erster Term , zweiter Term . Hier wird eine Fläche mit einem Volumen addiert. Mindestens irgendwelche Normierungsfaktoren fehlen hier. --91.23.70.219 23:37, 30. Apr. 2016 (CEST)
- Da wird kein Volumen addiert, und belegt ist die Formel auch. --Mnchnstnr (Diskussion) 04:47, 1. Mai 2016 (CEST)
geometrische lösung ziegenproblen 2d
[Quelltext bearbeiten]
Ich hatte mal diese Aufgabe bekommen und hier einen geometrischen Lösungsweg benutzt. r1 ist der Radius der Wiese(Hauptfläche). r2 ist der Radius der (Hauptfläche/2). verbindung ist die Hilfslinie zur Ermittlung des Durchgangspunktes am äußeren Radius. r3 ist die Strecke zwischen Ziegenpflock und Durchgangspunkt, also der gesuchte Radius. (nicht signierter Beitrag von Mattes.Sch. (Diskussion | Beiträge) 17:25, 1. Mai 2016 (CEST))
- Und warum sollte das so sein? Auf den ersten Blick falsch ist deine ebenfalls hochgeladene Skizze Datei:Mathematik ziegenproblem grafik.jpg. --Mnchnstnr (Diskussion) 20:28, 2. Mai 2016 (CEST)
ja, die erste grafik war leider die falsche, konnte diese aber nicht mehr löschen. ich kann gerne eine detailierte zeichnung mit rechenschritt hochladen. hoffe hier nix falsch gemacht zu haben. (nicht signierter Beitrag von Mattes.Sch. (Diskussion | Beiträge) 08:43, 3. Mai 2016 (CEST))
- Ich denke, da muss man gar nicht nachrechnen. Die Lösung einer transzendenten Gleichung kann doch nicht mit Zirkel und Lineal konstruiert werden. Grüße -- HilberTraum (d, m) 10:26, 3. Mai 2016 (CEST)
Ich bin der Sache nochmals nachgegangen, der Beitrag von mir sollte gelöscht werden. Bei den Berechnungen lag ich nur 3 Stellen hinter dem Komma richtig. Es lag wohl damals an dem Taschenrechner. Dennoch war es eine schnelle fast perfekte Möglichkeit das Problem graphisch zu lösen. Hier mein Lösungsweg, grob gesehen: R1=1; A1=Π; R2=Wurzel(0,5); A2=Π/2; c=Wurzel(1,5); β=inv cos(Wurzel(0,5)/Wurzel(1,5); α=90°-β; r=2*sinα/sin90°;

Gruß und Danke (nicht signierter Beitrag von Mattes.Sch. (Diskussion | Beiträge) 13:14, 3. Mai 2016 (CEST))
Geometrische Näherungslösung
[Quelltext bearbeiten]Der aktuelle Abschnitt besitzt einige wikipediatechnische Probleme:
- Es fehlen Belege. Ohne diese ist das ganze formal ein Verstoß gegen WP:TF und man mag die Relevanz des Inhalts anzweifeln. Auch wenn man hier aufgrund elementarmathematischen Inhalts argumentieren mag, dass Belege zumindest nicht zur Sicherung der Korrektheit des Inhalts benötigt werden.
- Der folgende Schlusssatz ist irgendwo zwischen Falsch und verwirrend: "Zur Verdeutlichung: Wäre die Fläche der kreisförmigen Wiese etwa , könnte davon die Ziege ca. nicht abgrasen." Zunächst ist nicht die Fläche der (ganzen) kreisförmigen Wiese, sondern die Hälfte. Dementsprechend kann die Ziege der halben Wiese nicht abgrasen (was sie aber bei der "exakten" numerischen Lösung könnte). Sinnvoller wäre hier wohl auch relative Angaben, d.h. um wie viel Prozent die geometrische Approximation von der numerischen Approximation abweicht (für Fläche oder Radius).
--Kmhkmh (Diskussion) 16:56, 7. Jan. 2018 (CET)
- Danke für deinen Hinweis, den groben Fehler habe ich sofort ausgebessert. M. E. macht es schon Sinn den Fehler zumindest auch in zu beschreiben. Ich werde deinen Gedanken aufgreifen und eine prozentuelle Angabe versuchen. Petrus3743 (Diskussion) 17:36, 7. Jan. 2018 (CET)
- Ich habe den relativen Fehler für Fläche und Radius nachgetragen. So ist gut erkennbar wie sich der relative Fehler vom konstruierten Radius auf die Fläche auswirkt. --Petrus3743 (Diskussion) 19:02, 7. Jan. 2018 (CET)
Näherungslösung mit 42 (Douglas Adams)
[Quelltext bearbeiten]Und die 42 ist doch die Antwort auf die Frage "nach dem Sinn des Lebens, dem Universum und dem ganzen Rest". Beim Ziegenproblem gibt die 42 als Antwort die Näherungslösung
mit einem noch besseren relativen Fehler als im Hauptartikel von
Wer übrigens dabei an den Einfluss böser Mächte glaubt, dem sei mitgeteilt, dass
ist. --Apio22 (Diskussion) 19:42, 10. Jun. 2021 (CEST)
- Ja, das ist richtig, der relative Fehler ist in der Näherungslösung mit 42 um (!) besser. Die Konstruktion im Artikel besticht aber durch ihren sehr geringen Aufwand. Mit Gruß--Petrus3743 (Diskussion) 00:32, 8. Nov. 2021 (CET)


















