Triangulierte Kategorie

Triangulierte Kategorie ist ein Begriff aus der homologischen Algebra. Triangulierte Kategorien bieten einen gemeinsamen Rahmen für derivierte Kategorien und für die stabilen Modulkategorien der Darstellungstheorie. Ursprünglich wurden sie durch Verdier eingeführt, um derivierte Funktoren der algebraischen Geometrie zu studieren.

Definition

Eine triangulierte Kategorie besteht aus

• einer additiven Kategorie ${\mathcal {C}}$,
• einem additiven Funktor $T\colon {\mathcal {C}}\rightarrow {\mathcal {C}}$, der eine Äquivalenz von Kategorien ^(a) ist, und
• einer Klasse von Tripeln von Morphismen $A\,{\xrightarrow {f}}\,B\,{\xrightarrow {g}}\,C\,{\xrightarrow {h}}\,T(A)$ in ${\mathcal {C}}$. Elemente $(f,g,h)$ dieser Klasse nennt man ausgezeichnete Tripel.

Dabei verlangt man, dass die folgenden vier Axiome gelten: ^(b)

(TR1)

• Zu jedem Objekt $X$ aus ${\mathcal {C}}$ ist das Tripel $X\,{\xrightarrow {\operatorname {Id} _{X}}}\,X\rightarrow \,0\,\rightarrow T(X)$ ausgezeichnet.
• Zu jedem Morphismus $A\,{\xrightarrow {f}}\,B$ aus ${\mathcal {C}}$ gibt es mindestens ein ausgezeichnetes Tripel der Form $A\,{\xrightarrow {f}}\,B\,{\xrightarrow {g}}\,C\,{\xrightarrow {h}}\,T(A)$.
• Ein Tripel ist genau dann ausgezeichnet, wenn es zu einem ausgezeichneten Tripel isomorph ist. Das heißt: Ist das Diagramm
  
  kommutativ, und sind die senkrechten Morphismen Isomorphismen, dann ist die untere Zeile genau dann ein ausgezeichnetes Tripel, wenn die obere Zeile ein ausgezeichnetes Tripel ist.

(T2)

Ist $A\,{\xrightarrow {f}}\,B\,{\xrightarrow {g}}\,C\,{\xrightarrow {h}}\,T(A)$ ausgezeichnet, dann ist auch $B\,{\xrightarrow {g}}\,C\,{\xrightarrow {h}}\,T(A)\,{\xrightarrow {-T(f)}}\,T(B)$ ausgezeichnet.

(TR3)

Kommutiert das linke Quadrat im Diagramm

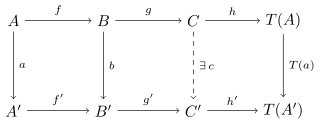
und sind die beiden Zeilen ausgezeichnete Tripel, dann gibt es (mindestens) einen Morphismus $c$ derart, dass das ganze Diagramm kommutiert.

(T4) Schwaches Oktaederaxiom

Ist $h=g\circ f$, dann gibt es ausgezeichnete Tripel $(f,f',f'')$, $(g,g',g'')$, $(h,h',h'')$ und $(j,j',j'')$ derart, dass das folgende „Zopfdiagramm“ ^(c) kommutiert.

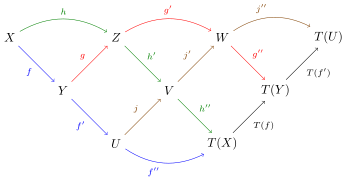
Beispiele

Häufig definiert man die Klasse der ausgezeichneten Tripel, indem man eine Klasse von Standardtripeln beschreibt und dann definiert: Ein Tripel ist genau dann ausgezeichnet, wenn es zu einem Standardtripel isomorph ist.

1. Sei ${\mathcal {A}}$ eine abelsche Kategorie. Dann ist auch die Kategorie $\mathop {Ch} ({\mathcal {A}})$ aller Kettenkomplexe in ${\mathcal {A}}$ abelsch. Analog zur herkömmlichen Homotopie-Kategorie bildet man die Homotopie-Kategorie $K({\mathcal {A}})$, indem man kettenhomotope Morphismen in $\mathop {Ch} ({\mathcal {A}})$ miteinander identifiziert. Diese Kategorie ist selbst nicht abelsch, aber doch trianguliert, wobei:
   • $T$ ist die Verschiebung $T(A)_{*}=A[-1]_{*}$, das heißt $T(A)_{n}=A_{n-1}$ und $d_{n}^{T(A)}=-d_{n-1}^{A}$.
   • Die Standardtripel sind die Tripel der Form $A_{*}\,{\xrightarrow {f_{*}}}\,B_{*}\,{\xrightarrow {i_{*}}}\,C(f)_{*}\,{\xrightarrow {j_{*}}}\,A[-1]_{*}$ für jeden Morphismus $A_{*}\,{\xrightarrow {f_{*}}}\,B_{*}$ aus $\mathop {Ch} ({\mathcal {A}})$, wobei $C(f)_{*}$ der Abbildungskegel ist und $i_{*}$, $j_{*}$ die entsprechenden Strukturabbildungen sind.

Literatur

• Sergei I. Gelfand, Yuri I. Manin: Methods of Homological Algebra. 2. Auflage. Springer, Berlin 2003, ISBN 978-3-642-07813-2. 
• Dieter Happel: Triangulated Categories in the Representation Theory of Finite Dimensional Algebras (= London Mathematical Society Lecture Note Series. Nr. 119). Cambridge University Press, 1988, ISBN 0-521-33922-7. 
• Amnon Neeman: Triangulated Categories (= Annals of Mathematics Studies. Nr. 146). Princeton University Press, 2001, ISBN 0-691-08685-0. 
• Wolfgang Soergel: Derivierte Kategorien und Funktoren. (PDF) Mathematisches Institut, Universität Freiburg, 7. April 2017, abgerufen am 8. April 2017 (Vorlesungsskript). 
• Charles A. Weibel: An introduction to homological algebra (= Cambridge Studies in Advanced Mathematics. Nr. 38). Cambridge University Press, 1994, ISBN 0-521-43500-5, Kapitel 10. 
• Alexander Zimmermann: Representation Theory: A Homological Algebra Point of View (= Algebra and Applications. Nr. 19). Springer, Cham 2014, ISBN 978-3-319-07968-4, §3.4. 

Anmerkungen

 

Viele Quellen verlangen sogar einen Isomorphismus von Kategorien, was manche Aussagen vereinfacht. Die stabile Modulkategorie ist ein Beispiel, wo $T$ – in diesem Fall der Heller-Operator – kein Isomorphismus von Kategorien ist.

 

Axiome nach Paul Balmers Rezension eines Artikels von J. Peter May

 

Diese diagrammatische Darstellung des Oktaederaxioms ist von May, der ein Sinuswelle-Diagramm von J. F. Adams als seine Inspiration angibt.