Benutzer:Googolplexian1221/Modulform

Bei der sog. j-Funktion - hier im kolorierten Schaubild - handelt es sich um eine Modulfunktion. Ihre außerordentliche Symmetrie zeichnet sich durch eine unendliche Anzahl von Funktionalgleichungen (darunter 1-Periodizität und $j(-1/z)=j(z)$) bei gleichzeitiger komplexer Differenzierbarkeit aus.

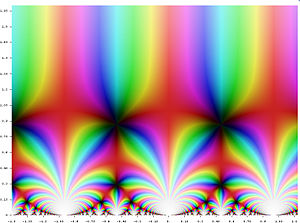
In der Mathematik sind Modulformen eine bestimmte Gattung von Funktionen, die eine überaus starke Form der Symmetrie besitzen, und aufgrund ihrer sehr breiten Anwendungsmöglichkeiten wie zum Beispiel in algebraischer, algorithmischer und analytischer Zahlentheorie, Topologie, Darstellungstheorie, Gruppentheorie, komplexer, algebraischer bzw. arithmetischer Geometrie, diskreter Mathematik, Kombinatorik, Funktionentheorie, Stringtheorie, Quantenphysik, Differentialgleichungen und Knotentheorie zu den bedeutendsten Objekten innerhalb der modernen Mathematik bzw. theoretischen Physik gehören.

In der klassischen Form handelt es sich um auf der oberen Halbebene der komplexen Zahlen meromorphe Funktionen, die ein bestimmtes Transformationsverhalten bezüglich ihrer Funktionswerte respektieren, und am Rand ihres Definitionsbereichs kein zu starkes Wachstum besitzen. In einigen Anwendungen verlangt man jedoch einschränkend, dass Modulformen holomorphe Funktionen sind, was ihnen nochmal erheblich mehr Struktur verleiht. Wichtiger Spezialfall ist der Begriff der Modulfunktion, der zusätzlich eine Form der absoluten Invarianz fordert, was eine höhere Anforderung als denen einer Modulform darstellt. Ihre Entdeckungsgeschichte lässt bis in die Anfänge des 19. Jahrhunderts zurückverfolgen, wo sie besonders mit Namen wie Carl Friedrich Gauß, Gotthold Eisenstein und Carl Gustav Jacobi assoziiert sind. Umfangreiche Forschungsprogramme ab dem 20. Jahrhundert haben jedoch zu sehr weitreichenden Verallgemeinerungen von „klassischen Modulformen“ geführt, und den Begriff der automorphen Formen geprägt, die in der modernen Mathematik primär als Objekte der Darstellungstheorie gesehen werden.

Modulformen werden als Kandidaten für eine Vereinheitlichung großer Bereiche der Mathematik und theoretischen Physik gesehen. Damit ist gemeint, dass sie Brücken zwischen mathematischen aber auch physikalischen Theorien bauen, die längere Zeit als verschieden angesehen wurden und teils eine völlig unterschiedliche mathematische Historie und Tradition haben. In manchen Fällen sind solche Zusammenhänge in der Vergangenheit schon gezeigt worden, in anderen Fällen, besonders im Umfeld der Zahlentheorie und Darstellungstheorie, werden sie bis heute nur vermutet. Sehr kurz beschreiben lassen sich diese Zusammenhänge durch ein „gemeinsames Vorhandensein von Symmetrie“. Vereinheitlichende mathematische Theorien sind deshalb von Interesse, da sie gewissermaßen die tiefere „Architektur der Mathematik“ aufzeigen, und durch die dadurch entstehenden Einsichten neue Anwendungsmöglichkeiten schaffen können. In etwa eröffnet sich die Möglichkeiten, Probleme einer Theorie äquivalent in eine andere Theorie zu übertragen, und gegebenenfalls mit den dort vorhandenen Methoden zu lösen. Auch in der theoretischen Physik gelten Modulformen als Bestandteil innerhalb mathematischer Theorien, die tiefere Strukturen hinter dem Aufbau des Universums erklären könnten - etwa im Umfeld „Großer vereinheitlichter Theorien“ (GUT) - ähnlich wie die Riemannsche Geometrie aus der Mathematik die Grundlage für Albert Einsteins Relativitätstheorie bildete, die sich später experimentell bestätigen ließ.

Der mathematische Hintergedanke bei der Definition einer Modulform ist, ein Objekt mit „so viel Struktur wie möglich“ auszustatten. Die Philosophie dahinter besagt, dass solche Objekte zwar unter Hinzunahme von Eigenschaften immer seltener, aber dadurch zugleich in der Theorie „immer mächtiger“ werden.

Dieser Artikel befasst sich primär mit den klassischen elliptischen Modulformen. Darüber hinaus wurden viele weitere Arten von Modulformen gefunden, zum Beispiel Jacobiformen, Siegelsche Modulformen, Hilbertsche Modulformen sowie p-adische Modulformen.

Einführung

Trotz sehr zahlreicher Anwendungen stechen einige Entdeckungen und Vermutungen um den Themenkomplex der Modulformen bzw. automorphen Formen besonders hervor:

• Holomorphen Modulformen, und allgemeiner auch gewissen automorphen Formen bzw. Darstellungen, können sog. L-Funktionen zugeordnet werden. Ist die betroffene Modulform eine sog. normalisierte Hecke-Eigenform, so besitzen diese L-Funktionen ein Euler-Produkt. Gleichzeitig impliziert die modulare Symmetrie eine Spiegelung des Abbildungsverhaltens der L-Funktion an einer vertikalen Geraden, der sog. kritischen Geraden. Die Große Riemannsche Vermutung besagt, dass sämtliche nicht-triviale Nullstellen dieser L-Funktionen auf dieser kritischen Geraden liegen. Prototyp ist die Riemannsche Zeta-Funktion, die zur Jacobischen Theta-Funktion, einer Modulform „halbganzen Gewichts“, korrespondiert. Eine Konsequenz dieser Aussage wäre eine Form der Pseudozufälligkeit in der Verteilung der Primzahlen. Von einem Beweis dieser Vermutung ist man, selbst im Spezialfall der klassischen Riemannschen Vermutung, noch weit entfernt.

• Zu Beginn des 20. Jahrhunderts nutzten Godfrey Harold Hardy und Srinivasa Ramanujan die Modularität der Dedekindschen Eta-Funktion, um eine asymptotische Formel für die Partitionsfunktion $p(n)$ herzuleiten, nämlich

$p(n)\sim {\frac {1}{4{\sqrt {3}}n}}e^{\pi {\sqrt {\frac {2n}{3}}}},\quad n\to \infty ,\qquad$ (mit der Kreiszahl $\pi =3,141\ldots$ und der Eulerschen Zahl $e=2,718\ldots$)

Es zählt $p(n)$ die Anzahl der Möglichkeiten, wie oft sich die Zahl $n$ als Summe natürlicher Zahlen unter Missachtung der Reihenfolge schreiben lässt, etwa $p(4)=5$, denn $1+1+1+1=1+1+2=2+2=1+3=4$. Im Jahr 1937 konnte Hans Rademacher, wieder mit Hilfe der vorhandenen Modularität, sogar eine exakte Formel angeben.

• Im Jahr 1952 konnte Kurt Heegner durch Anwendung vornehmlich Weberscher Modulfunktionen sämtliche imaginärquadratischen Zahlkörper mit Klassenzahl 1 klassifizieren, also solche, in deren Ganzheitsring eine eindeutige Primfaktorzerlegung existiert. Es gibt genau 9 solche imaginärquadratische Zahlkörper, nämlich $\mathbb {Q} ({\sqrt {-1}}),\mathbb {Q} ({\sqrt {-2}}),\mathbb {Q} ({\sqrt {-3}}),\mathbb {Q} ({\sqrt {-7}}),\mathbb {Q} ({\sqrt {-11}}),\mathbb {Q} ({\sqrt {-19}}),\mathbb {Q} ({\sqrt {-43}}),\mathbb {Q} ({\sqrt {-67}})$ und $\mathbb {Q} ({\sqrt {-163}})$, womit Heegner eine Vermutung von Carl Friedrich Gauß bestätigte. Unmittelbar mit Modulformen verknüpft sind in diesem Kontext die numerische Kuriosität

$e^{\pi {\sqrt {163}}}=262537412640768743,99999999999925007259\ldots \qquad$

sowie der bis heute genutzte Chudnovsky-Algorithmus zur schnellen Berechnung der Kreiszahl $\pi$.

• Im Jahr 1974 bewies Pierre Deligne die Weil-Vermutungen vollständig. Diese treffen eine Aussage über die Lösungsanzahlen von Varietäten über endlichen Körpern, mit zahlreichen Anwendungen in der Mathematik. Der Beweis umfasste ebenfalls die besonders schwierige lokale Riemannsche Vermutung, und gehört zu den größten mathematischen Durchbrüchen des 20. Jahrhunderts. Eine direkte Konsequenz ist die Ramanujan-Vermutung, die eine scharfe obere Grenze für die Fourier-Koeffizienten von Spitzenformen (Modulformen mit bestimmten Eigenschaften), liefert. Deligne erhielt für diese Leistungen 1978 die Fields-Medaille.

Aus Radioaufnahmen des Event Horizon Telescope berechnete Darstellung, die das supermassereiche Schwarze Loch der Galaxie M87 zeigt.

• Es ist durch wegweisende Arbeiten von Jacob Bekenstein und Stephen Hawking in den 1970er Jahren bekannt, dass schwarze Löcher eine thermodynamische Entropie besitzen und daher aus einer Sammlung mikroskopischer Quantenzustände bestehen sollten (siehe auch Bekenstein-Hawking-Entropie). Im Rahmen der Superstringtheorie können gewisse Anzahlen mikroskopischer Zustände in Verbindung gebracht werden, die das quantenstatistische System eines schwarzen Lochs bilden - was ihr thermodynamisches Verhalten aus einer fundamentaleren Perspektive erklärt. Der grundlegende Zusammenhang zu Modulformen ergibt sich aus der Beobachtung, dass in der einfachsten superstring-theoretischen Konstruktion die erzeugende Funktion der Anzahl der mikroskopischen Zustände eine Modulform ist. In einer Richtung fungiert die modulare Symmetrie als mächtiger Leitfaden für die Berechnung von quantengravitativen Effekten auf die Entropie des schwarzen Lochs. In der anderen Richtung hat dieser Zusammenhang zur Entdeckung überraschender Beziehungen zwischen den „Mock-Modulformen“ - erste Beispiele wurden von Srinivasa Ramanujan bereits in der 1910ern konstruiert - und einer Klasse stringtheoretischer schwarzer Löcher geführt, was eine unendliche Anzahl neuer Beispiele für Mock-Modulformen liefert.

• Richard Borcherds zeigte 1992 mit der Hilfe sog. Vertex-Algebren im Rahmen des Monstrous moonshine (gelegentlich auch Moonshine theory, dt: „Mondscheintheorie“), dass es einen überraschenden Zusammenhang zwischen den Fourier-Koeffizienten der j-Funktion - einer Modulfunktion - und der Monstergruppe gibt. Die Monstergruppe ist mit ca. $8\times 10^{53}$ Elementen die größte unter den 26 sporadischen Gruppen, die sich im Rahmen der Klassifikation aller endlichen einfachen Gruppen in keine der dort gegebenen Klassen (mit je unendlich vielen Vertretern) einordnen lassen. Die Monstergruppe kann zum Beispiel als Automorphismengruppe einer kommutativen, nicht-assoziativen Algebra auf einem 196883-dimensionalen Raum realisiert werden - und zum Beispiel ist 196884 genau der erste Fourier-Koeffizient der j-Funktion. Borcherds erhielt für diese Leistung 1998 die Fields-Medaille.

• Im Jahr 1995 konnten Andrew Wiles und Richard Taylor im Rahmen des Modularitätssatzes zeigen, dass alle semi-stabilen elliptischen Kurven modular sind, also von einer Modulform „abstammen“. Dahinter verbirgt sich eine Parametrisierung elliptischer Kurven durch Modulformen, ähnlich wie zum Beispiel Sinus und Kosinus den Einheitskreis parametrisieren. Jedoch geht die Aussage des Satzes viel tiefer und impliziert eine „zahlentheoretische Beziehung“ zwischen elliptischen Kurven und Modulformen. Eine Konsequenz des Modularitätssatzes ist der Große Satz von Fermat und sein Beweis wird als einer der Höhepunkte der Mathematik des 20. Jahrhunderts gesehen. Im Umfeld der bis heute ungelösten Vermutung von Birch und Swinnerton-Dyer, einem Millennium-Problem der Mathematik, werden zudem Zusammenhänge zwischen der Anzahl rationaler Punkte auf elliptischen Kurven und den „analytischen Eigenschaften“ ihrer Modulformen (bzw. deren L-Funktionen), vermutet.

• Im Jahr 2016 löste Maryna Viazovska mit Hilfe der Theorie der Modulformen das Problem der dichtester Kugelpackungen in 8 Dimensionen. Dies gilt als einer der größten Durchbrüche der diskreten Mathematik der letzten Jahrzehnte. Viazovska erhielt für diese Leistung im Jahr 2022 die Fields-Medaille.

Geschichte

Die Anfänge der Theorie gehen auf Carl Friedrich Gauß zurück, der Transformationen spezieller Modulformen unter der Modulgruppe im Rahmen seiner Theorie des arithmetisch-geometrischen Mittels im Komplexen betrachtete (ein Fundamentalbereich zu $\Gamma (2)$ findet sich in seinen Aufzeichnungen schon 1805). Begründer der klassischen (rein analytischen) Theorie der Modulformen des 19. Jahrhunderts sind Richard Dedekind, Felix Klein, Leopold Kronecker, Karl Weierstraß, Carl Gustav Jacobi, Gotthold Eisenstein und Henri Poincaré. Ein bekanntes Beispiel für die Anwendung von Modulformen in der Zahlentheorie war der Satz von Jacobi (Anzahl der Darstellungen einer Zahl durch vier Quadrate). Die moderne Theorie der Modulformen entstand in der ersten Hälfte des 20. Jahrhunderts durch Erich Hecke und Carl Ludwig Siegel, die Anwendungen in der Zahlentheorie verfolgten. Hier spielt die Theorie der Hecke-Operatoren, die im Raum der Modulformen wirken, und mit ihnen definierter Dirichletreihen (Hecke L-Reihe) eine besondere Rolle. Modulformen in Termen der Darstellungstheorie stammen von Robert Langlands (Langlands-Programm). p-adische Modulformen treten zuerst bei Nicholas Katz und Jean-Pierre Serre auf. Modulformen spielten auch eine zentrale Rolle im Beweis der Vermutung von Fermat (Modularitätssatz, der wiederum ein Spezialfall der 2006 bewiesenen Serre-Vermutung ist), die Modulformen mit Galoisdarstellungen der absoluten Galoisgruppe von Zahlkörpern verbindet. Sowohl beim Beweis der Lösung des Gaußschen Klassenzahlproblems durch Kurt Heegner als auch des letzten Teils der Weil-Vermutungen (Riemann-Hypothese) und damit verbunden der Ramanujan-Vermutung durch Pierre Deligne spielten Modulformen eine wichtige Rolle wie auch beim Beweis von Maryna Viazovska (2016), dass das E8-Gitter in acht Dimensionen und das Leech-Gitter in 24 Dimensionen dichteste Kugelpackungen liefern (die Thetafunktionen dieser beiden Gitter sind Modulformen, siehe unten). Modulformen kodieren häufig arithmetische Informationen der algebraischen Zahlkörper, sind aber viel einfacher rechnerisch zugänglich, teilweise schon mit Computeralgebra-Programmen, und die Anzahl linear unabhängiger Modulformen bestimmten Typs ist beschränkt.

Definition elliptischer Modulformen

Vorbereitung

Es sei

$\mathbb {H} :=\{z\in \mathbb {C} \mid \mathrm {Im} (z)>0\}$

die obere Halbebene, d. h. die Menge aller komplexen Zahlen mit positivem Imaginärteil. Es ist aus der klassischen Funktionentheorie bekannt, dass die Gruppe ${\text{SL}}_{2}(\mathbb {R} )$ via Möbiustransformation auf $\mathbb {H}$ operiert. Dabei werden, wie bei einer Gruppenoperation üblich, die Elemente $M\in {\text{SL}}_{2}(\mathbb {R} )$ als Abbildungen $\mathbb {H} \to \mathbb {H}$ aufgefasst. Man setzt:

${\begin{pmatrix}a&b\\c&d\end{pmatrix}}\langle z\rangle :={\frac {az+b}{cz+d}}.$

Über Möbiustransformation kann damit eine Aktion auf dem Vektorraum der auf ganz $\mathbb {H}$ meromorphen bzw. holomorphen Funktionen ${\mathcal {M}}(\mathbb {H} )$ bzw. ${\mathcal {O}}(\mathbb {H} )$ definiert werden. Dafür wird ein $k\in \mathbb {Z}$ fixiert. Man definiert dann den Peterssonschen Strichoperator durch

$f|_{k}M(z):=(cz+d)^{-k}f\left({\frac {az+b}{cz+d}}\right)=(cz+d)^{-k}f(M\langle z\rangle ),\qquad M:={\begin{pmatrix}a&b\\c&d\end{pmatrix}}.$

Offenbar ist dann $f|_{k}M$ wieder in ${\mathcal {M}}(\mathbb {H} )$ bzw. ${\mathcal {O}}(\mathbb {H} )$. Es gilt zudem für alle $M,N\in {\text{SL}}_{2}(\mathbb {R} )$ die Rechenregel

$(f|_{k}M)|_{k}N=f|_{k}(MN),$

womit der Peterssonsche Strichoperator eine Operation auf dem Raum der meromorphen bzw. holomorphen Funktionen auf der oberen Halbebene definiert.

Jede holomorphe und zugleich 1-periodische Funktion auf der oberen Halbebene besitzt eine Fourier-Entwicklung

$f(z)=\sum _{n=-\infty }^{\infty }a_{n}e^{2\pi izn}$

mit irgendwelchen komplexen Koeffizeinten $a_{n}$, die eindeutig bestimmt sind. In diesem Kontext ist es üblich, $q:=e^{2\pi iz}$ zu definieren, und abkürzend

$f(z)=\sum _{n=-\infty }^{\infty }a_{n}q^{n}$

zu schreiben. Ist $f$ lediglich meromorph in $\mathbb {H}$, besitzt in $i\infty$ jedoch keine Häufung an Polstellen, ist also holomorph auf einer Halbebene $\mathbb {H} _{r_{0}}:=\{z\in \mathbb {H} \colon \mathrm {Im} (z)>r_{0}\}$ für ein $r_{0}>0$, so kann auf jener eingeschränkten Halbebene $\mathbb {H} _{r_{0}}$ wiederum eine Fourier-Reihe oberen Typs angegeben werden.

Die volle Modulgruppe

Die volle Modulgruppe ist definiert durch

${\text{SL}}_{2}(\mathbb {Z} )=\left\{\left.{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\right|a,b,c,d\in \mathbb {Z} ,\ ad-bc=1\right\}.$

Es handelt sich also um die Kollektion aller $2\times 2$-Matrizen mit ganzen Einträgen, deren Determinante gleich 1 ist. Jede Matrix in der vollen Modulgruppe hat also eine ebenfalls ganzzahlige Inverse mit Determinante 1. Offenbar ist sie eine echte Untergruppe von ${\text{SL}}_{2}(\mathbb {R} )$. Gelegentlich wird abkürzend $\Gamma :={\text{SL}}_{2}(\mathbb {Z} )$ geschrieben. Sie wird durch die Matrizen

$S={\begin{pmatrix}0&-1\\1&0\end{pmatrix}},\qquad T={\begin{pmatrix}1&1\\0&1\end{pmatrix}}$

erzeugt. Diese Matrizen beschreiben geometrisch eine Spiegelung an einem Kreis (Inversion) und eine Translation.

Manche Autoren bezeichnen auch die projektive spezielle lineare Gruppe $\mathrm {PSL} _{2}(\mathbb {Z} )$ als volle Modulgruppe, in der Matrizen $M$ und $-M$ identifiziert werden. Sie ist der Quotient von ${\text{SL}}_{2}(\mathbb {Z} )$ nach ihrem Zentrum $\{\pm I_{2}\}$ und der Einheitsmatrix $I_{2}$.

Modulformen zur vollen Modulgruppe

Definition

Für eine ganze Zahl $k$ heißt eine holomorphe bzw. meromorphe Funktion $f$ auf der oberen Halbebene eine holomorphe bzw. meromorphe elliptische Modulform vom Gewicht $k$ zur Gruppe ${\mbox{SL}}_{2}(\mathbb {Z} )$, wenn sie folgende Eigenschaften erfüllt:

• Sie ist invariant unter dem Peterssonschen Strichoperator bezüglich $k$, also $f|_{k}M=f$ für alle $M\in {\mbox{SL}}_{2}(\mathbb {Z} )$. Äquivalent gelten simultan die Funktionalgleichungen

$f\!\left({\frac {az+b}{cz+d}}\right)=(cz+d)^{k}f(z)$ für alle $z\in \mathbb {H}$ und $a,b,c,d\in \mathbb {Z}$ mit $ad-bc=1.$

Insbesondere gilt mit der Wahl $M=T={\begin{pmatrix}1&1\\0&1\end{pmatrix}}$ stets $f(z+1)=f(z)$.

• Sie ist „holomorph bzw. meromorph im Unendlichen“. Das bedeutet, dass sie für alle $z$ mit hinreichend großem Imaginärteil in eine Fourier-Reihe von der Form

$f(z)=\sum _{n=-n_{0}}^{\infty }a_{n}q^{n}$

mit einem $n_{0}\in \mathbb {N} _{0}$ entwickelbar ist, wobei im holomorphen Fall sogar $n_{0}=0$ gewählt werden kann und die betroffene Fourier-Reihe auf der gesamten oberen Halbebene konvergiert.

Eine Modulform von Gewicht $k=0$ nennt man auch Modulfunktion. Modulfunktionen haben ein besonders einfaches Verhalten unter der Modulgruppe, da der Faktor $(cz+d)^{0}=1$ entfällt:

$f\left({\frac {az+b}{cz+d}}\right)=f(z).$

Holomorphe Modulfunktionen sind uninteressant, da aufgrund des Satzes von Liouville die einzigen holomorphen Modulfunktionen die konstanten Funktionen sind. Man nennt die holomorphen Modulformen auch ganze Modulformen. Verschwindet eine solche ganze Modulform darüber hinaus im Unendlichen $\mathrm {Im} (z)\to \infty$ (in der Spitze, englisch cusp, $q=0$), so nennt man sie Spitzenform. Die j-Funktion ist dagegen eine in der oberen Halbebene holomorphe Modulfunktion bis auf einen einfachen Pol in der Spitze, also ein Beispiel für Meromorphie. Aus der Definition folgt, dass eine Modulform für ungerades $k$ identisch verschwindet.

Die Abbildung stellt die berühmte Modulfigur dar, die zum Beispiel von M. C. Escher in mehreren Graphiken künstlerisch dargestellt wurde.

Das Verhalten der Modulform vom Gewicht $k$ unter diesen Erzeugenden ist

$f(-1/z)=z^{k}f(z),\qquad f(z+1)=f(z)$

und aus letzterer Gleichung ergibt sich, dass die Modulform periodisch ist. Daher ist die Fourierentwicklung ${\tilde {f}}(q)$ für $0<|q|<1$ wohldefiniert und holomorph bzw. meromorph. Mit den Fourierkoeffizienten $a_{n}$ hat man die Fourierreihe (auch q-Entwicklung genannt)

$f(z)=\sum _{n=-m}^{\infty }a_{n}e^{2i\pi nz}=\sum _{n=-m}^{\infty }a_{n}q^{n}$,

wobei $m$ die Ordnung des Pols von $f$ in der Spitze $q=0$ genannt wird (Imaginärteil von $z$ gegen Unendlich). Die Modulform ist bei negativen Fouriergliedern meromorph in der Spitze. Bei einer Spitzenform verschwindet $f$ bei $q=0$ ($a_{0}=0$), das heißt, die nichtverschwindenden Fourierkoeffizienten beginnen bei einem positiven $n$, das dann Ordnung der Nullstelle von $f$ in der Spitze genannt wird.

In der komplexen Ebene ist eine Modulform durch ihre Werte im Fundamentalbereich $\mathbb {H} /\Gamma$ definiert, der in der nebenstehenden Abbildung grau gefärbt ist. Er ist ein Dreieck mit einer Spitze im Unendlichen. Jedes der durch Geraden oder Kreise begrenzten fundamentalen Dreiecke entsteht durch Anwendung von Operationen der Modulgruppe auf den Fundamentalbereich. Die Anwendung der Modulgruppe lässt sich beliebig fortsetzen und ergibt eine immer feinere Einteilung, die aber in der Abbildung an einem bestimmten Punkt abgebrochen wurde.

Modulformen zu Kongruenzuntergruppen

Statt für ${\text{SL}}(2,\mathbb {Z} )$ werden Modulformen auch für diskrete Untergruppen dieser Gruppe betrachtet, insbesondere für die sogenannten Kongruenzuntergruppen der Modulgruppe ($N$ ist eine positive ganze Zahl):

$\Gamma _{0}(N)=\left\{\left.{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in {\text{SL}}(2,\mathbb {Z} )\right|c\equiv 0{\pmod {N}}\right\}$

$\Gamma (N)=\left\{\left.{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in {\text{SL}}(2,\mathbb {Z} )\right|c\equiv b\equiv 0{\pmod {N}},\quad a\equiv d\equiv 1{\pmod {N}}\right\}$

Die Zahl $N$ heißt die Stufe der zugeordneten Modulformen. $\Gamma (N)$ heißt auch die Hauptkongruenzgruppe der Stufe $N$. Jede Untergruppe von $SL(2,\mathbb {Z} )$, die die Hauptkongruenzgruppe für eine Stufe $N$ als Untergruppe enthält, wird Kongruenzuntergruppe genannt.

Bisweilen betrachtet man auch die Kongruenzuntergruppe

$\Gamma _{1}(N)=\left\{\left.{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in {\text{SL}}(2,\mathbb {Z} )\right|a\equiv d\equiv 1{\pmod {N}},\quad c\equiv 0{\pmod {N}}\right\},$

die eine Mittelstellung einnimmt zwischen $\Gamma _{0}$ (modulo $N$ äquivalent zu oberer Dreiecksmatrix) und $\Gamma$ (modulo $N$ äquivalent zur Einheitsmatrix). Es gilt $\Gamma (N)\subseteq \Gamma _{1}(N)\subseteq \Gamma _{0}(N)\subseteq SL(2,\mathbb {Z} )$ und $\Gamma (1)=\Gamma _{1}(1)=\Gamma _{0}(1)=SL(2,\mathbb {Z} )$.

Der Index der Kongruenzuntergruppen als Untergruppen von $SL(2,\mathbb {Z} )$ ist endlich und lässt sich explizit angeben. So ist:

$\left[\,SL(2,\mathbb {Z} )\colon \Gamma _{0}(N)\,\right]=N\prod _{p\mid N}\left(1+{\frac {1}{p}}\right)$

$\left[\,\Gamma _{0}(N)\colon \Gamma (N)\,\right]=N^{2}\prod _{p\mid N}\left(1-{\frac {1}{p}}\right)$

Die Modulformen zu den Kongruenzuntergruppen $\Gamma _{0}$ und $\Gamma _{1}$ haben Fourierentwicklungen in $q$; die von $\Gamma (N)$ für $N\geq 2$ nicht unbedingt, da die Matrix ($a=d=1,b=1,c=0$) in der Transformationsmatrix nicht dazugehört (sie haben eine Fourierentwicklung in $q^{1/N}$). Es lässt sich aber immer zu einer Modulform für $\Gamma (N)$ eine solche für $\Gamma _{1}(N^{2})$ zuordnen (die eine Fourierentwicklung in $q$ hat). Auch gibt es für Kongruenzuntergruppen kein so einfaches Kriterium für Spitzenformen (der konstante Fourierterm muss nicht unbedingt verschwinden wie bei der vollen Modulgruppe). Neben Modulformen mit Transformationsverhalten wie bei der vollen Modulgruppe diskutiert werden auch solche mit erweitertem Transformationsverhalten (Multiplikation mit einem Dirichlet-Charakter) betrachtet.

Mit diesen Kongruenzuntergruppen kann man die Quotientenräume wie $H\backslash \Gamma (N)=Y(N)$ bilden, die durch Hinzunahme endlich vieler Punkte (Cusps, Spitzen der Kongruenzuntergruppe) in der erweiterten oberen Halbebene $H^{*}$ kompaktifiziert werden, der entsprechende kompaktifizierte Quotientenraum heißt dann $X(N)$. Entsprechend spricht man bei der Kongruenzuntergruppe $\Gamma _{0}(N)$ von $Y_{0}(N)$ bzw. $X_{0}(N)$ und bei $\Gamma _{1}(N)$ von $Y_{1}(N),X_{1}(N)$. Nach Kompaktifizierung erhält man kompakte Riemannsche Flächen unterschiedlichen topologischen Geschlechts $g$. Die verschiedenen $X,Y$ heißen auch Modulkurven.

Zum Beispiel ist $X(5)$ die Riemannsphäre (Geschlecht 0) mit 12 Spitzen, die wie das Ikosaeder angeordnet sind. $X(7)$ ist die Klein-Quartik mit Geschlecht 3 und 24 Spitzen. $X_{0}(N)$ ist die klassische Modulkurve und wird auch häufig einfach nur als Modulkurve bezeichnet.

Modulkurven parametrisieren Äquivalenzklassen von elliptischen Kurven abhängig von der Art der Kongruenzuntergruppe und lassen sich rein algebraisch definieren und so auch über anderen Körpern als $\mathbb {C}$ betrachten. Sie sind in der arithmetischen Geometrie von Bedeutung.

Beispiele

Die einfachsten Beispiele für ganze Modulformen vom Gewicht $k$ sind die sogenannten Eisensteinreihen $G_{k}$, für eine Modulfunktion die j-Funktion oder absolute Invariante und für eine Spitzenform die Diskriminante $\Delta$.

Unter den Erzeugenden der Modulgruppe transformiert die Eisensteinreihe:

$E_{k}(-1/\tau )=\tau ^{k}E_{k}(\tau )$

$E_{k}(\tau +1)=E_{k}(\tau )$

Eigenschaften und Theorieaspekte

Valenzformel und Vektorräume der Modulformen

Volle Modulgruppe

Für ungerades $k$ ist stets $f=0$, die folgenden Aussagen gelten daher für gerades $k$.

Summen und Produkte von Modulformen sind wieder Modulformen. Die Modulformen vom Gewicht $k$ bilden einen $\mathbb {C}$-Vektorraum, ebenso die ganzen Modulformen und auch die Spitzenformen.

Bezeichnet man diese Vektorräume mit $\mathbb {V} _{k},\mathbb {M} _{k}$ und $\mathbb {S} _{k}$, so gilt:

$\mathbb {S} _{k}\subset \mathbb {M} _{k}\subset \mathbb {V} _{k}$

Für die Dimension dieser Vektorräume gilt ($k$ sei eine positive gerade ganze Zahl):

$\mathrm {dim} \,\mathbb {M} _{k}={\begin{cases}\left[{\frac {k}{12}}\right],&{\mbox{falls}}\;k\equiv 2\;(\mathrm {mod} \ 12)\\\left[{\frac {k}{12}}\right]+1,&{\mbox{falls}}\;k\not \equiv 2\;(\mathrm {mod} \ 12)\end{cases}}$

$\mathrm {dim} \,\mathbb {S} _{k}={\begin{cases}\left[{\frac {k}{12}}\right]-1,&{\mbox{falls}}\;k\equiv 2\;(\mathrm {mod} \ 12)\\\left[{\frac {k}{12}}\right],&{\mbox{falls}}\;k\not \equiv 2\;(\mathrm {mod} \ 12)\end{cases}}$

Da durch die Multiplikation mit der Spitzenform $\Delta$ (Diskriminante) vom Gewicht 12 ein Isomorphismus von $\mathbb {M} _{k-12}$ nach $\mathbb {S} _{k}$ gegeben ist, gilt

$\mathrm {dim} \,\mathbb {S} _{k}=\mathrm {dim} \,\mathbb {M} _{k-12},\quad \mathrm {falls} \quad k\geq 12.$

Die Modulräume $\mathbb {M} _{k}$ für $k=0,4,6,8,10,14$ sind eindimensional und werden erzeugt von den $1,E_{4},E_{6},E_{4}^{2},E_{4}\cdot E_{6},E_{4}^{2}\cdot E_{6}$ und für $k=12$ zweidimensional, erzeugt von $(E_{4}^{3},E_{6}^{2})$ mit den Eisensteinreihen $E_{4},E_{6}$. Allgemein kann man zeigen, dass alle Elemente von $\mathbb {M} _{k}$ durch Polynome in $E_{4},E_{6}$ erzeugt werden:

$f(z)=\sum _{a,b\in \mathbb {N} \atop 4a+6b=k}\alpha _{a\,,\,b}E_{4}^{a}(z)\cdot E_{6}^{b}(z)$

mit Konstanten $\alpha _{a,b}$. Es ist aber häufig nützlicher, Basen von Eigenformen der Hecke-Operatoren zu verwenden (Atkin-Lehner-Theorie).

Hans Petersson führte das Petersson-Skalarprodukt im Raum der Spitzenformen ein und machte diese damit zu einem Hilbertraum. Man kann mit dem Satz von Riemann-Roch Aussagen über die Dimension der Vektorräume der Spitzenformen machen. Eisensteinreihen sind bezüglich des Petersson-Skalarprodukts orthogonal zu den Spitzenformen.

Ein Grund für die Nützlichkeit von Modulformen in unterschiedlichsten Anwendung ist, dass sie zwar häufig unterschiedliche Beschreibungen in den verschiedensten Anwendungen haben, man aber sofort Verbindungen unter den Modulformen findet, da die Vektorräume von relativ kleiner Dimension sind.

Hecke-Theorie

→ Hauptartikel: Hecke-Operator

Anwendungen

Elliptische Funktionen und Gitter

Die Modulgruppe hat die wichtige Eigenschaft, dass sie Gitter in der komplexen Ebene auf sich abbildet. Diese Gitter werden von zwei komplexen Zahlen $\omega _{1},\omega _{2}\in \mathbb {C} \setminus \{0\}$ mit $\tau ={\tfrac {\omega _{1}}{\omega _{2}}}\not \in \mathbb {R}$ aufgespannt:

$\Lambda :=\left\{m\omega _{1}+n\omega _{2}\mid m,n\in \mathbb {Z} \right\}$

Sie lassen sich als Parallelogramme in der komplexen Zahlenebene darstellen. Eine andere Basis des Gitters, gegeben durch zwei komplexe Zahlen $\alpha _{1},\alpha _{2}$, spannt genau dann dasselbe Gitter auf, wenn die beiden Basen durch ein Element der Modulgruppe ineinander transformiert werden (das folgt aus der Bedingung, dass die Determinante gleich 1 ist und aus der Ganzzahligkeit):

${\begin{pmatrix}\alpha _{1}\\\alpha _{2}\end{pmatrix}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}\omega _{1}\\\omega _{2}\end{pmatrix}}$

Setzt man $\tau ={\tfrac {\omega _{1}}{\omega _{2}}}$, ergibt sich die oben angegebene Transformationsformel $\tau \to {\tfrac {a\tau +b}{c\tau +d}}$ über eine Möbiustransformation.

Eisensteinreihen sind auf natürliche Weise auf diesen Gittern definiert:

$E_{k}(\Lambda )=\sum _{(0,0)\neq (m,n)\in \mathbb {Z} ^{2}}{\frac {1}{(m\omega _{1}+n\omega _{2})^{k}}}$

Oder mit $\tau ={\tfrac {\omega _{1}}{\omega _{2}}}$ (also einem $\tau$ aus der oberen Halbebene):

$E_{k}(\tau )=\sum _{(0,0)\neq (m,n)\in \mathbb {Z} ^{2}}{\frac {1}{(m+n\tau )^{k}}}$

Da das Gitter invariant unter der Modulgruppe ist, gilt dies auch für die Eisensteinreihen. Sie sind ganze Modulformen vom Gewicht $k$, wobei $k$ gerade ist (sonst würde die Modulform identisch verschwinden, da über alle Gitterpunkte $\lambda$ summiert wird, worunter sich auch $-\lambda$ befindet). Damit die Reihen absolut konvergieren, muss auch $k$ größer als 2 sein.

Der Zusammenhang mit Gittern ergibt auch eine Verbindung von Modulformen zu elliptischen Funktionen, die als doppeltperiodische, meromorphe Funktionen auf einem solchen Gitter definiert sind (werden die Seiten des Gitters miteinander identifiziert, ergibt sich ein Torus mit topologischem Geschlecht $g=1$, die Riemannsche Fläche der elliptischen Funktionen). Am einfachsten wird das durch Betrachtung der Weierstraßschen ℘-Funktion deutlich. Meromorphe Modulformen vom Gewicht 0 sind auf den Isomorphieklassen der den elliptischen Funktionen zugrundeliegenden Gittern definiert. Die j-Invariante einer elliptischen Funktion kennzeichnet diese Isomorphieklassen, die damit von dieser Funktion der oberen Halbebene eindeutig parametrisiert werden. Sie ist eine Modulform vom Gewicht 0 und lässt sich als rationale Funktion aus Eisensteinreihen vom Gewicht 4 und 6 bilden, mit der modularen Diskriminante im Nenner, einer Modulfunktion vom Gewicht 12 (sie steht wiederum mit der Dedekindschen η-Funktion in Verbindung). Die j-Funktion hat viele interessante Eigenschaften, die sie wichtig für die Zahlentheorie (Konstruktion algebraischer Zahlkörper) und Gruppentheorie (die Fourierkoeffizienten ihrer q-Entwicklung stehen mit der Darstellung der Monstergruppe in Verbindung, moonshine) machen.

Modularitätssatz und elliptische Kurven

→ Hauptartikel: Modularitätssatz

Irrationalitätsbeweis der Apéry-Konstante

→ Hauptartikel: Apéry-Konstante

1987 konnte Frits Beukers die Irrationalität von $\zeta (3)$ mit Hilfe der Theorie der Eisensteinreihen beweisen. Dafür betrachtete er die Funktion

$F(z)={\frac {1}{40}}\left(E_{4}(z)-36E_{4}(6z)-28E_{4}(2z)+63E_{4}(3z)\right),$

die eine Modulform zum Gewicht 4 für die Kongruenzuntergruppe $\Gamma _{1}(6)$ ist. Die zu diesem $F$ korrespondierende L-Funktion ist dann

$L(F,s)=6\left(1-{\frac {36}{6^{s}}}-{\frac {28}{2^{s}}}+{\frac {63}{3^{s}}}\right)\zeta (s)\zeta (s-3).$

Das Argument bezieht sich letztlich auf eine Technik, die Konvergenzradien von Umkehrfunktionen lokal injektiver, meromorpher Funktionen ausnutzt. Mit der gleichen Methode lassen sich auch $\zeta (2)={\tfrac {\pi ^{2}}{6}}\notin \mathbb {Q}$ und $8\zeta (3)-5{\sqrt {5}}L(\chi _{5};3)\notin \mathbb {Q} ({\sqrt {5}})$ zeigen, wobei der Charakter $\chi _{5}$ das Legendre-Symbol modulo 5 ist. Die Techniken lassen sich jedoch laut Beukers selbst höchstwahrscheinlich nicht auf die Fälle $\zeta (5),\zeta (7),\dotsc$ übertragen, geben jedoch Einblick in algebraisch geometrische und modulare Interpretationen der Apery-Zahlen.

Verallgemeinerungen

Automorphe Formen

Modulfunktionen lassen sich durch Erweiterung der Art des Transformationsverhaltens und für andere Gruppen als die Modulgruppe verallgemeinern.

Zunächst wurden oben nur Modulformen zu ganzzahligem Gewicht $k$ betrachtet, es gibt aber auch solche zu rationalen Werten, die auch eine Rolle in der Zahlentheorie spielen, so benutzte Jerrold Tunnell Modulformen zum Gewicht $k=3/2$ bei der Lösung des Problems kongruenter Zahlen.

Beispielsweise kann man Funktionen betrachten, die sich durch Multiplikation mit einem automorphen Faktor transformieren:

$f\left({\frac {az+b}{cz+d}}\right)=\varepsilon (a,b,c,d)(cz+d)^{k}f(z)$

mit dem automorphen Faktor $\varepsilon (a,b,c,d)(cz+d)^{k}$, wobei $|\varepsilon (a,b,c,d)|=1$. Das sind Beispiele für automorphe Funktionen. Ein Beispiel ist die Dedekindsche Etafunktion. In der algebraischen Zahlentheorie werden auch häufig Modulfunktionen zur Kongruenzuntergruppe $\Gamma _{0}(N)$ betrachtet mit einem automorphen Faktor, der mit dem Dirichlet-Charakter $\chi {\pmod {N}}$ gebildet wird (Modulformen vom Gewicht $k$, Nebentypus $\chi$ und Stufe $N$):

$f\left({\frac {az+b}{cz+d}}\right)=\chi (d)(cz+d)^{k}f(z)$

Sie sind für $z$ in der oberen Halbebene definiert und holomorph in der Spitze.

Automorphe Formen sind für topologische Gruppen $G$ (Lie-Gruppen) definiert und deren diskrete Untergruppen $\Gamma$. Das entspricht im Fall der Modulformen für die Modulgruppe $SL(2,\mathbf {Z} )$ der Modulgruppe selbst als diskreter Untergruppe der Liegruppe $SL(2,\mathbf {R} )$ oder den Kongruenzuntergruppen als diskreten Untergruppe der Modulgruppe. Das Transformationsgesetz wird hier allgemein mit Automorphiefaktoren definiert. Automorphe Formen sind Eigenfunktionen bestimmter Casimir-Operatoren von $G$ (das entspricht bei den Modulfunktionen der Tatsache, dass diese analytische Funktionen in zwei Dimensionen sind, die die Laplacegleichung erfüllen, was dem Casimir-Operator für $SL(2,\mathbf {R} )$ entspricht) und erfüllen wie die Modulformen bestimmte Wachstumsbedingungen. Sie wurden schon im 19. Jahrhundert für Fuchssche Gruppen (diskrete Untergruppen von $SL(2,\mathbf {R} )$) von Henri Poincaré betrachtet und in der Zahlentheorie Anfang des 20. Jahrhunderts von David Hilbert (Hilbertsche Modulformen für total reelle Zahlkörper $F$ zur allgemeinen linearen Gruppe $GL_{2}^{+}({\mathcal {O}}_{F})$ über dem Ring der ganzen Zahlen des Zahlkörpers, definiert als Modulform auf dem $m$-fachen Produkt der oberen Halbebene, mit $m$ als Grad von $F$ über den rationalen Zahlen).

Ein weiteres Beispiel automorpher Formen in mehreren komplexen Variablen sind Siegelsche Modulformen, die im siegelschen Halbraum definiert sind und automorphe Formen zur symplektischen Gruppe sind. Sie spielen eine ähnliche Rolle für die Parametrisierung abelscher Varietäten wie Modulformen für die Parametrisierung von elliptischen Funktionen (als jeweilige Modulräume) und wurden von Carl Ludwig Siegel ursprünglich in der Theorie quadratischer Formen betrachtet.

Auch Jacobiformen sind automorphe Funktionen in mehreren Variablen, zu ihnen gehören zum Beispiel die Weierstraßsche ℘-Funktion und die Jacobische Thetafunktion.

Automorphe Formen spielen eine wesentliche Rolle im Langlands-Programm, wo algebraische Gruppen in einem zahlentheoretischen Kontext betrachtet werden (als algebraische Gruppen über dem Adelring eines algebraischen Zahlkörpers) und deren Darstellungstheorie eine besondere Rolle spielt.

Weitere Beispiele von Erweiterungen des Konzepts von Modulformen sind die Mock-Thetafunktionen von S. Ramanujan bzw. Mock-Modulformen. Sie sind selbst keine Modulformen, lassen sich aber durch Addition einer nicht-holomorphen Komponente (Schatten der Mock-Modulform genannt) zu einer Modulform vervollständigen und fanden spektakuläre Anwendung in der Theorie der Partitionen durch Ken Ono, Jan Hendrik Bruinier und Kathrin Bringmann. Sie stehen nach Sander Zwegers in Zusammenhang mit Maaß-Formen bzw. Maaß-Wellenformen von Hans Maaß, nicht-analytischen automorphen Formen, die als Eigenfunktionen des invarianten (hyperbolischen) Laplace-Operators zum Gewicht $k$ sind. Mock-Modulformen sind der holomorphe Anteil einer schwachen Maaßform, wobei sich das schwach auf die verlangten Wachstumsbedingungen bezieht.

Siegelsche und Hilbertsche Modulformen und Modulkurven sind Beispiele für Shimura-Varietäten.

Literatur

• Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Aufl., Springer, Berlin (2006), ISBN 3-540-31764-3.
• Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. 2. Aufl., Springer, Berlin (2007) ISBN 978-3-540-49324-2.
• Jean-Pierre Serre: A course in arithmetic. Springer, 1973.
• Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Springer, 1995, Kapitel 4, S. 238–291, Online, PDF.
• Serge Lang: Introduction to Modular forms. Springer, Grundlehren der mathematischen Wissenschaften, 1976.
• Neal Koblitz: Introduction to Elliptic Curves and Modular Forms. Springer, 1984.
• L. J. P. Kilford: Modular forms, a classical and computational introduction. Imperial College Press, London 2008.
• T. Miyake: Modular forms. Springer, 1989.

Weblinks

• Gabor Wiese, verschiedene Vorlesungen zu Modulformen
• Igor Dolgachev, Lectures on Modular Forms, PDF
• The L-functions and modular forms data base

Einzelnachweise und Anmerkungen

Kategorie:Funktionentheorie Kategorie:Analytische Zahlentheorie Kategorie:Gruppentheorie Kategorie:Mathematische Funktion