Diskussion:Fibonacci-Folge/Archiv/1

Diese Seite ist ein Archiv abgeschlossener Diskussionen. Ihr Inhalt sollte daher nicht mehr verändert werden. Benutze bitte die aktuelle Diskussionsseite, auch um eine archivierte Diskussion weiterzuführen.

Um einen Abschnitt dieser Seite zu verlinken, klicke im Inhaltsverzeichnis auf den Abschnitt und kopiere dann Seitenname und Abschnittsüberschrift aus der Adresszeile deines Browsers, beispielsweise

[[Diskussion:Fibonacci-Folge/Archiv/1#Thema 1]]

oder als Weblink zur Verlinkung außerhalb der Wikipedia

https://de.wikipedia.org/wiki/Diskussion:Fibonacci-Folge/Archiv/1#Thema_1

Programmierung

Es gibt 3 mir bekannte Prinzipien, um die Fibonacci-Zahlen zu berechnen:

1. rekursiv in quadratischer Laufzeit
2. iterativ in linearer Laufzeit
3. direkt in konstanter Laufzeit

Für die ersten beiden könnte ich ein Java-Programm schreiben, für die dritte die Formel TeXen. Ist Java OK? Die Programmiersprache, die hier benutzt wurde, kenne ich nicht, und Pseudocode finde ich furchtbar. --Head 00:15, 5. Sep 2003 (CEST)

Wenn's nach mir geht, können wir den Basic-Dialekt gerne in Java umschreiben. Eine Referenzimplementierung in Java zu 2. gibt's auf meiner Homepage (www.jonelo.de/java/bigal_de.html). Sourcecode ist im jar ;-) Jonelo 12:59, 5. Sep 2003 (CEST)

Die verwendete Programmiersprache ist QBasic (oder Basic - kA), ist eigentlich bekannt, aber hoffnungslos veraltet. floklk

Noch 'ne Meinung: Da Java ein Produkt und keine Programmiersprache ist, ist Pseudocode hier viel besser angebracht. Der Artikel sieht so einfach nur scheusslich aus, mit je einem Beispiel aus Python, Java und Pseudocode. Der Nächste kommt dann wohl mit VisualBasic, .NET, Cobol, Haskell, Lisp, Brainfuck, Dolog, C/C++, Rexx, Perl, Tcl, Delphi, Fortran, XYZ-Assembler, Postscript (Ja, Postscript ist eine Programmiersprache), M4, Redcode, awk oder Gofer an. ---

Nun, um genau zu sein ist Java ein Produkt, ein Trademark und natürlich auch eine Programmiersprache! Da sie in der Regel leicht zu lesen und plattformunabhänig ist, ist es wohl Geschmacksache was mehr Sinn macht: Pseudocode oder Java. Deinem zweiten Argument "zu viel Code im Artikel" stimme ich Dir aber hingegen voll zu. Meiner Meinung nach ist weniger oft mehr und ein ganzes Programm reinpasten ist wirklich overkill. Gibt's da noch andere Meinungen zum Artikel verschlanken/verschönern? Jonelo 22:43, 28. Apr 2004 (CEST)

hallo head, ich denke, du hast es nicht so gemeint, aber es könnte so mißverstanden werden:

1. rekursiv == quadratischer Laufzeit
2. iterativ == linearer Laufzeit

selbstverständlich läßt sich das ganze auch

1. rekursiv UND linear, bzw.
2. iterativ UND quadratisch berechnen.

zur programmiersprache: ich finde pseudocode ok, was ich nicht ok finde, sind 4 verschiedenen programmiersprachen in einem einzelnen artikel ( pseudo, basic, python, java). mfg Wzwz 23:16, 2. Mai 2004 (CEST)

Vier Programme dazu finde ich auch zuviel. Nebenbei ist die "iterative" Berechnung im Java-Programm die explizite Formel von Binet, kein iteratives Auswerten der Rekursionsgleichung. --SirJective 12:56, 5. Mai 2004 (CEST)

Ich finde die Aufführung von 4 verschiedenen Algorithmen per seitenlangem Quellkode in einem WP-Artikel völlig absurd. Wenn niemand protestiert, lösche ich demnächst den Beitrag von Benutzer:Took vom 27.02.04. Es bliebe dann nur das kleine Basicprogramm übrig. Hätte nichts dagegen, das auch zu löschen, muss aber nicht sein. --Wolfgangbeyer 23:24, 7. Jul 2004 (CEST)

Kein Widerspruch? Dann lösche ich das mal. Modifiziere auch mal das Basicprogramm, da es alles andere als schön ist, denn es berechnet pro Durchlauf gleich 2 Zahlen. Wem soll sowas überhaupt was bringen? Wenn jemand auch nur einen Funken von Programmierkenntnissen hat, dann schreibt er so ein Programm auf der Stelle hin (was simpleres gibts ja fast nicht) und wenn er keine hat, dann sagts ihm auch wenig. Aber ok ... --Wolfgangbeyer 10:52, 10. Jul 2004 (CEST)

Zahl / Zahlen

Gibt es einen besonderen Grund, warum der Artikel entgegen der Konventionen einen Pluraleintrag hat? Wenn man sich eine ganz bestimmte Zahl ansieht, die den Kriterien der Zahlen genügt, dann ist es üblich den Begriff in der Einzahl zu verwenden. Stern 00:36, 28. Apr 2004 (CEST)

In diesem Artikel geht es um eine bestimmte Zahlenfolge, deren einzelne Glieder nicht (ohne eine ziemlich willkuerlich aussehende explizite Formel) ohne die anderen Glieder definiert werden koennen. Oder weisst du einen Weg, eine Fibonacci-Zahl zu definieren, ohne alle (kleineren) Fibonacci-Zahlen zu definieren - und zwar ohne die Formel von Binet? Bei Fermat-Zahlen zum Beispiel ist das anders, die sind unabhaengig voneinander als Zahlen einer bestimmten Form definiert. --SirJective 12:56, 5. Mai 2004 (CEST)

Und wenn man den artikel nach Fibonacci-Zahlenfolge verschiebt? --Wiki Wichtel sowie KatEgo 23:38, 7. Jul 2004 (CEST)

Keine schlechte Idee. Ich hätte jedenfalls nichts dagegen. --Wolfgangbeyer 23:19, 9. Jul 2004 (CEST)

So richtig überzeugt mich das nicht, man kann von jeder natürlichen Zahl sagen, ob sie Fibonacci-Zahl ist oder nicht. Und würde ein Suchender (unter Berücksichtgung der Singular-Konvention) denn nicht einen Artikel zur Fibonacci-Zahl suchen (statt Fibonacci-Zahlenfolge) ? --Callimachos 09:30, 10. Jul 2004 (CEST)

Das ist natürlich richtig, aber die Fibonacci-Zahlen werde so gut wie immer in ihrer Gesamtheit betrachtet oder zumindest in Bezug auf ihrer unmittelbaren Nachbarn, anders als z. B. die rationalen Zahlen, wo man sich auch mal dafür interessiert, ob z. B. π eine ist. Einen entsprechenden Redirect bei Fibonacci-Zahl muss es natürlich geben und gibt es auch. Das google-Trefferverhältnis Fibonacci-Zahlen : Fibonacci-Folge : Fibonacci-Zahl : Fibonacci-Zahlenfolge beträgt übrigens ca. 6100:5200:1700:100. Das spricht meiner Ansicht nach eindeutig für Fibonacci-Folge. Ich mach' das jetzt einfach mal. --Wolfgangbeyer 10:25, 10. Jul 2004 (CEST)

Seltsam: Die Verschiebe-Operation hat nicht funktioniert. Ich dachte, das geht auch dann wenn dort schon ein Redirect steht. Selbst das löschen des Redirects hat nichts genützt. Schade, denn nun steht die ganze Versionsgeschichte unter Fibonacci-Zahlen. --Wolfgangbeyer 10:47, 10. Jul 2004 (CEST)

Programm-Quellcodes

Ich bin durchaus ein Freund von Quellcodes, aber müssen es denn die Quellcodes von drei verschiedenen Programmiersprachen sein? Ich kann auch noch LOGO, Lisp, REXX, tcl und AWK beitragen. Im Prinzip sollten zwei Quellcodes reichen, und zwar den rekursiven und einen iterativen Ansatz. Und das am besten in einer neutralen Form, die sich nicht auf eine bestimmte Programiersprache bezieht. --Arbol01 11:26, 17. Aug 2004 (CEST)

Formelversionen

Die Folge würde auch mit f(n) = f(n-1) + f(n-2) funktionieren, dann müsste man allerdings n > 1 festlegen, ist also wohl eher Geschmackssache. Interessanter ist, dass f0 mal mit 0 und mal mit 1 festgelegt wird, so dass man darüber philosophieren könnte, ob die Null eine fibonaccizahl ist oder nicht. Kennt jemand die Primärquelle? -Hati 12:08, 26. Aug 2004 (CEST)

Weitere Zahlenreihen

könnte man die auch erwähnen?

Lucas

Wie Fibonacci (mit f0=f1=1), aber mit f0=1 und f1=3; würde wohl besser zu Kaninchen passen, die ja nicht genau einen Nachkommen haben. -Hati

Padovan

entdeckt 1924 von dem frz. Architekturstudenten Gérard Cordonnier, 1928 vom niederländischen benediktinermönch und Architekten Hans van der Laan: f(n) = f(n-2)+ f(n-3) mit n>3 und f0=f1=f3=1
(auf Kaninchen angewandt, könnte die Verzögerung der Tragzeit entsprechen). -Hati

Chaos

f(n) = f[n - f(n-1)] + f[n-(fn-2)] mit n>1 und f0=f1=1
wäre eine nette Programmier-Übung und liefert Pseudozufallszahlen. -Hati 12:08, 26. Aug 2004 (CEST)

Hm, welches von diesen f's meint denn die Fibonacci-Funktion und welche die Zufallszahlenfunktion? Ist das denn überhaupt beschränkt? Sieht jedenfalls gefährlich aus: Wenn man damit Punkte im Raum würfeln will, könnten die unter Umständen alle auf einer Fläche im Raum liegen. Hatte das Problem mal im Rahmen meiner Physik-Diplomarbeit, als ich per Monte-Carlo-Methode ein vieldimensionales Problem (Integral) lösen wollte. Zum Glück habe ich damals schon (ca. 1976) privat begeistert mit bescheidenen Computergrafiken experimentiert und mich irgendwann über die regelmäßigen Muster gewundert, die man erhält, wenn man viele Rechtecke mit zufälligen Seitenlängen und Mitten würfelt. Als ich dann im Handbuch des verwendeten Basic-Dialekts was von Zufallszahlen auf der Basis von Fibonacci-Zahlen las, war mir alles klar. Hätte schlecht ausgehen können für meine Diplomarbeit ;-). --Wolfgangbeyer 00:26, 5. Sep 2004 (CEST)

Da sind wir wohl nicht mehr bei der Fibonaccio-Funktion sondern bei einer Iterationsanweisung, bei der die Zahl der Rückschritte nochmals eine Rückschrittschleife enthält. Dadurch entsteht eine Zahlenreihe, die einer Zufallsreihe sehr ähnlich ist, aber durch den Algorithmus exakt determiniert ist. Bei exakt gleichem Anfangswert wird also immer die gleiche Zahlenreihe generiert. Eine andere Zahlenreihe entsteht dann, wenn man einen anderen Startwert benutzt. Ob jetzt computer diesen oder einen anderen deterministischen Algorithmus verwenden (Iteration der Zeltfunktion ginge auch aber nicht bei jedem Startwert) weiß ich nicht. Wenn man aber immer eine andere "Zufalls"zahlrenreihe haben will, holt sich der Computer als Startwert die Systemzeit (16stellig?) als Startwert. -Hati 16:27, 5. Sep 2004 (CEST)

Kaninchen

Dem Biologen sträuben sich natürlich die Haare, wenn man mit f0=0 aus dem Nichts ein Kaninchenpaar zaubert. Da wäre f0=1 "biologischer". Für die Programmierer: Das geht noch viel einfacher mit Excel und hat den Vorteil, dass man die Zahlenreihe gleich als Diagramm darstellen kann und sich mit Parametern spielen kann: f(n) = a*f(n-1) + b*f(n-2). Mit Der Veriation von f0 und f1 kommen da die erstaunlichsten Zahlenfolgen mit Gleichgewichtswerten oder Oszillationen heraus, die sich ganz gut zur Modellierung von dynamischen Systemen wie Populationen eignen.
Konsequenterweise muss natürlich ein "geschleichtsreifes" Kaninchenpaar wieder ein Kaninchenpaar hervorbringen. Das ganze ginge übrigens eleganter mit Blattläusen während der sommerzeit, da diese sich ungeschlechtlich fortpflanzen. Da kann man dann tatsächlucb von einer einzigen Blattlaus ausgehen.
-Hati 12:08, 26. Aug 2004 (CEST)

Vorschlag für Kaninchen-Formulierungsänderungen:

1. Zu Beginn gibt es ein Kaninchenpaar. Zu Beginn gibt es ein Kaninchen [Wenn man von Paar spricht, geht man bei Säugetieren von Mänchen und Weibchen aus. Und gebärfahige Männchen ... ;-)]
2. Jedes neugeborene Kaninchen wird nach 2 Monaten entspricht 2 Iterationszyklen) gebärfähig.
3. Jedes gebärfähige Kaninchen [statt -paar] bringt jeden Monat ein weiteres zur Welt.
4. Kaninchen leben ewig.
5. Kaninchen haben einen unbegrenzten Lebensraum.
6. Kaninchen pflanzen sich ungeschlechtlich fort.

Den folgenden Satz würde ich ganz streichen, da er etwas verwirrend und sprachlich nicht ganz korrekt ist: Jeden Monat kommt zu der Anzahl der Paare, die im letzten Monat gelebt haben, die dazu, die im vorletzten gelebt haben, da diese sich nun vermehren. Das entspricht aber gerade der oben angegebenen Rekursionsformel.
statt dessen (*grübel grübel*) -Hati 12:20, 26. Aug 2004 (CEST)

Also Kaninchen pflanzen sich ungeschlechtlich fort. gefällt mir gar nicht (zu wenig realistisch und zu lustlos ;-)). Aber Deine Kritik war schon berechtigt. Was hälst Du von der jetzigen Variante?

Ist so ok. Ergänzung durch eine realistischeres Beispiel: Ungeschlechtliche Fortpflanzung der Blattlaus im Frühling und Sommer: Da kann man tatsächlich von einem weiblichen Individuum ausgehen, das Junge lebend zur Welt bringt, die schon nach kurzer Zeit wieder lebende Junge gebären. -Hati 16:31, 5. Sep 2004 (CEST)

$f_{0}=0$

Ich habe wenig Hoffnung, das dadurch dauerhaft etwas vermieden wird, nämlich das jemand aus welchen Gründen auch immer definiert, dass $f_{0}=1$ ist. Die rekursive Formel ist da sehr unklar, da sie sich auf Vorgänger festlegt.

Wendet man aber die allgemeine Lucas-Folge $U_{n}(P,Q)={\frac {a^{n}-b^{n}}{a-b}}$ mit P = 1 und Q = -1 bzw. die Formel von Binet an, dann wird klar ersichtlich, das f_0 = 0 sein muß:

Die Fibonaccifolge läßt sich über die allgemeine Formel $U_{n}(1,-1)={\frac {a^{n}-b^{n}}{a-b}}$ mit a = ${\frac {1+{\sqrt {5}}}{2}}$ und b = ${\frac {1-{\sqrt {5}}}{2}}$ erzeugen. Dabei ist $f_{0}=U_{0}(1,-1)={\frac {a^{0}-b^{0}}{a-b}}={\frac {1-1}{a-b}}={\frac {0}{a-b}}=0$

Damit ist gezeigt, daß $f_{0}=0$ ist. --Arbol01 21:57, 22. Nov 2004 (CET)

Laut der original Definition im original Skript von Fibonacci fängt die Folge mit 1 an. Wieso wird die Fibonacci-Folge anders definiert, als es Fibonacci definiert hat? --Dtail 10:04, 25. Nov. 2008 (CET)

Lukas-Folge

Habe ja nicht prinzipiell was dagegen, wenn ein Bezug zur Lukas-Folge hergestellt wird. Ich würde das aber auf gar keinen Fall in dieser erschlagenden Ausführlichkeit an den Anfang stellen sondern weit nach unten in ein eigenes Kapitel. Versuche mal, den Artikel mit den Augen eines Laien zu lesen - der schnallt doch völlig ab, selbst wenn er die Rekursionsformel schon kennt. Auch die Parameter 1,-1 fallen für ihn ja völlig unmotiviert vom Himmel. Im Prinzip würde es auch völlig reichen, darauf hinzuweisen, dass ein Bezug zur Lukas-Folge besteht, und die ganze Mathematik dorthin zu verlagern. Wenn unbedingt hier, dann am besten nach dem Goldenen Schnitt z. B. unter Bezug zur Lukas-Folge. Bitte Artikel generell so strukturieren, dass das einfach vorne und das komplizierte weiter hinten steht. --Wolfgangbeyer 00:29, 23. Nov 2004 (CET)

Finde den Abschnitt zu den Lukas-Zahlen schon ungemein formellastig, da könnte man sicher einige Zwischenschritte weglassen. Dafür steht die eigentliche Definition $f(n)=U_{n}(1,-1)$ nirgendwo explizit da, sondern man muss sie sich indirekt aus der Formelwüste klauben. Was soll eigentlich an dieser Definition iterativ sein? --Wolfgangbeyer 00:50, 23. Nov 2004 (CET)

Iterativ? Hmmmm, naja sie ist nicht rekursiv. Ok, sie wird direkt berechnet. Aber ich denke, du kannst das besser Formulieren.

Statt $f(n)=U_{n}(1,-1)$ könnte man natürlich kurz $f(n)=U_{n}$ schreiben, wobei es natürlich unendlich viele $f(n)=U_{n}$ gibt. Wenn Du eine Idee hast, wie man es besser integrieren kann, dann mach es. Wenn mir an der Änderung etwas nicht gefällt, dann kann ich es wieder ändern, bzw. wenn es, wie bei der Mandelbrot-Menge, über meinen Horizont geht, mich aus dem Artikel raushalten werde.

Ich halte es trotzdem für sinnvoll, die Lucas-Folge an erster Stelle zu nennen, weil "Idioten" (dazu zähle ich mich auch), die wilkürlich F(0)=1 setzen, statt F(0)=0. Die rekursive Darstellung läßt das zu, die direkte Darstellung aber nicht. --Arbol01 01:16, 23. Nov 2004 (CET)

Das als Grund für die Einführung der Lukas-Folge ist nicht einsichtig. Wer sagt denn, dass man $f(n)=U_{n}(1,-1)$ definieren muss und nicht $f(n)=U_{n+1}(1,-1)$? Es gibt keine richtigen und falschen Definitionen in der Mathematik, sondern nur mehr oder weniger nützliche. Daher hat diese Argumentation kein Gewicht. --Wolfgangbeyer 18:57, 23. Nov 2004 (CET)

Nachtrag: Es ist durchaus nicht selbstverständlich, dass das einfache vor dem komplizierten kommt. Bestes Beispiel dagegen ist der Binomialkoeffizient, bei dem das Allgemeine vor dem Speziellen kommt, und eben nicht das Einfache vor dem Komplizierten. Nebenbei habe ich Binomialkoeffizient nicht strukturiert. --Arbol01 01:41, 23. Nov 2004 (CET)

Das kann ich nicht erkennen. In Binomialkoeffizient geht es von anfang an um Binomialkoeffizienten und um nichts komplizierteres. Hier aber wolltest Du die Fibonacci-Folge über etwas einführen, das erheblich komplizierter als das Artikelthema selbst ist. --Wolfgangbeyer 18:57, 23. Nov 2004 (CET)

Wie dem auch sei, ich habe jetzt den Formellastigen Teil nach hinten verschoben, dafür aber die Formel von Binet an diese Stelle gesetzt, an der vorher die Lucas-Folge war. Und ganz nach vorne habe ich die Kaninchen gesetzt. --Arbol01 19:11, 23. Nov 2004 (CET)

Evtl. hast Du die Bedeutung des Begriffs "Wikisource" missverstanden. Das ist keine Sammlung zum Auslagern von Source-Code im Sinne von Computerprogrammen, sondern eine Sammlung von ganz gewöhnlichen Texten. Ich bin auch kein Freund von langatmigen Programm-Listings in Wikipedia-Artikeln, so dass ich das hier eigentlich nicht unbedingt vermisse. Aber es ist nur eine Frage der Zeit, bis hier wieder jemand so was reinschreibt - wenn wir Pech haben doppelt so umfangreich. --Wolfgangbeyer 19:45, 23. Nov 2004 (CET)

Hoppla, sehe erst jetzt den Weblink auf den Quellkode. Das verhindert vielleicht doch, dass er wieder hier reinkommt ;-). --Wolfgangbeyer 19:50, 23. Nov 2004 (CET)

Jein, vielleicht ist es mal so gedacht gewesen. Jedenfalls wimmelt es, im eglischsprachigen Wikisource-Teil, vin Programmlistings. Da fallen die beiden Fibonacci-Listings überhapt nicht auf. Das mußt Du dir wirklich mal ansehen.

Ich würde es nie wagen, in den deutschsprachigen Teil der Wikisource Programmlistings, oder Listen und Tabellen mit Prim- oder sonstigen Zahlen unterzubringen.

Wenn jemand wieder Listings im Artikel Fibonacci-Folge unterbringt, dann ist in dem ausgelagerten Listing-Teil noch genug platz.

Hier, um sich ein Bild zu machen: http://wikisource.org/wiki/Main_Page:English http://wikisource.org/wiki/Wikisource:Source_code http://wikisource.org/wiki/Wikisource:Mathematics. --Arbol01 19:57, 23. Nov 2004 (CET)

Rekursion oder Iteration

Seid ihr euch sicher, dass Fibonacci und Konsorten rekursiv (also durch eine Proozedur, die sich selbst aufruft), oder nicht doch iterativ, also durch eine Prozedur die nacheinander abläuft, wobei bei jedem Durchlauf der zuletzt errechnete Wert übergeben wird? Siehe die verlinkten Programm-Beispiele die für mich schwer nach Iteration ausschauen. Siehe dazu auch Heinz-Otto Peitgen et al., Bausteine des Chaos, 1992, Klett-Cotta, ISBN 3-6-08-95888-7 -Hati 18:21, 26. Nov 2004 (CET)

Die Frage verstehe ich nicht! Keine Funktion kann den Anspruch erheben, ausschließlich durch Rekursion, Iteration oder auch nur direkt darstellen. Eine Funktion, für die es einen rekursiven Algorithmus gibt, existiert auch einen iterativen Algorithmus (Arbol01)

Stimmt schon - so wie es da steht, ist die Bezeichnung iterativ passender. --Wolfgangbeyer 10:29, 27. Nov 2004 (CET)

Oder? Jetzt bin ich etwas verwirrt. Man spricht von einer Rekursionsformel aber nicht von einer Iterationsformel. Rekursiv heißt selbstbezüglich, und das ist es ja. Vielleicht muss man bedenken, ob man von der Formel oder einer programmtechnischen Umsetzung spricht. Im iterativen Algorithmus tritt der rekursive Charakter zurück, da man Zuweisungen zu verschieden Variablen macht, die aber letztlich zur selben Folge gehören. Da Iteration nur ausdrückt, dass viele Schritte notwendig sind, ist Rekursion hier schon treffender. --Wolfgangbeyer 10:48, 27. Nov 2004 (CET)rekursiv onder iterativ

Rekursiv ist, wen eine Funktion r wieder eine funktion r aufruft die wiederum r aufruft, und so weiter, bis eine Abbruchbedingung erfüllt ist:

(!5) = 5*(!4) = 5*4*(!3) = 5*4*3*(!2) =5*4*3*2*(!1) = 5*4*3*2*1

Iterativ ist, wenn die Berechnung in einer Schleife abläuft:

w=5
f=1
do i = 1 to w
  f=f*i
end
say fakultät f

Das ist der prinzipielle Unterschied zwischen Rekursiv und Iterativ. Später mehr! --Arbol01 11:04, 27. Nov 2004 (CET)

Schon klar, das ist das, was ich oben mit programmtechnischer Umsetzung bezeichnet habe. Um die geht es aber im Artikel gar nicht sondern um die mathematische Definition. Und die ist selbstbezüglich also eine Rekursionsformel. --Wolfgangbeyer 13:52, 27. Nov 2004 (CET)

Da stellt sich mir wiederum eine Frage: Die folgende Funktion zu Berechnung des Binomialkoeffizienten ist iterativ realisiert:

#include <stdio.h>

unsigned int ggt(unsigned int m, unsigned int n)
{
  unsigned int c=0;
  do
  {
    if (m < n)
    {
      if ((n % m) > 0)
      {
        n %= m;
      }
      else
      {
        c = m;
      }
    }
    if (m > n)
    {
      if ((m % n) > 0)
      {
        m %= n;
      }
      else
      {
        c = n;
      }
    }
  }
  while (c == 0);
  return(c);
}

unsigned int bin_koeff(unsigned int n, unsigned int k)
{
  unsigned int na = n;
  unsigned int ka = k;
  unsigned int t;
  if (na == ka) ka = 0;
  if (na == 0)  return(0);
  if (ka == 0)  return(1);
  if (ka == 1)  return(na);
  if ((ka > 1) && (na > 0))
  {
    do
    {
      na *= (n-1);
      ka *= (k-1);
      t   = ggt(na,ka);
      na /= t;
      ka /= t;
      n--;
      k--;
    }
    while (k > 1);
  }
  return(na / ka);
}

int main()
{
  unsigned int a, b, ergebnis;
  scanf("%d",&a);
  scanf("%d",&b);
  ergebnis = bin_koeff(a,b);
  printf(" %d ueber %d = %d \n",a,b,ergebnis);
  return 0;
}

Ist sie nach mathematischer Definition dennoch rekursiv? Es würde mich wundern.

Die rekursive Realisation der gleichen Funktion ist:

MAIN
  DEFINE ergebnis INTEGER,
         wert1    INTEGER,
         wert2    INTEGER
  PROMPT "n : " FOR wert1
  PROMPT "k : " FOR wert2
  CALL binomial_koeffizient(wert1,wert2) RETURNING ergebnis
  DISPLAY ergebnis
END MAIN

FUNCTION binomial_koeffizient(n,k)
  DEFINE ergebnis1 INTEGER,
         ergebnis2 INTEGER,
         n         INTEGER,
         k         INTEGER
  IF ((k = 0) AND (n >= 0)) OR ((k = n) AND (k >= 0)) THEN
    LET ergebnis1 = 1
    RETURN ergebnis1
  END IF
  IF (n > k) AND (k > 0) THEN
    CALL binomial_koeffizient(n-1,k-1) RETURNING ergebnis1
    CALL binomial_koeffizient(n-1,k)   RETURNING ergebnis2
    LET ergebnis1 = ergebnis1 + ergebnis2
    RETURN ergebnis1
  END IF
END FUNCTION

--Arbol01 14:37, 27. Nov 2004 (CET)

"Ist sie nach mathematischer Definition dennoch rekursiv?" Diese Frage gibt für mich keinen Sinn und beruht vielleicht auf einem Mißverständnis. Du stellst ein iteratives Verfahren vor. Die mathematische Definition, von der ich sprach, bezog sich auf die Struktur der Formel im Artikel. Und die würde ich, so wie sie da steht, rekursiv nennen. Das heißt nicht, dass man f(n) nicht über ein iteratives Verfahren berechnen kann. --Wolfgangbeyer 16:18, 27. Nov 2004 (CET)

Ah jetzt verstehe ich! Aber dann drücke es auch so aus. Ich verstand deine Antwort so, als ob die iterative Darstellung der Fäkultät dem Mathematischen Sinne nach rekursiv sei.

Das F(n) = F(n-1) + F(n-2) rekursiv ist, ist unbestreitbar. --Arbol01 17:33, 27. Nov 2004 (CET)

Überarbeitung

Habe mir doch noch mal die Zeit genommen, diesen Artikel etwas umzugestalten:

• Worte sind zwar oft leichter verständlich als Formeln, aber im vorliegenden Fall ist es eher umgekehrt: Die Rekursionsformel zusammen mit dem Satz, dass jede Zahl die Summe iherer beiden Vorgänger ist, dürfte erheblich leichter nachvollziehbar sein, als die Schilderung der Kaninchenpopulation. Ich wette, die meisten Leser müssen erst dreimal nachdenken, bevor sie darin die simple Rekursionsformel wiedererkennen. Daher ist die Rekursionsformel am Anfang ausnahmsweise besser aufgehoben.
• Im Prinzip ist es in der Mathematik eine Frage des Geschmacks, welche Aussagen man als Definition und welche man als abgeleitete Beziehungen darstellt. Im Rahmen der Wikipedia sehe ich keien Sinn, irgendetwas anderes als in Übereinstimmung mit der Mathematikgeschichte die Rekursionsformel als Definition vorzustellen. Die Formel von Binet gehört daher an eine spätere Stelle im Text.
• Die Lucas-Folge geht ja über das eigentlich Thema des Artikel weit hinaus. Habe daher mal alles, was damit zusammenhängt in ein einziges Kapitel gesteckt. Auch die Umformung in die Formel von Binet müssen wir daher nicht mit zig Rechenschritten nachvollziehen, sondern es genügt, den Weg anzudeuten. Da damit diese Beziehung für den allgemeinen Fall bewiesen ist, muss sie ja nicht noch explizit für f₂ bewiesen werden. Auch die Herleitung der Rekursionsformel erübrigt sich damit, denn sie zeigt nichts anderes als die innere Widerspruchsfreiheit der Mathematik. Ganz abgesehen beruht sie auf der Beziehung $U_{n+2}=PU_{n}-QU_{n+1}$, die völlig vom Himmel fällt. Selbst unter Lucas-Folge finde ich sie nicht. --Wolfgangbeyer 00:44, 8. Dez 2004 (CET)

Vieleicht nicht unter Lucas-Folge, so aber doch unter Fibonacci numbers unter Generalizations. Ich halte es doch mal für angebracht, über die Grenze zu schauen. --Arbol01 01:55, 8. Dez 2004 (CET)

Hallo Arbol01, ich habe meine Änderungen ausführlich begründet. Wenn Du das einfach komplett revertierts, erwarte ich schon einen Kommentar zu meinen Argumenten. Der ganze Abschnitt zur Lucas-Zahlen ist reichlich verwirrend für den Leser. Du sagst dem Leser nicht, wovon Du ausgehst, wo Du hin willst und warum. Zusätzlich zu meinen obigen Einwänden: Wen interessiert, dass ab U₂ die Ausdrücke a und b benötigt werden? Ich habe absolut nichts gegen einen Blick über den Zaun, aber Du solltest in diesen Abschnitt einen Roten Faden reinbringen. Im Übrigen ist Dir offenbar entgangen, dass ich die Schreibweise f(n) in die für Folgen übliche Schreibweise f_n umgewandelt habe. --Wolfgangbeyer 22:05, 8. Dez 2004 (CET)

Eine Antwort: Ich bin durchaus nicht mit deiner Begründung über deine Änderung zufrieden (allerdings habe ich auch keinen Anspruch auf eine solche ausführliche Begründung). Ich möchte für jeden, den es interessiert, einen weiteren Weg, oder besser gesagt ein komplettes Bild bieten, und nicht nur eine 08/15-Antwort, wie sie im täglichen Schulbetrieb, und vielleicht auch sonstwo, Usus ist (Der Spiegel 50/6.12.04 - Die Magie der Zahlen). Anders gesagt ich will dem, den es interessiert, die Möglichkeiten bieten, die ich während meiner Schulzeit, und auch sonst, nicht hatte. Und dazu gehört auch dieses hochkomplizierte Gebiet dazu. Ich halte keinen Menschen für so Doof, das er es nicht verstehen könnte. Tatsächlich ist mir natürlich auch klar, das jeder Mensch das sich alles selbst noch mal erarbeiten (errechnen) muß. Zumindest will ich aber jedem diese Wege bieten.

Ja, das mit dem f(n) ist mir entgangen, bzw. wollte ich erst mal abwarten.

Nicht unbedingt als Handreichung, folgende Überlegung: Ich nehme meinen Abschnitt, und baue ihn in die Lucas-Folgen ein. Nicht um Dir einen Gefallen zu tun, oder dir zuzugestehen, der Artikel Fibonacci-Folge wäre dein Artikel (auch wenn Du ihn initiert hast). --Arbol01 22:23, 8. Dez 2004 (CET)

Noch etwas: Eine Enzykliopädie ist weder ein Roman, noch ein Fachbuch. Dein Wunsch nach einem roten Faden ist verständlich, aber schwierig, bis unmöglich. Warum? Weil die Intention eines Lesers, die in diesem Falle die Hauptrolle spielt, eine ganz unterschiedliche ist. Der eine Leser hat einen Standpunkt, der nächste einen anderen, und beide Leser fassen den Artikel dementsprechend unterschiedlich auf. Bei einem Roman führt der Autor durch eine Geschichte, die dann ja wirklich eindimensional sein muß, und in einem Lehrbuch ist das ähnlich. Die Mathematik ist aber nicht eindimensional, sondern ein ganzes Universum, bei der man im Idealfall von jedem Punkt zu jedem anderen Punkt kommt. --Arbol01 22:32, 8. Dez 2004 (CET)

Eine Enzyklopädie soll demjenigen, der über ein Thema etwas wissen will, helfen, dieses Wissen zu erlangen. Wenn nur derjenige mit einem Artikel etwas anfangen kann, der es eh schon weiß, kann man sich die Mühe sparen. Insofern sollte ein Enzyklopädie Artikel durchaus vom Einfachen zum Schweren gehen und nicht umgekehrt, sonst wendet sich der Leser einem anderen Thema zu. Wenn jetzt das Argument kommt, "dann ist der Leser meines Artikels nicht wert", dann ist das ziemlich arrogant. Wiki dient nicht der geistigen Selbstbefriedigung seiner Autoren. Wenn jemand wirklich über ein Thema Bescheid weiß und nicht nur so tut als ob, weil er sich hier und da etwas angelesen hat, dann kann er diese Information auch strukturiert (d.h. mit Rotem Faden) rüberbringen. --217.255.10.102 09:25, 9. Dez 2004 (CET)

Zuerst zu deinem Vorwurf: Wenn ich wirklich der Ansicht wäre: "dann ist der Leser meines Artikels nicht wert", dann würde ich hier gar nicht erst schreiben. Mein Ziel ist ja, etwas, was ich auch weiß, oder zumimdest erfahren habe, anderen weiterzuvermitteln. Und ich bin auch nicht der Ansicht, man solle um Himmelswillen immer vom leichten zum Schweren gehen. Nein, man soll und muß auch den Weg vom "schweren" zum einfachen nehmen. Der Aha-Effekt, der Erfolg ist um so größer. Du sprichst wie derjenige, der immer nur den Wanderweg benutzt, und die Nase über diejenigen rümpfst, die freikletternd ihren Weg anders suchen. Einfach geht immer. In diesem Fall hat fast jedes Programmierhandbuch, jeder Programmierkurs die rekursive Programmierung der Fibonacci-Folge. Wo bleibt da die Herausforderung. --Arbol01 17:27, 9. Dez 2004 (CET)

Ich komme mal auf Dein obiges "Angebot" zurück und setze eine gestraffte Version ein. (Nebenbemerkung zur Vermeidung von Missverständnissen: 217.255.10.102 bin nicht ich. Ich stimme ihm auch nur partiell(!) zu.) --Wolfgangbeyer 23:39, 9. Dez 2004 (CET)

Ich habe es auch nicht geglaubt! --Arbol01 00:49, 10. Dez 2004 (CET)

f(0)=1?

Habe mal ein wenig gegoogelt: f₀=1 habe ich nicht gefunden. Damit müsste man auch alle Formeln weiter unten anpassen. Allerdings wird häufig mit f₁=1 begonnen, d. h. f₀=0 ausgelassen, oft aber in Kombination mit einer bestimmten praktischen Situation, in der die Fibonacci-Zahlen auftauchen und situationsbedingt mit 1 beginnen. Habe mal eine entsprechende Formulierung gewählt. --Wolfgangbeyer 21:25, 20. Jan 2005 (CET)

Fibonacci und die Kaninchen

In wie weit sieht man denn die Fibonacci-Zahlen in einer Kaninchen-Population? ich erkenne eher sowas wie eine klassisdche exponentielle zunahme.

danke, --Abdull 00:23, 23. Jan 2005 (CET)

Da empfehle ich den Zahlenteufel von Hans Magnus Enzensberger. Da ist es sehr anschaulich beschrieben. Im übriegen ist es umgekehrt. Die Fibonacci-Folge soll das Wachstum einer Kaninchenpopulation erklären, und nicht die Kaninchenpopulation die Fibonacci-Folge.

Angenommen man beginnt mit einem Kaninchenpärchen zu einem Zeitpunkt Null. Erst nach zwei Monaten kann ein Pärchen Junge bekommen, und zwar der Einfachheithalber ein Pärchen. Danach bekommt dann ein Pärchen jeden Monat Junge (immer noch der Einfacherhalber Pärchen):

0    1    2    3    4    5    6 ...

1 -> 1 -> 1 -> 1 -> 1 -> 1 -> 1 ...
          1 -> 1 -> 1 -> 1 -> 1 
               1 -> 1 -> 1 -> 1
                    1 -> 1 -> 1
                    1 -> 1 -> 1
                         1 -> 1
                         1 -> 1 ...
                         1 -> 1
                              1
                              1
                              1
                              1
                              1 ...

Und so weiter. So ungefähr klappt das auch mit der Verästelung bei Bäumen. --Arbol01 00:43, 23. Jan 2005 (CET)

Ach ja, natürlich nur bei einem unbegrenzten Lebensraum, Unsterblichkeit, immer Pärchen und kein Inzuchtproblem. --Arbol01 00:48, 23. Jan 2005 (CET)

Verallgemeinerung

Das die Fibonacci-Folge (Folgen ?) mit der allgemeinen Lucas-Folge zu tun hat, habe ich schon mal erwähnt. Das hat aber mit dem, worauf ich hier hinaus will nur am Rande zu tun.

Die Fibonacci-Folge läßt sich über die Formel von Binet:

$f_{n}={\frac {1}{\sqrt {5}}}(a^{n}-b^{n})$ mit a = ${\frac {1+{\sqrt {5}}}{2}}$ und b = ${\frac {1-{\sqrt {5}}}{2}}$

herleiten. Das steht ja auch im Artikel. Aber das ist nicht die einzige Folge dieser Art. Es gibt unzählige Folgen der Form:

$f_{n}={\frac {1}{\sqrt {x}}}(a^{n}-b^{n})$ mit a = ${\frac {1+{\sqrt {x}}}{2}}$ und b = ${\frac {1-{\sqrt {x}}}{2}}$

Die einzelnen Glieder dieser verallgemeinerten Folge sind $a_{0}=0\ ,\ a_{1}=1\ ,\ a_{2}=1\ ,\ a_{3}={\frac {3+x}{4}}\ ,\ a_{5}=...$. Leider bin ich noch weiter gekommen. --Arbol01 16:55, 17. Mär 2005 (CET)

Jede zweistufige lineare Rekursion

$a_{n+1}=ua_{n}+va_{n-1}$

hat eine explizite Lösungsformel, die entweder die Form

$a_{n}=c_{1}\lambda _{1}^{n}+c_{2}\lambda _{2}^{n}$

oder

$a_{n}=c_{1}\lambda ^{n}+c_{2}n\lambda ^{n}$

hat. Umgekehrt erfüllt jede Folge dieser Form eine zweistufige lineare Rekursion, in Deinem Fall

$a_{n+1}=a_{n}-{\frac {1-x}{4}}\cdot a_{n-1}.$

Steht das hier in der WP nicht schon irgendwo?--Gunther 18:59, 17. Mär 2005 (CET)

Das wüßte ich auch gerne. Wenn nicht, dann sollte es irgendwo stehen. Warum nicht unter verallgemeinerung der Fibonacci-Folgen? --Arbol01 19:06, 17. Mär 2005 (CET)

Es gibt eine (ziemlich unverständliche) Fassung unter Lineare Differenzengleichung. Habe diesen Artikel als "überarbeitungswürdig" eingetragen, vielleicht verbessert er sich ja von selbst :-)--Gunther 23:56, 17. Mär 2005 (CET)

Zu Deiner Verallgemeinerung siehe Wikipedia:Was Wikipedia nicht ist, Punkt 2. Das fällt alles wie gesagt unter die Lösungstheorie linearer Rekursionen, aber welche besonderen Eigenschaften hat Deine Verallgemeinerung?

Versteh' mich nicht falsch, es ist nun einmal extrem schwierig, in der Elementarmathematik Konzepte zu finden, die nicht schon Hunderte anderer betrachtet haben.--Gunther 09:09, 18. Mär 2005 (CET)

Mit Punkt 1. spielst Du wahrscheinlich auf "Wikipedia dient nicht der Theoriefindung, sondern der Theoriedarstellung. In ihr sollten weder neue Theorien, Modelle, Konzepte, Methoden aufgestellt noch neue Begriffe etabliert werden. Ebenso unerwünscht sind nicht nachprüfbare Aussagen. Ziel des Enzyklopädieprojektes ist die Zusammenstellung bekannten Wissens." an. Das trifft es in diesem Fall aber nicht, da es unzählige dieser Folgen gibt, und es bestimmt nicht neu ist.

Das besondere der allgemeinen rekursiven Formel ist halt, das man ein (nicht ganz) beliebiges x einsetzen kann, und man bekommt die entsprechende Folge:

x = 5: 0, 1, 1, 2, 3, 5, 8, ... (Fibonacci-Folge) $a_{n+1}=a_{n-1}+a_{n}$

x = 9: 0, 1, 1, 3, 5, 11, 21, 43, ... (Jacobstal-Folge) $a_{n+1}=2*a_{n-1}+a_{n}$

Kurz gesagt: Für x = 4m+1 bekommt man die rekursive Folge $a_{n+1}=m*a_{n-1}+a_{n}$ wenn ich alles richtig verstanden habe. --Arbol01 09:57, 18. Mär 2005 (CET)

Trotzdem wählst Du eine spezielle Klasse aus, und diese Betrachtung ist "neu". Eine etwas übertriebener Vergleich wäre ein Abschnitt in reelle Zahl über Zahlen, deren dezimale Nachkommastellen alle gerade sind. Natürlich sind reelle Zahlen nicht neu, aber gerade diese Unterklasse zu betrachten ist es.--Gunther 10:14, 18. Mär 2005 (CET)

Es gibt in Wikipedia auch einen Grundsatz: "Ignoriere die Regeln". Das heißt nicht, das man machen soll, was man will.

Mir geht es letzendlich immer noch um die Lucas-Folgen. Die Fibonacci-Folge und die Jacobsthal-Folge (das sind die beiden bekannten Folgen) gehören zu den folgen, die durch das Schema $a={\frac {1+{\sqrt {x}}}{2}}$ und b = ${\frac {1-{\sqrt {x}}}{2}}$ miteinander, und mit der allgemeinen Lucas-Folge verbunden sind. Es gibt da noch wenigstens zwei andere spezielle Formen der Lucas-Folge. Eine davon ist dergestalt, daß bei beistimmten P und Q die beiden Lösungen der quadratischen Gleichung natürliche Zahlen sin. Die andere Form habe ich nicht parat.

Ausserdem gibt es noch den kleinen Fermatschen Satz als Spezialfall der allgemeinen Lucas-Folge. --Arbol01 10:38, 18. Mär 2005 (CET)

Habe mal einen verständlichen Teil zu Lineare Differenzengleichung hinzugefügt.--Gunther 16:28, 18. Mär 2005 (CET)

n > 2 ist überflüssig

Der Zusatz, das für die Fibonacci-Folge $a_{n}=a_{n-1}+a_{n-2}\$ erst ab n=2 gilt ist überflüssig und falsch. Da der Umkehrschluß $a_{n-2}=a_{n}-a_{n-1}\$ gilt. Die Folge läßt sich also nach hinten verlängern:

... 8 5 -3 2 -1 1 0 1 1 2 3 5 8 13 21 34 55 89 144 233 ... . 

$a_{0}=1$ und $a_{1}=1$ gelten natürlich weiterhin. --Arbol01 23:02, 26. Nov 2005 (CET)

Hallo Arbol01. Ich denke, die Einschränkung n >= 2 ist nicht überflüssig, und falsch ist sie schon gar nicht. Jede Folge muss einen Definitionsberech haben, und der ist hier {0, 1, 2, 3, ...} und eben nicht Z (ganze Zahlen). Bei jeder rekursiven Definition gibt es einen oder mehrere Startwerte, und dann eben eine Vorschrift, die ab einem bestimmten n (hier 2) auf frühere Werte zurückgreift. ich möchte daher die Einschränkung wieder aufnehmen. Konnte ich dich überzeugen? Gruß von --Wasseralm 23:39, 26. Nov 2005 (CET)

Hallo ihr beiden, ich war einfach so frei, und habe das Bildungsgesetz - wie ich hoffe - etwas flüssiger formuliert. In dieser neuen Version sollte unmittelbar herauskommen, dass $n\geq 2$ eine sinnvolle Ergänzung ist.--JFKCom 23:51, 26. Nov 2005 (CET)

Wenn wir statt einer Aufzählung von 3 Gleichungen einen Satz hinschreiben, dann geben auch die Aufzählungspunkte keine Sinn mehr. Habe daher einen anderen Vorschlag formuliert. --Wolfgangbeyer 01:37, 27. Nov 2005 (CET)

Naja, ehe ich hier einen Edit-War auslöse beuge ich mich der Mehrheit. Nichtsdestotrotz halte ich die Einschränkung $n\geq 2$ für überflüssig, da, wie sich aus der in Z erweiterte Konstrukt kein Widerspruch ergibt, wenn man die rekursive Bildungsregel für alle n $a_{n}=a_{n-1}+a_{n-2}\$ sein läßt. Erst wenn die erweiterung nach Z zu einem Widerspruch führen würde, wäre so eine Einschränkung angebracht. --Arbol01 02:02, 27. Nov 2005 (CET)

Ich wollte eigentlich nicht für $n\geq 2$ plädieren sondern nur gegen die Aufzählungszeichen, die durch den Satz zerrissen wurden. Hinsichtlich $n\geq 2$ bin ich eher neutral. --Wolfgangbeyer 02:21, 27. Nov 2005 (CET)

Die Frage ist nicht, ob diese Fortsetzung möglich ist, sondern ob sie üblich ist und ob sie relevante Anwendungen hat. Primär ist die Fibonacci-Folge eine Folge, also indiziert durch positive oder nichtnegative ganze Zahlen.--80.136.185.54 03:15, 27. Nov 2005 (CET)

Also mir gefällt die momentane Version auch ziemlich gut. Gruß --Wasseralm 13:53, 27. Nov 2005 (CET)

Es ist eine Einschränkung, durchaus zulässig. Viel früher waren die negativen Zahlen nicht anerkannt, etwas früher waren die imaginären Zahlen nicht anerkannt. Auch Einschränkungen. Erst als gezeigt wurde, daß sinnvolle Ergebnisse durch einen erweiterten Einschränkungsradius gewonnen werden konnten, war man bereit Einschränkungen zugunsten einer erweiterten Sichtweise aufzugeben. Warum sollte dies heute anders sein? Für das Verständnis sind Einschränkungen und deren Aufhebung ein wertvolles Hilfsmittel. --Helmut Rasinger 13:22, 19. Okt. 2006 (CEST)

Fibonacci-Folge und Lucas-Folge

Um gleich die Luft rauszulassen: Ich meine die Folge 2, 1, 3, 4, 7, 11, ... und nicht die allgemeinen Lucas-Folgen U(P,Q) und V(P,Q).

Zwischen der Fibonacci-Folge und der Lucas-Folge gibt es Verbindungen. Das sich ein Glied der Lucas-Folge aus der Summe zweier Glieder der Fibonacci-Folge bilden läßt $L_{n}=f_{n-1}+f_{n+1}\$ habe ich schon in Lucas-Folge erwähnt. Es gibt da aber noch eine andere Formel, die mehr die Fibonacci-Folge betrifft: $f_{2n}=f_{n}\cdot L_{n}$. In Worten: Das Produkt der n.ten Fibonacci-Zahl mit der n.ten Lucas-Zahl ist gleich der Fibonacci-Zahl an der doppelten Position. --Arbol01 01:07, 23. Feb 2006 (CET)

"Jeden Monat kommt zu der Anzahl der Paare, die im letzten Monat gelebt haben, eine Anzahl von neugeborenen Paaren hinzu, die gleich der Anzahl der Paare ist, die bereits im vorletzten Monat gelebt haben, da genau diese geschlechtsreif sind und sich nun vermehren. Das entspricht aber gerade der oben angegebenen Rekursionsformel."

Ich glaube, das sollte anders formuliert werden.. diese Erklärung stimmt zwar genau mit der Rekursionsvorschrift überein, nicht jedoch mit der tatsächlichen Vermehrung der Kaninchen. z.B: 3 + 5 = 8, die 8 kommt aber nicht aus dieser Addition zustande, sondern aus 5 (Anzahl der Kaninchenpaare, die es bereits gibt) plus 2 (unter den 5 Kaninchenpaaren gibt es 2, die bereits jedes Monat werfen) plus 1 (Nachkommen des Kaninchenpaares, welches im 4. Monat geboren wurde und nun im 6. Monat zum ersten Mal wirft).

Kann auch sein dass ich mich irre, bitte um eure Meinung! liebe grüße

Ich glaube, Du irrst dich nicht. Aber für die Berechnung macht das ja keinen Unterschied. In der Realität wird ein Weibliches Kaninchen nicht immer die gleiche Zahl an Nachkommen werfen, alte Kaninichen werden sterben, ab einer gewissen Bevölkerungsdichte wird die Geburtenrate zurück gehen, ... . Wichtig ist, das die Näherung stimmt. --Arbol01 17:46, 2. Apr 2006 (CEST)

Die angeblichen "Fibonacci"-Zahlen.

Wie im englischen Pendant zu lesen ist, stammen die Zahlen nicht von Fibonacci!

Sie wurden bereits 1600 Jahre zuvor in Indien entdeckt.

Unglaublich, dass sich solche Misnomen so verbreiten. Habe es in jedem Fall im ersten Abschnitt korrigiert. --Gentlemanx 14:58, 15. Sep 2006 (CEST)

Auch in der alten Version stand nichts davon, dass Fibonacci der erste gewesen sei.--Gunther 15:18, 14. Sep 2006 (CEST)

Auf diesen Firlefanz soll ich jetzt wohl nicht eingehen, oder? Troll woanders 'rum! --Gentlemanx 14:58, 15. Sep 2006 (CEST)

Sorry, aber aus meiner Sicht ist so etwas wie „die angeblichen ‚Fibonacci‘-Zahlen“ Firlefanz. In der Mathematik interessiert sich niemand dafür, ob der Mensch jetzt die Benennung nach ihm verdient hat oder nicht. Sie heißen Fibonacci-Zahlen, so versteht jeder, was gemeint ist, das ist das einzige, was zählt.

Ansonsten: WP:WQ--Gunther 15:01, 15. Sep 2006 (CEST)

Herleitung der Formel von Binet

Der Ansatz $f(n)=a^{n}$ ist so falsch, weil die Fibonacci Folge offensichtlich keine geometrische Folge ist. Die Lösung von $a^{2}=a+1$ ergibt ja schließlich auch zwei Funktionen. Die Formulierung "aus der Rekursionsformel folgt" verdeutlicht sogar, das es sich nicht um eine Herleitung handelt, ich kann ja nicht das gesuchte Ergebnis vorraussetzen.

Selbst der richtige(re) Ansatz, dass es sich um die Linearkombination von 2 geometrischen Folgen handelt wäre unzulässlich (unbekannt); und ein analytischer Ansatz ohne diese Voraussetzung ist relativ kompliziert. Deshalb schlage ich vor an dieser Stelle stattdessen einfach allgemein auf Lösungsverfahren für rekursiv definierte Funtionen zu verweisen. --145.253.184.242 13:01, 19. Sep 2006 (CEST)

Etwas ausführlichere Fassung der Beweisskizze: Setzt man für die Rekursionsformel Lösungen der Form $f_{n}=a^{n}$ an, so erhält man die Aussage, dass das genau dann funktioniert, wenn $a$ die quadratische Gleichung löst. Da die Folge durch die beiden Anfangsglieder bestimmt ist und man mit einer geeigneten Linearkombination der beiden Lösungen $\Phi ^{n}$ und $\Psi ^{n}$ die gewünschten Anfangswerte erhält, folgt die Behauptung. QED. Ist ein einwandfreier Beweis.--Gunther 00:30, 26. Sep 2006 (CEST)

Hallo Gunther Ich habe sinngemäß den Satz: Aus der Lösung von a²=a+1 folgt die obige Formel.

Umgeschrieben zu: ... folgt $\lbrace \Psi ,\Phi \rbrace$ und führt später zur obigen Formel. Einverstanden?

Die Herleitung ist angedeutet, es ist vielleicht auch nicht der richtige Platz diese hier ausführlich darzulegen. Wo kann man dies denn tun? Eine Unterseite? Ein Link auf die Herleitung wäre ganz gut. --Helmut Rasinger 12:18, 19. Okt. 2006 (CEST)

Steht alles unter Lineare Differenzengleichung.--Gunther 00:08, 30. Okt. 2006 (CET)

Fibonaccibeispiele in verschiedenen Programmiersprachen

Ich bin etwas verwirrt von den 2 Beispielen, das sieht doch beides aus wie C++, aber über dem 2ten steht (sinngemass) 'und jetzt noch ein Beispiel in C++'.

Günter

Korrektur: Das erste Beispiel ist nicht C++, aber WAS ist es?

Egal: Für einen derartig trivialen Algorithmus einen Programmcode aufzuführen, auch noch in verschieden Sprachen, ist nun wirklich nicht die Aufgabe einer Enzyklopädie. Wir sind doch kein Anfängerprogrammierkursskript. --Wolfgangbeyer 01:06, 14. Jan. 2007 (CET)

Frage eines mathematisch Unbegabten...

.. hat es einen besonderen Hintergrund warum exakt jede 3. Stelle der Fibonacci-Folge eine gerade Zahl ist ? (die 0 lässt man natürlich ausser Acht ;) ).

0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 ... usw.

Ich beschäftige mich im Normalfall nicht mit Mathematik, es ist mir nur beim Anblick der genannten Zahlenfolge im Artikel aufgefallen und gleichzeitig habe ich aber nichts darüber im Artikel selbst gefunden.

danke für eventuelle Hinweise.

Creo 11:05, 23. Jul. 2007 (CEST)

Ja. Das ist die immer wieder kehrende Folge aus

gerade + ungerade = ungerade

ungerade + ungerade = gerade

ungerade + gerde = ungerade.

--Simon-Martin 11:52, 23. Jul. 2007 (CEST)

omg darauf hätte ich auch als unbegabter selbst kommen müssen .. :-/ Grundschul-Logik .. und nichts ist hängen geblieben ;) .. danke dir auf jeden Fall für die Erleuchtung

Creo 15:26, 23. Jul. 2007 (CEST)

Fibonacci bei den Zweierpotenzen

Die erste(n) Stellen von bestimmten (einem Muster folgenden) Zweierpotenzen ergeben die Fibonacci Folge:

2^07 = 128
2^11 = 2048
2^15 = 32768
2^19 = 524288
2^23 = 8388608
2^27 = 134217728
2^31 = 2147483648
2^35 = 34359738368

Auffällig ist hier: Die Fibonacci Folge taucht in den ersten Stellen der Folge

F(n) = 16 * F(n-1) = 2^4 * F(n-1)

auf, für den Startwert

F(0) = 2^7

oder absolut:

F(n) = 2^(7+4*n)

Die Zahlen nehmen außerdem solange nur um eine Stelle zu, solange die zugehörigen Zahlen der Fibonacci Folge ihre Stellenzahl behalten, der Sprung um eine bzw. zwei Stellen findet gleichzeitig statt: siehe Übergang zwischen 2^23 und 2^27.

--87.180.77.159 21:00, 2. Aug. 2007 (CEST)

Ich habe eine zweite, m. E. einfachere Herleitung der Binet-Formel eingefügt. Man könnte daher m. E. die erste Herleitung streichen. Ich halte es aber nicht für meine Aufgabe, das zu tun. --Hanfried.lenz 17:36, 27. Aug. 2007 (CEST).

Dies wurde von einem anderen Benutzer noch etwas umformuliert, m. E. sogar etwas verbessert, z. B. durch Verwendung bereits benutzter großen griechischen Buchstaben, von denen ich leider nicht weiß, wie man sie eintippen kann. --Hanfried.lenz 21:17, 27. Aug. 2007 (CEST).

Hallo Hanfried. Mir gefällt deine Herleitung, wobei ich den Schritt zu $g(n)=a\Phi ^{n}+b\Psi ^{n}$ nicht ganz nachvollziehen kann. Ist das ein unbekannter Ansatz wo man die "Anfangsbedingungen" bestimmen sollte oder bezieht sich das auf den Abschnitt oberhalb? Die Syntax die man hier verwendet ist fast ähnlich zur Tex-Syntax (siehe Hilfe:Mathematische_Symbole bzw. Hilfe:TeX). mfg --Montag 17:00, 28. Aug. 2007 (CEST)

"Beste Approximation"?

Hintergrund ist der Umstand, dass die rationalen Zahlen, die den zugrunde liegenden Goldenen Schnitt am besten approximieren, Brüche von aufeinanderfolgenden Fibonacci-Zahlen sind. – Gibt es dafür eine Quelle (mit geeigneter Definition von am besten), oder ist das irgendwie trivial? -- Paul E. 23:14, 25. Sep. 2007 (CEST)

Das folgt aus der Kettenbruchzerlegung von $\Phi$: Bricht man die (bei irrationalen Zahlen unendliche) Kettenbruchentwicklung irgendwann ab, erhält man eine rationale Zahl. Diese rationale Zahl approximiert die irrationale Zahl am besten im Sinne von: Um die irrationale Zahl noch besser anzunähern, muss man den Nenner des Bruchs erhöhen. Die Details gibt es auf der Seite zu Kettenbrüchen. Viele Grüße, -- octo 07:15, 6. Jul. 2009 (CEST)

Einleitung

Eine ausführlichere Einleitung für nicht-Mathematiker wäre sehr wünschenswert.. Holstenbär 15:04, 14. Mär. 2008 (CET)

Ist mir auch aufgefallen. Wissende wir brauchen euch! ;) – Metoc 21:42, 15. Apr. 2008 (CEST)

Trivia?

Ich habe den Abschnitt umgetitelt in "Rezeptionen in Kunst und Unterhaltung", denn die "Fibonacci-Folge" findet sich durchgehend immer wieder und ist deshalb eigentlich keine Nebensächlichkeit. Es wäre m. E. auch besser, aus der Stichwortliste in diesem Abschnitt einen Fließtext zu machen, der die Vielfalt der Aufnahmen und deren qualitative Unterschiede im Zusammenhang erläutert. --Felistoria 23:49, 12. Apr. 2008 (CEST)

Frage an euch

fn=fn-1+fn-2 fuer n groesser gleich 2
Das steht dort... f0=0, f1=1
Ich bin einfach mal hingegangen und habe Zahlen eingesetzt...
Theoretisch sollte es dann so aussehen zu Anfang: 0,1,1,2,3,5 (1+1=2, 1+2=3, 2+3=5, etc.)
f0=0
f1=1
f2=f2-1+f2-2=1
So weit so gut... 0,1,1
f3=f3-1+f3-2=3 (2+1=3)
Wo finde ich die 2 oder habe ich hier einen Haenger in meinem Gedankengang?

f_3-1+f_3-2=f₂+f₁=1+1=2 --Rat 10:37, 21. Sep. 2008 (CEST)

Zeckendorf-Theorem

Liebe Hauptautoren,

Könnte jemand von euch hier ein paar Beispiele (z.B. für die Zahlen 1,2,3,4) angeben. Die Formulierung ist leider zu wenige anschaulich, als dass man das Prinzip verstehen können. Es dankt herzlich im voraus Peu 15:17, 21. Okt. 2008 (CEST)

Liege ich hiermit richtig ?

	F0 0	F1 1	F2 1	F3 2	F4 3	F5 5	F6 8	Fn ...
1	0	0	1	0	0	0	0	...
2	0	0	0	1	0	0	0	...
3	0	0	0	0	1	0	0	...
4	0	0	1	0	1	0	0	...
5	0	0	0	0	0	1	0	...
6	0	0	1	0	0	1	0	...
7	0	0	0	1	0	1	0	...
8	0	0	1	0	0	0	1	...
9	0	0	1	0	0	0	1	...
usw.

Gespannt, ob ich Antwort erhalte :) --Peu 16:44, 21. Okt. 2008 (CEST)

Da F₁==F₂, kann nur, indem F₁ ignoriert wird, eine eindeutige Zeckendorf-Repreäsentation erzeugt werden[1]... Offenbar lag ich so ganz nah an richtig... --Peu 17:10, 21. Okt. 2008 (CEST)

Die Nullen (F₀) können auch raus... --Peu 17:15, 21. Okt. 2008 (CEST)

...da hat sich ein Fehler eingeschlichen...

das ist das erste mal das ich das mache... aber da hat sich ein fehler eingeschlichen...

im artikel steht: 3.524.578, 5.702.887, 9.224.465 allerdings wäre 9.227.465 an dieser stelle richtig...

erledigt, Danke --Peu 23:37, 21. Okt. 2008 (CEST)

'Zufällige' Fibonacci-Folge

Im Artikel Embree-Trefethen-Konstante wird die 'zufällige Fibonacci-Folge' erwähnt. Vielleicht könnte man die auch noch beschreiben? --Cspan64 18:25, 7. Dez. 2008 (CET)

Kaninchen-Gleichnis

Die Fibonacci-Folge funktioniert am Kaninchenbeispiel nur dann, wenn die Großelterngeneration nach ihrem zweiten Wurf stirbt. Sonst ist es eine simple exponentielle Vermehrung zur Basis 2 (2^n). Fibonacci ging wohl in seinem Beispiel von einem "Ideal-Kaninchen" aus, dass nach dem ersten Monat geschlechtsreif ist und exakt ein Paar wirft. Am zweiten Monat ein weiteres Paar wirft und dann verstirbt und damit aus der Zählung ausscheidet. Zum korrekten Verständnis wäre zu betonen, dass die Zählung den lebenden Paaren und nicht den Individuen gilt.

Die in der aktuellen Seite abliegende Vorschrift

1. Zu Beginn gibt es ein Paar geschlechtsreifer Kaninchen.
2. Jedes neugeborene Paar wird im zweiten Lebensmonat geschlechtsreif.
3. Jedes geschlechtsreife Paar wirft pro Monat ein weiteres Paar.
4. Die Tiere befinden sich in einem abgeschlossenen Raum („in quodam loco, qui erat undique pariete circundatus“), so dass kein Tier die Population verlassen und keines von außen hinzukommen kann.

müsste beispielsweise folgendermaßen modifiziert werden:

1. Zu Beginn gibt es ein Paar geschlechtsreifer Kaninchen.
2. Jedes neugeborene Paar wird im zweiten Lebensmonat geschlechtsreif.
3. Jedes geschlechtsreife Paar wirft pro Monat ein weiteres Paar.
4. Nachdem ein Paar zum zweiten Mal geworfen hat, verstirbt es.
5. Die Tiere befinden sich in einem abgeschlossenen Raum („in quodam loco, qui erat undique pariete circundatus“), so dass kein Tier die Population verlassen und keines von außen hinzukommen kann.

In der englischen Wiki-Seite ist es korrekt geschildert. (nicht signierter Beitrag von 195.127.43.185 (Diskussion | Beiträge) 12:00, 12. Mär. 2009)

Nein, du irrst dich. Sämtliche Paare des Vormonats existieren weiterhin, und für sämtliche Paare des Vor-Vormonats kommt ein Paar dazu. Zum Beispiel hier und hier hat es jemand aufgemalt. Wie du siehst, stirbt keines. Bei deiner Version kommt die Folge 1, 1, 2, 2, 3, 4, … heraus. --80.129.93.127 16:27, 12. Mär. 2009 (CET)

Deine Folge ist übrigens die ebenfalls interessante und selbstverständlich mit der Fibonacci-Folge verwandte Padovan-Folge (Folge A000931 in OEIS). --80.129.93.127 18:30, 12. Mär. 2009 (CET)

"Explizite" Darstellung

Wieso nennt man die explizite Darstellung explizit? Laut Wikipedia bedeutet explizit "Darlegung, Entwirrung, Erläuterung, Deutung". Allerdings ist die explizite Darstellung keinesfalls entwirrt, sondern das Gegenteil. Sie braucht wesentlich mehr Rechenschritte und ist viel komplizierter, als die einzelnen Zahlen einfach nacheinander Auszurechnen. Eigentlich ist es doch nur ein Umweg um mit mehr Aufwand auf daselbe Ergebnis zu kommen. Wieso wird das nirgens erwähnt? Was haltet ihr davon? --Popelmaus 07:14, 2. Mai 2009 (CEST)

Es ist bestimmt "nicht rekursiv" gemeint, und eine Darstellung mit (allerdings ebenfalls nicht völlig klar definierten) elementaren Funktionen. Man kann vor allem den Koeffizienten des asymptotisch exponentiellen Wachstums direkt daraus ablesen. Die Behauptungen "wesentlich mehr Rechenschritte", "viel komplizierter" und "Umweg" sind so nicht richtig. Die im Abschnitt "Näherungsformel für große Zahlen" angegebene exakte Formel, die aus der "expliziten Darstellung" direkt folgt, dürfte für große Indizes die schnellste einfache Berechnungsmöglichkeit sein. --80.129.76.232 08:39, 2. Mai 2009 (CEST)

Fibonacci in der Natur

Blütenstand des Romanesco mit fraktalen Strukturen und Fibonacci-Spiralen.

Vielleicht sollte man hier auch den Romanesco mit aufführen. (nicht signierter Beitrag von 194.25.30.1 (Diskussion | Beiträge) 11:48, 8. Okt. 2009 (CEST))

Man sollte diesen Abschnitt dringend überarbeiten. Das versteht doch kein Mensch und ist z.T. irreführend. Z.B. "Viele Pflanzen weisen in ihrem Bauplan Spiralen auf, deren Anzahl durch Fibonacci-Zahlen gegeben sind ..."? Sicherlich ist hier gemeint daß die Anzahl der Elemente (z.B. Samenkörner) bestimmten F-Zahlen entsprechen (gemäß dem Bild). Weiter mit "... der Winkel zwischen architektonisch benachbarten Blättern oder Samen bezüglich der Pflanzenachse der Goldene Winkel ist." Was soll architektonisch benachbart heißen? Bei 137.5 Grad handelt es sich doch nicht mehr um Nachbarschaft (bei einem Achsenabstand der den Größenverhältnissen der Blume entspricht), das ist weit entfernt. Über den radialen Abstand wird auch gar nichts gesagt, der muß sich aber auch ändern wenn sich eine Spirale ergeben soll. Dann steht zu lesen "Die Spiralen werden daher von Pflanzenelementen gebildet, deren Platznummern sich durch die Fibonacci-Zahl im Nenner unterscheiden und damit fast in die gleiche Richtung weisen." Wo oder was ist denn hier die Platznummer? Eine Koordinatenangabe als Funktion von F-Zahlen wobei jedes Pflanzenelement n durch F_n o.ä. gegeben ist könnte ich mir vorstellen. Im kartesischen oder besser noch im polaren Koordinatensysten ließe sich so eine Spirale erzeugen. Aber was hat das alles mit der Blume zu tun? Wie ist denn hier die Zuordnung? So ist der Abschnitt eher löschwürdig. (nicht signierter Beitrag von 212.147.5.100 (Diskussion | Beiträge) 16:54, 22. Dez. 2009 (CET))

weiteres Beispiel: Varroa-Milbe

bei der Vermehrung der Varroa-Milbe in der Bienenbrut geht man davon aus, daß die Mutter 3-mal verdeckelungsbereite Zellen aufsucht und über die Verdeckelungsdauer von 12 Tagen einen Sohn und zwei vermehrungsfähige Töchter liefert

die daraus sich ergebende Fibonacci-Folge ergibt sich dann zu 1 - 3 - 9 - 26 -76 - 210, also annähernd 3 exp n

die Bestätigung hierfür liefert das Zählen der nach einer durchgeführten (chemischen) Behandlung heruntergefallenen toten Milben, wo nach etwa 8 Brutperioden (entspricht 4 Monaten ungestörter Vermehrung) bis zu 10.000 Exemplare gefunden werden können

eine Grenze liegt nur in der im Bienenvolk geschätzten Gesamtzahl von ca. 60.000 Bienen und zusätzlich darin, daß in den heißen Sommermonaten die Legetätigkeit der Bienenkönigin eine Talsohle (eine Art Diapause) aufweist - trotzdem ist bei der Ende August endenden Brutzeit unentrinnbar das Todesurteil für das Bienenvolk gesprochen

-- kauhl-meersburg (nicht signierter Beitrag von Kauhl-mbg (Diskussion | Beiträge) 21:37, 21. Nov. 2009 (CET))

Mathematische Strenge und Verständnis im Abschnitt: Herleitung mittels Differenzengleichung

Aus verschiedenen Gründen kommt es gelegentlich vor, daß die ausgeführten mathematischen Gedanken noch nicht der vollen mathematischen Strenge genügen. Glücklicherweise ist es aber so, daß in vielen Fällen durch kleine Modifikationen die volle Strenge erreicht und auch das mathematische Verständnis verbessert wird. Ich möchte dies an folgender Altfassung vom 13.3. vorführen. Die ursprünglichen Überlegungen sind formal so nicht zulässig, da der Ansatz $f_{n}=x^{n}$ unzuläsig ist. Denn die Fibonacci-Folge ist offensichtlich keine geometrische Folge. Dieser Fehler findet sich leider häufig. Außerdem finden sich noch die Rudimente $\Phi$ und $\Psi$ einer abweichenden Notation.

„Eine andere Herleitungsmöglichkeit folgt aus der Theorie zu linearen Differenzengleichungen:

Angenommen, die Fibonacci-Folge kann als Potenzfunktion $f_{n}=x^{n},n\in \mathbb {N}$ dargestellt werden. Dann ergibt sich

$f_{n}-f_{n-1}-f_{n-2}=x^{n}-x^{n-1}-x^{n-2}=(x^{2}-x-1)x^{n-2}$

durch Herausheben.

Wenn also $x$ so gewählt wird, dass $x^{2}-x-1=0$ ist, wird $f_{n}=f_{n-1}+f_{n-2}$, also die Rekursion der Fibonaccifolge. Das tritt ein, wenn $x$ das reziproke Teilverhältnis $\Phi$ des goldenen Schnitts oder sein algebraisch konjugiertes $\Psi$ ist. Die Folgen $\Phi ^{0},\Phi ^{1},\Phi ^{2},\dots$ und $\Psi ^{0},\Psi ^{1},\Psi ^{2},\dots$ sind Lösungen der Rekursionsgleichung. Außerdem wird die fibonaccische Rekursionsformel auch durch Linearkombinationen der beiden Lösungen, $g_{n}=c_{1}\Phi ^{n}+c_{2}\Psi ^{n}$, erfüllt.

Bestimmt man die Koeffizienten $c_{1}$ und $c_{2}$ so, dass sich wie bei der Fibonaccifolge $g_{0}=0$ und $g_{1}=1$ ergibt, erhält man die Binet-Formel. Dazu sind zwei einfache lineare Gleichungen zu lösen.“

---

Die mathematische Idee dahinter ist jedoch so gut, daß durch eine kleine Modifikation des Textes die volle mathematische Strenge erreicht wird:

Sei $C_{n}=x^{n},n\in \mathbb {N} _{0}$ eine geometrische Folge, so ergibt sich:

$C_{n+1}-C_{n}-C_{n-1}=x^{n+1}-x^{n}-x^{n-1}=(x^{2}-x-1)x^{n-1}$

Wenn also $x$ so gewählt wird, dass die charakteristische Gleichung $x^{2}-x-1=0$ erfüllt ist (also $x=\varphi$ oder $x=\psi \$), wird $C_{n+1}=C_{n}+C_{n-1}$, d.h. $C_{n}$ erfüllt die Fibonacci-Rekursion mit dem Rekursionsanfang $C_{0}=1$ und $C_{0}=x$.

Wichtig ist also folgende Erkenntnis:

Die rekursive Folge $A_{0}=1$, $A_{1}=\varphi$, $A_{n+1}=A_{n}+A_{n-1}$ hat die explizite Darstellung $A_{n}=\varphi ^{n}$. Ebenso $B_{0}=1$, $B_{1}=\psi \$, $B_{n}=\psi ^{n}\$

Mit $A_{n}$ und $B_{n}$ genügt auch jede Linearkombination $L_{n}=\alpha A_{n}+\beta B_{n}$der Fibonacci-Rekursion $L_{n+1}=L_{n}+L_{n-1}$. Mit Hilfe eines linearen Gleichungssystems ergibt sich $\alpha ={\frac {1}{\sqrt {5}}}$ und $\beta =-{\frac {1}{\sqrt {5}}}$ damit $L_{0}={\frac {\varphi ^{0}-\psi ^{0}}{\sqrt {5}}}=0=f_{0}$ und $L_{1}={\frac {\varphi ^{1}-\psi ^{1}}{\sqrt {5}}}=1=f_{1}$. Folglich ergibt sich explizit $F_{n}={\frac {A_{n}-B_{n}}{\sqrt {5}}}={\frac {\varphi ^{n}-\psi ^{n}}{\sqrt {5}}}$.

Für $\alpha =\beta =1$ ergibt sich $L_{0}=2$ und $L_{1}=1$, d.h. die klassische Lucas-Folge mit explizit $L_{n}=A_{n}+B_{n}=\varphi ^{n}+\psi ^{n}$. --Skraemer 13:51, 13. Mär. 2010 (CET)

Ist bei der Formel von Moivre-Binet die Gauß-Klammer nicht fehl an Platz, wird Sie nicht nur bei dem weglassen der hinteren Formel benötigt? (nicht signierter Beitrag von 92.193.8.219 (Diskussion) 09:00, 22. Jun. 2010 (CEST))

Müsste es nicht "...erfüllt die Fibonacci-Rekursion mit dem Rekursionsanfang $C_{0}=1$ und $C_{1}=x$." heißen? Also eine 1 statt einer 0 am zweiten C? -- Epaminaidos 00:58, 7. Okt. 2010 (CEST)

So ist es, ich habe es korrigiert. --91.32.87.198 14:11, 7. Okt. 2010 (CEST)

"Negafibonacci"

habe ich nirgends außerhalb Wikipedia und Co. belegt gefunden, abgesehen von [2], wo es etwas anderes bedeutet. Die Bezeichnung erscheint mir auch höchst überflüssig. --91.32.81.210 16:25, 13. Jan. 2011 (CET)

Donald E. Knuth: The Art Of Computer Programming, Volume 4., Seite 36 in diesem Preview: http://www-cs-faculty.stanford.edu/~uno/fasc1a.ps.gz . Das von dir angegebene Textstück referenziert per [41] genau dieses Buch. --Daniel5Ko 17:40, 13. Jan. 2011 (CET)

Hmm, da ist es, wenn ich es richtig sehe, eine Wortbildung analog zu einem früher eingeführten "negadecimal system". Die Schreibweise ist dann auch entsprechend "negaFibonacci" und nicht "Negafibonacci", und die Bezeichnung "negaFibonacci numbers" (nur das erste Wort kursiv) ergibt sich dabei als Rückbildung aus dem "negaFibonacci number system" (alles kursiv). Wenn man all das nicht vorhat, ist die Bezeichnung unverständlich. Ich würde sie immer noch entfernen, solange man nicht die Knuthsche Konstruktion erläutert. --91.32.81.210 18:36, 13. Jan. 2011 (CET)

"Die in den negativen Indexbereich erweiterte Negafibonacci-Folge" (Betonung von mir) ist sowieso falsch. Es ist ja lediglich der Teil gemeint, der aus $F_{k}$ mit $k<1$ besteht. Wie dem auch sei. Mir ist eigentlich ziemlich egal, was mit der Passage passiert. Ich wollte lediglich eine Quelle angeben, für den Fall, dass jemand etwas annehmbares basteln möchte. --Daniel5Ko 20:09, 13. Jan. 2011 (CET)

Danke für die Recherche, auch von mir aus kann das gerne jemand damit erweitern. Ich entferne aber das meiner Ansicht nach eher irreführende "so genannte Negafibonacci-Folge". --91.32.81.210 20:25, 13. Jan. 2011 (CET)

Kaninchenproblem; Fibonacci-Folge

Liber abbaci, MS Biblioteca Nazionale di Firenze, Codice Magliabechiano cs cI 2616, fol. 124r: Berechnung der „Kaninchenaufgabe“ mit Fibonacci-Reihe

Ich habe ein kleines Problem mit der bisherigen Darstellung des Kaninchenproblems, dieses soll ja eigentlichdie Fibonacci-Folge darstellen, dafür müsste man aber mit einem geschlechtsunreifen Paar anfangen, da auch die Fibnacci-Folge mit [1;1;2...]anfängt es ist also 2 die ersten beiden Monate nur ein Paar vorhanden --95.112.213.74 22:45, 5. Mai 2009 (CEST)

Bei Fibonacci selbst ist (laut dem Artikel, ich habe es nicht nachgeprüft) der Index um eins verschoben, die originale Fibonacci-Folge beginnt also mit 1, 2, 3, 5, 8, … --80.129.96.156 23:34, 5. Mai 2009 (CEST)

Um das mal aufzuklären, weil ich es aus Unachtsamkeit auch schon falsch wiedergegeben habe und es in der Literatur sehr oft falsch dargestellt wird:

Der Liber abbaci liegt mir in der Ausgabe von Boncompagni vor, hier findet Ihr online eine Abschrift der Kaninchenaufgabe mit englischer Übersetzung. Jedes Paar bringt im Monat ein Paar zur Welt, das seinerseits ab dem zweiten Monat ein Paar zur Welt bringt ("cum natura eorum sit per singulum mensem aliud par germinare; et in secundo mense ab eorum natiuitate germinant"), denn die Empfängnis und der Beginn der Austragungszeit liegen im Monat vor der Geburt, wie sich aus der Aussage zum 2. und 3. Monat ergibt. Der Text läßt das erste Paar aber bereits im ersten Monat das zweite Paar werfen und fängt die Reihe deshalb genaugenommen weder mit "1, 2", noch mit "1, 1, 2", sondern mit "2, 3, 5" an:

• primo mense: paria duo
• secundo mense: paria 3
• tercio mense: paria 5
• quarto mense: paria 8
• quinto mense: paria 13

...

• undecimo mense: paria 233
• ultimo mense: paria 377

In der von Boncompagni zugrundegelegten Handschrift, aus der Heinz Lüneburg (Angaben im Artikel Leonardo Fibonacci) die beiden Seiten mit der Kaninchenaufgabe in Photographien reproduziert (er fand sie so unwichtig für Leonardo und das Gewese in der Literatur darüber so übertrieben, daß er sie im Text seines Buches nicht besprechen mochte, der Leser sollte sie sich in der Reproduktion stattdessen selbst anschauen!) findet sich auf dem rechten Rand von f. 124r (oben verlinkt) eine auch von Boncompagni nachgedruckte Zahlenkolonne, die an den Anfang zwar den Eintrug "parium" mit der Zahl 1 (also "An Paaren: 1") stellt, dann aber, wie im Text, erst im folgenden Eintrag mit der Monatszählung und der Zahl 2 für den "ersten Monat" beginnt.

Weil Lüneburg es sich dann doch nicht ganz verkneifen konnte, das verhaßte Thema wenigstens abfällig anzusprechen, schreibt er hierzu (p.197): "Er [Lüneburgs eigener Leser] wird dort [in der Photographie der Handschrift] feststellen, daß Fibonacci die nach ihm benannte Serie mit F₀ = 1 und F₁ = 2 beginnen läßt. Seine Arbeiten würden also von der Zeitschrift 'The Fibonacci Qua[r]terly' nicht zur Publikation angenommen, wie man etwa der Seite 2 des Umschlags des Maiheftres des Jahres 1991 dieser Zeitschrift entnehmen kann." --Otfried Lieberknecht 20:47, 17. Feb. 2011 (CET)

Danke für die Aufklärung! Man kann aber, wie Lüneburg, es auch so sehen, dass bei Fibonacci die Folge mit F₀ = 1 (also im nullten Monat) beginnt. Der Umschlag des Maiheftes von 1991 von "The Fibonacci Quarterly" ist hier, an dieser Vorgabe hat sich wohl auch nichts geändert. Der Index ist dann jedenfalls um zwei verschoben. --91.32.82.234 11:42, 18. Feb. 2011 (CET)

Ihr habt sicher beide recht, was Monat 0 betrifft, aber in der ausdrücklichen Formulierung get es erst mit Monat 1 los. Vielen Dank übrigens für das Link, jetzt weiß ich endlich genau, wie er das meinte. Daß jemand das noch mal eigens nachguckt und verlinkt hätte ihn als leidenschaftlichen Spaziergänger auf der Suche nach Antworten auf nebensächliche Fragen bestimmt gefreut! --Otfried Lieberknecht 13:20, 18. Feb. 2011 (CET)

Erzeugende Funktion

Da scheinbar andauernd verkehrt korrigiert wird, hier mal 'ne kurze Herleitung: Wir starten mit Haskell-Folklore, von der wir wissen, dass die Fib-Folge, beginnend mit $0,1$, definiert werden kann als

fibs = 0 : 1 : zipWith (+) fibs (tail fibs)

Übersetzen wir das in eine erzeugende Funktion $F$, so lautet die Gleichung $F(x)=0+x+x^{2}(F(x)+F(x)/x)$. Nun weiter:

${\begin{aligned}F(x)&=0+x+x^{2}(F(x)+F(x)/x)\\F(x)&=0+x+x^{2}F(x)+xF(x)\\F(x)(1-x-x^{2})&=x\\F(x)&={\frac {x}{1-x-x^{2}}}\end{aligned}}$

Vielleicht könnte man das auch einigermaßen vernünftig (insbesondere der Start mit Haskell-Folklore ist ein wenig faul ;) ) in den Artikel einbauen. So oder so kann man nun per "Siehe Disk." möglicherweise lehrreicher/konstruktiver revertieren^^... --Daniel5Ko 00:19, 2. Feb. 2011 (CET)

Die Fib-Folge beginnend mit $1,1$ kann definiert werden als

fibs = 1 : 1 : zipWith (+) fibs (tail fibs)

Übersetzen wir das in eine erzeugende Funktion $F$, so lautet die Gleichung $F(x)=1+x+x^{2}(F(x)+(F(x)-1)/x)$. Nun weiter:

${\begin{aligned}F(x)&=1+x+x^{2}(F(x)+(F(x)-1)/x)\\F(x)&=1+x+x^{2}F(x)+xF(x)-x\\F(x)(1-x-x^{2})&=1\\F(x)&={\frac {1}{1-x-x^{2}}}\end{aligned}}$

Aber dieser Folgenstart ist halt nicht der im Artikel verwendete... --Daniel5Ko 00:19, 2. Feb. 2011 (CET)

Ergänzung

Die Zahlen spielen auch in dem historischen Roman "Das königliche Spiel" der Autorin Katherine Neville eine Schlüsselrolle. Kann dies bitte der Autor noch in dem Artikel ergänzen? Viele Grüße, AK -- 217.252.149.140 14:46, 4. Mai 2011 (CEST)

Teilbarkeit

Ich konnte den Fakt nirgendwo finden, dass stets (nur) jede (n+1)-te Fibonacci-Zahl durch n teilbar ist. --W. Kronf *@* 22:56, 10. Mai 2011 (CEST)

Das ist kein Fakt, sondern stimmt beispielsweise für n = 2, 3 und 7, aber nicht für n = 4 und 5 ([3]). --91.32.85.106 23:27, 10. Mai 2011 (CEST)

Oh, dann war ich wohl zu voreilig. Trotzdem sollte dies erwähnt werden. --W. Kronf *@* 23:58, 10. Mai 2011 (CEST)

Die Primzahl p teilt die Fibonacci-Zahl

--> f_{p-1}, wenn 5 quadratischer Rest modulo p ist,

--> f_5, wenn p=5 ist,

--> f_{p+1}, wenn 5 quadratischer Nichtrest modulo p ist.

--M. Hammer-Kruse 13:13, 22. Jun. 2011 (CEST)

P.S.: Das ist so auch nur ein Teil der ganzen Wahrheit. Denn wegen f_n|f_m, wenn n|m ist p natürlich auch Teiler aller Fibonacci-Zahlen mit einem Vielfachen des genannten Index. Jener Index gehört aber nicht unbedingt zur kleinsten Finbonacci-Zahl, die von p geteilt wird. Beispiel 47|987=f_16. 5 ist kein quadratischer Rest modulo 47. 47 teilt also auf jeden Fall f_48. In diesem Fall aber auch schon die Fibonacci-Zahl, die auf einem Drittel der Strecke liegt.

--M. Hammer-Kruse 13:20, 22. Jun. 2011 (CEST)

Könntest du dafür bitte eine Quelle angeben? Dann könnte man das sicher einfügen. Bei der Suche bin ich übrigens gerade auf [4] gestoßen, wo ebenfalls interessante Dinge stehen, die aufgenommen werden könnten. --W. Kronf *@* 13:24, 22. Jun. 2011 (CEST)

Keine Ahnung, wo das schon steht. Ich habe es mir neulich hergeleitet. Der Beweis ist relativ einfach. Den habe ich im ICE zwischen Hamburg und Hannover fertiggestellt gehabt. --M. Hammer-Kruse 13:55, 22. Jun. 2011 (CEST)

Ich habe den Beweis jetzt notiert: http://sternenreise.com/Verschiedenes/Fibonacci-Teilbarkeit.pdf --M. Hammer-Kruse 18:43, 23. Jun. 2011 (CEST)

tool - lateralus

gudn tach!
da es hier auf der talk page anscheinend noch nicht angesprochen, verlinke ich mal auf talk:Lateralus#Fibonacci. (etwaige weitere diskussion bitte dort fuehren und nicht hier.) -- seth 14:05, 2. Jun. 2011 (CEST)

Zeckendorf

Die Formulierung des Zeckendorfsatzes stimmt nicht, denn: mit die Folge 1, 1, 2, 3, 5, 8, ... gilt:

$\!3=0f_{1}+0f_{2}+0f_{3}+1f_{4}+0f_{6}+0.....$

mit $c_{4}=1,c_{i}=0,i\neq 4$

aber auch:

$\!3=1f_{1}+0f_{2}+1f_{3}+0f_{4}+0f_{6}+0.....$

mit $c_{1}=1,c_{3}=1,c_{i}=0,i\neq 1,i\neq 3$

Zwei Representationen die beide die Bedingungen erfuellen. (nicht signierter Beitrag von 82.75.140.46 (Diskussion) 16:53, 17. Okt. 2011‎ (CEST))

Die Summe von Zeckendorf beginnt aber mit 0-mal oder 1-mal $f_{2}$, die zweite Darstellung ist also ungültig. --79.204.239.7 17:10, 17. Okt. 2011 (CEST)

Von mir dieselbe Vermutung: Die Formulierung des Satzes stimmt nicht, denn es heißt: "dass jede natürliche Zahl n größer Null eindeutig als Summe voneinander verschiedener, nicht direkt aufeinanderfolgender Fibonacci-Zahlen geschrieben werden kann." Dies scheint mir aber z.B. für die 5 und die 13 nicht zu stimmen, es lassen sich keine verschiedenen, nicht direkt aufeinander folgenden Fibonacci-Zahlen finden, die in Summe 5 oder 13 ergeben. Es sei denn man nähme 0+5 bzw. 0+13, was aber den ganzen Satz redundant und damit sinnlos erscheinen ließe. Oder irre ich mich da vielleicht? -- 2.214.174.103 19:28, 1. Mär. 2012 (CET)

Diese Summe darf auch nur aus einer einzigen Zahl bestehen. Genau wird es nicht durch den informellen Satz, sondern durch die zur Erläuterung angegebene Formel (eingeleitet mit "Das heißt, [...]") beschrieben. --84.130.188.196 19:38, 1. Mär. 2012 (CET)

Erzeugende Funktion

die Formel nach Multiplikation mit z ist falsch, denn die linke Seite müsste offensichtlich noch über l summiert werden, denn so ist die rechte Seite eine Potenzreihe, die linke Seite aber eine verschied. endliche Summe (nicht signierter Beitrag von 131.220.192.3 (Diskussion) 20:09, 11. Dez. 2011 (CET))

Bild

Ein Kachelmuster aus Quadraten, deren Kantenlängen der Fibonacci-Folge entsprechen.

Ich halte dieses Bild als Einleitungsbild für irreführend, da es mit der Herleitung und Anwendung der Fibonacci-Zahlen wenig zu tun hat. Ich fände sowas passender und OmA-tauglicher. Wenn keiner widerspricht würde ich mal die Grafikwerkstatt beauftragen. --Siehe-auch-Löscher (Diskussion) 12:56, 27. Nov. 2013 (CET)

Ich finde schon, dass das Bild die Herleitung und Anwendung (goldene Spirale) illustriert. Die Kaninchen des Namensgebers sind vergleichsweise kurios und etwas verwirrend wegen der idealisierenden Annahmen (es wird pro Paar immer genau ein Pärchen pro Zeitabschnitt geboren, das dann ewig lebt). Dennoch, oder gerade deswegen, wäre ein Bild dazu keine schlechte Idee. Die auf Commons taugen leider nicht so viel (Datei:FibonacciRabbits.svg, Datei:FibonacciRabbit.svg, Datei:Time plaque on Millennium milepost - geograph.org.uk - 847338.jpg). --84.130.178.239 10:35, 29. Nov. 2013 (CET)

Ja, wahrscheinlich hast Du recht. Die Hasenreihe ist auch nicht so anschaulich. Am einfachsten ist hier eigentlich die Formel. --Siehe-auch-Löscher (Diskussion) 21:10, 12. Dez. 2013 (CET)

Lateralus (Lied)

Jemand hat das Lied bei Rezeption in Kunst hinzugefügt es wurde sofort mit "wurde schon x-mal rausgenommen" gelöscht. Nun ist das aber kaum ne Begründung. Also warum ist das nicht bedeutend, aber Dinge wie:

Das Cover des Debütalbums der kanadischen Band The Organ, Grab That Gun, wurde von David Cuesta mithilfe eines auf der Fibonacci-Folge basierenden Rasters entworfen.

Das Lied ist ein sehr erfolgreicher Metalsong, basiert tatsächlich auf Fibonacci-Zahlen,ich verstehe den Auscchluss hier nicht. -BrankoJ - Diskussion 19:55, 12. Dez. 2013 (CET)

Wir benötigen einen brauchbaren Beleg gemäß WP:Q, siehe auch #tool - lateralus. Mit einwandfreiem Beleg wäre die Information dann auch zunächst einmal vor allem für das Lied und die Band relevant. --84.130.246.63 21:03, 12. Dez. 2013 (CET)

Bitte weitere Diskussion auf Diskussion:Lateralus (Lied). --Kronf @ 21:04, 12. Dez. 2013 (CET)

Ich würd' ja vorschlagen, den ganzen "Rezeption[...]"s-Abschnitt zu löschen. Er ist aus meiner Sicht sowieso vor allem an den Haaren herbeigezogenes Zeug, das niemanden interessiert.

Mit der Löschung erspart man sich dann hier u.a. die Diskussion darüber, warum das, was dasteht, relevanter/sinnvoller/wasauchimmer ist, als Lateralus. --Daniel5Ko (Diskussion) 21:25, 12. Dez. 2013 (CET)

Gegen den Abschnitt ab an sich habe ich nichts. Solange dort simple Erwähnungen in Filmen, Cover von Bands ohne eigenen Artikeln oder auch einzelne Sendungen einer Serie drinnen stehen, sehe ich die direkte Relevanz für den Artikel nicht gegeben. Interessant wäre höchstens eine historische Abhandlung über verschiedene Benutzungen der Fibonacci-Zahlen im Laufe der Zeit oder Ähnliches. -BrankoJ - Diskussion 21:43, 12. Dez. 2013 (CET)

Ich habe den Lateralus-Hinweis erneut gelöscht! Er war von BrancoJ wieder eingetragen worden. (Zusammenfassungstext: 13:34, 22. Feb. 2014‎ BrankoJ (Diskussion | Beiträge)‎ K . . (38.187 Bytes) (+351)‎ . . (→‎Rezeptionen in Kunst und Unterhaltung: Lateralus mit eindeutiger Quelle hinzugefügt. Das Abstreiten der Richtigkeit dieser Quelle ist wohl wesentlich mehr Theoriefindung)) Mitsamt derselben Quelle war der Hinweis bereits im Dez. 2013 gelöscht worden und es bestand doch Einigkeit darüber, dass es eine stichhaltigere Begründung braucht. Die Sache nach 10 Wochen unverändert (ohne neue Erkenntnisse) wieder reinzuschieben, grenzt schon an Vandalismus, zumal der Wiedereintrag vom selben Benutzer vorgenommen wurde, der seinerzeit (in https://de.wikipedia.org/wiki/Diskussion:Lateralus_%28Lied%29 ) eingeräumt hatte, er werde nicht mehr darauf bestehen. --M. Hammer-Kruse (Diskussion) 20:58, 22. Feb. 2014 (CET)

Die sogenannte Einigkeit bestand, nach meiner Erwähnung von dem Beleg, der verwendet wurde, leider nur aus dem Kommentar von Hammer-Kruse. Ich habe meinen Entschluss, das zu akzeptieren, fallen lassen, da ich es nicht zulassen werde, dass Tatsachen nicht in die Wikipedia aufgenommen werden, nur weil ein Benutzer sich in den Kopf gesetzt hat, diese trotz Quellen nicht anzuerkennen.

Ich kann es nur wiederholen, es handelt es sich um eine große Zeitschrift speziell für Rockmusik. Diesen Beleg nicht zu akzeptieren, auf eine Fehlinformation in der Zeitschrift zu bestehen und sein eigenes Urteil über das von einem Fachjournalisten zu legen, ist kein verständlicher Grund für eine Nichtaufnahme in die Wikipedia (zumal hier vieles andere auch nicht belegt ist) --BrankoJ - Diskussion 20:23, 23. Feb. 2014 (CET)

(Mal wieder ausgerückt, sonst werden irgendwann die Zeilen zu kurz): Die Behauptung um die es hier geht, ist seit dem Nov. 2009 bereits 17 Mal im Artikel gelöscht worden, und zwar von mindestens sieben unterschiedlichen Bearbeitern. Dass hier "vieles andere auch nicht belegt" ist, ist ja kein Grund, alles mögliche als Wahrheit darzustellen. ("Herr Wachtmeister, der da parkt aber auch falsch. Wieso soll gerade ich denn mein Auto hier wegfahren?"). Und Presseerzeugnisse gibt es viele. So würde ich die große deutsche Tageszeitung mit den vier Buchstaben auch nicht als Beleg für irgendetwas akzeptieren. Und dass der vermeintliche Beleg keiner ist, das habe ich doch in der Sache schon drüben (auf der Diskussionsseite zum Lied) am 17. Dez. 2013 dargestellt. Ganz im Gegenteil: Er sagt deutlich, dass der Fibonnacci-Bezug im Nachhinein konstruiert wurde. --M. Hammer-Kruse (Diskussion) 21:06, 23. Feb. 2014 (CET)

Neben den Argument, dass die Zeitung kein Beleg ist, erwähntest du noch folgendes als Argument gegen den Beleg

"The song also switches between 9/8, 8/8 and 7/8 time signatures, with the number 987 being the 17th number of the Fibonacci sequence." Das ist nun so hanebüchen wie nur etwas. Damit ist auch jeder Walzer eine Hommage an die Fibonnacci-Folge, weil der 3/4 Takt auf die F.-Zahl 34 hinweist.

"In mapping the numerical representation of the Fibonacci sequence, an eternal spiral shape can be formed, which Keenan uses as a metaphor for finding strength within yourself in the lyric, ‘Spiral out, keep going.’" Das ist nun eher Esoterik als ein Bezug zur Fibonnacci-Folge.

Ich sehe in beiden kein Argument, dass für eine spätere Konstruktion spricht. Die 987 wurde von der Band selbst als Fibonacci-Zahl erkannt und in Interviews erwähnt, wenn Mozart auf 34 in seinem Walzer eingeht, kann das gerne dann auch irgendwo drinnestehen. Das da auch Esoterik drinne ist, mag schön sein, aber ich verstehe das Argument nicht in Bezug auf die spätere Konstruktion der Verwendung von der Folge.

Zudem kann man Loudwire wohl auch nicht ohne weiteres mit der Bild gleichsetzen. --BrankoJ - Diskussion 21:32, 23. Feb. 2014 (CET)

Beginn mit 1 statt 0

Auch eine falsche Übersetzung der Fibonacci-Folge, die am 1. beginnt, ist 1, dann 2, hält es Hinzufügen der beiden vorangegangenen. schließlich geht 1, 1, 2, 3, 5, 8, 13, 21. Das Voriobov sagen, Corbalan, Kolman und Polya. Aber die spanischen Wikipedia-Experten sagen, dass emìeza 0, dann 1, 1, 2, und so gegen den Strom, gegen die Geschichte und gegen die Problemstellung. Nun, es war ein paar Kaninchen. Und keine Null-Paare, lieber Bernard, der Herr und Meister der Bosheit und Tücke und Dummheit, die vor 12 Jahren über engavetan. (nicht signierter Beitrag von 190.118.20.8 (Diskussion) 00:25, 22. Feb. 2014 (CET))

Habe zwar nicht verstanden, wer da von Lima aus warum gedisst wurde, aber ich stimme zu, dass die Folge mit f_1=1 beginnend definiert werden sollte. Das ist nach meiner Einschätzung üblicher (etwa auch im Fibonacci Quarterly, Fibonacci selbst und auch das Zeckendorf-Theorem beginnen sogar erst mit f_2) und auch leichter zu verstehen, da so nicht gleich zu Beginn mögliche Verwirrungen mit der 0 provoziert werden (aus 0 Kaninchenpaaren kann zweifellos nicht 1 Kaninchenpaar entstehen). Am Index ändert sich dadurch nichts, die Fortsetzung zu f_0=0 kann zusammen mit der auf die negativen Zahlen erwähnt werden. --84.130.160.30 15:26, 22. Feb. 2014 (CET)

Induktiver Beweis der Formel von Moivre-Binet

Die Formulierung "Für den Induktionsschritt sei die Formel schon bis n bewiesen..." scheint mir nicht sehr glücklich gewählt.

Beim Induktionsschritt muss lediglich gezeigt werden, dass die Formel für n+1 stimmt, FALLS sie für n (oder alle Werte bis n) stimmt. Ob sie das wirklich tut braucht uns dabei im Moment nicht zu beschäftigen (das ergibt sich dann rückwirkend zusammen mit dem Induktions-Anfang).

Eine bessere Formulierung wäre (meiner E. nach) z.B.: "Angenommen die Formel gelte für alle Werte bis n. Wir zeigen nun, dass sie dann notwendigerweise auch für n+1 gelten muss. ..." --Safrazap (Diskussion) 02:23, 26. Okt. 2014 (CET)

Ich denke, dass ist nicht zwingend notwendig, aber zumindest bringt es das Prinzip deutlicher herüber, habe es daher geändert.--BrankoJ - Diskussion 11:36, 26. Okt. 2014 (CET)

Meine Oma

Mein Kumpel und ich haben zusammen einen IQ von 268, aber Mathematik interessiert uns nicht. Sondern Filme. Wir sind auch durch einen Film auf Fibonacci aufmerksam geworden und haben das gleich mal gegoogelt. Das Prinzip der logischen Folge haben wir wohl verstanden und da kommt dann 21 nach der 13, aber die Formeln und die Tabellen machen überhaupt keinen Sinn. Das scheint so, als sei "n" nur die Durchnummerierung und "f von n" ergibt dann im Detail keinen Sinn, wenn man die Formel anwendet. Meine Oma versteht das garantiert nicht.

"f von n" ist in meinem Universum die Funktion von "n", also das, was passiert, wenn ich eine Zahl in eine Formel stecke. Oder nicht? "Die Summe zweier benachbarter Zahlen" - also die Drei zum Beispiel hat die Zwei und die Vier als Nachbarn, welche nehme ich denn da? Beide? Prima, Sechs ist immer gut. So wie das da in der Einleitung steht, da kommen alle ungeraden Zahlen raus oder nur Blödsinn, denn es ist ja eigentlich die Summe aus der eins und dann jeder weiteren folgenden Zahl der Reihe gemeint, die in der Reihe davor kam und nicht danach.

Okay, Ihr seid Wikipedi-Autoren und vielleicht sogar Mathematiker oder Schlimmeres und formulieren liegt euch nicht, aber denkt mal an meine Oma und an Allgemeinverständlichkeit. Man kann erwarten, dass ein überdurchschnittlich begabter Mensch daraus schlau wird, denn wenn nicht, dann schicken die Grauen die Autoren zurück zu ihren Heimatplaneten, das soll jetzt keine Drohung sein. (nicht signierter Beitrag von 91.64.217.103 (Diskussion) 00:16, 29. Apr. 2015 (CEST))

Funktionsplot der Fibonacci-Folge

Ich glaube nicht, dass Wikipedia-Autoren tatsächlich Schlimmeres als Mathematiker sind. Vermutlich haben sie aber zusammen genommen einen IQ von mehr als 268, insofern sind hier kleine Lesergruppen schon stark im Hintertreffen. Ich versuche die Sache trotzdem mal zu erklären. Die Notation $f_{n}$ ist nur eine andere Schreibweise für $f(n)$, also den Funktionswert der Funktion $f$ an der Stelle $n$, wobei für $n$ nur natürliche Zahlen eingesetzt werden dürfen. Die Funktion $f$ ist bei der Fibonacci-Folge zunächst nicht formelmäßig, sondern nur indirekt über die Rekursion

$f(n)=f(n-1)+f(n-2)$

für $n=3,4,5,\ldots$ gegeben, wobei $f(1)=1$ und $f(2)=1$ die beiden Startwerte sind. Um beispielsweise $f(3)$ zu bestimmen, rechnet man

$f(3)=f(2)+f(1)=1+1=2$

und um $f(4)$ zu bestimmen

$f(4)=f(3)+f(2)=(f(2)+f(1))+f(2)=(1+1)+1=3$.

Man kann die Funktion $f$ sogar explizit angeben, nur ist das eine etwas kompliziertere Formel, siehe den Abschnitt Fibonacci-Folge#Formel von Moivre-Binet. Grüße, --Quartl (Diskussion) 12:37, 29. Apr. 2015 (CEST)

Die Formulierung in der Einleitung war vielleicht etwas missverständlich, allerdings sind ja im Artikel direkt danach weitere Definitionen angegeben, sowohl formal als auch in Worten. Die Einleitung darf durchaus etwas informell sein und muss nicht schon jede Frage beantworten oder jeden Zweifel ausräumen. Dennoch habe ich die informelle Formulierung noch schärfer zu fassen versucht. --84.130.171.163 14:06, 30. Apr. 2015 (CEST)

Merke: Eine Funktion (oder eine Folge, die - das ist ganz richtig erkannt - auch eine bestimmte Art Funktion ist) ist nicht immer (wie zumeist der Schule und wie, Scherz beiseite, noch bis ins 19. Jahrhundert auch von Mathematikern stillschweigend angenommen wurde) durch eine Rechenvorschrift (/Formel) gegeben.

Alles, was sagt: ich gebe Dir eine Zahl (hier n) und du gibst mir dann eine andere, klar bestimmte andere Zahl (hier: die n-te Fibonaccizahl), ist eine Funktion.

Verständlich genug? Damit sollte das spezifische Problem behoben sein.

In dem Fall ist die Funktion eben rekursiv definiert ("rekursiv" ist noch nicht schlimm, oder?). Wobei man zeigen kann - aber da braucht man dann, salopp gesagt, "wirklich Mathematik dazu" - daß man in diesem Fall schon so eine Rechenvorschrift finden kann, das ist dann die, wo diese Quadratwurzeln von 5 drin vorkommen. --2001:A61:2129:6701:CC12:5A64:35BA:4505 19:42, 22. Nov. 2015 (CET)

Verwandtschaft mit dem Goldenen Schnitt

unter der Überschrift: "Verwandtschaft mit dem Goldenen Schnitt" steht:

Die Zahl Φ ist irrational. Das bedeutet, dass sie sich nicht durch ein Verhältnis zweier ganzer Zahlen darstellen lässt, ...

so weit, so gut.

Es steht weiter:

... Am besten lässt sich Φ durch Quotienten zweier aufeinander folgender Fibonacci-Zahlen darstellen. ...

Hier passt was nicht. Gerade wurde (richtig) geschrieben, dass Φ sich nicht als Quotient zweier ganzer Zahlen darstellen lässt und auf einmal geht es doch als Quotient zweier aufeinander folgender Fibonacci-Zahlen. Fibonacci-Zahlen sind aber ganze Zahlen! Hier muss sicher etwas mit Grenzwert rein ;) (nicht signierter Beitrag von 2A00:C1A0:8182:300:15BD:D4B1:DA25:983E (Diskussion | Beiträge) 17:48, 20. Mai 2015 (CEST))

Ich habe „darstellen“ durch „approximieren“ ersetzt. Zur Optimalität der Näherung siehe Kettenbruch#Beste Näherungen. --Quartl (Diskussion) 08:59, 21. Mai 2015 (CEST)

Kein Fraktal ...

Ich nehme an, das gehört nicht zu den Fraktalen? Weil alles, was sich so irgendwie ins Unendliche begibt und schöne Bildchen ergibt wird vom Durchschnittsleser mit Fraktal und Apfelmännchen verbunden ... --Peter2 (Diskussion) 19:33, 20. Mai 2015 (CEST)

Nicht alles, was sich ins Unendliche begibt und schöne Bildchen ergibt, ist automatisch ein Fraktal. Für eine genauere Definition siehe Fraktal#Fraktale Dimension; Selbstähnlichkeit. Der Menge der Fibonacci-Zahlen kann man soweit ich weiß keine fraktale Dimension zuweisen. Grüße, --Quartl (Diskussion) 09:06, 21. Mai 2015 (CEST)

Spiral Zahlen

Nach mehrmaligen lesen habe ich das mit der Anzahl der Spiralen auch verstanden. Aber vielleicht hat jemand eine Idee, wie man das etwas einfacher formulieren könnte. Insbesonders bei der Graphik "[...]farblicher Markierung der Fibonacci-Spiralen 8, 13, 21, 34." dachte ich das die Kennzahl der Spirale etwas anderes ist, als die Anzahl, wie oft sie auf einen Kreis passt. Vielleicht bin ich aber auch besonders doof und das ist schon verständlich genug206.123.146.39 18:50, 30. Mai 2015 (CEST)

Reihenfolge der Abschnitte

Ich finde die Reihenfolge ehrlich gesagt etwas seltsam. "Definition" und "Eigenschaften" sind mathematische Abschnitte, dann kommt "Fibonacci-Folgen in der Natur", danach mit "Berechnung" wieder ein mathematischer Abschnitt, danach "Geschichte". Aus meiner Sicht wäre die "natürlichere" Reihenfolge, zuerst die mathematischen Abschnitte abzuhandeln, danach "Geschichte" und danach "Fibonacci-Folgen in der Natur". Wie seht ihr das? --Rsteinkampf (Diskussion) 12:49, 18. Feb. 2018 (CET)

Ich halte deinen Vorschlag für sinnvoll. --Digamma (Diskussion) 19:41, 18. Feb. 2018 (CET)

Ja, deine "natürlichere" Reihenfolge wäre besser. --Nomen4Omen (Diskussion) 12:42, 19. Feb. 2018 (CET)

Gänseblümchen

Gänseblümchen haben 34, 55 oder 89 Blütenbätter. Eine Zahl dazwischen ist nicht möglich. MfG Harry8 16:06, 29. Mai 2018 (CEST)

Dazu: Spektrum.de: "Sie liebt mich, sie liebt mich nicht" Gruß--Udo (Diskussion) 16:58, 29. Mai 2018 (CEST)

Start mit 0 oder 1

Im 1ten Satz der Einleitung erfahren wir, dass die Fibonacci-Folge ursprünglich mit 1 begann (also 1 1 2 3 5 ) aber in moderner Schreibweise häufig mit 0 (also 0 1 1 2 3 ). Aber noch im gleichen Absatz wird die 0 als optional gekennzeichnet. Im Abschnitt #Definition der Fibonacci-Folge geht sie ebenfalls mit 1 los. Die 0 ist dort Teil der Erweiterung auf negative Zahlen. In #Verwandschaft mit dem Goldenen Schnitt brauchen wir fn+1/fn. Das funktioniert auch nicht für f1=0. Ob #Eigenschaften mit 0 oder 1 oder beidem funktioniert, ist leider nicht angegeben.

Ich neige dazu, den Artikel mit f(1)=1 zu starten und dann f(0)=0 nur im Zusammenhang mit negaFibonacci zu benutzen. --Hfst (Diskussion) 14:05, 8. Sep. 2019 (CEST)

Die "Encyclopedia of Integer Sequences" beschreibt die Folge mit "0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ..", also mit führender 0. Das entspricht F(n) = F(n-1) + F(n-2) with F(0) = 0 and F(1) = 1. Warum sie optional ist, steht in der Einleitung im ersten Satz (alte vs neue Schreibweise). Ich sehe da keinen Widerspruch.

Die führende 0 liefert auch dem nicht-Mathematiker eine einfache Erklärung, warum die Folge in der alten Schreibweise mit zweimal der Zahl 1 beginnt und dann erst mit 2 und 3 weitergeht, denn

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …

Wir müssen auf beide Schreibweisen hinweisen, da es sie gibt; die Erwähnung der optionalen 0 in der Einleitung wegzulassen, halte ich für falsch. -- ^ηeonZERO  19:08, 11. Sep. 2019 (CEST)

Die Folge mit 0 beginnen zu lassen bedeutet nicht, dass man $f_{1}=1$ aufgeben muss, da man man ja auch den Index bei 0 beginnen lassen kann und damit alle Eigenschaften oder Formulierungen die auf $f_{1}=1$ beruhen auch in diesem Fall unverändert gelten.--Kmhkmh (Diskussion) 17:38, 8. Nov. 2019 (CET)

Ganz meine Meinung! $f_{0}=0$ und $f_{1}=1$ und $f_{2}=1.$ 0 ist die Symmetrieachse. Und der Herr Fibonacci hat die Benennung ab 1 nun mal so eingeführt. --Nomen4Omen (Diskussion) 18:00, 8. Nov. 2019 (CET)

Wie Leonardo von Pisa das damals formuliert hat, spielt eigentlich keine Rolle, sondern wie Mathematiker das heute handhaben. (Newton würde die heutige Formulierung seiner Gesetze auch nicht wiedererkennen.) --Digamma (Diskussion) 20:41, 10. Nov. 2019 (CET)

Archivierung dieses Abschnittes wurde gewünscht von: GS63 (Diskussion) 22:03, 8. Nov. 2019 (CET)

Änderungen von 217.246.178.85 zurückgesetzt

Die Änderungen stammen von mir, wobei ich die meisten versehentlich selber durch überschreiben mit der falschen Bearbeitungsversion "zurückgesetzt" habe.

Konkret hat Rmcharb nur eine von mir hinzugefügte Dezimalstelle zurückgesetzt. Die hatte ich eingefügt, weil 1,618033... nach einer rationalen Zahl aussieht (scheinbare Periode am Ende!), und der Hinweis, dass $\Phi$ irrational ist, erst viel später im Artikel auftaucht. Das Problem(chen) kann auch dadurch gelöst werden, dass ein gerundeter Wert (1,618034) angegeben wird.

Weitere Änderungen waren:

• $\Phi$ wurde bei ersten Auftreten erklärt. Dies könnte auch dadurch geschehen, dass die Abschnitte 2.1 (Beziehungen zwischen den Folgegliedern) und 2.1 (Verwandtschaft mit dem Goldenen Schnitt) vertauscht werden.
• Die Formel $f_{2n}=f_{n+1}^{2}-f_{n-1}^{2}$ als weitere Beziehung zwischen den Folgegliedern
• Die Formel $f_{2n+1}=f_{n}^{2}+f_{n+1}^{2}$ wurde in $f_{2n+1}=f_{n+1}^{2}+f_{n}^{2}$ geändert, um sie zur eingefügten Formel zu parallelisieren.

Mit Ausnahme der zusätzlichen 9 in 1,6180339... sind die anderen Änderungen in der Version vom 19. Juli 2017, 12:34 Uhr enthalten.

Und jetzt stell ich dies als Änderungsvorschläge zur Diskussion.

-- Helmut w.k. (Diskussion) 13:47, 19. Jul. 2017 (CEST)

Fibonacci-Zahlen, die nicht alle Ziffern enthalten

Sollen wir die Liste der ersten Fibonacci-Zahlen bis zur größten bekannten Fibonacci-Zahl, deren Dezimaldarstellung nicht alle zehn Ziffern enthält, erweitern? --92.216.164.225 14:10, 22. Okt. 2018 (CEST)

Ich halte das nicht für eine wesentliche Eigenschaft. Deshalb: nein. --Digamma (Diskussion) 21:37, 22. Okt. 2018 (CEST)

Auch meine Ansicht. Sonst müsste man auch hexadezimal, oktal und ternär denken. Im Binärsystem darf man wohl annehmen, dass alle 2 Ziffern vorkommen. --Nomen4Omen (Diskussion) 22:31, 22. Okt. 2018 (CEST)

Die kleinste Fibonacci-Zahl mit allen Dezimalziffern ist F₆₁, und die größte bekannte Fibonacci-Zahl, deren Dezimaldarstellung nicht alle zehn Ziffern enthält, ist F₂₈₅. --92.216.164.225 08:52, 23. Okt. 2018 (CEST)

Link "Goldener Schnitt"

Warum verweist der Link "Goldener Schnitt" in der Einleitung nicht auf "Goldener Schnitt"? --77.0.141.214 16:14, 7. Aug. 2019 (CEST)

Tut er doch. --Digamma (Diskussion) 16:19, 7. Aug. 2019 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: StatistikusMaximus (Diskussion) 18:42, 31. Mär. 2020 (CEST)

Verlauf

Man sollte erwähnen, dass die Größe der Zahlen einer Exponentialfunktion folgt und daher entsprechend schnell zunimmt. Die 1000. Zahl ist (Mit dem Computer bestimmt):

43.466.557.686.937.456.435.688.527.675. .040.625.802.564.660.517.371.780.402.481.729.089.536.555.417.949.051.890.403.879. .840.079.255.169.295.922.593.080.322.634.775.209.689.623.239.873.322.471.161.642. .996.440.906.533.187.938.298.969.649.928.516.003.704.476.137.795.166.849.228.875

ca. 4,35 * 10²⁰⁸ Gelesen:

Potenzdarstellung 1	Potenzdarstellung 2	Zahlworte
43.466 * 106 * 34	43 * 10207 + 466 *10204	43 Quattuortrigintilliarden 466 Quattuortrigintillionen
557.696 * 106 * 33	557 * 10201 + 696 *10198	557 Tretrigintilliarden 686 Tretrigintillionen
937.456 * 106 * 32	937 * 10195 + 456 * 10192	937 Duotrigintilliarden 456 Duotrigintillionen
435.688 * 106 * 31	435 * 10189 + 688 * 10186	435 Untrigintilliarden 688 Untrigintillionen
527.675 * 106 * 30	527 * 10183 + 675 * 10180	527 Trigintilliarden 675 Trigintillionen
40.625 * 106 * 29	40 * 10177 + 625 * 10174	40 Novemvigintilliarden 625 Novemvigintillionen
802.564 * 106 * 28	802 * 10171 + 564 * 10168	802 Oktovigintilliarden 564 Oktovigintillionen
660.517 * 106 * 27	660 * 10165 + 517 * 10162	660 Septenvigintilliarden 517 Septenvigintillionen
371.780 * 106 * 26	371 * 10159 + 780 * 10156	371 Sexvigintilliarden 780 Sexvigintillionen
402.481 * 106 * 25	402 * 10153 + 481 * 10150	402 Quinvigintilliarden 481 Quinvigintillionen
729.089 * 106 * 24	729 * 10147 + 89 * 10144	729 Quattuorvigintilliarden 89 Quattuorvigintillionen
536.555 * 106 * 23	536 * 10141 + 555 * 10138	536 Trevigintilliarden 555 Trevigintillionen
417.949 * 106 * 22	417 * 10135 + 949 * 10132	417 Duovigintilliarden 949 Duovigintillionen
51.890 * 106 * 21	51 * 10129 + 890 * 10126	51 Unvigintilliarden 890 Unvigintillionen
403.879 * 106 * 20	403 * 10123 + 879 * 10120	403 Vigintilliarden 879 Vigintillionen
840.079 * 106 * 19	840 * 10117 + 79 * 10114	840 Novemdezilliarden 79 Novemdezillionen
255.169 * 106 * 18	255 * 10111 + 169 * 10108	255 Oktodezilliarden 169 Oktodezillionen
295.922 * 106 * 17	295 * 10105 + 922 * 10102	295 Septendezilliarden 922 Septendezillionen
593.080 * 106 * 16	593 * 1099 + 80 * 1096	593 Sexdezilliarden 80 Sexdezillionen
322.634 * 106 * 15	322 * 1093 + 634 * 1090	322 Quindezilliarden 634 Quindezillionen
775.209 * 106 * 14	775 * 1087 + 209 * 1084	775 Quattuordezilliarden 209 Quattuordezillionen
689.623 * 106 * 13	689 * 1082 + 623 * 1078	689 Tredezilliarden 623 Tredezillionen
239.873 * 106 * 12	239 * 1075 + 873 * 1072	239 Duodezilliarden 873 Duodezillionen
322.471 * 106 * 11	322 * 1069 + 471 * 1066	322 Undezilliarden 471 Undezillionen
161.642 * 106 * 10	161 * 1063 + 642 * 1060	161 Dezilliarden 642 Dezillionen
996.440 * 106 * 9	996 * 1057 + 440 * 1054	996 Nonilliarden 440 Nonillionen
906.533 * 106 * 8	906 * 1051 + 533 * 1048	906 Oktilliarden 533 Oktillionen
187.938 * 106 * 7	187 * 1045 + 938 * 1042	187 Septilliarden 938 Septillionen
298.969 * 106 * 6	298 * 1039 + 969 * 1036	298 Sextilliarden 969 Sextillionen
649.928 * 106 * 5	649 * 1033 + 928 * 1030	649 Quintilliarden 928 Quintillionen
516.003 * 106 * 4	516 * 1027 + 3 * 1024	516 Quadrilliarden 3 Quadrillionen
704.476 * 106 * 3	704 * 1021 + 476 * 1018	704 Trilliarden 476 Trillionen
137.795 * 106 * 2	137 * 1015 + 795 * 1012	137 Billiarden 795 Billionen
166.849 * 106 * 1	166 * 109 + 849 * 106	166 Milliarden 849 Millionen
228.875 * 106 * 0	228 * 103 + 875 * 100	228-tausend 875

ÅñŧóñŜûŝî (Ð) 00:09, 30. Dez. 2018 (CET)

OK, um wieviel größer ist die 1001. Zahl, wie lautet deren Quotient? Kann bewiesen werden, dass dieser eine irrationale Zahl ist? Gruß! GS63 (Diskussion) 00:51, 30. Dez. 2018 (CET)

Der Quotient zweier natürlicher Zahlen ist natürlich immer eine rationale Zahl und keine irrationale. --Digamma (Diskussion) 13:20, 30. Dez. 2018 (CET)

Hm, hast ja recht. Wollte fragen, ob ausgeschlossen ist, dass sie restlos dezimalbrüchig darstellbar ist. Aber beim genauen formulieren fällt mir auf, dass es für eine derart willkürliche Forderung selbstverständlich keine Klassifikation geben wird, die ich aber irrtümlich mit "irrationale Zahl" bezeichnete. Gruß! GS63 (Diskussion) 17:29, 30. Dez. 2018 (CET)

Die 1001. könnte ich berechnen, aber ich habe keinen Programmquelltext für eine Division beliebig großer - als Strings gespeicherter - Zahlen. ÅñŧóñŜûŝî (Ð) 00:56, 30. Dez. 2018 (CET)

So beeindruckend groß die Zahlen jetzt sind, sie sind IMHO von der Unendlichkeit immer noch (fast) so weit entfernt wie 1, 1, 2, 3, 5, ... .

Und übrigens – das Exponentielle steht schon im Artikel unter Fibonacci-Folge#Formel von Moivre/Binet und wurde demnach im Jahr 1718, also vor mehr als 300 Jahren gefunden. --Nomen4Omen (Diskussion) 12:09, 30. Dez. 2018 (CET)

Diese Formel ist gewiss die einer Exponentialfunktion, aber der Begriff steht nicht direkt im Artikel. Ich finde, man sollte nicht nur schöne Herleitungen schreiben, sondern auch darauf achten, wichtige Begriffe nicht zu vergessen. Was es meine Anfangsinfo hier angeht: mit einem Tool, welches erlaubt, extrem viele Stellen zu handhaben (durch Workarounds der Operationen), würde die Annäherung an den goldenen Schnitt gut verdeutlichen. Inwieweit man hier diesen "Psi-term" bentzen kann, wird aus dem Artikel nicht ersichtlich. ÅñŧóñŜûŝî (Ð) 18:14, 30. Dez. 2018 (CET)

---

Neuer Abschnitt "Herleitung der alternierenden Näherung"

Ich fügte den neuen Abschnitt "Herleitung der alternierenden Näherung" ein; die zu beweisende Aussage lässt sich kurz und mit recht elementaren Mitteln aus der de Moivre-Binet-Darstellung herleiten.

Noch passender wäre vielleicht, wenn ich das als aufklappbaren "Beweis" an die entsprechende Aussage im Kopftext setzen könnte; diese Art der Darstellung sah ich in einem anderen mathematischen Wikipedia-Artikel (weiß natürlich nicht mehr, in welchem), finde das aber mit sinnvollem Zeitaufwand nicht wieder. Schützenhilfe?

Mit Gruß und Dank für dieselbe, --Psychironiker (Diskussion) 23:51, 20. Jun. 2019 (CEST)

Inzwischen fand ich zufällig die Syntax zum Aufklappen in einem anderen Artikel wieder, der Belang ist also fast erledigt. Meine Herleitung der alternierenden Näherung ist einklappbar gestaltet, so dass die Übersichtlichkeit des Artikels nicht leidet. Allerdings sind am Kopf der eingeklappten Darstellung noch zwei Leerzeilen, die dort nicht sein müssten. Wer weiß, wie die zum Verschwinden gebracht werden?

--Psychironiker (Diskussion) 16:57, 11. Jul. 2019 (CEST)

Induktiver Beweis

1. Einverstanden mit der Weglassung des Bruchs 1/Φ.
2. Das mit n und n−1 ist zwar absolut korrekt. Die vorherige Überlegung ist aber auch richtig, und auf sie wird im Artikel starke Induktionsvoraussetzung explizit Bezug genommen, so dass das so stehen bleiben sollte. Es sei denn, du findest noch ein besseres Beispiel für einen Fall starker Induktion.

--Nomen4Omen (Diskussion) 20:20, 9. Jul. 2019 (CEST)

Ich las im Artikel über vollständige Induktion nach und kann dem nicht folgen. Denn dort heißt es in der Passage, von der aus auf die Fibonacci-Folge verwiesen wird:

"Es kann überdies vorkommen, dass mehr als eine Anfangsaussage vorab zu zeigen ist" (Hervorhebungen von mir);

dort wird also nicht behauptet, dass derlei bei einer starke Induktion im Allgemeinen gegeben wäre, und auch nicht, dass das Prinzip der starken Induktion hierdurch erklärt wäre. Eher ist der Induktionsbeweis von de Moivre-Binet ein Beispiel für eine (zusätzliche) Mehrstufigkeit des Induktionsanfangs, der für gewisse starke Induktionen erforderlich ist. Der Verweis im verlinkten Aritkel leidet daher nicht, wenn mit n und n-1 argumentiert wird. - Ansonsten finde ich nach wie vor, dass die Annahme der Gültigkeit der Aussage für alle Werte von 0 bis n ein (vor allem Anfänger verwirrender) Fremdkörper in der Logik des hier zu führenden Beweises ist.

Natürlich wäre recht konstruktiv, wenn mir ein besseres Beispiel für eine Induktion einfiele, die mit starker Voraussetzng zumindest wesentlich einfacher zu führen ist. Das wird aber wohl leider etwas dauern. Vielleicht ist jemand anders schneller?

--Psychironiker (Diskussion) 18:06, 11. Jul. 2019 (CEST)

Ich denke, alles ist korrekt, was du dazu bemerkst, nur: nicht nur der Induktionsanfang ist mehrstufig, sondern auch die Rekursionsformel. In der »schwachen« Induktion wird nur auf einen Vorgänger rekurriert (»Schluss von n auf n+1«, und eben nicht: »Schluss von n-1 und n auf n+1«). Und Folgendes: Der induktive Beweis von de Moivre-Binet gelingt ganz besonders einfach mit der starken Induktion. Außerdem sehe ich das mit dem Fremdkörper nicht so, ich sehe nur die Keule, die das Problem erledigt. (Keulen hat man aber oft in der Mathematik. Man nimmt, welche man findet und welche am besten passt.) --Nomen4Omen (Diskussion) 22:01, 11. Jul. 2019 (CEST)

Video nicht mehr verfügbar

Das Video zum Weblink [5] ist nicht mehr verfügbar.--Hs-berlin (Diskussion) 18:38, 20. Aug. 2019 (CEST)

Ich habe den Link repariert, danke für die Anmerkung. -- HilberTraum (d, m) 20:47, 20. Aug. 2019 (CEST)

Zum Abschnitt "Erzeugende Funktion"

Der vorgefundene Herleitung des Zusammenhangs zwischen Fibonacci-Zahlen und den Binomialkoeffizienten aus der erzeugenden Funktion $\textstyle \sum _{n=0}^{\infty }f_{n}z^{n}$ ist fehlerhaft, denn dann müsste die Beziehung $\textstyle f_{n}=\sum _{k=0}^{n}{\tbinom {n-k-1}{k}}$ auch für $n=0$ gelten. Das aber trifft nicht zu:

$\textstyle f_{0}=0$, aber $\textstyle \sum _{k=0}^{0}{\tbinom {0-k-1}{k}}={\tbinom {0-0-1}{0}}=1.$

Entsprechend enthält in der angegebenen Umformung

$\textstyle \sum _{0\leq k\leq l}{\tbinom {l}{k}}z^{l+k+1}=\sum _{n\geq 0}z^{n}\sum _{k=0}^{n}{\tbinom {n-k-1}{k}}$

die rechte Seite einen Summanden mit der 0-ten Potenz von z , die linke Seite aber nicht. Da war anscheinend der Wunsch (nach Herleitbarkeit der Formel aus der angegebenen erzeugenden Funktion) der Vater des Gedankens; die behauptete Umsummierung existiert aber nicht.

Drittens ist die angegebene Entwicklung der Potenzreihe keine "Entwicklung um $z=0$"; eine Entwicklungsstelle wie etwa bei einer Taylorreihe wird für die Herleitung nicht benötigt.

Viertens wird auch der angegebene Konvergenzradius nicht benötigt; hinreichend ist, dass die erzeugende Funktion (für irgendein dem Betrage nach hinreichend kleines $z$) überhaupt konvergiert. Aber letzteres ist eher eine Stilfrage.

Ich bemühte mich, in einer Neufassung diese Fehler zu bessern.

--Psychironiker (Diskussion) 08:43, 29. Jun. 2019 (CEST)

Herleitungen-Binet Formeln

Also aus meiner Sich nicht nimmt das inzwischen überhand. Primäres Ziel eines enziklopädische Artikels die wichtigsten Apekte eine knapp und übersichtlich zusammenzufassen, streng genommen sind da überhaupt keine Herleitung oder Beweise nötig. Natürlich kann man sie trotzdem dort einarbeiten, wenn sie kurz sind, das organisch ergibt und sie den Artikel nicht unnötig aufblähen. Aber der Punkt ist aus meiner Sicht längst überschritten. Umfangreiche technische Details, Beweis/Herleitungsvarianten oder Sammlungen gehören nicht in diesen Artikel.

Man kann das gegebenenfalls in einen separaten Artikel auslagern. Hier wäre zum Beispiel ein eigener zu Binet-Formel möglich, bei dem wenn er nicht zu lang ist verschiedene Herleitungsvariationen angeben kann. Ansonsten gibt es für so etwas intern das [:wikibooks:de:Beweisarchiv|Beweisarchiv] oder auch extern das [ProofWiki], wohin man die Inhalte verschieben und dann hier verlinken kann.--Kmhkmh (Diskussion) 19:09, 29. Jun. 2019 (CEST)

zum Abschnitt "Stammbäume"

In der vorgefundenen Version fand ich verbesserungswürdig:

A. Die genannte "Ahnenmenge" ist keine Menge im mathematischen Sinn.

"Apis mellifera" ist keine Bezeichnung männlicher Honigbienen (wie die vorgefundene Satzkonstruktion nachlegt), sondern der Art insgesamt. Zudem ist das latinische Wort "Apis" weiblich.

Die eingefügten Angaben "(n = 1)" usw. waren nicht definiert. Beim ersten Lesen konnten sie auch für die Anzahl der in je einer Generation betrachteten Tiere gehalten werden.

Die Einführung der "Genom"-Begrifflichkeit trägt nicht zum Verständnis des Zusammenhangs bei.

Der vorgefundene Text nannte erst die Anzahl der Eltern in einer Vorläufergeneration, schob dann die sachliche Begründung als Beifügung in Klammern hinterher. Das lässt sich günstiger lösen.

Auch lässt sich unschwer präziser formulieren, welche Fibonacci-Zahl in welcher Generation welche Anzahl welcher Bienen beschreibt.

B. Die Homologie des Modell zum Kaninchen-Problem Fibonaccis war nicht erläutert.

--Psychironiker (Diskussion) 11:54, 6. Jul. 2019 (CEST)

zum Abschnitt "Fettsäuren"

A: Zur Begründung von Änderungen an der vorgefundenen Formulierung:

Nicht jede aliphatische Monocarbonsäure ist unverzweigt (Gegenbeispiel Isobuttersäure). Die neue Formulierung vermeidet eine solche Implikation.

Weiter ist die verunklare Formulierung vermeidbar, der aufgeführte mathematische Zusammenhang folge "unter anderem" daraus, dass bei den bezeichneten Substanzen keine benachbarten Doppelbindungen auftreten. Woraus sollte das denn noch folgen? Eine weitere Voraussetzung ist nicht erforderlich.

B. Eine Erläuterung des Zusammenhangs ist angefügt.

--Psychironiker (Diskussion) 17:42, 6. Jul. 2019 (CEST)

Kaninchen-Population

Die Baum-Darstellung im Unterabschnitt Antike und Mittelalter in Europa ist zwar optisch ansprechend und plakativ. Jedoch wäre es wünschenswert, wenn die im Fließtext links neben der Grafik aneinander gereihten Erläuterungen prägnant und übersichtlich zusammen mit grafischen Elementen in einem Bild untergebracht würden, sozusagen als zusammenfassende Kurzinformation. Hier ein Vorschlag:

Kaninchen-Population nach Fibonacci

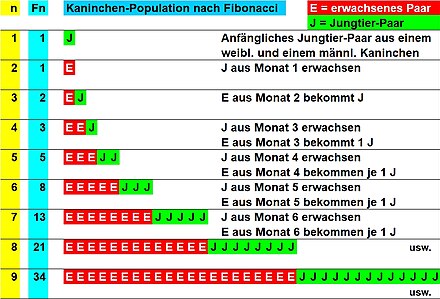
Für Meinungen hierzu wäre ich dankbar. Gegebenenfalls würde ich die Grafik gerne einbinden. Beste Grüße --Mabit1 (Diskussion) 20:42, 9. Sep. 2020 (CEST)

Das ist eine schöne Theorie, aber sie krankt daran daß sie nicht stimmt. Siehe Text , den ich eingetragen habe.StatistikusMaximus (Diskussion) 20:28, 3. Okt. 2020 (CEST)

@StatistikusMaximus: Ein Beleg bzw. Literaturhinweis zu deiner Fußnote wäre wünschwert.--Kmhkmh (Diskussion) 06:30, 4. Okt. 2020 (CEST)

@StatistikusMaximus: Wie schon von Kmhkmh angemerkt, handelt es sich bestenfalls um eine Fußnote und nicht um einen Einzelnachweis. Auf keinen Fall gehört diese Anmerkung in den Abschnitt „Einzelnachweise“. Ohne Beleg muss sie dort entfernt werden. Fibonacci hat, wie ja schon im Artikel erwähnt, ein idealisiertes mathematisches Modell unter vereinfachenden Prämissen entworfen, um die mathematische Entwicklung seiner Zahlenfolge zu verdeutlichen.

Der Link http://informatik.rostfrank.de/info/lex12/fibonacci.html schwächt übrigens die von Dir beschriebene Realitätsferne ab.

Mein Vorschlag: Entweder die Anmerkung ersatzlos streichen oder an geeigneter Stelle, dann aber, mit einem belastbaren Weblink oder Einzelnachweis versehen, in den Artikel platzieren. Beste Grüße --Mabit1 (Diskussion) 10:42, 4. Okt. 2020 (CEST)

Auch meine Ansicht. Denn ich kann mir nicht vorstellen, dass es jemand gibt, der die Fibonacci-Kaninchen für bare Münze nimmt und nicht als eine math. „Idealisierung“ begreift. –Nomen4Omen (Diskussion) 11:18, 4. Okt. 2020 (CEST)

Wir haben solche Populationen mehrfach statistisch ausgewertet und anders als bei Bakterien und Viren läuft es bei den Säugetieren eben genau NICHT so ab, wie sich das die Nichtbiologen gerne vorstellen. Bitte die Kanickel raus oder ausdrücklich belegen. Wenn, dann kann man die Bakterien nehmen, die erfüllen progressives Wachstum noch am Besten, solange das Nahrungsangebot in der Petrischale passt. StatistikusMaximus (Diskussion) 01:57, 10. Okt. 2020 (CEST)

Und das Beispiel von Rostfrank taug schon einmal gar nicht, da es von einem Informatiker kommt, die sehr gerne solche Anleihen in der Tierwelt machen und ihre Theorien verbreiten, sie aber niemals gegenprüfen. Zudem ist es einfach nur abgeschrieben. Dass Mäuse und Ratten ihre Populationen der Nahrung anpassen, ist bekannter Fakt und seit 20 Jahren in den Biobüchern. Leider wird in Informatikstudiengängen so etwas nicht gelehrt, daher kommen solche Leute sehr gerne mit ihren Theorien um die Ecke. Klassisches Beispiel ist das Jäger-Beute-Schema und dem sich angelich einstellenden Gleichgewicht aus den 1930er Jahren, das nach wie vor den Köpfen herumspukt,welches sich aber mit einer einfachen DGl widerlegen lässt. StatistikusMaximus (Diskussion) 02:00, 10. Okt. 2020 (CEST)

Irgendwie geht mMn. jetzt etwas am Thema vorbei. Niemand behauptet, dass die Fibonaccifolge die tatsächliche Kaninchenvermehrung realistisch modelliert. In den Artikel gehört das Thema trotzdem aus historischen Gründen, weil Fibonacci die Folge nun einmal dazu benutzt hat, um die Kaninchenvermehrung zu modellieren.

Es spricht auch nichts dagegen eine Anmerkung zur tatsächlichen Vermehrung zu verfassen, diese ist aber eben zu belegen mit der entsprechenden Fachliteratur, sowie das in WP eben üblich ist. Es reicht in WP im Normalfall eben nicht nur hinzuschreiben, was richtig ist (oder was man persönlich weiß), sondern man muss auch angeben, wo man das nachlesen kann, d. h. im WP-Jargon die Aussage belegen.--Kmhkmh (Diskussion) 04:18, 10. Okt. 2020 (CEST)

Wir müssen 2 Dinge unterscheiden:

• es ist eine historische Tatsache, dass es Modelle für die Kaninchenpopulation gibt, die zu einer Fibonacci-Folge führen. Alleine aus der geschichtlichen Tatsache, dass seid Ewigkeiten gelehrt werden gehören die hier rein.
• davon unabhängig existiert die Frage, ob und unter welchen Randbedingungen das Modell gut ist. Punkt 3 ist nach einigen Monaten falsch, Punkt 1 ist fragwürdig usw. Im Rahmen dieses Artikels aber eher ein Randthema, dass mit einem Satz der Art "Tatsächlich beschreibt das Modell die Kaninchenpopulatio schlecht, da die Aspekte x, y und z nicht berücksichtigt werden. EN dazu".

Kurz und klein: das Thema ist Fibonacci, nicht Kaninchen. --Hfst (Diskussion) 09:28, 10. Okt. 2020 (CEST)

zu der Frage nach dem Bild: da finde ich die Baumdarstellung intuitiver und ausreichend. --Hfst (Diskussion) 09:51, 10. Okt. 2020 (CEST)

In der Fußnote steht heute:

Dazu muss festgestellt werden, dass dies ein theoretisches Gedankenmodell ist, welches sich in der Praxis nicht so abbildet. Der Grund liegt in den individuellen Genen der Kaninchenmütter und der sich verändernden Geburtenrate. Es gibt Mütter, die über die Zeit zunehmend mehr Nachkommen haben, wenn sie mehr gebären konnten, während andere weniger Nachkommen haben, nachdem sie einen großen Wurf hatten. Zudem passen Kaninchen wie auch Mäuse ihre Wurfgröße genetisch festgelegt an das Nahrungsangebot an, indem sie Gene an und abschalten, welche die Fertilität steuern und Keimverzögerung sowie Befruchtungswillen beeinflussen.

Dazu ein paar Bemerkungen:

1. Das Modell kann nur ein durchschnittliches Kaninchen beschreiben. Das heißt, das beschriebene Fortpflanzungsverhalten bildet einen Durchschnitt ab. Wenn ich die individuellen Gene modellieren will lande ich in einer anderen Klasse von Modellen, den Monte-Carlo-Modellen. Im Vergleich zu Wildkaninchen#Fortpflanzung und Entwicklung ist Fibonacci etwas optimistisch, da reale Kaninchen sich erst nach ca. 2 Jahren fortpflanzen.
2. Das Thema Nahrungsangebot spielt hier keine Rolle, da der abgeschlossene Modellraum natürlich auch genügend Nahrung bereit stellt.
3. Echte Kaninchen sterben, das heißt das Modell gilt nur für vielleicht 60 Iterationen / Monaten.

Kurz und klein. Die Fußnote ist, so lange sie unbelegt ist WP:OR. Sie verbessert auch nicht das Verständnis für den Artikelgegenstand. Daher sollte sie entfallen.--Hfst (Diskussion) 22:20, 10. Okt. 2020 (CEST)

Danke, Hfst, für die ausführliche Stellungnahme. Demnach plädiere auch ich, wie schon weiter oben in meinem ursprünglichen Vorschlag als Alternative formuliert, für die ersatzlose Streichung der Fußnote. Beste Grüße --Mabit1 (Diskussion) 23:28, 10. Okt. 2020 (CEST)

Änderungen bei Identität von Cassini

Wieso linken wir die Simson-Identität?StatistikusMaximus (Diskussion) 20:20, 3. Okt. 2020 (CEST)

Ich verstehe die Frage nicht. Das ist doch nur ein anderer Name für dieselbe Identität, oder nicht? --Digamma (Diskussion) 22:31, 3. Okt. 2020 (CEST)

Ja, die Identität ist unter beiden Namen bekannt, so wie es im Zielartikel auch steht.--Kmhkmh (Diskussion) 06:20, 4. Okt. 2020 (CEST)