Diskussion:Statischer Auftrieb/Archiv

Diese Seite ist ein Archiv abgeschlossener Diskussionen. Ihr Inhalt sollte daher nicht mehr verändert werden. Benutze bitte die aktuelle Diskussionsseite, auch um eine archivierte Diskussion weiterzuführen.

Um einen Abschnitt dieser Seite zu verlinken, klicke im Inhaltsverzeichnis auf den Abschnitt und kopiere dann Seitenname und Abschnittsüberschrift aus der Adresszeile deines Browsers, beispielsweise

[[Diskussion:Statischer Auftrieb/Archiv#Thema 1]]

oder als Weblink zur Verlinkung außerhalb der Wikipedia

https://de.wikipedia.org/wiki/Diskussion:Statischer_Auftrieb/Archiv#Thema_1

Spoiler

hallo Hohun, schau dir mal den Artikel Spoiler an. von der Wortbedeutung gesehen hast recht, jedoch werden zumindest im Automobilbereich häufig so ziemlich alle aerodynamisch wirksamen Anbauten als Spoiler bezeichnet. (wenn auch nur laienhaft: Verlust von Auftrieb = Gewinn Abtrieb-es ist eine Betrachtungsfrage). Ich bin auf dem Gebiet kein Experte und wollte eigentlich auch nur eine Definition für Auf- und Abtrieb in der steht, daß abtrieb physikalisch negativer Auftrieb ist. Natürlich müssen da auch Spoiler erwähnt werden. Bin jetzt hier so zufrieden ;) Hadhuey 07:58, 26. Apr 2004 (CEST)

Hallo, Hadhuey - Danke für den Hinweis, Spoiler muß ich dann auch noch einmal angehen :-) Luftschiffe erzeugen den Auf- und Abtrieb übrigens tatsächlich mit der Hülle, die Steuerflächen sind ja weit hinter dem Schwerpunkt und können daher (wie das Höhenleitwerk beim Flugzeug) nur den Anstellwinkel ändern. Beim Strömungsabriß an der Hülle können Luftschiffe, die gerade dynamischen Abtrieb erzeugen, sogar aufwärts "abschmieren" :-) --HoHun 09:57, 26. Apr 2004 (CEST)

stümmt-hab heute tagsüber etwas darüber nachgegrübelt-natürlich erzeugt der rumpf den eigentlichen auftrieb und nicht nur die steuerflächen-Hadhuey 16:53, 26. Apr 2004 (CEST)

gegenkraft zum auftrieb

1. ich mag mich irren, aber der abtrieb ist doch nie im leben die gegenkraft zum auftrieb. nach der physikalischen definition aus dem artikel ist der abtrieb auch ein auftrieb. nur nennt man ihn im automoblil bereich abtrieb weil der auftrieb nach unten gerichtet ist und die bezeichnung auftrieb nur zu verwechslungen führen würde. vondaher gilt das der abtrieb ein nach unten (in richtung der schwerkraft) gerichtete auftrieb ist.
2. schön das ich hier wieder auf die schwachsinnige erklärung für den dynamischen auftrieb treffe den mir schon mein prof um physikstudium vorgehalten hat (das bezieht sich jetzt nur auf die wirbel als ursache für den auftrieb). aber ich bin ja lernwillig, also weiss jemand wo ich ne ähnlichen deutschen text zu A Physical Description of Lift (den link hab ich von flugzeug) finde? wie man bestimmt wiedermal an meinem beitrag sieht bin ich alles andere als sprachbegabt und die übersetzung des fachtextes ist für einen wie mich extrem anstrengend.

--SK-Genius 22:22, 28. Okt 2004 (CEST)

Strömungsmechanik ist kein einfaches Thema. Schon Newton hat sich daran die Finger verbrannt. Die m.E. pseudowissenschaftliche Phantasie, dass Auftrieb auf einen vertikal beschleunigten Massestrom beruhen soll, widerspricht der Potenzialtheorie. Schaue die die Stromlinien einer Halbkugel mit planer Oberfläche parallel zur Anströmung an: Der Lauf der Stromlinien von An- und Abströmung sind zueinander symmetrisch. das Gleiche gilt für eine gewölbte Platte mit Anstellwinkel=0, um gleich noch mit den unterschiedlichen Weglängen aufzuräumen. Das, was hinten nach unten abströmt ist vor dem Flügel auch nach oben gekommen. In der Profiltheorie wirst du bei einer Potenzialströmung an der Berandung eines hinreichend großen Kontrollvolumen niemals eine Vertikalkomponete haben wohl aber Auftrieb. Ich habe in gängigen Fachbüchern (Schlichting, Truckenbrodt, Schade, Kunz) sowie in den Skripten meiner Lehrveranstaltungen noch nie eine Herleitung für den Auftrieb nach der von Eberhardt getroffenen Impulsbilanz gefunden. Er schimpft dafür lieber auf Bernoulli, ohne jemals zu sagen, was daran nicht stimmt. Bernoulli kannst du dir aus Impuls- und Masseerhaltung unter best. Annahmen (Rotorfreiheit, Inkompressibilität, Stromfaden) herleiten. Und wenn ich hier den (subsonischen) Windkanal einschalte und mit einem Betzmanometer die Differenz zwischen dem Druck an einer statischen Sonde im Kanal und den Druck der ruhenden Atmposphäre außerhalb des Kanals messe und das mit dem Rechenergebnis nach Bernoulli vergleiche, scheint da auch was dran zu sein. Auch wenn bei viskosen Strömungen die Wandhaftbedingung gilt, so ist der statische Druck über die Grenzschicht annährend konstant - siehe Prandtl'sche Grenzschichthypothese.

Niemals würde ich behaupten, ich hätte Strömungmechanik einschliesslich das Phänomen des Auftriebs vollständig gerafft und ich bin für plausible Nachweise der Eberhardt'schen Theorie jederzeit offen. Etwas habe ich jedoch im Studium gelernt: Strömungsmechanik ist erstens anders und zweitens als man denkt. Mit einem "gesunden (physikalischen) Menschenverstand" kommt i.d.R. hier nicht weit. Formulierungen wie beispielsweise "abgedrenkte Luftmassen" sind ausschließlich Begriffe der Laienaerodynamik. --79.193.254.179 15:15, 4. Jan. 2008 (CET)

laienaerodynamik?

also, ich habe in aerodynamik (im studiengang luft- und raumfahrttechnik) gelernt, dass auftrieb durch strömungsumlenkung entsteht, und durch nicht anderes (was mir durch die impulsbilanz auch plausibel scheint), und die potenzialtheorie hat mit der ursache des auftriebs gar nichts zu tun- sie ist nur ein modell um den auftrieb berechenbar zu machen.77.130.11.247 10:24, 5. Dez. 2008 (CET)

Was sagt die Gewichtskraft...

..des Menschen in der Beispielrechnung aus? --NB > ?! > +/- 23:43, 4. Mai 2007 (CEST)

Falls Du die Stelle meinst, die Du vermutlich meinst: Garnichts. Man wollte damit offenbar etwas veranschaulichen, ist aber auf halber Strecke liegengeblieben - oder es wurde irgendwann zereditiert.--Thuringius 01:32, 5. Mai 2007 (CEST)

Danke, sah ich genauso, wollte nur die mir eingebaute menschliche Irrtumsfähigkeit nicht unnötig beanspruchen... ;-) --NB > ?! > +/- 08:06, 5. Mai 2007 (CEST)

Habe mal die Einheiten in der Rechung (gramm pro Liter und Liter) in die richtigen SI-Einheiten umgeändert. Sonst kann man die Rechnung ja nicht richtig nachvollziehen. Das mit der Gewichtskraft hab ich auch rausgenommen. --217.226.52.129 21:32, 10. Jul. 2008 (CEST)

Aha. Wurde natürlich gleich wieder Rückgängig gemacht. Deshalb nochmal zur Erklärung: Wenn ich mit "Gramm pro Liter" und "Liter" rechne anstatt mit "kg/m³" und "m³", komme ich am Ende nicht auf "Newton". Denn 1 N = 1 kgm/s² und nicht "gm/s²". Außerdem Wird die Dichte der Luft in der nachfolgenden Tabelle ebenfalls in der Einheit "kg/m^3" angegeben. --217.226.52.129 23:00, 10. Jul. 2008 (CEST)

Das 'g' in der Formel für die Auftriebskraft steht für die Schwerebeschleunigung und nicht für die Gewichtskraft wie im Artikel steht, oder? --132.230.1.28 14:40, 14. Apr. 2009 (CEST)

Richtig, aber das Produkt aller drei Größen rechts vom Gleichheitszeichen entspricht der Gewichtskraft des verdrängten Mediums. Gruß --Quezon95 15:35, 14. Apr. 2009 (CEST)

Satz

Zitat:Andererseits entsteht kein Auftrieb, wenn unter keiner der Körperflächen ausreichend Fluid vorhanden ist; zum Beispiel an einem senkrecht stehenden geraden Zylinder, der bis auf den Grund gedrückt wird.
Natürlich würde an diesem Zylinder Auftrieb entstehen. Wurde hier etwas falsch verstanden oder nur unglücklich formuliert?--Thuringius 15:26, 28. Feb. 2008 (CET)

Qubric hat Skript Hydromechanik 3.5.1 Nr.3 als Referenz angegeben. Bin mir aber selber unsicher, ob das so richtig ist.--WikiJourney 20:24, 28. Feb. 2008 (CET)

Ja, ich bin mir aber nicht sicher, welche Stelle er meint und ich bezweifle, dass das Beispiel mit dem Zylinder dort vorkommt, das ziemlicher Unsinn ist. Sobald Teile eines Körpers einem Druckverlauf ausgesetzt sind, wirkt ein Auftrieb, auch wenn der Zylinder aus Blei und auf dem Grund festgemauert ist. Die Formulierung "unter keiner der Körperflächen" klingt nicht sehr glücklich. Gemeint dürfte sein, dass kein statischer Auftrieb auf Körper wirkt, wenn sie in Richtung der Schwerewirkung nicht von Fluid umflossen werden können. Das trifft bestenfalls zB auf den ebenen Boden eines Schwimmbeckens zu. Das auf diesen kein Auftrieb wirkt, bedarf wohl keiner Erläuterung im Artikel.--Thuringius 21:48, 28. Feb. 2008 (CET)

Zitat 3.5.1.nr.3 im Skript: "3. Liegt der Körper so auf dem Boden, daß kein Fluid – auch keine molekulare Fluidschicht ! – unter den Körper dringen kann, so ist die „Auf“kraft Null und es ist kein Auftrieb vorhanden, d.h. der Körper wird dann mit der „Ab“kraft auf den Gefäßboden gedrückt." Ich verstehe das so: Wo kein Fluid ist, dort kann kein Druck sein. Auftrieb richtet sich nach oben, also muß der Druck unterhalb des Körpers sein. Ist unterhalb kein Fluid dann gibts auch kein Auftrieb Qubric 23:23, 28. Feb. 2008 (CET)

Das ist völlig unverständlich. Ein Körper mit einer Höhenausdehnung größer als Null wird in einer Umgebung mit einem Druckgradienten einer Auftriebskraft augesetzt sein. Es muss kein Fluid "unter" ihm sein - hier stolpert der Text schon über die Oben-Unten-Definition. Wenn kein Fluid zwischen Körper und Untergrund dringen kann, bedeutet das nur, dass der Körper entweder schwerer ist als die verdrängte Fluidmasse oder dass die Auftriebskraft die Adhäsionskraft mit dem Untergrund nicht überwinden kann. Die Auftriebskraft ist unvermeidlich vorhanden, aber addiert sich mit einer Gegenkraft zu Null. Die Kraft ist also da, aber nur statisch (ohne Bewegung). Vielleicht meinte man das.--Thuringius 00:51, 29. Feb. 2008 (CET)

Welcher Druckgradient sollte den Auftrieb bewirken, wenn nicht der unterhalb des Körpers? Eine Kraft muß irgendwo ansetzen und in eine bestimmte Richtung drängen, ansonsten kann sie keine Wirkung haben. Auftrieb kann - wie der Name es verdeutlicht - nur von unten wirken. Eine Kraft ist nicht unvermeidlich (wie jeder Judoka weiß) wenn man sich ihr nicht in den Weg stellt. Wäre sie statisch (potentiell) vorhanden, dann würde ein leichter Zylinder nicht einfach auf dem Grund bleiben.Qubric 19:25, 29. Feb. 2008 (CET)

Ich glaube ich verstehe, der Druck muss ja tatsächlich eine Angriffsfläche haben, die die Kraft nach oben wirken lässt.Der Zylinder taugt als Beispiel, ist aber recht speziell. Man könnte die Aussage sicher mit einer etwas allgemeineren Beschreibung vervollständigen.--Thuringius 01:02, 1. Mär. 2008 (CET)

Sandys Luftkuppel vieleicht Qubric 19:04, 5. Mär. 2008 (CET)

Vielleicht, bin mir aber auch da nicht sicher. Die Frage könnte man so verallgemeinern: Kann bei einer von allen Seiten horizontal auf einen Körper wirkenden Kraft ein nach oben wirkender Vektor resultieren, wenn die horizontale Kraft nach oben hin abnimmt? Inzwischen glaube ich aber eher, dass die Webquelle doch recht hat.--Thuringius 06:50, 6. Mär. 2008 (CET)

Auf eine senkrechte Fläche wirkt nur der Druck von der Seite, da alle anderen Vektoren sich gegenseitig aufheben (in großer Tiefe ist der Auftrieb derselbe wie in geringer Tiefe, aber der Seitendruck nimmt zu). Ist die Fläche schief, dann haben die nach unten gerichteten Vektoren vergleichsweise mehr Angriffsfläche, die Differenz entspricht genau der vertikalen Projektionsfläche. Auf die Unterseite eines auf Grund liegenden Körpers wirkt dagegen nur der Druck, der auch von oben wirkt, also die Summe (das Integral) der vertikalen Projektionsflächen mal dem jeweiligen Wasserdruck.

Denkt man in diesem Zusammenhang an einen Badewannenstöpsel und dessen Auftriebsverhalten, so ist diese Aussage mit dem zylinderförmigen Körper eigentlich trivial. --80.142.194.14 21:38, 10. Jul. 2008 (CEST)

Nochmal langsam zum Verständnis: Auftrieb grundsätzlich nicht in eine bestimmte Richtung?

Der Einleitungssatz des Artikels lautet: "Als Auftrieb wird diejenige Kraft bezeichnet, die eine Flüssigkeit oder ein Gas auf einen Körper (oder auf ein Gasvolumen) ausübt." Von einer bestimmten Richtung (nach oben oder senkrecht zu irgendwas, z.B. Strömungsrichtung) ist hier erstmal nicht die Rede. Ich würde darunter laienhaft einfach den "Druck" verstehen, der von außen auf den Körper einwirkt.

Erst im nächsten Satz heißt es dann "Eine physikalisch gesehen gleiche Kraft wie der Auftrieb, die aber in die entgegengesetzte Richtung wirkt, nennt man Abtrieb." Entgegengesetzte Richtung, wenn doch der Auftrieb gar keine Eigen-Richtung hat? Streng genommen wäre die logische Konsequenz, dass der Abtrieb diejenige Kraft ist, die der Körper auf das ihn umgebende Gas oder die ihn umgebende Flüssigkeit ausübt.

Der dritte und letzte Satz der Einleitung macht's nicht klarer: "Man unterscheidet den entgegen der Schwerkraft wirkenden statischen Auftrieb vom rechtwinklig zur Anströmung wirkenden dynamischen Auftrieb." Das macht für mich nur dann Sinn, wenn ich unter Auftrieb das verstehen würde, was ich darunter bis vor kurzem verstand (nämlich bis zur Lektüre des ersten Satzes dieser Einleitung).

Bitte um eine für einen Laien (= der durchschnittliche Wikipedia-Leser und Adressat des Artikels) verständliche Erklärung. --Snevern 09:08, 11. Nov. 2009 (CET)

== Hallo Snevern, dieser Artikel ist leider inzwischen totaler Schrott, weil hier sich lauter Schlaumeier mit Halbwissen einen Edit-War liefern. Wenn du was über Auftrieb wissen willst, geh in die Bücherei und hol dir ein gutes Buch, möglichst ein Hochschul-Lehrbuch. Ich habe es aufgegeben hier einzugreifen. Viel Erfolg --Hbquax 19:33, 15. Nov. 2009 (CET)

Leider gehöre ich nun mal zu denen, die solches Wissen lieber in der Wikipedia lesen und es anderen da auch zugänglich machen wollen. Aber trotzdem danke, Hbquax! Immerhin hast du geantwortet - die Schlaumeier nicht. --Snevern 19:49, 15. Nov. 2009 (CET)

Änderung vom 23.11.2009: Auftrieb eines auf dem Boden stehenden Körpers

So, hab den Satz mal wieder gelöscht. Entscheidend für den Auftrieb ist ja nicht, ob der Zylinder von unten nass oder trocken ist, sondern welcher Druck dort herrscht. Und dort herrscht natürlich der Druck des Fluids am Rand der Aufstandsfläche. Es seid denn der Körper wäre am Boden festgeklebt, aber dann wäre er auch kein freier Körper mehr, sondern Teil des Grundes. Vor dem Revertieren bitte zuhause in der Badewanne testen. Und nein, der Badewannestöpsel zählt nicht, der Druck auf der Rückseite des Stöpsels ist der Druck im Abflussrohr und hat mit dem Wasserdruck in der Badewanne nichts zu tun (anderes System) --Hbquax 17:52, 23. Nov. 2009 (CET)

Hallöchen, es kommt nicht auf den Druck an, sondern auf den vertikalen Druckvektor. Der ist auf dem Grund so groß wie auf der Oberseite des Körpers. -- Qubric 20:47, 2. Mär. 2010 (CET)

siehe Saugnapf. Das gleiche Prinzip gilt bspw. bei Glasplatten, die übereinander liegen und aneinander zu "kleben" scheinen wenn eine von ihnen angehoben wird--Qubric 20:29, 3. Mär. 2010 (CET)

Abtrieb und Tragflügel

Ich habe die folgenden Bereiche herausgenommen, weil sie unter Tragflügel und Spoiler /Autosport besser behandelt sind oder werden sollten. "Abtrieb" als Unterpunkt von "Auftrieb" ist sehr unglücklich und sollte deshalb nur als Beispiel und Verweis drin sein. ich hoffe die anderen Autoren können so mitgehen. Die Erklärung der Zirkulation und der Karroserieform geht über den Inhalt des Artikels Auftrieb hinaus . Folgendes habe ich entfernt:

der Rennwagen an sich, daher der Heckflügel

Vom Prinzip her stört ein Profil bei dynamischem Auftrieb die Strömung so, als ob sich dort ein Wirbel befände, der sich auf der Saugseite mit der Anströmung dreht und auf der Druckseite entgegengesetzt dazu - nicht genug, um die Strömung umzukehren, die Luft dreht sich also nicht um eine Flugzeug-Tragfläche. Entscheidend für das Entstehen dieses Wirbels ist das Bilden eines Wirbels an der Tragflächenhinterkante, des sogenannten Anfahrwirbels. Durch Bewegung der Tragfläche aus der Ruhe heraus (Start) entsteht an der Hinterkante eine Instabilität der beginnenden Luftströmung und das Auftreten von Wirbeln. War die Strömung anfangs wirbelfrei (Ruhe), dann führt das zu einem Gegenwirbel, sodass die Gesamtrotation des Wirbelsystems (Zirkulation) unverändert bleibt (Satz von Thomson). Dieser Gegenwirbel sorgt dann für einen hinreichend großen Geschwindigkeitsunterschied von Strömungen auf der Ober- und Unterseite einer Tragfläche. Nach einer Gesetzmäßigkeit, die man den Helmholtzschen Wirbelsatz nennt, kann ein Wirbelfaden nicht mitten in der Strömung plötzlich zu Ende sein. Der Wirbel, der ein Flugzeug trägt, setzt sich an beiden Enden der Tragflächen U-förmig nach hinten fort, als ein gewaltiges Wirbelpaar, die sog. Wirbelschleppe. Beispiel für eine Kombination von statischem und dynamischen Auftrieb:

Abtrieb

Eine in Richtung der Schwerkraft wirkende Auftriebskraft wird bei bestimmten Anwendungen als Abtrieb bezeichnet. Abtrieb, die Kraft, mit der ein Körper auf den Boden gedrückt wird, spielt im Autosport eine wichtige Rolle, weil dort ein möglichst hoher Anpressdruck des Fahrzeuges auf die Straße erwünscht ist, um eine hohe Bodenhaftung, und damit hohe Kurvengeschwindigkeiten zu erzielen. Abtrieb bezeichnet dabei den dynamischen Abtrieb durch aerodynamische Flächen, die bei Rennwagen Flügel genannt werden. Die im Automobilbau ebenfalls verwendeten Spoiler verhindern die Entstehung dynamischen Auftriebs, der durch die aerodynamischen Eigenschaften der Karosserieform erzeugt wird. Je höher der Abtrieb ist, desto höher ist die mögliche Seitenführungskraft in Kurven. Der höhere Abtrieb geht jedoch einher mit einem höheren Luftwiderstand, der sich negativ auf die Höchstgeschwindigkeit auswirkt.""

OLMuseum 22:48, 29. Dez. 2009 (CET)

Der dynamische Auftrieb enthält jetzt keine Erklärung mehr, er wird nur mathematisch beschrieben, den Omatest würde der Abschnitt nicht mehr bestehen.--Thuringius 14:06, 30. Dez. 2009 (CET)

Den letzten Einwand von Thuringius habe ich gerade dadurch gelöst, dass ich Links auf dei Seiten eingebaut habe, wo das erklärt wird. Mein Text selber ist hoffentlich oma-tauglich genug. --Dogbert66 14:45, 30. Dez. 2009 (CET)

Die Kuh am Ende

...ich weiß nicht ob das passt.
Sollte der Beitrag zur Kuh nicht in einer Begriffsklärungsseite stehen und nicht am Ende des "physikalischen" Auftriebs (Wie richtig oder falsch der Artikel ist kann ich nicht beurteilen). --Telcontar 00:01, 18. Feb 2005 (CET)

Was hat eine Kuh mit der Physik zu tun? Haha. (nicht signierter Beitrag von 62.178.88.82 (Diskussion) 20:37, 13. Apr. 2011 (CEST))

Richtung des dynamischen Auftriebs

Hi! Ich habe irgendwie das Gefühl, dass die Richtung des dynamischen Auftriebs nicht Rechtwinklig zur Anströmungsrichtung sein kann. In welche Richtung denn überhaupt , is doch im Dreidimensionalen Raum? Hat das nicht vielleciht irgendwas mit Einfalls- und Ausfalls-Winkel zu tun oder bin ich da völlig auf dem Holzweg?? Würde mich über ne schnelle Antwort freuen, sonst beschäftigt mich das die nächsten Tage :-) TSChabba

Hallo, TSChabba! Doch, es ist so! Der dynamische Auftrieb ist immer im rechten Winkel zur Anblasrichtung nach oben gerichtet. Der Auftrieb ist eine Komponente der Luftkraft. Die andere Komponente der Luftkraft ist der Widerstand (auch Rücktrieb), die entgegen der Flugrichtung wirkt. Die Luftkraft (als Resultierende aus Auftrieb und Widerstand) wirkt lotrecht nach oben und genau entgegengesetzt dem Gewicht des Luftfahrzeugs. (Anmerkung: Anstelle des Begriffs Anblasrichtung wird auch oft auch Anströmrichtung verwendet). Bei einem Flug auf abwärts geneigter Bahn (Gleitflug) liefert eine Teilkraft der Schwerkraft (als Komponente des Gewichts) in Flugrichtung die erforderliche Zugkraft (Vortrieb), die dem Widerstand entgegenwirkt. Die andere Teilkraft der Schwerkraft wirkt (ebenfalls als Komponente des Gewichts) genau entgegen dem Auftrieb. Somit herrscht im freien Flug ein Gleichgewicht aller Kräfte, die gemeinsam am Druckpunkt des Profils wirken. (Diese Ausführungen sind dem Standart-Lehrbuch zur Ausbildung von Luftfahrzeugführern entnommen). Leider hab ich keine Möglichkeit ein anschauliches Bildchen beizufügen! Doch hoffe ich, dir dennoch mit diesen Erklärungen geholfen zu haben? Ein Tip noch! Wenn in deiner Nähe ein Luftsportverein ist, frag mal nach ob, wann und wo die in den Wintermonaten ihre theoretische Schulung abhalten. Die freuen sich meist über Gastzuhörer (in der Hoffnung auf neue Mitglieder)!!!

MfG, der Holzwurm, am 25.09.05

Noch deutlicher (und mit nur zehn Jahren Verspätung): Der dynamische Auftrieb ist so definiert, dass er senkrecht zur Anströmrichtung ist. Die durch die Umströmung erzeugte Kraft wird begrifflich in zwei Komponenten zerlegt. Der Anteil parallel zur Anströmrichtung wird Strömungswiderstand genannt. Den Anteil senkrecht zur Anströmrichtung nennt man Auftrieb.---<)kmk(>- (Diskussion) 19:08, 2. Sep. 2014 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: Keine Änderung am Artikel erforderlich.---<)kmk(>- (Diskussion) 19:09, 2. Sep. 2014 (CEST)

Kunstflugzeuge, die auf dem Kopf fliegen

Kunstflugzeuge, die auf dem Kopf fliegen zeigen ganz eindeutig auf, daß diese Erklärung von Auftrieb nicht richtig sein kann. Des weiteren fliegen auch Papierflieger und Flugzeuge mit symetrischen Tragflügeln. Daher sollte dieser Artikel, der im Wiederspruch zum Tragflügelartikel steht, nochmals überdacht oder durchdiskutiert werden. Leptokurtosis999 (nachgetragen)

Was stört dich denn genau? Bei symmetrischen Profilen kommt noch der Anstellwinkel zum Tragen. durch ihn entsteht eine unsymmetrische Anströmung und damit ein unterschiedlicher Druck zwischen Ober- und Unterseite (=Auftrieb). Hadhuey 19:48, 16. Aug 2005 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: Der Artikel hat seit längerem nur noch den statischen Auftrieb zum Thema.---<)kmk(>- (Diskussion) 19:12, 2. Sep. 2014 (CEST)

Richtung des dynamischen Auftriebs

Es ist eine Definition, dass die Richtung des Auftriebs 'normal', d.h. senkrecht zur Strömungsrichtung steht. Da es sich in der Tat um ein 3-dimensionales Phänomen handelt, ist die Strömung als Feld zu betrachten und der Auftrieb zeigt in Richtung der Normalen der relevanten Strömungsfläche (hier: Fläche des Tragflügels).

Der (dynamische) Auftrieb ist üblicherweise so definiert, dass er senkrecht zur Anströmrichtung steht. Die Anströmung erfolgt im Allgemeinen nicht parallel zu den relevanten Oberflächen. Entsprechend zeigt der Auftrieb nicht notwendigerweise senkrecht zu den umströmten Flächen Es wäre etwas unbequem für weitergehende Kräftebetrachtungen, wenn der Auftrieb eines Flugzeug von der Oberfläche abhinge, die man jeweils betrachtet.---<)kmk(>- (Diskussion) 19:21, 2. Sep. 2014 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: Dieser Artikel hat seit längerem nur noch den statischen Auftrieb zum Thema.---<)kmk(>- (Diskussion) 19:22, 2. Sep. 2014 (CEST)

Super Sehrohr

Zitat Artikel

. Etwas einfacher wird es durch das Ausfahren des Sehrohrs über die Wasseroberfläche, wodurch ein U-Boot wie ein Überwasserfahrzeug in einen stabiles Gleichgewicht bezüglich der Tauchtiefe gebracht wird.

Mein physikalisches Verständnis würde sagen, dass ein kleines Sehrohr schwerlich ein tonnenschweres Schiff stablisieren kann. Oder was meint ihr? --Abdull 10:14, 1. Mär 2005 (CET)

Bin bei´m Lesen des Artikels auch etwas stutzig über diese Aussage geworden!! Bisher war ich immer der Auffassung, dass einfach soviel Wasser in die Ballasttanks geflutet wird, bis das U-Boot genau so schwer ist (oder zum Tauchen auch schwerer) wie (als) die von ihm verdrängte Wassermasse und somit kein Auftrieb mehr vorhanden ist (schlicht und ergreifend, doch das archimedische Prinzip, oder)!? Allerdings lerne ich gerne dazu, doch dafür sollte mir mal jemand eine physikalisch plausible Erlärung abgeben, wodurch bei einem U-Boot das - über die Wasseroberfläche - ausgefahrene Sehrohr ein stabiles Gleichgewicht bezüglich der Tauchtiefe bewirken soll!? Ach, noch´ne Frage: wie erreicht man denn das besagte stabile Gleichgewicht, bei Tauchbooten ohne ausfahrbares Sehrohr?? MfG, PG, am 25.09.05

Wenn ein U-Boot unter Wasser seine Hoehe halten kann, ohne seine Ruder zu benutzen, dann hat es effektiv die gleiche Dichte (kg/m^3) wie Wasser. Da es quasi 'schwebt', kann es die Hoehe alleine durch die Ruder veraendern, ohne die Ballasttanks zu benutzen. Es ist also instabil gegen Stoerungen, z.B. Dichteaenderungen des Wassers wegen Temperaturschwankungen. Jetzt versetz dasselbe Boot (immer noch gleiche Dichte wie Wasser) mal in die Situation, dass ein bisschen was aus dem Wasser rausguckt (sagen wir 1% des Volumens). Jetzt tragen nur noch 99% des Volumens zum Auftrieb im Wasser bei (wenn man den statischen Auftrieb des 1% in Luft mal vernachlaessigt) mit der Folge, dass das Boot weniger Auftrieb hat. Es wird also wieder zurueck ins Wasser sinken, bis wieder 100% unter Wasser sind. Andersrum. Das Boot ist stabil und 5m Sehrohr schauen aus dem Wasser. Jetz drueck das Boot mal gedanklich unter Wasser, was passiert? Das Boot hat eine zu geringe Dichte, um ganz unter Wasser zu bleiben und wird wieder auftauchen, bis wieder 5m Sehrohr aus dem Wasser gucken. Das Argument, das sei doch viel zu wenig gegenueber dem Gesamtgewicht aendert nichts an dem Kraeftegleichgewicht. Sicherlich wird das Boot nicht jede Wellenbewegung nachvollziehen (soll's ja auch nicht), aber stabilisiert ist es.

Im Prinzip war die Anmerkung richtig. Nur ist das Verhältnis der Masse des Sehrohrs zu der des gesamten Uboots typischerweise so krass, das die Diskussion des Effekts akademisch wird. Ein modernes Uboot der Klasse 216 Bundesmarine wiegt etwa 2000 Tonnen. Das Sehrohr wird bestenfalls ein paar hundert Kilogramm auf die Waage bringen. Das ist ein Verhältnis von 1 zu 10 Tausend. Entsprechend lange müsste man auf ausgleichende Bewegungen warten.---<)kmk(>- (Diskussion) 19:48, 2. Sep. 2014 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: Die Anmerkung mit dem Sehrohr ist nicht mehr im Artikel.---<)kmk(>- (Diskussion) 19:47, 2. Sep. 2014 (CEST)

Auftrieb beim Diskuswerfen

Ihr wisst sicherlich alle was ein diskus ist.Es ist ein Sportgerät der Leichtathletik und ist eine runde relativ flache Scheibe. Jetzt habe ich eine Frage zum Auftrieb dieses Objektes. Ich habe gelesen (siehe Diskuswerfen ), dass beim Abwurf der Diskus einen Abtrieb erfährt und kurz danach einen Auftrieb der ihn weit segeln lässt. Da ich selber Diskuswerfer bin interessiert mich jetzt wie denn dieser Auftrieb überhaupt zu stande kommt. Ich weiss nur dass, wenn man den Diskus beim Abwurf eine schnelle Rotation verleiht, er auch umso weiter und stabiler fliegt. Ist der Auftrieb nichts anderes als der Luftwiederstand unter der Scheibe oder enstehen da irgendwelche Verwirbelungen oder sowas?! Würde mich echt mal interessieren! freue mich auf jede Antwort :) Jonas

Wenn ich mir die Erklärung so angucke kommen dort mehrere Effekte zusammen. Die Eigenrotoation stabilisierte den Diskus, so kommt er nicht ins Trudeln und behält seine Lage (Winkel der Scheibe) während des gesamten Fluges bei. Je mehr Masse im Außenring ist, umso höher ist die Stabilität bei gleicher Umdrehungsgeschwindigkeit (Massenträgheitsmoment).

Bei der Flugbahn handelt es sich grundsätzlich um eine Wurfparabel, die mit aerodynamischen Effekten überlagert ist. Im ersten Teil (siehe Skizze im Artikel) wird der Diskus in einem bestimmten Winkel abgeworfen. Durch seine Fluglage entsteht Abtrieb. Ab einem bestimmten Punkt in der Flugbahn wechselt der Anströmwinkel. Die Luft wird bei geringem Winkel um den Diskus herum fließen. Dabei wird Auftrieb wie bei einem Flugzeug erzeugt. Ab einem bestimmten höheren Winkel in der letzten Flugphase wird die Strömung über dem Diskus abreißen und turbulent werden. Sie greift dann wie bei einem Drachen (oder einem Stein) unter den Diskus und er fällt auf diesem Luftpolster zum Aufschlag. Im Gegensatz zu Flugzeugflügeln hat der Diskus ein symmetrischen Profil. Das bedeutet, dass er, wenn er genau horizontal fliegt, keinen Auftrieb erhält. (Kunstflug-Flugzeuge haben übrigens auch häufig ein symmetrisches Tragflächenprofil) Ich hoffe das hilft dir weiter.Hadhuey 19:26, 25. Sep 2005 (CEST)

Vielen Dank für die Antwort! Jonas

Archivierung dieses Abschnittes wurde gewünscht von: ---<)kmk(>- (Diskussion) 19:49, 2. Sep. 2014 (CEST)

lebhafte wissenschaft

"Es ist am Flughafen von Rio de Janeiro schon vorgekommen, dass jemand verbotenenerweise ein gesperrtes Gelände am Flughafenzaun befahren hat und vom Wirbelpaar eines landenden Flugzeugs mit seinem Auto meterweit in die Luft geschleudert und schwer verletzt wurde - er kannte den Helmholtz'schen Wirbelsatz nicht."

DAS ist ne echt coole Formulierung :) Wird dem Opfer nicht so gefallen, aber ich war nicht mehr zu halten.

Die Formulierung ist längst nicht mehr im Artikel. Da der statische Auftrieb nichts mit Wirbelpaaren zu tun hat, sollte sie auch nicht wieder eingefügt werden.---<)kmk(>- (Diskussion) 19:56, 2. Sep. 2014 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: Diese Anmerkung hat sich überlebt.---<)kmk(>- (Diskussion) 19:56, 2. Sep. 2014 (CEST)

Sog

kann bitte jemand, der sich mit der Sache auskennt, den Auftrieb auf geeignete weise mit dem Sog verknüpfen? Das hängt doch sehr eng zusammen, oder?... -- D. Dÿsentrieb ⇌ 13:29, 11. Mai 2006 (CEST)

Es gibt keinen Zusammenhang mit dem statischen Auftrieb -- und nur der ist seit ein paar Jahren Thema dieses Artikels.---<)kmk(>- (Diskussion) 19:52, 2. Sep. 2014 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: keine Änderung nötig---<)kmk(>- (Diskussion) 19:52, 2. Sep. 2014 (CEST)

Abtrieb/Spoiler

Hallo zusammen!

Also ich arbeite im Bereich Rennwagen und dies auch schon seit einigen Jahren, deshalb muss ich leider ein wenig wiedersprechen. Spoiler dienen nicht nur um Auftrieb zu vernichten, wie der Name suggeriert. Dies gilt sicherlich bei Serienfahrzeugen, die mit "Spoilern" getunt werden, nicht aber für den professionellen Rennsport. So wird z.B. bei DTM-Fahrzeugen Abtrieb in Größenordnungen von mehreren hundert Kilogramm generiert, so dass die Fahrzeug bei höheren Geschwindigkeiten theoretisch an der Decke fahren könnten. Das wäre sicherlich nicht möglich, wenn man nur Auftrieb vernichten würde. Dies wird nicht nur mit "Spoilern" erreicht sondern mit speziell geformaten Unterböden, den so genannten Diffusoren, und mit "richtigen" Flügeln, die natürlich umgekehr verwendet werden, wie am Flugzeug.

--Keiler1965 12:06, 1. Jun 2006 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: Spoiler sind hier nicht mehr Thema, seit der Artikel ausschließlich den statischen Auftrieb darstellt.---<)kmk(>- (Diskussion) 19:58, 2. Sep. 2014 (CEST)

Artikel zum Auftrieb zusammenfassen ?

Hallo Freunde der Luftfahrt, eine kurze Volltextsuche hat ergeben, dass der aerodynamische Auftrieb in mehreren Artikeln mehr oder weniger gut beschrieben wird. Jedesmal entwickelt sich hierzu eine spannende Fachdiskussion. Hier das Ergebnis meiner kleinen Recherche: In den Artikeln Auftrieb, Fliegen (Fortbewegung), Tragfläche und Flugzeug wird eine Erklärung des Phänomens versucht. In Deltaflügel und Magnus-Effekt werden spezielle Aspekte des Themas behandelt. In Strömung nach Bernoulli und Venturi wird erstaunlicherweise keine Erklärung des Auftriebs geliefert, man findet aber noch Spuren in der Diskussion... Wäre es evtl. sinnvoll, das irgendwie zusammenzufassen? Also vielleicht einen Hauptartikel (oder Kategorie?) Auftrieb, von Flugzeug und Tragflügel Links zu Auftrieb setzen und von dort aus auf Themen wie Deltaflügel, Magnus und Bernoulli verweisen. Nur mal so als Idee. Möglicherweise würde das einen Aufschrei geben, aber es würde doch auf Dauer die Übersichtlichkeit verbessern, und alle die sich für das anscheinend sehr spannende Thema Auftrieb interessieren könnten an einer Stelle diskutieren. Schönes Wochenende  :-) --Hbquax 11:21, 16. Jun. 2007 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: Die angeregte Zusammenfassung geschah in Form des Artikels Dynamischer Auftrieb.---<)kmk(>- (Diskussion) 20:00, 2. Sep. 2014 (CEST)

fehlende Informationen und Quellenangabe

Lieber KaiMartin, in dem Artikel zum Thema Auftrieb habe ich bewusst die folgende Textpassage von Ihnen entfernt: "Das hydrostatische Paradox sagt aus, dass der Druck nur von der Tiefe und nicht von der Form eines Fluids abhängt. Daher ist die Auftriebskraft unabhängig von der Menge des Fluids, in das der Körper eingetaucht ist." Dort fehlt schließlich die Quellenangabe zu meiner beim Grin-Verlag veröffentlichten Arbeit und die kurze Aussage ist zudem unvollständig!. Diesen physikalischen Zusammenhang hatte ich unter der Leitung von dem Physiker Dr. Hecht aus Leipzig erkannt, ehemals Leibniz-Institut. Inhalt meiner dazu geschriebenen Arbeit: 1. der Effekt tritt ein 2. wann er immer eintritt 3. warum er dann immer eintritt 4. wie sich dann die Auftriebskraft berechnet 5. dass der Effekt auf beliebig große Gefäße und Gefäßabstände erweiterbar ist 6. dass der Effekt somit auch technisch nutzbar ist Quelle: Robert Stach, 2012, Extension of the Archimedean Principle, München, GRIN Verlag GmbH, Bitte beachten Sie dies, vielen Dank für Ihr Verständnis!--77.12.249.205 08:57, 9. Jan. 2013 (CET)

Der Begriff Hydrostatische Paradox ist ein wenig älter als 2012. Siehe auch die in Hydrostatisches Paradoxon angegebenen Quellen.---<)kmk(>- (Diskussion) 18:40, 9. Jan. 2013 (CET)

Ich hoffe für Sie, dass das nur ein Spaß war! Es geht nicht um das Hydrostatische Paradoxon von Blaise Pascal, welches jedem Physiker geläufig ist! Es geht um die Aussage: "Die Auftriebskraft ist unabhängig von der Menge des Fluids, in das der Körper eingetaucht ist". Sie sind derjenige, der dies zuerst am 02.Feb.2012 um 02:27 Uhr ergänzt hat! Dazu findet man in der Fachliteratur nur die Veröffentlichung von Dr. Hecht und mir. Bei Wikipedia steht geschrieben: Einer der Grundsätze der Wissenschaftsethik, die unter anderem in fachspezifischen Ethikcodes ihren Ausdruck findet, lautet: Benutzte Vorlagen sind in angemessener Weise anzugeben. Wer einer Fachpublikation wichtige Anregungen entnimmt, dies aber verschweigt und sie nicht zitiert, verstößt gegen diesen Grundsatz. Woher haben Sie die Information?! --77.12.249.205 19:50, 9. Jan. 2013 (CET)

Zitat Archimedisches Prinzip: "Die Auftriebskraft eines Körpers in einem Medium ist genauso groß wie die Gewichtskraft des vom Körper verdrängten Mediums." Das "genauso groß" impliziert unmittelbar eine Nicht-Abhängigkeit von anderen denkbaren Parametern wie etwa der Farbe des Fluids über seine Viskosität oder eben seiner Form. Das ist auch in dieser Form so weit Allgemeinwissen, dass es mir in der Schule im Physikunterricht beigebracht wurde.---<)kmk(>- (Diskussion) 18:17, 10. Jan. 2013 (CET)

"Das Prinzip gilt demnach auch, wenn etwa die vorhandene Flüssigkeit ein geringeres Volumen besitzt als der eingetauchte Teil des Schwimmkörpers." (aus der Version vom 10. November 2011 des Artkels, also vor der 2012 erfolgten Veröffentlichung von Robert Stach). --Joerg 130 (Diskussion) 18:38, 10. Jan. 2013 (CET)

Vielen Dank für die Informationen, auch ich bin an einer sachlichen und korrekten Lösung interessiert! Durch die zuletzt hinzugefügten Informationen wird ersichtlich, wo genau das Missverständnis zwischen uns liegt. Es wird auch deutlich, dass Sie den Sachverhalt nicht anders kannten und deshalb nicht gegen das Urheberrecht verstoßen haben! Man sollte dabei jetzt ganz genau hinsehen. Meine veröffentlichte Arbeit bezieht sich auf einen anderen Sachverhalt. Meine Experimente verdeutlichen Folgendes: Ein Schwimmkörper der vollständig unter die Wasseroberfläche gedrückt wird und dabei weniger Volumen des Fluids verdrängt, als er selbst an Körpervolumen besitzt, erhält bereits seine maximale Auftriebskraft. Dies obwohl die Gewichtskraft der verdrängten Flüssigkeit geringer ist, als die des Körpers- laut dem archimedischen Prinzip müsste der Körper zu Boden sinken. Die Experimente dazu habe ich Herrn Dr. Hecht ausführlich vorgeführt, der daraufhin sehr erstaunt war. Wer möchte kann diese Experimente gerne zu jeder Zeit wiederholen, ich würde sie auch gerne erneut vorzeigen. Nicht nur über die Experimente, auch über die klassische Herleitung der Auftriebskraft kann man sehen, dass der von mir zuvor überlegte Sachverhalt auch tatsächlich eintreten kann! Dazu muss man zur Herleitung wissen: Der Schweredruck in Flüssigkeiten nimmt linear mit der Tiefe zu und ist in einer bestimmten Tiefe nach allen Richtungen gleich groß. Aus diesem Grund wirkt, auf einen unter Wasser gedrückten Schwimmkörper, ober- und unterhalb ein unterschiedlicher Schweredruck. Kraft entspricht dem Produkt aus Druck und Fläche, d.h. es entsteht eine nach oben gerichtete Auftriebskraft. Die eigentliche Raffinesse besteht darin: durch das hydrostatische Paradoxon ist der Schweredruck unabhängig von dem Flüssigkeitsvolumen. Deshalb erhält der vollständig unter Wasser gedrückte Schwimmkörper bereits seine maximale Auftriebskraft. Der Schweredruck ober- und unterhalb des Körpers ändert sich nicht, damit ändert sich auch nicht die Auftriebskraft, sie bleibt maximal- auch bei weniger verdrängtem Volumen an Flüssigkeit, als es das archimedische Prinzip verlangt! --77.184.209.189 21:03, 10. Jan. 2013 (CET)

Herzlichen Dank für Ihre Verständigungsbereitschaft! Gehe ich zu Recht davon aus, dass der von Ihnen hier erwähnte Versuch auf http://www.hausarbeiten.de/faecher/vorschau/191038.html , Fig. 1 - 5 vollständig beschrieben ist? Das dort geschilderte Ergebnis erstaunt mich (Dr.-Ing.) jedoch überhaupt nicht. Nach meinem Eindruck liegt das Missverständnis an anderer Stelle: An einem unterschiedlichen Verständnis, was denn das "verdrängte Volumen" sei. Hier scheint mir der Artikel in der Version vom 10. November 2011 leichter verständlich als die aktuelle Fassung (Siehe http://de.wikipedia.org/w/index.php?title=Auftrieb&oldid=95818227 ) . Ändern Sie doch mal Ihren Versuch so, dass Sie das Glas bis zum Rand füllen, bevor sie den Körper dazu tun. Nun läuft natürlich Flüssigkeit über, das Volumen der überlaufenden Flüssigkeit ist (bis auf Nebeneffekte durch die Oberflächenspannung) auch bei dem engen Glas gleich dem des Körpers (Nachtrag: Bei schwimmendem Körper nur des Volumens des eingetauchten Anteils.) . Die Situation im Glas unterscheidet sich danach nicht von der nach Ihrer Versuchsdurchführung. In allen übrigen Punkten stimme ich Ihrer obigen Erklärung ausdrücklich zu. Offenbar ist die in Lehrbüchern übliche Beschreibung für die Situation geringer Flüssigkeitsvolumina aber tatsächlich irreführend. Dies aufgezeigt zu haben, ist sicher Ihr Verdienst. Auch möchte ich meine Hochachtung vor dem offensichtlich großen Aufwand Ihrer Arbeit ausdrücklich betonen.--Joerg 130 (Diskussion) 22:00, 10. Jan. 2013 (CET)

Für meine Arbeit möchte ich keine Anerkennung und dennoch ist es mir wichtig, physikalische Zusammenhänge richtig darzustellen! Allein aus der Vorschau ist mein Zusammenhang nicht vollständig erkennbar, wir sollten uns daher weiteren Teilen der Arbeit widmen. Es ist verständlich, dass das geschilderte Ergebnis Sie nicht erstaunt, weil Sie noch wie folgt denken: "das Volumen der überlaufenden Flüssigkeit ist (bis auf Nebeneffekte durch die Oberflächenspannung) auch bei dem engen Glas gleich dem des Körpers. Das dies eben nicht der Fall ist, war schließlich die Grundlage für meine Arbeit! Weil für das Hochladen von Dateien bei Wikipedia eine Wartezeit von 4 Tagen nach Anmeldung nötig ist, habe ich für Sie eine eigene Internetseite bereitgestellt. Dort können Sie auf die Arbeit zugreifen. Auf den Seiten 5 und 6 finden Sie die dazu nötigen Angaben. PS: Auch der Physiker Dr. Hecht hatte anfangs genau wie Sie argumentiert. Nach dem Vorzeigen der Experimente und der schriftlichen Arbeit dazu, erkannte er aber schnell den Sachverhalt. Ich bin auch nicht verärgert über Ihre Reaktion, schließlich hätte ich an Ihrer Stelle mit Sicherheit ähnlich gehandelt. http://www.physikfreund.de/ Einen freundlichen Gruß aus MD --Majorante (Diskussion) 11:36, 11. Jan. 2013 (CET)

Herzlichen Dank für die Datei! Ich habe sie inzwischen heruntergeladen, bei erster Durchsicht sah ich allerdings nichts, was meiner Auffassung widerspricht. Für eine genauere Durchsicht werde ich mehr Zeit brauchen; ich muss mich aber jetzt um anderes kümmern. --Joerg 130 (Diskussion) 13:46, 11. Jan. 2013 (CET)

Genau, Ruhe bewahren! Physikalische Zusammenhänge sind schließlich zeitlos gültig. Ich werde ebenfalls die Zeit nutzen. Der schriftliche Teil liegt Ihnen bereits vor, sodass ich mich dazu entschlossen habe, den Sachverhalt auch in einem Video zu verdeutlichen. Vielen Dank, im Voraus!--Majorante (Diskussion) 16:14, 11. Jan. 2013 (CET)

"Jede Arbeit wird exakt so gedruckt, wie der Autor sie als Word- oder PDF-Datei einreicht, eine Lektorierung findet nicht statt." (Zitat aus der Wikipedia-Seite zum GRIN Verlag). --Joerg 130 (Diskussion) 23:11, 9. Jan. 2013 (CET)

In den von KaiMartin genannten Quellenangaben wird der Zusammenhang nicht erwähnt: Experimentalphysik 1 - Mechanik und Wärme. 2. Auflage. Springer-Verlag, Berlin, Heidelberg, New York 2001 und Willi Bohl, Wolfgang Elmendorf: Technische Strömungslehre. 13. Auflage. Vogel-Buchverlag, Würzburg Über die beim Grin-Verlag veröffentlichten Texte sollten Sie wissen: "Kopien und Ausdrucke dürfen nur zum privaten Gebrauch angefertigt werden. Die Herstellung und Verbreitung weiterer Kopien ist nur mit ausdrücklicher Genehmigung des Urhebers oder Verlags gestattet. Wird aus einer Arbeit wörtlich zitiert, muss der Autor genannt werden (sonst liegt eine Urheberrechtsverletzung vor)". Wenn bekannt ist, dass keine Lektorierung stattfindet, warum hat KaiMartin dann den Inhalt übernommen?! Entfernen Sie den Inhalt oder geben Sie die dazu richtigen Quellen an!--77.184.209.189 07:23, 10. Jan. 2013 (CET) Als

Die Sätze "Das hydrostatische Paradox sagt aus, dass der Druck nur von der Tiefe und nicht von der Form eines Fluids abhängt. Daher ist die Auftriebskraft unabhängig von der Menge des Fluids, in das der Körper eingetaucht ist." beschreiben einen mir seit (der mehrere Jahrzehnte zurückliegenden) Schulzeit bekannten Sachverhalt. Ich bezweifele, dass die (offenbar mit erheblichem Aufwand erstellte) Arbeit von Robert Stach KaiMartin überhaupt bekannt war, ich kannte sie bis gestern nicht. Nach den Angaben auf http://www.hausarbeiten.de/faecher/vorschau/191038.html ist der Verdienst dieser Arbeit bestenfalls, auf missverständliche Formulierungen in der Fachliteratur hinzuweisen, keinesfalls aber neue physikalische Erkenntnis. --Joerg 130 (Diskussion) 12:00, 10. Jan. 2013 (CET)

Von Ihrer Seite ist dies eine Vermutung, die Sie bis jetzt in keiner Weise durch andere Quellen belegen konnten! Desweiteren stellen Sie sich über die Meinung von dem Physiker Dr. Hecht und Kollegen! Wenn auch Sie den Sachverhalt sachlich klären möchten, bitte ich Sie mir dazu Ihre Quellen aus der Fachliteratur aufzuzeigen, vielen Dank!--77.184.209.189 12:42, 10. Jan. 2013 (CET)

Ich halte die Aussage "Daher ist die Auftriebskraft unabhängig von der Menge des Fluids, in das der Körper eingetaucht ist." für derart offensichtlich, dass es dazu keinerlei Fachliteratur bedarf. Wenn der mir nicht bekannte Dr. Hecht anderer Meinung sein sollte, möge er das bitte hier erläutern. --Joerg 130 (Diskussion) 13:19, 10. Jan. 2013 (CET)

Mir wurde dazu geraten, die Diskussion jetzt zu beenden, weil sich die Rechtsanwälte darum kümmern.--77.184.209.189 13:31, 10. Jan. 2013 (CET)

Sehr geehrter Joerg 130,

inzwischen haben mir viele Fachleute auf meine Nachfrage geantwortet. Die Fachleute sind: Prof. Dr. rer. nat. habil. Holger Schanz von der Hochschule Magdeburg-Stendal, Univ.Prof. Dr.Dr. Ulrich Berger von der WU Vienna, Department of Economics Institute for Analytical Economics, Dr. rer. nat (Physik) Frank Schorr aus der Kanzlei Diehl und Partner. Die Fachleute sind einstimmig der Meinung, dass meine veröffentlichte Arbeit keinen neuen physikalischen Zusammenhang enthält. Die Fachleute betonen weiterhin, dass auch der fett markierte Teil in der folgenden Aussage zweifelsfrei falsch ist: "Das hydrostatische Paradox sagt aus, dass der Druck nur von der Tiefe und nicht von der Form eines Fluids abhängt. Daher ist die Auftriebskraft unabhängig von der Menge des Fluids, in das der Körper eingetaucht ist." . Zudem wird dazu ergänzt:" Sie sollten aber bei aller Begeisterung nicht über das Ziel hinausschießen. Zum Beispiel war es natürlich bereits bekannt, wie sich schwimmende Körper in engen Gefäßen verhalten, es handelt sich also nicht um eine "Entdeckung". "Ich halte Ihre Schlussfolgerung, Sie hätten das Archimedische Prinzip (AP) "erweitert" oder für kleine Flüssigkeitsvolumina "widerlegt", für stark übertrieben." "Im Endeffekt läuft Ihr Argument doch darauf hinaus, dass bei kleinen Volumina der schwimmende Körper weniger Wasser verdrängt als seiner Gewichtskraft entspricht, was Ihnen zufolge dem AP widerspricht. Nun muss man sagen, dass in der Tat das AP in vielen populärwissenschaftlichen Darstellungen so formuliert wird, dass ein schwimmender Körper so weit eintaucht, dass das Gewicht des verdrängten Wassers genau dem Gewicht des Körpers entspricht. Sie argumentieren, dass sich im schmalen Gefäß so wenig Wasser befindet, dass dessen gesamtes Gewicht kleiner als das des schwimmenden Körpers ist, dass also dieser gar nicht soviel Wasser verdrängen kann, wie es das AP fordert. Dieses Argument beruht aber lediglich auf einer speziellen, engen Interpretation des Wortes "verdrängt". Die populäre Version des AP betrachtet aber offenbar das "verdrängte" Wasservolumen als jenes, welcher der Teil des schwimmenden Körpers einnimmt, der sich unter der Wasseroberfläche befindet. Dadurch ergibt sich die scheinbar paradoxe Situation, dass ein Schwimmkörper in einem schmalen Gefäß mehr Wasser "verdrängen" kann, als sich überhaupt im Gefäß befindet. Es ergibt sich aber keine Notwendigkeit für eine Erweiterung des AP, und dieses wird durch diese Beobachtung auch nicht widerlegt." Dafür und für die hier entstandene Diskussion möchte ich mich bei Ihnen entschuldigen. Mit freundlichen Grüßen --Majorante (Diskussion) 07:38, 12. Jan. 2013 (CET)

Sehr geehrter Majorante, es freut mich, dass wir uns da einig geworden sind. Wenn ich richtig verstehe, ist Ihre Arbeit an einer berufsbildenden Schule entstanden. Soweit ich das beurteilen kann, haben Sie dabei das dort übliche theoretische Niveau deutlich überschritten. Das zeigt Mut, und das verdient Anerkennung, ebenso wie der Mut, jahrtausendealte Darstellungen (durch versuchte Erweiterung) in Frage zu stellen. Und ich meine, Ihre Überlegungen zeigen auch ein hohes Maß an Intelligenz. Ich kenne Ihr Alter und Ihre berufliche Planung nicht; falls Sie die Möglichkeit zu weitergehender theoretischer, z.B. akademischer Ausbildung haben, sollten Sie diese m.E. ergreifen.

Ich bin nicht sicher, ob Sie sich oben verschrieben haben. Den Satz "Daher ist die Auftriebskraft unabhängig von der Menge des Fluids, in das der Körper eingetaucht ist." halte ich für richtig, natürlich unter der unausgesprochenen Nebenbedingung, dass bei gegebener Geometrie die Menge des Fluids zum vollständigen Eintauchen oder Aufschwimmen des Körpers ausreicht und dieser auch soweit eingetaucht ist. Aber vielleicht ist er mehrdeutig, man sollte das wohl anders formulieren. Herzliche Grüße --Joerg 130 (Diskussion) 12:37, 12. Jan. 2013 (CET)

Sehr geehrter Joerg 130,

zuerst vielen Dank für Ihr großes Lob an mich! Auch bei KaiMartin möchte ich mich sehr bedanken! Hatte er sich doch meinem Problem angenommen und mir die von ihm benutzte Quelle aufgezeigt. In dem aufgezeigten Artikel bei Wikipedia in der Version vom 10. November 2011, steht geschrieben: Gleichwohl ist die verdrängte Masse m= p * V kein tatsächlicher Körper, sondern eine durch den verdrängenden Körper geprägte Verformung (V) des Fluides (relativ zu ihrem Oberflächenspiegel), welcher eine virtuelle Dichte zugemessen wird. Die Auftriebskraft wird demnach allein durch die Summe der (von Druckdifferenzen verursachten) Kräfte an allen exakt übereinanderliegenden vertikalen Projektionsflächen (der Verformung) bewirkt, welche sich jeweils direkt unter und über dem Fluid befinden bzw. angrenzen. Das Prinzip gilt demnach auch, wenn etwa die vorhandene Flüssigkeit ein geringeres Volumen besitzt als der eingetauchte Teil des Schwimmkörpers. Ich denke auch, dass KaiMartin mit seiner Formulierung Recht hat: Das hydrostatische Paradox sagt aus, dass der Druck nur von der Tiefe und nicht von der Form eines Fluids abhängt. Daher ist die Auftriebskraft unabhängig von der Menge des Fluids, in das der Körper eingetaucht ist. Laut meiner damaligen Aussage könnte man den von KaiMartin geschriebenen Text jetzt wie folgt ergänzen: Das hydrostatische Paradox sagt aus, dass der Druck nur von der Tiefe und nicht von der Form eines Fluids abhängt. Daher ist die maximale Auftriebskraft auf einen vollständig eingetauchten Schwimmkörpers bereits möglich, wenn er dabei weniger Volumen an Flüssigkeit verdrängt, als es das archimedische Prinzip verlangt. Die scheinbar paradoxe Situation, ist gar nicht paradox. Dies wollte ich in meiner Arbeit auch deutlich machen. Der Schwimmkörper mit einem Volumen von 562cm³ wird von den 400 cm³ Wasser (400 ml) vollständig umschlossen. Habe ich den Körper tief unter die Wasseroberfläche gedrückt und anschließend losgelassen, so erfolgte immer eine schnelle Aufwärtsbewegung. Dabei hatte der Schwimmkörper ein Gewicht von 501g. Damit ist das archimedische Prinzip für diesen einen speziellen Sachverhalt in der Tat verletzt und sollte ergänzt werden! Viele Leute haben dazu voreilig ihr Urteil gefällt, ohne dies zu hinterfragen, bzw. experimentell zu testen. Der Sachverhalt ist noch nicht offiziell und wird vielleicht nie genutzt werden. Ich bitte euch so sehr, mir dabei zu helfen! Ein physikalischer Zusammenhang ist schließlich ein Zusammenhang, der sich unter gleichen Bedingungen immer wieder wiederholt. Bitte wiederholt deshalb meine Versuche und überprüft dies erneut. Am wichtigsten war mir immer der technische Nutzen dabei für die Industrie in Deutschland. Ich hatte mich auch entgegen der Patentanmeldung für eine Veröffentlichung entschieden. Wenn nicht von mir, so kann dies dann vielleicht von anderen Menschen aus der Region sinnvoll genutzt werden. Abgesehen von meinen dazu überlegten Anwendungen haben die Leute vielleicht noch ganz andere, bessere Ideen. Hier noch einmal die Arbeit zum Download: http://www.physikfreund.de/ Vielen Dank, euer Robert--Majorante (Diskussion) 11:01, 14. Jan. 2013 (CET)

hallo robert,

bei wikipedia ist das "du" als anrede üblich. auch wenn mich das hier nichts angeht, finde ich deine argumentation doch interessant. deine experimente habe ich mit rohren, diverser durchmesser wiederholt. um den sachverhalt optisch darzustellen, sind die benutzten massestücke in deiner arbeit die beste möglichkeit. du verdeutlichst die maximale auftriebskraft mit dem schwebezustand-das ist clever. dafür kannst du den schwimmkörper aber auch mit wasser befüllen, das ist dann auf 1 gramm genau. wenn aber optische aspekte keine rolle spielen, zeige ich dir, wie du die maximale auftriebskraftr ohne massestücke genauer messen kannst. mit der überlaufmethode zuerst das körpervolumen bestimmen, notiz machen. dann stellst du das leere gefäß auf deine digitalwaage und stellst sie danach auf null. hast du das wasser in dein gefäß gefüllt, mache eine notiz vom angezeigten gewicht, danach ebenfalls die waage nullen. zum schluss drückst du den leeren schwimmkörper unter die wasseroberfläche und mit actio=reactio zeigt deine digitalwaage die auftriebskraft deines schwimmkörpers an. wie du schon sagst, ist dies die maximal mögliche auftriebskraft auf den körper, sie ist gleich der kraft in einem größeren gefäß, rohr. fachlich ist das von dir geschriebene richtig, sei stolz drauf, kleiner kämpfer! (nicht signierter Beitrag von Geoid110 (Diskussion | Beiträge) 09:25, 15. Jan. 2013 (CET))

Sehr geehrter Joerg 130, wie schon KaiMartin richtig sagt, hängt die Auftriebskraft nur von der Tiefe des eingetauchten Körpers ab und nicht von der Flüssigkeitsmenge. Soweit ist alles richtig und sollte auch dabei bleiben! Jedoch ist V immer das Körpervolumen. Aus der klassischen Herleitung habe ich dies damals gesehen. Sogar Prof. Dr. Schanz sieht dies genauso, dass V immer das Körpervolumen ist. Weil bisher immer galt, dass das Volumen(Fluid) immer größer oder gleich dem Volumen(Körper) ist, bestand natürlich keinerlei Notwendigkeit, dies zu korrigieren. Ich habe aber den Spezialfall erkannt und ihn mit Experimenten aufgezeigt: das Volumen(Fluid) tatsächlich kleiner als Volumen(Körper) sein kann und das es daher nicht immer richtig ist, zu sagen: V(Fluid) ist immer größer oder gleich V(Körper). Dem Physiker Dr. Hecht durfte ich dies immerhin vor Ort vorführen, auch wenn er anfangs besonders skeptisch war. Wie bereits in meiner Arbeit geschrieben, gilt für die Auftriebskraft immer: Auftriebskraft = Volumen(Körper) * Dichte(Fluid) * Schwerebeschleunigung. Nur die folgende Aussage sollte daher verbessert werden: Dabei ist V das vom Körper verdrängte Volumen des Fluids. Joerg 130, Sie sind wie ein Stratege, wenn ich dies hier mal sagen darf! Sie haben schließlich die ganze Diskussion auf die alles entscheidende Frage drauf hin gelenkt. Den meisten Ingenieuren und sogar Physikern ist die sich dabei stellende Frage gar nicht aufgefallen. Vielen Dank! Mit freundlichen Grüßen --Majorante (Diskussion) 12:24, 16. Jan. 2013 (CET)

Hallo Joerg, mir erzählte ein ehemaliger Physik-Kommilitone davon. Zuerst schreibt ihr hier: „Der statische Auftrieb entspricht der Gewichtskraft des verdrängten Fluids (Fluidvolumens).“ und im Anschluss wurde hier geschrieben: „die Auftriebskraft ist unabhängig von der Menge des Fluids, in das der Körper eingetaucht ist“. Dies steht aber zueinander im Widerspruch! Dafür brauche ich nicht mein Physik-Diplom, auch ein Ingenieur der Elektrotechnik muss man nicht sein. Warum Majorante hier soviel Kritik bekommen hat, verstehe ich nicht. Dass die Auftriebskraft unabhängig von der Menge des Fluids ist, macht doch nur für sein spezielles Experiment einen Sinn! Wie Majorante schon sagte: „wenn der Schwimmkörper weniger Volumen an Flüssigkeit verdrängt, als seinem Körpervolumen entspricht.“ Ohne dieses Beispiel ist die zweite Aussage hier sinnwidrig! Hallo Majorante, einen Besuch an der Uni Magdeburg kann ich dir nur ans Herz legen! Am 1. Juni findet zum achten Mal die Lange Nacht der Wissenschaft statt, oder komm einfach zu einer Vorlesung von Herrn Dr. Streitenberger, anspruchsvoll und zugleich unterhaltsam! Alles Gute und viel Erfolg auf deinem weiteren Lebensweg wünsche ich dir!--77.12.252.130 17:47, 25. Mär. 2013 (CET)

Die obige Diskussion ist zweifellos erheblich ausgeufert. Der Satz „Der statische Auftrieb entspricht der Gewichtskraft des verdrängten Fluids (Fluidvolumens).“ wurde missverstanden, er provoziert dieses Missverständnis allerdings auch. Ein Beispiel: Was passiert, wenn ein Schiff aus offenem Gewässer in eine enge Schleusenkammer fährt? Was passiert, wenn sich die Schleusentore schließen? Was ist anders, was genauso, wenn das Schiff stattdessen mit einem Kran in eine bereits geschlossene, um das verdrängte Volumen leergepumpte Schleusenkammer gehoben wird? --Joerg 130 (Diskussion) 19:22, 25. Mär. 2013 (CET)

Eine konkrete Problemlösung, also eine Umformulierung des missverstanden Satzes, wäre z.B. : "Daher ist die Auftriebskraft nicht abhängig von der Menge des Fluids, in das der Körper eingetaucht ist und ihn umgibt, sondern von der Menge des vom Körper verdrängten Fluidvolumens." --Retorte (Diskussion) 12:46, 6. Apr. 2014 (CEST)

Schwerkraft

Da die Wiki eine akkurat gewissenhafte Seite ist. In der Gleichung sollte berücksichtigt werden, dass die Schwerkraft - so wie die Höhe von Unter- wie Oberseite des Schwimmkörpers - ebenso höhenabhängig ist.

kleiner Denkanstoss ..

qubric (14:25, 6. Jul 2014 (CEST), Datum/Uhrzeit nachträglich eingefügt, siehe Hilfe:Signatur)

Das ist doch bei den üblichen Größen der betrachteten Körper nicht von Bedeutung. Wenn im Einzelfall doch (ein Ballon von mehreren Kilometern Höhe?), wird man erst Recht berücksichtigen müssen, dass auch die Dichte des Fluids höhenabhängig ist. Wir brauchen dann also ein Volumenintegral, mit dem wir unsere Leser überfordern. Was soll das? --Joerg 130 (Diskussion) 15:14, 6. Jul. 2014 (CEST)

Eigener Artikel für statischen Auftrieb

Die meisten Wikis haben jeweils einen Artikel für statischen und dynamischen Auftrieb. Damit braucht man auch nicht mehr 2 Links auf die englische Wiki.

Archivierung dieses Abschnittes wurde gewünscht von: Ist seit ein paar Jahren auch hier in WP-de der Fall. ---<)kmk(>- (Diskussion) 00:02, 2. Jun. 2016 (CEST)

Zylinder - stimmt das?

Hier wurde die Behauptung in den Artikel eingebaut, ein dicht auf dem Boden stehender Zylinder erfahre keinen Auftrieb. Ich bezweifle die Richtigkeit dieser Behauptung und plädiere dafür, sie entweder stichhaltig zu belegen oder zu entfernen.--Balliballi (Diskussion) 14:14, 23. Mai 2016 (CEST)

Einfach mal ausprobieren - macht eigentlich jeder Lehrer mal im Physikunterricht vor. Hier ist's ausführlich erklärt. OLMuseum (Diskussion) 11:35, 24. Mai 2016 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: Die Aussage ist völlig korrekt. Keine inhaltliche Korrektur am Artikel erforderlich.---<)kmk(>- (Diskussion) 00:25, 2. Jun. 2016 (CEST)

auftrieb duch vakum

ich habe eine ide und zwar könte man fom prinzip her anstelle eines leichtgases wie helium oder wasserstof ein vakum verwenden natürlich muste dzu ein kompromis einegangen werden da ein vakum zu halten nicht einfach ist und der gewichtforteil damit schon wider flöten gehen könte ein kompromis wäre es ein leichgas mit starken unterdruck zu verwenden(nicht signierter Beitrag von 78.51.48.156 (Diskussion) )

Eine durchaus schlüssige Idee, die aber schon seit einigen hundert Jahren bekannt ist. Vom Prinzip her ist das möglich, aber es bringt wegen des konstruktiven Aufwandes keine Vorteile, da die Hülle eine hohe Festigkeit (=hohes Gewicht) haben müsste.--Thuringius 23:14, 7. Nov. 2007 (CET)

Vielleicht kann man diese Idee einschließlich historischer Referenz in den Artikel einbringen.---<)kmk(>- (Diskussion) 20:09, 2. Sep. 2014 (CEST)

Zusammenhang Gravitation

Ich finde nirgends im Artikel den Zusammenhang mit Gravitation.. Auftrieb entsteht ja, weil eben die dichtere Masse staerker von der Erde angezogen wird als die weniger dichte (zb Luftblase im Wasser). Weil das Wasser dichter ist uebt es (durch die Gravitation) mehr Kraft auf die Luftblase aus, was ja den Effekt hat, das die Luft nach oben gedraengt wird. Diese Kraft waere der AUftrieb.. ich finde diesen Vorgang nirgends im Artikel genauer erklaert :(

Der Artikel sagt auch "Mit Auftrieb wird eine Kraft bezeichnet, die eine Flüssigkeit oder ein Gas ..." Aber stimmt das? EIn Stein in einem Glas voll Sand sinkt durch leichte Erschuetterungen nach unten.. So ist ja auch das Metal(da es das schwerste ist) zum erdkern gewandert und die Dichte wird praktisch immer weniger je naeher an die Oberflaeche man kommt. WIrd das immernoch auftrieb genannt?

--Marenz 12:01, 7. Okt. 2007 (CEST)

• Der Zusammenhang mit der Gravitation erfolgt über die mehrfach im Artikel erwähnte Gewichtskraft. Mit einer Ergänzung durch eine anschauliche Erklärung mit Druck und Drängen wie von Dir angedeutet, könnte ich mich anfreunden.
• Ja, auch bei Steinen im Boden und bei Vorgängen im Erdinneren nennt man es "Auftrieb". Die Kontinente, die auf dem Mantel schwimmen könnte man sehr gut als Beispiel in den Artikel integrieren.

---<)kmk(>- (Diskussion) 20:07, 2. Sep. 2014 (CEST)

Um genau zu sein: es braucht ein Kraftfeld, das muss aber nicht zwingend Gravitation sein. Gegenbeispiel: eine Zentrifuge: ein Rohr gefüllt mit Flüssigkeit das sich dreht. Teilchen in der Flüssigkeit, die eine kleinere Dichte haben als die Flüssigkeit gehen nach innen, solche mit grösserer nach aussen. Dies ist auch (statischer) Auftrieb! Siehe Dichtegradientenzentrifugation / Ultrazentrifuge

Allgemein ist dieser Artikel sehr schlecht.. Woher kommt der Auftrieb? (Druckunterschied / -gradient auf Flächen senkrecht zum Gradient, hervorgerufen durch entweder Gravitation oder Rotation oder ...) Dies sollte meiner Meinung nach besser hervorgehoben werden (Archimedisches Prinzip: Die Skizze dort sollte auch hier sein) 130.60.166.148 09:17, 2. Dez. 2014 (CET)

Überarbeitung mit neuen Quellen sinnvoll.

Der Artikel muss dringend mit überarbeitet und mit mehr/neuen Quellen belegt werden. Die Einzige Quelle die hier angegeben wurde bezieht sich auf den letzten Absatz und hat mit dem restlichen Thema wenig zu tun. Für einen qualitativ hochwertigen Artikel sind auf Quellen gestützte Angaben wohl das Mindeste. (nicht signierter Beitrag von Felix Stollberger (Diskussion | Beiträge) 21:55, 1. Jun. 2016 (CEST))

Der Artikel referiert im Hauptteil Grundlagenwissen, das sich in einführenden Lehrbüchern der Physik inhaltlich wieder findet. Diese Aussagen sind ohne ernsthaften Recherche-Aufwand leicht zu überprüfen. Damit sind die in WP:Beleg geforderten Grundsätze erfüllt. Explizite Einzelnachweise sind nicht erforderlich, schon gar nicht "dringend".---<)kmk(>- (Diskussion) 23:51, 1. Jun. 2016 (CEST)

Wieso schwimmt die Münze auf dem Quecksilber?

Die Bildunterschrift behauptet, die britische Ein-Pfund-Münze schwimme aufgrund ihres Auftriebs auf dem Quecksilber. Da die Dichte des Neusilbers, aus dem die Münze geprägt ist (8,48 g/cm^3), mehr als die Hälfte der Dichte des Quecksilbers beträgt (13,5 g/cm^3), müßte sie, wenn die Bildunterschrift stimmen würde, mehr als zur Hälfte eintauchen. (Die Dichte der Legierung: 70% * 8,92 g/cm^3 (Kupfer) + 24,5% * 7,14 g/cm^3 (Zink) + 5,5% * 8,908 g/cm^3 (Nickel) = 8,48 g/cm^3.)

Auf dem Foto ist aber durch das Muster auf dem Münzrand deutlich genug zu sehen, daß die Münze so gut wie gar nicht in das Quecksilber eintaucht. Ihr statischer Auftrieb kann also höchstens einen vernachlässigbar kleinen Teil dazu beitragen, daß sie schwimmt.

Die Bildunterschrift zu demselben Foto im englischen Artikel über das Quecksilber gibt für das Neusilber der Münze eine zu geringe Dichte an, aber sie erwähnt wenigstens, daß auch die Oberflächenspannung eine Rolle spielt: "A pound coin (density ~7.6 g/cm^3) floats in mercury due to the combination of the buoyant force and surface tension."

Das Foto zeigt offensichtlich, daß die Münze nicht vom Auftrieb, sondern praktisch ganz von der Oberflächenspannung des Quecksilbers getragen wird. Die Bildunterschriften zeigen, daß das, was man sieht, manchmal nicht bis ins Bewußtsein vordringt. Gruß--Liberatus (Diskussion) 21:47, 10. Feb. 2016 (CET)

Danke für den Hinweis. Du hast völlig Recht: Das Quecksilber benetzt die Münze nicht. Sie taucht nicht wie ein Boot ein, sondern liegt auf der Oberfläche auf und drückt eine Delle hinein. Das hat zwei Folgen: Zum einen ist durch die Wölbung nicht klar zu erkennen, wie tief der untere Rand der Münze unter dem Spiegel des Quecksilbers liegt. Zum anderen muss man zur Berechnung des Auftriebs das Volumen der Luft jenseits des Randes der Münze hinzu nehmen. Ähnlich wie bei einem [[[Wasserläufer]] ist das kein statischen Auftrieb im engeren Sinn.

Insgesamt macht das die Münze zu einem wenig geeigneten Beispiel, um das Phänomen eindrücklich zu illustrieren. Ich suche mal auf Commons nach einem besseren Beispiel.---<)kmk(>- (Diskussion) 00:18, 2. Jun. 2016 (CEST)

Fliegen oder fahren oder was?

Im Laufe der Zeit wechselte die Bezeichnung für das korrekte Verhalten von Ballons mehrfach zwischen "fliegen", "abheben", "schweben" und "fahren", wobei derzeit "fahren" favorisiert wird. Das Fahren der Ballone passt aber nicht recht zum Schwimmen der Schiffe. Bekanntlich wurde die Bezeichnung "Ballonfahrt" in Analogie zur "Schifffahrt" gebildet. Wenn also die Ballone "fahren", dann sollten erst recht die Schiffe "fahren" und nicht "schwimmen". Hier geht es aber nicht ums Fahren im Sinne von Fortbewegung, sondern um die Wirkung des Auftriebs. Und die führt beim Schiff nur zum "Schwimmen", denn fürs "Fahren" sind Segel oder Schiffsschraube erforderlich. Entsprechend führt der Auftrieb beim Ballon nicht zum (Vorwärts-) "Fahren", sondern nur zum "Schweben". Ich schlage eine entprechende Änderung vor.--Balliballi (Diskussion) 12:42, 2. Aug. 2016 (CEST)

Ja, im Sinne des Auftriebs ist Schweben die richtige Zustandsbeschreibung. Ansonsten fahren Ballons schon länger, als Flugzeuge fliegen können. Hadhuey (Diskussion) 13:09, 2. Aug. 2016 (CEST)

Schiffe fahren noch viel länger. Neben der Bezeichnung "Ballonfahrt" gibt es übrigens durchaus auch die Bezeichnung Ballonflug, dagegen vom einem "Schiffsschwimm" hab ich noch nichts gehört. Also wenn schon "Ballonfahrt", dann bitte erst recht auch "Schifffahrt".--Balliballi (Diskussion) 13:45, 2. Aug. 2016 (CEST)

Oberflächenspannung?

Bzgl. diesem Edit von Benutzer:Ulfbastel habe ich Zweifel. Da ich aber nicht weis, wie das zu berechnen ist, habe ich unter "Wikipedia:Auskunft#Metallmünze in Quecksilber ~ Oberflächenspannung?" nach Hilfe gefragt.

--arilou (Diskussion) 09:42, 26. Mär. 2019 (CET)

Der Edit ist völlig in Ordnung.

Die Differenz der Dichten reicht aus, um einen Schwimmzustand zu erklären, die Oberflächenspannung ist in diesem Fall nicht relevant:

• Quecksilber: 13,55 g/cm³
• Eisen/Legierung: 7 oder 8 g/cm³ / Nordisches Gold: 7 g/cm³

Ein leichteres Material schwimmt also auf einem fast doppelt so schweren Fluid, ragt schon deshalb zu 50 % aus dem Flüssigkeitsspiegel.

• Sie hat statischen Auftrieb im Umfang einer Münze aus Quecksilber, aber nur die halbe Gewichtskraft, also die einer Münze aus Eisen
• Ein theoretischer Beitrag der Oberflächenspannung ist vernachlässigbar winzig.

Mit Oberflächenspannung gibt es auch Effekte; dann liegt aber gerade umgekehrt ein schwerer (dichterer) Körper auf einem leichteren Medium und wird durch nette Effekte an der Oberfläche gehalten. Ebene Schnipsel aus Aluminiumfolie könnte man geschickt auf eine Wasseroberfläche auflegen; drückt man sie unter die Oberfläche, dann sinken sie.

Die Münze würde hingegen auch dann wieder aus dem Fluid aufschwimmen, wenn sie tief unter die Oberfläche gedrückt würde.

Jeder Zustand in der Realität ist immer ein Zusammenwirken vieler physikalischer Effekte, von denen manche dominieren und andere in der aktuellen Konstellation vernachlässigbar sind. Bei unserem Thema kommen theoretisch folgende Annahmen und mögliche Effekte zusammen:

• Inkompressibles homogenes Medium
  • Ist bei Wasser gut erfüllt, aber wäre bei Hunderten von Metern Tiefenunterschied nicht gegeben.
  • Große Wassermengen in der realen Welt sind geschichtet in unterschiedliche Temperaturen, in unterschiedliche Salzgehalte, und deshalb unterschiedliche Dichten (die auch widersinnig geschichtet sein können; Blasen von leichterem Wasser können unter Schichten von schwererem Wasser liegen).
  • Inkompressibilität kommt ganz gut hin, aber über Kilometer Wassertiefe wird Wasser doch minimal weiter komprimiert.
• Statischer Zustand
  • In der realen Welt gibt es immer Störungen; etwas Wind, eine leichte Drift im Wasser, Schwingungsbewegungen in Luft und Wasser.
  • Der Körper kann stark gegen das Fluid bewegt sein; das bringt erhebliche Effekte bis hin zum Gleiten (dynamischer Auftrieb).
• Oberflächenspannung
  • Bei einem kleinen Körper an der Oberfläche beeinflussend.
• Adhäsion, Kohäsion, Reibung, dynamische Volumenverdrängung:
  • In entsprechenden Konstellationen relevant.

Ahoi --Schiefbauer (Diskussion) 10:29, 26. Mär. 2019 (CET)

Auch wenn der statische Auftrieb alleine groß genug ist, trägt die Oberflächenspannung zum Schwimmen bei. Es scheint mir deshalb ungerechtfertigt zu sein, den Satz so zu formulieren, als würde der statische Auftrieb alleine das Schwimmen begründen. --BlackEyedLion (Diskussion) 11:09, 26. Mär. 2019 (CET)

"Die Differenz der Dichten reicht aus, um einen Schwimmzustand zu erklären, die Oberflächenspannung ist in diesem Fall nicht relevant"

Ähm - sicher? Die Münze erfährt im Schwerefeld eine Gewichtskraft F_g. Dieser wirken entgegen:

1. F_a aus dem Archimedischen Auftrieb und
2. F_o aus der Oberflächenspannung.

Wie du selbst schreibst, kann ein Stück Alufolie mit Dichte ~ 2,7 g/cm³ auf Wasser mit Dichte 1 g/cm³ obenauf schwimmen. Die Kraftkomponente F_a übernimmt hier gerade mal ¹/₃ der Gewichtskraft! --> Offensichtlich ist F_o in manchen Fällen mitnichten vernachlässigbar.

Deshalb möchte ich das in diesem Fall nachgerechnet sehen. (Hätt' ich die Formeln, würd' ich 's ja selber machen.)

Außerdem: Gerade Quecksilber ist so ziemlich die Flüssigkeit mit der stärksten Oberflächenspannung, fast 8* so stark wie bei Wasser. Das lässt mich vermuten, dass hier F_o besonders relevant sein kann.

--arilou (Diskussion) 11:22, 26. Mär. 2019 (CET)

(BK)Tut mir leid, aber hier kann der statische Auftrieb alleine das Schwimmen begründen. Denn vereinfacht gesagt, verhindert die Oberflächenspannung nur, dass ein Körper die Oberfläche nicht durchbrechen kann. Kann der Körper die Oberfläche nicht durchbrechen, dann kann er ein höheres spezifisches Gewicht haben als die Flüssigkeit, und schwimmt trotzdem oben auf. Und ob ein Körper die Oberfläche durchbrechen kann oder nicht, dafür ist vor allem die Form und als zweiter Faktor die Oberflächenspannung ausschlaggebend. Klar hat auch die Masse des Körpers einen Einfluss, nicht aber das spezifische Gewicht des Körpers. Auf der anderen Seite kann die Grösse der Mulde, oder die Verdrängung, relativ einfach berechnet werden. Denn sie entspricht dem Volumen des zu verdrängenden Quecksilber, und darauf hat die Masse der Münze einen Einfluss. Und hierbei gilt; Hat der Körper (hier Münze) ein kleiner spezifisches Gewicht als die Flüssigkeit (hier Quecksilber) schwimmt er immer, egal wie gross oder wie klein die Oberflächenspannung ist. --Bobo11 (Diskussion) 11:24, 26. Mär. 2019 (CET)

Die Oberfläche kann undurchbrochen (besser: unbenetzt) bleiben, und der Körper geht trotzdem unter. Er muss nur schwer genug sein, um F_g > (F_a + F_o) zu bewirken. --arilou (Diskussion) 11:35, 26. Mär. 2019 (CET)

Wie gesagt - ich würde das gerne mal gerechnet sehen. Schon aus bloßem Interesse - ist doch 'ne spannende Frage ;-)

--arilou (Diskussion) 11:37, 26. Mär. 2019 (CET)

Ich relativiere mich mal ein wenig betreffend der Situation im Quecksilber:

• In der Münzen-Konstellation gäbe es einen messbaren Einfluss, er ist aber nicht erforderlich, um das Schwimmen der Münze zu erklären.

Unser Artikel soll einen Effekt verständlich erklären und beschreiben; das Münzen-Foto wäre insofern zur Illustration ungeeignet, wenn es die Sachverhalte verkompliziert und durch spürbare Zusatzeffekte für Verwirrung sorgt.

• Wenn man sich mit statischem Auftrieb beschäftigt, dann geht es um Schiffe, Boote, Flöße und dergleichen. Hier ist Oberflächenspannung definitiv vernachlässigbar und geht in keine Berechnung mit ein, weil der theoretische Effekt um Größenordnungen von den Messungenauigkeiten der klar dominanten Effekte erschlagen wird.
• Nur für so ein Mini-Gebilde wie eine Münze wird die Fragestellung überhaupt betrachtenswert.

Zur Kombination Münze-Quecksilber:

• Ein Blick auf das Foto zeigt, dass sich Quecksilber in dieser Kombination anscheinend stark „hydrophob“ verhält.
  • Die Fluidoberfläche ist deutlich nach unten eingedrückt.
  • Das sieht mir nach einem spürbaren Einfluss in absolut kleinen Systemen aus.
• Maßgeblich sind unsere folgenden Artikel:
  • Kontaktwinkel
  • Youngsche Gleichung
  • Oberflächenspannung
• Für die Münze im Quecksilber wüsste ich ungefähr, wie ich das rechnen müsste, aber mir fehlen konkrete Daten, und ich hatte sowas zuletzt vor rund vierzig Jahren mal ausgerechnet.
  • Überschlagsmäßig und mit Schätzungen über Winkel und gegoogleten geometrischen Daten einer Pfund-Münze (die aber keine Masse von 0,5 kg zu haben scheint, seltsam) komme ich maximal auf einen einstelligen Prozentbereich, der den Einfluss der Oberflächenspannung gegenüber dem Auftrieb ausmacht; vielleicht aber sogar unter 1 %.

Vielleicht mal in unserer Physik-Redaktion anfragen, ob da jemand Routine mit Oberflächenspannung hätte.

• Eine fertig durchgerechnete Muster-Rechnung für die Konstellation „fester kreisförmiger Körper auf Fluid-Oberfläche schwimmend“ müsste sich eigentlich in einer Aufgabensammlung Physik (oder Materialkunde) für Schlaumeier finden, und wenn man das gesichert irgendwo als Rechenbeispiel nachlesen kann, dann brauchen nur die Durchmesser und Winkel eingesetzt werden und es ergibt sich die Vertikalkraft (Schubspannung) für beliebige Fälle. Für Kapillaren gibt es das haufenweise.
• IngInnen bevorzugen es, sowas vorgekaut in Formelsammlungen nachzuschlagen und dann nur noch situationsgerecht anzuwenden.

Die Verformung der Fluid-Oberfläche gegenüber der Horizontalen gibt dem Schwimmkörper eine zusätzliche Vertikalkomponente der Grenzflächenkraft („Haftspannung“) mit, und diese beeinflusst die Resultierende aller äußeren Kräfte. Allerdings kann das positiv oder negativ ausfallen, und rein rechnerisch könnte das den Auftrieb sogar mindern. Weil ich aber mit Quecksilber keinerlei Erfahrung habe, sondern mich allenfalls mit Wasser auskenne, mag ich das jedoch heute nicht mehr vertiefen.

Maßgeblich für die Relevanz der Oberflächenspannung ist das Verhältnis von Wasserlinienlänge zu Volumen bzw. Masse.

• Bei einer auf zehnfache Abmessungen vergrößerten Münze geht die Relevanz der Oberflächenspannung auf ein Hundertstel gegenüber der alltagstauglichen Münze zurück.
• Nur bei absolut winzigen Gebilden, also sehr klein gegenüber einem Ruderboot oder Öltanker, ist das überhaupt diskutabel.
• Dann ist das spektakuläre Foto aber ggf. ungeeignet, um das umseitige Thema zu illustrieren.

Ahoi --Schiefbauer (Diskussion) 12:32, 26. Mär. 2019 (CET)

Hi Schiefbauer, arilou, beinahe erwartrt waren diese Zweifel, aber so umfangreich hatte ich es nicht erwartet. Erstmalhabe ich es tatsächlich deswegen editiert, weil eben der Oberflächenspannungsbeitrag in diesem Lemma nicht relevant ist. Dass er dennoch maßgeblich den Schwimmzustand beeinflussen kann, schließe ich nicht aus. Daher ist das Bild etwas ungeeignet (nicht die Materialkombination). Ich hätte da ein Bild aus einem Quecksilberschalter machen können, wo ein Eisenteil (der Magnetanker) vertikal (durch die Glasröhre begrenzt) im Hg schwimmt. Auch da ist die Oberflächenspannung sehr zu sehen, leider sieht man ja nie den eintauchenden Teil des Schwimmkörpers (der ist erstaunlich gering, gäbe also eine gute Illiustration). Den Hg-Schalter habe ich leider wegen der Kinder entsorgt. Hier seht ihr mein Bild von vor der Zerlegung...--Ulf 17:33, 26. Mär. 2019 (CET)

Es gibt in dem gezeigten System nicht nur einfach eine Oberflächenspannung, sondern drei verschiedene Grenzflächenenergien: jeweils eine an der Grenzfläche Münze-Quecksilber, Münze-Umgebungsatmosphäre sowie Quecksilber-Umgebungsatmosphäre. Der Auftrieb der Münze kommt alleine durch die Verdrängung des Wassers zustande. Es ist dabei egal, ob und wie weit die Münze eintaucht. Wenn es sich bei der Flüssigkeit nicht um Quecksilber, sondern um Wasser handeln würde, dann würde die Münze untertauchen. Auch dabei entstehen aber neue Grenzflächen: die Münze, die vor dem Eintauchen Grenzflächen mit der Atmosphäre hatte, hat diese beim Untertauchen durch Grenzflächen mit dem Wasser eingetauscht. Auch wenn die Grenzflächenenergien sich dadurch verändern: auf den Auftrieb, den die Münze erfährt, hat das keine Auswirkung. --Blutgretchen (Diskussion) 21:52, 26. Mär. 2019 (CET)

Drei Grenzflächenenergien gibt es nur, wenn drei Fluide aneinanderstoßen; nehmen wir mal Wasser, Öltropfen und Luft.

• Dann gibt es auch drei Grenzflächenwinkel, die zusammen 360° ergeben und die ein Maß für die Spannung/Kraft sind.
• Hier ist ein Beteiligter ein starrer Körper; dann gibt es nur noch einen freien Winkel (weil die Münzkante 180° sind und bleiben, sich nicht verformt). Wenn nichts verformt dann auch keine Grenzflächenenergie.
• Wenn nur starre Körper aneinanderstoßen, dann ist null Grenzflächenenergie.

Es gibt eine durch Oberflächenspannung verursachte, der Gewichtskraft entgegenwirkende Komponente, die also ähnlich wie der Auftrieb wirkt. Zwei Gründe:

• Kreisförmiger ebener Aluminiumblechschnipsel auf Wasser.
  • Habe ich inzwischen mal spaßeshalber ausgestanzt, 1 cm Durchmesser, 0,3 mm Stärke, „schwimmt“, säuft auf einen Puster hin ab.
  • Gewicht minus Auftrieb lassen 1,7 g/cm³ übrig; diese Kraft muss von irgendwas aufgebracht werden, und das ist die Vertikalkomponente der Haftspannung.
  • Leider ist das so fummlig, dass sich der Winkel (der maßgeblich für die Grenzflächenkraft ist) nicht abschätzen ließ. Aber dafür gibt es ja Bücher.
• Kapillarwirkung
  • Die Wassersäule steht im Rohr über dem Umgebungsniveau.
  • Nach reiner Hydrostatik müsste der Wasserspiegel im Röhrchen genau die gleiche Höhe haben wie das umgebende Medium; was kommunistische Röhren so erwarten lassen.
  • Die Arbeit gegenüber dem Nullspiegel muss die Flüssigkeit im Röhrchen irgendwie aufbringen, und die Gewichtskraft der Wassersäule über Null muss irgendwer verantworten. Das ist eine Kraftkomponente, die wie der Auftrieb der Gewichtskraft entgegenwirkt.

Heißt: In die Kräftebilanz muss die Vertikalkomponente der Haftspannung einbezogen werden; genauso wie Auftrieb und Gewichtskraft. Bei leichten kleinen Körpern spielt sie ggf. die entscheidende Rolle. Sie ist aber auf wenige Moleküle in der Wirkung begrenzt, und nur linienförmig entlang der Wasserlinie. Damit ist die absolute Ausdehnung des Körpers maßgeblich. Bei einem kleinen leichten Starrkörper noch relevante Größenordnung, bei einem Öltanker auch noch vorhanden, aber angesichts dessen Dimensionen im Vergleich zu einigen Molekülen in der Wasserlinie und des Verhältnisses zwischen statischem Auftrieb und Oberflächenspannung weit im Jenseits.

Am Rande gefragt: Gibt es eigentlich Materialkombinationen, bei denen ich negative Kapillarwirkung bekäme? Also Röhrchen in Fluid gehalten, und der Spiegel im Röhrchen liegt unterhalb des Umgebungsniveaus, weil das irgendwie hydrophob wäre oder so?

Ahoi --Schiefbauer (Diskussion) 11:15, 31. Mär. 2019 (CEST)

Nur zwei Zitate: Drei Grenzflächenenergien gibt es nur, wenn drei Fluide aneinanderstoßen; nehmen wir mal Wasser, Öltropfen und Luft. und Wenn nichts verformt dann auch keine Grenzflächenenergie. Mit Verlaub Schiefbauer, aber das ist völliger Unsinn. Natürlich gibt es zwischen Feststoffen und anderen Phasen (fluide ebenso wie feste) Grenzflächenenergien. Evtl. liegt darin das Missverständnis. Ich empfehle Dir als ersten Schritt mal unsere Artikel Grenzflächenenergie und Oberflächenenergie zu lesen. Und zu deiner Frage "am Rande": Natürlich gibt es auch Kapillarwirkung, bei der der Säulenstand in der Kapillare unter dem Spiegel einer Flüssigkeit liegt, in die ein Rohr eingetaucht wird: Das ist immer dann der Fall, wenn der Kontaktwinkel zwischen der Flüssigkeit, dem Röhrenmaterial und der umgebenden Atmosphäre >90° beträgt (also z. B. wenn Du an der normalen Umgebungsluft ein Teflonröhrchen in Wasser eintauchst). Ach ja...über die kommunistischen Röhren musste ich sehr schmunzeln ;) Ahoi! --Blutgretchen (Diskussion) 23:01, 31. Mär. 2019 (CEST)

Konvexe Körper

JoKalliauer: Bei einem nicht konvexen Körper dächte ich zunächst an einen Körper mit Einbuchtungen. Warum sollte das Gesagte bei diesen Körpern nicht gelten? Oder was versteht man sonst unter nicht konvexen Körpern? Flächige Körper ohne Volumen? Körper mit negativem Volumen? --Diwas (Diskussion) 00:22, 21. Feb. 2020 (CET)

konvex und konkav

das ist ein I-Profil

@Diwas: Konvexe Körper sind nach außen gebaucht. Es gibt keine konkaven Körper (außer vl. bei der Antimaterie oder so). Aber es gibt nicht konvexe Körper (beispielsweise konkave Linsen, oder was du als Einbuchtungen bezeichnest). Beispielswesise ein I-Profil (Bild rechts), dort herscht an der Unterseite des oberen Flansches ein kleiner Druck als an der Oberseite des unteren Flansches (wenn er so wie rechts dargestellt liegt). Außerdem habe ich nur eine Aussage über konvexe Körper gemacht, ich hab nicht gesagt, dass es bei anderen Körpern anders ist. Hat man einen nicht konvexen Körper hat sind OMA-taugliche-Definitionen für die Ober- und Unterseiten kompliziert.  — Johannes Kalliauer - Diskussion | Beiträge 17:57, 21. Feb. 2020 (CET)

Ich hätte als Unterseite ohnehin jeweils die wirksamen Anteile der Oberflächen des Körpers angesehen, du hast aber recht, dass das nicht jedem Leser bewusst ist. So ganz zufrieden, war ich mit der Formulierung Oberseite und Unterseite noch nie. Denn auch bei konvexen Körpern sind ja die Oberseite und Unterseite und die jeweiligen Drücke und Kraftvektoren nicht einheitlich. Was ist jetzt allgemeinverständlicher: vereinfacht oder genau und in Einzelheiten? Das war sicher eine gute Idee. Lustigerweise (im Bezug zur Diskussion eins drunter bevor ich diese gelesen und die heutigen (nein, gestrigen) Bearbeitungen gesehen hatte) habe ich heute (nein, das war gestern) offline schon überlegt, wie man an einem einfachen Beispiel erläutern kann, dass es etwas komplizierter wird, den Auftrieb zu berechnen, wenn die Flächen jeweils nicht in einheitlicher Tiefe liegen und der Druck nicht überall nur vertikal wirkt. Ich dachte dabei an ein Prisma dessen Erzeugenden (diese Bezeichnung fehlte mir gerade) horizontal liegen. Daher grübelte ich, wie man die Erzeugenden von den anderen Kanten des Prismas sprachlich unterscheiden kann. Es wäre wünschenswert, aber nicht Pflicht, in einem eigenen Anschnitt, darauf einzugehen, wie die Auftriebskraft errechnet wird, wenn nicht alle Flächen in nur horizontaler oder vertikaler Ebene liegen. Schiefbauer hatte mir das hier dankenswerterweise recht ausführlich dargelegt, obwohl ich mit meiner provokanten Frage vor allem darauf hinweisen wollte, dass hydrostatischer Druck an vertikalen Flächen keine vertikalen Kräfte ausüben kann. --Diwas (Diskussion) 02:13, 5:47, 22. Feb. 2020 (CET)

@Diwas: Scherzantwort: Wenn man eine rauhe vertikale Fläche hat dann übt ein hydrostatischer Druck lokal sehrwohl zu vertikalen Kräften.  — Johannes Kalliauer - Diskussion | Beiträge 17:01, 22. Feb. 2020 (CET)

Archivierung dieses Abschnittes wurde gewünscht von:  — Johannes Kalliauer - Diskussion | Beiträge 17:01, 22. Feb. 2020 (CET)

OmA-Formulierung des Erzeugenden sind

Im Falle eines Prismas (z.B. eines Zylinders) des Erzeugenden parallel zum Schwerefeld sind ist der statische Auftrieb die resultierende Kraft aus den beiden Kräften die an der Unter- und Oberseite angreifen. JoKalliauer: Mags du diesen Satz noch einmal OmA-tauglich formulieren? Den Satz verstehen vermutlich eher 0 ppm als 0,000128 ppm der Weltbevölkerung. --Diwas (Diskussion) 00:37, 21. Feb. 2020 (CET)

@Diwas:Was Erzeugende eines Prismas sind lernt man in der Pflichtschule (zumindest in Österreich). Da etwas 1,2 Prozent der Weltbevölkerung Deutsch als Muttersprache haben sollten das etwa 10000ppm der Weltbevölkerung verstehen, ob jetzt eine Null auf oder ab ist mir jetzt egal aber deine Rechnung ist ja um ca. 8 dezimale Größenordnungen daneben. Vielleicht nennt man die Geraden der Mantelfläche in Deutschland anders, aber dann sind wir trotzden noch bei ca. 1000ppm.

PS Wenn du etwas nicht verständlich findest streiche es raus, vereinfache es, solange es nicht explizit falsch ist werde ich nichts dagegen haben.

 — Johannes Kalliauer - Diskussion | Beiträge 18:11, 21. Feb. 2020 (CET)

Danke für die Erhellung. Ich kann nicht ausschließen, dass die Bezeichnung in meiner Schulzeit erwähnt wurde, aber der Speicherbereich später bereinigt wurde. Ich denke aber weiterhin, dass sehr viele Leser damit nichts anfangen konnten. Der Grammatikfehler, den ich nicht klar identifizieren konnte, hatte mich davon überzeugt, dass das so nicht stimmen kann und eine Nachfrage effizienter sei als grübeln oder recherchieren. Übrigens erwähnt Prisma (Geometrie) die Erzeugenden nicht. Unter Erzeugende ist etwas mathematisches beschrieben, von dem ich nicht weiß, ob es einen Bezug zu Prismen hat. --Diwas (Diskussion) 02:32, 2:40, 22. Feb. 2020 (CET)

Vielleicht hat es auch nur mein Geometrie-Lehrer es so erzählt, oder ich habe irgendetwas verwechselt. — Johannes Kalliauer - Diskussion | Beiträge 17:01, 22. Feb. 2020 (CET)

Falsch verstanden hast du nichts, das hab ich ja mittlerweile ergoogelt. Die Bezeichnung ist ja auch sinnig, wenn man sich die Erzeugung drehsymmetrischer Körper anschaut, besonders bei Rotationskörpern. --Diwas (Diskussion) 17:38, 22. Feb. 2020 (CET)

Archivierung dieses Abschnittes wurde gewünscht von:  — Johannes Kalliauer - Diskussion | Beiträge 17:01, 22. Feb. 2020 (CET)

in das der Körper eingetaucht ist.

entweder in das der Körper eingetaucht wird oder in dem der Körper eingetaucht ist. Es ginge auch in das der Körper eingetaucht worden ist. Ra-raisch (Diskussion) 10:45, 3. Jun. 2015 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von:  — Johannes Kalliauer - Diskussion | Beiträge 16:45, 26. Feb. 2020 (CET)

erledigtErledigt Ra-raisch (Diskussion) 12:26, 27. Feb. 2020 (CET)

Auftriebskraft mit dem Betrag

korrekt wäre sicherlich auch vektoriell $F_{\mathrm {A} }^{1}=-g^{1}\rho V$ ist ja hier beschrieben Archimedisches_Prinzip Ra-raisch (Diskussion) 12:18, 3. Jun. 2015 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von:  — Johannes Kalliauer - Diskussion | Beiträge 16:46, 26. Feb. 2020 (CET)

erledigtErledigtRa-raisch (Diskussion) 12:26, 27. Feb. 2020 (CET)

"Auftrieb" auch bei schwereren Objekten?

Anlass meiner Frage ist dieser Edit/Teil-Revert.

Das archimedische Prinzip gilt natürlich auch für Objekte, die schwerer als das umgebende Medium sind, z.B. einem Stein im Wasser. Im ganzen Artikel ist aber nicht 1 solches Beispiel. Nun meine Frage:

Spricht man auch von "statischem Auftrieb", wenn nicht einmal eine Komponente des Objekts leichter als das Medium ist? Denn eigentlich ist es dann ja "statischer Abtrieb" - oder "negativer statischer Auftrieb"?

Im Beispiel: Egal welchen Kubikmillimeter des Steins man betrachtet - jeder ist schwerer als Wasser. Anders z.B. bei einem U-Boot: Die Stahl-Bordwand ist zwar schwerer, der Innenraum aber leichter. Die Bordwand erzeugt eine Abtriebskraft, der Innenraum den Auftrieb.

--arilou (Diskussion) 09:24, 23. Aug. 2018 (CEST)

@Arilou: Auftrieb wird gem. aktuellen Artikel als der Effekt und nicht als die Kraft angesehen.

Luftfahrzeug scheint mir korrekt zu sein.

 — Johannes Kalliauer - Diskussion | Beiträge 16:51, 26. Feb. 2020 (CET)

Archivierung dieses Abschnittes wurde gewünscht von:  — Johannes Kalliauer - Diskussion | Beiträge 16:51, 26. Feb. 2020 (CET)

arilou Ergänzung: Auch auf einen Goldbarren in Luft wirkt ein statischer Auftrieb und damit eine statische Auftriebskraft, die den Wägewert reduziert. --Diwas (Diskussion) 04:02, 3. Mär. 2020 (CET)

Anmerkung

Zum einen ist folgendes Inhalt redundant: "Und g rho V ist [seine] Gewichtskraft." Am Anfang des Absatzes steht: "Der statische Auftrieb entspricht der Gewichtskraft des verdrängten Fluids." Vielleicht könnte man beide Formulierungen zusammenführen.

Weiterhin könnte man in Kapitel "Ursache und Größe" wie in der Einleitung beschrieben zusätzlich erwähnen, dass die Auftriebskraft der Gewichtskraft eines im Fluid befindlichen Körpers entgegengesetzt ist, um ein grundlegendes Verständnis über den Sachverhalt zu gewährleisten. --Retorte (Diskussion) 12:45, 6. Apr. 2014 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: Hadhuey (Diskussion) 07:48, 29. Feb. 2020 (CET)

Widersprüchliche Edits

In Spezial:Diff/196957771 behauptet User:Maschinist1968

Wegen des höheren Salzgehalts im Toten Meer ist die Dichte des Wassers höher als etwa in der Nordsee. Daraus resultiert ein stärkerer sichtbarer Auftrieb (Schwimmer tauchen nicht so weit ein) und wegen der Dichte auch ein stärkerer statischer Auftrieb.

(von mir drei Tage!?!(kontrolliert das hier keiner?) später gelöscht), hingegen in Spezial:Diff/197081011 wiederspricht User:Maschinist1968 sich selbst:

 Fährt dieses Schiff von der [[Nordsee) in die Elbe, wechselt es also vom Salzwasser ins Süßwasser, so sinkt es im Süßwasser (das eine geringere Dichte hat als Salzwasser) weiter tiefer ein und hat dadurch dann noch mehr Auftrieb.

(von mir korrigiert).

@Maschinist1968: Zuerst behauptest du in Salzwasser hat man mehr Auftrieb, dann behauptest du in Süßwasser hat man mehr Auftrieb, wenn ein Körper frei schwimmt. Die Auftriebskraft hängt nur vom Gewicht hab, aufgrund von Gleichgewicht, das verdrängte Volumen ist nur unterschiedlich.

 — Johannes Kalliauer - Diskussion | Beiträge 11:09, 23. Feb. 2020 (CET)

Das Tote Meer hat einen extrem hohen Salzgehalt, . Hab zumindest ich in der Schule gelernt.--Maschinist1968 (Diskussion) 11:24, 23. Feb. 2020 (CET)

Drum steht im Bildtext "wegen der Dichte" --Maschinist1968 (Diskussion) 11:26, 23. Feb. 2020 (CET)

@Maschinist1968: Wenn wir schon deine Webseite hernehmen dort steht F_A=F_G, also ist die Auftriebskraft eines schwimmenden Objektes unabhängig von der Dichte des Fluides! (Das Volumen ändert sich jedoch).

 — Johannes Kalliauer - Diskussion | Beiträge 11:32, 23. Feb. 2020 (CET)

Und das glaubt der vorgebliche "TU-Absolvent" beim Anblick des Zeitunglesenden im Toten Meer? --Maschinist1968 (Diskussion) 12:54, 23. Feb. 2020 (CET)

...und deswegen empfiehlst du mir in diesem PA auf meiner Disk. eine Nachhilfe?--Maschinist1968 (Diskussion) 17:52, 23. Feb. 2020 (CET)

Sicher klingt der Beitrag auf deiner Disk (etwas) oberlehrerhaft. Immerhin hat er sich aber bemüht, versöhnlich zu sein. Es entspricht meiner Ansicht nach dem Wikiprinzip, dass Autoren bei der Artikelarbeit hinzulernen. Ich denke, wir alle haben bei der Arbeit an diesem Artikel hinzugelernt. --Diwas (Diskussion) 03:14, 24. Feb. 2020 (CET)

Archivierung dieses Abschnittes wurde gewünscht von: Kein Einstein (Diskussion) 11:50, 29. Feb. 2020 (CET)

Bearbeitungen in der Nacht von Sonntag auf Montag

Die vergangene Nacht hatte der sachlichen Richtigkeit unseres Artikels nicht gutgetan.

„wirkt dann wegen der größeren Einsinktiefe mehr Auftriebskraft, wegen des erhöhten Gewichts aber“

• Das ist missverständlich.
• Das stärker beladene Schiff ist ein anderer Körper, hat eine andere Gewichtskraft und, sofern schwimend, eine betragsmäßig dann wieder genauso große Auftriebskraft.
• Es sind aber zwei unterschiedliche Körper, zwei ganz andere Situationen, auch wenn vielleicht noch derselbe Name an dem Fährschiff dransteht.
• Deshalb ist diese Erörterung maximal verunglückt.
• Der Abschlusssatz lautet dann: „das Gewicht der Fähre bleibt konstant“
  • Nein, die Fähre hat wegen mehr Autos mehr Masse bekommen, deshalb größere Gewichtskraft, und dementsprechend in gleichem Maße gestiegene Auftriebskraft. Die Erörterung mit den Drücken dazwischen ist hier Nonsens.

„wird der (hydro)statische Auftrieb fälschlicherweise mit der Auftriebskraft gleichgesetzt“

• Da ist nichts „fälschlicherweise“.
• Unterschieden werden könnte höchstens das Phänomen Auftrieb von der Auftriebskraft, was hier auch schon mehrfach klargestellt wurde; die Vokabel „Auftrieb“ wird landläufig auch als Kurzwort für „Auftriebskraft“ verwendet.
• Hydrostatischer Auftrieb und Auftriebskraft sind identisch, sofern man in beiden Fällen eine Kraft meint.
  • Die sonstige Wortklauberei des Absatzes ist gegenstandslos.

Einen „optisch erkennbaren Auftrieb“ oder „sichtbaren Auftrieb“ gibt es nicht, dass ist konfuses Kindergartengeplapper und hat in unserem Artikel nichts verloren.

• Zu beobachten wäre lediglich, dass ein Körper stabil an der Grenzfläche zweier Medien schwimmt.
• Dabei müssen mehrere Medien (beliebig oft) horizontal geschichtet mit unterschiedlicher Dichte vorliegen; die dichteren unten.
  • Die unterschiedliche Dichte kann aus einer völlig anderen chemischen Substanz herrühren, oder anderer Temperatur oder anderem Salzgehalt usw.
  • Die Medien müssen hinreichend die Anforderungen an Fluide erfüllen und sollen in unserem statischen Fall praktisch in Ruhe sein.
• Notwendig wäre, dass auf eine leichte Kraftwirkung von oben, einen Stupser, der Körper auch eine Rückstellkraft erfährt und sich anschließend sofort wieder in die alte Ruhelage begibt.
  • Macht er das nicht, dann ist die umgebende Dichte gleichverteilt und jede vertikale Position ist möglich; es liegt keine Grenzfläche zweier Medien vor.
  • Das wäre bei einem Heißluftballon in homogenem Temperaturbereich der Fall; dann liegt es am Zufall oder leichten Windstößen, welche vertikale Höhe gerade eingenommen wird.
• Beobachtet werden kann nur: Schwimmt, geht unter, steigt in die Höhe.
  • Etwas anderes oder einen optischen oder sichtbaren Auftrieb gibt es nicht.

„eine scheinbare Verminderung der Gewichtskraft tritt aber nur zusammen mit der Gewichtskraft des Kaörpers auf“

• Das suggeriert, es wäre eine Gewichtskraft des Körpers für den Auftrieb erforderlich.
  • Das ist schlicht falsch.
  • Der Auftrieb liegt auch dann vor, wenn null Masse und null Gewichtskraft dem Körper zuzuordnen wären.
  • Nehmen wir an, unser Körper wäre von einem ultraleichten, superstabilen Kunststoff als ultradünne Membran umgeben. Im Inneren stellen wir ein Vakuum her.
  • Die Auftriebskraft ist die Gewichtskraft des verdrängten Mediums, die Masse und Gewichtskraft des Körpers dürfen Null sein.
• Es gibt drei Fälle:
  1. Auftriebskraft kleiner als Gewichtskraft des Körpers: Körper sinkt auf Boden
  2. Auftriebskraft gleich Gewichtskraft des Körpers: Körper ändert seine Vertikalposition nicht.
     • Gibt es eine Grenzfläche zweier Medien, dann schwimmt er stabil auf dieser Oberfläche. (Sofern er nicht seitlich umkippt und nicht geflutet wird.)
     • Gibt es keine Grenzfläche, dann schwebt er beliebig. Seifenblasen.
  3. Auftriebskraft größer als Gewichtskraft des Körpers: Körper steigt in die Höhe; vielleicht ein Wetterballon.
• Im ersten und dritten Fall würde man nicht von einem statischen Gesamtzustand sprechen.
  • In allen drei Fällen liegt jedoch der hydrostatische Auftrieb vor, weil sich dieser lediglich aus den Dichte- und Druckverhältnissen des unbewegten umgebenden Mediums begründet.
• Ein vierter Fall wäre noch eine zusätzliche äußere Kraft; bisher hatten wir immer stillschweigend vorausgesetzt, der Körper wäre frei im Medium.
  • Das gesunkene Wrack erfährt eine Stützkraft durch den Boden, gleichzeitig haben seine Strukturen (Stahl- oder Holzrumpf, jedoch leck) immer noch ihren statischen Auftrieb.
  • Der Heliumballon an seiner Schnur wird von dieser festgehalten und dadurch am Aufsteigen gehindert, damit er nicht seine umweltschädliche Mikroplastik-Wirkung auf die Tierwelt entfalten kann.
• In der gängigen Formulierung des Archimedischen Prinzips kommt die Gewichtskraft des Körpers überhaupt nicht vor.
  • Es werden nur zwei Bilanzgrößen miteinander verglichen:
    1. Gewichtskraft des verdrängten Mediums.
    2. Von der Konstellation bewirkte Auftriebskraft.
  • Es wird festgestellt, dass beide den gleichen Betrag haben (sie haben entgegengesetzte Richtung).
  • Ist gleichzeitig die Definition der Auftriebskraft.
  • Mehr ist nicht.

Eine Zuordnung von „Ursache“ und „Wirkung“ zu physikalischen Beobachtungen ist immer problematisch.

• Das ist eine menschengemachte Perspektive.
• Davon weiß die Natur nichts. Die weiß sowieso von nix.
• Die Natur kann durch Gleichungen beschrieben werden, und in denen steht: Das eine hat den gleichen Zahlenwert wie das andere.
• Von den Absichten des Menschen hängt es ab, den einen Effekt bewusst herbeizuführen, um den zugehörigen zu bewirken. Der Natur ist es egal; sie sagt nur etwas über das Gesamtsystem. Je nachdem was vom Menschen direkt veranlasst wurde, nennt er dies die Ursache. Geht genauso andersrum.

Solche Artikelbearbeitungen sind extrem anstrengend. Ahoi --Schiefbauer (Diskussion) 10:54, 24. Feb. 2020 (CET)

@Schiefbauer: Gut Ausgearbeitet! Stimme in allen(!) Punkten zu. Ich finde ebenfalls Version Spezial:Permanenter_Link/197086922 besser als die jetzige. Vermutlich ist es besser wir alle (alle Autoren) versuchen die Intention von allen Edits seither in die alte Version Spezial:Permanenter_Link/197086922 einzuarbeiten, sofern sinnvoll. Anstatt zu versuchen eine mMn inhaltlich falsche/irreführende Version irgendwie korrektzubiegen.  — Johannes Kalliauer - Diskussion | Beiträge 12:40, 24. Feb. 2020 (CET)

"Der Abschlusssatz lautet dann: „das Gewicht der Fähre bleibt konstant“ - Nein, die Fähre hat wegen mehr Autos mehr Masse bekommen,"

Das check ich jetzt nicht, wenn die beladene Fähre von der Nordsee auf die Elbe fährt, woher kommt dann das Auto geflogen? --Maschinist1968 (Diskussion) 12:51, 24. Feb. 2020 (CET)

Der Absatz im Artikel fängt an mit „Auf ein voll beladenes Fährschiff, das tiefer ins Wasser einsinkt und mehr Wasser verdrängt als im unbeladenen Zustand“.

@Maschinist1968: Die Aussage „das Gewicht der Fähre bleibt konstant“ stammt von Maschinist1968 in Spezial:Diff/197107488.

Die aktuelle Version ist so missverständlich, dass wir die nicht sinnvoll fehlerfrei biegen können; ich bin für ein Zurücksetzen auf Spezial:Permanenter_Link/197086922.

 — Johannes Kalliauer - Diskussion | Beiträge 13:12, 24. Feb. 2020 (CET)

Archivierung dieses Abschnittes wurde gewünscht von: Kein Einstein (Diskussion) 11:51, 29. Feb. 2020 (CET)

sichtbare Auftrieb

Eine wissenschaftliche Suche nach "sichtbarer Auftrieb" hat zu keinen einzigen Treffer (außer einem in der Sozialforschung) geführt. Ich bezeifle das dieser Terminus existiert (WP:TF). Außerdem ist das was als sichtbare Auftrieb bezeichnet wird (den man wohl eher als effektiven Auftrieb bezeichnen würde) immer ident mit Null, wenn sich der Körper in Ruhe befindet. Wenn sich der Körper nicht in Ruhe befindet ist mMn out of scope für statischer Auftrieb.  — Johannes Kalliauer - Diskussion | Beiträge 09:05, 23. Feb. 2020 (CET)

Bezüglich:

Fälschlicherweise wird oft der „sichtbare Auftrieb“ eines Körpers, also die resultierende Kraft aus Gewichtskraft des Körpers und der Auftriebskraft, als „statischer Auftrieb“ angesehen. 

...darum stand der Ausdruck auch unter Anführungszeichen! Nicht verständlich? Auf zahlreichen Websites wird das Gesehene als Auftrieb beschrieben, weil umgangssprachlich es so gehandhabt wird. Diese Diskrepanz gehört beschrieben! Es können auch andere Worte sein. Das Beispiel mit dem Schiff allein ist zuwenig.

--Maschinist1968 (Diskussion) 10:39, 23. Feb. 2020 (CET)

Dann kann man das auch einfacher schreiben

Fälschlicherweise wird oft der „sichtbare Auftrieb“ eines Körpers, also eine Kraft mit dem Betrag null, als „statischer Auftrieb“ angesehen. 

Als nächstes beschreibt man dann Gleichgewicht als

Die Summe alle Kräfte ist der „sichtbare Auftrieb“.

„Auf zahlreichen Websites wird das Gesehene als Auftrieb beschrieben, weil umgangssprachlich es so gehandhabt wird.“

Kannst du diese Webseiten aufzeigen, ich kenne keine solche?

Es gibt viel Blödsinn in Wikipedia und noch mehr in Literatur und vermutlich am meisten auf div. Webseiten.

In der Wikipedia kann man Blödsinn leicht korrigiern, in der Sekudärliterautur muss man seinen Hausverstand verwenden ob man das nur eingeschränkt anwenden kann, und auf unseriosen Webseiten muss man damit rechnen, dass man Falschinformationen bekommt.

 — Johannes Kalliauer - Diskussion | Beiträge 10:59, 23. Feb. 2020 (CET)

Diese Website unterscheidet zwischen Auftriebskraft und Auftrieb, vl. sollte WP das auch tun? --Maschinist1968 (Diskussion) 11:05, 23. Feb. 2020 (CET)

Beispielsweise:

Der statische Auftrieb bewirkt, dass Schiffe schwimmen, Heißluftballone schweben, in Wasser Luftblasen bzw. in Luft heiße Abgase und Gewitterwolken aufsteigen. Er wird durch die Auftriebskraft verursacht, eine der Schwerkraft entgegengesetzte Kraft, die auf einen ruhenden Körper, der in eine Flüssigkeit oder ein Gas eintaucht, einwirkt.

--Maschinist1968 (Diskussion) 11:21, 23. Feb. 2020 (CET)

@Maschinist1968: (Bearbeitungskonflikt) Sobald es effektiven Auftrieb gibt (Also sich der Heißluftballon nach oben bewegt) ist es nicht mehr statisch, daher imho nicht hier.  — Johannes Kalliauer - Diskussion | Beiträge 11:22, 23. Feb. 2020 (CET) zurückgezogen  — Johannes Kalliauer - Diskussion | Beiträge 11:28, 23. Feb. 2020 (CET)

@Maschinist1968: Wo unterscheidet Diese Website zwischen Auftriebskraft und Auftrieb? Der oben genannte Satz zeigt genau das auf was derzeit hier im Artikel beschrieben wird.  — Johannes Kalliauer - Diskussion | Beiträge 11:28, 23. Feb. 2020 (CET)

...im 2. Absatz, fett gedruckt.--Maschinist1968 (Diskussion) 11:33, 23. Feb. 2020 (CET)

Ich lese da:

In der Flüssigkeit bzw. in dem Gas muss also der Gewichtskraft des Körpers eine Kraft entgegenwirken. Diese Kraft nennt man Auftriebskraft , die Erscheinung selbst Auftrieb

--Maschinist1968 (Diskussion) 11:40, 23. Feb. 2020 (CET)

@Maschinist1968: Die Erscheinung dass eine Auftriebskraft herscht nennt man Auftrieb. Also bedeuten sie das Gleiche, das eine ist die Kraft das andere der Effekt den diese Kraft hervorruft.  — Johannes Kalliauer - Diskussion | Beiträge 11:55, 23. Feb. 2020 (CET)

Nein, der Auftrieb ist die Wirkung der Auftriebskraft, wegschleudern ist die Wirkung der Zentrifugalkraft, hinunterfallen oder der freie Fall sind die Wirkung der Schwerkraft,..

Bedeuten alle nicht das gleiche.

Der statische Auftrieb bewirkt, dass Schiffe schwimmen, Heißluftballone schweben, in Wasser Luftblasen bzw. in Luft heiße Abgase und Gewitterwolken aufsteigen. Er wird durch die Auftriebskraft verursacht, eine der Schwerkraft entgegengesetzte Kraft, die auf einen ruhenden Körper, der in eine Flüssigkeit oder ein Gas eintaucht, einwirkt.

Gruß --Maschinist1968 (Diskussion) 20:12, 23. Feb. 2020 (CET)

@Maschinist1968: Das ist ein Henne-Ei Problem, ähnlich wie drückt das Haus auf den Boden oder der Boden gegen das Haus. Ersetzte mal statische Auftrieb mit Auftriebskraft und dann ließt sich der Satz so:

Die Auftriebskraft bewirkt, dass Schiffe schwimmen, Heißluftballone schweben, in Wasser Luftblasen bzw. in Luft heiße Abgase und Gewitterwolken aufsteigen. Sie entspricht der Auftriebskraft, die, eine der Schwerkraft entgegengesetzte Kraft verursacht, die auf einen ruhenden Körper, der in eine Flüssigkeit oder ein Gas eintaucht, einwirkt.

Insofern spezifiziert dieser Satz nicht welche Bedeutung er hat.

Wenn du einen Beleg finden kannst der explizit sagt, dass der Auftrieb=Auftriebskraft-Gewichtskraft ist, können wir weiterreden, aber so ist es müssig. Solange das nicht ist müssen wir uns darüber ausschweigen. Wenn du einen Beleg findest, können wir sagen, dass es in der Literatur uneinheitlich geregelt ist und man es aus dem Zusammenhang herauslesen können muss. Wenn steht:

Wenn der Auftrieb negativ ist sinkt der Heißluftballon.

heißt das Auftrieb=Auftriebskraft-Gewichtskraft, wenn aber steht

Der Auftrieb kleiner als die Gewichtskraft sinkt der Heißluftballon.

heißt das dass Auftrieb=Auftriebskraft ist. Ich kann mir vorstellen, dass es beide Bedeutungen geben kann. Mir scheint zweiteres geläufiger zu sein und, zweitens glaube ich dass das Auftreten der Aufgriebskraft als Auftrieb bezeichnet wird, aber der Auftrieb sich nicht quantifizieren lässt, daher sind sind mMn meine beide Beispiele eine falsche Verwendung des Begriffes Auftrieb.

 — Johannes Kalliauer - Diskussion | Beiträge 10:09, 24. Feb. 2020 (CET)

Archivierung dieses Abschnittes wurde gewünscht von: Hadhuey (Diskussion) 11:02, 1. Mär. 2020 (CET)

Katamaran

Als Laie erlaube ich mir die Bemerkung, dass ich den Abschnitt über den Auftrieb von Schiffen nicht so recht verstehe. Vielleicht könnte man ihn eindeutiger und klarer formulieren. Ich verstehe, dass das Gesamtgewicht des Schiffes dem Gesamtgewicht des verdrängten Wassers entspricht ("actio = reactio"). Warum jetzt aber nur der eingetauchte Teil des Schiffes seinen Auftrieb bewirken soll, obwohl angeblich - so muss man den Text verstehen - s ä m t l i c h e Hohlräume des Schiffes zur relativ geringeren Dichte (?) des physikalischen Körpers "Schiff" beitragen, bleibt unklar. - Und in diesem Zusammenhang sollte man auch erklären, wie der scheinbar (?) grössere Auftrieb des Katamarans oder gar des Trimarans zu erklären ist, denn er taucht erheblich weniger ins Wasser ein, so dass er viel schneller fahren kann als ein sog. Verdränger-Schiff. (Vermutlich kommt man dann nicht mehr um die zusätzliche Darstellung des Begriffs der von Wasser "benetzten" Fläche harum. - Diesen Begriff müsste man dann wohl aber auch bei der Darstellung des Auftriebs von Schiffen benutzen und erklären.) <kreuz des südens>

Anders ausgedrückt: Man müsste erklären, dass ein Schiff zwar genau so viel Wasser verdrängt wie es wiegt, dass sich sein Gewicht aber auf eine grosse Wasserfläche verteilt. Man könnte dies an einer Untertasse aus normal dünnem Porzellan im Spülbecken verdeutlichen: Lässt man die Untertasse senkrecht ins Wasser gleiten, versinkt sie sofort - denn Porzellan ist schwerer als Wasser. Setzt man sie aber vorsichtig horizontal auf die Wasseroberfläche, schwimmt sie. - Und diesen Effekt müsste man in "laienhafter" Sprache verdeutlichen. <kreuz des südens>

Hallo, beim statischen Auftrieb, also wenn das Schiff sich nicht bewegt, ist das Volumen des eingetauchten Teils des Schiffes und seine Masse im Gleichgewicht zum verdrängten Wasser, (nicht das Gesamtvolumen des Schiffes).

Bei einigen Schiffen auch noch dynamischer Auftrieb ins Spiel, sobald sie sich im Wasser bewegen. Dann wirken zusätzliche Kräfte durch die Strömung, die z.B. den Rumpf geschwindigkeitsabhängig ein klein wenig aus dem Wasser heben können. Das nennt man beim Schiff gleiten. Schau dir mal den Artikel Verdränger und Gleiter an. Grüße Hadhuey (nicht signierter Beitrag von Hadhuey (Diskussion | Beiträge) 10:00, 1. Dez. 2008‎)

Den Vergleich "Lässt man die Untertasse senkrecht ins Wasser gleiten, versinkt sie sofort - denn Porzellan ist schwerer als Wasser. Setzt man sie aber vorsichtig horizontal auf die Wasseroberfläche, schwimmt sie." könnte als anschauliches Beispiel in den Artikel eingebaut werden. --Maschinist1968 (Diskussion) 15:09, 2. Mär. 2020 (CET)

Gleiter

Gleiter in Bewegung

@Maschinist1968: Ich bezeichne die Untertasse einfach als Salatschüssel, weil's da anschaulicher ist. Dein Beispiel hat damit zu tun, dass wenn ich eine Salatschüssel quer ins Wasser gebe, dass nur das Mateiralvolumen der Schüssel verdrängt wird -->untergeht, aber wenn ich sie hineinlege, dann verdrängt sie das Ganze Schüsselluftvolumen -->schwimmt. Da Schiffe (im gegensatz zu offenen Booten) idR geschlossene Hohlkammern haben, können sie zwar umkippen, aber nicht untergehen, daher hier nicht anwendbar.

Man muss bedenken, dass die genannten schiffe wahnsinnig leicht gebaut sind.

Und wie @Hadhuey: gesagt hat es gibt Gleiter die so schnell fahren, dass sich Wasser mehr wie ein Festkörper als wie ein Fluid verhällt.

Frage wurde mMn bereits vor ~11,75Jahren zufriedenstellend beantwortet, daher wieder {{Erledigt}}.

 — Johannes Kalliauer - Diskussion | Beiträge 20:05, 2. Mär. 2020 (CET)

Archivierung dieses Abschnittes wurde gewünscht von: Hadhuey (Diskussion) und  — Johannes Kalliauer - Diskussion | Beiträge 20:05, 2. Mär. 2020 (CET)-

Wasserläufer

Wasserläufer beim ... Vorlage:Nsfw

Lichtbrechung durch Dellen

Auftrieb in rot markiert

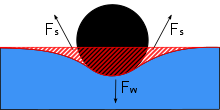
Wasserläufer nutzen die Oberflächenspannung aus um nicht in das Wasser einzudringen, hierbei üben Sie einen Druck auf die Wasseroberfläche aus, sodass sich das Wasser "eindellt". Das Eindringvolumen entspricht dem Dellenvolumen. Durch die feinen Haare spannen sie ein "offenes Gefäß" auf Wasser wie ein geschlosses Gefäß Wasser verdrängen kann. Aufgrund der Oberflächenspannung dringt kein Wasser in das "offene Gefäß".  — Johannes Kalliauer - Diskussion | Beiträge 13:02, 1. Mär. 2020 (CET)

Von User:Diwas geändert  — Johannes Kalliauer - Diskussion | Beiträge 22:20, 1. Mär. 2020 (CET)

Archivierung dieses Abschnittes wurde gewünscht von: Hadhuey (Diskussion) 12:06, 2. Mär. 2020 (CET)

Wenn es entsprechende Belege gibt, wäre ein eigener Abschnitt zum Zusammenwirken von Oberflächenspannung und Auftriebskraft denkbar, das ist aber optional. --Diwas (Diskussion) 02:31, 4. Mär. 2020 (CET)

falsche Herleitung

Gedankenexperiment: Ein Becher Wasser, ein gläserner Hohlkörper und ein Eisenklotz, beide mit demselben Volumen. Der Eisenklotz wird im Wasser untergehen, der Hohlkörper schwimmt.

WP: Auf die Unterseite des Körpers wirkt ein höherer Druck als auf die Oberseite.

Auf beide Körper wirkt auf die Unterseite ein höherer Druck als auf die Oberseite und warum hat dann der Eisenklotz weniger Auftrieb? Und wenn der Eisenklotz eine senkrecht hängende Eisenplatte gleichen Volumens wäre, wäre der Höhenunterschied noch größer und trotzdem geht sie unter.

Der hydrostatische Druck ist definiert nach dem Pascal'schen Gesetz:

$p(h)=\rho gh+p_{0}$

Das Schaubild ist insofern verwirrend, weil der hydrostatische Druck nicht nur auf den Boden wirkt, sondern auch auf die Gefäßwand und auf jeden eingetauchten Körper, aber je nach Tiefe unterschiedlich ist. (Änderungswunsch gerade bei Wikipedia:Grafikwerkstatt#Hydrostatischer Druck )

So entspricht beispielsweise der auf einen Taucher wirkende Wasserdruck in einem ruhenden Gewässer der Summe

aus dem Luftdruck, der auf die Gewässeroberfläche wirkt plus dem hydrostatischen Druck des Wassers selbst.

Der Eisenklotz übt auf das Wasser auch einen Gewichtsdruck aus,

$p(h)=\rho gh+p_{0}+p_{E}$

Und der gläserne Körper ebenso:

$p(h)=\rho gh+p_{0}+p_{G}$

Das verdrängte Wasser wird auf die Seite geschoben, hat dort keinen Platz, also wird es im Becher nach oben geschoben und der Wasserspiegel im Becher steigt (das hat auch Archimedes gewusst). Gemäß dem Pascal'schen Paradoxon hängt der hydrostatische Druck nicht vom Wasservolumen abhängt sondern nur von der gestiegenen Füllhöhe, also dem Gewichtsdruck des nach oben verdrängten Wassers.

$p(h)=\rho gh+p_{0}+p_{W}$

Wir lassen den Wasserstand konstant:

Das ergibt für das verdrängte Wasser in der grafischen Statik einen Kraftpfeil nach oben und für jeden eingetauchten Körper einen Kraftpfeil nach unten. Der statische Auftrieb ist die dann resultierende Kraft.

Der statische Auftrieb (des Eisenkörpers oder des gläsernen Körpers entspricht der Gewichtskraft des Körpers abzüglich der Gewichtskraft des verdrängten Fluids.

»Die Ursache für die Auftriebskraft eines Körpers liegt in der Verringerung des hydrostatischen Drucks, den das verdrängte Wasser nun nicht mehr ausübt.«

Bei nicht konstantem Wasserstand erhöht sich der hydrostatische Druck, der auf die Unterseite des eingetauchten Gegenstands wirkt um den Gewichtsdruck der höheren Wassersäule, also des verdrängten Fluids.

Der hydrostatische Druck wirkt ja nach allen Seiten, sonst bräuchte ja ein U-Boot auf der Unterseite nicht wasserdicht sein oder deshalb wird der Luftkörper in einer Taucherglocke zusammengepresst...

Der statische Auftrieb (des Eisenkörpers oder des gläsernen Körpers entspricht der Gewichtskraft des Körpers abzüglich der Gewichtskraft des verdrängten Fluids.

Darum kann der ganze falsche Sermon im Artikel entfernt und ersetzt werden

alte Version

Textvorschlag

== Ursache und Größe == Die Ursache für die Auftriebskraft liegt darin, dass der hydrostatische Druck von der Höhe des betrachteten Orts abhängt. Auf die Unterseite des Körpers wirkt ein höherer Druck als auf die Oberseite. Wenn kein Fluid an die Unterseite des Körpers gelangen kann, dann gilt das archimedische Prinzip nicht. In diesem Fall kann sich dennoch eine Auftriebskraft ergeben. Der statische Auftrieb entspricht der Gewichtskraft der entsprechenden Verformung des Fluids. Das Fluid kann eine Flüssigkeit wie Wasser oder auch ein Gas wie etwa Luft sein. Dieser Zusammenhang ist als archimedisches Prinzip bekannt. Auf einen Körper, der in ein Fluid mit der Dichte $\rho$ getaucht ist, wirkt also eine Auftriebskraft $F_{\mathrm {A} }$ mit dem Betrag: (…)

== Ursache und Größe == Der statische Auftrieb eines Körpers in einem Fluid entspricht der Gewichtskraft des Körpers abzüglich der Gewichtskraft des verdrängten Fluids. Das Fluid kann eine Flüssigkeit wie Wasser oder auch ein Gas wie etwa Luft sein. Dieser Zusammenhang ist als archimedisches Prinzip bekannt. Die Ursache für die Auftriebskraft eines Körpers liegt im hydrostatischen Druck, den das verdrängte Fluid ausübt. Ist der hydrostatische Gegendruck geringer als der Gewichtsdruck des eingetauchten Körpers, so sinkt der Gegenstand ein, ist er höher, so schwimmt er im Fluid. Auf einen Körper, der in ein Fluid mit der Dichte $\rho$ getaucht ist, wirkt also eine Auftriebskraft $F_{\mathrm {A} }$ mit dem Betrag: (…)

Der Trugschluss resultiert daraus, dass

• Auftriebskraft
• mit dem Auftrieb gleichgesetzt / verwechselt wird.

Die Auftriebskraft ist der hydrostatische Druck an der Unterseite.

Der Auftrieb ist die Summe der Kräfte aus der hydrostatischen Druckdifferenz (= Differenz unten minus oben) plus Gewichtskraft des Gegenstandes minus Gewichtskraft des verdrängten Wasserkörpers.

Siehe auch (Douglas C. Giancoli: Physik. ISBN 3868940235 S. 460 (eingeschränkte Vorschau in der Google-Buchsuche)) wo in der Abbildung die Gewichtskraftpfeile des Gegenstandes und des verdrängten Wassers weggelassen wurden (weil es ja um die Auftriebskraft geht), die aber für den Auftrieb wesentlich sind, sonst wäre ja der Auftrieb unabhängig vom Gewicht…

…wenn es nicht Physikbücher gäbe (Hans Moor: Physikalische Grundlagen. ISBN 3519050501 (eingeschränkte Vorschau in der Google-Buchsuche), die in die Auftriebskraft Dichte und Gewicht einbeziehen würden…

… und solche, die die Auftriebskraft mit der Gewichtskraft des verdrängten Wasservolumens gleichsetzen. (Physik. S. 7 (eingeschränkte Vorschau in der Google-Buchsuche))

--Maschinist1968 (Diskussion) 09:15, 17. Feb. 2020 (CET)

fehlerhafte Kritik

Ich stimme weder deiner Analyse zu noch möchte ich deinen Textvorschlag umgesetzt sehen. Also müsen wir diskutieren.
Ich folge deinem Gedankenexperiment. Du schreibst: „Auf beide Körper wirkt auf die Unterseite ein höherer Druck als auf die Oberseite und warum hat dann der Eisenklotz weniger Auftrieb? Und wenn der Eisenklotz eine senkrecht hängende Eisenplatte gleichen Volumens wäre, wäre der Höhenunterschied noch größer und trotzdem geht sie unter.“ - Und ich verstehe nur mit Mühe, was du vielleicht meinst. Ist für dich "Auftrieb" so etwas wie "relativer (sic!) Gewichtskraftverlust"? So wie ich Auftrieb verstehe und in Literatur finde (übrigens in allen drei von dir verlinkten Büchern) ist Auftrieb und Auftriebskraft in der Regel synonym, wenn man sich sprachlich etwas mehr Mühe gibt ist Auftrieb das Phänomen, dass (durch die Auftriebskraft) weniger Gewichtskraft vorhanden zu sein scheint. Also "Gewichtskraftverlust" - aber der Eisenklotz deines Beispiels hat mehr (!) Auftrieb als der Hohlkörper (da er ganz eintaucht), nicht weniger. Das er dennoch untertaucht liegt an der größeren Gewichtskraft als beim Hohlkörper.
Zu deinem zweiten Einwand: Bei einer senkrecht hängenden Eisenplatte wäre zwar der Höhenunterschied größer, es geht aber nicht nur um den Druck (mir scheint, du setzt Druck und Kraft gleich?) sondern es geht um die aufgrund des Drucks wirkende Kraft. Und da ergibt sich zwar eine größere Druckdifferenz aber gleichzeitig weniger Fläche (oben wie unten, bei der Platte verglichen mit dem Klotz), sodass die Kraft (vulgo: Auftrieb) beidesmal gleich ist.
Das Verständnis deines Beispiels sollten wir erst klären. Aber ich kann mir die Anmerkung nicht verkneifen, dass die von dir kritisierte "alte Version" (die natürlich besser formuliert werden kann) der Erklärung entspricht, die gemäß diverser Lehrplänen den Schülern vorgesetzt wird. Gruß Kein Einstein (Diskussion) 21:29, 17. Feb. 2020 (CET)

Ich muss da Kein Einstein leider zustimmen. Du kannst Auftrieb nicht mit Beispielen betrachen, bei denen die Flüssigkeit "im Becher hochgedrückt wird". Du kannst die Auftriebskraft nur "statisch" bei gleicher Eintauchtriefe betrachten und sie mit der Gewichtskraft vergleichen. Beim Hohlkörper wird sich an einer Stelle ein Gleichgewicht mit dem Gewicht des Körpers einstellen, beim Eisenklotz nicht-deshalb geht er unter. Das Gewicht hat keinen Einfluss auf die statische Auftriebskraft, die auf den Körper wirkt. Das Gewicht spielt nur eine Rolle für die verbleibende Kraft, die man aufwenden muss um den Körper unterzutauchen bzw. am Sinken zu hindern. Diese Verbleibende Kraft wird gern je nach Richtung als Auftrieb oder Abtrieb bezeichnet, sie ist aber nicht identisch mit dem statischen Auftrieb durch das Wasser. Hadhuey (Diskussion) 22:11, 17. Feb. 2020 (CET)

Vielleicht noch als Zusatz: Die Eingangsdefinition lautet: Der statische Auftrieb ist eine der Schwerkraft entgegengesetzte Kraft auf einen Körper in Flüssigkeiten oder Gasen. Dort ist die Gewichtskraft nicht einbezogen. Es ist nur die statische Auftriebskraft durch das Fluid gemeint. Vielleicht sollte man das stärker herausarbeiten, bevor mann zu Frage Schwimmen/Tauchen kommt. Hadhuey (Diskussion) 22:22, 17. Feb. 2020 (CET)

Ja es ist die Unzulänglichkeit der Sprache Diese Verbleibende Kraft wird gern je nach Richtung als Auftrieb oder Abtrieb bezeichnet und "der Eisenklotz deines Beispiels hat mehr (!) Auftrieb als der Hohlkörper". Genau diese Diskrepanz sollte Wikipedia auseinanderdröseln.

Vielleicht kannst Du @Kein Einstein: damit leben:

Die Auftriebkraft  eines Körpers in einem Fluid entspricht der Gewichtskraft des verdrängten Fluids.[(ref)Jürgen Schatz, Robert Tammer: Erste Hilfe - Chemie und Physik für Mediziner. ISBN 3662583011 S. 95 (eingeschränkte Vorschau in der Google-Buchsuche).(/ref)] Das Fluid kann eine Flüssigkeit wie Wasser oder auch ein Gas wie etwa Luft sein. Dieser Zusammenhang ist als archimedisches Prinzip bekannt. Die Gewichtskraft des verdrängten Fluids bewirkt einen hydrostatischen Druck, der als Auftrieb der Schwerkraft entgegenwirkt. Ist der hydrostatische Gegendruck geringer als der Gewichtsdruck des eingetauchten Körpers, so sinkt der Gegenstand ein, ist er höher, so schwimmt er im Fluid, ist er gleich, so ist der Gegenstand im Fluid in Schwebe. Ein voll beladenes Fährschiff, das tiefer in Wasser einsinkt als ein leeres Fährschiff gleicher Bauart hat wegen der größeren Einsinktiefe mehr Auftrieb, weil es mehr Wasser verdrängt.

@Hadhuey:"Die Gewichtskraft des verdrängten Fluids bewirkt einen hydrostatischen Druck, der als Auftrieb der Schwerkraft entgegenwirkt." ist ja gleichbedeutend mit "Die Ursache für die Auftriebskraft eines Körpers liegt im hydrostatischen Druck, den das verdrängte Fluid ausübt.", aber klarer erklärt. Oder wie oben: "Das verdrängte Wasser wird auf die Seite geschoben, hat dort keinen Platz, also wird es im Becher nach oben geschoben und der Wasserspiegel im Becher steigt (das hat auch Archimedes gewusst). Gemäß dem Pascal'schen Paradoxon hängt der hydrostatische Druck nicht vom Wasservolumen ab sondern nur von der gestiegenen Füllhöhe, also dem Gewichtsdruck des nach oben verdrängten Wassers."

Denn wie das Gewicht des verdrängten Wasservolumens Einfluß hätte, ist für Laien nicht plausibel, erst durch den um das verdrängte Volumen gestiegenen Wasserspiegel, der einen hydrostatischen Druck ausübt, wird das Ganze verständlicher.

Nimmt man einen wassergefüllten Becher und setzt ein Trinkglas hinein, so verdrängt das Trinkglas Wasservolumen, im gleichen Maße steigt der Wasserspiegel im Becher. Gemäß dem Pascal'schen Paradoxon hängt der hydrostatische Druck nicht vom Wasservolumen ab sondern nur vom Gewicht der darüberlagernden Wassersäule (plus Luftdruck). Steigt die Füllhöhe im Becher, steigt auch der hydrostatische Druck um den Betrag wie der Gewichtsdruck des nach oben verdrängten Wasservolumens.

--Maschinist1968 (Diskussion) 01:34, 18. Feb. 2020 (CET)

@Maschinist1968: Nein, mit deinem Vorschlag kann ich nicht leben. Es ist der falsche Weg, wenn du mit einem neuen Textvorschlag kommst statt dich mit meinen Argumenten auseinanderzusetzen. Immerhin glaube ich, dir in zwei zentralen Punkten fachlich widersprochen zu haben.

Dein Vorschlag leidet auch daran, dass „die Gewichtskraft des verdrängten Fluids“ nichts bewirken kann, auch keinen „hydrostatischen Druck“. Das ist sprachlich murks und ein verdrängtes Fluid ist bisweilen einfach weg (dein Becher kann auch randvoll sein zu Beginn) und dennoch muss die Formulierung funktionieren...

Bevor wir nicht fachlich dein Problem geklärt haben, sind Formulierungsvorschläge zu früh. Kein Einstein (Diskussion) 13:04, 18. Feb. 2020 (CET)

@Kein Einstein:

So, und ich soll jetzt meine Kristallkugel polieren und herausfinden, was du meinst, welche Argumente dir wichtig sind. Ich sehe, Du hast Null Interesse, den Artikel zu verbessern, und in dieser Diskussion geht's nur darum, wer recht hat / wer den Größeren hat. Mir ist meine Lebenszeit zu schade, mit unreif Pubertären in Kilo-Meta-Diskussionen deren BlaBla durchzukauen. Wenn es dir um die Sache und den Inhalt geht, dann schreibe Deine Version hier herein.

Derzeit muss ich davon ausgehen, dass dir die Version "Wenn kein Fluid an die Unterseite des Körpers gelangen kann, dann gilt das archimedische Prinzip nicht." besser passt. Das wird aber weiter oben diskutiert (Diskussion:Statischer Auftrieb#Unsinn "keine Auftriebskraft, wenn nicht Fluid an Unterseite". Oder "Die Ursache für die Auftriebskraft liegt darin, dass der hydrostatische Druck von der Höhe des betrachteten Orts abhängt." Das checkst nur du.

Sollen alle Häkler der Nation (häkeln ist österreichisch für verarschen (Duden)) ihre verqueren Ansichten in die Wikipedia schreiben. Ich kann ja in anderen Artikeln Wikipedia oder die Welt verbessern. --Maschinist1968 (Diskussion) 01:19, 19. Feb. 2020 (CET)

Das liegt möglicherweise durchaus an meiner eigenen Betriebsblindheit, aber für mich sind in den zentralen beiden Abschnitten meines Kommentars von 21:29, 17. Feb. 2020, genau zwei Kritikpunkte an deiner Argumentation (deines Textvorschlags) enthalten. Aber lassen wir's, so wurde ich zumindest mal wieder in die unreif-pubertär-Schublade gepackt, das hatte ich zuletzt vor mehreren Jahrzehnten. Mit deiner nun erfolgten Überarbeitung gehe ich mit - also ist die Welt ein wenig besser als noch gestern, was will man mehr... Gruß Kein Einstein (Diskussion) 17:39, 19. Feb. 2020 (CET)

Frage eines Laien:

• Wie berechnet sich die Auftriebskraft, wenn wie im Artikel erwähnt, die Unterseite eines Körpers, nicht vom Fluid erreicht werden kann, wo doch, bekanntermaßen? Druckkräfte immer? senkrecht, in dem Falle also seitlich oder nach unten, wirken? --Diwas (Diskussion) 04:42, 19. Feb. 2020 (CET)

Anmerkung zum Textvorschlag:

• Ist der hydrostatische Gegendruck geringer als der Gewichtsdruck des eingetauchten Körpers, so sinkt der Gegenstand ein, ist er höher, so schwimmt er im Fluid. Wenn, dann muss in der Formulierung berücksichtigt werden, dass sich der Auftrieb mit der Eintauchtiefe ändert.
• Die Zweideitigkeit von Auftrieb ist ebenfalls zu berücksichtigen. Gewöhnlich ist damit wohl eher nur die Kraft gemeint, die das Fluid ausübt, nicht die Resultierende aus Gewichtskraft und Wirkung des Fluids. --Diwas (Diskussion) 04:42, 19. Feb. 2020 (CET)

@Maschinist1968:

Also, ich bin Schiffbauingenieur, mache Hydrostatik seit Jahrzehnten, und mein Schutzpatron ist St. Archimedes.

An einer Allgemeinverständlichkeit des bisherigen Artikeltextes oder Details einer Formulierung mag poliert und geschärft werden, der Sachverhalt war und ist richtig.

Wir bilden das Druckintegral, das heißt für jedes Stückelchen Körperoberfläche des Körpers (hier mal vereinfacht als fest und starr angenommenen Körpers mit glatter geschlossener Oberfläche) fragen wir uns, welcher Druck mit welchem Betrag in welcher Richtung wirkt.

• Das wird um den gesamten Körper herum für jedes Fitzelchen gemacht.
• Bei gängigen Körpern wie etwa einem Schiff kann man sich den Bereich oberhalb der Wasseroberfläche sparen, weil sich der Luftdruck in der Höhe nicht so arg ändert und der Luftdruck auch auf die Wasseroberfläche wirkt und nur einen konstanten Summanden auf alles mitliefert.
• Außerdem heißt das statischer Auftrieb, wir nehmen also eine Situation ohne Bewegungen an; Schiff liegt ruhig, Wasseroberfläche ist spiegelglatt, keine Strömungen in Wasser oder Luft. Wenn sowas auftreten sollte, müsste das extra berechnet werden und ist nicht statisch.
• Dann nehmen wir außerdem noch an, dass Wasser inkompressibel ist, und damit folgt der Wasserdruck linear der Wassertiefe.
• Außerdem hätten Oberflächenspannungen keinen messbaren Einfluss und wir haben ein ideales Fluid (newtonsch).
• Und wenn man jetzt nach den Spielregeln der Mathematik die Druckverteilung integriert, dann hat das denselben Zahlenwert wie die Gewichtskraft des verdrängten Mediums.
• Alle horizontalen Komponenten heben sich gegenseitig auf; interessant sind nur noch die vertikalen Komponenten. Die können bei komplizierten Formen des Körpers durchaus lustig werden; es kommt aber trotzdem sauber heraus, weil bei einer Einbuchtung ein Teil vertikal nach oben Auftrieb liefert und darunter das Gegenstück wieder nach unten drückt.
• Das liefert sogar noch sauber die Spezialfälle; ein U-Boot oder Wrack liegt auf felsigem Untergrund auf, oder auf Kieselsteinen, oder in Schlamm oder Sand. Hier ist der Druck ggf. abschätzbar geringer oder Null.
• Grundsätzlich muss für saubere Rechnung das Gewässer so groß sein, dass die Höhe des Wasserspiegels nicht messbar durch den Eintauchvorgang beeinflusst wird. Bei einem Hühnerei im Zahnputzbecher stimmt das nicht mehr; dann muss man auch sauber mit den Koordinaten relativ zum jeweiligen Flüssigkeitsspiegel arbeiten, vorher und nachher. Auf den Effekt hat das keinerlei Einfluss; deshalb ist auch der letzte Textvorschlag schlicht falsch.

Den ganzen Vorgang für die typische Situation nennt man Auftrieb, genauer statischen Auftrieb; und die durch Verdrängung des umgebenden Mediums entstehende Kraftkomponente nennt man Auftriebskraft. Wer kurz angebunden ist, kann zur Auftriebskraft auch Auftrieb sagen, wie zwischen Gewicht und Gewichtskraft auch üblicherweise kein Unterschied bestünde. „Gewicht“ in haarspaltender Begrifflichkeit wäre eine Eigenschaft nichtrelativistisch massebehafteter Körper in einem Gravitationsfeld; geschenkt.

Der im Textvorschlag eingebrachte „Gewichtsdruck des eingetauchten Körpers“ ist barer Unsinn; sowas gibt es nicht und hat auch in unserem Artikel nix am Suchen.

Alle Betrachtungen ob Holz oder Eisen oder Glas und hochkant oder quer und tief oder flach sind völlig gegenstandslos.

Die Auftriebskraft hat den gleichen Wert wie die Gewichtskraft des verdrängten Mediums. Die Darstellung „Gewichtskraft des Körpers abzüglich der Gewichtskraft des verdrängten Fluids“ ist schlicht falsch.

Wenn die Auftriebskraft größer ist als die Gewichtskraft des Körpers, dann bestünde keine statische Situation, das heißt unser U-Boot schießt nach oben und durchbricht die Wasseroberfläche. Erst danach stellt sich wieder eine statische Lage ein.

• Das gibt es auch an Land, wenn Bauwerke in schlammigem Untergrund etwas Auftrieb erfahren und mit ihrer Fundamentwanne aufschwimmen (Bonner Schürmann-Bau war so ein Millionengrab).
• Bei einer Seemine (Ankertaumine) bindet man einen Schwimmkörper unterhalb der Wasseroberfläche an einen Grundanker. Das Dings würde gern zur Wasseroberfläche aufsteigen, weil die Auftriebskraft größer ist als die Gewichtskraft des Körpers, aber auf das Ankertau wird eine Zugkraft ausgeübt und mit dem Anker zusammen ergibt sich wieder ein statischer Zustand.
• Alle Betrachtungen gelten analog auch ganz sauber für einen Heißluftballon in kalter Umgebungsluft.

„also wird es im Becher nach oben geschoben“ – das ist Nonsens; dann muss auch sauber mit dem Wasserspiegel in der veränderten Konstellation gerechnet werden, und nicht eine völlig andere Situation.

Zusammengefasst: Unsere derzeitige Textfassung ist inhaltlich richtig und nicht der angeblich „ganze falsche Sermon“ – letztere Charakterisierung träfe allerdings auf die Vorschläge zu.

• Ursache ist eine Differenz statischer Druckkomponenten, die sauber zusammengezählt genau die Gewichtskraft des verdrängten Mediums ergeben. Nur und nur über diese Betrachtung lassen sich alle Sonderfälle korrekt erfassen. Damit funktioniert es sogar, wenn das umgebende Medium nicht inkompressibel wäre, und wenn es mit unterschiedlichen Dichten (Temperatur, Salzgehalt) keine lineare hydrostatische Druckverteilung gibt. Es funktioniert sogar noch, wenn Dynamik im Spiel wäre, heißt dann aber nicht mehr statischer Auftrieb.
• Hinterher, nachdem wir für jedes Fitzelchen die Druckwirkung des verdrängten Mediums aufsummiert hatten, bekommen wir eine einzige, integrale, Größe heraus, nämlich die Auftriebskraft. Mit dieser auf einen einzelnen Zahlenwert zusammengefassten Bilanzgröße lassen sich aber keinerlei Betrachtungen mehr für unterschiedliche Fälle anstellen; das geht nur, wenn man das Fitzelchen für Fitzelchen, somit differenziell, betrachtet.

Basierend darauf mag man umseitig einzelne Formulierungen klarer und präziser und unmissverständlicher herausarbeiten; aber der Effekt ist korrekt dargestellt, mitnichten ein „Trugschluss“, wohingegen die gegen die angeblich „falsche Herleitung“ vorgetragene Argumentation in sich völlig verwirrt ist.

@Diwas:

• Der Kniff liegt in „Druckintegral“, das heißt für jedes Stückelchen Körperoberfläche summieren wir auf, welcher Druck mit welchem Betrag in welcher Richtung wirkt.
  • Wenn Teile der Körperoberfläche auf dem Grund aufsitzen, dann fallen diese mit Null Druck oder mit einem abgeschätzt reduziertem Druck aus der Saldierung heraus.
  • Das passiert bei Wracks, oder auch bei U-Booten mit Grundberührung.
  • Es hängt von der Art des Meeresbodens ab: Modder, Sand, grobe Kiesel, große Felsbrocken.
  • Bei harten spitzen unterstützenden Elementen sind die paar Kontaktflächen zu vernachlässigen; Schlick und Sand absorbieren durch ihre Zähigkeit vielleicht die Hälfte, können aber auf kurze Distanzen noch den Wasserdruck durchreichen, jedoch nicht mehr auf mehrere Meter. Es gibt experimentell ermittelte Tabellen dafür, bei welchem Untergrund man welche Flächenbereiche prozentual abziehen muss. Maßgeblich ist die Fluid-Definition: kann in Ruhe keine Schubspannungen aufnehmen – Schmodder kann das jedoch und reicht den Wasserdruck der Umgebung dann nicht mehr durch.
  • Für U-Boote ist das im Allgemeinen das Aus: Wenn es auf Sandboden aufliegt, dann ist die erreichbare Auftriebsreserve dafür nicht ausgelegt und es kommt nie wieder hoch. Weiß man auch bei der Bergung von Wracks im Schlick – die kriegt man oft nicht mal dann mehr raus, wenn der ganze Rumpf durch Pumpen mit Luft gefüllt ist. Weil wenn Oberkante Wrack tiefer als zehn Meter dann dort 1 bar und maximaler Auftrieb eines luftgefüllten Wracks aber auch nur entsprechend 1 bar und für jeden Meter tiefer als etwa 8–9 Meter bräuchte es zusätzliche „Leichter“; also lange Kähne backbord und steuerbord vertäut, die zusätzlich heben müssen. Deshalb wird mit Wasserstrahlen der Schlick unter dem Wrack weggespült, damit der Wasserdruck wieder von unten wirken kann. Mit Gummistiefeln in Schlamm das gleiche: Der Stiefel bleibt stecken, du kannst auf Socken weiterlaufen.
• Zweideutigkeit von Auftrieb – ja, siehe oben, Gewicht meint sowohl als Kurzwort die Gewichtskraft wie auch den Gravitationseffekt. Auftrieb meint sowohl kurz die Auftriebskraft wie auch die Konstellation und die Effekte. Es sagt auch niemand statt „ich habe ein Gewicht von 70 Kilo“, er würde mit einer Gewichtskraft von 686,7 Newton vom Planeten angezogen, oder hätte eine Eigenmasse von 70 Kilogramm. Wenn doch, sollte eine andere Fakultät einbezogen werden.

Ahoi --Schiefbauer (Diskussion) 11:09, 19. Feb. 2020 (CET)

@Schiefbauer:. Ich bin 100% einverstanden mit deinen Ausführungen und gebe zu, zeitweilig auf dem Schlauch gestanden zu sein. Mittlerweile hoffe ich, alles auseinandergedröselt zu haben (siehe Artikel). Es geht kürzer und einfacher:

"Die Auftriebskraft eines in einem Fluid eingetauchten Körpers wirkt deswegen, weil an der Unterseite der hydrostatische Druck (auch Gravitationsdruck genannt) größer ist als an der Oberseite. Die resultierende Kraft aus beiden Kräften ist der statische Auftrieb."

Gruß --Maschinist1968 (Diskussion) 14:05, 19. Feb. 2020 (CET)

Nichtsdestotrotz bin ich der Ansicht, dass bei U-Booten oder Wracks im Schlick die Adhäsionskräfte eine wesentlichere Rolle spielen, wie bei zwei Glasplatten mit Wasserschicht dazwischen. Sonst müsstest Du wenn du im tiefen Wasser am Beckenboden stehst den Auftrieb verlieren. --Maschinist1968 (Diskussion) 14:18, 19. Feb. 2020 (CET)

Danke Schiefbauer für die Erklärungen und Danke Maschinist1968 für die Verbesserungen. Insbesondere für die Entfernung der Behauptung , ohne Wasser auf der Unterseite gäbe es (statischen) Auftrieb. --Diwas (Diskussion) 16:02, 19. Feb. 2020 (CET)

Sorry mein Fehler

@Maschinist1968:Danke für Spezial:Diff/197175847, hatte ich falsch gelesen, füge stattdessen eine Neue Quelle ein.  — Johannes Kalliauer - Diskussion | Beiträge 21:50, 25. Feb. 2020 (CET)

Dan lies vorher hier 5 Zeilen drüber. --Maschinist1968 (Diskussion) 22:02, 25. Feb. 2020 (CET)

@Maschinist1968: Nein im Gewicht der Flüssigkeit steckt nicht die dichte drinnen, weil das Volumen invers zur Dichte ist (https://link.springer.com/chapter/10.1007%2F978-3-322-89910-1_16 ) damit kürzt sich die Dichte heraus.

Da ich nun auch einen mMn Schlampigkeitsfehler gemacht habe, beantworte ich wird dir diese Frage zum min 12Mal (und halte mich nicht ganz an don't feed the trols gem. Spezial:Diff/197126518), indem ich dir die Literatur herauszitiere:

„Die Bedingungen fiir das Gleichgewicht eines schwim-menden Korpers sind daher: 1. das Eigengewicht G des Kor-pers muB gleich sein dem Auftrieb der Fliissigkeit:“

– https://link.springer.com/chapter/10.1007%2F978-3-642-99127-1_4

„https://link.springer.com/content/pdf/10.1007%2F978-3-662-54847-9.pdf“

„Gesamtgewicht -P -, das Gewicht aller der Schwerkraft unterliegenden Teile des fertig ausgerüsteten und beladenen Schiffes in t, ist gleich dem Auftrieb.“

– https://link.springer.com/chapter/10.1007%2F978-3-642-50701-4_1

„Schwimmgleichgewicht ${\frac {\text{Eintauchendes V}}{\text{Gesamtvolumen}}}={\frac {\text{Dichte d. schwimmenden Körpers}}{\text{Dichte der Flüssigkeit}}}$“

– https://link.springer.com/chapter/10.1007%2F978-3-322-89910-1_16

„and for a floating object on a liquid, the weight of the displaced liquid is the weight of the object.Clifford A. Pickover: Archimedes to Hawking. Oxford University Press USA - OSO, 2008, ISBN 978-0-19-533611-5, S. 41. “

– https://en.wikipedia.org/wiki/Buoyancy

 — Johannes Kalliauer - Diskussion | Beiträge 22:31, 25. Feb. 2020 (CET)

@JoKalliauer: Und hast du auch einen Beleg für die Dichteunabhängigkeit? Die ist ja das Strittige. --Maschinist1968 (Diskussion) 12:26, 26. Feb. 2020 (CET)

@Maschinist1968: Die Auftriebskraft (wenn sie im Gleichgewicht mit der Gewichtskraft ist) ist abhängig von der Masse des Körpers aber nicht von der Dichte des Fluides. (bitte spezifiziere von welcher Dichte du redest)

Also ich soll zeigen, dass das Gewichtskraft des Schiffes nicht von der Dichte des Fluides abhängt?:

„Definition

$F_{g}=mg\,$,

where m is mass and g is local acceleration of free fall.

Remarks

• When the reference frame is Earth, this quantity comprises not only the local gravitational force, but also the local centrifugal force due to the rotation of the Earth, a force which varies with latitude.
• The effect of atmospheric buoyancy is excluded in the weight.
• In common parlance, the name "weight" continues to be used where "mass" is meant, but this practice is deprecated.“

– ISO 80000-4:2006, Quantities and units - Part 4: Mechanics (Zitiert von https://en.wikipedia.org/wiki/Weight#ISO_definition)

Sowohl die Masse $m$ als auch die Fallbeschleunigung $g$ sind (wenn man von der lokalen Massenanziehung absieht) von der Dichte des Fluides unabhängig.

Daraus folgt |F_A|=|F_G|=m*|g| und voilà: Der Betrag ist von der Dichte des Fluides unabhängig. (Das Vorzeichen/Die Orientierung&die Richtung auch, auch wenn es hier nicht gezeigt wird.)

 — Johannes Kalliauer - Diskussion | Beiträge 15:32, 26. Feb. 2020 (CET)

Ein Schiff wird kommen…

Ausgangsbasis (Version 09:01, 24. Feb. 2020‎):

Auf ein voll beladenes Fährschiff, das tiefer ins Wasser einsinkt und mehr Wasser verdrängt als im unbeladenen Zustand, wirkt dann wegen der größeren Einsinktiefe mehr Auftriebskraft, wegen des erhöhten Gewichts aber weniger hydrostatischer Auftrieb (darum sinkt es ja ein). Fährt dieses Schiff von der Nordsee in die Elbe, wechselt es also vom Salzwasser ins Süßwasser, so sinkt es im Süßwasser (das eine geringere Dichte hat als Salzwasser) wie ein Schwimmer tiefer ein. Weil die hydrostatischen Drücke wegen der verringerten Dichte des Wassers sinken, so sinkt auch die Auftriebskraft, das Gewicht der Fähre bleibt konstant, resultierend sinkt der (hydro)statische Auftrieb im leichteren Medium.

In manchen Texten wird der (hydro)statische Auftrieb fälschlicherweise mit der Auftriebskraft gleichgesetzt, eine scheinbare Verminderung der Gewichtskraft tritt aber nur zusammen mit der Gewichtskraft des Körpers auf, der (hydro)statische Auftrieb ist daher die aus Auftriebskraft und Gewichtskraft resultierende Kraft. Der (hydro)statische Auftrieb (das scheinbar verringerte Gewicht) sollte auch nicht mit dem optisch erkennbaren Auftrieb verwechselt werden.

---

Änderung (Version 10:45, 24. Feb. 2020)‎

Auf ein voll beladenes Fährschiff, das tiefer ins Wasser einsinkt und mehr Wasser verdrängt als im unbeladenen Zustand, wirkt dann wegen der größeren Einsinktiefe mehr Auftriebskraft, wegen des erhöhten Gewichts. Fährt dieses Schiff von der Nordsee in die Elbe, wechselt es also vom Salzwasser ins Süßwasser, so sinkt es im Süßwasser (das eine geringere Dichte hat als Salzwasser) tiefer ein. Weil die hydrostatischen Drücke bei gleicher Tiefe der verringerten Dichte des Wassers sinken, so würde bei gleichen Eindringvolumen auch die Auftriebskraft sinken, da aber das Gewicht der Fähre konstant bleibt, muss sinkt es tiefer ein um die gleiche Auftriebskraft zu erhalten, daher ist die Auftriebskraft von der Dichte des Fluides unabhängig.

In der Literatur wird der (hydro)statische Auftrieb mit der Auftriebskraft gleichgesetzt.

---

Irgendwie ist das kein gutes verständliches Deutsch "wirkt dann wegen der größeren Einsinktiefe mehr Auftriebskraft, wegen des erhöhten Gewichts" und "Weil die hydrostatischen Drücke bei gleicher Tiefe der verringerten Dichte des Wassers sinken, so würde bei gleichen Eindringvolumen auch die Auftriebskraft sinken". --Maschinist1968 (Diskussion) 12:33, 24. Feb. 2020 (CET)

„Ich finde ebenfalls Version Spezial:Permanenter_Link/197086922 besser als die jetzige. Vermutlich ist es besser wir alle (alle Autoren) versuchen die Intention von allen Edits seither in die alte Version einzuarbeiten, sofern sinnvoll. Anstatt zu versuchen eine mMn inhaltlich falsche/irreführende Version irgendwie korrektzubiegen.“

– JoKalliauer in Spezial:Diff/197121042

Besser es ist unverständlich als falsch. Wenn es unverständlich ist, hat man wenigsten keinen Schaden angerichtet, hingegen wenn es falsch sind, führen zu so Diskussionen wie die, die wir hier führen müssen. (Weil irgendwer dann glaubt es besser zu wissen (hat er ja in der Wikipedia so gelesen).)

 — Johannes Kalliauer - Diskussion | Beiträge 12:47, 24. Feb. 2020 (CET)

Und was hältst du davon:

Auf ein voll beladenes Fährschiff, das tiefer ins Wasser einsinkt und mehr Wasser verdrängt als im unbeladenen Zustand, wirkt dann wegen der größeren Einsinktiefe mehr Auftriebskraft, als im unbeladenen Zustand und es hat mehr Auftrieb ( = mehr Verlust an Gewichtskraft), hätte sie weniger Auftrieb, würde sie eventuell sinken. Fährt dieses beladene Schiff von der Nordsee in die Elbe, wechselt es also vom Salzwasser ins Süßwasser, so sinkt es wie auch ein Schwimmer im Süßwasser (das eine geringere Dichte hat als Salzwasser) tiefer ein. Wegen der geringeren Dichte sinken die hydrostatischen Drücke des Wassers und ebenso der Auftrieb. Weil der Verlust (!) an Gewichtskraft sinkt, wirkt nun eine höhere Gewichtskraft und deshalb sinkt die Fähre im Süßwasser weiter ein obwohl das Gewicht der Fähre konstant bleibt.

--Maschinist1968 (Diskussion) 13:17, 24. Feb. 2020 (CET)

Du musst mal runterkommen vom Irrglauben, dass die Dichte des Wassers keine Rolle spielte. Oder schwimmst Du im Süßwasser gleich untergetaucht wie in Salzwasser (oder im Toten Meer)? --Maschinist1968 (Diskussion) 13:20, 24. Feb. 2020 (CET)

Falsch, wenn ein Schiff in Gleichgewicht ist, dann kann auch der Auftrieb (genaugenommen die Auftriebskraft) nicht sinken, sofern es nicht entladen wird. Beweis steht in Statischer_Auftrieb#Ursache_und_Größe. Wie oft muss ich dir das noch sagen?

1. Spezial:Diff/197116914
2. Spezial:Diff/197081333/197083037
3. Spezial:Diff/197120357
4. Spezial:Diff/197115657
5. Spezial:Diff/197082009
6. sorry hab' nicht alle gefunden ... (und von denen von Schiefbauer und anderen zu schweigen z.B. Spezial:Diff/197104037 oder Spezial:Diff/197117199)

 — Johannes Kalliauer - Diskussion | Beiträge 13:40, 24. Feb. 2020 (CET)

Alkoholometer: hier zeigt die Skala nicht die Dichte der Flüssigkeit, sondern ihren Gehalt an Alkohol (Dichte kleiner als die von Wasser) an, darum nehmen die Skalenwerte nach oben hin zu; Ablesewert: 44 % vol. Alkohol

Bitte erkläre hier die Dichtebestimmung mithilfe des Auftriebs eines Aräometers, wenn nach deinem Irrglauben der Auftrieb nicht von der Dichte des verdrängten Volumens des verdrängten Fluids abhängt. Auf die Erklärung vom Universitätsassistenten und Doktor in spe bin ich seeeehr gespannt. --Maschinist1968 (Diskussion) 13:50, 24. Feb. 2020 (CET) @JoKalliauer:. Ich "lausche". --Maschinist1968 (Diskussion) 14:10, 24. Feb. 2020 (CET)

@Maschinist1968: Gem w:en:WP:You_must_feed_the_trolls antworte ich dir auf diese Frage ein min. 9 und somit letztes Mal, jetzt sollte die Erklärung selbst für fachfremde Admin klar sein.

Es ist zu einem gewissen Grad nicht meine Aufgabe dir Nachhilfe zu gehen, siehe Benutzer_Diskussion:Maschinist1968#Wikipedia_ist_nicht_dein(e)_NachhilfelehrerIn

Leider das falsches Bild gewählt, bei einem Gewichtsaräometer hättest du recht, aber bei einem Skalenaräometer nicht.

Bei einem Skalenaräometer hängt das Eindringvolumen von der Dichte ab aber die Auftriebskraft nicht, beim Gewichtsaräometer ist das Volumen (als Starrkörper betachtet) konstant, dort wäre es anders.

Bei einem Skalenaräometer ist das Eindringvolumen indirekt propotional zur Dichte, wenn man diese Volumen mit der Dichte multiziert, kürzt sich die Dichte heraus.

Beweis

Die Auftriebskraft hängt von der Dichte und vom Volumen ab: ${\vec {F}}_{\mathrm {A} }=-\iiint {\vec {g}}(z)\rho _{\mathrm {fluid} }(z)\mathrm {d} V_{\mathrm {Eindringung} }$ Gleichzeitig gilt Gleichgewicht: Auftriebskraft+Gewichtskraft=0. Die Gewichtskraft ist idR von der Masse des Körpers vorgegeben, daher gibt die Masse des Körpers auch die Auftriebskraft vor: ${\vec {F}}_{\mathrm {A} }=-\iiint {\vec {g}}(z)\rho _{\text{körper}}(z)\mathrm {d} V_{\text{körper}}$ Da beide Gleichungen für die Auftriebskraft notwendig sind, gilt: ${\vec {F}}_{\mathrm {A} }=-\iiint {\vec {g}}(z)\rho _{\mathrm {fluid} }(z)\mathrm {d} V_{\mathrm {Eindringung} }=-\iiint {\vec {g}}(z)\rho _{\text{körper}}(z)\mathrm {d} V_{\text{körper}}$. Für homogene Dichten und ein homogenes Schwerefeld folgt mit $V_{\mathrm {Eindringung} }(\rho _{\mathrm {fluid} })={\frac {m_{\text{körper}}}{{\rho }_{\mathrm {fluid} }}}$: $-{\vec {F}}_{\mathrm {A} }={\vec {g}}\rho _{\mathrm {fluid} }V_{\mathrm {Eindringung} }(\rho _{\mathrm {fluid} })={\vec {g}}\rho _{\mathrm {fluid} }\,{\frac {m_{\text{körper}}}{{\rho }_{\mathrm {fluid} }}}=-{\vec {g}}\,m_{\text{körper}}$, somit ist bewiesen, dass die Auftriebskraft unahängig von der Dichte ist.

Du kannst gerne konkreter nachfragen, aber diese eine Frage beantworte ich dir gem. w:en:WP:Do not feed the trolls nicht mehr, du hast jetzt schon min 9 Antworten auf diese konkrete Frage.

Ich melde niemanden auf VM-Seiten (zumindest bisher), aber du kannst es auch wie bei Setzung (Bauwesen) eskalieren lassen und es dir von einem Admin erklären lassen, aber ich glaube kaum, dass es ausführlicher/verständlicher erklärt wird.

 — Johannes Kalliauer - Diskussion | Beiträge 15:13, 24. Feb. 2020 (CET)

@JoKalliauer: Tja, so isses, wenn die Argumente ausgehen, wird der Kontrahent beschimpft (»Beleidigungen sind die Argumente jener, die über keine Argumente verfügen.« Jean-Jacques Rousseau).

…Es steht sogar in deinem Ausklapptext: (ausnahmsweise fett, nur zur Hervorhebung:) "Die Auftriebskraft hängt von der Dichte und vom Volumen ab:". Von der Dichte des Fluids und vom verdrängten Volumen. Und als Archimedisches Prinzip: "„Der statische Auftrieb eines Körpers in einem Medium ist genauso groß wie die Gewichtskraft des vom Körper verdrängten Mediums.“. 20 Liter verdrängtes Salzwasser haben ein anderes Gewicht als 20 Liter verdrängtes Süßwasser, also wird der Körper in Süßwasser stärker einsinken und dann, Hausnummer, 21 Liter verdrängen. Die resultierende Auftriebskraft ist je nach Einsinktiefe anders, weil von der Dichte abhängig.

"Bei einem Skalenaräometer hängt das Eindringvolumen von der Dichte ab aber die Auftriebskraft nicht"

• "Während bei dem Gewichts-Aräometer das eingetauchte Volumen unverändert bleibt, und daher das spezifische Gewicht dem Gewicht des eingetauchten Körpers gerade proportional ist [es wird so viel Gewicht aufgelegt, bis die Volumen-Messmarke erreicht ist]], bleibt bei dem Volumen-Aräometer das Gewicht des schwimmenden Körpers unverändert, und es ist folglich das spezifische Gewicht der verdrängten Flüssigkeit dem eingetauchten Volumen umgekehrt proportional."(Peter Münch: Lehrbuch der Physik. ISBN 3738794514 S. 90 (eingeschränkte Vorschau in der Google-Buchsuche).)
• ausnahmsweise fett, nur zur Hervorhebung: "Die Dichtebestimmung geschieht "direkt durch Bestimmung des Auftriebs, welchen ein Körper von bekanntem Raumgehalt in der Flüssigkeit erleidet (hydrostatische Methode)" (Johann Friedrich Domke, Ernst Reimerdes: Handbuch der Aräometrie. ISBN 3642512003 (eingeschränkte Vorschau in der Google-Buchsuche).) --Maschinist1968 (Diskussion) 16:08, 24. Feb. 2020 (CET)

Du checkst es eben nicht. Ich kann damit leben. Gibt solche und solche.

Drum wäre es wieder mal an der Zeit, inhaltlich zu arbeiten:

Auf ein voll beladenes Fährschiff, das tiefer ins Wasser einsinkt und mehr Wasser verdrängt als im unbeladenen Zustand, wirkt dann wegen der größeren Einsinktiefe mehr Auftriebskraft, als im unbeladenen Zustand und es hat mehr Auftrieb ( = mehr Verlust an Gewichtskraft). Fährt dieses beladene Schiff von der Nordsee in die Elbe, wechselt es also vom Salzwasser ins Süßwasser, so sinkt es im Süßwasser (das eine geringere Dichte hat als Salzwasser) tiefer ein. Wegen der geringeren Dichte nehmen die hydrostatischen Drücke des Wassers und ebenso der Auftrieb ab. Weil der Verlust (!) an Gewichtskraft geringer wird, wirkt nun eine höhere Gewichtskraft und deshalb sinkt die Fähre im Süßwasser weiter ein obwohl das Gewicht der Fähre konstant bleibt.

(nicht signierter Beitrag von Maschinist1968 (Diskussion | Beiträge) 24. Februar 2020, 16:16:36 Uhr)

Darf ich dich an die schlichte, andernorts von Schiffbauer ausgesprochene Wahrheit erinnern: Die Auftriebskraft auf das Schiff ist in Nordsee und Elbe gleich, nämlich gleich seiner (unveränderten) Gewichtskraft. Dein Text unterliegt diesem Denkfehler weiterhin. Kein Einstein (Diskussion) 16:28, 24. Feb. 2020 (CET)

@Kein Einstein:Aha, und deswegen liegt ein Schwimmer im Süßwasser tiefer/nicht tiefer als im Salzwasser und der fast obenauf schwebende Zeitungsleser im Bild ist nur ein Fotogag und die Münze am Bild schwimmt gar nicht auf Quecksilber, sondern wurde auf erstarrtes Quecksilber draufgelegt, sie hat gar keinen höheren Auftrieb… Die Auftriebskraft in Luft und in Wasser ist dann auch "gleich seiner (unveränderten) Gewichtskraft" auch gleich. Können wir die Fallschirme daheim lassen...

Apropos Stumpfsinn, der aktuelle Text lautet:

Fährt ein Schiff mit einer konstanten Masse von der Nordsee in die Elbe, wechselt es also vom Salzwasser ins Süßwasser, so sinkt es im Süßwasser (das eine geringere Dichte hat als Salzwasser) tiefer ein. Der hydrostatische Druck ist in gleicher Eindringtiefer, bei gleichen Oberflächendruck proportinal zu Dichte. Die Auftriebskraft ist bei konstanten Eindringvolumen proportional zur Dichte. Das Gewicht der Fähre ist idR unabhängig von der Dichte des Fluides und aufgrund von Gleichgewicht ist die Auftriebskraft unabhängig von der Dichte des Fluides. Um die gleiche Auftriebskraft verhällts ich das Eindringvolumen indirekt proportial zur homogenen Dichte des Fluides. Die Auftriebskraft ist somit von der Dichte des Fluides unabhängig.

Abgesehen von der "konstanten Masse" und dem "Eindringvolumen", die nicht laienfreundlich/verständlich sind, 10 Orthografiefehler/unkorrigierte Tippfehler in 6 Sätzen ("Eindringtiefer", "gleichen", "proportinal", "zu", "konstanten", "idR" (nicht barrierefrei), "von", "verhällt", "s ich", "proportial" . Sind hier wirklich Akademiker am Werk? Oder könnte, auch bei emotionalem Stress, die Vorschau benutzt werden? Oder eine Nachschau, stand ja stundenlang so drin. --Maschinist1968 (Diskussion) 16:56, 24. Feb. 2020 (CET)

Ich habe zwei Bitten an dich, Maschinist1968. Erstens trage bitte deinen Teil dazu bei, die Debatte hier nicht (wieder/mehr) ins Persönliche abgleiten zu lassen, das ist sicher nicht hilfreich und du würdest dir solche ad hominem - Argumentationen auch verbitten. Zweitens tritt geistig nochmal einen Schritt zurück und schau dir die Kräftebilanz des Schiffes an. Ich sehe (lass uns nicht über Oberflächeneffenkte, Auftrieb in Luft oder Effekte durch Strömung/Fahrtgeschwindigkeit reden) die Gewichtskraft nach unten, die Auftriebskraft nach oben. Fertig. Wären nicht beide Kräfte gleich groß, dann würde nach dem Grundgesetz der Mechanik eine Beschleunigung die Folge sein. Wir betrachten aber den statischen Fall, also das Kräftegleichgewicht und voila: Da die Gewichtskraft des Schiffes sich nicht verändert ist beidesmal die Auftriebskraft gleich groß. Du verwendest das Wort Auftrieb(skraft) nicht im Sinne der Physik und der Literatur, mein entsprechender Hinweis von letzter Woche hat dich ggf. zu wenig erreicht. Bitte lass das mal sacken. Kein Einstein (Diskussion) 17:03, 24. Feb. 2020 (CET)

Nach BK: Der Fallschirm funktioniert anders. Luft liefert mir nicht genügend Auftriebskraft, um meine Fallbeschleunigung nach unten auf 0 zu reduzieren. Der Witz ist ja das angesprochene Kräftegleichgewicht, das gilt fürs Schiff, für den Zeitungleser, für die Münze - davon reden wir. Kein Einstein (Diskussion) 17:03, 24. Feb. 2020 (CET)

@Kein Einstein:Ich sehe das Bild im Artikel mit dem untergetauchten Körper vor mir. Die Gewichtskraft nach unten (sagen wir 10kg), die Auftriebskraft nach oben, vereinfacht, 15 kg (Auftrieb = Verringerung des Gewichts um -15kg) (Resultierende Kraft nach oben 5 kg). Fertig. Beide sind nicht gleich groß und nach dem Grundgesetz der Mechanik bewegt sich der Körper alsbald nach oben und schwimmt dann. Und wenn (wegen geringerer Dichte des Fluids) die hydrostatischen Drücke abnehmen, voilà, ändert sich auch die Auftriebskraft. Wir betrachten das neue Kräftegleichgewicht: 10 kg konstante Gewichtskraft nach unten und die verringerte Auftriebskraft sagen wir 13kg nach oben (Resultierend 3 kg nach oben; weniger Auftrieb, daher Einsinken). Das Schiff sinkt weiter ein, obwohl die Masse konstant blieb. Die Auftriebskraft abhängig von der Dichte des umgebenden Fluids. Oder was sehe ich da falsch? --Maschinist1968 (Diskussion) 17:27, 24. Feb. 2020 (CET)

Ich ignoriere deine Einheit kg und werde stattdessen kN schreiben.

Ich folge deiner Argumentation (die aber nicht zum Schiff in Elbe und Nordsee passt, dazu später) bis zu "Wir betrachten das neue Kräftegleichgewicht" --> Hier meinst du nicht Kräftegleichgewicht (denn dazu gehört notwendig die resultierende Kraft 0N), also meinst du vermutlich die "neue Kräftebilanz"? Wenn du nach oben 13kN hast, dann musst du immernoch einen nicht voll aufgetauchten Körper betrachten (dann ist deine Bilanz nachvollziehbar), aber das bedeutet: der Körper steigt weiter auf bis er so weit das Fluid verlassen hat, dass er nur noch Fluid der Gewichtskraft 10kN verdrängt und stabil schwimmt.

Bei dir lese ich aus deiner Schilderung, dass der Körper aber bereits bei der 13kN-Auftriebskraft "schwimmen" soll. Schwimmen geht genau so, dass er 10kN (nicht 13 oder sonstwas) Auftriebskraft erfährt. Sonst steigt er noch weiter auf (was natürlich auch dann erfolgen kann, wenn er schon teilweise aus dem Fluid ragt). Schwimmendes Schiff: Kraftpfeil der Gewichtskraft gegengleich Kraftpfeil der Auftriebskraft (stehendes Auto: Kraftpfeil der Gewichtskraft gegengleich Kraftpfeil der Normalkraft von der Straße ...).

Wechselt der (schwimmende) Körper (im Kräftegleichgewicht) nun in ein Medium kleinerer Dichte, dann muss er, um weiter/erneut Fluid der Gewichtskraft 10kN zu verdrängen, tiefer eintauchen. Ja, er ist tiefer drin im Fluid. Nein, er hat nicht "mehr oder weniger Auftrieb" - die Bedingung für Schwimmen ist und bleibt 10kN Auftriebskraft. Kein Einstein (Diskussion) 17:55, 24. Feb. 2020 (CET)

Nachtrag: Oder ist es so, dass du beim anderen Fluid wieder "voll unter Wasser" begonnen hast, dann verstehe ich deine 13kN - aber muss erneut darauf insistieren, dass das Schiff dann zwar im Vergleich zum untergetauchten Schiff davor mit geringerer Kraft und damit geringerer Beschleunigung nach oben geht - aber beidesmal ist das nicht der Fall des Schwimmens, von dem im Artikel gesprochen wird. Es ist _nicht_ so, dass wir beim Auftrieb einen untergetauchten Tischtennisball und einen untergetauchten gleich großen sandgefüllten Tischtennisball vergleichend betrachten, die diskutierten Beispiele im gerade verhandelten Kontext sind das schwimmende Schiff in Nordsee/Elbe, der schwimmende Zeitungsleser in Badewanne/Totem Meer, die schwimmende Pfundmünze in Quecksilber. Kein Einstein (Diskussion) 18:07, 24. Feb. 2020 (CET)

Ich meine ein Kräftepolygon. Wenn der Körper mit 10kN Gewichtskraft 10kN Auftriebskraft erfährt, dann schwimmt er nicht (auf), sondern er schwebt im Fluid (wie es im Artikel von mir beschrieben wurde und noch immer drinsteht). Der 2. Vergleich begann in meinem Kopf wieder im untergetauchten Zustand, sorry, habe ich nicht kommuniziert. Im leichteren Medium muss die Auftriebskraft geringer sein, sonst würde er nicht einsinken, geht gar nicht anders. Schwebt der Körper in beliebiger Tiefe in Salzwasser, so sinkt er wenn er in Süßwasser kommt, weil der Auftrieb geringer wird. Befindet sich derselbe Körper im Toten Meer, dann wird er obenaufschwimmen. Ich denke, Du bist schon mal in Süßwasser und in Salzwasser geschwommen. In Salzwasser schwimmt man nicht so weit eingetaucht, wie in Süßwasser, weil der Auftrieb/die Auftriebskraft größer ist. Beides ist von der Dichte des verdrängten Fluids abhängig. Ebenso bei der Fähre. Gruß --Maschinist1968 (Diskussion) 18:54, 24. Feb. 2020 (CET)

Das wissen auch die Taucher, Zitat: "Die unterschiedlichen Auftriebseigenschaften zwischen Süß- und Salzwasser beeinflussen den Auftrieb, wobei Salzwasser einen höheren Auftrieb hat als Süßwasser und entsprechend den Einsatz von mehr Blei erfordert. Verantwortlich für den höheren Auftrieb des Salzwassers ist - wie die Vermutung nahe legt - die höhere Salzkonzentration." perfekt tarieren. --Maschinist1968 (Diskussion) 19:04, 24. Feb. 2020 (CET)

Die Aufklärung einer Sprachverwirrung

Ich glaube, ich verstehe nun den Kern dieses Streitpunktes. Es ist ein Missverständnis, worüber genau gesprochen wird. Wir müssen unterscheiden:

1. Szenario 1 (Maschinist1968): Ein Körper befindet sich mitten im Fluid, wird dort beispielsweise festgehalten. Wir wollen wahlweise sein weiteres Schicksal (nach Loslassen: schwimmt er auf, schwebt er, sinkt er ab) verstehen oder einfach messen, mit welcher Kraft wir ihn festhalten müssen, damit er seine Lage nicht verändert. Ich bevorzuge für die weitere Diskussion die letztere Variante. Den Unterschied, den wir zur Gewichtskraft des Körpers ohne Fluid messen können, nennen wir Auftriebskraft. Die so verstandene Auftriebskraft ist natürlich von der Dichte des Fluids abhängig - da sich das eingetauchte Volumen des Körpers und damit das verdrängte Volumen des Fluids nicht verändert.
2. Szenario 2 (Kein Einstein): Ein Körper schwimmt an der Grenzfläche Fluid-Luft, etwa das Schiff, der Zeitungsleser, die Münze im Quecksilber. Hier liegt offenkundig ein statischer Fall mit einem Kräftegleichgewicht vor. Die Gewichtskraft des Körpers wird genau kompensiert durch die Auftriebskraft. Auftriebskraft ist also die Kraft, die das (Ab-)Sinken verhindert. Die so verstandene Auftriebskraft ist natürlich nicht von der Dichte des Fluids abhängig - da sich die Gewichtskraft und damit die vorliegende Auftriebskraft nicht ändert, stattdessen sich (bei Bedarf, also bei Dichteänderung) das eingetauchte Volumen des Körpers verändert.

Ernsthafte Frage: Kannst du der Darstellung bei beiden Punkten so weit folgen und zustimmen? Das wäre der erste nötige Schritt für Artikelverbesserungen. Kein Einstein (Diskussion) 19:37, 24. Feb. 2020 (CET)

Natürlich kann ich folgen, das Einsinkvolumen ändert sich doch wegen des geänderten Auftriebs. Ein Henne-Ei-Problem? Ich gehe aber davon aus, dass das Archimedische Prinzip auch an der Oberfläche gilt (und es keine Ausnahme gibt), also dass die Einsinktiefe/das Volumen Resultat des geänderten Auftriebs ist und nicht umgekehrt. Und auch hier mischt die Dichte mit. Gruß --Maschinist1968 (Diskussion) 19:51, 24. Feb. 2020 (CET)

Naja. Natürlich mischt die Dichte (bei Szenario 2) bei der Einsinktiefe mit. Aber nicht (bei Szenario 2) bei der Auftriebskraft als solcher. Das war der Streitpunkt. Und gerade schreibst du (ich nehme an, weiter auf das Schiff in Nordsee/Elbe bezogen), dass sich der Auftrieb änderte („wegen des geänderten Auftriebs“) - äh, nein, der Auftrieb hat sich (wir sind weiter an der Oberfläche, also Szenario 2) nicht verändert. Wir schreiben eine Enzyklopädie, da muss man noch mehr als im Zwiegspräch zwischen uns darauf achten, dass richtige auch richtig zu sagen. Ich denke (ohne den Dialog zwischen dir und JoKalliauer ganz gelesen zu haben), da hätten sich einige Mitarbeiter hier viele Stunden an Diskussion sparen können. Gruß zurück Kein Einstein (Diskussion) 20:01, 24. Feb. 2020 (CET)

Und sinkt nun ein Taucher, der sich für die Nordsee so austariert hat dass er gerade noch schwimmt, zum Grund, wenn er in einen einmündenden Süßwasserstrom kommt? --Maschinist1968 (Diskussion) 00:23, 25. Feb. 2020 (CET)

Ja. ---<)kmk(>- (Diskussion) 00:47, 25. Feb. 2020 (CET)

Allgemeiner: Wenn in der Naturwissenschaft davon die Rede ist, dass eine Änderung von Parameter A eines Systems zur Folge hat, dass sich die Größe B in einer bestimmten Weise ändert, dann ist erstmal die instantane Auswirkung gemeint -- also ohne dass das System mit seinem Verhalten auf die Änderung reagiert und einen neuen Gleichgewichtszustand erreicht hat. Natürlich kann man den Fall, dass das System reagiert hat, sinnvoll beschreiben. Nur teilt man diesen Umstand dann der Leserschaft mit.
Als Beispiel, das absichtlich nicht den statischen Druck zum Inhalt hat, nehme ich das System "Motorflugzeug" im Geradeaus-Flug. Der Parameter B, dessen Änderung betrachtet wird, soll die Drehzahl des Propellers sein. Eine Erhöhung der Drehzahl führt praktisch instantan zu einem stärkeren Vortrieb. Mehr lässt sich aus der bisher gegebenen Information über das System nicht ablesen. Tatsächlich sind für den weiteren Verlauf verschiedene Szenarien plausibel:

• Der (Auto-) Pilot hält mit Hilfe des Höhenruders die Flughöhe konstant. Dann führt die höhere Drehzahl des Propellers zu einer Beschleunigung bis zu einer Geschwindigkeit, bei der die Zusätzliche Luftreibung gerade zu groß ist wie der zusätzliche Vortrieb.
• Der (Auto-) Pilot behält alle Ruder in der gleichen Stellung bei, die sie vor der Erhöhung der Drehzahl hatten. Dann geht das Flugzeug nach einer kurzen Beschleunigungsphase in einen Steigflug über. Der Steigflug hält so lange an, bis weitere äußere Umstände den Vortrieb begrenzen -- etwa ein durch die Höhe verminderter Luftdruck. Das Flugzeug geht dann in einen Geradeaus-Flug über, allerdings in größerer Höhe und bei größerer Geschwindigkeit als am Anfang des "Experiments".
• Der (Auto-) Pilot hält sowohl die Höhe als auch die Geschwindigkeit konstant, indem er mit Hilfe der Querruder die Tragflächen um einen passenden Winkel seitwärts kippt. Dadurch neigt sich der dynamische Auftrieb ein Stück zur Seite und das Flugzeug fliegt mit leichter Unterstützung durch das Seitenruder in gleichbleibender Höhe einen Kreis. Diese Beschreibung klingt vielleicht etwas konstruiert. Tatsächlich ist das genau die Art, wie man idealerweise eine Kurve einleitet: Erst beschleunigen, dann mit dem Querruder rollen und mit dem Seitenruder dafür sorgen, dass die Nase voll im Fahrtwind steht.

Mein Vorschlag für den Artikel: Wir sollten uns an die oben beschriebene allgemeine Konvention halten. Das heißt, ohne explizite Erwähnung, dass die Reaktion des Systems eingeschlossen ist, ist (nur) die unmittelbare, instantane Wirkung gemeint. Da, wo es die reale Situation nahe legt, wie etwa beim Schiff, dass vom Salzwasser ins Süßwasser wechselt, sollten die Reaktion mit der Folge eines neuen Gleichgewichts ausdrücklich als solche erwähnt werden. Viele Grüße, ---<)kmk(>- (Diskussion) 02:03, 25. Feb. 2020 (CET)

Und, formulierst du aus dieser weisen Erkenntnis einen Lösungsvorschlag oder wirst du bloß Teil des Problems? --Maschinist1968 (Diskussion) 10:51, 25. Feb. 2020 (CET)

Auf ein voll beladenes Fährschiff, das tiefer ins Wasser einsinkt und mehr Wasser verdrängt als im unbeladenen Zustand, wirkt dann wegen der größeren Einsinktiefe mehr Auftriebskraft, als im unbeladenen Zustand und es hat mehr Auftrieb ( = mehr Verlust an Gewichtskraft). Fährt dieses beladene Schiff von der Nordsee in die Elbe, wechselt es also vom Salzwasser ins Süßwasser, so sinkt es im Süßwasser (das eine geringere Dichte hat als Salzwasser) tiefer ein. Wegen der geringeren Dichte nehmen die hydrostatischen Drücke des Wassers und ebenso der Auftrieb ab. Weil der Verlust (!) an Gewichtskraft geringer wird, wirkt nun eine höhere Gewichtskraft und deshalb sinkt die Fähre im Süßwasser weiter ein obwohl das Gewicht der Fähre konstant bleibt.

Was machst du draus? --Maschinist1968 (Diskussion) 10:56, 25. Feb. 2020 (CET)

Ich bin zwar nicht direkt angesprochen, aber meine Version wäre:

Ein voll beladenes Fährschiff sinkt tiefer ins Wasser ein und verdrängt mehr Wasser als im unbeladenen Zustand, dadurch wird die größere zum Schwimmen benötigte Auftriebskraft erzeugt (Ergänzung?: falls das Schiff nicht überladen ist - es wird untergehen wenn die zur Kompensation der Gewichtskraft nötige Auftriebskraft nicht erzeugt werden kann). Fährt dieses beladene Schiff von der Nordsee in die Elbe, wechselt es also vom Salzwasser ins Süßwasser, so sinkt es im Süßwasser (das eine geringere Dichte hat als Salzwasser) tiefer ein. Hier wird die zum Schwimmen nötige unveränderte Auftriebskraft erst durch ein größeres verdrängtes Flüssigkeitsvolumen erreicht (Ergänzung?: falls die Flüssigkeit eine zu geringere Dichte hat, was beispielsweise bei aufsteigenden Methanblasen im Meerwasser geschehen kann, kann auch hier ein Sinken des Schiffes die Folge sein). 

Kritik an deiner Fassung insbesondere wegen der Verknüfung von mehr Gewichtskraft und mehr Auftriebskraft oben und im unteren Teil wegen des Plurals bei "Drücke", der "Flüssigkeitsmenge" (Volumen? Masse?) und einer "wirkenden Gewichtskraft" im Unterschied zum Gewicht - das ist ähnlich daneben wie das, was ich dir bei unserer letzten Diskussion oben zum "geänderten Auftrieb" sagen will. Kein Einstein (Diskussion) 11:32, 25. Feb. 2020 (CET)

Ich würde voll belades vs. leeres Schiff einen Absatz machen. Und einen getrennten Absatz Süß- vs. Salzwasser. Zwei Effekte auf einmal zu erklären ist wohl etwas verwirrend, weil sich die effekte tw. aufheben.  — Johannes Kalliauer - Diskussion | Beiträge 11:40, 25. Feb. 2020 (CET)

Ich vertraue den Beladern einer Fähre, dass sie Ahmung oder Freibord im Auge behalten und sich an ihre Sicherheitsvorschriften halten (wovon die Betriebserlaubnis / Konzession abhängt) und deswegen das Schiff nicht überladen (die Einsinkmarke wäre eine nette Artikelergänzung).

Aber warum soll die Auftriebskraft konstant bleiben? Der größere Tiefgang muss nur bei der Beladung berücksichtigt werden wie ein Pilot, der die Betankungsmenge von der Beladung abhängig macht.

Und die Methanblasen stehen an anderer Stelle im Artikel. Muss ja nicht jeder Sonderfall (wenn 100 Möven zufliegen und sich aufs Schiff setzen oder draufscheissen) in den Absatz gepackt werden. Einfach bleiben! Gruß --Maschinist1968 (Diskussion) 13:17, 25. Feb. 2020 (CET)

Die Auftriebskraft für das (jeweils) schwimmende Schiff (vorher: Nordsee; nachher: Elbe) ist doch gleich der Gewichtskraft des Schiffes. Da hat sich nix daran geändert. Wie Kai-Martin oben sagte: Entweder schauen wir uns die momentane Änderung an oder die jeweiligen Gleichgewichtszustände - und ich argumentiere die ganze Zeit erkennbar mit Letzterem. Kein Einstein (Diskussion) 13:22, 25. Feb. 2020 (CET)

Bitte bitte bitte lies dir das archimedische Prinzip durch und wovon die Auftriebskraft abhängt. Sie muss höher sein, sonst bringt der nächste Mövenklecks das Schiff zum Untergehen. Lach. --Maschinist1968 (Diskussion) 13:39, 25. Feb. 2020 (CET)

Bitte sortiere deine Gedanken bzw. lies das, was da steht. Wenn ein Möwenklecks dazu kommt, dann ist das der "Belade"-Fall. Die unveränderte Auftriebskraft steht beim Nordsee-Elbe-Fall. Drücke ich mich wirklich so unverständlich aus? Kein Einstein (Diskussion) 14:08, 25. Feb. 2020 (CET)

"Die Auftriebskraft für das (jeweils) schwimmende Schiff (vorher: Nordsee; nachher: Elbe) ist doch gleich der Gewichtskraft des Schiffes. Da hat sich nix daran geändert"

Wir haben im Kräftegleichgewicht die Gewichtskraft des Schiffes und den (dichteabhängigen) hydrostatischen Gegendruck von unten, der größer sein muss als die Gewichtskraft, sonst wäre der Körper im Fluid in Schwebe. Damit der Körper aufschwimt und oben bleibt muss der Auftrieb größer sein als die Gewichtskraft.

In der Nordsee und in der Elbe hat das Schiff dieselbe Gewichtskraft, aber von unten wirken unterschiedliche hydrostatische Drücke, die unterschiedliches Einsinken erst bewirken.

Gruß --Maschinist1968 (Diskussion) 14:53, 25. Feb. 2020 (CET)

Widerspruch in einem zentralen Punkt: Damit ein Körper aufschwimmt (also aus dem Inneren des Fluids auftaucht) muss die Auftriebskraft größer sein als die Gewichtskraft. Aber nicht, damit der Körper an der Oberfläche schwimmt. Der Unterschied zwischen Schweben und Schwimmen ist, dass an der Grenzfläche ein stabiles Geleichgewicht (aufgrund vorhandener Rückstellkräfte durch Differenz Auftriebskraft-Gewichtskraft) vorliegt, beim Schweben ein indifferentes Gleichgewicht. Meinst du wirklich, beim Schwimmen an der Oberfläche ist die Auftriebskraft GRÖßER als die Gewichtskraft??? Kein Einstein (Diskussion) 15:13, 25. Feb. 2020 (CET)

(quetsch)'Ja, meine ich. Im Wasser. In der Luft ist sie kleiner. Sonst saufst du ab. --Maschinist1968 (Diskussion) 16:58, 25. Feb. 2020 (CET)

(mitquetsch): Wenn die Auftriebskraft größer wäre als die Gewichtskraft, dann hätten wir eine resultierende Kraft nach oben. Also eine beschleunigte Bewegung.

Ich habe es dir schon mit dem Auto auf dem Boden zu erläutern versucht: Beide Kräfte müssen im statischen Fall (betragsmäßig) gleich sein. F=ma und so. Kein Einstein (Diskussion) 17:04, 25. Feb. 2020 (CET)

Die bschleunigte Bewegung hast du nach einem Sprung ins Wasser, sie wird aber an der Oberfläche durch den fehlenden Auftrieb in Luft gestoppt. --Maschinist1968 (Diskussion) 17:17, 25. Feb. 2020 (CET)

Wir verstehen uns (mal wieder) nicht (gleich): Ein Schiff ruht, schwimmend auf der spiegelglatten See. Es ist da schon immer, taucht weder gerade ein noch kommt es "von unten". Da ist doch keine Kraft auf das Schiff nach oben - zumindest nicht in der Bilanz, die resultierende Kraft aus F_A und F_G ist genau 0. (Betrachtungen des Auftriebs in Luft helfen da nicht, vermindern nur den Wägewert des Schiffs, ich glaube nicht, dass du das meinst). Kein Einstein (Diskussion) 17:25, 25. Feb. 2020 (CET)

Schön, das meinst du also wohl nicht. Aber ebenso falsch wie die Vorstellung von der größeren Auftriebskraft als notwendige Bedingung beim Schwimmen ist die Idee, die du nun eingebaut hast. Ich zitiere: „Ist die Gewichtskraft des eingetauchten Körpers (auf den keine sonstige Krafteinwirkung wirkt) größer als die aktuell wirkende Auftriebskraft, so sinkt der Körper im Fluid ab bis beide Kräfte sich ausgleichen (weil der Auftrieb mit der Tiefe zunimmt)“ - wenn das Schiff voll eingetaucht ist, dann ist die Auftriebskraft konstant, egal in welcher Tiefe. Oder willst du die Kompressibilität des Wassers thematisieren? Wenn man davon absehen kann, dann ist die Differenz des hydrostatischen Drucks "unten" und "oben" am Köper/Schiff stets gleich. Anders gesagt: Gemäß deiner Formulierung müsste die Münze im Wasser in einer bestimmten Tiefe schweben, wenn der Auftrieb mit der Tiefe zunimmt. Willst du das sagen? Kein Einstein (Diskussion) 15:57, 25. Feb. 2020 (CET)

Da gebe ich dir recht. Die Differenz ist nur an der Oberfläche mit steigender Eintauchtiefe ungleich, untergetaucht ist sie konstant. --Maschinist1968 (Diskussion) 17:13, 25. Feb. 2020 (CET)

Einigung bei |F_A| = |F_G| --Maschinist1968 (Diskussion) 18:58, 25. Feb. 2020 (CET)

Jetzt fehlt nur mehr der Bildtext "Wegen des höheren Salzgehalts im Toten Meer ist die Dichte des Wassers höher als etwa in der Nordsee, dies führt aufgrund gleicher Auftriebskraft zu einer geringeren Einsinktiefe.".

Unterschiedliche Dichte, gleiches Gewicht --> mehr Auftrieb --> weniger Einsinken. Sind ja unterschiedliche Fluide und unterschiedliche Dichten. --Maschinist1968 (Diskussion) 19:20, 25. Feb. 2020 (CET)

Die Auftriebskraft ist nicht von der Dichte des Fluids abhängig. (Wohl aber das verdrängte Volumen und damit die Eintauchtiefe. Freibord wird beim Wechsel von Süß- zu Salzwasser größer) Denn, wenns schwimmt, ist die Auftriebskraft immer im Gleichgewicht mit der Gewichtskraft.

Pauls erster Enkel (Diskussion) 22:18, 27. Feb. 2020 (CET)

zurück aufs Schiff

Fährt ein Schiff von der Nordsee in die Elbe und wechselt somit vom Salzwasser ins Süßwasser (das eine geringere Dichte hat als Salzwasser), würde im Süßwasser bei unveränderter Eintauchtiefe die Auftriebskraft abnehmen. Daher sinkt das Schiff tiefer ein als im Salzwasser, die Wasserverdrängung steigt und die Auftriebskraft steht mit der Gewichtskraft des Schiffes wieder im Gleichgewicht.

oder

Fährt dieses beladene Schiff von der Nordsee in die Elbe und wechselt somit vom Salzwasser ins Süßwasser (das eine geringere Dichte hat als Salzwasser) hat es nun weniger hydrostatischen Gegendruck und somit weniger Auftrieb als in der Nordsee und deshalb sinkt es im Süßwasser tiefer ein (wodurch sich aber wieder der Auftrieb entsprechend der Einsinktiefe oder gestiegenen Wasserverdrängung  ändert).

Irgendwie wird bei der Version oben der Umstand, dass sich der Auftrieb wegen zweier Ursachen ändert, nicht so durchsichtig erklärt. "würde im Süßwasser bei unveränderter Eintauchtiefe die Auftriebskraft abnehmen" ist zudem zu vage. --Maschinist1968 (Diskussion) 18:23, 25. Feb. 2020 (CET)

Kompromiss:

Fährt dieses beladene Schiff von der Nordsee in die Elbe und wechselt somit vom Salzwasser ins Süßwasser (das eine geringere Dichte hat als Salzwasser) hat es nun weniger hydrostatischen Gegendruck und somit weniger Auftrieb als in der Nordsee und deshalb sinkt es im Süßwasser tiefer ein (wodurch sich aber wieder der Auftrieb entsprechend der Einsinktiefe oder gestiegenen Wasserverdrängung ändert, weil sich letztendlich beim Schwimmen an der Oberfläche ein Kräftegleichgewicht einstellt). 

--Maschinist1968 (Diskussion) 18:55, 25. Feb. 2020 (CET)

Komplettüberarbeitung

Ich war dann mal mutig und habe meine Komplettüberarbeitung in den Artikel gestellt. In der bisherigen Fassung gab es diverse Dopplungen und viele Auslassungen, was durch Einzel-Nachbesserungen eher schlimmer wurde. Hoffentlich habe ich keine Streitpunkte neu aufgewärmt, mir ging es primär um eine bessere Struktur. Kein Einstein (Diskussion) 00:10, 28. Feb. 2020 (CET)

Tabula rasa. Musste sein. Schaut gut aus. Lob. --Maschinist1968 (Diskussion) 14:22, 28. Feb. 2020 (CET)

Luftballon

Im Artikel stand mal:

"In der Atmosphäre kann der Ballon dann auch durch Windströmungen auf und ab oder horizontal bewegt werden. Da die Luftdichte mit steigender Höhe abnimmt, gibt es für jedes Füllgas bei bestimmtem Volumen eine Grenzhöhe, bis zu der ein Ballon steigen kann. Diese Eigenschaft muss bei Wetterballons, die mithilfe von aufzeichnenden Messgeräten Wetterdaten sammeln, beachtet werden. Umgekehrt können, um das teure Füllgas Helium zu sparen, kleinere Ballons gewählt werden, wenn nur tiefere Luftschichten untersucht oder Fotoaufnahmen aus geringerer Höhe gemacht werden sollen. Wegen des mit der Höhe abnehmenden Luftdrucks dehnen sich Luftballone beim Aufsteigen auf und können deswegen auch zerplatzen, anstatt von Winden weitergetragen zu werden."

---

Das Beispiel mit dem Luftdruck wäre interessant, weil mit der Volumenausdehnung der Auftrieb zunimmt oder mangels hydrostatischen Drucks abnimmt oder gleich bleibt... --Maschinist1968 (Diskussion) 14:21, 28. Feb. 2020 (CET)

Wie willst du dieses Beispiel einsetzen? Hier geht es übrigens um die Prallhöhe. Das ist die Höhe, bei der ein Ballon prall ist. Steigt er noch weiter, so steigt der Innendruck über den Atmosphärendruck. Dann geht entweder ein Sicherheitsventil auf, oder der Ballon platzt wenn er weiter steigt. Der Auftrieb ändert sich nicht solange der Druck im Ballon dem der Atmosphäre entspricht. Hadhuey (Diskussion) 19:30, 28. Feb. 2020 (CET)

nach oben gezogen

@Kein Einstein: Ein vollkommen fließfähiges (=nicht viskoses) Fluid, von denen wir hier, glaub ich, immer reden, wenn wir salopp von Fluiden reden, hat eine Querdehungszahl von µ=0.5 und kann daher ausschließlich hydrostatische Druckspannungen aufnehmen, daher wird der Körper wohl nach oben gedrückt und nicht nach oben gezogen?  — Johannes Kalliauer - Diskussion | Beiträge 17:44, 28. Feb. 2020 (CET)

Geschmackssache. Habe ich den Gesamtbestand von zwei Luftballonverkäufern aufgekauft und schwebe nun sanft nach oben, fühle ich mich wohl eher gezogen. Physikalisch sauber wäre wohl gedrückt (aber diese Disk läuft wohl noch auf WD:RP). Kein Einstein (Diskussion) 22:04, 28. Feb. 2020 (CET)

Körper wird leichter

@Kein Einstein: Zumindest ich weiß nicht was "leichter" in Spezial:Diff/197241210 bedeutet und gehört erklärt. Ich hätte instiktiv leichtheit mit Körpergewicht, also mit weniger Masse_(Physik) verbunden, aber jetzt würde ich es eher mit Gewichtskraft verbinden, aber ich würde es jedenfalls nicht wie du mit Wägewert gleichsetzen.  — Johannes Kalliauer - Diskussion | Beiträge 17:28, 28. Feb. 2020 (CET)

Ein Körper ist leichter, wenn er weniger Gewicht hat (omA-taugliche Belegstelle). Und bei Gewicht kannst du dir aus dem Kontext aussuchen, was du meinst. Hier beziehe ich mich, wie der anschließende Satz zeigt, auf die Gewichtskraft (die scheinbar - wie der Satz davor sagt - geringer ist). Wenn du das anders formuliert besser findest: Nur zu. Kein Einstein (Diskussion) 22:02, 28. Feb. 2020 (CET)

@Kein Einstein: Die Gewichtskraft ist doch konstant egal, ob im Fluid oder außerhalb, der Wägewert (das scheinbare Gewicht) wird weniger.  — Johannes Kalliauer - Diskussion | Beiträge 22:55, 28. Feb. 2020 (CET)

Es geht um die Alltagserfahrung, wir sind oben in der Einleitung und der Neuling will sehen, worum es eigentlich geht. Du denkst (entschuldige bitte, du weißt hoffentlich, wie es gemeint ist) als Fachidiot in physikalischen Schubladen. 99,9% der Leute da draußen haben kein Problem damit zu sagen, im Wasser fühlen sie sich leichter...

Wie gesagtM Satz vorher "scheinbar", im Satz nachher "Gewichtskraft". Wenn du das noch deutlicher klarstellen willst, eght das sicher auch geschickt. Mir fallen aber sofort 99 ungeschickte (weil Laien-unverständliche) Möglichkeiten ein... Kein Einstein (Diskussion) 23:22, 28. Feb. 2020 (CET)

Ich hoffe es gibt eine anerkannte Definition von Gewichtskraft, sonst sollte das umschrieben werden. --Diwas (Diskussion) 06:41, 29. Feb. 2020 (CET)

@Diwas:<Sarkasmus>Es gibt eine, es gibt sogar viele anerkannte Definitionen von Gewichtskraft, siehe Gewicht.</Sarkasmus>

Ich würde vorschlagen

„Der Wägewert des Körper ist leichter geworden ...“

oder zumindest

„Der Körper ist scheinbar leichter geworden“

aber aktuelle Version impliziert, dass die Masse_(Physik) oder die Gewichtskraft geringer werden wurde, beides falsch, daher muss es imho umgeschrieben oder entfernt werden.  — Johannes Kalliauer - Diskussion | Beiträge 08:24, 29. Feb. 2020 (CET)

So besser? Gleich zu Beginn mit Wägewert zu arbeiten halte ich für eine Zumutung (für den Leser), das "scheinbar" zu verdoppeln, ist stilistisch doof. Ich habe es mit einer anderen Umschreibung versucht. Kein Einstein (Diskussion) 12:14, 29. Feb. 2020 (CET)

Die Abbildung File:Ligji_i_arkimeditt.png stellt ja genau den Wägewert dar.

Ok den Begriff kennt man noch nicht, aber dafür gibt es ja Wikilinks.

Aktuelle Version gefällt mir.

 — Johannes Kalliauer - Diskussion | Beiträge 12:45, 29. Feb. 2020 (CET)

Zur unbewiesenen Theorie, der Auftrieb an der Oberfläche hinge NICHT von der Dichte ab

Ad Kein Einsteins Szenario2:

Münze im Quecksilber. "Die Gewichtskraft des Körpers wird genau kompensiert durch die Aufriebskraft"

Du transferierst die Münze in Wasser (geringere Dichte). Was passiert und warum? Theorieverfechter, bitte erklärt mir das Unverständlche. --Maschinist1968 (Diskussion) 12:47, 25. Feb. 2020 (CET)

@Maschinist1968: Wenn ich eine Münze in Wasser (zumindest bei reinem H₂O) werfe geht sie unter, und sie ist erst dadurch im Gleichgewicht, dass sie von einer externen Oberflächenkraft (dem Festkörper Untergrund) in der Lage gehalten wird. Das die Münze von einer externen Kraft beinflusst wird ist es nicht Szenario2.  — Johannes Kalliauer - Diskussion | Beiträge 12:55, 25. Feb. 2020 (CET)

Ja warum geht sie denn unter, wenn ihr Auftrieb (in der Zehntelsekunde an der Oberfläche) nicht von der Dichte abhängt? --Maschinist1968 (Diskussion) 12:59, 25. Feb. 2020 (CET)

Ich habe keinen Ping erhalten, aus bereits erläuterten Gründen. Aber ich lese ja ohnehin hier mit...

@Maschinist1968: Wenn ich in Szenario "schwimmt" schreibe, dann meine ich damit (wie bei den angeg. Beispielen) ein Schwimmen, nicht ein "kurzzeitig auf Höhe der Grenzfläche Flüssigkeit - Luft befindlich". Die Münze in Wasser ist Szenario 1. Ich messe, dass die Auftriebskraft geringer ist als die Gewichtskraft, daher wird die Münze nach unten beschleunigt. Kein Einstein (Diskussion) 13:06, 25. Feb. 2020 (CET)

Und die Auftriebskraft in Wasser ist deshalb (auch an der Oberfläche) geringer, weil Wasser eine geringere Dichte als Quecksilber hat, oder? --Maschinist1968 (Diskussion) 13:23, 25. Feb. 2020 (CET)

Dichte --> Auftriebskraft --> mehr oder weniger Einsinken

statt

Mehr Einsinktiefe wegen dichteunabhängiger Auftriebskraft (bei konstantem Gewicht).

Das ist die aufzulösende Diskrepanz.

--Maschinist1968 (Diskussion) 13:30, 25. Feb. 2020 (CET)

Aus dem Artikel zwecks Neuformulierung entfernter Text:

Das Gewicht der Fähre ist i. d. R. unabhängig von der Dichte des Fluides und aufgrund des sich einstellenden Gleichgewichts ist die Auftriebskraft, die auf ein gegebenes schwimmenses Objekt wirkt, unabhängig von der Dichte des Fluides. Bei konstanter Gewichtskraft des schwimmenden Körpers und damit konstanter Auftriebskraft verhällt sich das Eindringvolumen (verdrängtes Fluidvolumen) indirekt proportial zur homogenen Dichte des Fluides. Die Auftriebskraft ist bei gegebener Masse des schwimmenden Körpers somit von der Dichte des Fluides unabhängig.

--Maschinist1968 (Diskussion) 14:22, 25. Feb. 2020 (CET)

@JoKalliauer:@Kein Einstein: Und bitte keine eigene Theoriefindung mehr im Artikel, Belege für die Theorie extern suchen und angeben! WP gibt bekanntes Wissen wieder. Gruß --Maschinist1968 (Diskussion) 14:36, 25. Feb. 2020 (CET)

Der Beleg fehlt auch bei Statischer_Auftrieb#physikalische_Herleitung . Bitte ergänzen, sonst wird das Strittige demnächst entfernt. --Maschinist1968 (Diskussion) 16:27, 25. Feb. 2020 (CET)

@Maschinist1968:

Was ist denn da noch strittig?

Sofern $\|{\vec {F}}_{\mathrm {A} }\|=\|{\vec {F}}_{\mathrm {G} }\|$ (zu dem hast du ja selbst einen Beleg gebracht: Spezial:Diff/197081182) in irgendeiner Form bleibt hänge ich nicht an der Herleitung.

Wenn strittiges entfernt wird, entferne mal nur das strittige mit Begründung (nicht den ganzen Absatz). Inhalte die dann nicht mehr hineinpassen, bitte in einem anderen Edit, um die jeweiligen unterschiedlichen Begründungen nachvollziehen zu können.

 — Johannes Kalliauer - Diskussion | Beiträge 18:05, 25. Feb. 2020 (CET)

Kein Einstein meinte (16:27, 25. Feb. 2020‎ Umgeschrieben auf das, worum es in diesem Abschnitt offenbar nunmehr geht: Wie tief ein Schiff einsinkt. Meinethalben ist die "physikalische Herleitung" übrigens komplett entbehrlich. Wenn wir uns beim Schiff auf ein verbales |F_A| = |F_G| einigen können ).

Kein Einsteins "komplett entbehrlich", ich meine "Beleg fehlt". Netter Konsens. --Maschinist1968 (Diskussion) 18:28, 25. Feb. 2020 (CET)

Hier bitte ein Beleg für den Maschinenbauer: "Ein nicht vollständig in eine Flüssigkeit eingetauchter Körper erfährt eine Auftriebskraft, die gleich der Gewichtskraft des vom Körper unterhalb der Oberfläche verdrängten Flüssigkeitsvolumen ist.. (ref)Werner Skolaut: Maschinenbau. ISBN 978-3-827-42554-6, S. 703 (eingeschränkte Vorschau in der Google-Buchsuche).(/ref) Und im Gewicht der Flüssigkeit steckt die Dichte. Gruß --Maschinist1968 (Diskussion) 21:58, 25. Feb. 2020 (CET)

Nein im Gewicht der Flüssigkeit steckt nicht die Dichte drinnen, weil das Volumen invers zur Dichte ist (https://link.springer.com/chapter/10.1007%2F978-3-322-89910-1_16 ) damit kürzt sich die Dichte heraus, belege siehe: Spezial:Diff/197177440.  — Johannes Kalliauer - Diskussion | Beiträge 22:33, 25. Feb. 2020 (CET)

Dann musst du auch den Artikel Salzwasser ändern, Zitat "Durch den Gehalt von etwa 3,5 % Salzen ist die Dichte von Meerwasser um gut 3 % höher als Süßwasser gleicher Temperatur, etwa 1,025 kg/l bei 25 °C. Diese Dichteerhöhung vergrößert den Auftrieb, so dass z. B. Schiffe in Salzwasser weniger tief eintauchen – oder mehr laden können – als in Süßwasser.". --Maschinist1968 (Diskussion) 22:42, 25. Feb. 2020 (CET)

Es ist korrekt wenn man mit dem Auftrieb, die Auftriebskraft pro Volumen meint, aber ja ich werde mir das anschauen und versuchen es klarer zu formulieren.  — Johannes Kalliauer - Diskussion | Beiträge 22:45, 25. Feb. 2020 (CET)

Und auch Schüler lernen es demnach falsch Physikaufgaben. Schlimm diese Welt. Oder hier Mehr Tiefgang in der Elbe. --Maschinist1968 (Diskussion) 22:48, 25. Feb. 2020 (CET)

Ich konnte beim überfliegen in beiden Links keinen Fehler finden. Ich vermute dieser steckt in den Schlussfolgerungen die daraus gezogen werden.  — Johannes Kalliauer - Diskussion | Beiträge 22:53, 25. Feb. 2020 (CET)

Es gibt in der zweiten Quelle einige Fehler/Unklarheiten, wie wir sie hier auch wiederholt gemacht haben. Keine klare Angabe welcher Zustand oder Prozeß betrachtet wird (schwimmend oder untergetaucht, instantan oder Gleichgewicht), keine klare Angabe welche Parameter als konstant definiert werden und keine klare Nennung der Bezüge, also z. B. Auftrieb (bezogen auf den verdrängenden Körper vs. bezogen pro Volumeneinheit des verdrängten Fluids.)

Die Fehler/Unklarheiten in der Quelle sind etwa:

• Ein Kö[r]per schwimmt, wenn die Auftriebskraft größer als die Gewichtskraft sind. Aber sobald sich das Gleichgewicht eingestellt hat, sind beide Kräfte gleich. Von welcher Auftriebskraft wird hier gesprochen, im untergetauchten oder im schwimmenden Zustand?
• [...] Dadurch ändert sich die mittlere Dichte des U-Bootes, was zu mehr oder weniger Auftrieb führt. Dass das den Auftrieb (die Auftriebskraft) ändert, stimmt nur, wenn man das Wasser im Tank dem umgebenden Wasser, nicht aber dem Volumen des U-Bootes zurechnet.
• [...] und im dritten Fall ist die Auftriebskraft größer als die Gewichtskraft. Da fehlt wieder die Angabe, dass sich die Aussage nur auf den Ungleichgewichtszustand bezieht, nach dem Einpendeln aber beides gleich ist. --Diwas (Diskussion) 03:00, 26. Feb. 2020 (CET)

Und diese Lademarken für See- und Süßwasser, die auf Schiffe gepinselt werden, alles sinnloseste Zeit- und Geldverschwendung… --Maschinist1968 (Diskussion) 22:57, 25. Feb. 2020 (CET)

Das Eindringvolumen ist eine Funktion der Fluiddichte, aber nicht die Auftriebskraft.  — Johannes Kalliauer - Diskussion | Beiträge 22:58, 25. Feb. 2020 (CET)

"Somit hängt die Eindringtiefe mit der Dichte des Fluides zusammen, nicht jedoch die Auftriebskraft." Gähn. Von oben wirkt die Gewichtskraft, von unten der dichteabhängige hydrostatische Druck (vulgo die Auftriebskraft) und die Resultierende beider bewirkt, ob das Schiff einsinkt oder nicht. Kein Einstein hat dies schon bejaht, doch jetzt werden die wasserdichteabhängigen Lademarken abgeschafft, weil JoKalliauer die Physik neu erfunden hat.--Maschinist1968 (Diskussion) 23:07, 25. Feb. 2020 (CET)

Bitte beachte, welchen Zustand du anschaust: Den Moment des jähen Wechsels der Fluiddichte oder den Gleichgewichtszustand, der sich danach dann einstellt. Ähnliches wollte, glaube ich, KaiMartin schon sagen: Die instantane Wirkung oder die Folge eines neuen Gleichgewichts. Kein Einstein (Diskussion) 23:25, 25. Feb. 2020 (CET)

...und auch [Physik für Tauchprofis – Auftrieb und Tarierung. (eingeschränkte Vorschau in der Google-Buchsuche). Physikbücher für Taucher] müssen jetzt umgeschrieben werden. Und der Gesetzgeber muss die Eichung von Schiffen neu verordnen. Die Welt ist im Umbruch, Waaaahnsinn. --Maschinist1968 (Diskussion) 23:28, 25. Feb. 2020 (CET)

<sarkasmus>Ich bin ja Universitätsasisstent, wenn mir nichts besseres einfällt, dann erfinde ich neue phys. Gesetze, dass mach ich in der Arbeit genau gleich, das ist bei uns in der Wissenschaft so üblich, und dann lassen wir uns so was einfallen wie z.B. Antimaterie.</sarkasmus>; im Ernst: Wenn ein Schiff in Ruhe ist, dann gilt Gleichgewicht, also die Resultierende ist Null unabhänig von der Einsinktiefe. Ich sag ja die ganze Zeit, dass die Tiefe (alias Lademarke) von der Fluiddichte abhängt, aber eben nicht die Auftriebskraft eines frei schwimmenden Schiffes. Wie Kein_Einstein sagt: Es ist die Frage welches Szenario (konstantes Volumen oder frei schwebend)  — Johannes Kalliauer - Diskussion | Beiträge 23:30, 25. Feb. 2020 (CET)

@Maschinist1968: Wenn du schon den Sachverhalt, um den es geht, nicht sauber prüfst (welches Szenario, wir hatten das doch schon öfter), dann schütte bitte nicht unfundiertes ad-hominem-Bashing aufgrund von Self-Publishing-Qualitätsmedien-Erzeugnissen auf deine Mitdiskutanten. Können wir uns bitte darauf einigen? Kein Einstein (Diskussion) 00:09, 26. Feb. 2020 (CET)

Szenario frei schwebend

Von oben wirkt auf den vollständig eingetauchten Taucher samt Bleigewichten sein Gewicht. Von unten wirkt eine gleich große Auftriebskraft, er schwebt im Wasser und ist im Gleichgewicht. Er lässt Luft in seine Tarierweste und steigt dadurch auf und ist nicht mehr im Gleichgewicht. Sobald er die Oberfläche durchstößt, stellt sich ein Gleichgewicht aus Gewichtskraft und Auftriebskraft ein, sein Kopf ragt aus dem Wasser (weniger untergetauchtes Volumen, weniger Auftrieb). Dann bläst er nocheinmal die Tarierweste auf, er bekommt mehr Auftrieb. Im nächsten Gleichgewicht ragen auch die Schultern heraus. Im Gleichgewicht ist die Gewichtskraft gleich zur Auftriebskraft pro Volumen. Nichtsdestotrotz ist die Auftriebskraft [egal ob pro großem oder kleineren Volumen] IMMER abhängig von der Dichte des Fluids, was ja auch das Archimedische Prinzip besagt, das auch an der Oberfläche gilt. --Maschinist1968 (Diskussion) 00:33, 26. Feb. 2020 (CET)

Wie bei vielen unserer Beiträge, fehlen hier die Bezüge. Welche Volumina meinst Du? Beim Aufblasen steigt das Volumen des gesamten Tauchers. An der Oberfläche stellt sich wieder das alte eingetauchte Volumen ein. Das Volumen des gesamten Tauchers bleibt größer als zu Anfang. Welche Auftriebskraft meinst Du? Gut, das ist für mich in den ersten Sätzen noch nachvollziehbar, bei weniger Auftrieb wird es schon schwieriger; wenn Du meinst, weniger als nach dem ersten Aufblasen und wieder soviel wie zu Anfang, stimmt es. Welchen Auftrieb nach dem Aufblasen meinst Du, unmittelbar beim Aufblasen oder aber nachdem sich das Gleichgewicht eingestellt hat? Wenn man das nicht jedesmal klarstellt, wird es immer Missverständnisse geben und niemand kann prüfen, ob die Aussagen stimmen oder nicht. Auftriebskraft pro Volumen Was meinst du damit? Welches Volumen meinst Du, das eingetauchte = verdrängte oder das Volumen des ganzen Tauchers? Auftriebskraft pro Liter wäre die Dichte des Fluids. Die Auftriebkraft pro Liter verdrängten Fluids ist natürlich proportional zu dessen Dichte. Auftriebskraft, die auf den aufgetauchten Taucher wirkt, ist, nachdem sich das Gleichgewicht eingestellt hat, unabhängig von der Dichte des Fluids immer gleich der Gewichtskraft des Tauchers. Die Auftriebskraft, die auf den untergetauchten Taucher wirkt, ist von seinem Volumen (einschließlich Gewichte und Tarierweste) und der Dichte des Fluids abhängig. Wir schreiben alle oft, ohne die Bezüge, Szenarien, Zeitpunkte usw. anzugeben, daher reden wir oft aneinander vorbei, und bei den Lesern des Artikels wird es nicht anders sein. --Diwas (Diskussion) 03:48, 26. Feb. 2020 (CET)

ad "Auftriebskraft, die auf den aufgetauchten Taucher wirkt, ist, nachdem sich das Gleichgewicht eingestellt hat, unabhängig von der Dichte des Fluids immer gleich der Gewichtskraft des Tauchers."

Entsprechend dem Gewicht des Tauchers sinkt er mehr oder weniger ein, entsprechend des dabei verdrängten Volumens und der Einsinktiefe bildet sich eine Auftriebskraft, die dann mit der Gewichtskraft in Gleichgewicht steht. Verständlich. Die wirkende Auftriebskraft ist dabei abhängig vom verdrängten Volumen und der Dichte des verdrängten Volumens (Archimedisches Gesetz). Kleines Gewicht --> kleines Volumen (geringe Einsinktiefe, wenig Auftriebskraft im Gleichgewicht) | Großes Gewicht --> großes Volumen (große Einsinktiefe, große Auftriebskraft im Gleichgewicht). Aber die Dichte hat immer Einfluß auf die Auftriebskraft.

Salzwasser: Großes Gewicht --> großes Volumen (große Einsinktiefe, große Auftriebskraft im Gleichgewicht)

Süßwasser: Großes Gewicht --> größeres Volumen (größere Einsinktiefe, größere Auftriebskraft im Gleichgewicht)

Das Archimedische Prinzip ist auch an der Oberfläche gültig, auch wenn sich ein Gleichgewicht einstellt. Wenn der Taucher in den Wellen schaukelt. Laufend wird das Volumen verändert, laufend wird mehr oder weniger Wasser, mit hoher oder geringerer Dichte, verdrängt.

@Diwas:--Maschinist1968 (Diskussion) 12:18, 26. Feb. 2020 (CET)

Du fängst richtig an, aber irgendwo kommt dann wieder die Idee auf, ein unveränderter Schwimmkörper würde im Gleichgewicht in Salzwasser eine andere Auftriebskraft als in Süßwasser erfahren. Die Auftriebskraft ist die selbe, es ändert sich das verdrängte Volumen, was die veränderte Dichte ausgleicht:

Salzwasser: Großes Gewicht --> großes Volumen (große Einsinktiefe, große Auftriebskraft im Gleichgewicht)

Süßwasser: Großes Gewicht --> größeres Volumen (größere Einsinktiefe, große Auftriebskraft im Gleichgewicht)

Die Dichte beeinflusst, die Auftriebskraft eines bestimmten Fluidvolumens. Die Auftriebskraft, die auf einen schwimmenden Körper im statischen Gleichgewicht wirkt, ergibt sich aus dem Produkt von verdrängtem Fluidvolumen und dessen Dichte und ist gleich der Gewichtskraft des schwimmenden Körpers. An der Oberfläche von Quecksilber ist das verdrängte Volumen sehr klein, da die Dichte sehr groß ist. Bei zwei identischen an der Oberfläche im Gleichgewicht schwimmenden Körpern, einer in Alkohol, einer in Salzwasser beeinflusst die Fluiddichte das verdrängte Volumen umgekehrt proportional ohne die Auftriebskraft zu verändern.

Ja das Archimedische Prinzip gilt auch beim an der Oberfläche schwimmenden Körper. Der Körper verdrängt immer soviel Fluidmasse wie er selbst Masse hat. Bei größer Fluiddichte kleines verdrängtes Fluidvolumen (wenig Einsinken), bei kleiner Fluiddichte großes Fluidvolumen (tieferes Einsinken). Daraus ergibt sich immer die Auftriebskraft gleich der Gewichtskraft des Körpers (solange er nicht ganz untertaucht). --Diwas (Diskussion) 20:39, 26. Feb. 2020 (CET)

Da die Dichte des Eises 0,920 Kilogramm pro Liter beträgt (Meerwasser 1,025 Kilogramm/Liter), müssen sich 90 % des Volumens der Eisberge unter der Wasseroberfläche befinden.

Da die Dichte des Eises 0,920 Kilogramm pro Liter beträgt (Meerwasser 1,025 Kilogramm/Liter), müssen sich 90 % des Volumens der Eisberge unter der Wasseroberfläche befinden.

...aber der Auftrieb hängt ja nicht von der Dichte ab... Wenn das die Eisberge wüssten. --Maschinist1968 (Diskussion) 02:27, 5. Mär. 2020 (CET)

Das wissen sie, sie wissen, dass sie so tief einsinken dürfen, dass die verdrängte Fluidmasse, gleich der eigenen Masse ist. Und da bei Eis zu Wasser die Dichte nur wenig abweicht, nutzen sie das schamlos aus und sinken zu 90 % ein. Denn sie können sich leicht ausrechnen, dass sie erst dann ein Fluidvolumen verdrängt haben, dessen Masse gleich der Eismasse ist, wenn sie ein Fluidvolumen von 90 % ihres eigenen Volumens verdrängt haben. „Auftrieb“ wird sicher mehrdeutig verwendet, damit kann vieles gemeint sein, die Auftriebskraft ist aber unabhängig von der Fluiddichte gleich der Gewichtskraft des an der Oberfläche schwimmenden Körpers. --Diwas (Diskussion) 03:47, 5. Mär. 2020 (CET)

Schwimmende Münze

Eine Münze schwimmt in flüssigem Quecksilber aufgrund des statischen Auftriebes

"Eine Münze schwimmt in flüssigem Quecksilber aufgrund des statischen Auftriebes" wurde mit diesem Edit zu "Eine Münze schwimmt in flüssigem Quecksilber aufgrund der Oberflächenspannung." und das Bild wurde dann mit den nächsten Edit entfernt (→‎Schwimmen: Bild entfernt. Münze auf Quecksilber ist kein anschauliches Beispiel, weil nicht klar ist, welche Kräfte hier wirken.).

Die Oberflächenspannung von Quecksilber als horizontale Kraft von 0,47476 N/m wirkt stärker als die Auftriebskraft zwischen Münze und Quecksilber (Dichte von Kupfer = 8,920 g/cm³, Dichte von Quecksilber = 13,534 g/cm³) ?

Nach der Young-Laplace-Gleichung In einem kugelförmigen Tropfen des Radius $r$, beispielsweise einem kleinen Wassertropfen oder einer Gasblase in einer Flüssigkeit, herrscht aufgrund der Oberflächenspannung $\gamma$ an der Grenzfläche Flüssigkeit/Gas ein um $\Delta p$ erhöhter Druck:

$\Delta p={\frac {2\cdot \gamma }{r}}$

Der Druck wird also umso größer, je kleiner der Kugelradius ist.

… wird der Druck umso kleiner je größer der Kugelradius ist und eine plane Oberfläche ist quasi die Oberfläche einer Riesenkugel.

Also ist der Gegendruck eher klein. --Maschinist1968 (Diskussion) 14:52, 2. Mär. 2020 (CET)

Oben schreibst du die Oberflächenspannung wirkt stärker als die Auftriebskraft, unten schreibst du, der Druck sei wegen der planen Oberfläche eher klein. Mags du mir das noch einmal klären? --Diwas (Diskussion) 01:18, 4. Mär. 2020 (CET)

(quetsch) Du hast das Fragezeichen "oben" übersehen. --Maschinist1968 (Diskussion) 00:24, 5. Mär. 2020 (CET)

Oh ja stimmt. Dann hast du genau das dargestellt, was ich erwartet hab: Der statische Auftrieb ist hier das entscheidende. --Diwas (Diskussion) 00:38, 5. Mär. 2020 (CET)

Dieses Beispiel ist hochgradig verwirrend; die Münze schwimmt auch ohne Oberflächenspannung, weil Quecksilber eine doppelt so hohe Dichte hat als übliches Münzmetall. Würde die Münze einmalig vollständig untergetaucht, käme sie trotzdem wieder an die Oberfläche.

Die Oberflächenspannung bewirkt kein „Schwimmen“ im Sinne des statischen Auftriebs, sondern wirkt nur dem initialen Durchbrechen durch die Oberfläche entgegen.

Würden die Tierchen einmalig vollständig untergetaucht, blieben sie ggf. unten; es sei denn der Tierkörper wäre im Mittel leichter als Wasser. Ich sehe allerdings die Leichen toter Fliegen grad unterhalb des Bierschaums treiben; also vermutlich knapp unter der Dichte des Wassers.

Die Sachverhalte haben schon mindestens einem Bearbeiter gehörig den Kopf verdreht; wir sollten unsere Leser nicht grundlos mit noch mehr Effekten verwirren, die mit dem statischen Auftrieb überhaupt nichts zu tun haben.

Ahoi --Schiefbauer (Diskussion) 12:46, 4. Mär. 2020 (CET)

Strittiges Bild/Strittiger Effekt --> nicht im Artikel (ohne Beleg) mMn  — Johannes Kalliauer - Diskussion | Beiträge 18:53, 4. Mär. 2020 (CET)

Also was nun? Mit diesem Edit will Benutzer:JoKalliauer in den Artikel ohne Beleg seine TF reindrücken, der Effekt hinge von der Oberflächenspannung ab, aber fordert selbst einen Beleg für den Auftrieb als Ursache? Bitte erst mal vor der eigenen Tür kehren. Und J.K. ist nicht hier Herr der Diskussion, der Diskussionen abdreht. Erledigt wird üblicherweise vom Fragesteller oder wenn 14 Tage kein Beitrag kam. --Maschinist1968 (Diskussion) 00:24, 5. Mär. 2020 (CET)

Zu dem Problem gibt es im Archiv unter "Oberflächenspannung?” (dort) einen Kilometer Diskussion mit dem Ergebnis, dass die Oberflächenspannung geringsten Einfluss hat (und deswegen das Bild erhalten blieb?). --Maschinist1968 (Diskussion) 03:24, 5. Mär. 2020 (CET)

Untertrieb

Das Gegenteil des hydrostatischen Auftriebs wird Untertrieb genannt

• Das ist mal wieder so ein Satz von glamouröser Unbestimmtheit.
• Was soll ein „Gegenteil“ denn sein? Wie definiert sich sowas?
• Den Ausdruck gibt es in der Fachsprache ausschließlich bei U-Booten klassischer Art, also mit Tauchtanks.
• „Untertrieb“ ist keine Kraft, sondern bezeichnet den Zustand „Gewichtskraft größer Auftriebskraft“.
• Heißt: Auch beim „Untertrieb“ gibt es trotzdem einen Auftrieb und eine Auftriebskraft, sie ist auch genauso groß wie immer, es ist auch mitnichten irgendwie ein angebliches „Gegenteil“, die trotzdem vorhandene Auftriebskraft ist bloß kleiner als die Gewichtskraft.
• Für Sinkvorgänge, insbesondere die unerwünschten, außerhalb der Unterwasserfahrzeuge wird dieser fachsprachliche Begriff nicht verwendet.
• Je länger man googelt, desto schlimmer wird dieser Artikel.

Ahoi --Schiefbauer (Diskussion) 12:47, 4. Mär. 2020 (CET)

@Schiefbauer: Dein letzter Satz hat meinen Tag gerettet. Gruß Kein Einstein (Diskussion) 19:55, 4. Mär. 2020 (CET)

Mir auch. :-) Das scheint ein U-Boot-Spezifischer Begriff zu sein. Belege dazu wären noch gut. Viele Grüße Hadhuey (Diskussion) 16:51, 6. Mär. 2020 (CET)

Einfacher Versuch zum fehlenden Auftrieb, wenn kein Fluid einen Druck an der Unterseite aufbauen kann

Zur Frage, ob in verschiedenene Situationen das Fluid Auftrieb erzeugen kann, wenn ein Körper nicht frei im Fluid untergetaucht schwimmt, sondern anderes Material mit der Unterseite des Körpers in kontakt steht gibt es ja unterschiedliche Standpunkte. Zurück zur Ursprungsfrage: Herrscht Einigkeit darüber, dass kein Auftrieb wirkt, wenn weder dass Fluid noch etwas anderes Druck auf die Unterseite ausüben kann?

Beispiel: Ein Zylinder steht senkrecht im Wasser. An seiner Unterseite herrscht der normale Luftdruck, weil das Wasser, dass nur die Mantelfläche erreicht, dort keinen Druck aufbauen kann und die Luft an der Unterseite (Grundfläche) in Verbindung steht mit der normaldruckigen Luft über der Wasseroberfläche. Übt hier nur die Luft einen Auftrieb aus oder auch das horizontal um den Zylinder verteilte Wasser? --Diwas (Diskussion) 02:28, 4. Mär. 2020 (CET)

@Diwas:

Aufgrund des darüberliegenen Gewichtes steht die Luftschicht unter Druck (~Auftrieb) wenn sie mit der Luft über der Wasseroberfläche verbunden ist würde sie Ausströmen. Genau das passiert bei Erdöl/Erdgas-Bohrungen. Es sei denn es ist ein Festkörper der das Gewicht trägt, der muss dann die Spannungen aufnehmen die die Luft nicht aufnimmt.

Also unter einem Objekt muss es irgendetwas geben, dass das Gewicht des Zylinders und des Wassers trägt. Also hat dieser Körper hohe Druckspannungen. Bei einem (idealen) Fluid können dies nur die hydrostatischen Spannungen sein und somit ein statischer Auftrieb. Bei allem anderen gibt es einen Körper der diese Kräfte aufnimmt, tw. auch dynamischen Auftrieb genannt (Boden verformt sich über Jahrezehnte bis mehrere Jahrtausende, daher gibt es am selben Ort auch nur alle paar Jahrzehnete Erdbeben bzw. Vulkanausbrüche).

Ich glaube wir gehen da in Theorien die ich nicht unter statische Auftrieb fallen.

 — Johannes Kalliauer - Diskussion | Beiträge 08:33, 4. Mär. 2020 (CET)

Ächz.

• Den Versuch gibt es schon, wurde vor 350 Jahren in Magdeburg gemacht.
  • Man stelle sich statt der gedachten Ebene zwischen den Halbkugeln eine zwei Meter dicke Betonwand vor, die auf beiden Seiten mit einer Gummidecke belegt ist. Auf diesen mögen sich beidseitig die Halbkugeln fest„saugen“, und sie werden wie bisher vom Luftdruck auf die Wand gedrückt.
  • Jeder Handtuchhaken auf der Fliese per Saugnapf funktioniert genauso.
  • Es ist wohl über ein halbes Jahrhundert her, da hatten wir im Physikunterricht an so einen Handtuchhaken eine Federwaage gehakelt. Und es passte. Und die Federwaage war sogar schon in Newton.
  • Man drehe die Betonwand oder Badezimmerfliesen um 90° und nehme Wasser statt Luft.
• Es hängt, wie ich vor Wochen schon mal zum selben Thema ausgeführt hatte, von der Art des Untergrundes ab.
  • Warum kann eigentlich ein Sachverhalt nicht mal geklärt und abgeschlossen werden, sondern taucht zyklisch immer wieder von vorn auf?
  • Es setzt voraus, dass es ein praktisch die Bedingungen für ein „Fluid“ erfüllendes, die Druckkräfte in alle Richtungen ungehindert weitergebendes Medium geben würde.
  • Ein Fluid ist etwas, das in Ruhe keine Schubspannungen aufnehmen kann. Wasser, Luft und sogar Honig machen das für unsere Zwecke hinreichend gut.
  • Das Fluid muss auch an die Unterseite gelangen können und die Druckwirkung aus der sonstigen Umgebung auf die Unterfläche weiterleiten können.
• Sandboden kann Kräfte aufnehmen und ist deshalb kein Fluid.
  • Wir erinnern uns, insbesondere Beton-Ingenieure, dass schiffsladungsweise Sand aus Australien in die Wüstenstädte Arabiens verschifft wird. Dort wird es für den Beton der bekanntlich höchsten Gebäude der Welt benötigt.
  • Sandkörner aus Flüssen haben meist noch viele Kanten. Eine Sandschüttung kann Querkräfte aufnehmen, weil sich die vielen Kanten ineinander verhaken und auf je mehr Strecke Sandkörner kleine Kraftkomponenten aufnehmen desto mehr Kraft in den Untergrund abgeleitet wird.
  • Sand in den Wüsten ist eher kugelig, weil vielfach die Dünen rauf- und runtergeweht und abgeschliffen. Sand aus den Wüsten Arabiens ist für Beton ungeeignet, weil die Kügelchen leicht aneinander vorbeigleiten können und sich nicht genug verhakeln.
  • Für den Sand in den Nord- und Ostsee-Flussmündungen gilt, dass ungefähr einen Meter von der Berührungsstelle Schiffswrack-Sand-Wasser die weiterleitende Wirkung des Modders soweit abgebaut und durch Verhakelung in den Untergrund umgelenkt wurde, dass es keinen technisch relevanten Auftrieb mehr gibt.
  • Heißt, dass ein zehn Meter breites Wrack mit den inneren acht Metern genauso fest auf dem Grund liegt, als ob es dort in Stahlbeton eingegossen wäre. In der umlaufenden Randzone nimmt der noch umgelenkte Druckanteil nichtlinear und materialbedingt ab; die liefern teils Auftrieb, teils leiten sie schon Querkraft ab.
  • Wenn ein Wrack eine Weile auf dem Grund liegt, dann drückt es allmählich Wasser zwischen den Sandkörnern heraus. Der Untergrund unter einem Wrack ist fester und trockener als der freie Meeresboden, über den wir barfuß laufen würden.
  • Geologen werden sich mit Schichten unter Deckgebirge und deren Beweglichkeit besser auskennen als ich.
• Weil hier weiter oben im Abschnitt Bodenkräfte erörtert wurden:
  • Auf den Meeresboden wirken die Gewichtskräfte von Stahlschiffsrumpf, Wassersäule darüber und 1 bar für Luftsäule bis zum Mond.
  • Wenn eine Wasserschicht zwischen Schiffsrumpf und Meeresboden eindringen kann und diese den Umgebungsdruck widerstandsfrei weiterleiten kann, dann wirkt dieser Druck in Richtung oben auf den Schiffsboden und in gleicher Höhe nach unten auf den Meeresboden.
  • Genau dieser Druck auf den Schiffsboden ist die Ursache für unseren Auftrieb.
  • Wenn keine Wasserschicht dann kein Auftrieb. Dann liegt der Schiffskörper halt direkt auf dem Meeresboden.
• Und weil irgendwo viel weiter oben mal die zwei Glasplatten auftauchten und in Zweifel gezogen wurden:
  • Die viskosen und molekularen Kräfte der Flüssigkeit sind vernachlässigbar klein gegenüber der Wirkung des Luftdrucks auf einen halben oder ganzen Quadratmeter.
  • Ich unterstelle mal, dass das Wasser oder sowas ist und kein Kunstharzkleber.
  • Wenn der Spalt schmal und durchgängig mit Wasser befüllt ist, dann kann nicht synchron zum Auseinanderziehen der Glasplatten schnell genug Luft von der Seite eindringen und den Druckausgleich herstellen.
  • Somit halten die beiden Glasplatten bis in Höhe des Kavitationsdrucks des Wassers zusammen.
  • Nur wenn die Benetzung nicht vollständig wäre, also trockene Kanäle die Luft von der Seite aus hereinleiten könnten, oder der Spalt einigermaßen breit ist, dass das Wasser schnell genug vom Rand nach innen fließen könnte, bekäme man die beiden Glasplatten ohne Schwermaschinen auseinander. Einen ganzen oder selbst einen halben Quadratmeter bringt der stärkste Mann nicht auseinander.
  • Das wusste man schon vor 350 Jahren in Magedburg, womit ich den Bogen zum Anfang geschafft hätte.

Ahoi --Schiefbauer (Diskussion) 12:46, 4. Mär. 2020 (CET)

Warum wirkt dann auf Pfeiler am Meeresgrund ein hydrostatischer Auftrieb (Detlef Aigner, Gerhard Bollrich: Handbuch der Hydraulik. ISBN 978-3-410-21341-3, S. 100 (eingeschränkte Vorschau in der Google-Buchsuche).), der "die Standsicherheit gefährden" kann ? --Maschinist1968 (Diskussion) 23:55, 5. Mär. 2020 (CET)

@Maschinist1968:Weil zwischen Untergrund und Pfeiler Wasser ist.  — Johannes Kalliauer - Diskussion | Beiträge 00:08, 6. Mär. 2020 (CET)

Also Unter dem Bauwerk ist Wasser und der Erddruck, aber unter dem U-Boot im Schlamm nicht? Merkwürdig? Der Pfeiler hätte Auftrieb, aber das (auftauchfähige) U-Boot nicht? --Maschinist1968 (Diskussion) 00:15, 6. Mär. 2020 (CET)

@Maschinist1968: Ich sag nicht, dass es beim U-Boot nicht wirk, ich sag nur, dass es dann nicht wirkt, wenn kein Wasser darunter ist. Einfacheres Beispiel: Stell dir ein U-Boot in einem Güterschiff vor. Auf das Schiff wirkt der Auftrieb, auf das U-Boot nur indirket. Bzw. @Diwas: Konservendosen-Beispiel unten ist noch viel besser!  — Johannes Kalliauer - Diskussion | Beiträge 09:36, 7. Mär. 2020 (CET)

Und was wirkt dann auf den Pfeiler? --Maschinist1968 (Diskussion) 12:53, 9. Mär. 2020 (CET)

Unter beiden Bildern wird darauf hingewiesen, dass der Boden bzw. die Gründung durchlässig sein muss. Das Wasser kann nur Auftrieb erzeugen, wenn es die Unterseite des Pfeilers, der Gründung oder eines Körpers erreicht, der die Auftriebskraft an den Pfeiler übertragen kann. --Diwas (Diskussion) 00:14, 10. Mär. 2020 (CET)

Erneuter Versuch, die grundsätzliche Aussage zu klären, dass ohne Fluiddruck von unten kein Auftrieb entsteht

Bei aller Berechtigung der Diskussionen: Oben werden sehr viele Fragen kombiniert, daher noch einmal ganz einfach: Ein gewöhnliches Spülbecken wird so hoch mit Wasser gefüllt, dass eine leere senkrecht stehende Konservendose gerade nicht überflutet wird. Drückt man die Dose senkrecht ins Wasser, spürt man einen deutlichen Auftrieb. Der Abfluss ist mittels eines offenen zweiten oder eines offenen Überlaufs mit der umgebenden Luft verbunden. Der Abfluss wird geöffnet und die Dose, ohne das Wasser in sie eindringt, auf den Abfluss positioniert. Die Dose bleibt stehen, da kein Auftrieb (abgesehen des geringen der Luft auf das dünne Blech) mehr wirkt, denn das wenige sickernde Wasser fließt ab und hat so keine Möglichkeit Druck aufzubauen. Wohlgemerkt, obwohl die Dose seitlich von Wasser umgeben ist und sie mit der enthaltenen Luft deutlich geringere Dichte hat, als das Wasser rund um ihre Mantelfläche. --Diwas (Diskussion) 02:32, 6. Mär. 2020 (CET)

Damit hast du über dem Abfluss einen Saugdruck wie von einer Strahlpumpe. --Maschinist1968 (Diskussion) 14:29, 6. Mär. 2020 (CET)

Es gibt keinen Saugdruck, nur umgebenden Luftduck. Wir betrachten hier ein statischen System. Bei einer Pumpe strömt die Flüssigkeit (=Dynamisches System). Ich dachte eigentlich auch, das wäre geklärt. Schönen Gruß aus Magdeburg übrigens ;-) Hadhuey (Diskussion) 16:49, 6. Mär. 2020 (CET)

Maschinist1968: Das überzeugt mich nicht. Die Fließgeschwindigkeit ist eher niedrig. Die Fläche der Dosenwandunterseite ist extrem gering. Es gibt keinen merklichen Unterschied, ob die offene Seite oben oder unten ist. Selbst wenn auch die zweite Grund-/Deckfläche ausgeschnitten wird, bleibt die Dose am Boden und wird nicht aufgetrieben, sondern das Wasser aus dem Doseninneren läuft ab; also kein Auftrieb erkennbar, obwohl der Auftrieb sehr deutlich zu spüren war, als (abseits des Ablaufs) unter der Dose Wasserdruck wirken konnte. Immer wenn der Falz unten ohne eine anschließende Fläche allein verbleibt, ist die Fläche extrem gering, wo ein dynamischer Abtrieb angreifen könnte. Ich bin sicher das klappt auch mit einer weichen Dichtung. --Diwas (Diskussion) 04:00, 7. Mär. 2020 (CET)

@Maschinist1968: Saugdruck ist mMn ein irreführender Begriff, Unterdruck wäre passender. Unter der Dose herrscht aber Normaldruck, weil durch den Abfluss Luft zuströmen kann (Also es ist kein Vakuum.) Würde keine Luft hinströmen(Vakuum), würde die Dose vom darüberliegeneden Lufdruck sogar nach unten gezogen gedrückt werden(Abtrieb?/Untertrieb?), ich glaube das meinst du mit Saugdruck. Auch wenn ich den Begriff Saugdruck nicht kenne, verstehe ich so viel, dass ich sagen würde, dass Diwas einen korrekten physikalsichen Effekt korrekt beschreibt. @Diwas: gutes Beispiel.  — Johannes Kalliauer - Diskussion | Beiträge 09:36, 7. Mär. 2020 (CET)

Richtig: Es gibt physikalisch gesehen keinen "Saugdruck". Es kann nur einen verringerten Druck gegenüber der betrachtenen Umgebung geben, weil es keinen negativen Druck gibt. Einen zum Bezugssystem verringerten Druck nennt man in der Technik "Unterdruck". Für unsere statischen Betrachtungen sollten wir aber auch nicht mit "Unterdruck" arbeiten, sondern entweder mit Vakuum als Bezugswert oder wenigstens mit dem geringsten im Bezugssystem vorkommenden Druck. Das wäre hier der Luftdruck. Bei allem anderen kommt nur Verwirrung heraus. Hadhuey (Diskussion) 09:58, 7. Mär. 2020 (CET)

In Festkörpern gibt es negative hydrostatische Druckspannungen (alisas Zug) aber in idealen Fluiden wurde Zug imho zu einem Schubbruch führen und damit kann man in idealen Fluiden imho keinen negativen Druck aufbringen.

@Hadhuey: Aber ein Wassertropfen (kein ideales Fluid) das am Wasserhahn hängt, nimmt aufgrung von Adhäsion?/Oberflächenspannung?/Kohässion?/warum-auch-immer sehrwohl Zugspannungen auf.

 — Johannes Kalliauer - Diskussion | Beiträge 11:09, 7. Mär. 2020 (CET)

Ein ideales Fluid hat keinen Dampfdruck, keine gelösten Gase und noch nicht einmal Moleküle. Kavitation und Bläschenbildung sind damit ausgeschlossen. Und ohne einen durch intermolekulare Kräfte vermittelten Zusammenhalt fehlt sogar ein Mechanismus, der hinter einem Zerreißen stehen könnte. Entsprechend würde ich bei einem idealen Fluid sogar eine beliebig hohe Zugspannung für möglich halten. Aber man kann sich natürlich darüber streiten, was genau ein "ideales Fluid" ausmacht. Bei realem Fluiden demonstriert jeder mehr als zehn Meter hohe Baum, dass Wasser in Kapillaren deutlich Zugspannung und damit negativen Druck aushalten kann ohne zu zerreißen. ---<)kmk(>- (Diskussion) 02:21, 11. Mär. 2020 (CET)

mini

@KaiMartin: Aufgrund von Kapillarität, kann Wasser in Bäumen >100Meter steigen, siehe Hyperion_(Baum), das hat was mit der Oberflächenspannung/Adhässion von Wasser zu tun aber mMn nichts mit hydrostatischen Spannungzuständen.

Jede Abweichung von isotrophen (alias hydrostatischen) Spannungszuständen, nennt man deviatorische Spannungen. Wenn es deviatorische Spannungen gibt es Schubspannungen und umgekehrt. Der Unterschied zwischen Druck und Zug ist der: Wenn man ein Kontinuum (Festkörper oder Fluid) unter großen (hydrostatischen) Druck gibt plastifiziert der Körper in Richtung eines hyrostatischen Spannungszustandes (er kann ja nicht aus, das maximale Volumen ist vorgegeben). Bei homogenen (keine Schwerkraft) hydrostatischen Zug hingegen, führt eine Abweichung des hydrostatischen Spannungszustandes die größer ist als die Schubfestigkeit (bei idealen Fluiden=0) zu einem Schubbruch und somit zu Vakuum (Das Fluid nutzt nicht das gesammte Volumen aus). Zu sagen es gibt hydostatische Zugspannungen in idealen Fluiden ist eine rein theoretisch Lösung, bei der jede Störung (zB Temperatur >0K) zu einem Versagen führt, das ist wie zu sagen ein gerade Knickstab knickt nie, weil er nicht weiß ob er rechts oder links ausknicken soll (Ich vermute man kann auch belegen, dass ideale Fluide keinen Zug aufnehmen können). Sobald wir ein Schwerefeld einführen und das haben wir ja im Falle eines statischen Auftriebes idR gegeben ist, ist es hingegen mMn wieder klar: Der Wasserspiegel sinkt und darüber ist Vakuum.  — Johannes Kalliauer - Diskussion | Beiträge 10:54, 11. Mär. 2020 (CET)

Wenn unter der Dose Luft ist, dann gibt es Auftrieb in Luft, der wird wegen des Gewichts der Dose so gering sein, dass sie stehen bleibt oder Unterdruck.--Maschinist1968 (Diskussion) 12:01, 7. Mär. 2020 (CET)

Ja, es gibt Auftrieb in Luft, es ging ja aber gerade um den nicht vorhandenen Auftrieb in Wasser, das nur die Mantelfläche erreicht. --Diwas (Diskussion) 23:09, 7. Mär. 2020 (CET)

Gravitation

Sollte es nicht sehr große Schnittmengen zwischen der Gravitation und dem Auftrieb geben, und sollte man das nicht erwähnen? (nicht signierter Beitrag von 213.142.96.28 (Diskussion) 23:46, 21. Okt. 2022 (CEST))

Magst du genauer sagen, welche "Schnittmengen" du meinst? Es sind beides Kräfte, die man im Alltag erfährt. Und sonst? Kein Einstein (Diskussion) 14:29, 22. Okt. 2022 (CEST)

Heißluftballon

Im Artikel steht:Ein Heißluftballon steigt beispielsweise so weit auf, bis er eine Luftschicht geringerer Dichte erreicht hat, die einen geringeren Auftrieb verursacht und die gleiche Dichte wie der Ballon hat. Das ist zumindest ein Missverständnis fördernd: Ein Heißluftballon (und auch ein Luftschiff) ist unten offen (bzw. hat Ballonetts). D.h. auch die Dichte des Traggases und damit des Ballons reduziert sich beim Aufstieg. Wenn im Ballon immer die doppelte Außentemperatur wäre, wäre der Auftrieb immer die halbe Ballongröße*Luftdichte der aktuellen Höhe. In der Realität schwebt ein Heißluftballon nie, sondern fährt vertikal Zick-Zack wegen der Abkühlung und dem Nachheizen.

Mein Vorschlag ist im Beispiel den Heißluftballon durch einen (druckfesten) Folienluftballon mit konstantem Gewicht und konstantem Volumen zu ersetzten. Das ist aus meiner Sicht einfacher zu erklären und zu verstehen. --Schrauber5 (Diskussion) 15:54, 20. Mai 2024 (CEST)

Ich verstehe dein Problem und deinen Ansatz. Aber ich gebe zu bedenken, dass ein druckfester und volumenkonstanter Ballon auch eine ganz schöne Herausforderung für den Leser ist.... Kein Einstein (Diskussion) 17:15, 20. Mai 2024 (CEST)