Diskussion:Weltraumlift/Archiv/1

Diese Seite ist ein Archiv abgeschlossener Diskussionen. Ihr Inhalt sollte daher nicht mehr verändert werden. Benutze bitte die aktuelle Diskussionsseite, auch um eine archivierte Diskussion weiterzuführen.

Um einen Abschnitt dieser Seite zu verlinken, klicke im Inhaltsverzeichnis auf den Abschnitt und kopiere dann Seitenname und Abschnittsüberschrift aus der Adresszeile deines Browsers, beispielsweise

[[Diskussion:Weltraumlift/Archiv/1#Thema 1]]

oder als Weblink zur Verlinkung außerhalb der Wikipedia

https://de.wikipedia.org/wiki/Diskussion:Weltraumlift/Archiv/1#Thema_1

"Erfindung"

"Bekannt wurden diese Ideen in der Öffentlichkeit, als Arthur C. Clarke sie 1978 als Teil eines Romans (The Fountains of Paradise) vorstellte."

Ich bin relativ sicher das dies schon vorher in bekannten Science Fiction Roman benutzt wurde, z.B. von Robert A. Heinlein oder Larry Niven. Wenn ich eine Quelle finde werde ich den Artikel ändern.

Sicher wurde der Lift schon vorher in der Literatur verwendet, aber erst durch Fountains of Paradise wurde die Idee bekannt. JE 17:34, 23. Mär 2006 (CET)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Unfallgefahr

Was passiert eigentlich wenn das Seil mal runterfällt? dürfte einen ganz hübschen Krater geben.. 790 08:49, 9. Aug 2005 (CEST)

wenn der schwerpunkt des seiles im geo ist, duerfte es nicht runterfallen, solange es nicht unterhalb des geo gekappt wird.

wenn dies passiert, muss man immernoch bedenken, dass das "seil" nicht auf eine stelle faellt sondern sich auf eine ziemliche flaeche verteilt. desweiteren muessten warscheinlich noch viele dinge um das seil herumbebaut werden (z.B. stromleitungen, schienen, messgeraete), so dass es sich eher um einen turm handelt, der in einzellne handlichen segmenten an fallschirmen zu boden gleiten koennte (wuerde dann natuerlich vorraussetzen, dass in einem k-fall das seil an den entsprechenden segmentenden getrennt wird.

aber das ist natuerlich alles spekulation ;) Elvis_untot 42 12:04, 27. Sep 2005 (CEST)

Das dürfte sich eher verteilen, die Abschnitte werden ja wohl nicht alle an einer Stelle in die Erdathmosphäre eintreten. (unterschiedliche Bahngeschwindigkeit). Ich denke sogar das Teile die oberhalb einer bestimmten Höhe sind, den Eintritt gar nicht überstehen und verglühen.

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Last den Mist mit den Zukunftsromanen raus

Der Artikel hier selber ist schon Zukunftsmusik, jetzt möchten einige IP's den ganzen Artikel auch noch mit Zukunftsromanen wie Robert A. Heinlein oder Larry Niven untermaueren. Das hat nichts mit einem fundierten wissenschaftlichen Erkenntnissen oder handwerklichem Können oder historischen Beispiellösungen zu tun, die ein Lexikon erwähnen könnte oder sollte. Wer seinen Ideen einbringen will, soll sich bei Geocities eine Freewaredomain registieren und hier als Link einbinden. Ansonsten gelangen wir hier ganz schnell beim geistigen Dünnschiß an. --84.176.69.247 20:14, 1. Nov 2005 (CET)

Es geht hier um Visionen. Viele der heutigen Technologien waren mal Elemente in Zukunftsromanen. --212.204.77.149 12:47, 9. Nov. 2009 (CET)

Ich bin dafür, die weitere Diskussion zu stoppen. Ernsthaft. Viele Beiträge dieser Diskussion sind in der Tat laienhafte SciFi-Theorien und vielen Teilnehmern fehlt offenbar schlicht der physikalische, mathematische und ingenieurwissenschaftliche Hintergund für diese Diskussion. Ich möchte niemendem persönlich zu nahe treten, muss aber schon mal was geraderücken: Einerseits werden Haken in den Himmel gehängt, seitenlange Hobby-Berechnungen mit fehlerhaften Einheiten angestellt, Nano-Materialien im Orbit aufgehängt aber andererseits recht simple physikalische Sachverhalte außer acht gelassen. Das geht vielleicht noch, dass jeder mal seine persönliche Sicht zu einem Thema verkündet, das ansonsten im professionellen Zusammenhang von Experten und Forschern von NASA und EADS beleuchtet wird. Aber am Ende muss auch ein bisschen wissenschaftliche Seriösität Eingang in dieses Medium finden. Sonst besteht in meinen Augen die Gefahr, dass wir das Niveau von Toilettensprüchen nicht wesentlich überschreiten. Auch scheint mir niemand mal die Überlegung angestellt zu haben, warum das nicht schon längst mal umgesetzt oder wenigstens ausprobiert wurde? Glaubt Ihr wirklich, da wäre ein von Braun oder andere Vordenker nicht schon mal drauf gekommen und hätten das durchdacht? Jede Wette, das haben die auch schon mal überlegt, aber am Ende wieder verworfen. Weil sie klug waren. Also nochmal meine dringende Bitte: Diskussion stoppen. Und wer weiterhin Visionen hat, kann ja mal einen Roman schreiben oder sollte vielleicht mal einen Arzt aufsuchen. (nicht signierter Kommentar von Airchiller (Diskussion | Beiträge) 00:31, 12. Nov. 2009 (CET))

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Fadenlänge

im artikel heisst es das es gelungen sei einen 100m lange nanofaserfaden herzustellen beim artikel kohlenstoff (siehe modifikation) steht aber nur etwas von 20-50 cm... hat jemadn dazu eine quelle? MfG

Da in dem Bereich höchst aktiv geforscht sind, gibt der eine die Länge wirtschaftlich herstellbarer Fäden an, der andere die Maximallänge eines jemals im Labor hergestellten Fadens, der dritte die Länge der Fäden, von denen er glaubt, dass sie in zwei Jahren wirtschaftlich herstellbar wären. Die Zahlen sind also allesamt mit Vorsicht zu genießen und darüber hinaus äußerst vorläufig. Joachim Durchholz 10:49, 21. Okt. 2008 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Dyneema: © oder ®?

Mit welchem Zeichen soll Dyneema gekennzeichnet werden: © oder ®? --84.61.99.165 17:45, 30. Mär 2006 (CEST)

Guck dir die Bedeutung von © und ® an, dann weißt du, dass ® richtig ist, da es sich um eine eingetragene Marke handelt. Sofern es eben eine solche ist. --RokerHRO 17:24, 26. Mai 2006 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Windeinfluss

wie siehts eigentlich mit dem Windeinfluss aus? immerhin muss man schon bei Hochhäusern stark darauf achten. zusammen mit der tatsache das 'seil' schon aufgrund der drehbewegung der erde sicher irgendwelche verrenkungen machen müsste, wenn ein gewicht hochtransportiert wird, muss das seil doch sicher deutlich länger als die hier berechnete länge werden?

wenn du dir die Länge des Seil ansiehst( ich habe etwas von 100.000 km gehört) und das mit der Höhe des Luftraums (<25km ) vergleichst, dürfte sich das Auspendeln. Außerdem wird zumindestens bei Liftport die Geometrie an die Unterschiedlichen Umgebungen angepasst. D.h. die unteren Sektionen sind eher rund( um keine WIndlasten aufkommen zulassen), die oberen eher flach um bei Mikrometeoriten-durchschlägen noch genügend Restmaterial zu haben.

Lass doch den Wind meinetwegen mit 200 km/h wehen. Was ist das schon im Vergleich zu den rund 10.000 km/h, die die Last drauf hat wenn sie aus dem geostat. Orbit runterkommt? -- Kyber 17:17, 26. Mai 2006 (CEST)

Die beiden Geschwindigkeiten haben miteinander nichts zu tun: die Windgeschwindigkeit ist die, gegen die das Seil stabilisiert werden muss, die Absturzgeschwindigkeit die, die erst bei Ausfall der Stabilisierung zum Tragen kommt. (Letzteres Thema wird an anderer Stelle behandelt.) Joachim Durchholz 10:54, 21. Okt. 2008 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Jerome Pearson

• Jerome Pearson in der [Washingtonpost] zu seinem SBIR-Preis [[1]]

Ob das eher so ist, das er wie eine von vielen einen Preis für seine SF bekommen hat?

"Bradley C. Edwards, president and founder of Carbon Designs Inc., is the driving force behind the space elevator" [[2]] finde ich auch keinen so tollen Experten für den Weltraumlift - eher für Finanzierng seiner Carbon-Forschung o.ä.

Hat das schon mal jemand nachgerechnet, ob das physikalisch überhaupt funktioniert. (Selbst wenn wir so stabile Seile hätten.) Oder ist das alles nur aus der PM 11/1981 (ab Seite 10) abgeschrieben?

-- Kyber 23:03, 4. Jun 2006 (CEST)

Die NASA hat einen Wettbewerb ausgeschrieben, hält das Ganze also für prinzipiell machbar. Insofern beantworten die Fachleute Deine Frage mit "ja, funktioniert physikalisch". Joachim Durchholz 10:56, 21. Okt. 2008 (CEST)

Nein. Die Nasa hat in Teilbereichen Ausschreibungen. Dabei geht es nur um Motivation für Grundlagenforschung. Ein Projekt "Weltraumlift" ist wahrscheinlich nicht machbar. Z.B wegen Schwingungen und Stabilisierung (siehe auch "Wind") 91.15.244.18 23:17, 12. Apr. 2009 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Auswirkungen

„Es ist denkbar, dass ein Weltraumlift die Transportkosten von derzeit 20.000 bis zu 80.000 US-Dollar pro kg nach seiner Armortisierungszeit auf bis zu 200 US-Dollar pro kg reduzieren könnte“ - dieser Satz ist bespielhaft für hinterhältiges Marketinggeschwätz, das dazu dient, ahnungslose Laien und besonders doofe JournalistInnen hereinzulegen. Denn

• es sind in den 20. - 80.00 $ herkömmlicher Raketentechnik die Entwicklungskosten etc und damit auch die Amortisation bereits enthalten und

• es fehlt eine Schätzung der Investitionskosten für den Lift und daher

• ist es keineswegs gesichert, dass ein solches Monstrum jemals amortisiert werden könnte.

Ich schau' bald mal wieder vorbei hier, und wenn sich die Kundigen bis dahin nicht etwas Mühe gegeben haben, setzt es ein QS-Bapperl. --Lycopithecus 14:31, 10. Dez. 2007 (CET)

habe ne quelle dazu und etwas geaendert, aber man sollte den satz noch komplett umschreiben. was die nutzlast bei raketen kostet, habe ich leider nichts gefunden. das billigste scheint momentan unter 7.000€ für LEO zu sein (siehe Trägerrakete Eintrag bei Eurockot, jedoch ohne Quelle) den QS-Bapperl darfst du gerne draufmachen, aber bitte mit kommentar drunter, sonst kümmert sich keienr drum und dieser eintrag ist auch zu versteckt mitten auf der seite gelandet. Elvis untot 15:03, 13. Dez. 2007 (CET)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Seilmaterial

hi, nur mal so im artikel steht nirgends das man schon einmaterial gefunden hat obwol es solche gäbe, weiss jemand mehr? ob es realisierbar ist oder nicht?

Hallo,
In der Doku 2057 beschreibt der japanische Physiker Kaku, die Fortschritte des Materials. 
http://www.imdb.com/title/tt0977682/
Grüsse Bernd

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Energieversorgung

Für die Energieversorgung gibt es vielleicht eine sehr elegante Lösung.

Hierzu folgende Annahme: Der Lift wird sehr nahe vom Äquator in Peru auf dem Cayambe verankert. [3] Das Hilfsseil wir in östlicher in 300km Entfernnung verankert. Der Lift ist mit dem zweiten Band über eine Hilfsseil von ca. 400km Länge verbunden. Damit dies nicht beim Start 300km auf dem Boden liegt, wird es in durch eine keine Hilfsstation in vielleicht 100km Höhe abgefangen. Das muss man sich so vorstellen, als würde man einen dicken Knoten in ein Seil machen um das runterrutschen zu verhindern. Beim hochfahren wird dann ständig ein kleiner zug vom Hilfsseil in Drehrichtung der Erde ausgeübt. Hierdurch wird der Lift ständig beschleunigt.

Das Liftsystem besteht aus zwei Bändern von z.B. 50 und 500mm Breite. Dem Hilfsband, dem Lift und einem Hilfslift am Hilsseil. Haupt, Verbindungsseil und Hilfsseil bilden etwa ein Trapetz.

Bei Verwendung von Kohlenstoff Nanoröhren ist es wahrscheinlich möglich das Halteseil selbst mit einem Hilfsseil als Stromleiter zu verwenden. Allerdings habe ich bis jetzt noch keine Informationen gefunden, ob der Type von Nanofassern mit der höchsten Zugkraft auch zu der Sorte gehört welche eine sehr hohe Leitfähigkeit aufweisen. (ca. 1000x besser als Kupfer)

Hier folgende Annahmen: Liftmasse (Lm): 10.000kg Gewichtskraft am Boden (LF): Lm*G=98,1kN Anfangsgeschwindigkeit (v0): 20,4m/s (73,44km/h) der Liftkabine Maximale Geschwindigkeit .: 111,1m/s (400km/h) Maximaler Energigbedarf ..: LF*v0=2MW Seildimension Hauptband ..:(500x0,1mm) (am Boden) Seildimension Nebenband ..:( 50x0,1mm) (am Boden) Hier folgt ein Querschnitt des Nebenbandes von ......; 5mm^2

Arbeitet man z.B mit einer Spannung 50.000V so währen anfangs 40A(=Amper) nötig. Da die Leitfähigkeit vielleicht um den Faktor 1000 besser ist als in Kupfer, entspricht das einem Strom von 8mA/mm^2 in Kupfer für das Hilfsband und 800µA im Hauptband. Weiterhin wird das Band natürlich immer breiter bzw. dicker. Das hat zur Folge das von den 2MW Leistung weniger als 600W in Wärme umgewandelt werden. Da die Schwerkraft mit der Höhe abnimmt, sinkt auch Gewichtskraft des Liftes. Der Lift würde mit zunehmender Höhe langsam schneller bis zu einer maximalen Geschwindigkeit von 400km/h. Der Energiebedarf würde ständig mit E=E0/r^2 abnehmen.

Hier eine keine Liste mit Zeiten und Höhen über dem Boden:

Fahrtzeit |Höhe in km | G(h) in Stunden |über dem Meer| m/s^2

       0,0|     6,0 | 9,78
       1,0|    73,6
       2,0|   153,4
       5,0|   394,1
      11,9| 1.012,6 | 7,27
      25,0| 2.601,9 | 4,90
      48,4| 8.245,1 | 1,79
     117,2|35.786,0 | 0,0   (Geo-Orbit in 4Tagen 21h und 7m)

Da der Winkel zum Hilfsband immer schlechter wird, währe es denkbar das Hilfband z.B. beweglich auf einer Eisenbahn anzubinden, hierdurch könnte der Winkelverkleinerung entgegengewirkt werden. Eventuell ist es auch möglich den Lift bis zu einem gewissen Grad im mittleren Bereich stärker in Bahnrichtung zu beschleunigen.

Naja, 1000fach bessere elektrische Leitfähigkeit als Kupfer erreicht man aber mit keinem bekannten Material, auch Kohlenstoffnanoröhren nicht. Da müsste man schon Supraleiter nehmen und das Seil dann stark kühlen. Das wird also nix. --RokerHRO 18:50, 11. Feb. 2007 (CET)

Offenbar wurde die Wärmeleitfähigkeit mit der elektrischen Leitfähigkeit gleichgesetzt... --1-1111 09:03, 9. Feb. 2010 (CET)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Energiebedarf

"The low energy requirements for moving payloads up and down the elevator could make it possible to achieve cost to orbit <$10/kg." http://trs.nis.nasa.gov/archive/00000535/ Also, wenn die NASA mir für weniger als 10$ ein kg um knapp 10.000km/h beschleunigt + verzögert, sollte ich vielleicht mal mit denen ins Geschäft kommen. Bei E = 0,5 * m * v² komme ich auf jeweils 0,5 * 2589² kg m²/s² = 3,35 MJ pro kg .. und das für <10$

Kleiner Einwurf hier: Dir ist schon klar, dass 1 KWh exakt 3.6 MJ entspricht und für etwas weniger als 10$ zu haben ist? Die Erzeugungskosten liegen übrigens im Bereich von 1 Cent/kWh. --Jogy 20:47, 21. Okt. 2007 (CEST)

Auweia, das kommt davon, wenn ich mich auf Joule einlasse - und dann noch von den Mega blenden lasse. -- Kyber 23:07, 21. Okt. 2007 (CEST)

Auch stell´ ich es mir spannend vor, wie man das Seil für diesen Weltraumlift in seiner ganzen Länge auf die entspr. Bahngeschwindigkeit beschleunigt. Ansonsten würde es sich nämlich um die Erde wickeln. :-\

Oder habe ich da jetzt was übersehen?

>Naja, das Seil wird wohl komplett zusammengerollt auf GEO gebracht >und von dort nach oben und nach unten abgewickelt. >Sodass der Schwerpunkt immer auf GEO bleibt.

Darüber muß ich nochmal nachdenken. Zum einen baumelt´s rauf und runter. Zum anderen haben die beiden Enden 11.000 km/h.

Und das ändert noch nichts an der höhenabh. Geschwindigkeit der (Nutz-)Last.

Vielleicht findet sich in deren Linkliste was dazu *[[4]] -- Kyber 15:35, 27. Mai 2006 (CEST)

• Jerome Pearson in der [Washingtonpost] zu seinem SBIR-Preis [[5]]

Denkbar wäre auch, dass das Seil erst im Weltraum produziert wird, was zwar nicht unbedingt einfach ist, aber zumindest die gigantischen Kosten die notwendig wären um ein Kabel der notwendigen Länge/Masse in eine Umlaufbahn zu bringen unterbieten könnte. Im Buch "Roter Mars" von Kim St. Robinson kommt ein derartiger Space-Elevator vor und der wurde von Robotern auf einem eingefangen Asteroiden durch Abbau der Ressourcen des Asteroiden "gebastelt" - ziemlich nettes Konzept, wenngleich nicht unbedingt realistischer :)

Hallo an alle,
zum Energieverbrauch beim Beschleunigen der Nutzlast:
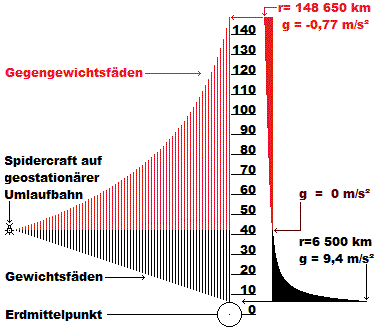
Wenn der Weltraumlift durch ein ausreichend grosses Fliehgewicht oberhalb der geostationären Umlaufbahn gespannt wird, dann stammt die Energie zum Beschleunigen der Nutzlast direkt aus der Erdrotation, die dadurch ein klein wenig langsamer wird.
Im Idealfall zeigt die dabei entstehende Corioliskraft immer genau quer zum Weltraumlift, so dass man nur die Energie zum Hochheben der Nutzlast verbraucht.
Wenn das Seil höher als bis in eine Höhe von 143.800 km über der Erdoberfläche führt, kann man sogar Energie aus der Erdrotation gewinnen.
Leider kommt es dann bald zu Störungen durch die Mondgravitation.
http://members.chello.at/karl.bednarik/GEOSYN-3.jpg
Wenn man aber immer die gleiche Menge an Planetoiden-Rohstoffen zur Erde hinab transportiert, dann sind alle Kräftebilanzen und Energiebilanzen völlig ausgeglichen.
Mit freundlichen Grüssen,
Karl Bednarik 09:11, 5. Jul 2006 (CEST).

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Elastizität

So ein langes Seil ist ja keine starre Stange. Schon bei den Fahrstühlen in Wolkenkratzern war Überschwingen ein Problem. Wenn die Gondel am Erdboden anfährt und beschleunigt wird sie das Seil doch wohl erstmal um ein paar km strecken. Wird man da drin nicht Seekrank, wenn man ständig vor und zurückbeschleunigt wird? -- Kyber 22:44, 11. Apr. 2007 (CEST)

Schwingungen und Resonanzen werden oft als mögliches Problem genannt. Da muss gar nicht der Ruck der Gondel schuld sein, allein Windstöße können schon erhebliche Probleme verursachen. Ich weiß nur im Moment nicht mehr, wo ich das gelesen habe, sobald mir die Quelle wieder unterkommt, werde ich das dem Artikel hinzufügen. -- Wilfried Elmenreich 20:49, 12. Apr. 2007 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Realisierbarkeit?

Es mag ja an meinem eher sporadischen Interesse an diesem Thema liegen. Aber bisher konnte ich zum genannten Thema nur „globale“ Berechnungen entdecken: Fliehkraft, gelegentlich „etwas Coriolis“ usw.

Was mir fehlt ist eine Betrachtung im Detail. Modelle, die das physikalische Verhalten der Konstruktion betrachten – im Gegenssatz zu solchen, die einen oder ein paar Massepunkte „irgendwo“ herumwirbeln lassen.

Brücken- und Liftbauer (um mal Leute mit einigermaßen vergleichbaren „Interessen“ zu erwähnen) geben sich ja auch nicht mit einer maximalen Tragekraft, ein paar Sicherheitsreserven und der Zugspannung von Stahl („eine Sorte!“) zufrieden.

Hier haben wir ein (bislang theoretisches) System, das nur auf den ersten Blick einfacher aufgebaut ist:

1. das „Seil“ dürfte IMO schon wegen der Betriebssicherheit kaum aus einem einzelnen Element bestehen.
2. Sein Querschnitt, möglicherweise seine Zusammensetzung, ändert sich über die Länge fortlaufend.
3. auch die einwirkenden Kräfte scheinen mir bestenfalls in Ausnahmefällen etwas Konstantes an sich zu haben.
4. …

Wie wirkt sich das alles (und mehr) in der Summe aus? Wird das Seil vielleicht aufgespult? Verwindet es sich? Immerhin wird es fortwährend seitlich und keineswegs konstant beschleunigt und schon Newton wußte, daß so etwas nicht ohne Folgen bleibt. Die einwirkenden Kräfte sind vielartig (der Atmosphärenwiderstand scheint mir keineswegs vernachlässigbar – und wenn es dabei nur um die integrale Wirkung über die Betriebsdauer ginge! Und, weil wir ja überhaupt keinen Einfluß ausüben: wie sieht die Reaktio der Atmösphäre aus? „Schleppwirbelstürme mit ≥1200km/h?“), daran bewegte Gegenständen werden auch Schwingungen vielerlei Art auslösen … Also: gibt es dazu etwas ernsthaftes? Wenn ja: her mit dem Link! (Und wenn sich herausstellt, daß es da leider ein „kleines“, aber unlösbares Problem geben sollte: lieber ein Ende mit Schrecken …)

Ich habe mal die Differentialgleichung dafür aufgestellt, wie der Seilquerschnitt aussehen müsste, damit die vom Eigengewicht ausgelöste Zugkraft pro Quadratmeter überall die gleiche ist. Corioliskräfte und Störeinflüsse habe ich außen vor gelassen, dafür reichte (und reicht) mein mathematisches Rüstzeug nicht.

Ergebnis: die maximale Seildicke wächst exponentiell (!) mit der Differenz aus Schwerkraft (hohe Schwerkraft = mehr Last) und dem Quadrat der Rotationsgeschwindigkeit (hohe Rotation = mehr Fliehkraft = weniger Last).

So gesehen ist es erstaunlich, dass ein Weltraumaufzug überhaupt denkbar ist. Etwas weniger Rotation oder mehr Schwerkraft, und selbst die Bindungskräfte zwischen Atomen wären nicht mehr genug. Aber ich denke mal, bei der NASA haben sie das durchgerechnet.

Die englische Wikipedia schreibt etwas von einer benötigten Zugfestigkeit von 65 GPa, verfügbaren Zugfestigkeiten um die 52 GPa, und theoretischen Zugfestigkeiten für Kohlenstoffnanoröhrchen zwischen 140 und 170 GPa. Man müsste also die Nanoröhrchen näher an die theoretischen Grenzen heranbringen und hätte dann immer noch gut zu tun, um das Seil stark genug für Nutzlast und Sicherheitsreserve zu machen - das ist alles äußerst knapp, aber vielleicht(!) gerade noch machbar.

Joachim Durchholz 11:49, 21. Okt. 2008 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Dyneema ist nicht geeignet

Nach den Informationen, die man zu Dyneema findet (z.B. http://www.ehlers-seilerwarenfabrik.de/techdat.html ), ist es völlig ungeeignet, weil es unter Dauerbelastung anfängt zu kriechen. Das Seil würde also immer länger und dünner werden und endlich reißen.

Mit Kevlar (HMPA) müsste es allerdings gehen, weil Kevlar nicht kriecht und etwa die gleiche Zugfestigkeit hat, wie Dyneema, ist allerdings etwas schwerer.

--Mdiekel 14:28, 2. Okt. 2007 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Schwerelos? Oder: Unterstützung des Seils durch Ballons

Tut wohl nichts zur Sache, da die höchste Belastung wohl sowieso irgendwo in der Mitte auftrit - mal abgeshen von all den anderen Problemen - aber weiss eigentlich jemand, weshalb das Kabel nich schwerelos gemacht wird ... gemacht werden kann? --Alien4 05:33, 28. Jul. 2008 (CEST)

Man ist im Weltraumlift nur schwerelos, wenn man die Station im geostationären Orbit erreicht. Die Idee ist doch, dass das Seil (halbwegs) gerade vom Boden bis zum Gegengewicht verläuft, d.h. über die ganze Länge die gleichen Winkelgeschwindigkeit hat. Man braucht für Schwerelosigkeit (d.h. Fliehkraft=Schwerkraft) aber immer höhere Winkelgeschwindigkeiten, je tiefer man kommt (was ich jetzt nicht nachweisen will), d.h. wenn man von der Erde aus aufwärts fährt, wird der Effekt 1 lauten, dass die Gravitation abnimmt und die Zentrifugalkraft zunimmt, man fühlt sich also immer leichter, bis man auf der geostationären Höhe ankommt. Fährt man weiter, hängt man plötzlich an der Decke. Die Kraft, die einen an die Decke drückt, wird bei zunehmender Höhe immer größer; und wenn man zu hoch fährt, übersteigt sie auch die Anziehungskraft der Erde.

Das gilt auch für jeden betrachteten Meter Liftseil. Auf Bodenhöhe hat ein Meter Seil ein Gewicht X und im stationären Orbit hat ein Meter Seil das Gewicht 0. Auf halbem Weg hat es ein Gewicht in der Gegend von X/2 (kein Bock auf Formelsuchen, wird de facto nicht genau die Hälfte sein). Diese Gewicht integrieren sich auf und führen dazu, dass auf Höhe des stationären Orbits ein Gewicht nach unten zieht, dass bei meiner linearen Näherung 18 Millionen mal X beträgt. Damit es nicht runterfällt, muss der Teil des Seiles, der außerhalb des stationären Orbits liegt, mit dem gleichen Gewicht nach außen ziehen. Man kann das System optimieren, indem man das Seil zur Mitte hin dicker macht und am Rand möglichst dünn, aber ich denke, mit 1kg pro Meter Tragseil liege ich weit unten in der Schätzung. Es sind dann also ca 18.000 TONNEN Liftseil, die unterhalb des stationären Orbits baumeln und zerren und gehalten werden wollen. Dazu kommen dann noch vielleicht 200 Tonnen Nutzlast, die am Seil unterwegs sind und beinah vernachlässigt werden können...

Es gibt aber auch noch den Coriolis-Effekt (der meiner Meinung nach oben in der Diskussion noch lange nicht richtig gesehen wird). Du musst Deine Tangentialgeschwindigkeit von 0,463km/s (oben wurde fälschlich mit 42000km Erdumfang gerechnet) auf mehr als 3km/s erhöhen, sonst bleibst Du hinter dem Seil zurück. Die dafür nötige Beschleunigung spürst Du ebenfalls.

--Rolf b 11:17, 1. Aug. 2008 (CEST)

Wohl schon nur ein theoretisches Gedankenexperiment. Wenn ich einen Balon habe, kann ich daran ein Seil aufhängen. Dann kann ich darüber einen weiteren Balon haben, an dem ich ein weiteres Seil aufhängen könnte. Daran könnte man theoretisch jetzt von einem zum nächsten raufklettern. Wie weit man damit kommen könnte, und damit evtl. ein bisschen die Atmosphäre ausnützen könnte, damit die Last am (bis jetzt theoretischen, so viel ich weiss, sind sie noch nicht mal mit den Nano-Röhrchen so weit) Seil evtl. zumindest bis dort verringern könnte. So viel Lastminderung ist es vielleicht nicht, dass weiss ich zuwenig. Natürlich müsste, damit ein technisches Gerät: Lift daran rauffahren könnte, das Konstrukt etwas technischer sein. Natürlich gäbe es auch da viele technische Schwierigkeiten: technische Regulierung der Auftriebsgase, usw. Ob so was die Last, und damit die Anforderungen an das Seil selber, evtl. verringern könnte? Natürlich würde das dann wieder mit einer erhöhten Komplexität in die (Auftriebs-) Technik erkauft. --Alien4 01:54, 6. Dez. 2008 (CET)

Diese Idee durchdenke ich auch schon eine Weile, so könnten zumindest im erdnahen Bereich bis zu max. 40 km Höhe das Eigengewicht des Seiles bis auf Null reduziert werden. Philipp Schmagold, Witzenhausen

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Corioliskraft

Was macht denn z.B. der Coriolis-Effekt http://de.wikipedia.org/wiki/Corioliskraft mit einer Masse, die an diesem Seil rauf- oder runtergelassen wird?

Auf der Höhe des geostat. Orbit müßte die Masse eine Bahngeschwindigkeit von 3075m/s haben, also 11070 km/h. Auf der Erdoberfläche dagegen 42000km/24h = 1750 km/h = 486m/s

Ich glaube, dass die Auswirkungen dieser Kraft noch lange nicht klar herausgestellt sind. Sie ist an 2 Stellen zu beachten.

Beim Bau des Lifts: Seilstücke bewegen sich in einem rotierenden System entlang des Radius, mit der Folge, dass abgesenkte Seilteile der Baustation im Orbit vorauseilen und dass die Gegengewichtteile zurückbleiben. Dem kann man auf 2 Arten begegnen:

• Warten - Schwer- und Fliehkräfte wirken an den Enden und das Ganze pendelt sich schließlich aus
• Raketen entlang des Seiles

Das ist aber eine Einmalinvestition. Sobald das Seil hängt und ausgependelt ist, verändern die Teile des Lifts ihren Radius nicht mehr und erleben daher auch keine Corioliskräfte mehr. Solange man Elastizitätseffekte vernachlässigt...

Beim Transport einer Last: Wie oben gezeigt, muss die Last von 463m/s auf über 3000 m/s beschleunigt werden, d.h. die kinetische Energie eines Kilogramms Fracht muss von ca 107 KJ auf ca 4500 KJ steigen. Mehr als das 42-Fache. Karl Bednarik schrieb am 05.06.2006, dass die Transportgondel diese Energie aus dem Tragseil holen kann, d.h. seitlich verbiegen und Zugkräfte darauf ausüben. Das Kräfteparallelogramm ist extrem flach und damit ist die Zugkraft, die auf das Seil ausgeübt wird, um ein Vielfaches höher als das Gewicht der Gondel. Das Gegengewicht muss genug Zug ausüben, um dadurch nicht zum Absturz gebracht zu werden. Dazu kommt, dass das Tragseil an der Stelle, wo die Gondel ist, gebogen wird, was noch höhere Materialanforderungen stellt. Alternativ führt man einen Raketenantrieb mit, der immerhin die Masse der Gondel nicht tragen muss und daher schwächer sein kann als der Antrieb einer herkömmlichen Weltraumrakete. Das umgekehrte Problem besteht auf dem Weg nach unten, hier muss man gegen die Corioliskraft bremsen.

"Das 42-fache an kinetischer Energie" klingt eindrucksvoll, ist es aber nicht - der begrenzende Faktor ist hier, wieviel Watt ich brauche. Und wenn ich (unrealistischerweise) annehme, dass das Kilogramm in 1000 Sekunden hochgezogen wird, komme ich mit 4,393 kW aus, was nicht wirklich viel ist.

Die Energiebetrachtung ist nicht das Problem, sondern die Kraft, sprich, welche Belastungen auf das Seil wirken.

Joachim Durchholz 12:17, 21. Okt. 2008 (CEST)

Liftport behauptet, dass dadurch der Teil des Kabel unterhalb der Gondel "nur" um 1 Grad gegenüber der Vertikalen verbogen wird. Allerdings gehen sie auch nur von 200km/h Aufstiegsgeschwindigkeit aus, was 7,5 Tage bis zum Geo-Orbit bedeutet. 1 Grad auf 36000km Höhe sind 628km, um die sich der Schnittpunkt mit dem geostationären Orbit verschiebt. Oha. Ganz schöne Pendelei. Gibt es irgendwo Quellen, wo das plausibel durchgerechnet wird?

Es ist völlig egal, ob das Seil um 6 Meter, 600 km oder 6000 km ausgelenkt ist. Was zählt, ist die Belastung, und eine Auslenkung um 1 Grad verursacht halt eine gewisse Biegebelastung, die sich noch dazu auf die Länge von 18.000 km verteilt. Ich halte das für ziemlich vernachlässigbar.

Joachim Durchholz 12:17, 21. Okt. 2008 (CEST)

Übrigens liest man häufig, dass der Lift energieneutral sein kann, indem man im Weltraum Rohstoffe schürft und diese am Lift runterfährt, während andere Gondeln hochfahren. Aber das macht es noch schlimmer. Denn die Rohstoffe müssen gegen die Corioliskraft gebremst werden, und wenn man das nicht per Rakete macht, muss man die Bremsung ebenfalls über Spannungskräfte im Tragseiles erreichen.

Sie müssen eben nicht gegen die Corioliskraft gebremst werden. Die Kräfte durch auf- und absteigende Lasten heben sich genau auf, und damit ist kein Energieverbrauch nötig.

Das ist genauso, wie wenn Du ein Gewicht an einem Flaschenzug bewegst. Du kannst nur dieses eine Gewicht bewegen, dann musst Du sowohl beim Hochziehen als auch beim Hinunterlassen Energie aufwenden. Oder Du kannst ein Gegengewicht anbringen, dann gleichen sich die Kraftbilanzen aus und Du musst nur noch die Energie für die Reibung aufbringen.

Joachim Durchholz 12:17, 21. Okt. 2008 (CEST)

Zu dieser Idee gehört auch, dass man die potentielle Energie zum Heben einer Gondel aus der potentiellen Energie gewinnt, die beim Absenken einer anderen Gondel frei wird. Das geht auf mehrere Arten:

• Wie bei einer Gondelbahn - mit einem Zugseil. Der Weltraumlift bestünde also aus einer "Umlenkrolle" am oberen Ende, einem "Sicherungsseil", das die Umlenkrolle auf der richtigen Höhe hält, einem Gegengewicht außerhalb der geostationären Bahn, das die Umlenkrolle trägt, und einem "Tragseil", das entlang des Sicherungsseiles geführt wird, über die Umlenkrolle läuft und an dessen Enden die Gondeln hängen. Ich denke, dass man das gleich vergessen kann. Hier entstehen im Betrieb weitere Corioliskräfte und die Tatsache, dass die Umlenkrolle das Tragseil biegen muss, macht seinen Bau nicht einfacher.
• Alternativ durch 2 Zugseile, die ein Gegengewicht am Ende haben und an der "Umlenkrolle" vorbei laufen. Irgendwie stellt man einen Kraftschluß mit der Umlenkrolle her, damit ein Kraftausgleich zwischen den beiden Seilen erfolgen kann. Die Corioliskräfte entlang der Seile bestehen weiterhin und ihre Enden, draußen im Raum, würden dadurch auch noch verbogen werden. Das Seil muss also nach wie vor biegsam sein.
• Durch Speichern der potentiellen Energie der herabfahrenden Gondel auf chemische oder mechanische Art. Dieser Speicher macht die Gondel schwerer und ist mit ziemlicher Sicherheit verlustbehaftet.

Die Corioliskräfte der beiden Seilhälften gleichen sich weitgehend aus. Allerdings wäre so ein Seil aus anderen Gründen vollkommen ungeeignet, weil ein derart langes Seil keine Zugkräfte übertragen kann - zuviel Eigenschwingungen, zuviel Reibung wenn man Eigenschwingungen durch Führungsrollen ausgleicht, zuviel Probleme mit variierenden Seildicken, zuviel Probleme mit der Längselastizität des Seils (wenn das Seil sich konstant bewegt, ist das kein Problem, aber beim Anfahren und Abbremsen wird die Sache äußerst schwierig).

Man will die potenzielle Energie daher elektrisch nutzen: die herunterfahrenden Kapseln werden per Lineargenerator gebremst, die herauffahrenden Kapseln per Linearmotor beschleunigt. Umwandlungsverluste gibt es, aber es geht ja auch nur darum, die Transportkosten zu senken, nicht, sie auf Null zu bringen :-)

Den Linearmotor für die aufsteigenden Kapseln benötigt die Angelegenheit sowieso, und ob die absteigenden Kapseln nun per Linearmotor oder per Wirbelstrombremse vom Runterkrachen abgehalten werden, das Gewicht ist im Grunde das gleiche... also denke ich, dass man da einfach um kleines Geld den Energiebedarf um x% senken will.

Joachim Durchholz 12:17, 21. Okt. 2008 (CEST)

Diese Aspekte müssten zumindest im Artikel erwähnt werden und wenn es Quellen gibt, die die Lösung dieser Probleme diskutieren, müssen sie angeführt werden. Ansonsten ist der Weltraumlift Fiction mit fehlerhafter Science. --Rolf b 12:59, 1. Aug. 2008 (CEST)

Zu den Problemen, die Du da ansprichst, habe ich jetzt die Gegenargumente geliefert. Da wir offenkundig beide Halblaien sind, sollten wir die Aufzählung der tatsächlich artikelrelevanten Probleme wohl eher den besser Informierten überlassen.

Joachim Durchholz 12:17, 21. Okt. 2008 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Aktio = Reaktio und Corioliskraft

"Im Idealfall zeigt die dabei entstehende Corioliskraft immer genau quer zum Weltraumlift, so dass man nur die Energie zum Hochheben der Nutzlast verbraucht."

Nach dem 2. Newtonschen Axiom gilt Aktio = Reaktio D.h. jede Kraft braucht eine gleich große Gegenkraft.

Ein Seil nimmt nur Kräfte in Längsrichtung auf. Die quer wirkende Corioliskraft ist in der Tat ein nicht zu unterschätzendes Problem.

Will man die Corioliskraft durch das Seil auf die Erde ableiten, so muß es leicht schräg stehen. Ansonsten wirkt die Kraft am Endpunkt senkrecht auf der Erde. Und damit läßt sich nunmal keine Kraft in Rotationsrichtung ableiten. Allerdings ist ein schräg stehendes Seil in Ruhe nicht stabil. Daher braucht man mehrere Seile. Im Idealfall 3 Seile in Form einer Pyramide. Dann ist es möglich die Corioliskräfte abzuleiten.

Auch pendelt ein Seil ohne Reibung nicht aus. Das heißt, man muß Schwingungen aktiv auf der Erde bzw. im Welltall dämpfen.

Wieso spielt die Corioliskraft eine Rolle? Ein Lift am Äquator hat das Problem doch gar nicht. -- Joachim Durchholz 11:26, 23. Apr. 2009 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Quellen

In der aktuellen Ausgabe der IEEE Spectrum Mitgliederzeitschrift ist ein ausführlicher Bericht zu dem Thema? (10.09.05)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Toter Weblink

Ich habe mal alle Links kontrolliert.

Link 3 ("What is the Space Elevator? Institute for Scientific Research, Inc.") scheint überlastet/defekt zu sein, dito "Institute for Scientific Research Konzept des Space Elevator und FAQs" und http://isr.us generell. Ich habe sie mal dringelassen, wenn die Seite dauerhaft nicht erreichbar ist, sollte sie entfernt werden.

Der Link zum Max-Born-Team ist dauerhaft entfernt ("requested page does not exist"), den habe ich entfernt. Hier ist (falls die Seite wieder erscheinen sollte) der Originaleintrag: Space Elevator (Max-Born-Team 2006) Weltraumfahrstuhl-Konstruktion 2006 (Schüler/Jungstudierenden Projekt)

Joachim Durchholz 12:27, 21. Okt. 2008 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Zugfestigkeit

In dem Beitrag ist mehrfach von der erforderlichen Zugfestigkeit des Materials die Rede. Diese Angabe ist aber so prinzipiell falsch: Tatsächlich kommt es auf das Verhältnis der Zugfestigkeit zur Dichte des Werkstoffs an.

Hier gibt es einen neuen Werkstoff: Graphen. Der Elastizitätsmodul entspricht mit ca. 1020 GPa dem von normalen Graphit entlang der Basalebenen und ist fast so groß wie die des Diamants. Wissenschaftler der New Yorker Columbia University veröffentlichten 2008 weitergehende Messergebnisse, in denen sie hervorhoben, dass Graphen die höchste Reißfestigkeit aufweise, die je ermittelt wurde.

Archivierung dieses Abschnittes wurde gewünscht von: arilou (Diskussion) 13:41, 24. Okt. 2014 (CEST)

Auswirkungen - Energiebilanz

Die Grafik scheint mir etwas ungenau zu sein. Der Scheitelpunkt der Gesamtkurve müsste doch genau in der Höhe der Geostationären Umlaufbahn (35.786 Kilometer) liegen. Es wäre auch sinnvoll, diese Höhe in der Grafik besonders zu kennzeichnen. Die Grafik zeigt jedoch den Scheitelpunkt bei ca. 42.000 Kilometern. Gibt es einen Grund für diese Abweichung, oder ist es nur ungenau gezeichnet? -- Rfc 09:46, 30. Jun 2006 (CEST)

Hallo Rfc,
Der Unterschied entsteht dadurch, das zur Höhe der geostationären Umlaufbahn noch der Erdradius von 6378,15 km dazu kommt.
An dieser Stelle der x-Achse haben auch die Energiekurven ihren y-Nulldurchgang.
Mit freundlichen Grüssen,
Karl Bednarik 08:43, 5. Jul 2006 (CEST).

Hallo Karl, verstanden. Sollte das vielleicht in der Grafik verdeutlicht werden? Man könnte die Erdoberfläche und die Höhe des geostationären Orbits in der Grafik markieren und benennen. Das würde die Grafik anschaulicher machen. --Rfc 11:47, 7. Jul 2006 (CEST)

Hallo Rfc,
ist es so besser?
Mit freundlichen Grüssen,
Karl Bednarik 13:08, 7. Jul 2006 (CEST).

Perfekt! Danke. -- Rfc 10:06, 11. Jul 2006 (CEST)

Hallo Karl, angeregt durch das Buch "Limit" von Frank Schätzing habe ich mich mit dem Thema Weltraumlift näher auseinander gesetzt. Dabei bin ich auf Deinen Beitrag zur Energiebilanz gestoßen. Deine Angaben hinsichtlich des Energiebedarfs zum Hochheben einer Masse von 1kg von der Erdoberfläche zum geostationären Punkt berücksichtigt nur die erforderliche potenzielle Energie (also senkrecht zur Erdoberfläche). Damit die Masse m=1kg jedoch immer senkrecht über dem gleichen Punkt steht (entlang eines gedachten senkrechten Seils), muss dieser Masse noch zusätzliche kinetische Energie zugeführt werden, um die Winkelgeschwindigkeit der Erddrehung auch bei größer werdendem Abstand von der Erde beizubehalten. Diese kinetische Energie errechnet sich zu 1/2*m*Omega^2*(r2^2 - r1^2). Zahlenmäßig entspricht die erforderliche kinetische Energie genau dem Wert, der als Gewinn durch die Fliehkraft in Deiner Grafik ausgewiesen ist.

Für den Transport von der Erdoberfläche zum geostationären Punkt ist also die in der Grafik angegebene Energiezufuhr von 48.500 kJ für die potenziele (höhenbedingte) Energie plus 5116 kJ kinetische Energie zum Erhalt der gleichen Winkelgeschwindigkeit erforderlich. Entsprechendes gilt dann auch für den Weitertransport zu einem gedachten Punkt der 143.800km über der Erdoberfläche ist. Durch die jenseits des geostationären Punktes zunehmende Fliehkraft gewinnt man zwar die potenzielle Energie zurück. Dafür muss aber weiterhin kinetische Energie zugeführt werden, damit die Masse weiterhin senkrecht über dem gleichen Erdpunkt verbleibt. Diese Energie entspricht wiederum dem in Deiner Grafik gezeigten Anteil an Energiegewinn durch die Fliehkraft. Bis zum 143.800 km-Punkt muss als eine Energie von 61.000 kJ in Form von kinetischer Energie aufgewendet werden. --Joachim Claus 16:52, 8. Feb. 2010 (CET)

Hallo Joachim,
die von Dir beschriebene zusätzliche Energiemenge stammt
aus der Abbremsung der Erdrotation.
In 143.800 km Höhe befindet sich ein massereiches Fliehgewicht,
welches das Seil straff gespannt hält.
Der Antrieb des Aufzuges muss nur jene Kraft überwinden,
die parallel zum Seil zeigt.
Die Querkraft verschiebt das Fliehgewicht geringfügig nach hinten.
Dadurch erhöht sich die Kraft parallel zum Seil nur geringfügig.
Der Aufzug wird von der Querkraft zwar in seine Führungsschienen
gedrückt, aber das wird ein Eisenbahnzug auch.
Der Aufzug und der Eisenbahnzug muss die Querkraft nicht überwinden.
Das Fliehgewicht verliert zwar kinetische Energie, aber sobald
Schwerkraft und Fliehkraft einen kleineren Winkel als 180 Grad
bilden, entsteht eine Rückstellkraft, die das Fliehgewicht beschleunigt.
Um eine geringere Verformung des Seiles zu erreichen, könnte
man Planetoidenmaterial auf die Erde hinunter transportieren.
Für die Seilbelastung sind viele massearme Aufzüge ausserdem
besser als ein massreicher Aufzug.
Bild: http://members.chello.at/karl.bednarik/GEOSYN-3.jpg
Im Idealfall verhält sich das Seil wie ein starrer, senkrechter Turm.
Dann liegen genau jene Bedingungen vor, die auch in einer Kreiselpumpe vorliegen.
Mit freundlichen Grüssen,
-- Karl Bednarik 06:51, 9. Feb. 2010 (CET).

Zur Berechnung der Reißfestigkeit: Man nehme zunächst mal einen sehr hohen Zylinder und berechne sein Gewicht.

$F=A\cdot d\cdot g\cdot h$ (A=Querschnittsfläche d=Dichte g=Erdbeschleunigung h=Höhe)

Da jedoch g mit der Höhe variiert müssen wir die letzten beiden Buchstaben als Integral formulieren, nämlich

$F=A\cdot d\cdot \int _{r_{0}}^{r_{1}}g\,dr=A\cdot d\cdot \int _{r_{0}}^{r_{1}}{\frac {\mu }{r^{2}}}-r\cdot w^{2}\,dr=A\cdot d\cdot [\mu \cdot ({\frac {1}{r_{0}}}-{\frac {1}{r_{1}}})+{\frac {w^{2}}{2}}\cdot ({r_{0}}^{2}-{r_{1}}^{2})]$

u=Erdmasse * Gravitationskonstante, w = Winkelgeschwindigkeit der Erde~Pi/43200s

Zur Ermittlung der Reißfestigkeit einfach das “A” in der rechten Formel weglassen.--Willi windhauch 13:52, 7. Jan. 2011 (CET)

Eine Frage ließ der Hauptartikel unbeantwortet. Wie hoch muss man mit dem Lift fahren, um sich ausklinken zu können, ohne auf die Erde zurück zu fallen. Will man beispielsweise in eine niedrige Erdumlaufbahn einschwenken, so fährt man 23 760 km hoch und lässt sich einfach fallen. Beim tiefsten Bahnpunkt zündet man die Bremsraketen, nimmt dadurch ca. 2 100m/s an Geschwindigkeit weg und erhält damit eine niedrige (kreisförmige)Erdumlaufbahn in 350 km Höhe. Will man die Erde verlassen, so verlängert man die Entfernung Erdmittelpunkt-Synchronbahn um den Faktor 2^(1/3).

--Willi windhauch 20:56, 28. Jan. 2011 (CET)

Beim Einrichten der Aufzugsseile stellen wir uns vor, eine Spinne in einer geostationären Umlaufbahn möchte einen Faden zur Erdoberfläche hinunter lassen. Wieviel Faden muss sie in der Gegenrichtung spinnen, damit sie ihre Umlaufbahn beibehalten kann?

Dazu muss man nur den Inhalt der eckigen Klammer in der obigen Gleichung mit 0 gleich setzen und durch w² kürzen und dann u/w² einfach durch (r_g)^3 ersetzen.

r_g=[Erdmittelpunkt_geostationäre Bahn] r_0=[Erdmittelpunkt_unteres Seilende] r_1=[Erdmittelpunkt_oberes Seilende]

Wir lösen nach r_1 auf und bilden nachfolgenden Differentialquotienten, bei dem sich r_g wieder rauskürzt.

$r_{1}={\frac {r_{0}}{2}}\cdot \left({\sqrt {1+{\frac {8\cdot r_{g}^{3}}{r_{0}^{3}}}}}-1\right)\rightarrow {\frac {dr_{1}}{dr_{0}}}={\frac {2+{\frac {r_{1}}{r_{0}}}}{2+{\frac {r_{0}}{r_{1}}}}}$

Anhand dieses Differentialquotienten kann man auch ohne Rechnung gleich sehen, dass zu Anfang für jeden Meter nach unten, nach oben ebenfalls ein Meter gesponnen werden muss. Das ändert sich aber, je weiter man nach unten kommt. Kurz vor der Erdoberfläche schaut’s dann so aus!

dr_1/dr_0=(2+148 650/6500)/(2+6500/148 650)~12,17

Gleichzeitig mit einem nach unten gesponnenen Meter müssen nach oben 12,17 Meter gesponnen werden. Ich hoffe, das kommt in der Grafik einigermaßen rüber.

--Willi windhauch 23:43, 15. Sep. 2011 (CEST)

Hallo Willi windhauch,
ich habe mir hier die genauesten Ausgangswerte zusammen geschrieben,
und bekomme bei der Berechnung ganz ähnliche Ergebnisse wie Du:
Benutzer_Diskussion:Karl_Bednarik#Energiebilanz_des_Weltraumliftes
Die Energiebilanz und die Seillänge besitzen das selbe Integral.
Mit freundlichen Grüssen,
-- Karl Bednarik 08:57, 16. Sep. 2011 (CEST).

Graphen Weltraumlift

Dichte von Graphen = 2.260 kg/m^3
Schichtdicke von Graphen = 0,000 000 000 335 m
Zugfestigkeit von Graphen = 42 N/m = 125.373.134.328 N/m^2
Gravitationskonstante * Erdmasse = GM = 398.600.441.800.000 m^3/s^2
Siderischer Tag = 86.164,098 903 697 3 s
Winkelgeschwindigkeit der Erde = w = 0,000 072 921 151 467 rad/s
Äquatorradius der Erde = 6.378.160 m
Geostationärer Radius = Dritte Wurzel von (GM/w^2) = 42.164.172 m
2260*(398600441800000*((1/6378160)-(1/42164172))+(0,000072921151467*0,000072921151467/2)*(6378160*6378160-42164172*42164172))=
= Zugbelastung = 109.434.716.471 N/m^2
Prozent Belastung von Graphen = 87,287 %
-- Karl Bednarik 10:06, 8. Jan. 2011 (CET)
Allgemeine Lösung für die Erde:
Zugbelastung = Dichte (in kg/m^3) * 48.422.440,916 N/m^2
Gravitations- und Fliehkraft-Potentialdifferenz = 48.422.440,916 J/kg
-- Karl Bednarik 12:57, 8. Jan. 2011 (CET)

Nicht-rotierendes und unendlich langes Seil:
Der Erdäquator würde mit 465,1 m/s unter dem unteren Seil-Ende hinweg rotieren.
Am Besten verbindet man das untere Seil-Ende mit einer Raumstation,
die in 100 km Höhe, wo die Luft schon sehr dünn ist, am Seil hängt.
Zugbelastung = 141.237.754.849 N/m^2
Prozent Belastung von Graphen = 112,654 %
Das stellt kein Problem dar, denn man kann die Querschittsfläche
des Seiles bei Bedarf an den richtigen Stellen vergrößern.
Gravitations-Potentialdifferenz = 62.494.581,792 J/kg
Ein Seil von der Erde zum Mond ist also realisierbar.
Man benötigt dafür eine kreisrunde, drehbare, schwimmende Insel am Nordpol,
unter der sich die Erde in etwa einem Tag hindurch drehen kann.
Ein Turm soll verhindern, dass das Seil zum Mond über die Polar-Region scheuert.
Eventuell kann man im Bereich der Polar-Region auch Trage-Ballone einsetzen,
denn eine längere Strecke weit verläuft das Seil innerhalb der dichteren Erdatmosphäre.
-- Karl Bednarik 08:14, 9. Jan. 2011 (CET)
Der Grund dafür ist, dass sich der Mond, vom Nordpol aus gesehen, immer in der Nähe des Horizontes bewegt.
-- Karl Bednarik 09:51, 10. Jan. 2011 (CET)
Ein Bild dazu:
http://members.chello.at/karl.bednarik/ERDEMOND.PNG
-- Karl Bednarik 00:38, 11. Jan. 2011 (CET)

Ein paar Bezeichnungen:
V(x) .... Potentialfunktion für Position x am Seil
V'(x).... Ableitung dieser Potentialfunktion
r(x) .... Radius des Seils bei Position x
ρ .... Dichte des Seilmaterials

Man kann die Zugspannung am Seil dann als Integral ausdrücken:
${\frac {1}{r^{2}(x)\ \pi }}\int _{x_{0}}^{x}dy\ \rho \ r^{2}(y)\ \pi \ V'(y)$
Man will eventuell, dass die Spannung über die ganze Länge gleich groß ist.

Vorausgesetzt, dass V(x₀) = -∞ ist, kann man das durch folgende Abhängigkeit des Seilradius erreichen:
$r(x)=r_{0}\ e^{a\ V(x)}$
wobei a eine Konstante ist; die Zugspannung ist dann ${\frac {\rho }{2a}}$

Im Fall des Weltraumlifts ist die Potentialfunktion
$V(x)=-{\frac {GM}{x}}-{\frac {\omega ^{2}x^{2}}{2}}$
und diese ist bei x=0 und x=∞ auch gleich -∞, d.h. theoretisch müsste das Seil von einer Punktmasse bis in die Unendlichkeit reichen, aber man kommt näherungsweise hin, wenn das nicht ganz stimmt.
Usr2 21:34, 12. Jan. 2011 (CET)

Fortsetzung:
Wenn man beim Weltraumlift aus Graphen (mit den Werten von Karl Bednarik) etwa 50% Sicherheitsabstand von der Zerreißspannung einhält, dann nimmt man ca. a = 1,8 * 10^-8 s²/m².
Betrachten wir den unteren Bereich des Seils, von x₀ = 6378 km bis x₁ = 42164 km, die Zugspannung beträgt hier:
${\frac {\rho }{2a}}(1-e^{2a\ (-{\frac {GM}{x_{0}}}-{\frac {\omega ^{2}x_{0}^{2}}{2}}+{\frac {GM}{x}}+{\frac {\omega ^{2}x^{2}}{2}})})$
Man erhält dann einen Quotienten der Durchmesser r(x₁)/r(x₀) = 2,39, und die Zugspannung von 36,5 GPa bei x₁
Um die selbe Zugkraft vom unteren wie vom oberen Teil des Seils zu erhalten, muss das Seil bis in die Höhe von 150159 km reichen.

mfg,
Usr2 22:40, 12. Jan. 2011 (CET)

Hallo Usr2,
zur Sicherheit habe ich noch ein paar Rückfragen:
Was bedeuten die 1,8 * 10^-8 s²/m²?
Ist wirklich der Durchmesser gemeint, und nicht die Querschnittsfläche?
36,5 GPa sind aber nicht 50 % von 125 GPa.
150159 km ist der Abstand vom Erdmittelpunkt.
Hier sind noch ein paar Zahlenwerte:
Benutzer Diskussion:Karl Bednarik#Energiebilanz des Weltraumliftes
Mit freundlichen Grüssen,
-- Karl Bednarik 05:30, 13. Jan. 2011 (CET)
Korrektur:
-- Karl Bednarik 05:41, 13. Jan. 2011 (CET)

Hallo Karl Bednarik,
da war ich wohl etwas durcheinander und habe etwas verkürzt geschrieben: Die 1,8 * 10^-8 s²/m² erhält man einfach, wenn man die Formel nach a auflöst:
$a={\frac {\rho }{2\sigma }}$
und für die Zugspannung σ die halbe Zerreißspannung einsetzt.
Es handelt sich also um eine Größe der Dimension Dichte pro Spannung, und die Einheit kann man auch als (kg/m³)/Pa schreiben.

Es ist der Durchmesser gemeint; allerdings ändert sich nur der Wert der Konstanten a, wenn man die Formel für die Querschnittsfläche will, man könnte es auch so mit der Querschnittsfläche A ausdrücken:
$A=A_{0}\ e^{b\ V(x)}$ und
$b={\frac {\rho }{\sigma }}=2a$

Dann habe ich den durch die Näherung, dass die Erde punktförmig ist, erhaltenen Wert von a genommen und in die Formel für das Seil eingesetzt, das erst beim Erdäquatorradius von 6378 km beginnt. Dadurch ist die Belastung natürlich vor allem im unteren Bereich niedriger, und beim geostationären Punkt ist sie gleich der Spannung im Modell mit punktförmiger Erde multipliziert mit $(1-e^{2a\ (-{\frac {GM}{x_{0}}}-{\frac {\omega ^{2}x_{0}^{2}}{2}}+{\frac {GM}{x_{1}}}+{\frac {\omega ^{2}x_{1}^{2}}{2}})})$.

Und 150159 km ist vom Erdmittelpunkt aus, ja.

Man könnte also das Seil in der Mitte noch etwas dünner machen, so dass es die halbe Zerreißspannung ausnutzt, mit dem Parameter a = 1,28159 * 10^-8 s²/m², und dem Quotienten der Radien:
$e^{a\ ({\frac {GM}{x_{0}}}+{\frac {\omega ^{2}x_{0}^{2}}{2}}-{\frac {GM}{x_{1}}}-{\frac {\omega ^{2}x_{1}^{2}}{2}})}=1,86004$

mfg,
Usr2 06:49, 13. Jan. 2011 (CET)

Nachtrag: Den letzten Wert des Parameters a habe ich numerisch errechnet, weil es keine Darstellung in elementaren Funktionen mehr gibt, wenn das Seil nicht bei einer punktförmigen Erde anfängt.

mfg,
Usr2 06:53, 13. Jan. 2011 (CET)

Hallo Usr2,
jetzt gibt es auch ein Diagramm dazu.
Mit freundlichen Grüssen,
-- Karl Bednarik 14:45, 13. Jan. 2011 (CET)

Hallo Karl Bednarik, das Diagramm enthält noch den Fehler, den ich zuerst gemacht habe: Wenn man die halbe Zerreißspannung ausnutzen will, muss a = 1,28159 * 10^-8 s²/m² sein, und der maximale Durchmesser ist nur das 1,86004-fache des Anfangsdurchmessers.

mfg,

Usr2 16:46, 13. Jan. 2011 (CET)

(Erster Teil)
Hallo Usr2,
das muss nicht unbedingt ein Fehler sein.
Ich ging davon aus, dass am unteren Ende des Seiles, beim Radius von 6.378.160 m,
eine Last von 50 % der Reissfestigkeit, also von 62.686.567.164 N/m^2 am Seil hängt.
Das führt zu dem steilen Anstieg am Anfang der Kurven.
Bei 42.164.172 m Radius erreicht die Kurve für den Durchmesser das Maximum
mit einem Faktor von 2,3787.
Am oberen Ende des Seiles, beim Radius von 150.158.384 m, muss dann ebenfalls
eine Last von 62.686.567.164 N/m^2 hängen, die nach oben zieht.
Sind meine Überlegungen richtig?
Ich habe diese Kurven durch iterative Integration mit 1440 Schritten von 100.000 m Länge
gewonnen, so dass eine gewisse Ungenauigkeit des Faktors möglich ist.
Die iterative Integration ist eine Möglichkeit, die Gleichungen schrittweise zu überprüfen.
Mit freundlichen Grüssen,
-- Karl Bednarik 03:58, 14. Jan. 2011 (CET).

(Zweiter Teil)
Hallo Usr2,
jetzt habe ich noch eine genauere iterative Integration durchgeführt:
35787 Schritte von 1000 m Länge ergeben einen Querschnittsfaktor von
5,7294, und einen Durchmesserfaktor von 2,3936.
(Die vorige Iteration habe ich mit Excel durchgeführt.)

Hier ist das Programm in MSV C++ 6.0 unter Windows 32:
(Das "kleiner als Zeichen" würde im Text Störungen verursachen.)

SelectObject (hdc, GetStockObject (OEM_FIXED_FONT)); // Schriftart
st = 1000; // m Schrittgrösse
er = 6378160 + 0.5 * st; // m Erdradius
sr = 42164172 + 0.5 * st; // m Synchronradius
ma = 2260 * st; // kg Masse
fe = 125373134328 * 0.5; // N/m^2 Festigkeit
su = fe; // N/m^2 Kraftsumme Anfangswert
gm = 398600441800000; // GM
wq = 0.000072921151467 * 0.000072921151467; // w^2
z = 0; // Schrittzähler
for( r = er; r (kleiner als Zeichen) sr; r = r + st ) // alle Radien
{
z = z + 1; // Schrittzähler
sf = su / fe; // Verdickungsfaktor am Anfang 1
su = su + sf * ma * gm / ( r * r ) - sf * ma * wq * r; // Kraftsumme
}
sg = sqrt( sf ); // Durchmesser
strcpy( m, " z = " );
gcvt( z, 20, n );
strcat( m, n );
TextOut( hdc, 100, 100, m, strlen( m ) ); // Zähler
strcpy( m, " sf = " );
gcvt( sf, 20, n );
strcat( m, n );
TextOut( hdc, 100, 150, m, strlen( m ) ); // Querschnittsfläche
strcpy( m, " sg = " );
gcvt( sg, 20, n );
strcat( m, n );
TextOut( hdc, 100, 200, m, strlen( m ) ); // Durchmesser

Mit freundlichen Grüssen,
-- Karl Bednarik 06:02, 14. Jan. 2011 (CET).

(Dritter Teil)
Hallo Usr2,
wenn man unten und oben keine Last anhängt, und das Seil
nur bei Bedarf verdickt, weil 50 % der Reissfestigkeit
überschritten werden, dann entstehen diese Kurven:
http://members.chello.at/karl.bednarik/GRAPLIF3.PNG
Erst ab 11.528.000 m Radius ist dann eine Verdickung notwendig.
Das Maximum ist dann bei einem Durchmesserfaktor von
1,4505 (Excel) oder genauer 1,4519 (MSVC).
Mit freundlichen Grüssen,
-- Karl Bednarik 14:39, 14. Jan. 2011 (CET).

(Vierter Teil)
Hallo Usr2,
hier ist noch eine Überlagerung beider Bilder:
http://members.chello.at/karl.bednarik/GRAPLIF5.PNG
Mit freundlichen Grüssen,
-- Karl Bednarik 18:30, 14. Jan. 2011 (CET).

Hallo Karl Bednarik,
beim Seil mit konstantem Durchmesser komme ich auf 11550 km.
Es ist vollkommen richtig, dass man oben eine zusätzliche Last anhängen sollte, denn sonst droht der Weltraumlift zu kollabieren, sobald man von unten Fracht hinauftransportiert. Unten ist der Lift in der Erde verankert, und man kann dann ungefähr 6,4*10⁹ kg/m² hinauftransportieren.
Genau genommen sollte man die Last am oberen Ende etwas kleiner machen, so dass die tolerierte Materialbelastung nicht überschritten wird, wenn man die Fracht mit einem Aufzug ganz nach oben transportiert. Für die Kräfte gilt dann, wenn die Fracht noch ganz unten ist
$m_{Endlast}\cdot (\omega ^{2}x_{Ende}-{\frac {GM}{x_{Ende}^{2}}})=F_{oben}=F_{unten}=(m_{Aufzug}+m_{Fracht})\cdot g$
und wenn die Fracht ganz oben ist:
$F_{oben}=(m_{Endlast}+m_{Aufzug}+m_{Fracht})\cdot (\omega ^{2}x_{Ende}-{\frac {GM}{x_{Ende}^{2}}})$
$F_{oben}=m_{Endlast}\cdot (1+{\frac {1}{g}}\cdot (\omega ^{2}x_{Ende}-{\frac {GM}{x_{Ende}^{2}}}))\cdot (\omega ^{2}x_{Ende}-{\frac {GM}{x_{Ende}^{2}}})$
Deshalb sollte man nur das 0,92596-fache der vorher geplanten Endlast verwenden (der Kehrwert des mittleren Faktors in der letzten Formel), absolut 7,43414*10¹⁰ kg pro m² Seilquerschnitt.
mfg,
Usr2 22:26, 14. Jan. 2011 (CET)

Nachtrag, wegen der Textformatierung: Man kann in HTML (und deshalb auch hier) das Kürzel &lt; für das Kleiner-als-Zeichen verwenden. Wenn man den Code zwischen
<source lang="cpp">
</source>
einschließt, dann wird auch die Formatierung schöner, und die Kleiner-als-Zeichen sollten auch keine Probleme machen (&lt; funktioniert im Source-Block aber nicht mehr).
mfg,
Usr2 22:38, 14. Jan. 2011 (CET)

Noch eine Frage: Wie stellt man eigentlich so lange Graphenblätter her, und wie verbindet man sie (vor allem beim Verdicken des Seils), so dass die Verbindungsstellen genügend Kraft übertragen?
mfg,
Usr2 22:50, 14. Jan. 2011 (CET)

Hallo Usr2,
derzeit kann man 76 cm (30 inch) breite, endlose Bänder aus Graphen berstellen, indem man eine monoatomare Schicht aus Kohlenstoff auf eine Folie aus inertem Trägermaterial, wie zum Beispiel Kupfer, durch chemische Gasphasenabscheidung (CVD) aufbringt, und dann das Trägermaterial auflöst.
Während des Auflösens des Kupfers verwendet man auf der anderen Seite der Graphen-Schicht eine Hilfsträger-Schicht aus Kunststoff.
Von der Hilfsträger-Schicht kann man dann das Graphen durch Adhäsion auf andere Flächen übertragen.
Das ist bereits Stand der Technik:
http://www.canli.dicp.ac.cn/Gruop%20Seminars%20Pdf/20100814dqyu.pdf

Ich habe dazu noch ein paar Ideen:
Wenn man für die Hilfsträger-Schicht Polystyrol verwendet, dann kann man diese in Aceton auflösen, oder sie bei 400 °C zu Styrol verdampfen lassen.
Der Siedepunkt von Kupfer liegt bei Normaldruck bei 2927 °C, und ist im Vakuum sicher etwas niedriger.
Der Schmelzpunkt von Graphit und vermutlich auch von Graphen liegt bei 3700 °C.
Rein theoretisch könnte man das Kupfer im Hochvakuum des Weltraumes einfach verdampfen lassen.
Dazu benötigt man im Weltraum nur einen grösseren Parabolspiegel.
Bei hohen Temperaturen haben die Kohlenstoffatome des Graphen eine gewisse Beweglichkeit, so dass dadurch Fehler in seiner Molekularstruktur ausheilen können.
An Stelle der chemischen Gasphasenabscheidung könnte man dann den Kohlenstoff einfach im Hochvakuum aufdampfen.
Das gasförmige Kupfer lässt man dann auf einer Graphitplatte oder Graphitwalze kondensieren, und erzeugt so wieder eine Kupferfolie zur weiteren Verwendung.
Das Graphen kann man an einigen Stellen mit Fluor zu Fluorgraphan (CF)n umwandeln, bei dem an jedem Kohlenstoffatom ein Fluoratom hängt, immer abwechselnd eines oben und eines unten.
Graphan (CH)n sieht so aus:
http://en.wikipedia.org/wiki/File:Graphane.png
Mit metallischem Lithium könnte man dann zwei Fluorgraphan-Schichten durch die Wurtzsche Synthese mit einander verbinden.
Dabei entstehen Atombindungen zwischen den Kohlenstoffatomen, die sehr belastbar sind.
R'-C-F + 2 Li = R'-C-Li + LiF
R'-C-Li + F-C-R" = R'-C-C-R" + LiF
Runde Seile sind anfälliger für Mikrometeoriten als flache Bänder, und an flachen Bändern können sich die Laufrollen der Liftkabine auch besser festhalten.
Ein 1 m breites Band aus 10.000 Lagen Graphen wäre 3,35 Mikrometer dick, und hielte 420.000 N aus, was 42,8 Tonnen Masse bei Erdschwerkraft bedeutet.
Im geostationären Orbit würde das Band bei 1 m Breite aus 57.294 Lagen Graphen bestehen, und 19,19 Mikrometer dick sein, um die 50 % Festigkeits-Vorgabe einzuhalten.

Graf Hombugs Konzept:
Zur Energieversorgung der Liftkabine könnte man einen nicht abgeschirmten, nuklear-thermischen Turbogenerator verwenden, den man an den Stromkabeln 500 m hinter der Liftkabine her ziehen würde, denn Abstand ist die beste Abschirmung.
Mit 200 Megawatt Nettoleistung könnte dieser Turbogenerator 20 Tonnen Masse bei Erdschwerkraft mit 1 km/s hoch heben, so dass die Kabine des Weltraumliftes nach 10 Stunden die geostationäre Umlaufbahn erreichen könnte.
Von diesen 20.000 kg Masse würden auf die Liftkabine und den nuklear-thermischen Turbogenerator je 10.000 kg Masse enfallen, nur wäre das Volumen der Liftkabine wesentlich größer als das Volumen des Turbogenerators 500 m darunter.
Natürlich müsste man ruckartige Beschleunigungen vermeiden, um das Graphen-Band nicht zu sehr zu belasten.
Bei 1 m/s^2 Beschleunigung würden 20.000 kg Masse ungefähr wie 22.000 kg Masse auf der Erdoberfläche wirken, denn insgesamt wäre das eine Veränderung von 9,81 m/s^2 auf nur 10,81 m/s^2, so dass das Graphen-Band ungefähr zur Hälfte seiner Reissfestigkeit belastet werden würde, und die Passagiere kaum etwas von ihrer Gewichtszunahme spüren würden.
Nach 5 Minuten würde die Liftkabine 45 km Höhe erreichen, bei einem Luftdruck von nur 0,36 Prozent des Druckes auf der Erdoberfläche hätte sie dann 300 m/s, was ungefähr der dortigen Schallgeschwindigkeit entspricht, und nach 17 Minuten würde die Liftkabine in 500 km Höhe 1 km/s erreichen.
So lange sich die Kabine des Weltraumliftes auf der Erdoberfläche befinden würde, würde der nuklear-thermische Turbogenerator in einem 500 m tiefen Schacht ruhen, der als Strahlungsabschirmung dienen würde.
Ein Bild dazu:
http://members.chello.at/karl.bednarik/NUKLTURB.PNG
Mit freundlichen Grüssen,
-- Karl Bednarik 04:32, 15. Jan. 2011 (CET). Noch ein Bild dazu:
http://members.chello.at/karl.bednarik/GRAPSYNT.PNG
-- Karl Bednarik 07:00, 15. Jan. 2011 (CET).

Hallo Karl Bednarik,
um die Kraft vom Lift auf das Seil bzw. Band zu übertragen, müsste genügend Druck angewendet werden, damit die oberste Graphenschicht sich nicht ablöst (weil sie unmöglich das gesamte Gewicht tragen kann). Als Graphit-Graphit-Haftreibungskoeffizient habe ich Werte von 0,1 gefunden (und 0,5 im Vakuum), aber dabei handelt es sich wohl um polykristallinen Graphit mit zufälliger Orientierung. Hier wird ein Reibungskoeffizient zwischen Schichten von 0,03 angegeben:
http://iopscience.iop.org/1367-2630/12/12/125009/fulltext
Deshalb müssten die Laufrollen mindestens das 33-fache des Gewichtes an Kraft auf das Band übertragen.
Zur Gesamtmasse des Seils:

$m=\rho \int _{6378km}^{150159km}dxA_{Boden}e^{{\frac {\rho }{\sigma }}(-{\frac {GM}{x}}-{\frac {\omega ^{2}x^{2}}{2}}+{\frac {GM}{x_{0}}}+{\frac {\omega ^{2}x_{0}^{2}}{2}})}$
m = A_Boden*1,19782*10¹² kg
Bei 3,35*10^-6 Quadratmetern am Boden wären das 4.012.690 kg. Dazu kommt noch die Endmasse von 249.044 kg, insgesamt also 4.261.734 kg.
Man könnte aber mit einem dünnen Band und einem kleinen Lift anfangen. Wenn man mit einer einzelnen Schicht arbeiten kann (die immerhin 420 Newton aushält), dann wären das ca. 426 kg, die man mit einer konventionellen Rakte problemlos in den geostationären Orbit transportieren kann (auch 10 Schichten wären kein Problem). Dazu käme noch einiges an Ausrüstung für die Herstellung des Graphen. Ein kleiner Lift könnte dann Grahpit nach oben bringen und die neuen Graphenschichten an das Band heften (2 Lifte - gleichzeitig nach oben und nach unten).
Abgesehen von anderen Problemen ist es aber sicher auch schwierig, am Anfang das Band herabzulassen, denn es wird buchstäblich vom Winde verweht werden (vielleicht sollte man besser einen 30 km hohen Turm bauen, um die Probleme der unteren Atmosphäre zu umgehen).
mfg,
Usr2 22:17, 15. Jan. 2011 (CET)

(Teil eins)
Hallo Usr2,
es existiert dann auch noch das Problem, dass die jeweils oberste Schicht des Graphens durch die Adhäsion an den Laufrollen der Liftkabine kleben bleiben könnte.
Auf eine ähnliche Weise hat man die ersten Graphen-Proben aus Graphit hergestellt.
Um den Zusammenhalt sämtlicher Graphen-Schichten zu gewährleisten, könnte man etwa 0,1 % bis 1 % aller Atome punktuell durch die Wurtzsche Synthese mit einander atomar verbinden.
Vielleicht kann man solche Atombindungen zwischen den Schichten auch durch den Beschuss mit Ionen erzeugen.
Ein mehrere Atome grosses Loch durch zwei benachbarte Graphen-Schichten würde dann zu einer Art Modell einer Einstein-Rosen-Brücke ausheilen.
Der andere chemische Grenzfall wären Graphan-Schichten, die man durch Wasserstoff-Abspaltung zu mehreren Diamant-ähnlichen Schichten verbindet.
Graphan entsteht aus Graphen durch Behandlung mit atomarem Wasserstoff.
Graphan geht bei 400 °C durch Wasserstoff-Abspaltung wieder in Graphen über.
Die Reissfestigkeit von Graphan und Diamant-Ebenen müsste man noch bestimmen.
Ein ganz anderes Problem ist, dass sämtliche Erdsatelliten, ganz gleich mit welcher Bahnneigung, pro Umrundung zwei mal die Ebene des Erdäquators durchqueren müssen.
Igendwann befindet sich dann irgend ein Satellit und das Welraumseil gleichzeitig an der gleichen Stelle, und die meisten Satelliten besitzen keinen Treibstoff für eine Kursänderung.
Mit freundlichen Grüssen,
-- Karl Bednarik 06:38, 16. Jan. 2011 (CET).
(Teil zwei)
Ein halbiertes Verbindungsloch zwischen zwei Graphen-Ebenen:
http://members.chello.at/karl.bednarik/GRAPEBE5.PNG
-- Karl Bednarik 09:50, 16. Jan. 2011 (CET).
(Teil drei)
Hallo Usr2,
wenn in zwei 1 m breiten Bändern auf 1 m Länge 1000 Löcher von 1 nm Durchmesser gleichmässig verteilt sind, dann wird die Festigkeit der Bänder höchstens um 1/1000.000.000 verringert.
Unter diesen Bedingungen befinden sich auf 1000 km Länge der Bänder aber 1.000.000.000 Löcher.
Diese 1.000.000.000 Löcher haben zusammen mehr Reissfestigkeit zwischen den Bändern als die Bänder selbst.
Am Besten schiesst man schnelle Kohlenstoff-Ionen durch mehrlagige Bänder aus Graphen.
Dadurch entsteht ein Kanal, der mit heissen Kohlenstoff-Radikalen gefüllt ist, die sehr bindungsfreudig sind.
Das könnte man als molekulares Punktschweissen bezeichnen.
Die oberste und die unterste Graphenschicht könnte man auf der Aussenseite fluorieren, um die Adhäsion zu den Rollen der Liftkabine zu vermindern.
Die Gewichtsbelastung regelt sich automatisch.
Am oberen Ende des Seiles hängt eine Masse die das Seil mit seiner halben Zugfestgkeit belastet.
Wenn das Seil selbst mit seiner Masse ausgewogen zwischen Gravitation und Zentrifugalkraft ist, dann zieht es an seiner Bodenverankerung ebenfalls mit seiner halben Zugfestgkeit.
Wenn man nun unten eine Last anhängt, die maximal seiner halben Zugfestgkeit entspricht, dann wird bloss die Bodenverankerung um diesen Betrag entlastet.
Laut der ESA befinden sich über 600.000 Objekte mit einem Durchmesser größer als 1 cm in Umlaufbahnen um die Erde.
Das bedeutet, dass es 1.200.000 Durchgangspunkte durch die Äquatorebene der Erde gibt, wobei die meisten dieser Durchgangspunkte mehrmals täglich durchflogen werden.
Das Weltraumseil streicht einmal täglich über eine Kreisfläche mit etwa 150.000 km Radius.
Während ein typischer Satellit etwa 1 m^2 Querschnittsfläche hat, hat das Weltraumseil 150.000.000 m^2 Querschnittsfläche, die man treffen kann.
Wie lange wird es wohl dauern, bis es getroffen wird?
Mit freundlichen Grüssen,
-- Karl Bednarik 07:02, 17. Jan. 2011 (CET).
(Teil vier)
Hallo Usr2,
Um das Weltraumband widerstandsfähiger gegen Einschläge zu machen, könnte man es bei gleicher Querschnittsfläche breiter und dünner machen.
Flache Weltraumbänder können von einem parallel zu seiner Fläche einschlagenden Teilchen durchschnitten werden.
Wenn man dem Weltraumband eine kleine mechanische Vorspannung zwischen seinen Schichten einbaut, dann bildet es ganz von selbst einen losen, geschlitzten Zylindermantel.
Am Besten wäre ein Halb-Zylindermantel, denn dieser wird von einem Objekt normalerweise nur einmal durchschlagen.
Nur der Bereich, wo das Weltraumband durch die Laufrollen der Liftkabine gezogen wird, wird dann noch von den Rollen flach gedrückt.
Mit freundlichen Grüssen,
-- Karl Bednarik 08:06, 17. Jan. 2011 (CET).

Mond

Man könnte doch den Mond und die Erde mit einem Seil verbinden. 217﹒125﹒121﹒169 10:51, 5. Jul 2006 (CEST)

Das erste Problem wäre dabei, dass sich dann die Erde unter dem Seil hindurch drehen müsste.
Das könnte man mit einer kreisrunden, schwimmenden Insel am Nordpol bewältigen, die sich in ungefähr einem Tag dreht.
Das zweite Problem wäre dabei, dass das Seil wesentlich weniger Fliehkraft in Erdnähe erzeugen würde (etwa 28*28 mal weniger).
Das würde deshalb Materialien von heute noch unbekannter Reissfestigkeit erfordern.
Mit freundlichen Grüssen,
Karl Bednarik 12:23, 5. Jul 2006 (CEST).

Was ist mit einem rotierenden Seil? Ein Schwerpunkt und um diesen ein beidseitig raus hängendes Seil rotierend. Dann würde das lange Ende in Abständen hohe Schichten der Atmo streifen und könnte dort Lasten aufnehmen. Das kurze Ende kann ein Gegengewicht halten, ebenso wie das lange Ende in unbeladenem Zustand eine hoch und runter gleitende Gondel, in der "Schwerkraft" herrscht. Wenn der Schwerpunkt nicht geostat wäre, sondern sich mit bewegen würde, müsste das Seil nicht lang sein und könnte vielleicht Lasten "sanft" aufnehmen. Mehrere kleinere Installationen in angrenzenden Höhen.

Ohne Atmo, nur auf dem Mond, hätte man nicht einmal Reibung.

Außerdem könnte man mit mehreren solchen Einrichtungen hinter einander aufgereiht eine Masse beschleunigen. (schleudern) 172.207.158.109 13:00, 5. Jul 2006 (CEST)

Diese Idee wird zum Beispiel hier diskutiert:
http://spacetethers.com/
Wenn ein Weltraumseil in Erdnähe die richtige Rotationsgeschwindigkeit hat, dann entwickelt es beim Eintauchen in die Atmosphäre nur wenig Reibung.
Mit freundlichen Grüssen,
Karl Bednarik 13:22, 5. Jul 2006 (CEST).

Das Beschleunigungsproblem bei rotierenden Weltraumseilen:
Ein Beispiel:
Erddurchmesser 12756 km,
Seillänge 1276 km, also 1/10 Erddurchmesser,
Umlaufgeschwindigkeit etwas weniger als 7900 m/s,
weil die Fliehkraft f = v * v / r ist, ist
die Fliehkraft beim Erdradius 1 g, und
die Fliehkraft beim Seilradius 10 g,
das ergibt hohe Belastungen von Seil und Nutzlast,
Länge einer halben Seilumrundung 2000 km,
Zeitdauer einer halben Seilumrundung etwas mehr als 4 min,
das ist nur etwas für harte Astronauten,
eine Abhilfe können nur längere Seile liefern,
und grossmuttertauglich wäre eine Seillänge vom Erddurchmesser.
Mit freundlichen Grüssen,
Karl Bednarik 09:11, 7. Jul 2006 (CEST).

Bild der Bewegungsphasen des Grossmutterseils:
http://members.chello.at/karl.bednarik/GROMUSEI.PNG
Mit freundlichen Grüssen,
Karl Bednarik 11:29, 7. Jul 2006 (CEST).

Jetzt auch in Wikipedia,
die Enden des Seils bewegen sich entlang von Kardioiden.

Umfangsgeschwindigkeit und Seillänge:
Nehmen wir einmal ein ganz gewöhnliches, zylindrisches Seil an.
Von diesem Seil nehmen wir verschieden lange Stücke.
Diese Materialproben beschleunigen wir in ihrer Rotation um ihre Mitte so lange bis sie reißen.
Alle Materialproben werden bei der gleichen Umfangsgeschwindigkeit reißen, ganz gleich, wie lang sie sind.
Warum? f=v*v/r.
Die Masse des Seils steigt linear mit seiner Länge.
Die Fliehkraft sinkt linear mit dem Radius.
Natürlich immer bei der gleichen Umfangsgeschwindigkeit.
Und bei nicht zylindrischen Seilen, zur Seilquerschnittsfläche:
In einem homogenen Gravitationsfeld, das wir aber nicht haben, sollte die Seilquerschnittsfläche nach oben hin exponentiell größer werden.
Bei einem kreisförmigen Querschnitt würde daher der Seildurchmesser mit der Quadratwurzel der exponentiellen Zunahme anwachsen.
Das Gravitationsfeld der Erde nimmt aber nach oben hin mit 1/r*r ab.
Das Fliehkraftfeld eines rotierenden Seils nimmt nach innen hin mit dem Radius ab.
Da gibt es noch einiges zu berechnen.
Wenn das Seil Bandförmig sein soll, dann gilt immer noch die Querschnittsfläche, aber nicht mehr sein Durchmesser.
Mit freundlichen Grüssen,
Karl Bednarik 17:15, 8. Jul 2006 (CEST).

Hallo an alle,
irgendwann sollten wir einen eigenen Artikel über rotierende Weltraumseile schreiben.
Mit freundlichen Grüssen,
Karl Bednarik 16:34, 10. Jul 2006 (CEST).

Wie soll der Lift auf dem Mond funktionieren? Der Mond rotiert doch viel langsamer, als die Erde. Ist da die geostationäre Umlaufbahn nicht höher? Naja, andererseits ist natürlcih die Masse geringer. Weiss das vielleicht jemand? -- Fr242 16:37, 04. Jul 2006 (CEST)

guggst du Geosynchrone Umlaufbahn und setzt die Daten vom Mond ein, ergibt 88.440 km Radius, oder gut das Doppelte wie bei der Erde. Nicht berücksichtigt ist hierbei der Einfluss der Erde auf den 'Mondsatellit' oder Mondweltraumlift, was man aber IMHO schon machen müsste, da der Abstand Erde-Mond ja mit ca 380.000 km nur knapp das vierfache der Umlaufbahn beträgt, die Erde aber die 81-fache Masse des Mondes hat und damit stärker an dem Satellit zieht als der Mond selbst (siehe Gravitation, da die Erde eine 81-fach höhere Masse hat als der Mond, überwiegt die Gravitation der Erde, wenn der Abstand Erde-Satellit nicht mindestens 9 mal so gross ist wie der Abstand Mond-Satellit, hier wäre er aber nur 3 bis 5 mal so gross). --fubar 17:12, 4. Jul 2006 (CEST)

Also, wenn ich es richtig kapiert habe, dann baut man den Lift auf dem Mond Richtung Erde, und durch die Gravitation der Erde bleibt dann der Lift "oben"? Und aus diesem Grund kann man ihn auch kürzer bauen. Oder vielleicht noch besser gesagt, man setzt den "Schwerpunkt" in den Lagrange-Punkt L₁. -- Fr242 18:07, 4. Jul 2006 (CEST)

Nein, es ist viel einfacher :-P Im Artikel ist es momentan falsch bzw missverständlich dargestellt, es geht hier nicht um geostationäre Bahnen oder Weltraumlifte zu oder durch diese, es werden auf der als Referenz genannten Seite http://www.star-tech-inc.com/spaceelevator.html mehrere verschiedene Konzepte vorgestellt, die sich nicht (wie es momentan leider der Fall ist) in einem Satz zusammenfassen lassen können. Interesannt ist von dieser Seite auch http://www.star-tech-inc.com/papers/als/lunar.pdf. --fubar 22:03, 4. Jul 2006 (CEST)

Davon abgesehen müssen Störeinflüsse nicht einmal "überwiegen". Schon geringe Einflüsse könnten sehr große Anstregungen zur Kompensation erforderlich machen. Schwankungen in der Bahnhöhe des Mondes könnten das Seil in Schwingungen versetzen, die mit gleitenden Gewichten ausgeglichen werden müssten. 217﹒125﹒121﹒169 10:51, 5. Jul 2006 (CEST)

Belastung der Basisstation?

Im Abschnitt "Errichtung des Turms als Basisstation" wird von einer maximalen Belastung von 62 Gigapascal zwischen Kabel und Basisstation gesprochen. Allerdings ist dies wie weiter oben geschrieben die maximale Belastung, die das Kabel laut NASA überhaupt aushalten muss. Da die gesamte Einrichtung jedoch geostationär ist, dürfte im Idealfall überhaupt keine Kraft zwischen Turm und Kabel wirken! Höchstens die Kraft, die notwendig ist, um Schwingungen im Kabel auszugleichen oder um ein gewissen "Übergewicht" im Weltraum zum Straffen des Kabels auszugleichen. Gibts also irgendwelche Belege für die Aussage im Artikel? -- Jan Krieg 02:38, 13. Mär. 2009 (CET)

Eine Angabe in Gigapascal ist kompletter Blödsinn, Kräfte werden in Newton angegeben. Wahrscheinlich ein Copy&Paste-Fehler. Hoffentlich findet jemand die Quelle, um das richtigzustellen. (Ich lass den Abschnitt drin: Die Bodenstation ist zwar kaum Zugkräften ausgesetzt, aber das Konstrukt kann ja schwingen und durch atmosphärische Turbulenzen oder den ganz normalen Betrieb in Resonanz kommen. Je nach Materialeigenschaften des Trägerseils kann das zum echten Problem werden.) -- Joachim Durchholz 11:18, 23. Apr. 2009 (CEST)

Nein, die Angabe in Pascal macht schon Sinn, da sie vom Durchmesser des Seils unabhängig ist. Somit weiß man, welche Zugfestigkeit das Seil haben muss, unabhängig von der endgültigen Dicke (welche dann von den zu befördernden Nutzlasten abhängig ist). -- Jan Krieg 16:56, 24. Apr. 2009 (CEST)

"Blödsinn - die Physik steht im Wege"

Im Roman funktioniert's vielleicht, in der Wirklichkeit wird es aber nicht gehen. Die Physik steht im Wege. Die zugehörige Mathematik ist die Mechanik, Kapitel "Impulserhaltungssatz".

Zur Erinnerung: Impuls gleich Masse mal Geschwindigkeit, I=mv.

Für den Laien (Nichtmathematiker, Nichtingenieure, Nichtphysiker) die anschauliche Schilderung: Ein Körper behält immer seinen Impuls bei, es sei denn es wirkt eine äußere Kraft. Was bedeutet das für den Fahrstuhl? Er hat einen Impuls I, der auf dem Weg zum obersten Punkt seines Orbits wesentlich erhöht werden muss, denn die Umlaufbahn wird ja länger und er will ja über dem gleichen Punkt geostationär stehenbleiben. Dazu muss die Geschwindigkleit wachsen - ergo: der Impuls muss erhöht werden und es ist ein äußere Kraft erforderlich, um in Drehrichtung zu beschleunigen. Dazu wird man (weil auf dem Weg ins Weltall) einen Raketenantrieb benutzen müssen. Wenn man wieder runter will, muss man die Rakete übrigens auch noch umdrehen können. Da stellt sich unmittelbar die Frage - wozu dann noch das Seil? Leute, lasst die Kirche im Dorf und das Seil am Boden. Wenn's ginge wäre auch von Braun schon drauf gekommen, verlasst Euch drauf...

Die Presse hat grad' nix zu schreiben, die Schweinegrippe ebbt schon wieder ab und der Impfstoff ist schon in Sicht, da poppt so ein Murks schon mal wieder hoch. (nicht signierter Beitrag von Airchiller (Diskussion | Beiträge) 00:31, 12. Nov. 2009 (CET))

Zum Impulserhaltungssatz verweise ich auf die Impulsbilanz des Weltraumliftes abgerufen am 12.11.09.

Das aktuell fehlende hochzugfeste Material war wohl auch in der Vergangenheit ein Problem. Dies bedeutet jedoch nicht, das auch in Zukunft die benötigten Komponenten fehlen. --Oliver 15:45, 12. Nov. 2009 (CET)

Die gezeigte Impulsbilanz betrachtet das statische System. Das reicht nicht aus. Da der Fahrstuhl hochfährt, muss die Gondel dynamisch betrachtet werden. Die Umlaufgeschwindigkeit der Gondel im Orbit ist aber ein Vielfaches der Umlaufgeschwindigkeit am Boden, demzufolge muss auch der Impuls vervielfacht werden. Wo soll bitte die Energie herkommen? Ich habe den Eindruck, hier verfestigt sich die Laienmeinung, man könne einfach senkrecht hochfahren und gut ist - das stimmt aber nicht. Zum Material: Bei den Auführungen zum "hochzugfesten Material" habe ich bei "800 N/m²" aufgehört zu gelesen. Nicht nur, dass es 800 N/mm² heißen muss - der Autor hat sich mal eben um Faktor 10e6 verrechnet oder vertippt oder wie auch immer - dann muss das Seil auch noch wohltemperiert und geprüft fehlerfrei sein. Die Belastung des Seils wäre bei 800N/mm² denn auch ständig nahe am technischen Limit - so legt man so ein Seil aber nicht aus, es fehlt der Sicherheitsfaktor. Und der Demontage-Ablauf? Beim runterkurbeln wird das Seil nämlich immer schneller, den Effekt kennen wir von den Pirouetten einer Eisläuferin. Und beim Unfall? Da schwirrt dann die Gondel davon? Mein persönliches Fazit: Aktien dieser Unternehmung würde ich nicht zum Kauf empfehlen! (nicht signierte Rückantwort von Airchiller (Diskussion | Beiträge) 00:31, 12. Nov. 2009 (CET))

Zur kinetischen Energie der Gondel siehe meinen Beitrag bei Der Energieerhaltungssatz läßt sich nicht überlisten. Die Zunahme/Abnahme des Drehimpulses der Gondel in Bezug auf die Erde ist analog dazu, dass die kinetische Energie der Gondel verändert wird. Und zur Machbarkeit: Heute sicherlich noch nicht realisierbar, aber wer hätte Anfang des 20. Jh. daran geglaubt, dass 1959 schon Menschen auf dem Mond landen? Und das Wissen wächst heute schneller denn je an. Also lassen wir uns überraschen ;-) -- Jan Krieg 18:49, 15. Dez. 2009 (CET)

In den 50ern war man auch davon überzeugt, dass PKWs in Zukunft von Mini-Kernreaktoren angetrieben werden. Die technische Umsetzung sein nur eine Frage der Zeit. Nicht alles, was auf den ersten Blick möglich erscheint ist auch möglich - Mondlandung hin oder her! (nicht signierter Beitrag von 88.73.198.60 (Diskussion) 08:15, 23. Apr. 2012 (CEST))

Mondseillänge

Dass das benötigte Kabel wegen der im Vergleich mit der Erde geringeren Schwerkraft niedrigeren Belastungen ausgesetzt wäre ist klar. Aber ich verstehe [aus dem Abschnitt Weltraumlist auf dem Mond heraus] nicht, wieso aufgrund der langsamen Rotation des Mondes ein Kabel bis zum luna-stationären Orbit mit knapp 100.000 km wesentlich länger wäre als bei einem Erd-Weltraumlift.
Wegen der geringeren Größe kann man doch näher heran, und sobald der Schwerpunkt in einem lunarstationären Orbit ist bewegt es sich doch mit der entsprechenden Eigengeschwindigkeit. Wieso müsste das Kabel also so viel länger sein als bei der Erde? -- Gohnarch^░░░░ 12:55, 28. Nov. 2009 (CET)

Die Erde dreht sich in 24 Stunden um sich selbst. Eine geostationäre Umlaufbahn hat man in der Höhe, in der die Umlaufbahn des Satelliten 24 Stunden beträgt. Der Mond dreht sich in 29 Tagen um sich selbst. Die Höhe der stationären Bahn ist proportional zur Rotationszeit des Zentralkörpers, also hast Du da Faktor 29. Sie ist aber auch proportional zur Wurzel der Masse. Da der Mond 1/81 der Erdmasse hat, ist die Höhe der lunarstationären Bahn um den Faktor 29/9=3,2 größer als die der geostationären (vom Mittelpunkt des Zentralkörpers aus gerechnet). --Asdert 22:58, 28. Nov. 2009 (CET)

Kannst Du das nicht ähnlich schön in den Artikel schreiben? Oder gehört da kein „weil“ hin? -- Gohnarch^░░░░ 20:44, 1. Dez. 2009 (CET)

In diesem Abschnitt geht es hauptsächlich um die Lagrange-Punkte, das lunastationäre Orbit ist ja nur in einem Nebensatz erwähnt. Wenn man die Berechnung des lunastationären Orbits detailliert, dann müsste man auch die Berechnung des Lagrange-Punkts detaillieren. Gehört das aber hier in den Artikel? Die Ergebnisse werden ja angegeben. Braucht man den Rechenweg? --Asdert 08:57, 2. Dez. 2009 (CET)

Weltraumschrott, Flugzeuge, Zielbahnhöhen der transportierten Objekte

Neben den ganzen anderen Problemen kommen noch ein paar dazu

ZB stellt ja der ganze Weltraumschrott eine Gefahr dar. Ich will mir nicht vorstellen was passiert wenn so ein schnelles Teil(chen) auf das Kabel trifft daß ja tendentiell eh schon am Limit ist.

Und daß man das Ganze nicht "im Griff" ;) hat, wie behauptet, zeigt ja daß schon ganze, funktionsfähige Satelliten ohne Vorwarnung kollidert sind. Dazu noch die Gefahr durch Flugzeuge, auch durch Terroranschläge.

Man kann auch nicht einfach hin und wieder ein neues Kabel ziehen. Abgesehen von der Katastrophe eines herabstürzenden "Kabels". Naja das weitaus meiste wird wohl verglühen. Und zu CO2...

Weiterhin werden ja nicht alle transportierten Objekte in einer geosynchronen Bahn gebraucht. Wohl die wenigsten. Um andere Bahen zu erreichen braucht man dann wieder Raketen benutzen die nicht unerhebliche Energien brauchen. Runter muß man bremsen etc. Um eine niedrige Umlaufbahn zu erreichen muß man die halbe zuvor investierte Energie wieder wegbremsen.... Unterwegs absetzen ist schwierig weil die Bahngeschwindigkeiten viel zu niedrig sind. Für jede Zielhöhe dürfte es einen Absetzpunkt geben von der der Körpen dann fallen kann um die richtige Geschwindigkeit für seine Umlaufbahn zu erreichen.

Wie auch immer, wäre gut weitere wirtschaftliche Volldesaster wie beim Space Shuttle (optimistisch hoch x) zu vermeiden. Das Geld kann man anderswo gebrauchen. ZB für die Installation einer nachhaltigen Energieversorgung. Lieber die Erde bewohnbar (eventuell auch noch mit ein bißchen Lebensqualität) erhalten. Es gibt keine Alternative. Auch da draußen nicht.

Wenn wir hier unten (unter den optimalen Bedingungen) nicht schaffen zu überleben werden wir es woanders auch nicht.

--95.116.148.99 12:09, 7. Okt. 2010 (CEST)

Zitat aus dem Artikel:
"Wird das Seil bis in eine Höhe von 143.800 Kilometer über der Erdoberfläche verlängert, kann diese (vorher aufgewendete) Energiemenge wieder zurückgewonnen werden."
Man kann sich jederzeit die Höhe aussuchen, die die gewünschte Summe aus kinetischer und potentieller Energie aufweist, um Objekte aller Art zu starten.
Letzten Endes ist ein Weltraumlift nur eine Zentrifugalpumpe, die von der Schwungmasse der Erde angetrieben wird.
-- Karl Bednarik 15:18, 7. Okt. 2010 (CEST).

Zwischenrechnungen/Konstanten

Karl Bednarik hat in den letzten Tagen eine Reihe von Konstanten bzw. Zwischenwerten für eine Energiebilanz eingestellt. Ich denke, dass diese nicht in den Artikel gehören, da sie erstens nicht unmittelbar speziefisch für den Weltraumlift sind, zweitens nicht ungewöhnlich/komplex genug, um überhaupt erklärend erwähnt werden zu müssen und drittens in der jetzigen Form den Abschnitt entstellen. Ich würde (vorschlagen) sie die nächsten Tage wieder zu entfernen!

Desweiteren halte ich Präzisierungen in den Zahlenwerten zwar für in Ordnung, die Genauigkeit die Karl Bednarik allerdings an den Tag legt, ist rein theoretischer Natur und dürfte wahrscheinlich schon durch leichte Dichteschwankungen, Temperaturänderungen etc. Makulatur werden. Ich denke hier wären an manchen Stellen Werte ohne Kommata eingänglicher.

-- Allesquarks 23:52, 2. Nov. 2010 (CET)

Hallo Allesquarks.

Das Gravitationspotential und das Zentrifugalkraftpotential der Erde hängt ausschliesslich von der Länge des siderischen Tages und dem Produkt aus der Gravitationskonstante und der Masse der Erde ab.

Diese Werte sind ausserordentlich genau bekannt und werden keinesfalls von Dichteschwankungen oder von Temperaturänderungen oder von sonst von irgend etwas beeinflusst.

Im Laufe der Jahrmillionen wird der siderische Tag aber ein wenig länger werden, weil der Mond die Erdrotation abbremst.

Die Werte und die Gleichungen dafür sind ausreichend ungewöhnlich und komplex, so dass ich selbst einige Zeit lang danach suchen musste.

Wir schreiben hier in der Wikipedia nicht nur für Diplomphysiker sondern auch für Grossmütter.

Ich bin selbst nur Chemotechniker, und weiss daher genau, wie schwer zugänglich solche Fragestellungen sind.

Mit freundlichen Grüssen,

-- Karl Bednarik 04:35, 4. Nov. 2010 (CET).

Ich sagte ja, dass das grundsätzlich zwar stimmt, aber alleine der Tidenhub macht beispielsweise deine letzte/n signifikante Stelle bei Seilhöhe und anderen radialen Angaben problematisch. Desweiteren gibt es bsp. Abweichungen im Gravitationspotential aufgrund von Dichteschwankungen in der Erdkruste (wobei ich diese jetzt nicht quantifizieren kann) zum Beipiel auf dem Meer oder Land. Die Energie zum Verlassen des Gravitationspotentials ist so genau angegeben, dass schon eine in Richtung centimetergenaue vertikale Positionierung als Startpunkt nötig wäre. Die Leser werden diese Angabe denke ich auch als Seillänge interpretieren, die aufgrund von thermischer Ausdehnung des Seils hier also viel zu genau angegeben ist.

Könntest du nicht anstatt dieser Legende Links auf die entsprechenden Thematiken legen (am besten direkt in den Zahlenwerten verlinken), wo das behandelt wird (die gibt es ja schließlich alle)? Oder das zumindest als Fußnote optisch weniger aufdringlich gestalten?

Ich sage auch nicht, dass die Gleichungen alle trivial sind, aber die Höhe der geostationären Bahn muss doch hier nicht ausgerechnet werden, sondern kann einfach benutzt werden.

-- Allesquarks 12:09, 4. Nov. 2010 (CET)

Ich habe nun die Berechnungen ausgelagert, und mit den Quellenangaben versehen. -- Karl Bednarik 12:50, 4. Nov. 2010 (CET).

Warum hat jemand diesen Hinweis gelöscht? Die Berechnungen dazu findet man hier. -- Karl Bednarik 04:24, 24. Nov. 2010 (CET).

weil in den Artikelraum keine Links auf die redaktionellen Seiten gehören, vgl. dazu http://de.wikipedia.org/wiki/Hilfe:Namensr%C3%A4ume#Regeln. Gruß --62.227.219.2 00:02, 25. Nov. 2010 (CET)

Danke für die Information, wo diese Angaben nicht hingehören.

Bitte um die Information, wo diese Angaben schon hingehören.

-- Karl Bednarik 06:22, 25. Nov. 2010 (CET).

Vielleicht auf eine Unterseite Weltraumlift/Berechnung? --Asdert 09:55, 25. Nov. 2010 (CET)

Ich habe nun genau das gemacht, was Asdert geschrieben hat, was sofort zur Löschung von Weltraumlift/Berechnung geführt hat.

Dazu habe ich die folgende Begründung erhalten:

"Hallo Karl! In dieser Form war dein Beitrag kein enzyklopädischer Artikel. Zur weiteren Verwendung hier der Inhalt. Grüße, Polarlys"

-- Karl Bednarik 17:12, 25. Nov. 2010 (CET).

Es war kein Rat von mir, sondern nur geraten. Ich weiß die Antwort auch nicht, deshalb habe ich "vielleicht" geschrieben und ein Fragezeichen hinzugefügt. Das als "falscher Rat" zu bezeichnen (siehe Edit-Kommentar) halte ich nicht für richtig. --Asdert 17:18, 25. Nov. 2010 (CET)

Den "falschen Rat" nehme ich natürlich sofort mit dem Ausdruck des Bedauerns zurück.

Es ist allerdings erstaunlich, dass Du zwar weisst, wo Angaben nicht hingehören, dass Du aber nicht weisst, wo Angaben schon hingehören.

Diese Art von Wissen führt zwar zu Löschungen, aber nicht zu neuen Informationen.

-- Karl Bednarik 17:48, 25. Nov. 2010 (CET).

Kannst Du mir das näher erläutern? --Asdert 21:16, 25. Nov. 2010 (CET)

Erläuterung:

Eine Reihe von Personen ist schnell zur Löschung von fremden Informationen bereit, die einen Formfehler enthalten.

Prinzip: Beim geringsten Fehler wirst Du gnadenlos ausgelöscht, so wie beim Egoshooter.

Die Anzahl der Personen, die erklären, wie man es besser machen kann, ist geringer.

Das liegt zumindest zum Teil daran, dass sie das selbst gar nicht wissen.

Am seltensten sind aber Personen, die einen Formfehler von selbst freundlich ausbessern.

Ich selbst vermeide es, fremde Informationen zu löschen, und versuche sie zu auszubessern, wenn ich kann.

Das erscheint mir höflicher und konstruktiver.

Scherz: Ich frage mich, was passiert, wenn unser Zeilenanfang den rechten Rand des Bildschirmfensters erreicht hat.

-- Karl Bednarik 04:08, 26. Nov. 2010 (CET).

Okay, dann hast Du mich verwechselt. Du hast mir zwar geschrieben "dass Du zwar weisst, wo Angaben nicht hingehören", aber wohl denjenigen IP-Nutzer gemeint, der Deinen Beitrag gelöscht hat. Das war nicht ich. Damit ist diese Sache für mich erledigt. Und wenn man weit genug einrückt, dann wird das logische Fenster größer als das physikalische und der Browser schenkt Dir einen horizontalen Scrollbalken.. --Asdert 12:06, 26. Nov. 2010 (CET)

ß oder ss

Wie sieht es in der Wikipedia bei der Verwendung von ß oder ss aus?
In einigen deutschsprachigen Ländern gibt es gar kein ß.
-- Karl Bednarik 09:57, 5. Nov. 2010 (CET).

Ja, in schweizbezogenen Artikeln wird kein ß verwendet. Der Weltraumlift dagegen hat nichts mit der Schweiz zu tun, da richtet man sich nach der normalen deutschen Rechtschreibung, siehe Wikipedia:Rechtschreibung#ss-ß-Regel. --Asdert 21:12, 5. Nov. 2010 (CET)

Und warum hat die Schweiz nichts mit dem Weltraumlift zu tun? Handelt es sich bei der Schweiz vielleicht um ein technologisch unterentwickeltes Volk? Also, ich glaube, dass das nicht so ist. (man beachte das "dass das") -- Karl Bednarik 03:45, 6. Nov. 2010 (CET)

Ein Wort: FAIL. Ich erläutere das mal eben kurz. Erstens hast du die Aussage nicht verstanden. Die Schweiz hat genau so viel mit dem Weltraumlift zu tun wie jeder andere Staat, aber der Weltraumlift eben nichts mit der Schweiz. Und genau darauf kommt es an. Lesen hilft; spätestens beim falschen Wiedergeben sollte es dann aber auch auffallen. Okay, kann ja mal passieren. Und dann aber auch noch neunmalkluk darauf hinweisen müssen, wie überflüssig das ß doch ist, indem man es verständnisverlustfrei durch ss ersetzen kann, nur um damit zu beweisen, dass man selbst außerstande ist, zwischen langem und kurzem Vokal zu unterscheiden und so jedem anderen klar macht, dass das ß doch für diejenigen Deutschsprachigen vonnöten ist, die das noch können. --★PowerZ_Diskussion 22:29, 2. Jan. 2012 (CET)

Wohin soll man weiter führende Erklärungen geben

Es handelt sich hier nicht um Erfindungen oder Theorien, sondern um harte Mathematik und Physik.
Wir schreiben hier in der Wikipedia nicht nur für Diplomphysiker sondern auch für Grossmütter.
Ich bin selbst nur Chemotechniker, und weiss daher genau, wie schwer zugänglich solche Fragestellungen sind, denn ich selbst habe drei Wochen lang vergeblich danach gesucht.
Die Werte und die Gleichungen dafür sind den meisten Menschen unbekannt, schwer zu finden, und entsprechend schwer verständlich.
Wollen wir wirklich sagen: "Lernt Physik und sucht euch die Formeln selbst zusammen."?
Wozu soll dann ein Nachschlagewerk wie die Wikipedia gut sein?
Dazu kommt noch, dass diese Berechnungen die Begründung für die im Artikel Weltraumlift angegebenen Zahlenwerte darstellen.
Die Berechnungen der Energiebilanz des Weltraumliftes.
-- Karl Bednarik 04:43, 26. Nov. 2010 (CET).

Bitte gib zunächst an, aus welcher Fachpublikation diese Berechnung stammt. Sollte sie von dir selbst erstellt worden sein, kann sie wegen WP:KTF nicht verwendet werden. Auf die Problematik der Übergenauigkeit wurdest du bereits mehrfach hingewiesen. --jergen ? 09:27, 26. Nov. 2010 (CET)

Energiebilanz

Gilt das Verbot selbst erstellter Berechnungen auch für Diagramme, wie bei diesem Bildchen, um das wirklich schade wäre?

Was ist, wenn die Fachpublikation von einem selbst stammt, wie bei der Dichtegradientenelektrophorese?

Ab welcher Komplexität gilt das Verbot selbst erstellter Berechnungen? 2*3=6 liegt bestimmt unter dieser Grenze.

Die Übergenauigkeit könnte ich ganz leicht eliminieren, aber das ist wohl nun nicht mehr notwendig.

Danke im Voraus für die Antworten. -- Karl Bednarik 12:58, 26. Nov. 2010 (CET).

Zusatzfrage:

Muss man die Herkunft von physikalischen Gleichungen, wie sie zum Beispiel in Geosynchrone Umlaufbahn vorkommen, auch belegen?

Ab welcher Komplexität der Gleichungen gilt das? Liegt v=at unter dieser Grenze?

Danke im Voraus für die Antwort. --Karl Bednarik 13:15, 26. Nov. 2010 (CET).

Erde-Mond-Seil

Graphen Weltraumlift

Geostationäres Welraumseil aus Graphen:
Dichte von Graphen = 2.260 kg/m^3
Schichtdicke von Graphen = 0,000 000 000 335 m
Zugfestigkeit von Graphen = 42 N/m = 125.373.134.328 N/m^2
Gravitationskonstante * Erdmasse = GM = 398.600.441.800.000 m^3/s^2
Siderischer Tag = 86.164,098 903 697 3 s
Winkelgeschwindigkeit der Erde = w = 0,000 072 921 151 467 rad/s
Äquatorradius der Erde = 6.378.160 m
Geostationärer Radius = Dritte Wurzel von (GM/w^2) = 42.164.172 m
2260*(398600441800000*((1/6378160)-(1/42164172))+(0,000072921151467*0,000072921151467/2)*(6378160*6378160-42164172*42164172))=
= Zugbelastung = 109.434.716.471 N/m^2
Prozent Belastung von Graphen = 87,287 %
Allgemeine Lösung für die Erde:
Zugbelastung = Dichte (in kg/m^3) * 48.422.440,916 N/m^2
Gravitations- und Fliehkraft-Potentialdifferenz = 48.422.440,916 J/kg

Nicht-rotierendes und unendlich langes Seil:
Der Erdäquator würde mit 465,1 m/s unter dem unteren Seil-Ende hinweg rotieren.
Am Besten verbindet man das untere Seil-Ende mit einer Raumstation,
die in 100 km Höhe, wo die Luft schon sehr dünn ist, am Seil hängt.
Zugbelastung = 141.237.754.849 N/m^2
Prozent Belastung von Graphen = 112,654 %
Das stellt kein Problem dar, denn man kann die Querschittsfläche
des Seiles bei Bedarf an den richtigen Stellen vergrößern.
Gravitations-Potentialdifferenz = 62.494.581,792 J/kg
Ein Seil von der Erde zum Mond ist also realisierbar.
Man benötigt dafür eine kreisrunde, drehbare, schwimmende Insel am Nordpol,
unter der sich die Erde in etwa einem Tag hindurch drehen kann.
Ein Turm soll verhindern, dass das Seil zum Mond über die Polar-Region scheuert.
Eventuell kann man im Bereich der Polar-Region auch Trage-Ballone einsetzen,
denn eine längere Strecke weit verläuft das Seil innerhalb der dichteren Erdatmosphäre.
-- Karl Bednarik 08:14, 9. Jan. 2011 (CET)
Der Grund dafür ist, dass sich der Mond, vom Nordpol aus gesehen, immer in der Nähe des Horizontes bewegt.
-- Karl Bednarik 09:51, 10. Jan. 2011 (CET)
Ein Bild dazu:
http://members.chello.at/karl.bednarik/ERDEMOND.PNG
-- Karl Bednarik 00:38, 11. Jan. 2011 (CET)

Hallo Karl Bednarik,

man hat dabei allerdings noch das Problem, dass die Mondentfernung vom Perigäum zum Apogäum um 42592 km variiert. Die Distanz zum Verankerungspunkt am Mond variiert wegen der Libration noch etwas mehr.

mfg,

Usr2 16:52, 13. Jan. 2011 (CET)

... und natürlich variiert die Entfernung zum Nordpol noch einmal etwas mehr, weil die Mondbahn gegenüber dem Erdäquator geneigt ist.

mfg,

Usr2 16:54, 13. Jan. 2011 (CET)

Hallo Karl Bednarik,

mal im Ernst, so hypergenaue Zahlenangaben sind doch bei einem so komplexen System völlig unpassend, wenn man nicht gerade bei der NASA arbeitet; allein die Näherung "Nicht-rotierendes und unendlich langes Seil" macht die meisten Nachkommastellen in der Praxis zu Zufallszahlen. Ebenfalls ist "Gravitationskonstante * Erdmasse = GM = 398.600.441.800.000 m^3/s^2" Unsinn, da die Gravitationskonstante nur auf 6 signifikante Stellen bekannt ist. Nichts gegen Hobby-Theorien, aber diese ist wohl etwas über das Ziel hinausgeschossen... --Jan Krieg 01:13, 28. Feb. 2011 (CET)

Hallo Jan Krieg,

das Produkt aus Gravitationskonstante und Erdmasse ist aus messtechnischen Gründen tatsächlich viel genauer bekannt, als die beiden Einzelgrößen.

Für die Berechnungen ist es besser, die höchste Genauigkeit der Werte zu verwenden, und dann erst das Endergebnis auf die gewünschte Genauigkeit zu runden.

Es handelt sich hier nicht um Hobby-Theorien, sondern um die mathematisch exakte Physik eines idealisierten Systems.

Ein komplexes System wäre es erst dann, wenn man die Masse des Mondes und die Masse der Sonne in die Berechnungen einbeziehen würde.

-- Karl Bednarik 08:09, 28. Feb. 2011 (CET).

Hier ist das offiziell geltende Produkt aus Gravitationskonstante und Erdmasse (GM): World Geodetic System 1984.

--Karl Bednarik 08:31, 28. Feb. 2011 (CET).

Danke für den Hinweis, das hatte ich übersehen, Gravitationskonstante#Genauigkeit ist dazu auch hilfreich. Zu der Genauigkeit an sich: Da es sich in der Tat um ein idealisiertes System handelt, finde ich solche exakten numerischen Angaben umständlich und der Übersichtlichkeit wenig dienlich. Denn in der Praxis führen eine Vielzahl von Störungen und Randeffekten dazu, dass z.B. die errechnete Zugbelastung von der tatsächlichen deutlich abweichen kann (durch auftretende Oszillationen etc.). Dadurch sind die exakten Ergebnisse im idealisierten Modell wenig wert. Just my 2 cents. (nicht signierter Beitrag von Jan Krieg (Diskussion | Beiträge) 18:00, 4. Mär. 2011 (CET))

Abbremsung der Erdrotation

Hier wird mehrmals die Abbremsung der Erdrotation durch den Lift erwähnt. Falls ein Lift tatsächlich praktisch und kostengünstig wäre, würden mehrere gebaut und dauerhaft betrieben. In welcher Grössenordnung würde die Abbremsung der Erdrotation bei einem Lift oder einem Dutzend Liften liegen? Könnte die Abbremsung innerhalb von ein paar Jahrhunderten, ein paar Jahrtausenden oder einem längeren Zeitraum bemerkbare Folgen für das Leben auf der Erde haben? Ich meine das jetzt nicht als meine Frage an die Auskunft, sondern als Frage an die vorhandene Forschung: Ist da schon mal drüber nachgedacht worden? Wenn ja, sollte es vielleicht erwähnt werden. Oder hab ich was überlesen?--91.54.19.199 15:10, 9. Feb. 2011 (CET)

Der Mond bremst die Erdrotation durch die Gezeitenreibung ab.
Dadurch gelangt der Mond auf eine höhere Umlaufbahn.
Die Masse des Mondes ist wesentlich größer, als alles, was die
Raumfahrt mit Hilfe der Weltraumlifte jemals zustande bringen kann.
Ausserdem würde der Transport von Rohstoffen und Passagieren aus
dem Weltraum auf die Erde die Erdrotation wieder beschleunigen.
http://de.wikipedia.org/wiki/Gezeitenreibung#R.C3.BCckwirkungen_auf_Erde_und_Mond_.28Gezeitenreibung.29
-- Karl Bednarik 04:37, 10. Feb. 2011 (CET)

Google-Labor: so geheim, dass niemand darüber sprechen darf?

Derzeit im Artikel: "Seit 2011 ist bekannt, dass Google Inc. in einem Google X genannten Labor, im geheimen an der Umsetzung eines Weltraumliftes arbeitet". Belegt wird das durch einen Spiegel-Online-Artikel, der die New York Times zitiert. Wenn man den dortigen Artikel Google’s Lab of Wildest Dreams liest, erfährt man, dass die NYT ein Dutzend Leute interviewt haben, von denen aber keiner zitiert werden will. Teils arbeiten sie in diesem Geheimlabor, teils aber auch anderswo bei Google. Wo das Labor ist, bleibt unklar. Was aber berichtet wird: dieses Geheimlabor kümmert sich um 100 Ideen, darunter auch den Weltraumlift. Und: "Although most of the ideas on the list are in the conceptual stage, nowhere near reality, two people briefed on the project said one product would be released by the end of the year, although they would not say what it was". Ist dieser Artikel für uns fundiert genug, dass man behaupten kann, dass das Geheimlabor existiert? Und wenn: ist es dann klar, dass man bereits "an der Umsetzung des Weltraumlifts arbeitet"? Woraus kann man schließen, welchen Stand das Weltraumlift-Projekt hat? Es mag zur Zeit eine pure Datensammlung zur Materialforschung sein. Es mag auch das eine Produkt sein, dass in ein paar Wochen auf den Markt kommt. *g* Google selbst gibt keinen Kommentar ab, weder zum Weltraumlift, noch zum Labor überhaupt. Meine Meinung: diese Quelle stützt die Aussage nicht. Entweder bessere Quelle anbringen oder Aussage löschen. --Asdert 22:01, 14. Nov. 2011 (CET)

Aussage gelöscht. --Asdert 17:06, 18. Nov. 2011 (CET)

Tageslänge

Seit ein paar Tagen gibt es einen Absatz über die größere Tageslänge auf der Erde. Wenn sowas schon auf der Seite untergebracht wird, sollte auch deutlich gemacht werden, dass die Änderung der Tageslänge nur absolut minmal und vor allem temporär ist: Trotz der hohen Umlaufbahnen sollte der Verlängerung der Tageslänge absolut vernachlässigbar sein (kann ich aber gerade nicht durch Formeln belegen). Zusätzlich ist die Verlängerung nur temporär: Wird ein Satellit nach oben transportiert, wird der Tag etwas länger. Irgendwann kommt er wieder runter und die Tageslänge verkürzt sich wieder um genau den Betrag, um den sie vorher länger geworden ist. Was denkt Ihr? -- Epaminaidos 23:05, 3. Jan. 2012 (CET)

Ich denke der Autor meint Masse, die dauerhaft oben bleibt. Ziel des Lifts ist es zuletzt eben auch, Basen auf anderen Planeten zu errichten; diese Masse bleibt dann da. Aber der Effekt ist so minimal, dass ich eine Erwähnung im Artikel für unangemessen halte. Selbst wenn man tausende Tonnen nach oben bringt, ist das verschwindend klein im Vergleich zur Erdmasse (ca. 6x10²⁴ Kg). Also: nicht relevant, raus damit. --★PowerZ_Diskussion 01:21, 4. Jan. 2012 (CET)

Der Mond bremst die Erdrotation durch die Gezeitenreibung ab. Dadurch gelangt der Mond auf eine höhere Umlaufbahn. Die Masse des Mondes ist wesentlich größer, als alles, was die Raumfahrt mit Hilfe der Weltraumlifte jemals zustande bringen kann. Ausserdem würde der Transport von Rohstoffen und Passagieren aus dem Weltraum auf die Erde die Erdrotation wieder beschleunigen.

http://de.wikipedia.org/wiki/Gezeitenreibung#R.C3.BCckwirkungen_auf_Erde_und_Mond_.28Gezeitenreibung.29
-- Karl Bednarik 05:54, 4. Jan. 2012 (CET).

Risiken durch Raumschrott etc?

Wie siehts mit Risiken durch Terror, Kriege, Naturkatastrophen, Konkurrenzneid, Flugzeuge und Weltraumschrott aus? Risiken durch "Unwissende" die einfach mal gucken wollen was passiert wenn man eine Rakete darauf abschießt etc. Gibt so Typen. Und Waffen verbreiten sich ja eher. Piloten, die den Leuten im Aufzug eine dolle Show bieten wollen und eventuell einen Fehler machen? Und je weiter sich so ein Projekt von den normalen Lebensbereichen entfernt um so wahrscheinlicher ist sowas. Mal ganz praktische Probleme....

Wie will man das Objekt gegen obige Risiken schützen? Ist eindeutig Höchstrisikotechnologie. Und die führt meist zu autoritären Strukturen bei dem Versuch das Objekt zu schützen.

Wäre doch schade wenn zB irgendein größeres Stück Raumschrott gegen das Seil knallt, das Seil steht ja praktisch und die niedrigen Umlaufgeschwindigkeiten sind enorm, und dann das Ganze zerbröselt und in verschiedenste Richtungen entschwebt oder fällt... theoretisch kann das, angesichts der Länge, überall auf der Erde runterkommen. Was nicht verglüht etc. Wird ja durch den Müll eh immer gefählicher ins All zu kommen. Und der Aufzug muß zwangsweise auch durch die Zone.

--95.116.151.214 23:18, 22. Feb. 2012 (CET)
Hallo 95.116.151.214,
Laut der ESA befinden sich über 600.000 Objekte mit einem Durchmesser größer als 1 cm in Umlaufbahnen um die Erde.
Das bedeutet, dass es 1.200.000 Durchgangspunkte durch die Äquatorebene der Erde gibt, wobei die meisten dieser Durchgangspunkte mehrmals täglich durchflogen werden.
Das Weltraumseil streicht einmal täglich über eine Kreisfläche mit etwa 150.000 km Radius.
Während ein typischer Satellit etwa 1 m^2 Querschnittsfläche hat, hat das Weltraumseil etwa 150.000.000 m^2 Querschnittsfläche, die man treffen kann.
Wie lange wird es wohl dauern, bis es getroffen wird?
Mit freundlichen Grüssen, -- Karl Bednarik 08:40, 23. Feb. 2012 (CET).
Die Antwort:
Wir haben also ein Rechteck von 150.000.000 m mal 450.000.000 m,
(näherungsweise die Kreisfläche wo alles hindurch fliegt),
und ein Rechteck von 150.000.000 m mal 1 m Kantenlänge,
(näherungsweise die Fläche des Weltraumliftes).
Wir haben viel mehr als 1.500.000 Durchgänge pro Tag,
(bei den erdnahen Umlaufbahnen wird das wesentlich mehr sein).
450.000.000 / 1.500.000 = 300
In viel weniger als 300 Tagen wird es dann einen Treffer geben.
Wenn der Weltraumlift nur 75.000.000 m lang ist, dann dauert es natürlich 4 mal länger.
Über die 35.786.000 m über der Erdoberfläche muss der Weltraumlift
aber in jedem Falle hinaus reichen, weil er sonst sofort abstürzt.
Wirklich lästig ist dabei, dass die Bahnebenen absolut aller
Satelliten durch den Schwerpunkt der Erde gehen müssen, und
daher zwangsläufig die Äquatorebene der Erde schneiden müssen.
-- Karl Bednarik 16:48, 23. Feb. 2012 (CET).
Korrektur:
Etwa 95 Prozent des Weltraummülls kreisen sehr schnell
innerhalb von 35.786.000 m über der Erdoberfläche.
Deshalb wird auch der kürzest mögliche Weltraumlift
in viel weniger als 300 Tagen getroffen.
Neue Berechnung:
Grosses Rechteck: 40.000.000 m mal 120.000.000 m,
Kleines Rechteck: 40.000.000 m mal 1 m,
Wesentlich mehr als 1.200.000 Durchgänge pro Tag,
Wesentlich weniger als 100 Tage zwischen den Treffern.
Der schnellere, tiefere Weltraummüll schafft sogar
zwei Durchgänge innerhalb von eineinhalb Stunden,
und ist daher 16 mal schlimmer, so dass wir leicht auf
weniger als 10 Tage zwischen den Treffern kommen.
-- Karl Bednarik 06:40, 24. Feb. 2012 (CET).

Was ist mit Helium- und Wasserstoff-Ballons als Zwischenstationen?

Man kann doch die ersten 20-40km mit Hilfe "normaler" Seile raufkommen, an denen so alle 50m ein Ballon befestigt ist der die Schwerkraft des Seils aufhebt. Man käme mit dieser Technik immerhin an die Atmosphärengrenze, was doch ein viel besserer Startpunkt ist als der Erdboden. Oder übersehe ich da was? (nicht signierter Beitrag von 95.208.205.179 (Diskussion) 01:03, 4. Dez. 2012 (CET))

40 km sind nur 1/1000 von rund 40000 km Mindestlänge des Weltraumliftes. 40 km sind nur 1/159 des Äquatorradius der Erde von 6378 km. Deshalb ist in 40 km Höhe die Schwerkraft der Erde nur sehr wenig geringer als auf der Erdoberfläche. Einen Vorteil würde aber der geringere Luftwiderstand in 40 km Höhe darstellen, was man beim Rockoon genutzt hat. -- Karl Bednarik (Diskussion) 10:17, 4. Dez. 2012 (CET).

Auf den Luftwiderstand kommt es doch auch in erster Linie an. Schließlich schweben Satelliten nicht irgendwo im Weltraum rum sondern müssen sowieso die Erde umkreisen damit sie nicht abstürzen. Und wenn sie das weitgehend verlustfrei machen wollen müssen sie das ausserhalb der Atmosphäre machen. In 40km Höhe kann die Rakete schon fast tangential starten bis sie die Geschwindigkeit erreicht, bei der sich die Nutzlast(Satellit) aufgrund seiner Trägheit spiralenförmig von der Erde entfernt. Dann braucht der Satellit nur abzuwarten bis er seine Wunschhöhe erreicht hat und bremst entsprechend etwas ab um aus der Spiralenbewegung eine Kreisbewegung zu machen. Die 40000km Mindestlänge beziehen sich doch auf ein anderes Design (mit Gegengewicht). (nicht signierter Beitrag von 95.208.205.179 (Diskussion) 14:59, 4. Dez. 2012 (CET))

In 40 km Höhe herrschen immer noch 98,76 % der Schwerkraft der Erde, aber weniger als 1 % des aerodynamischen Auftriebes von Tragflächen.

Deshalb muss auch eine in waagrechter Richtung fliegende Rakete schräg gestellt werden, um die Schwerkraft durch ihren Schub zu kompensieren.

Solange diese Rakete nicht nahe an die Kreisbahngeschwindigkeit von 7910 m/s heran gekommen ist, liefert die Fliehkraft nur wenig Auftrieb.

Bei der halben Kreisbahngeschwindigkeit sind das nur 25 % der Schwerkraft, und 75 % der Schwerkraft ziehen immer noch nach unten.

Am Ende einer spiralförmigen Aufstiegsbahn ist das Bremsen völlig unnötig, denn man behält den letzten Bahnradius ohnehin bei.

Bei einer elliptischen Aufstiegsbahn muss man am erdfernsten Punkt sogar beschleunigen, um in eine Kreisbahn zu gelangen.

Hier ist ein interessanter Artikel zu diesem Thema.

Besonders empfehlenswert sind die Diskussionsbeträge von Karl Bednarik und seine weiterführenden Links.

http://www.scilogs.de/kosmo/blog/go-for-launch/allgemein/2011-12-22/stratolaunch_system_checked

--Karl Bednarik (Diskussion) 07:38, 5. Dez. 2012 (CET)

Basisstation

Entweder ich kapiers nicht oder im Artikel ist ein Fehler unter dem Stichwort Basisstation. Sollte diese auf der Erde sein, müssten dort nur sehr geringe Kräfte auftretten, die Station also auch nicht so extrem verankert werden. Im Prinzip nur die Maximale last +sicherheit für zum Beispiel Virbrationen(warscheinlich im Tagesrhythmus oder so...) (nicht signierter Beitrag von JoeHeinZ (Diskussion | Beiträge) 15:12, 20. Jan. 2010 (CET))

Inhaltlich schlecht Anfang 2010:

In der Diskussion ist vieles einfach inhaltlich falsch. Leider hat es einiges davon offensichtlich in den Artikel geschafft, wovon ich das gröbste entfernt habe. Aber auch ansonsten ist der Artikel in meinen Augen schlecht: Es fehlt eine übergeordnete Gliederung. Stattdessen gibt es viele Unterpunkte, die einem einzelnen Autor mal wichtig waren. Des Weiteren wimmelt der Artikel von Details von aktuellen Entwicklungen und Spekulationen. Einerseits sind sie wichtig, da dies nunmal der aktuelle Stand der Forschung ist, andererseits sollte man kennzeichnen, dass diese nicht a priori das zukünftige Setup ausdrücken. Es wäre sogar denkbar, sie in einem Abschnitt derzeitige wahrscheinlichste Realisierung oder so was zu bündeln. Grundlagen fehlt leider vollkommen. Eine Übersetzung des englischen Artikels wäre qualitativ hochwertiger. (nicht signierter Beitrag von Allesquarks (Diskussion | Beiträge) 17:24, 3. Mär. 2010 (CET))

Falsche Aussage

Zitat: "Ein zusätzliches Problem ist die Energieversorgung des Satelliten, denn durch die Corioliskraft einer aufsteigenden Last wird er abgebremst. Dadurch verliert er an Höhe und ist nicht mehr geostationär. Um dem entgegen zu wirken, wird für jede Last ein korrigierender Raketenantrieb benötigt. " Ende des Zitats.

Das ist falsch, denn sobald die Corioliskraft den Satelliten nach hinten zieht, bildet das Seil einen kleinen Winkel zur Senkrechten, und beschleunigt dadurch den Satelliten unter Bremsung der Erdrotation.

Ein vereinfachtes Bild:

http://members.chello.at/karl.bednarik/GEOSYN-3.jpg

Der Transport der Last wird durch die Corioliskraft kaum behindert, da sie praktisch quer zur Bewegung der Last steht.

Genau die gleiche Situation entsteht, wenn ein Eisenbahnzug auf der Nordhalbkugel der Erde nach Süden fährt.

Auch dann wird der Zug auf Kosten der Erdrotation beschleunigt.

-- Karl Bednarik 04:04, 23. Okt. 2010 (CEST).

Gegenläufige Gondeln

Auch ich habe, wie einige vor mir, noch arge Vorstellungsprobleme in punkto Energieerhaltungssatz. Aber das soll an dieser Stelle nicht das Thema sein. Mich würde zunächst vielmehr interessieren, wieso weder im Artikel noch in Schätzings Roman das Prinzip angedacht ist, welches beim normalen Aufzug elementar ist: Das Gegengewicht. Verwendet man zwei aneinandergekoppelte Gondeln, die sich gegenläuig bewegen, so muss keine Masse mehr gehoben, sondern nur noch die Reibung überwunden werden. Jan Krieg hat so etwas schon weiter oben erwähnt, aber im Artikel steht nichts davon. --W. Kronf *@* 17:57, 9. Jul. 2011 (CEST)

Weltraumaufzug bei der Piratenpartei

auf dem Bundesparteitag bpt141 anfang 2014 in Bochum besprach die Piratenpartei einen Antrag den Bau eines Weltraumlifts mit ins Programm aufzunehmen. Dieses wurde mehrheitlich abgelehnt. Interessantes Detail oder uninteressantes Detail für einen Eintrag? (nicht signierter Beitrag von 89.204.138.212 (Diskussion) 00:39, 12. Jan. 2014 (CET))

Uninteressant. --Asdert (Diskussion) 17:56, 12. Jan. 2014 (CET)

Auswirkungen auf die Erdrotation?

Ich könnte mir vorstellen, dass diese Vorrichtung, sollte sie wirklich jemals realisierbar sein, eine negative auswirkung auf die Erdrotation haben könnte. Den das Ganze stellt ja eine gewisse Unwucht her, bzw. kann ich mir vorstellen, dass der Hebelarm bremsend wirkt. Gibt es dazu Studien oder Berechnungen? 87.165.164.76 20:07, 19. Nov. 2006 (CET)

jetzt mal ohne die genauen zahlen zu kennen, was so ein weltraumlift wiegen wuerde, die Erde wiegt 5,974 · 10^24 kg,l ich denke nicht, dass die menschheit in der lage ist in den naechsten paar jahren das aus der bahn zu schubsen.

um dir die dimensionen vorzustellen, nimm einen fußball und klebe ein haar daran, das ca 3* so lang ist wie der ball im durchmesser ist. und das haar ist warscheinlich immernoch zu dick im vergleich. Elvis untot 22:51, 19. Nov. 2006 (CET)

Es geht weniger darum, die Erde aus der Umlaufbahn zu bringen, als darum, wie sich das auf die Eigenrotation der Erde auswirkt. Das Wasser der Weltmeere jedenfalls wirkt sich bremsend auf die Rotation aus. Auch ein Zunami kann sich bremsend auswirken. 87.165.139.235 15:23, 24. Nov. 2006 (CET)

ok, nimm den ball irgendwohin, wo er schwerelos im vakuum schwebt. meinst du, dass sich das haar wirklich auf die rotation auswirkt? (in einer messbaren größe, vorallem, da die erde im vergleich eine viel höhere masse hat)

wie das wasser die rotation dr erde abschwaechen soll verstehe ich jedoch nicht so ganz. es ist ja nicht so, dass das wasser einen entgegengesetzen impuls besitzt. Elvis untot 15:49, 24. Nov. 2006 (CET)

Das Wasser der Ozeane wird durch die Anziehung des Mondes auch angezogen und bildet so die Gezeiten. Dieses Umherwabern der Wassermassen ist mit viel Reibung verbunden und die Energie dafür wird u.A. der Erdrotation entzogen. --RokerHRO 16:10, 24. Nov. 2006 (CET)

ja, aber da würde ich dem mond die hauptschuld geben. und man muss da auch wieder sehen, welche massen das sind und dann den vergleich des lifts dazu. Elvis untot 22:06, 24. Nov. 2006 (CET)

Ein Hebelarm an sich wirkt niemals bremsend. Er kann dann bremsen, wenn er Reibung mit einem äußeren Medium hat - da wäre allenfalls die Erdatmosphäre zu berücksichtigen, aber (a) wirkt sie sich gerade mal auf den ersten 100 von 64.000 Kilometern aus und (b) dreht sie sich im großen und ganzen ohnehin mit der Erde mit.

Ansonsten gelten die bereits gemachten Argumente zum Weltraumlift - selbst wenn wir pro Meter eine Tonne Gewicht annehmen (was garantiert zuviel ist), haben wir 64.000*1000 Tonnen = 64.000*1000*1000 kg = 64 * 10^9 kg = 6,4 * 10^10 kg. Die Erde mit 6 * 10^24 kg ist also immer noch um den Faktor 10^14 schwerer als der Lift. Zum Vergleich: ein Promille ist ein Tausendstel, als ein Faktor von 10^4; ein Promille von einem Promille ist 10^8, ein Promille von einem Promille von einem Promille 10^12, und dann sind wir immer noch um einen Faktor von 100 von den 10^14 entfernt...

Joachim Durchholz 11:07, 21. Okt. 2008 (CEST)

Wieso steht der Käse mit dem Verlängern der Tageslänge denn jetzt im Artikel drin? Ist doch völlig insignifikant die "Abbremsung".

--31.19.124.203 02:58, 28. Nov. 2012 (CET)

Also ich versuche mal etwas dazubeizutragen. Das Problem, das oben etwas unbeholfen mit Unwucht benannt wurde, ist das http://de.wikipedia.org/wiki/Tr%C3%A4gheitsmoment . Das Massenträgheitsmoment $J$ lässt sich bei bekannter Massenverteilung $\rho ({\vec {r}})$ eines Körpers aus folgendem Volumenintegral berechnen:

$J=\int _{V}{\vec {r}}_{\perp }\!^{2}\rho ({\vec {r}})\mathrm {d} V$.

Dabei ist ${\vec {r}}_{\perp }$ der zur Rotationsachse ${\vec {\omega }}$ (Winkelgeschwindigkeit) senkrechte Anteil von ${\vec {r}}$. Wie man sieht wirkt, sich die Entfernung zum Erdmittelpunkt quadratisch aus. Der geostationäre Orbit ist schon ca. 7 mal soweit vom Erdmittelpunkt entfernt, wie die Erdoberfläche. Oben ist zudem die Rede davon, dass das Gegengewicht in über 143.000 km Entfernung kreist. Das ist mehr als der 20-fache Erdradius und somit bremst eine zusätzliche Masse dort über 400 mal so stark wie auf der Erdoberfläche. Vielleicht kann das mal jemand genauer ausrechnen, der mehr Muße und Routine hat als ich. Vielleicht sind auch sämtliche Überlegungen dazu unsinnig, falls man das Gesamtsystem Erde-Mond betrachten müsste. Just my 2 Cents. Trillian 3 (Diskussion) 14:54, 10. Mai 2014 (CEST)

Mondlift

Wozu wäre der Mondlift zu gebrauchen? Quellen? Links? --Itu 18:31, 2. Jan. 2011 (CET)

Die Vorteile wären

1. keine gefährlichen Landungen
2. Landefähren würden nicht mehr benötigt (Kapseln könnten zwischen Erde und Mond pendeln und müssten nicht jedes mal erneut hergestellt und in die Erdumlaufbahn gebracht werden)
3. Strom statt schwerer Treibstoff für den Start => mehr kann billiger nach oben transportiert werden

--Impériale (Diskussion) 00:11, 7. Okt. 2014 (CEST)

Wie soll man sich denn an einem nur wenige mm dicken

"Seil" "festhalten"??????????? (nicht signierter Beitrag von 217.227.55.222 (Diskussion) 07:46, 6. Mai 2014 (CEST))

Wenige mm ist gut. Das Seil ist am Anfang wahrscheinlich schon einige Zentimeter dick und erreicht wahrscheinlich eine Dicke von 2,5 Metern. Wie man sich an diesen verschiedenen Durchmessern festhält kann ich dir aber leider auch nicht sagen. --Impériale (Diskussion) 00:27, 7. Okt. 2014 (CEST)

Graphen-Lift, konstanter Querschnitt

Beim Graphen ist ein konstanter Querschnitt möglich. Das Graphen liegt normalerweise als flaches Band vor. [6] Dieses Band könnte man auch bei gleicher Dicke verbreitern. Kleine Löcher, die der Weltraummüll schlägt, stören erst, wenn sie größer als zwölf Prozent der Breite des Bandes sind. Ausserhalb der Kletter-Walzen sollte das Graphen-Band die Form eines halben Zylindermantels haben, denn flache Bänder reissen bei Treffern, die von der Kante her kommen, und ganze Zylinder werden häufiger zweimal durchschlagen. -- Karl Bednarik (Diskussion) 05:27, 7. Okt. 2014 (CEST). Korrektur: -- Karl Bednarik (Diskussion) 05:27, 8. Okt. 2014 (CEST). Korrektur: -- Karl Bednarik (Diskussion) 05:34, 8. Okt. 2014 (CEST).

Geostationärer Orbit oder höher?

Im Artikel wird die ganze Zeit von einem geostationärem Orbit gesprochen, jedoch habe ich irgendwo mal gelesen, dass die Station eine etwas größere Höhe haben müsste, damit diese das Seil dann spannen könne. Was ist richtig? --Impériale (Diskussion) 00:16, 7. Okt. 2014 (CEST)

Energiebilanz beim Weltraumlift

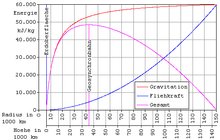
Der Schwerpunkt des gesamten Seilsystems muss mindestens im geostationärem Orbit liegen. Ein wenig höher stört aber nicht, und ist auch sicherer. Ein Graphen-Band mit konstantem Querschnitt, das bis in eine Höhe von 143.780 km über dem Erdäquator verlängert wird, ist im völligen Gleichgewicht zwischen Gravitationsbeschleunigung und Zentrifugalbeschleunigung. Diese Anordnung kann auch zur Zurückgewinnung der Aufstiegs-Energie verwendet werden. -- Karl Bednarik (Diskussion) 05:27, 7. Okt. 2014 (CEST). Korrektur: -- Karl Bednarik (Diskussion) 05:37, 7. Okt. 2014 (CEST).

Umlaufbahnen in niedrigeren Bahnen?

Wenn an dem Thema überhaupt etwas dran ist, würde ich es aus der Einleitung rausnehmen und nach ganz unten in ein Unterkapitel verschieben.

Wenn eine Station sich mit höherer Geschwindigkeit um die Erde dreht (beispielsweise einmal in 90 Minuten), würde sich doch das Seil von der Erdoberfläche aus ziemlich schnell aufwickeln?? Gut, wenn der Schwerpunkt von Station und Gegengewicht im geostationären Orbit bleibt, könnte die ganze Konstruktion weiter ortsfest mit der Erde rotieren, aber dann würde die Station fast mit ihrem gesamten Gewicht am Seil (gehalten vom Gegengewicht) hängen. Aber wie gesagt: eine Spezialdiskussion, die nichts in der Einleitung verloren hat. --Gerd-HH (Diskussion) 10:50, 23. Okt. 2014 (CEST)

Vermutlich war damit nur gemeint, was passiert, wenn ein antriebsloses Objekt unterhalb des geostationären Orbits aus einem normalen, geosynchronen Weltraumlift ausgeklinkt wird. Solch ein Objekt gelangt auf eine absteigende Bahn-Ellipse, und wird unterhalb einer bestimmten Mindest-Ausklink-Höhe in die Erdatmosphäre eintreten. Die Mindest-Ausklink-Höhe für eine stabile Bahn-Ellipse, die "hinten" um die Erdatmosphäre herum führt, muss ich noch berechnen. -- Karl Bednarik (Diskussion) 05:03, 24. Okt. 2014 (CEST).

Nachtrag: Oberhalb des geostationären Orbits gibt es eine Grenz-Ausklink-Höhe, ab der die aufsteigenden Bahn-Ellipsen in hyperbolische Fluchtbahnen übergehen. Diese hyperbolischen Fluchtbahnen sind für die Raumfahrt sehr nützlich. -- Karl Bednarik (Diskussion) 05:18, 24. Okt. 2014 (CEST).

Zweiter Nachtrag: Ein maßstabsgerechtes Bild der verschiedenen Ausklink-Bahnen:

http://members.chello.at/karl.bednarik/SATEBAH5.PNG

-- Karl Bednarik (Diskussion) 10:42, 24. Okt. 2014 (CEST).

Dritter Nachtrag: Numerische Abschätzung und ein neues Bild. Wenn man in 23558 km Höhe aussteigt, dann kommt man um die Erde herum. Wenn man in 46749 km Höhe aussteigt, dann kommt man von der Erde weg.

http://members.chello.at/karl.bednarik/SATEBAH6.PNG

-- Karl Bednarik (Diskussion) 06:59, 25. Okt. 2014 (CEST). Korrektur: -- Karl Bednarik (Diskussion) 07:34, 25. Okt. 2014 (CEST).

Schwerpunkt

Es stimmt nicht, dass der Schwerpunkt des Weltraumlifts auf der Höhe des geostationären Orbits wäre. Denn während die Summe der Fliehkräfte auf alle Massenpunkte des Weltraumlifts gleich der Fliehkraft ist, die bei Kontraktion der Gesamtmasse des Weltraumlifts auf den Schwerpunkt aufträte, ist das bei den Gravitationskräften nicht der Fall. Das liegt daran, dass die Fliehkraft in linearer Beziehung zum Radius $x$ steht ($F_{Z}=\omega ^{2}x$). Deshalb muss der Schwerpunkt oberhalb des geostationären Orbits liegen.

Beim Aufbau eines Weltraumlifts könnte man auf der Höhe des Schwerpunkts des Endprodukts starten, wobei man natürlich mit niedrigerer Winkelgeschwindigkeit startet. Beim Entfalten oder Zubauen muss dann Orbitalenergie hinzugefügt werden.

Beziehung von Bahnradius $x$ und Winkelgeschwindigkeit $\omega$ für Punktmassen auf Kreisbahnen:

$\omega ^{2}={\frac {GM}{x^{3}}}$

Bei einem dünnem Stab der Länge $l$, Querschnitt $A$ und Dichte $\rho$, der immer senkrecht ausgerichtet ist, kann man die gesamte Gravitationskraft durch folgendes Integral ausrechnen:

$\int _{x-{\frac {l}{2}}}^{x+{\frac {l}{2}}}A\rho {\frac {GM}{x'^{2}}}dx'$
$=GMA\rho ({\frac {1}{x-{\frac {l}{2}}}}-{\frac {1}{x+{\frac {l}{2}}}})$
$=GMA\rho {\frac {l}{x^{2}-{\frac {l^{2}}{4}}}}$

Mit der Gesamtmasse des Stabes $m=Al\rho$ ergibt das dann
${\frac {GMm}{x^{2}-{\frac {l^{2}}{4}}}}$

Damit kann man sehen, was die Beziehung von Bahnradius und Winkelgeschwindigkeit beim senkrechten dünnen Stab ist:

$\omega ^{2}={\frac {GM}{x(x^{2}-{\frac {l^{2}}{4}})}}$

Beim Weltraumlift wird die Dicke und somit die lineare Dichte $A\rho$ im Gegensatz zu meinem einfachen Stab-Modell nicht konstant sein, es gilt aber auch, dass die Winkelgeschwindigkeit für den Weltraumlift größer ist, als die Winkelgeschwindigkeit für eine Punktmasse im Schwerpunkt des Weltraumlifts.

Usr2 (Diskussion) 21:39, 26. Okt. 2014 (CET)

Nachtrag: Formel korrigiert, auf gleiche Konventionen wie im Abschnitt "Auswirkungen - Energiebilanz" gebracht. Usr2 (Diskussion) 20:41, 27. Okt. 2014 (CET)

Wenn man den vorgeschlagenen Weltraumlift aus dem Abschnitt "Auswirkungen - Energiebilanz" nimmt, kann man sich den Schwerpunkt $x_{S}$ ausrechnen:

$x_{S}={\frac {\int _{x0=6378000m}^{150159000m}dx\,x\,e^{-{\frac {GM}{x}}-{\frac {\omega ^{2}x^{2}}{2}}+{\frac {GM}{x_{0}}}+{\frac {\omega ^{2}x^{2}}{2}}}}{\int _{x0=6378000m}^{150159000m}dx\,e^{-{\frac {GM}{x}}-{\frac {\omega ^{2}x^{2}}{2}}+{\frac {GM}{x_{0}}}+{\frac {\omega ^{2}x^{2}}{2}}}}}$

Ergebnis nach numerischer Integration:

$x_{S}$ = 65558 km

Usr2 (Diskussion) 21:09, 27. Okt. 2014 (CET)

Hallo Usr2, wenn ein Lift mit konstantem Querschnitt vom Erdäquatorradius von 6378 km bis in die energetisch neutrale Höhe von 143780 km führt, dann sollten einander alle Kräfte gegeseitig aufheben, aber sein Schwerpunkt müsste dann in 71890 km Höhe liegen. Ist das richtig? Wenn man mit zwei unterschiedlich großen Rollen von Grahen-Band im geostationären Orbit in einer Höhe von 35786 km über dem Erdäquator beginnt, die zweite Rolle wäre dann 107994 km lang, dann müsste man sie nur unterschiedlich schnell abrollen. Dabei würde aber das Band nach unten dem geostationären Satelliten ein wenig voraus eilen, während das Band nach oben dem Satelliten hinterher eilen würde, weil beide Bänder zuerst die Kreisbahngeschwindigkeit des Satelliten hätten, während die Geschwindigkeit jedes Punktes des Liftes linear mit dem Abstand zum Erdmittelpunkt variiert. Mit freundlichen Grüßen, -- Karl Bednarik (Diskussion) 06:03, 28. Okt. 2014 (CET).

Hallo Karl Bednarik, der Schwerpunkt ist bei der von Dir angegebenen Höhe über dem Erdboden. Man müsste aber auf Schwerpunkthöhe (mit 2 gleich großen Rollen) anfangen, und dann während des Ausrollens nach und nach mit Raketentriebwerken Bahnenergie (bzw. Bahndrehimpuls) zuführen. Wenn man stattdessen auf geostationärer Höhe mit unterschiedlich großen Rollen anfängt und daher die Ausrollgeschwindigkeit unterschiedlich ist, dann wird sich die Mittelstation durch das Ausrollen senken.

Zum Coriolis-Problem: Man kann mit Drehimpuls-Erhaltung ausrechnen, wie sich eine schnelle Verlängerung (gleichzeitig nach oben und unten) auswirkt. Annahme: Die Rollen bleiben in der Mitte, während das Band (von Satelliten geführt) ausgerollt wird.

$m$ .... Gesamtmasse der Konstruktion

$m_{Z}$ .... noch aufgerollte Masse im Zentrum der Konstruktion

$A$ .... Querschnittsfläche des Bandes

$\rho$ .... Dichte des Bandes

$l$ .... Länge der Konstruktion

$x_{S}$ .... Abstand zwischen Erdmittelpunkt und Schwerpunkt der Konstruktion

$\omega$ .... Winkelgeschwindigkeit der Erdumkreisung

$L$ .... Drehimpuls der Konstruktion

Wir gehen in der Anfangssituation davon aus, dass die Konstruktion so schnell rotiert wie sie sich um die Erde bewegt und daher erstmal senkrecht bleibt.

Erstmal (eher nebenbei) zur Beziehung zwischen Winkelgeschwindigkeit $\omega$ und Schwerpunktposition $x_{S}$, Berechnung durch Gleichsetzen von Gravitationskraft (links, für den ausgerollten Teil übernehmen wir aus den Formeln des senkrechten Stabes von weiter oben) und Zentrifugalkraft (rechts):

$GM({\frac {m_{Z}}{x_{S}^{2}}}+{\frac {lA\rho }{x_{S}^{2}-{\frac {l^{2}}{4}}}})=m\omega ^{2}x_{S}$

Das ergibt umgestellt, mit Einsetzen von $m_{Z}=m-lA\rho$:

$\omega ^{2}={\frac {GM}{x_{S}^{3}}}+{\frac {GM}{x_{S}m}}lA\rho ({\frac {1}{xS^{2}-{\frac {l^{2}}{4}}}}-{\frac {1}{x_{S}^{2}}})$

Jetzt zum Drehimpuls, der ist einfach der Drehimpuls der Gesamtmasse als Punktmasse gedacht, plus Winkelgeschwindigkeit mal Trägheitsmoment (siehe im Artikel Trägheitsmoment unter Ein dünner Stab...) des ausgerollten Teils:

$L=\omega (mx_{S}^{2}+{\frac {l^{3}A\rho }{12}})$

Man vergrößere nun die Länge $l$ auf $l_{1}$, und zwar schnell genug, so dass sich während der Vergrößerung kaum etwas durch die Coriolis-Beschleunigung bewegt. In dieser kurzen Zeit kommt es daher auch kaum zu Gezeitenkräften, und deshalb bleibt der Drehimpuls erhalten. Die Konstruktion muss also nicht ganz so schnell mitrotieren, bzw. im rotierenden Bezugssystem sieht man eine Gegenrotation mit Winkelgeschwindigkeit $\omega _{1}$. Drehimpulsbilanz:

$\omega (mx_{S}^{2}+{\frac {l^{3}A\rho }{12}})=\omega (mx_{S}^{2}+{\frac {l_{1}^{3}A\rho }{12}})-\omega _{1}{\frac {l_{1}^{3}A\rho }{12}}$

Aufgelöst nach $\omega _{1}$:

$\omega _{1}=\omega (1-({\frac {l}{l_{1}}})^{3})$

Wenn also $l$ = 0 war, dann gegen-rotiert die Konstruktion nun mit der vollen Winkelgeschwindigkeit, sonst um weniger.

Man beachte, dass das $\omega$ in der letzten Formel mit der $\omega ^{2}$-Formel etwas weiter oben äausgerechnet werden kann, indem man $l$ (nicht $l_{1}$) einsetzt. Da jetzt aber die Länge größer ist, reicht dieses $\omega$ nicht mehr für eine geordnete Kreisbahn aus. Man muss also sowohl die Gegenrotation als auch die nun zu kleine Bahn-Winkelgeschwindigkeit ausgleichen. Bei der Gegenrotation können die Gezeitenkräfte helfen.

Usr2 (Diskussion) 23:52, 28. Okt. 2014 (CET)

Hallo Usr2, leider habe ich noch vier Fragen. Hat nicht der geostationäre Satellit in Position und Rotation bereits die Winkelgeschwindigkeit der Erde? Wenn man vom geostationären Satelliten in richtiger Weise beide Bänder ungleich schnell ausrollt, müssten sich dann nicht die Gravitationskraft des unteren Bandes und die Zentrifugalkraft des oberen Bandes genau ausgleichen? Die beiden Bänder werden ja nicht ausgestoßen, sie hängen ja freiwillig heraus. Wenn zum Beispiel der geostationäre Satellit zu sinken beginnt, dann rollt man mehr oberes Band aus, um ihn durch mehr Zentrifugalkraft wieder anzuheben. Wenn man einen stabförmigen geostationären Satelliten hat, der nicht auf den Schwerpunkt der Erde zeigt, was dämpft dann seine von den Gezeitenkräften ausgelösten Schwingungen? Was bedeutet der dritte Satz in der Einleitung: "Umlaufbahnen in niedrigeren Bahnen sind theoretisch nur sehr schwer möglich"? Mit Dank für die Antworten im Voraus, und mit freundlichen Grüßen, -- Karl Bednarik (Diskussion) 03:50, 29. Okt. 2014 (CET). Ergänzung: -- Karl Bednarik (Diskussion) 04:11, 29. Okt. 2014 (CET).

Hallo Karl Bednarik, Fragen sind gut, denn so sehe ich, dass ich mir in meinem letzten Beitrag ein falsches Modell gebaut habe. Du hast recht, man fängt beim geostationären Orbit an, wie von Dir beschrieben (und mein Modell nimmt an, dass die Bänder ausgestoßen werden). Die letzte Formel $\omega _{1}=\omega (1-({\frac {l}{l_{1}}})^{3})$ nimmt zwar einen starren Körper an, ansonsten stimmt sie aber noch, wenn kein Drehimpuls zugeführt wird. Allerdings ist das Band offensichtlich nicht starr, und die Coriolis-Beschleunigung eines kurzen Ausrollvorgangs führt z.B. entlang des gesamten inneren Bandes zur gleichen Geschwindigkeitsänderung, was dann unterschiedlichen Winkelgeschwindigkeiten (in Bezug auf das geostationäre Zentrum) führt, sodass die näher beim geostationären Zentrum liegenden Teile etwas vorauseilen.

Man könnte bei einem stabförmigem Satelliten die Schwingungen mit Hilfe der Reibung zwischen den äußeren und den dazu drehbaren inneren Teilen des Satelliten bewerkstelligen, oder mit einem flüssigkeitsgefülltem Behälter in der Mitte. Praktisch gesehen gibt es zumindest Magnet-Dämpfer, das sind mit Öl gefüllte Behälter an den Enden des Satelliten, die Permanentmagnete enthalten. Die Permanentmagneten richten sich immer nach dem Erdmagnetfeld aus und sorgen so für mehr Reibung, als nur die Trägheit eines flüssigkeitsgefüllten Behälters:

https://ia600509.us.archive.org/23/items/nasa_techdoc_19930015538/19930015538.pdf

Der genannte Satz in der Einleitung des Artikels kommt mir auch seltsam vor. Vielleicht wollte jemand andeuten, dass man auch einen kürzeren Weltraumlift bauen könnte, der ständig mit Raketentriebwerken stabil gehalten wird (ohne jetzt nach dem Sinn zu fragen...).

Usr2 (Diskussion) 15:45, 29. Okt. 2014 (CET)

Kritik am Abschnitt Technik

Ich finde es ja toll, dass Ihr den Artikel pflegt und auf der Diskussionsseite herumrechnet. Allerdings kommt mir der gesamte Abschnitt Technik etwas dürftig belegt vor. Alles was Ihr hier privat ausrechnet und in den Artikel einbaut, wäre Theoriefindung. Aber das wisst Ihr ja. Gruß, --Turnstange (Diskussion) 15:28, 28. Okt. 2014 (CET)

"Alles was Ihr hier privat ausrechnet und in den Artikel einbaut, wäre Theoriefindung" - Quatsch.

Was nach unangefochtenen Formeln aus der Physik (z.B. Gravitation, Fliehkraft) korrekt berechnet wurde, ist niemals Theoriefindung.

Im Gegenteil - logische Erklärung ist die einzige valide Ausnahme zur Belegpflicht.

--arilou (Diskussion) 15:35, 28. Okt. 2014 (CET)

Ungültiges Archivierungsziel

Die Zielangabe bei der automatischen Archivierung dieser Seite ist ungültig. Sie muss mit demselben Namen wie diese Seite beginnen. Wende dich bitte an meinen Besitzer, wenn das ein Problem darstellen sollte. ArchivBot (Diskussion) 04:47, 15. Dez. 2014 (CET)

Ich hoffe, dass die Archivierung jetzt funktioniert. MfG Harry8 08:43, 15. Dez. 2014 (CET)

Umlaufbahnen in niedrigeren Bahnen, Teil zwei

Der dritte Satz in der Einleitung: "Umlaufbahnen in niedrigeren Bahnen sind theoretisch nur sehr schwer möglich" ist schwer verständlich und zumindest erklärungsbedürftig. Vielleicht ist hier auch ein rotierendes Weltraumseil gemeint, wie in diesem Bild:
http://members.chello.at/karl.bednarik/GROMUSEI.PNG
-- Karl Bednarik (Diskussion) 06:51, 31. Okt. 2014 (CET).
Benutzer:Gerd-HH und Benutzer:Usr2 halten diesen Satz ebenfalls für fragwürdig. Ich lösche ihn daher probeweise. -- Karl Bednarik (Diskussion) 07:26, 1. Nov. 2014 (CET).

Diesen Satz habe ich so formuliert. Davor stand dort glaube ich "Umlaufbahnen in niedrigeren Bahnen sind nicht möglich", was meiner Meinung nach falsch ist, da man mit einem Gerät, welches sich in einer Höhe von über 100 km halten kann, einer Verbindung zum Boden und einer Gondel auch einen Weltraumlift hat. Theoretisch unmöglich ist das nicht, ob das aber in den Artikel gehört ist wieder eine andere Frage. --Impériale (Diskussion) 13:56, 9. Dez. 2014 (CET)

Ich verstehe immer noch nicht, wie das mit den niedrigen Umlaufbahnen gehen soll. Die Idee beim "Weltraumlift" ist doch, dass der Schwerpunkt im geostationären Orbit liegt (36000 km) und die Konstruktion dadurch ortsfest ist und schwebt. Jetzt steht es einem natürlich frei, an so einer Konstruktion in 1 oder 100 km Höhe eine kleine Aussichtskanzel anzuhängen. Aber meint ihr, man könnte so etwas auch mit einem Seil erreichen, das nur 1 oder 100 km lang ist?? Die ISS umrundet die Erde in ca. 90 Minuten, da bräuchte man wohl eine Kabeltrommel? --Gerd-HH (Diskussion) 09:41, 19. Mär. 2015 (CET)

Ich verstehe auch nicht, wie das mit den niedrigen Umlaufbahnen gehen soll. -- Karl Bednarik (Diskussion) 06:24, 20. Mär. 2015 (CET).

Es wäre z.B. möglich, dass die "Orbitalstation" ununterbrochen Schub leistet, um "geostationär" zu bleiben. Damit verliert sie natürlich ihren eigentlichen Vorteil, Objekte ohne Raketenantrieb ins All bringen zu können.

Da der ganze Artikel ziemliche "Spinnerei" ist, ist es schwierig abzugrenzen, was nun "wenig genug verrückt" ist, um erwähnt werden zu dürfen, und was "so aberwitzig" ist, dass es nicht genannt werden soll.

--arilou (Diskussion) 08:49, 23. Mär. 2015 (CET)

Vielleicht war ja auch die "space fountain" gemeint. Aber die oberen Enden von Türmen und Springbrunnen haben streng genommen gar keine Umlaufbahnen, weil sie einfach nur auf dem Boden stehen. Genau so gut könnte mein Kopf eine geostationäre Umlaufbahn haben.

Bild:

http://www.baenebooks.com/chapters/0671876864/067187686405.jpg

Text:

https://en.wikipedia.org/wiki/Space_fountain

-- Karl Bednarik (Diskussion) 08:16, 24. Mär. 2015 (CET).

Der Energieerhaltungssatz läßt sich nicht überlisten

Um einen Körper in eine Umlaufbahn zu bringen muß man sowohl seine potentielle wie auch seine kinetische Energie vergrößern. Die aufzuwendende Energie entspricht der Gesamtenergiedifferenz zwischen Erdoberfläche und der Umlaufbahn mit seinen charakteristisch großen Geschwindigkeiten. Bei dem Weltraumlift ist die kinetische Energieerhöhung ein bißchen versteckt. Oder wird einfach übersehen?

Ja, Du übersiehst da was: die Ineffizienz der Raketentechnik liegt daran, dass man den Treibstoff mit anheben muss. Elektrische Energie am Liftkabel nach oben zu transportieren erfordert keinen messbaren Massentransport, man muss also nur noch die Energie aufwenden, um die Nutzlast selbst anzuheben. (Wenn Du Dir anschaust, was für Monstren die heutigen Raketen sind und wie winzig die Nutzlast im Vergleich ist, kann Du Dir leicht ausmalen, welcher Faktor da eingespart wird.) -- Joachim Durchholz 11:25, 23. Apr. 2009 (CEST)

Die geostationäre Umlaufbahn zeichnet sich ja dadurch aus daß die Winkelgeschwindigkeit genau gleich der der Oberfläche ist. Die Geschwindigkeit ist dabei einfach proportional des Abstandes zur (Erd)Drehachse. Da der Abstand in der Umlaufbahn ca 6,6 mal so groß (wie der Erddurchmesser) ist ist auch die Geschwindigkeit 6,6 mal so groß wie díe der Erdoberfläche.

Wenn wir jetzt also einen Körper an einem Seil nach oben ziehen wird dieser Köper ohne die entsprechende Vergrößerung der horizontalen! Geschwindigkeit das Seil nach hinten ziehen und letzendlich den Sateliten bremsen. Bis er runterkommt und sich alles um die Erde wickelt. Was dann natürlich keiner vorhersehen konnte ;)

Man muß beim Hochziehen die horizontale Geschwindigkeit gemäß des Abstandes zur Erdachse vergrößern. Per Raketentriebwerk? Gibt da wohl keine andere Möglichkeit im Vakuum. Und damit wäre der Energieerghaltungsatz erfüllt. Die potentielle Energie kommt aus dem Aufzug...., die kinetische muß wohl per Raketentriebwerk erbracht werden.

Ist also kein wirklicher Unterschied zur (uneffektiven) "konventionellen" Methode per Rakete.

Man muß immer! den entsprechenden Energieunterschied aufbringen egal! wie mans macht. Und ich schätze alle Verfahren sind nicht sehr ökonomisch..... Wie auch das Space Shuttle daß die ursprünglich projektierten Kosten um mehr als das hundertfache überschritten hat. Der größte wirschaftliche Fehlschlag aller Zeiten.

Besser ist es imho sich die Erde bewohnbar und gemütlich zu erhalten. Es gibt keine Alternative.

Science fiction ist mehr fiction als science. (nicht signierter Beitrag von 89.61.216.157 (Diskussion | Beiträge) 13:50, 3. Apr. 2009 (CEST))

Nun, eine Möglichkeit, die der Weltraumlift dem Space Shuttle zum Ausgleichen der horizontalen Geschwindigkeit voraus hat, ist das Seil, an dem er aufgehängt ist. Wie schon richtig bemerkt, würde sich beim Hochziehen einer Last im Extremfall das Seil um die Erde wickeln. Allerdings mit der Betonung auf dem Extremfall. Falls die horizontale Kraft auf das Seil nicht zu groß ist, sollte es möglich sein, die verursachte Auslenkung im Seil durch die Aufhängung an der Basisstation und im Orbit aufzufangen. Zumal das Seil ja durch eine Verlängerung über die notwendige Länge im Orbit hinaus straff gehalten werden kann. Die ausgleichende Kraft kann dabei eine Gondel aufbringen, die zeitgleich zur aufwärtsfahrenden Gondel vom Orbit in Richtung Erde startet. Somit würden sich die kinetischen Energien der beiden Gondeln aufheben und die Basisstationen auf der Erde und im Orbit müssten nur die entstehenden Schwingungen auffangen.

Bei einer vertikalen Geschwindigkeit der Gondel von 150 m/s und einer Masse von 15.000 kg würde die horizontale Kraft, die direkt nach dem Start in Höhe des Äquators auf das Seil wirkt, etwa 1400 N betragen. In einer Höhe von 10.000 km über dem Äquator wäre die horizontale Kraft schon auf weniger als ein Viertel, etwa 340 N, gesunken. Daher denke ich, das die Auslenkung bei dem sehr massereichen Seil nicht besonders groß sein dürfte. Immerhin könnte man ja die vertikale Geschwindigkeit in Erdnähe niedrig halten und dann in Richtung Orbit immer mehr steigern, um die horizontale Kraft gleichmäßig zu halten. -- Jan Krieg 01:18, 4. Apr. 2009 (CEST)

Verlängert man das Seil über den geostationären Punkt hinaus läßt sich die Energie der Erdrotation nutzbar machen, indem entweder Nutzlast wie interplanetare oder interstellare Raumsonden auf praktisch beliebig hohe Geschwindikeiten beschleunigen ließe oder aber indem Gewichte über ein entsprechend langes Seil den Aufzugsschlitten mit hochziehen. Alternativ könnten diese Gewichte auch über das Dynamoprinzip ihre kinetische Energie in elektromagnetische umwandeln und etwa per Laser zur Basisstation oder direkt zum Schlitten transportieren. Dass die Energiebilanz des Weltraumliftes jenseits des geostationären Punktes positiv wird sieht man wenn man in der Grafik FLIHIHI_Energie_Weltraumlift.PNG die Abszisse entsprechend verlängert. Der blaue Graph der Fliekraft steigt exponentiell an, während der rosa Graph namens "Gesamt" im negativen Bereich letztendlich einen Energiegewinn ausweist.

Die Energie, oder vielmehr der Drehimpuls für das Hinausschleudern der Raumsonden und Opfergewichte zur Energieerzeugung, wird der Erdrotation entnommen wodurch sich die Tagesdauer verlängert. Auf mehr als 1 Monat Tagesdauer läßt sich dies aber selbst bei intensivster Nutzung durch die Menschheit nicht ausdehnen, weil sich dann der Mond sogar schneller um die Erde dreht als sie selbst und langfristig der Mond seinen Drehimpuls über die Gezeiten an die Erde abgeben würde und im Gegensatz zur heutigen Situation sogar seinen Abstand immer weiter verringern würde. (nicht signierter Beitrag von 89.12.118.158 (Diskussion) 22:20, 3. Sep. 2011 (CEST))

Diese Erklärung ist mir nicht ganz klar. Ich könnte das nachvollziehen, wenn es sich um einen völlig versteiften "Weltraumturm" handeln würde. Aber das Seil wäre ja in gewissen Grenzen flexibel. Wie kann die Erdrotation unter dieser Bedingung Energie auf die zu befördernde Masse übertragen? Oder nochmal anders ausgedrückt: Das Gewicht bewegt sich am Seil nach oben. Dabei wirkt die Corioliskraft dahingehend auf die Last ein, dass sie entgegen der Erdrotation horizontal am Seil zieht. Das Seil bekommt einen leichten Knick, wird aber letztlich durch die Zentrifugalkraft des Gegengewichtes straff genug gehalten, damit die Last oben ankommt. Ist das soweit richtig? Wenn ja, hieße das doch aber, dass die Energie, mit der die Corioliskraft ausgeglichen wird, eben nicht der Erdrotation entnommen würde, sondern vielmehr aus der Bahnenergie des Gegengewichtes im Orbit stammt, welches dadurch an Stelle der beförderten Last verlangsamt würde und folglich wieder beschleunigt werden müsste, um geostationär zu bleiben. Oder? 95.91.217.105 17:59, 28. Nov. 2014 (CET)

Hallo 95.91.217.105, der Schwerpunkt des gesamten Liftsystems, und natürlich auch der Schwerpunkt des Gegengewichtes, muss weit oberhalb der geostationären Umlaufbahn liegen. Dadurch kann der gesamte Weltraumlift winkelmässig nach hinten von der senkrechten oder radialen Ausrichtung abweichen, ohne dass er eine weitere Energiezufuhr benötigt, ausser der durch die Erdrotation. Ein Bild dazu:

http://members.chello.at/karl.bednarik/GEOSYN-3.jpg

Ähnliche Verhältnisse herrschen auch beim Hammerwurf. Mit freundlichen Grüssen, -- Karl Bednarik (Diskussion) 04:36, 29. Nov. 2014 (CET).

Alles klar, danke für den Hinweis 95.91.217.105 22:27, 30. Nov. 2014 (CET)

Hat da verstanden, wer da schreibt?

"bis sich dieser Trend auf geostationärem Orbit umkehrt, da ab dort die resultierende Kraft der Seilsegmente erdabgewandt wirkt."

Die Aufhängung des Seils wird vermutlich am Gegengewicht im Orbit platziert. Und auch eine Umlenkrolle wird dort gebraucht. Da in Zugrichtung nach oben alle Kräfte erhalten bleiben, weil nicht erkennbar ist, wer und wie die Zugkräfte abgetragen werden können, und durch die Umlenkrolle auch keine Kräfte abgetragen werden, muss die Seilstärke ab der Umlenkstelle mindestens gleich bleiben. Da das Seil als Endlosseil konzipiert wird, damit der Aufzug kontinuierlich fördern kann, weil er nur so wirtschaftlich sein kann, erledigt sich der Ansatz mit veränderlichen Seilstärken von selbst. (nicht signierter Beitrag von 188.107.36.123 (Diskussion) 09:07, 19. Aug. 2015 (CEST))

An Umlenkrollen und an umlaufende Endlosseile hat beim Weltraumlift bisher eigentlich niemand gedacht, obwohl das mit einem Band aus Graphen mit konstanter Querschnittsfläche realisierbar wäre. Bisher dachte man eher an ein ruhendes Seil mit variabler Querschnittsfläche, an dem eine kletterfähige Kabine hinaufläuft, ähnlich wie in diesem Bild:

http://members.chello.at/karl.bednarik/NUKLTURB.PNG

-- Karl Bednarik (Diskussion) 06:27, 20. Aug. 2015 (CEST).

Dyneema

Warum wird hier Dyneema diskutiert? Meines wissens ist Dyneema ein tolles Material, aber für statische Lasten ungeeignet. Mein Kentnisstand ist: Es hält extreme Lasten aus, wodurch man es gut als Segel, Seil oder schussichere Weste verwenden kann. Wenn es aber dauerhaft mit mehr als 10% seiner festigkeit belastet wird, dann kriecht es und wird damit länger und schwächer. Für viele Anwendungen macht das nichts, weil hier Spitzenlasten stossweise auftreten: Böhen beim Segeln, und auch ein Abseilen dauert selten mehr als eine Stunde. Trotzdem längt sich so ein Seil, was sich beim fliegen von Lenkdrachen durchaus bemerkbar. Karsten Schuhmann (nicht signierter Beitrag von 192.33.100.152 (Diskussion) 16:30, 18. Nov. 2015 (CET))

Dazu kommt noch die Erweichung bei Hitze, die Versprödung bei Kälte, und die Zersetzung durch die UV-Strahlung. Alle diese Bedingungen kommen im Weltraum vor. -- Karl Bednarik (Diskussion) 06:02, 19. Nov. 2015 (CET).

2003:4C:6E18:9001:54D8:D752:6CAC:74F7 (Diskussion | Beiträge) 22:21, 19. Nov. 2015 (CET))

Kabel ist ein "falscher Freund" in der Übersetzung ...

... bestenfalls Seemannsjargon, selbst da ist es aber nur ein Lehnwort aus dem Englischen. Es muss Seil heißen. Bei mir reagiert der Button Suchen/Ersetzen nicht, was muss ich da machen?

http://de.wikipedia.org/wiki/Kabel_(Begriffsklärung) (nicht signierter Beitrag von Frank Stephan (Diskussion | Beiträge) 11:29, 19. Sep. 2013 (CEST))

Zusätzliche Probleme

Das Seil des Lifts verhält sich wie eine sehr lange Saite und muß deshalb gegen Schwingungen gedämpft werden. Schwingungen entstehen nicht nur durch die Beschleunigungen und Fahrbewegungen des Lifts und dessen Corioliskräfte, sondern auch durch die Gezeitenwirkung von Mond und Sonne, durch elektromagnetische Induktion aus Weltraumwetter, also Sonnenaktivität und Strahlungsgürtel, durch Einschläge von Mikrometeoriten und Weltraumschrott, und vielleicht fällt jemandem noch was ein. Man muß äquatorial durch die Strahlungsgürtel durch, was nicht nur eine extreme Panzerung der Gondel erfordert, sondern das Seil in diesen Regionen außerdem schnell korrodieren lassen dürfte. Weiterhin sollte man vermeiden, Erdboden und Ionosphäre elektrisch kurzzuschließen. Sowohl Nanotubes als auch Graphen-Bänder sind elektrisch in gewissen Grenzen leitfähig, deshalb Anfälligkeit gegenüber Induktion und Kurzschluß-Gefahr. Es reicht also nicht aus, ein Seil zu installieren, welches sich selbst, das Gegengewicht und den Lift halten kann, sondern das Seil muß auch mit Schwingungsdämpfern, elektrischer Isolation und Korrosionsschutz vollgepackt werden. Hinzu kommt noch die Magnetbahn-Ausrüstung zum Tragen, Führen, Beschleunigen und Bremsen. (nicht signierter Beitrag von 178.11.215.204 (Diskussion) 09:00, 30. Jul 2016 (CEST))

Toll dass Sie darüber nachdenken, allerdings ist der Weltraumaufzug ein theoretisches Konzept.

Davon abgesehen:

• Wird das Seil nicht bereits von der Athmosphäre gedämpft?
• Bei Tausenden von Kilometern Länge läge der elektrische Widerstand des Seiles im Gigaohm - Bereich
• Der Weltraumlift ist in erster Linie dazu gedacht, sehr grosse Massen in den Orbit zu befördern - keine Menschen.
• Das orginale Konzept sieht keine Magnetbahn vor. Die Gondel zieht sich selbst in den Weltraum.

--Mraudi (Diskussion) 16:49, 14. Jun. 2018 (CEST)--

Archivierung dieses Abschnittes wurde gewünscht von: --PM3 05:11, 24. Aug. 2019 (CEST)

Fast alle Satelliten müssten weg

Aus meiner Sicht gibt es ein Killerargument gegen den Weltraumlift, das bislang nirgens erwähnt wurde: Jeglich Umlaufbahn* außerhalb der geostationären Bahn müsste früher oder später das Seil des Liftes kreuzen. Man müsste also zunächst alle (nicht-GEO-)Satelliten und sämtlichen Weltraumschrott beseitigen, da es sonst nur eine Frage der Zeit wäre, wann solch ein Objekt (mit erheblicher Differenzgeschwindigkeit) mit dem Seil kollidiert. Das Seil gegen eine Kollision mit einem ganzen Satelliten zu schützen, halte ich für unmöglich. Abgesehen von der gewaltigen Aufgabe, alle (nicht-GEO-)Satelliten und sämtlichen Weltraumschrott zu beseitigen, müssten dann alle Aufgaben, die heute durch Satelliten in diversen Bahnen übernommen werden, aus dem GEO erfolgen. Auch das halte ich für nicht durchführbar.

• )Spezialfall: Es gäbe auch noch eine begrenzte Zahl von synchronen Umlaufbahnen, die niemals das Seil kreuzen würden. Wenn solche Satelliten keinen Treibstoff mehr haben oder fehlerhaft sind, wird es aber auch gefährlich für das Seil.

Das ist richtig. Alle kreisenden Objekte gehen zwei mal pro Umlauf durch die Äquator-Ebene der Erde, und diese wird vom Weltraumlift ständig überstrichen. -- Karl Bednarik (Diskussion) 07:13, 22. Okt. 2016 (CEST).

Dagegen spricht: Trotz der vielen Satelliten ist die Chance von einem Zusammenstoss doch relativ gering, da im Weltall soviel Platz ist (vergleiche mit Flugzeugen); Trotzdem: Einzelne Zusammenstösse können präzise vorhergesagt werden und durch eine kleine Manöverkorrektur an der Spitze des Seiles vermieden werden. Alternativ gibt es die Ueberlegung, den Ankerpunkt des Weltraumlift auf einer beweglichen Plattform (Schiff?) zu befestigen. --Mraudi (Diskussion) 16:57, 14. Jun. 2018 (CEST)

Die Wahrscheinlichkeit, dass sich zwei Satelliten treffen, die zum Beispiel beide rund einen Quadratmeter groß sind, die ist gering. Wenn der Weltraumlift zum Beispiel rund einen Meter dick ist, dann hat er eine Fläche von rund 40 Millionen Quadratmetern. Die freie Kreisfläche, wo der Weltraumlift gerade nicht ist, ist rund 120 Millionen mal größer. Laut der ESA befinden sich über 600000 Objekte mit einem Durchmesser größer als 1 cm in Umlaufbahnen um die Erde. Das bedeutet, dass es 1,2 Millionen Durchgangspunkte durch die Äquatorebene der Erde gibt, wobei die meisten dieser Durchgangspunkte mehrmals täglich durchflogen werden. Nach spätestens 100 Tagen müsste also ein Einschlag stattfinden. Dazu kommt noch, dass die meisten Objekte mehr als zehnmal pro Tag umlaufen, und dass der Weltraumlift dicker als 1 m sein wird. So kommen wir auf einen Einschlag alle fünf Tage. -- Karl Bednarik (Diskussion) 10:04, 15. Jun. 2018 (CEST). Korrektur: -- Karl Bednarik (Diskussion) 10:39, 15. Jun. 2018 (CEST).

Nach den aktuellen Plänen wird der Weltraumlift nicht dicker als 1m werden. Von den 600000 Objekten die ESA verfolgt sind die wenigsten funktionierende Satelliten. ESA arbeitet derzeit an Möglichkeiten, diese Objekte einzufangen und zu de-orbiten. Wenn man das in Ihre detailreiche Rechnung mit einbezieht, kann evtl. von einem Einschlag pro Monat ausgehen, der durch ein Manöver verhindert werden muss. Durchaus machbar. Natürlich ist das Problem, dass Sie ansprechen nicht von der Hand zu weisen - aber das ist sicher kein Killerargument. LG --Mraudi (Diskussion) 19:24, 16. Jun. 2018 (CEST)

Den ungeheuer massereichen Weltraumlift seitlich zu bewegen, das wird schwierig sein, (mehr als 80 Millionen Tonnen träge Masse,) und auch eine Menge Energie kosten.

Ein Vorschlag zum deorbiten von kleineren Objekten:

https://www.e-stories.de/view-kurzgeschichten.phtml?33860

-- Karl Bednarik (Diskussion) 09:15, 17. Jun. 2018 (CEST).

Durch Massenverlagerung kann man steuern, welche Kraft auf die Bodenstation wirkt. Da es sich um eine "Schnur" handelt, sollte es reichen nur einen kurzen unteren Teil zu bewegen. Den Rest der Masse wird die Fliehkraft bewegen.

Andere Massenverlagerung sollte die Lage der Schnur in der Mitte auch leicht ändern. Auf die unglaubliche Länge bezogen sind 100 oder 1000 Meter Abweichung schon vernachlässigbar.

Vielen Dank für die Idee mit den Öltropfen.

Haben Sie den ISEC Report schon gelesen? https://isec.org/wp-content/uploads/2017/05/2014_ISEC_Space_Elevator_Architecture_and_Roadmap_Final_Report.pdf

Grüsse, --Mraudi (Diskussion) 22:58, 17. Jun. 2018 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: --PM3 05:11, 24. Aug. 2019 (CEST)

Trotz aller Begeisterung, realistisch bleiben

Der Inhalt diese Abschnitts wurde bereits zuvor ins Archiv verschoben, er ist also kein neuer Diskussions-Beitrag. Entweder da wird ein Artikel-Beitrag draus, oder der Autor möge das wiederholte Posten seiner Kritik unterlassen.

Da im Archiv nachzulesen, habe ich hier gelöscht.

--arilou (Diskussion) 09:24, 18. Aug. 2017 (CEST)

Mein Artikel war durchaus nicht als neuer Diskussionsbeitrag zu verstehen. Ich hatte ihn allerdings, aufgrund meiner Unerfahrenheit in Wikipedia, zuerst falsch eingeordnet.--Werren (Diskussion) 21:31, 18. Aug. 2017 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: --PM3 05:11, 24. Aug. 2019 (CEST)

Technische Fragen

Zwei Punkte: 1. Das Problem des Energietransports stellt sich im Prinzip nicht, weil das Fahrkunstprinzip angewendet werden könnte. In der praktischen Ausführung gäbe es nicht das Seil als Weltraumlift, sondern mehrere parallele. Die sind dann nicht an den Bodenstationen höhenfix verankert, sondern die Stationen können den Ankerpunkt einige hundert Meter oder Kilometer vertikal bewegen, also auslassen und einholen. Die Last wird also am Seil fixiert, dieses um eine gewisse Höhe ausgelassen, dann klammert sie sich am Nachbarseil fest und das erste Seil wird wieder eingeholt und das andere ausgelassen, und umgekehrt. Einen eigenen Antrieb und damit eine Energieversorgung für diesen benötigt die Last also überhaupt nicht, sie braucht genau wie ein Bergmann auf der Fahrkunst für den Auf- und Abstieg keine Energie aufzuwenden. 2. Man muß einfach damit rechnen bzw. dafür vorsorgen, daß die Anlage von einem größeren Objekt (Satellit, Flugzeug, Meteoroid, Raumstation) getroffen wird und es kein Mittel gibt, eine völlige Zerstörung an der getroffenen Stelle zu verhindern. Deshalb kann ein Spacelift keine "Eindrahtanlage" sein, sondern man hat sich eine Anordnung von vielen Mehrfach-Seilen, angeordnet in mehreren konzentrischen Kreisen und in gegenseitigem Abstand von einigen Kilometern, vorzustellen. Beispielsweise könnte man such zwei Kreise mit 45 und 55 km Radius vorstellen, auf denen jeweils 15 Basisstationen, gegeneinander um 12° versetzt, angeordnet sind. Von jeder Basisstation gehen 4-6 Einzelliftseile aus, so daß die komplette Anlage aus um die 150 Einzelseilen besteht. Diese Lifte sind netzartig in verschiedenen Höhen, so alle paar Kilometer, miteinander verbunden und bilden dadurch eine Art doppelwandigen Netzschlauch. So ein Kollisionsobjekt ist nun nach vernünftigen Annahmen maximal einige hundert Meter groß. Es wird beim Durchtritt durch die Anlage also wahrscheinlich nur die Seile einer der Bodenstationen zerstören. Die sind aber ober- und unterhalb der Schadensstelle mit den Parallelanlagen verbunden, die dadurch die Zugkräfte aufnehmen und abfangen können. Danach kann die Bruchstelle mit vergleichsweise geringem Gesamtschaden durch Einfügen eines "Spleißes" repariert werden, ein Totalverlust der Anlage kann so vermieden werden. Die schwerste wahrscheinliche Unfallfolge wäre die unwahrscheinliche Zerstörung einer Lastkabine. --77.6.56.219 06:04, 18. Mai 2019 (CEST)

(Müsste die Überschrift nicht eher „technische Antworten“ lauten?) - Zu 1.:Wie groß wäre die Amplitude; zu 2.:In welcher Größenordnung lägen die zu oszillierenden Massen? - Bitte antworte jeweils in nicht mehr als einem Satz. --87.147.189.228 09:21, 19. Mai 2019 (CEST)

Ganz allgemein betrachtet, werden die Quer-Schwingungen eine niedrige Frequenz und eine große Amplitude haben. Bei den Längs-Schwingungen wird die Frequenz höher und die Amplitude geringer sein. Die Längs-Schwingungen bringen ein hohes Risiko mit sich, dass das Seil reißt. Bei den Quer-Schwingungen wird eher ihre Dämpfung schwierig sein. -- Karl Bednarik (Diskussion) 05:13, 21. Mai 2019 (CEST).

Archivierung dieses Abschnittes wurde gewünscht von: --PM3 05:11, 24. Aug. 2019 (CEST)

Gravitationskrft und Fliehkraft

Die reale Zugspannung auf das Seil ist viel geringer, als wenn mit einer konstanten Gravitation von 9.8 m/s^2 gerechnet wird.

Gravitationskraft und Fliehkraft auf die einzelnen Seilsegmente wirken gegeneinander.

Die Gravitationskraft nimmt mit dem Quadrat des Radius ab.

Die Fliehkraft nimmt mit dem Radius zu. Am Radius der geostationären Umlaufbahn sind beide Kräfte gleich gross

Bereits auf doppelter Höhe vom Erdradius beträgt die Gewichtkraft nur noch 1/4.

Ausserdem zieht die Fliehkraft umso weiter Aussen gegen die Gravitationkraft und entlastet das Seil immer weiter.

Die höchste Belastung liegt auf Höhe der geostationären Umlaufbahn.

--77.56.188.185 19:29, 5. Aug. 2019 (CEST)

Diese Effekte wurden bereits hier im Artikel beschrieben:

In einem als homogen angenommenen Gravitationsfeld von 9,81 m/s² hätte Graphen eine Reißlänge von rund 5655 km. Tatsächlich wird aber die Schwerebeschleunigung mit zunehmender Höhe deutlich geringer, was die Reißlänge erhöht. Ein Band aus Graphen mit konstanter Querschnittsfläche würde in der Höhe der geostationären Umlaufbahn von 35.786 km über dem Erdäquator erst zu 87 % seiner Reißfestigkeit belastet werden.

Hier ist noch eine Berechnung zur Energiebilanz des Weltraumliftes:

Benutzer_Diskussion:Karl_Bednarik#Energiebilanz_des_Weltraumliftes

-- Karl Bednarik (Diskussion) 08:31, 6. Aug. 2019 (CEST).

Archivierung dieses Abschnittes wurde gewünscht von: --PM3 05:11, 24. Aug. 2019 (CEST)

Kleinst-Kernreaktor

Im Abschnitt über die Energierversorgung finde ich die Aussage, dass man den Lift mit einem "Kleinst-Kernreaktor" betreiben könnte, der in einigen 100 m hionter der Liftkabine hergezogen wird. Durch den Abstand könne man auf eine Abschirmung verzichten und so Gewicht sparen. Nun ist ein Kernreaktor auch ohne Abschirmung nicht ganz gewichtslos. Mindestens benötigt er größere Mengen eines Moderators, eine Turbine und einen Generator. Im Ergebnis bezweifele ich, dass sich mit Kerntechnik auch nur annähernd das für den Lift benötigte Leistungsgewicht erreichen lässt.
Die Passage ist gänzlich unbelegt. Ich nehme sie daher bis auf weiteres hinaus. ---<)kmk(>- (Diskussion) 03:18, 12. Aug. 2019 (CEST)

Solange keine bestimmte Steiggeschwindigkeit festgelegt wurde, solange kann die Leistung pro Gewicht jeden beliebigen Wert haben. Eventuell geht es eben ein wenig langsamer. Einige gute Reaktoren wurden für den Pluto (Marschflugkörper) und für die NERVA entwickelt. Die Masse einer Gasturbine mit Generator ist wesentlich geringer als die Masse des Reaktors selbst. Hier ist noch ein schönes buntes Bild dazu: http://members.chello.at/karl.bednarik/NUKLTURB.PNG -- Karl Bednarik (Diskussion) 04:10, 12. Aug. 2019 (CEST)

Nachtrag: Bereits in einer Höhe von 2642 Kilometern erreicht man mit der gleichen Leistung pro Gewicht die doppelte Steiggeschwindigkeit. -- Karl Bednarik (Diskussion) 04:45, 12. Aug. 2019 (CEST)

Zweiter Nachtrag: Ein Gas-cooled fast reactor benötigt keinen Moderator. https://en.wikipedia.org/wiki/Gas-cooled_fast_reactor Es geht aber auch noch einfacher mit einem BES-5 thermoelektrischen Generator. https://en.wikipedia.org/wiki/BES-5 Rund 400 Kilogramm Gewicht, rund 4000 Watt elektrische Leistung, daher rund 1 Meter pro Sekunde Steiggeschwindigkeit. Die ersten 2642 Kilometer schafft er in nur einem Monat, und dann geht es immer schneller. -- Karl Bednarik (Diskussion) 05:53, 12. Aug. 2019 (CEST)

Dritter Nachtrag: Der thermoelektrische Generator BES-5 hat bei einem elektrischen Wirkungsgrad von 4 Prozent eine elektrische Leistung von 10 Watt pro Kilogramm. Die Potentialsumme aus Gravitation und Zentrifugalkraft beim geostationären Radius beträgt 48.422.441 Joule pro Kilogramm. Daher benötigt der BES-5 4.842.244 Sekunden, um diese Energiemenge zu liefern. Das sind nur 56 Tage. Ein Gas-cooled fast reactor mit Brayton closed-cycle gas turbine hat einem elektrischen Wirkungsgrad von rund 40 Prozent. Daher wird er nur 5,6 Tage bis zum geostationären Radius benötigen, und mit 10 Metern pro Sekunde Steiggeschwindigkeit starten. Natürlich geht es mit dem Orion-Nukleartriebwerk noch schneller, aber die meisten Ionentriebwerke wird man abhängen. -- Karl Bednarik (Diskussion) 10:41, 12. Aug. 2019 (CEST)

Vierter Nachtrag: Betrachten wir nun die monokristallinen Silizium-Solarzellen. 1367 Watt pro Quadratmeter Solarkonstante. 22 Prozent elektrischer Wirkungsgrad. 300 Watt pro Quadratmeter elektrische Leistung. 1 Millimeter Schichtdicke. 1 Kubikdezimeter pro Quadratmeter. 3 Kilogramm pro Kubikdezimeter oder auch Quadratmeter. 100 Watt pro Kilogramm. Ebenfalls nur noch 5,6 Tage oder 484.224 Sekunden bis zum geostationären Radius. Diese Solarzellen werden in den kanadischen Wäldern viel weniger störend empfunden, als ein BES-5, falls sie herunter fallen sollten. -- Karl Bednarik (Diskussion) 16:52, 12. Aug. 2019 (CEST)

Fünfter Nachtrag: Natürlich besteht die Aufzugskabine nicht nur aus Solarzellen. Wenn alle anderen Bestandteile die gleiche Masse wie die Solarzellen haben, dann benötigt man zum Beispiel 11,2 Tage bis zum geostationären Radius. Der Elektromotor für den Antrieb kann einen Wirkungsgrad von rund 95 Prozent haben. Die Solarzellen müssen auf einer Achse montiert sein, die quer zum Lift-Seil, und die parallel zur Rotationsachse der Erde ausgerichtet ist. In 24 Stunden müssen die Solarzellen einmal herum gedreht werden, um auf die Sonne ausgerichtet zu bleiben. Dennoch werden sie beim geostationären Radius alle 24 Stunden mehr als 1 Stunde im Erdschatten sein, und in Erdnähe sogar bis zu 12 Stunden lang. Das alles verlängert die Reisezeit ein wenig. Wenn man wieder abwärts fahren will, dann verwendet man den Elektromotor für den Antrieb als Brems-Generator. Die überschüssige Energie wird man über Heiz-Widerstände abstrahlen müssen, wenn man sie nicht sinnvoll loswerden kann. -- Karl Bednarik (Diskussion) 04:45, 13. Aug. 2019 (CEST) Korrektur: -- Karl Bednarik (Diskussion) 05:42, 13. Aug. 2019 (CEST)

Hier sind die gewünschten Belege.
Bitte die Löschung rückgängig machen.
Die US-Raumfahrtbehörde NASA hat einen Reaktorkern von der Größe einer Küchenrolle mit zehn Kilowatt elektrischer Leistung erfolgreich getestet.
Der zehn-Kilowatt-Reaktor hat eine Gesamtmasse von 1500 Kilogramm.
https://en.wikipedia.org/wiki/Kilopower
https://www.nasa.gov/press-release/demonstration-proves-nuclear-fission-system-can-provide-space-exploration-power
-- Karl Bednarik (Diskussion) 07:10, 20. Aug. 2019 (CEST).

Ich sehe allerdings in der von Dir genannten Nasa-Quelle nirgendwo einen Weltraumlift als mögliches Anwendungsfeld. ---<)kmk(>- (Diskussion) 20:39, 20. Aug. 2019 (CEST)

Selbstverständlich ist alles, was im Weltraum elektrische Energie benötigt, ein Anwendungsfeld des Kilopower-Reaktors. Es steht ja auch nicht im Artikel über die Solarzellen, dass man sie auch für den Weltraumlift verwenden könnte. -- Karl Bednarik (Diskussion) 05:03, 21. Aug. 2019 (CEST).

Der Zweck der Wikipedia ist ausschließlich die Wiedergabe von Wissen, das in reputablen Quellen nachlesbar ist. Wenn das Thema "Energieversorgung eines Weltraumlifts" in der Literatur hinreichend breit diskutiert wird, dann kann man den Inhalt dieser Diskussion hier wiedergeben, mit Angabe von Quellen. --PM3 17:18, 23. Aug. 2019 (CEST)

Neben dieser formalen Geschichte hätte ich auch noch inhaltliche Zweifel. Es ist durchaus nicht ausgemacht, dass das Material des Kabels die (Neutronen)-Strahlung eines im wesentlichen ungeschirmten Reaktors auf die Dauer übersteht. Das sind so die Teufel, die in den Details stecken. ---<)kmk(>- (Diskussion) 18:23, 23. Aug. 2019 (CEST)

Wenn der Reaktor auf Leistung geschaltet ist, dann bestrahlt er nur sehr kurz die selbe Stelle des Kabels, weil er ja daran hinaufklettert. Der Weltraumlift stellt insgesamt ziemlich ungesichertes Wissen dar. Zum Beispiel würde er ständig von Weltraummüll getroffen werden und reißen. Siehe hier: Diskussion:Weltraumlift#Fast_alle_Satelliten_müssten_weg. -- Karl Bednarik (Diskussion) 04:39, 24. Aug. 2019 (CEST).

Bitte das Seiteinintro beachten: "Persönliche Betrachtungen zum Thema gehören nicht hierher." Relevante und wissenschaftlich fundierte Literatur zum Thema Weltraumlift recherchieren, Inhalt der Literatur mit dem umseitigen Artikelinhalt vergleichen, ggf. Artikel überarbeiten. So funktioniert Wikipedia. --PM3 05:14, 24. Aug. 2019 (CEST)

Wenn etwas naturwissenschaftlich grob falsch ist, dann kann es keine persönliche Betrachtung sein, wenn man darauf hinweist. -- Karl Bednarik (Diskussion) 05:53, 24. Aug. 2019 (CEST).

Wenn im Artikel ohne Beleg etwas behauptet wird, das man für "naturwissenschaftlich falsch" hält, dann ist ein Hinweis sinnvoll. Es ist dann entweder zu belegen oder zu entfernen. Alle darüber hinaus gehenden eigenen Überlegungen gehören definitiv nicht in die Wikipedia, weder in Artikel noch auf Diskussionsseiten. --PM3 12:25, 24. Aug. 2019 (CEST)

Und wenn im Artikel etwas entscheidendes weggelassen wird, wie zum Beispiel die https://en.wikipedia.org/wiki/Space_elevator_safety -- Karl Bednarik (Diskussion) 03:28, 25. Aug. 2019 (CEST)

Was in anderen Wikis steht, spielt überhaupt keine Rolle - siehe WP:WPIKQ und mein gestriger Beitrag von 05:14. --PM3 04:41, 25. Aug. 2019 (CEST)

Aber man darf die dort unter "References" angezeigten Artikel für die "Einzelnachweise" verwenden, wie zum Beispiel https://web.archive.org/web/20110716114451/http://www.spaceelevator.com/docs/acclarke.092079.se.3.html -- Karl Bednarik (Diskussion) 05:56, 25. Aug. 2019 (CEST)

Bei diesem Link handelt es sich um eine Einzeltheorie; die direkt wiederzugeben wäre Theorieetablierung. Soweit Clarkes Überlegungen eine breite Rezeption erfahren haben, zum Beispiel durch Wiedergabe in wissenschaftlichen Büchern anderer Autoren, kann man sie umseitig darstellen – und zwar explizit als eine Theorie Clarkes. Als gesichertes Wissen können wir eine Theorie nur darstellen, wenn sie „Stand der Wissenschaft“ ist, also der vorherrschenden Lehrmeinung in der Wissenschaft entspricht. --PM3 13:14, 25. Aug. 2019 (CEST)

Unsinn und furchtbares Geschwurbel

hab mir die sachliche Teilüberarbeitung erlaubt

bis "Technik" gröbsten Unsinn entfernt, der Arzutanov-Lift ist keine Ziolkowski-Variante, entschwurbelt, holpriger Journaille-Stil und Satzbau vereinfacht, Übertreibungen, unnötige Wiederholungen, tote Links, Füllworte ohne Informationswert entfernt, --2003:F2:83C1:2F01:F19F:865F:B758:FB7D 23:05, 7. Jan. 2018 (CET)

Reisslänge der Stahlseile

Die Reißlänge eines normalen Stahlseils ist im Artikel mit 4 bis 5 Kilometern angegeben. Das wäre die Festigkeit von Baustahl. Die tatsächliche Festigkeit von Stahlseilen ist mindestens 10x größer. Es gibt ja auch einen Eintrag nur zur Risslänge und da wird diese für verschiedene Stahlseile korrekt angegeben also bis maximal 70 km in etwa. (nicht signierter Beitrag von Dragonfly66 (Diskussion | Beiträge) 21:55, 27. Okt. 2020 (CET))

Ja, das scheint falsch zu sein, siehe etwa auch [7] als möglicher Beleg für eine Korrektur (65km), interessanterweise wird dort auch Kevlar mit einem Fakor von ca. 10 höher als hier momentan im Artikel angegeben und Carbon-Nanotubes sogar einen noch deutlicheren Faktor haben.--Naronnas (Diskussion) 23:03, 27. Okt. 2020 (CET)

Abschnitt: "Problemstellungen" o.Ä. fehlt komplett

Meiner Meinung nach ist ein Weltraumlift ausschließlich theoretischer Natur. Jedes noch so kleine Stück Weltraumschrott und jeder ausrangierte oder ausgefallene oder sonst irgendwie nicht steuerbare Satellit, der sich zwischen Gegengewicht und Erdboden befindet, wird zwangsweise irgendwann mit seiner Bahn den Punkt kreuzen, an dem das Tragseil durch den Weltraum schwingt... und dann ist Schicht im Schacht, bei den Geschwindigkeiten, die dort oben herrschen. Ich sehe derzeit auch keine sinnvolle und bezahlbare Möglichkeit, dieses Risiko zu eliminieren. Dieser Punkt sollte durchaus im Artikel angesprochen werden, denn es stellt meiner Meinung nach ein noch größeres und auch grundsätzlicheres Problem dar als die Konstruktion des Weltraumlifts an sich. Meinungen? Vorschläge? --Kaugummimann (disk, mail) 22:58, 9. Nov. 2020 (CET)

Die englische Wikipedia hat dazu einen eigenen Abschnitt sowei sogar einen eigenen Artikel. Zur konkreten Frage: Das Kabel muss kleinere Impakts einfach aushalten, bei größeren Objekten kann man entweder diese aktiv umleiten (aktive Satelliten selbst, inaktive/Schrott durch Einfangen oder Abschießen) oder aber das Aufzugkabel selbst ausweichen lassen (Beleg bezüglich Ausweichen, Seite 22). Gut belegt kann sowas gerne aufgenommen werden, ich habe leider selbst keine Zeit dafür das ordentlich zu formulieren.--Naronnas (Diskussion) 23:21, 9. Nov. 2020 (CET)

Anderer Abschnitt

Die Winkelgeschwindigkeit der Erde beträgt 0,0000729212 rad/s. Der Äquatorradius der Erde beträgt 6378160 m. Der geostationäre Radius beträgt 42164172 m. Die Rotationsgeschwindigkeit der Erde am Äquator beträgt 465,1 m/s. Die Kreisbahngeschwindigkeit beim geostationären Radius beträgt 3074,7 m/s. Weil in der Umgebung eines geostationären Satelliten dynamische Schwerelosigkeit herrscht, wird man das Seil mit einer Harpune abschießen müssen. Das Problem ist nur, dass das untere Ende des Seils die Rotationsgeschwindigkeit der Erde am Äquator haben muss, und dass das obere Ende des Seils die Kreisbahngeschwindigkeit beim geostationären Radius beibehalten muss. Alle anderen Punkte des Seils müssen genau die verschiedenen dazwischen liegenden Geschwindigkeiten haben, und das quer zu der Geschwindigkeit, mit der es abgeschossen wird. Die Länge des Seils wäre 35786012 m. Wenn man das Seil mit 1000 m/s abschießen würde, dann wäre seine Flugzeit 35786 s lang. Ein weiteres Problem wäre, wie man das Seil von den 1000 m/s Abschussgeschwindigkeit wieder abbremst. -- Karl Bednarik (Diskussion) 09:27, 8. Jul. 2021 (CEST).

Bei einer Abschussgeschwindigkeit von 10 m/s wäre die Flugzeit 41,4 Tage lang. Den Anfang des Seils müsste man mit 10 m/s nach unten, und mit 2609,6 m/s nach hinten abschießen. Den Geschwindigkeitsvektor nach unten behält man bei, während man den Geschwindigkeitsvektor nach hinten kontinuierlich verringern muss. -- Karl Bednarik (Diskussion) 10:16, 8. Jul. 2021 (CEST).

Es gibt zwei sich widersprechende Faktoren bei Weltraumkabeln die Probleme machen, die Länge des Kabels und die Winkelgeschwindigkeit:

• Wenn man ein Kabel haben möchte dass auf der Erdoberfläche auf einem festen Platz ist und "von alleine" im Orbit hängt, dann muss das Kabelende im Weltraum so lange sein, dass es bis zum Geostationären Orbit reicht. Die Umlaufgeschwindigkeit ist dort hoch genug um einen richtigen Orbit zu bilden, so dass das Kabel also nicht einfach herunterfällt und die Geschwindigkeit am Erd-Ende ist so gering dass das Kabel auf einem festen Platz über der Erdoberfläche hängt (die Winkelgeschwindigkeit beträgt dann also 360°/24h, die Geschwindigkeit über der Erdoberfläche ca 0km/h). Das sind dann aber eine Kabellänge von 35.786 km. Das ist sehr lang und das Kabel selbst wird dabei so schwer, dass es bei konstanter Dicke garantiert reißen würde, egal aus welchem Material (siehe dazu Reißlänge). Also muss man das Kabel an verschiedenen Stellen unterschiedlich dick machen, was wiederrum andere Probleme macht.
• Möchte man ein kürzeres Kabel verwenden, dann reicht es aber nicht bis in den Geostationären Orbit, das bedeutet dass man dann entweder ein Weltraum-Ende hat, das für einen Orbit viel zu langsam ist und herunterfällen würde (außer man hat einen aktiven Antrieb, der es ständig beschleunigt) oder ein Erd-Ende dass sich viel schneller bewegt als die Erdoberfläche (mit dem Problem der Luftreibung und einem gigantischen Überschnallknall wenn es an einem vorbeizieht). Die ISS etwa befindet sich ca 400km über der Erdoberfläche, umkreist die Erde aber in nur 90min (also Winkelgeschwindigkeit 360°/90min). Würde man von der ISS ein Kabel herunterhängen lassen, würde das mit grob 4.250km/h über die Erdoberfläche zischen. Wenn das "Kabel" dagegen auf der Erdoberfläche fest wäre (in dem Fall eher ein Turm), dann würde die ISS mit einer vergleichbaren Geschwindigkeit an dem Kabel vorbeiziehen. Bei solchen Geschwindigkeiten ist es mit "schnell mal auffischen" leider nicht getan. Zum Vergleich: diese Geschwindigkeiten entsprechen etwa mehr als dem was so eine Gewehrkugel hat wenn man sie abfeuert.
• Das "Problem" mit der Abschussgeschwindigkeit dagegen ließe sich leicht lösen indem man das Kabel an eine aktiv gesteuerte Rakete hängt die für die jeweilige Höhe die richtige Geschwindigkeit "einstellt"--Naronnas (Diskussion) 11:04, 8. Jul. 2021 (CEST)

Die "aktiv gesteuerte Rakete" soll entlang eines geostationären Radius bis in den GEO fliegen und dabei den Faden hinter sich abrollen? Ich glaube, diese Methode würde von einschlägigen Raumfahrtexperten nicht empfohlen. (Obwohl: man würde das Anheben eines großen Teils des Seils dabei einsparen...) --77.8.90.210 16:41, 12. Jul. 2021 (CEST)

Oder ein kreisendes und rotierendes Weltraumseil, das die Erde behutsam berührt. Weitere Einzelheiten stehen in der Bildbeschreibung. -- Karl Bednarik (Diskussion) 08:25, 9. Jul. 2021 (CEST). -- Karl Bednarik (Diskussion) 08:32, 9. Jul. 2021 (CEST).

Skyhook & Space Tether. https://www.youtube.com/watch?v=aoMOSa9kXPw -- Karl Bednarik (Diskussion) 09:24, 9. Jul. 2021 (CEST).

Repetitio non placet. Das steht alles schon im Archiv, einschließlich der idiotisch hohen Anzahl geltender Ziffern bei den Zahlenwerten. --95.116.12.223 14:10, 9. Jul. 2021 (CEST)

Repetitio est mater studiorum. Höflichkeit und Hilfsbereitschaft sind völlig unschädlich. Rundungsvorgänge macht man erst am Ende aller Berechnungen. -- Karl Bednarik (Diskussion) 08:37, 10. Jul. 2021 (CEST).

Wir studieren und wir kalkulieren nicht. Hier gehören nur die gebührend gerundeten Ergebnisse hin. --77.8.90.210 16:41, 12. Jul. 2021 (CEST)

Das gilt nur für die Artikelseiten. Das gilt nicht für die Diskussionsseiten. -- Karl Bednarik (Diskussion) 05:58, 13. Jul. 2021 (CEST).

Ich weiß nicht, warum Du es nicht verstehst, aber höhere Genauigkeiten bringen keinerlei zusätzlichen Erkenntniswert. Hier geht es um so simple Fragen wie "100 kg Payload" (realisierbar) oder "1 Mio. t Payload" (vollkommen utopisch). Irgendwelche Abschätzungen brauchen also lediglich Größenordnungen abzugrenzen, mehr nicht. Wenn Du Dich da exakter austoben willst, besorg Dir einen Entwicklerjob in dem Business - wer so etwas finanzieren soll, will es dann tatsächlich schon etwas genauer wissen. --77.8.141.101 19:47, 13. Jul. 2021 (CEST)

Funktionsmodell

Mich würde interessieren, warum man es nicht "einfach mal macht" bzw. schon gemacht hat. Idee: was wiegt denn ein "Seil" mit 1 kg Tragfähigkeit bei fünffacher Sicherheit aus Polyester lt. der Gleichung in vorstehendem Abschnitt? Sind das mehr als 100 kg? Falls nicht, könnte doch mal so eine Spule in den Orbit gebracht werden, am Ende mit einem kleinen Radarreflektor, damit man es wiederfindet, und dann abwickeln und zur Erde herunterlassen. Da könnte dann das Ende aufgefischt und da ein kleiner Gegenstand (Brief vom Präsidenten oder sowas) dran befestigt werden und dann der ganze Faden wieder aufgewickelt und der Brief zum Satelliten hochgezogen werden - anschließend wird ein Re-Entry-Körper damit weich auf der Erde gelandet oder zur ISS geschickt oder sowas. Wenn eine solche Demonstration mit überschaubarem Aufwand realisiert werden könnte, dann würde diese Space Elevator-Idee auch endlich mal ernstgenommen. Also: wäre das möglich, oder nicht? (Blöderweise funktioniert das Runterlassen und Wiederhochziehen nicht von der ISS aus, und GEO-Raumstationen gibt es ja nun einmal nicht.) --77.8.58.137 21:30, 7. Jul. 2021 (CEST)

Also: welche Masse hätte der Faden? --95.116.12.223 14:02, 9. Jul. 2021 (CEST)

Da dir die untenstehenden Antworten nicht reichen, hier eine direkte Antwort auf die Frage nach der Masse des Fadens: So wie du die Frage stellst ist das unklar. Von welcher Länge gehst du aus? Wenn du von einer Länge bis zum Geosynchronen Orbit (GEO) meinst, was hat dann die ISS damit zu tun? Wie auch immer, integrieren einfach die Gleichung von oben über r im Bereich R bis R_g, mit entsprechenden Zahlenwerte natürlich (R_g ist dann der Radius deines Zielorbits, aber nur der GEO ist so einfach zu betrachten, da sonst dass Seil zusätzlichen Kräften ausgesetzt ). Das musst du auch nicht selbst rechnen, einfach etwa in WolframAlpha abtippen.--Naronnas (Diskussion) 14:45, 9. Jul. 2021 (CEST)

Es ging immer nur um den geostationären Space elevator, und der ist nunmal so lang, wie die geostationäre Orbithöhe vorgibt. Außerdem führen wir keine Privatdiskussionen, sondern arbeiten an der Verbesserung des Artikels, und der ist keine Aufgaben- und Formelsammlung, sondern sollte Ergebnisse (das sind Zahlenwerte) angeben. Und mit der ISS hat das insofern zu tun, als daß die als LEO-Objekt nicht als Basis für den Weltraumlift in Frage kommt, aber ggf. als "Empfängerbriefkasten", wenn der Lift den Brief in ein Rendezvous-Fahrzeug steckt, das die ISS ansteuert und deswegen kein Hitzeschild oder dergl. für ein Deorbiting benötigt. - War schwierig? - Also: was wiegt der Faden? Nein, interessiert mich nicht, welche technischen Probleme der vielleicht hat oder ob er durch Mikrometoritenbeschuß zerstört werden kann, oder was weiß ich... --77.8.90.210 16:30, 12. Jul. 2021 (CEST)

Hast du mal einen Blick in das Paper geworfen [8]: Für Dichte = 1500 kg/m³, Stress T = 100 GPa (bzw 50 GPa wegen 2x Sicherheit), Startquerschnitt As = =1,5*10^7 m² (für einen 1000kg Aufzug) und Höhe Rg+h = 100000 km kommen sie auf 97.7*10^3 kg Seilmasse (und 52.7*10^3 kg Gegengewicht). Die Tragfähigkeit des Seils bzw. erlaubte Masse des Aufzuges sollte direkt proportional zur Querschnittsfläche sein (für 1 kg Aufzugmasse also 1/1000 des Wertes aus dem Paper) und wenn ich mir das Integral anschaue, kann man den Startquerschnitt aus dem Integral herausziehen. Dass sollten (ohne das jetzt wirklich gerechnet zu zu haben) also dann 97.7 kg Seil sein (gleiche Zusammenhänge auch für das Gegengewicht dann mit 52.7 kg)--Naronnas (Diskussion) 17:25, 12. Jul. 2021 (CEST)

Na prima. Da lag ich also mit ca. 100 kg Seil für 1 kg Nutzlast gar nicht so grob verkehrt. Womit sich durchaus die Frage stellt, warum man das nicht einfach mal macht, um einen Demonstrator zu haben. Eine Idee dabei wäre natürlich, beim Auf- und Abrollen immer neue zusätzliche Fäden von der Erdoberfläche hochzuziehen, um den vorhandenen Faden zu verstärken. Was ein etwas mühseliges Geschäft ist: um seine eigene Tragfähigkeit zu verdoppeln, müßte es Pi mal Daumen hundert Mal auf und ab gehen, wenn das Anfangsseil nur 1 kg Nutzlast heben kann, und das dauert natürlich bei 36.000 km Transportweg. (Die erreichbare Geschwindigkeit dürfte u. a. von der Größe der Solarpaneele abhängen, denn deren elektrische Leistung limitiert die Leistung der Motorwinde.) Zum Problem der Corioliskraft beim Heben und Senken: so ein WL ist ein ganz langer Gradientensatellit, der sich im Prinzip von alleine im Gravitationsfeld ausrichtet - dummerweise dabei aber heftig um seine Gleichgewichtslage pendelt, was bedeutet, daß ein Stück herausgelassenes Fadenende aber so ganz und gar nicht daran denkt, brav nach unten zu zeigen, sondern der Vertikalen viel lieber drastisch voreilt. Und dagegen hilft dann entweder die teure Bremsrakete, oder, viel simpler, ein Schwingungsdämpfer. Und das kann nach Lage der Dinge sinnvollerweise eigentlich nur eine hinreichend große Leiterschleife am Seilende sein, die vom Erdmagnetfeld angeregt wird und die potentielle Energie des Seils dissipiert. - Ist das jetzt zuviel TF, oder kann davon was in den Artikel? --77.8.141.101 19:35, 13. Jul. 2021 (CEST)

Deine Frage liegt zeitlich schon etwas zurück, dennoch: Ein Seil kann aus dem GEO oder darüber hinaus nicht einfach ab einer Spule abgewickelt werden in der Hoffnung, es würde den Weg zur Erde von selber finden. Das Ende müsste "gezogen" und das Seil dauerhaft unter kontrollierter Spannung gehalten werden. Alleine dieser Aspekt dürfte technisch eine absolute Höchstleistung werden. Ich erinnere mich an ein gescheitertes Experiment (wurde mehrfach mit einem Spaceshuttle ins All geflogen), bei dem ein langer Draht abgewickelt werden sollte. Im Feld wäre im Draht dann ein Stromfluss und damit ein Energiegewinn möglich gewesen - so zumindest die Idee. Die Winde verklemmte mehrfach und das Ganze wurde erfolglos abgebrochen. --194.230.148.36 00:23, 6. Jun. 2022 (CEST)

Von GEO hinunter werfen

Wenn man ein Objekt bei einem geostationären Satelliten, der 3075 m/s Umlaufgeschwindigkeit hat, auf rund 0,31*3075 m/s abbremst, dann trifft es die Erde senkrecht unterhalb des Satelliten, obwohl die Flugbahn des Objektes in beiden Bezugssystemen keine senkrechte Gerade ist. Obere Kurven im Bild: nicht-rotierendes System, untere Kurven im Bild: mit der Erde rotierendes System. http://s880616556.online.de/SATEBAH9.png Ob das richtig gerechnet ist, und ob das beim Errichten des Weltraumlifts hilft, das sind zwei gute Fragen. -- Karl Bednarik (Diskussion) 14:26, 5. Jul. 2022 (CEST).

Programm in Microsoft Visual C++ 6.0 in Win32 zum bequemen Nachrechnen: http://s880616556.online.de/SATEBAHN.TXT -- Karl Bednarik (Diskussion) 08:22, 6. Jul. 2022 (CEST).

Das Objekt kommt nach 15843 Sekunden (4,4 Stunden) mit 10355 Metern pro Sekunde herunter. http://s880616556.online.de/SATEBA18.png -- Karl Bednarik (Diskussion) 13:58, 7. Jul. 2022 (CEST).

Notwendigkeit des Äquators als Ort der Basisstation

Zu Beginn des Artikels wird kurz erwähnt, daß die Basisstation auf dem Äquator sein muß, auf den Grund dafür wird aber im weiteren Artikel nicht eingegangen. "Gefühlsmäßig" ist mir der Äquator ja klar, aber was sind die physikalischen Gründe? Ich hab auch in der englischsprachigen Artikelversion keine Erklärung gefunden. Ich vermute mal, es liegt daran, daß das Seil durch einen geostationären Punkt muß (der im Artikel ja immer wieder erwähnt wird, dazu wäre dann ein Verweis auf die geostationäre Umlaufbahn sinnvoll, richtig?), aber was würde denn passieren, wenn man die Basisstation anderswo, z. B. in den Alpen, errichten wollte? Wie würde sich das auf die Stabilität und Schwingungsverhalten auswirken? Für die Erde wären die Belastungen vermutlich zu groß, bei Monden oder Asteroiden aber vielleicht beherrschbar, z. B. zur direkten Anbindung eines Bergbaubetriebs? --Shugal (Diskussion) 01:34, 15. Aug. 2022 (CEST)

Die Zentrifugalkraft der Erdrotation wirkt immer von der Rotationsachse der Erde weg, während die Gravitationskraft der Erde immer zum Schwerpunkt der Erde hin wirkt. Wenn die Basisstation nicht auf dem Äquator der Erde liegen würde, dann würden diese beiden Kräfte nicht genau in die entgegengesetzten Richtungen wirken. Dieses Kräfteparallelogramm würde versuchen, die Basisstation in die Richtung zum Äquator zu ziehen. Auf dem Erdmond würde sich eine solche Abweichung leichter technisch bewältigen lassen, als auf der Erde, wo man schon am Rande des technisch machbaren ist. Bei den Asteroiden sind Weltraumlifte nicht notwendig, weil die Mikrogravitation eine freie Bewegung ermöglicht. -- Karl Bednarik (Diskussion) 10:20, 15. Aug. 2022 (CEST).

Nachtrag mit Bild: https://en.wikipedia.org/wiki/Lunar_space_elevator -- Karl Bednarik (Diskussion) 10:29, 15. Aug. 2022 (CEST).