Filtrierter Kolimes
Im mathematischen Teilgebiet der Kategorientheorie ist ein filtrierter Kolimes (auch direkter Limes oder induktiver Limes) ein spezieller Kolimes. Er kann in gewissen Fällen als Verallgemeinerung der Vereinigung betrachtet werden.
Elementare Definition (für teilgeordnete Indexmengen)
[Bearbeiten | Quelltext bearbeiten]Die Indexmenge sei eine feste gerichtete Menge.
Ein induktives System besteht aus Objekten (beispielsweise Mengen, Gruppen oder topologischen Räumen) für die Indizes sowie Übergangsabbildungen
- für ,
die mit der jeweiligen Struktur verträglich sind (d. h. Mengenabbildungen, Gruppenhomomorphismen, stetige Abbildungen topologischer Räume) und folgende Bedingungen erfüllen
- für alle die identische Abbildung auf und
- für alle .
Der induktive Limes eines induktiven Systems ist ein Objekt zusammen mit Abbildungen
- ,
die mit den kompatibel sind, d. h.
- für
mit der folgenden universellen Eigenschaft:
- Kompatible Systeme von Abbildungen der in ein beliebiges Testobjekt entsprechen Abbildungen von nach .
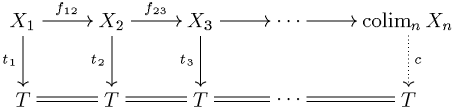
Das bedeutet: Wann immer Abbildungen gegeben sind, für die
- für
gilt, gibt es eine eindeutige Abbildung
- ,
von der die Abbildungen „herkommen“, d. h.
- .
Der induktive Limes eines induktiven Systems (Xi, fi,j) von Mengen kann explizit konstruiert werden als eine Menge von Äquivalenzklassen
in der disjunkten Vereinigung . Hierbei sollen Elemente und äquivalent sein, wenn ein existiert, für das gilt.