Kommakategorie

Eine Kommakategorie ist eine Konstruktion in der mathematischen Kategorientheorie, die 1963 von F. W. Lawvere eingeführt wurde. Der Name ergibt sich aus der ursprünglich von Lawvere verwendeten Notation.

Definition

Für die allgemeinste Konstruktion der Kommakategorie betrachtet man zwei Funktoren. Typischerweise ist einer von beiden auf der terminalen Kategorie definiert: viele kategorientheoretische Darstellungen betrachten nur diesen Fall.

Seien ${\mathcal {A}}$, ${\mathcal {B}}$ und ${\mathcal {C}}$ Kategorien, $T$ und $S$ Funktoren ${\mathcal {A}}{\xrightarrow {\;\;T\;\;}}{\mathcal {C}}{\xleftarrow {\;\;S\;\;}}{\mathcal {B}}$. Die Kommakategorie $(T\downarrow S)$ ist folgendermaßen definiert:

• Die Objekte sind Tripel $(\alpha ,\beta ,f)$, wobei $\alpha$ Objekt in ${\mathcal {A}}$, $\beta$ Objekt in ${\mathcal {B}}$ und $f:T(\alpha )\rightarrow S(\beta )$ Pfeil in ${\mathcal {C}}$ ist.
• Die Pfeile von $(\alpha ,\beta ,f)$ nach $(\alpha ',\beta ',f')$ sind Paare $(g,h)$, wobei $g\colon \alpha \rightarrow \alpha '$ und $h\colon \beta \rightarrow \beta '$ jeweils Pfeile in ${\mathcal {A}}$ und ${\mathcal {B}}$ sind, so dass das folgende Diagramm kommutiert:

${\begin{matrix}T(\alpha )&{\xrightarrow {T(g)}}&T(\alpha ')\\f{\Bigg \downarrow }&&{\Bigg \downarrow }f'\\S(\beta )&{\xrightarrow[{S(h)}]{}}&S(\beta ')\end{matrix}}$

Die Verkettung von Pfeilen ist durch $(g,h)\circ (g',h'):=(g\circ g',h\circ h')$ definiert.

Spezialfälle

Kategorie der Objekte unter A

Der erste Spezialfall tritt ein, wenn ${\mathcal {A}}={\boldsymbol {1}}$ terminal (d. h. es gibt genau ein Objekt und dessen Identität ist der einzige Morphismus) und $S$ identischer Funktor ist (also ${\mathcal {B}}={\mathcal {C}}$). Dann ist in obiger Definition $T(\alpha )=A$ für ein festes Objekt $A$ in ${\mathcal {C}}$. Die diesbezügliche Kommakategorie heißt Kategorie der Objekte unter $A$, geschrieben $(A\downarrow {\mathcal {C}})$. Die Objekte $(\alpha ,\beta ,f)$ können kurz $(\beta ,f)$ notiert werden, da die Festlegung von $A$ die Angabe von $\alpha$ überflüssig macht; $f:T(\alpha )\rightarrow S(\beta )$ notieren wir kurz als $f:A\rightarrow \beta$ - oft wird $f$ auch $i_{\beta }$ genannt, insbesondere, wenn es sich um Injektionen handelt. Ähnlich können wir die Darstellung eines Pfeils $(g,h):(B,i_{B})\rightarrow (B',i_{B'})$ auf $h:B\rightarrow B'$ reduzieren, da $g$ stets als $id_{A}$ gewählt wird. Das folgende Diagramm kommutiert:

$(A,id_{A})$ ist ein Anfangsobjekt von $(A\downarrow {\mathcal {C}})$. Ist $A$ bereits ein Anfangsobjekt von ${\mathcal {C}}$, so ist $(A\downarrow {\mathcal {C}})$ isomorph zu ${\mathcal {C}}$.

Beispiele:

• Die Kategorie der punktierten topologischen Räume ist isomorph zur Kategorie der topologischen Räume unter einem fest gewählten einpunktigen Raum.

• Die Kategorie der kommutativen, unitären $k$-Algebren für einen Körper $k$ ist isomorph zur Kategorie der kommutativen, unitären Ringe unter $k$.

Kategorie der Objekte über A

Analog können wir $T$ identisch und ${\mathcal {B}}$ terminal wählen. Wir erhalten dann die Kategorie der Objekte über $A$ (wobei $A$ das durch $S$ ausgewählte Objekt von ${\mathcal {C}}$ ist). Diese Kommakategorie notieren wir als $({\mathcal {C}}\downarrow A)$; in der algebraischen Geometrie ist die Bezeichnung ${\mathcal {C}}/A$ üblich. Sie ist das duale Konzept zu Objekten unter $A$. Die Objekte sind Paare $(\beta ,\pi _{\beta })$ mit $\pi _{\beta }:\beta \rightarrow A$; dabei steht $\pi$ für Projektion auf $A$. Ein Pfeil in der Kommakategorie mit Quelle $(B,\pi _{B})$ und Ziel $(B',\pi _{B'})$ wird durch eine Abbildung $g:B\rightarrow B'$ gegeben, die das folgende Diagramm kommutieren lässt:

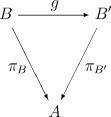
$A$ ist ein Endobjekt von $({\mathcal {C}}\downarrow A)$. Ist $A$ bereits ein Endobjekt von ${\mathcal {C}}$, so ist $({\mathcal {C}}\downarrow A)$ isomorph zu ${\mathcal {C}}$.

Einzelnachweise

V

Kategorientheorie