Diskussion:Dreieck/Archiv

Diese Seite ist ein Archiv abgeschlossener Diskussionen. Ihr Inhalt sollte daher nicht mehr verändert werden. Benutze bitte die aktuelle Diskussionsseite, auch um eine archivierte Diskussion weiterzuführen.

Um einen Abschnitt dieser Seite zu verlinken, klicke im Inhaltsverzeichnis auf den Abschnitt und kopiere dann Seitenname und Abschnittsüberschrift aus der Adresszeile deines Browsers, beispielsweise

[[Diskussion:Dreieck/Archiv#Thema 1]]

oder als Weblink zur Verlinkung außerhalb der Wikipedia

https://de.wikipedia.org/wiki/Diskussion:Dreieck/Archiv#Thema_1

Ikonographischer Akspekt des Dreiecks

In dem Artiel wird leider gar nicht auf das Dreieck in der Ikonographie, also als Symbol in der Mystik und Heraldik eingegangen! Ergänzung dringen notwendig.

Nein, ist sie nicht. Dieser Artikel beschäftigt sich mit dem Geometrischen Dreieck.

Für weitere Bedeutungen, siehe Begriffsklärungsseite. --Martin Thoma 13:50, 2. Sep. 2012 (CEST)

Dieser Abschnitt kann archiviert werden. --Martin Thoma 13:50, 2. Sep. 2012 (CEST)

Dreiecksarten

Also das ist ja mal Quatsch: "spitzwinklig Alle Winkel sind spitze Winkel, d.h. alle Winkel sind <90°."

In der Schule lernt man, dass ein Dreieck immer eine Winkelsumme von 180° besitzt!

Ich werde den Eintrag ändern! (Vorstehender nicht signierter Beitrag stammt von 62.214.232.31 (Diskussion • Beiträge) 18:58, 5. Jul 2006)

Hab's zurückgesetzt. Wenn Du Dein Problem nochmal etwas ausführlicher darstellst, kann ich Dir vielleicht weiterhelfen.--Gunther 20:33, 5. Jul 2006 (CEST)

Offensichtlich kann die Person es nicht. Das ist wohl erledigt. --Martin Thoma 13:46, 2. Sep. 2012 (CEST)

Dieser Abschnitt kann archiviert werden. --Martin Thoma 13:46, 2. Sep. 2012 (CEST)

Dreieck aus den drei Höhen

kann man aus der Angabe der drei Höhen ein Dreieck zeichnen? wie geht das? (AKW)(nicht signierter Beitrag von 80.218.27.138 (Diskussion) )

Ja, kann man. Ist vielleicht nicht ganz einfach und ohne Skizze schwer zu beschreiben. Grundsätzlich nähert man sich aber der Lösung durch die Voraussetzung, dass alle Seiten im umgekehrten Verhältnis zu den entsprechenden Höhen stehen. (Da ja die Fläche des Dreiecks Seite x Höhe / 2 ist - für alle Seiten). Durch eine Hilfsseite parallel zu einer Dreiecksseite, deren Länge man aus den Höhen errechnen kann ist das Dreieck konstruierbar. Wie gesagt - ohne Skizze nicht ganz einfach. Vielleicht mach ich das mal und ergänze den Artikel. Gehört hier aber glaube ich nicht her.-- Petflo2000 20:33, 15. Mär. 2007 (CET)

Ich hab den Beweis mal hier (Wikibooks) reingestellt: Dreieck aus drei Höhen -- Petflo2000 17:59, 16. Mär. 2007 (CET)

Dieser Abschnitt kann archiviert werden. --Martin Thoma 13:45, 2. Sep. 2012 (CEST)

a + b = c ???

Im Artikel steht »Die Gesamtlänge zweier Seiten eines Dreiecks ist immer größer oder gleich der Länge der dritten Seite.«, es wird auch auf die Dreiecksungleichung verwiesen. Ich habe aber ein Problem mit der Definition »Ein Dreieck wird durch drei Punkte definiert, die nicht auf einer Geraden liegen.«

Hintergrund: Wenn die Längen der Seiten a und b zusammen die Seitenlänge c ergeben sollen, folgt, dass der Winkel $\alpha$ = 0° sein müsste:

$\cos \alpha ={\frac {b^{2}+c^{2}-a^{2}}{2bc}}$

Wenn also c = a + b gilt, so kann man 2bc = 2 · b · ( a + b ) = 2b² + 2ab und c² = a² + b² + 2ab ersetzen.

So ergibt sich $\cos \alpha ={\frac {b^{2}+(a^{2}+b^{2}+2ab)-a^{2}}{2\cdot b\cdot (a+b)}}$

…oder vereinfacht $\cos \alpha ={\frac {2b^{2}+2ab}{2b^{2}+2ab}}$, was bedeutet (es kürzt sich ja alles raus), dass der Cosinus von Alpha = 1 ist, was ja nur bei Winkeln von 0° oder 360° vorkommen kann.

Habe ich einen Denkfehler?

Wenn ein Dreieck „erlaubt“ ist, bei dem der Winkel $\alpha$ = 0° hat, müsste die Grunddefinition dann nicht anders lauten, als „drei Punkte, die nicht auf einer Geraden liegen“ ? --84.168.118.208 00:47, 5. Apr. 2007 (CEST)

Du hast Recht. --Digamma 19:36, 11. Jun. 2007 (CEST)

Genau das habe ich mich auch gefragt! (nicht signierter Beitrag von 109.64.137.28 (Diskussion) 13:36, 27. Mai 2010 (CEST))

Ich habe es geändert --Digamma 13:45, 27. Mai 2010 (CEST)

fuer dreiecke ist auch a+b=c moeglich. haeufig werden die dann als ausgeartete/entartete dreiecke bezeichnet. googlebooks liefert beidpiele dafuer. woher stammt die definition, dass die drei punkte nicht auf einer gerade liegen duerfen? die ist mir neu. will man solche dreiecke ausschliessen, spricht man haeufig explizit von nicht-entarteten dreiecken. -- seth 22:12, 27. Mai 2010 (CEST)

Hallo seth, in der Schulmathematik wird für ein (zumindest stillschweigend )Dreieck vorausgesetzt, dass die Ecken nicht auf einer Geraden liegen. Ich habe aber persönlich nichts gegen ausgeartete Dreiecke. Nur sollte der Artikel konsistent sein. Und in der Definition steht: Ein Dreieck wird durch drei Punkte definiert, die nicht auf einer Geraden liegen. Wenn Du es ändern möchtest, nur zu. --Digamma 22:31, 28. Mai 2010 (CEST)

ok, wollte nur sichergehen, dass sich niemand gegen solche dreiecke straeubt. mal schauen, wann ich mir die zeit nehmen kann, auf jene im artikel hinzuweisen. -- seth 23:16, 28. Mai 2010 (CEST)

Bildbeschreibung fehlt bei [[Bild:Gleichseitiges-dreieck.png|300px|right]]

Der Artikel enthält ein Bild, dem eine Bildbeschreibung fehlt, überprüfe bitte, ob es sinnvoll ist, diese zu ergänzen. Gerade für blinde Benutzer ist diese Information sehr wichtig. Wenn du dich auskennst, dann statte bitte das Bild mit einer aussagekräftigen Bildbeschreibung aus. Suche dazu nach der Textstelle [[Bild:Gleichseitiges-dreieck.png|300px|right]] und ergänze sie.

Wenn du eine fehlende Bildbeschreibung ergänzen willst, kannst du im Zuge der Bearbeitung folgende Punkte prüfen:

• Namensraum Datei: Bilder sollte im Namensraum Datei liegen. Bitte ändere die alten Bezeichnungen Bild: und Image: in Datei:.
• Skalierung: Außerhalb von Infoboxen sollten keine festen Bildbreiten (zum Beispiel 100px) verwendet werden. Für den Fließtext im Artikelnamensraum gibt es Thumbnails in Verbindung mit der automatischen Skalierung. Um ein Bild/eine Grafik in besonderen Fällen dennoch größer oder kleiner darzustellen, kann der „upright“-Parameter verwendet werden. Damit erfolgt eine prozentuale Skalierung, die sich an den Benutzereinstellungen orientiert. --SpBot 22:10, 1. Mär. 2009 (CET)

Erledigt -- Petflo2000 15:43, 2. Mär. 2009 (CET)

Dieser Abschnitt kann archiviert werden. --Martin Thoma 13:34, 2. Sep. 2012 (CEST)

Das rechtwinklige Dreieck, Bezeichnungen in Bild

Die Bezeichnungen im Bild passen nicht zu dem Satz des Pythagoras.

c²=a²+b² im Bild b²=h²+q² oder a²=h²+p²

Vielleicht sollte das ergänzt werden

Reality (nicht signierter Beitrag von 93.130.132.174 (Diskussion | Beiträge) 15:26, 17. Apr. 2009 (CEST))

So wie ich das sehe, passen sowohl hier als auch im Artikel Satz des Pythagoras die Bezeichnungen im Text zu den Bildern.

Da das ganze schon 3 Jahre her ist und von einer IP angemerkt wurde (die ich leider nicht anschreiben kann), ist das vermutlich erledigt. --Martin Thoma 13:44, 2. Sep. 2012 (CEST)

Dieser Abschnitt kann archiviert werden. --Martin Thoma 13:44, 2. Sep. 2012 (CEST)

Symbolische Bedeutung

Herrlich genau, aber was ist mit dem Symbol Dreieck? So einen Verweis auf die Dreieinigkeit im christlichen Glauben etc... (nicht signierter Beitrag von 79.219.223.93 (Diskussion | Beiträge) 21:42, 12. Mai 2009 (CEST))

Dafür ist ganz oben ein Verweis auf die Begriffsklärungsseite. Dieser Artikel behandelt das geometrische Objekt Dreieck. --Martin Thoma 13:39, 2. Sep. 2012 (CEST)

Dieser Abschnitt kann archiviert werden. --Martin Thoma 13:39, 2. Sep. 2012 (CEST)

page offline

Java-Applet zur Veranschaulichung einiger Punkte im Dreieck (nicht signierter Beitrag von 92.230.67.168 (Diskussion | Beiträge) 09:42, 9. Aug. 2009 (CEST))

Ist immer noch 'page not found' (404). 14:47, 5. Mär. 2010 (CEST) -- User not found 14:51, 5. Mär. 2010 (CET)

hab den link nun geloescht. -- seth 15:23, 6. Mär. 2010 (CET)

Dieser Abschnitt kann archiviert werden. --Martin Thoma 13:39, 2. Sep. 2012 (CEST)

Zweierlei Formelzeichen für den Umfang

Bei den Formeln wird einmal (bei Umfang) ein kleines u und später (bei Flächeninhalt) ein großes U verwendet. Bitte vereinheitlichen. (nicht signierter Beitrag von 91.18.118.184 (Diskussion) 19:41, 7. Jul 2010 (CEST))

Wenn ich das richtig sehe, wird nun einheitlich das kleine u verwendet (siehe diff). --Martin Thoma 13:37, 2. Sep. 2012 (CEST)

Dieser Abschnitt kann archiviert werden. --Martin Thoma 13:37, 2. Sep. 2012 (CEST)

Punkt auf dreieck

Wie kann man, wenn man die drei Eckpunkte kennt herausfinden, ob ein Punkt im dreieck ligt? (ohne zeichnen und am besten in 3d)--213.209.76.169 17:50, 26. Feb. 2008 (CET)

War das mit dem Bild so beabsichtigt? --Caramdir 21:30, 15. Apr 2003 (CEST)

Baryzentrische Koordinaten --NeoUrfahraner 20:42, 26. Feb. 2008 (CET)

Ah, schön, das kannte ich noch nicht :-) Ich wollte mir schon etwas in dieser Richtung überlegen.

Die Frage ist damit beantwortet und seit 4 Jahren keine Aktivität mehr, also ist das wohl erledigt. --Martin Thoma 05:59, 17. Sep. 2012 (CEST)

Dieser Abschnitt kann archiviert werden. --Martin Thoma 05:59, 17. Sep. 2012 (CEST)

Ebene+Raum

Was bedeutet in der Tabelle der Satz in der Ebene unmöglich-ein Dreieck ist ein ebenes Gebilde-alles andere wäre ein Projektion Hadhuey 09:35, 2. Aug 2004 (CEST)

Nun, von mir stammt der Abschnitt nicht, Aber der Autor hat recht. Wenn man ein Dreieck nicht auf ein Blatt Papier malt, sondern auf die Oberfläche einer Kugel, dann kann dieses Dreieck drei 90° Winkel haben, bzw. hat drei 90° Winkel.

Ein Dreieck ist ein zweidimensionales Objekt, aber nicht zwangsläufig das Objekt einer Ebene. --Arbol01 09:53, 2. Aug 2004 (CEST)

Mein Vorschlag: Statt es zu diskutieren, schreibt man es einfach in den Artikel, denn solche Fragen + Diskussionen werden ja sicher noch öfter kommen. Ralf Pfeifer 12:40, 5. Sep 2004 (CEST)

Gemeint war damals diese Tabelle, die inzwischen nicht mehr im Artikel existiert. Also ist das Thema erledigt. --Martin Thoma 06:04, 17. Sep. 2012 (CEST)

Dieser Abschnitt kann archiviert werden. --Martin Thoma 06:04, 17. Sep. 2012 (CEST)

Definition

Die Definition erscheint mir ein wenig pompös. Warum nicht einfach "drei nicht kollineare Punkte, Ecken genannt, zusammen mit den Verbindungsstrecken, Seiten genannt" oder so? Denn präziser ist die derzeitige Fassung auch nicht:

• drei Geraden, die nicht parallel sind: da fehlt ein "paarweise"
• drei Geraden im Raum funktionieren nicht
• was heißt "eingeschlossen"? Die drei Geraden unterteilen die Ebene in sieben Teile, von denen vier an alle drei Geraden angrenzen. Welcher dieser vier Teile ist das Dreieck?

-- Gunther 18:24, 9. Apr 2005 (CEST)

Ich glaube da hat sich seit 2005 einiges getan (→ Dreieck#Definition_und_Eigenschaften):

Ein Dreieck wird durch drei Punkte definiert, die nicht auf einer Geraden liegen. Sie werden Ecken des Dreiecks genannt. Die Verbindungsstrecken zwischen je zwei Ecken heißen Seiten des Dreiecks.

Damit ist das Thema wohl erledigt. --Martin Thoma 06:08, 17. Sep. 2012 (CEST)

Dieser Abschnitt kann archiviert werden. --Martin Thoma 06:08, 17. Sep. 2012 (CEST)

Grundsatzfrage aus der Rechtschreibung

Es heißt nicht Winkl und Schenkl, sondern Winkel und Schenkel. Daher muß es richtig heißen: "Rechtwinkeliges Dreieck" und "Gleichschenkeliges Dreieck". MAP, 20.11.2011, 21:39 (MEZ) (ohne Benutzername signierter Beitrag von 46.207.107.61 (Diskussion) )

gudn tach!

nein, beide formen sind richtig, siehe duden: [2], [3]. -- seth 20:31, 24. Nov. 2011 (CET)

Dieser Abschnitt kann archiviert werden. arilou (Diskussion) 09:53, 5. Okt. 2012 (CEST)

Formelsammlung Trigonometrie

Die folgenden Artikel enthalten z.T. unfangreiche Formelsammlungen, die sich in wesentlichen Teilen überschneiden: Trigonometrie, Trigonometrische Funktion, Dreieck, Formelsammlung Geometrie#Dreieck, Formelsammlung Geometrie#Trigonometrie. Ich möchte vorschlagen, die Formeln in einer Formelsammlung Trigonometrie zusammenzufassen, entweder unter Formelsammlung Geometrie#Trigonometrie oder, auch wegen des Umfangs, in einem eigenen Artikel Formelsammlung Trigonometrie.

Ich habe die entsprechenden Absätze zunächt mal unter Benutzer:Duesentrieb/Trigonometrie zusammengefasst - dort müssten sie jetzt zusammengeführt und neu strukturiert werden. Für Anregungen und Kommentare wäre ich dankbar, wie auch für eine Inhaltliche überprüfung. Besprechen können wir das am besten auf der dortigen Diskussionsseite: Benutzer Diskussion:Duesentrieb/Trigonometrie. -- D. Düsentrieb ⇌ 14:21, 5. Okt 2004 (CEST)

Seit 2004 kein Kommentar dazu?

Dieser Abschnitt kann archiviert werden. arilou (Diskussion) 09:53, 5. Okt. 2012 (CEST)

Allgemeine Höhenformeln

Mir kommen die Formeln etwas merkwürdig vor, auf jeden Fall ist dies hier doch wohl falsch: $h_{a}=c\cdot \sin(\beta )$. Meines Wissens wäre das hier richtiger: $h_{a}=a\cdot \sin(\beta )$ Weil der Sinus ist ja Gegenkathete durch Hypothenuse, sprich ha durch a und nicht durch c! --GruppeCN 16:32, 5. Mai 2005 (CEST)

Scheinbar hat sich der Autor am falschen Dreieck orientiert, denn das Bild oben ist unüblich bezeichnet. Das sollte vielleicht mal geändert werden... --GruppeCN 17:01, 5. Mai 2005 (CEST)

Ich sehe nicht, welche Bezeichnungen unüblich sein sollen. Die Standardbezeichnungen sind $\alpha =\angle BAC$ und $a=BC$ usw. Mit diesen sind die angegebenen Formeln korrekt:

• Direktes Argument: Es sei $H_{A}$ der Höhenfußpunkt. Dann ist $c=AB$ die Hypotenuse und $h_{a}=AH_{A}$ die Gegenkathete von $B$ im rechtwinkligen Dreieck $ABH_{A}$.
• Symmetrieargument: Eine Formel muss richtig bleiben, wenn man die Bezeichnungen von Ecken, Seiten und Winkeln konsistent ändert. Wäre $h_{a}=a\sin \beta$ richtig, dann müsste auch $h_{a}=a\sin \gamma$ richtig sein (ersetze $A,B,C,a,b,c,\alpha ,\beta ,\gamma ,\ldots$ durch $A,C,B,a,c,b,\alpha ,\gamma ,\beta ,\ldots$), also $\sin \beta =\sin \gamma$, aber das ist im Allgemeinen falsch. Bei der richtigen Formel sind mögliche Permutationen

$h_{a}=c\sin \beta =b\sin \gamma ,$

aber diese beiden Ausdrücke sind nach dem Sinussatz gleich.

--Gunther 17:13, 5. Mai 2005 (CEST)

Unüblich stimmt nicht, da hab ich mich zu sehr an meinen Gewohnheiten orientiert. Allerdings ist nicht klar zu erkennen, für welches der dagestellten Dreiecke die Formeln gelten. In Bezug auf das Dreieck rechts daneben stimmen die nämlich nicht. --GruppeCN 16:31, 6. Mai 2005 (CEST)

Alle im Artikel dargestellten Dreiecke, die mit A, B, C, a, b, c, alpha, beta und gamma bezeichnet sind, stimmen überein. Was stimmt also deiner Meinung nicht? Meiner Meinung nach stimmt alles. Aber wir können es ja mal an ein paar Beispielen überprüfen. --Arbol01 17:52, 6. Mai 2005 (CEST)

Disku von 2005,

Dieser Abschnitt kann archiviert werden. arilou (Diskussion) 09:54, 5. Okt. 2012 (CEST)

Bezeichnungen am Dreieck

Anscheinend gibt es Leute, die nicht wissen, wie die korrekte Bezeichnung bei einem Dreieck ist. Hier also zum klarstellen:

• Die Ecken eines Dreiecks werden mit Großbuchstaben Bezeichnet: A, B und C
  • Die Ecke, die einen 90° Winkel $\left({\frac {\pi }{2}}\right)$ enthält ist automatisch C.
• Die Winkel werden mit den kleinen griechischen Buchstaben $\alpha$, $\beta$ und $\gamma$ bezeichnet.
• Die Seiten werden mit den kleinen Buchstaben a, b und c bezeichnet, wobei die entsprechende Seite immer der entsprechenden Ecke gegenüber liegt. Also Seite a liegt gegenüber von Ecke A und Winkel $\alpha$. Entsprechendes bei Seite b und Seite c --Arbol01 17:37, 5. Mai 2005 (CEST)

Man könnte der Vollständigkeit halber darauf hinweisen, dass Polygone mit mehr Ecken (insbesondere Vierecke) anders bezeichnet werden: dort ist $a=AB,b=BC,c=CD$ usw.--Gunther 18:13, 5. Mai 2005 (CEST)

In dem gegebenen Bild würde ich aber den Punkt, der jetzt B heißt, A nennen und entsprechend weiter. Des Weiteren könnte man darüber nachdenken, ob man noch die vektorielle Formulierung eines Dreiecks mit aufnimmt.

Ich habe das Bild mit der üblicheren Drehung des Dreiecks nach oben verschoben.--Gunther 16:24, 10. Jun 2005 (CEST)

Disku von 2005,

Dieser Abschnitt kann archiviert werden. arilou (Diskussion) 09:54, 5. Okt. 2012 (CEST)

Sonstige Formeln

Findet man $4Ar=abc$ und $\rho s=A$ schon irgendwo? --NeoUrfahraner 4. Jul 2005 18:17 (CEST)

Ja, in der Formelsammlung Trigonometrie, deren Name mir etwas unglücklich erscheint.--Gunther 4. Jul 2005 18:22 (CEST)

Dieser Abschnitt kann archiviert werden. arilou (Diskussion) 09:55, 5. Okt. 2012 (CEST)

"Trigon"?

Ist das Dreieck auch (auch im Deutschen?) ein "Trigon"? --Alien4 13:58, 8 November 2005 (CET)

Nie gehört, nur in abgeleiteten Wörtern wie Trigonalisierung.--Gunther 14:21, 8 November 2005 (CET)

Interessant -> Trigonometrie (, Pentagon, Tetraeder aber Tetragon) --Alien4 22:32, 8. Nov 2005 (CET)

Auch Pentagon ist im Deutschen eher unüblich. Tetragon habe ich noch nie gehört, auf englisch heißt da quadrilateral ("Vierseit").--Gunther 23:05, 8. Nov 2005 (CET)

Ich erinnere mich noch an meine Schulzeit, da hieß es immer Pentagon.. Trigon hab ich jedoch noch nie gehört

Dieser Abschnitt kann archiviert werden. arilou (Diskussion) 09:55, 5. Okt. 2012 (CEST)

Schreibweise

Was ist mit der Schreibweise "Hypothenuse" oder "Hypotenuse"? Letzteres erscheint mir viel zu lateinisch. Wortverwandtschaft oder ursprünglicher Ausdruck im Griechischen:

Aus: Henry George Liddell, Robert Scott, A Greek-English Lexicon:

hupothenar , to,

A. the part of the palm next the fingers, Ruf.Onom. 87, Poll.2.143.

2. = stêthos 111.2, base of the thumb, Orib.25.1.29.

3. the part opposite the stêthos, inner ridge of palm, Gal.

Daumen über der Handinnenfläche einknicken, fertig ist das rechtwinklige Dreieck!

Wortursprung oder eigentliches Fremdwort also "hypothenar" oder, mit geläuterter Endung, "Hypothenuse" ("us-e", grauslig). Neudeutsch erlaubt: Hypotenuse.

U. Ritter

Kluge (Ausgabe von 1967) meint hypo 'unten' + teinein 'spannen'. "-use" dürfte die Eindeutschung der Partizipendung ουσα sein.--Gunther 23:28, 8. Mär 2006 (CET)

Dieser Abschnitt kann archiviert werden. arilou (Diskussion) 10:15, 5. Okt. 2012 (CEST)

Sphärische Dreiecke

Der Satz zur Erklärung des "maximalen Exzesses" ist meiner Meinung nicht richtig. Ich beziehe mich auf folgenden Satz:

Der maximale Exzess von 360° tritt beim größtmöglichen "Dreieck" auf, das ein Viertel der Kugeloberfläche umspannt: mit 3 gestreckten Winkeln hat es eine Winkelsumme von 3 mal 180° und ε = 540° − 180° = 360°.

Zum einen kann die Formulierung "größtmöglichstes "Dreieck" nur gleichbedeutend mit "Dreieck mit maximalem Exzess" sein, weil eben dieser ein zum Kreis entartetes Dreieck voraussetzt (3x 180° Winkel). Dieser "Kreis" kann an beliebiger Stelle mit beliebigem Radius auf der Kugeloberfläche liegen, so dass der Begriff der "Größe" anders nicht definiert werden kann. Zum anderen ist aus diesen Gründen "Viertel der Kugeloberfläche" ebenfalls falsch. Mein Vorschlag:

Der maximale Exzess von 360° tritt beim einem "Dreieck" mit 3 auf 180° gestreckten Winkeln auf. Dieses zum Kreis entartete Dreieck hat die Winkelsumme 540° (3 mal 180°) und ε = 540° − 180° = 360°.

Oder habe ich als Mathe-Laie etwas Entscheidenes übersehen oder mißverstanden?

--Caracasa 18:55, 19. Jul 2006 (CEST)

Die Seiten des Dreiecks müssen Großkreise sein, alle auf diese Weise ausgearteten Dreiecke sind also Großkreise und damit gleich groß. Sie umfassen allerdings die Hälfte der Kugeloberfläche, und ich sehe auch keinen Grund, weshalb man nicht nach dem Prinzip "hier ist außen" noch größere Dreiecke betrachten sollte.--Gunther 20:02, 19. Jul 2006 (CEST)

Der Exzess ist doch trotzdem maximal, wenn die Seitenteil nicht Großkreise, sondern beliebige Kreise auf der Oberfläche sind, oder? Die Winkel sind dann ja immernoch 180°. Und sollte der Umstand, dass alle Punkte auf einem Kreis liegen, analog zu "Ein Dreieck wird durch drei Punkte definiert, die nicht auf einer Geraden liegen." ein Problem darstellen, dann wäre eben der entsprechende Grenzfall der maximale Exzess. Der "maximale Exzess" Fall auf einem Großkreis teilt die Kugel in zwei Hälften - so sehe ich das auch.

Mit dem "hier ist außen"-Prinzip meinst du doch den Umstand, dass sich auf der Kugeloberfläche kein "Innen" oder "Außen" definieren lässt oder? Dann wäre das größtmögliche sphärische Dreieck auf einer Kugel doch (grenzwertig) die gesamte Kugeloberfläche, wenn die Eckpunkte infinitisimal nahe beieinander liegen und wir die größere der beiden Fläche als den Flächeninhalt betrachten. Ich bin leider nicht ganz sicher, wie deine Bewertung des ganzen nun ausgefallen ist. Die zwei Sätze sind von der Logik ne harte Nuss. :)

--Caracasa 23:00, 19. Jul 2006 (CEST)

Sorry, ich wollte nicht kryptisch sein. Zum ersten Teil: Es gehört nun einmal zum Begriff "sphärisches Dreieck", dass die Seiten Großkreisbögen sind. Ganz entsprechend ist in der Ebene die Winkelsumme im Dreieck auch nur dann 180°, wenn man sich an die Definition von "ebenes Dreieck" hält und gekrümmte Seiten ausschließt. Zum zweiten Teil: Genau das meinte ich. Das ist offenbar ein Definitionsproblem, und solange wir keine gute Definition für sphärische Dreiecke und ihre Flächeninhalte (also welchen der beiden Teile der Kugel wir "Inneres" nennen) haben, halte ich den ganzen Absatz zum "maximalen" Exzess für Unsinn. (Wenn man es ganz genau nehmen will, dann wäre das ja ohnehin nur das Supremum und nicht das Maximum. Aber da sehe ich das kleinste Problem.)--Gunther 23:13, 19. Jul 2006 (CEST)

Danke. Hab die Definition zwar gelesen, aber diesen Punkt wohl einfach ignoriert. Den "maximalen Exzess" halte ich aber schon für wissenswert. Vielleicht mit dieser Formulierung?

Der maximale Exzess von 360° tritt beim einem "Dreieck" mit 3 auf 180° gestreckten Winkeln auf. Dieses zum Großkreis entartete Dreieck hat die Winkelsumme 540° (3 mal 180°) und ε = 540° − 180° = 360°.

In meinen Augen ist alles "grob Falsche" dann weg und man kann sich den Fall gut bildlich vorstellen. Sollte die Definition in Zukunft überarbeitet werden, kann ja noch ergänzt werden. Wie sind denn die Grundsätze der Wikipedia zu solchen Formulierungen? Im Zweifelsfall lieber nicht als ungenau? Bin noch zu frisch dabei. --Caracasa 23:38, 19. Jul 2006 (CEST)

von 2006,

Dieser Abschnitt kann archiviert werden. arilou (Diskussion) 10:15, 5. Okt. 2012 (CEST)

Ankreis

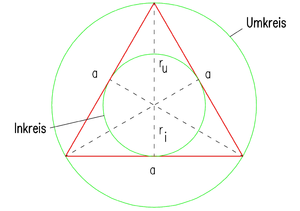
In der ersten Figur ist der Ankreis offensichtlich falsch geeichnet. 26. 8. 2007, --Hanfried.lenz 18:13, 26. Aug. 2007 (CEST).

Du hast recht. Ich habe die Grafik mal zeichnerisch erweitert. Der Ankreis ist so definiert, dass der Mittelpunkt auf der Winkelhalbierenden liegt. Das ist hier annähernd korrekt. Der Ankreis soll aber auch die Verlängerungen der Dreiecksseiten tangieren und das ist hier doch sehr weit daneben. Ich werde die Zeichnung bei Gelegenheit mal neu machen (soweit nicht vorher geändert).-- Petflo2000 18:08, 27. Aug. 2007 (CEST)

Dieser Abschnitt kann archiviert werden. arilou (Diskussion) 10:16, 5. Okt. 2012 (CEST)

Seite q

Mir ist aufgefallen, dass man bei den Dreiecken 3:4:5 die Seite q mit der Formel: U÷c=q berechnen kann. Zum Beispiel 12cm÷5cm=2,4cm. 79.197.132.139 20:20, 3. Apr. 2011 (CEST)

Ich weiß ja nicht, was du unter der "Seite q" verstehst. Wenn das einer der durch den Höhenfußpunkt begrenzten Abschnitte auf der Hypotenuse sein soll: Diese haben nach dem Kathetensatz von Euklid die Längen 1,8 und 3,2.

Möglicherweise meinst Du die Höhe h: Diese hat tatsächlich die Länge 2,4. Das folgt aber daraus, dass 12 das Doppelte des Flächeninhalts ist: 3 mal 4. In jedem rechtwinkligen Dreieck (a, b Katheten, c Hypotenuse) gilt A = ab/2 = c h /2. Daraus folgt h = ab/c. -- Digamma 21:24, 3. Apr. 2011 (CEST)

Dieser Abschnitt kann archiviert werden. arilou (Diskussion) 10:20, 5. Okt. 2012 (CEST)

folge

ich nehme ein beliebiges oder rechtwinkeliges dreieck-wenn man das so nennt-, von der hypotenuse zieh ich im recten winkel die höhe- bekomme zwei ungleiche dreiecke, dann spiegel ich das original über die hypotenuse-wie verhalten sich diese drei dreiecke von der oberfläche her zueinander?ist eine folge erkenbar? (nicht signierter Beitrag von 46.57.11.161 (Diskussion) 11:49, 7. Apr. 2011 (CEST))

Ich habe leider nicht verstanden, wie die drei Dreiecke entstehen. Was denn nun: ein beliebiges oder ein rechtwinkliges Dreieck? -- Digamma 15:56, 7. Apr. 2011 (CEST)

Da kommt nix mehr.

Dieser Abschnitt kann archiviert werden. arilou (Diskussion) 10:21, 5. Okt. 2012 (CEST)

Nicht-mathematische Verwendung des Begriffs Dreieck

Hallo zusammen,

momentan gibt es den Abschnitt Dreieck#Nicht-mathematische_Verwendung_als_Symbol im Artikel. Da es auch immer wieder Diskussionsbeiträge gibt, die das „Dreieck als Symbol“ hier im Artikel wollen, würde ich gerne diese Frage hier mal klären:

Welche Themen soll dieser Artikel behandeln?

Die Diskussionsbeiträge sind folgende:

• Diskussion:Dreieck#Dreieck_als_Symbol
• Diskussion:Dreieck/Archiv#Ikonographischer_Akspekt_des_Dreiecks
• Diskussion:Dreieck/Archiv#Symbolische_Bedeutung

Je nach dem, wie wir uns entscheiden, sollte eventuell folgendes gemacht werden:

• Abschnitt Dreieck#Nicht-mathematische_Verwendung_als_Symbol entfernen / ausbauen
• Den Hinweis zu beginn des Artikels „Dieser Artikel behandelt den geometrischen Begriff Dreieck; zu weiteren Bedeutungen siehe Dreieck (Begriffsklärung).“ ändern oder vielleicht sogar direkt darauf hinweisen, dass das Dreieck als Symbol auf der BKL zu finden ist
• Eventuell den Artikel in „Dreieck (Geometrie)“ umbenennen
• Vielleicht auf der Diskussionsseite deutlicher darauf hinweisen, dass es ausschließlich um Geometrie geht (wie?) und diese Diskussion verlinken.

Ich plädiere dafür, dass in diesem Artikel nur der geometrische Aspekt eines Dreiecks behandelt wird. Ich habe dafür folgende Gründe:

• Momentan behandelt der überwiegende Teil des Artikels bereits ausschließlich das „geometrische Dreieck“
• Es gibt für sehr viele weitere Bedeutungen viele weitere Artikel (39, falls es jemanden interessiert)
• Über den geometrischen Begriff lässt sich bereits sehr viel sagen und der Artikel ist auch ohne weitere Bedeutungen schon sehr lang

Aus Folge davon bin ich auch für eine ersatzlose Entfernung des Abschnitts Verwendung als Symbol (Permalink)

edit: Anscheinend hat Benutzer:Qniemiec damit angefangen, andere Bedeutungen hier mit hinein zu bringen (siehe [[4]]). Ich schreibe ihn auch mal an.

Grüße, --Martin Thoma 10:17, 16. Sep. 2012 (CEST)

Es dreht sich hier um die symbolische Verwendung der geometrischen Figur, insofern gehört es in diesen Artikel (btw: die neue Zwischenüberschrift halte ich für extrem misslungen). Bermudadreieck, Dreiecksbeziehung etc. haben bloß einen Namens- bzw einen Zahlwortbezug, die gehören zu Recht nicht hierher.--Fritzbruno (Diskussion) 10:31, 16. Sep. 2012 (CEST)

Ich wäre für die Einrichtung eines eigenen Artikels Dreieck (Symbol) und die Auslagerung der symbolischen Inhalte hier, vgl. Raute und Raute (Symbol). Viele Grüße, --Quartl (Diskussion) 10:43, 16. Sep. 2012 (CEST)

(edit conflict)

gudn tach!

danke fuer die zusammenstellung! grundsaetzlich stimme ich dir zu. auch im hinblick auf konsistenz - im kontext der anderen geom. artikel - wuerde die streichung angebracht sein, vgl. Stern (Geometrie), Quadrat (Geometrie), Kreis.

aaaber die loesung dieses problems halte ich nicht fuer einfach. denn bei den symbolhaften verwendungen (im nicht-mathematischen kontext) wird ja nicht nur das dreieck als wort benutzt, sondern vermutlich immer auch als geometrische figur. insofern halte ich ein hinweis im mathematischen artikel auf die symbolhafte verwendung (auch ausserhalb der mathematik) fuer nicht unangebracht. hab auch ein beispiel gefunden, bei dem mathe und nicht-mathe gemixt in einem artikel stehen: Pentagramm. und dann gibt es auch sowas: Fünfeck#Vorkommen.

die frage ist, ob eine BKL/BKS diese aufgabe ausreichend erfuellt/erfuellen darf, die symbolhaftigkeit des dreiecks zu beleuchten. besser waere ein eigener artikel Dreieck (Symbol) (oder so) analog zu z.b. Swastika, der jedoch erst mal geschrieben werden muesste. -- seth 10:51, 16. Sep. 2012 (CEST)

Einen Artikel "Dreieck (Symbol)" fände ich auch die beste Lösung. Die BKS ist auf jeden Fall der falsche Ort, um Inhalte unterzubringen.

Anmerkung: Die symbolische Bedeutung wurde hier zum ersten Mal in den Artikel gebracht. Benutzer:Qniemiec hat den Abschnitt nur innerhalb des Artikels verschoben. --Digamma (Diskussion) 11:07, 16. Sep. 2012 (CEST)

Danke für den Hinweis. Ich habe die Beiden auch mal auf diese Diskussion hingewiesen. --Martin Thoma 11:28, 16. Sep. 2012 (CEST)

Ja, die "Wildwuchsnatur" der Wikipedia führt leider dazu, dass man da manchmal nach einiger Zeit wieder etwas "aufräumen", also die Gliederung eines Artikels wieder etwas straffen, über den Text verteilte Beiträge zum selben Thema zusammenfassen muss etc. Was die momentane Diskussion angeht: Ich würde dafür plädieren, die mathematischen Aspekte des Dreiecks unter "Dreieck (Geometrie)" oder "Dreieck (Mathematik)" zu behandeln und den Überbegriff "Dreieck" für alles mit ihm verbundene, also auch seine symbolische Verwendung, offen zu halten. Ich erinnere mich daran, dass es dazu vor einiger Zeit eine ganz ähnliche Diskussion um den Begriff Batterie gab, den die meisten ja zugegebenermaßen nur als Bezeichnung für diese Dinger kennen, mit denen man irgendwelche Elektrogeräte betreibt. Mit Blick auf den Anspruch der Wikipedia, die große Internet-Enzyklopädie zu sein, und nicht nur ein Lexikon dieser oder jener Einzelbedeutungen, wurde das ganze dann in Batterie (Elektrotechnik) umgetauft.
Hier ist es, glaube ich, ähnlich: Das Dreieck (als solches) ist ein dermaßen fundamentales, ja was eigentlich?.... "Etwas", dass seine mathematische Bedeutung wirklich nur einen (wenn auch aus Mathematikersicht natürlich den wichtigsten ;-)) Teil all seiner Aspekte ausschöpft. Ich fände es also gut, wenn jemand, der "Dreieck" eingibt, damit erstmal auf eine Art Begriffsklärungsseite kommt, auf der dann ganz oben mit ein, zwei Sätzen gesagt wird, dass das Dreieck als "ein Ding mit drei Ecken" ;-)) eine der Urformen der Natur ist, und als solches auch uraltes menschliches Symbol mit diversen Konnotationen, von wo aus es dann zB. zu "Dreieck (Geometrie)", "Dreieck (Symbolik)" usw. weitergehen könnte, inkl. des Vorteils späterer Erweiterbarkeit. Das jedenfalls wäre mein Vorschlag.
Wie ich auch generell dafür bin, dass bei so allgemeinen Begriffen die Einengung auf die fachsprachliche Bedeutung in einer so universell angelegten Enzyklopädie wie der Wikipedia stets möglichst spät erfolgen sollte. Wurde ein Lemma für eine allein fachsprachliche Bedeutung "verbraucht", ist es jedenfalls - wie wir gerade sehen - sehr aufwändig, dass später wieder zu revidieren bzw. um weitere Bedeutungen zu erweitern. Je eher also so etwas rückgängig gemacht bzw. korrigiert wird, desto besser. Denn die Wikipedia hat ja hoffentlich noch eine lange Zukunft vor sich, und aus dieser Sicht ist es dann auch nicht zu spät, mal etwas schon eine Weile Eingefahrenes wieder beizubiegen ;-)). --Qniemiec (Diskussion) 12:30, 16. Sep. 2012 (CEST)

Was Du ansprichst, ist eine andere Frage, nämlich die, welche der Dreieck-Artikelseiten den Namen "Dreieck" führen soll. Die von dir angeregte "übergeordnete" Seite gibt es ja schon, nämlich als Begriffsklärungsseite unter dem Namen Dreieck (Begriffsklärung). Auf diese Seite wird im Kopf des Artikels Dreieck, im Begriffklärungshinweis verwiesen. --Digamma (Diskussion) 19:12, 16. Sep. 2012 (CEST)

eine Auslagerung in einen eigenen Artikel wäre ein brauchbarer Kompromiss (kein guter, für mich ist die Symbolwirkung nicht zu trennen von der geometrischen Figur - eher würde ich den trigonometrischen Teil auslagern wollen). Das müsste dann allerdings über einen Importwunsch geschehen, eine einfache Artikelneuanlage ginge nicht.--Fritzbruno (Diskussion) 12:11, 16. Sep. 2012 (CEST)

Also ich kann mit und ohne eine Auslagerungen leben, aber den mathematischen Teil zu zersplittern halte ich für eine denkbar schlechte Idee.--Kmhkmh (Diskussion) 12:21, 16. Sep. 2012 (CEST)

Noch 'n Vorschlag:

Verschieben von "Dreieck" nach "Dreieck (Mathematik)" und

Weiterleitung von "Dreieck" auf "Dreieck (Begriffsklärung)"

Begründung: Trotz meiner persönlichen Neigung, unter dem Begriff Dreieck erst mal an das geometrische Mathe-Ding zu denken, gibt es doch viele andere - auch verbreitete - Bedeutungen. Wenn ein WP-Nutzer einfach "Dreieck" in die Suche eingibt, ist wohl eine -hm- "Rückfrage" nötig, welches er meint -> BKS. Mit "Dreieck (Mathematik)" als erstgenannte Bedeutung.

Ach ja: Contra einen Abschnitt "Verwendung des Dreiecks als Symbol" hier im Artikel, das hat die Tendenz 'ne ewig lange Liste zu werden, wer wo wann mal ein Dreieck in sein Logo eingebaut hat.

--arilou (Diskussion) 09:16, 17. Sep. 2012 (CEST)

Wenn dann müsste Dreieck (Begriffsklärung) nach Dreieck verschoben werden. Ich habe eben in Google Books und Google die Verwendung des Begriffs "Dreieck" nachgeschlagen. Dort findet sich keine deutliche Tendenz zur geometrischen Bedeutung, sondern mindestens so häufig eine übertragene oder geografische Bedeutung, allerdings immer mit einem Zusatz ("magisches Dreieck", "goldenes Dreieck", ...).

Wenn man sich weiter Spezial:Linkliste/Dreieck anschaut, dann sieht man auch, dass innerhalb der Wikipedia die geometrische Bedeutung des Begriffs "Dreieck" gegenüber der symbolischen Bedeutung (die ja derzeit auch in diesem Artikel behandelt wird) stark überwiegt. Dreieck (Band) und Dreieck (Sternbild) haben ebenfalls wesentlich weniger interne Links (bei dem Sternbild sind 87 durch eine Navigationsleiste verursacht). Zu den beiden Orten gibt es noch keine Artikel.

Fazit: wenn ein Benutzer "Dreieck" ohne Zusatz eingibt meint er fast immer die geometrische Form und damit diesen Artikel hier. Daher wäre ich gegen eine Umbenennung in Dreieck (Mathematik). Viele Grüße, --Quartl (Diskussion) 11:31, 17. Sep. 2012 (CEST)

Das Fazit hinkt gewaltig, denn das würde bedeuten, dass in der WP Artikel und Artikelverlinkungen nachfrageorientiert erstellt werden. Das Gegenteil dürfte der Fall sein: Ich schreiben einen Artikel zu meinem Steckenpferd und verlinke ihn sinnvoll, statt: Oh, 25 Leute haben einen Artikel soundso gesucht, dann werde ich den mal erstellen und wie gewünscht verlinken. Als Argumentation ist das jedenfalls untauglich. Nebenbei: es dreht sich um das Dreieck (Geometrie).--Fritzbruno (Diskussion) 18:57, 17. Sep. 2012 (CEST)

Siehe die Tabelle in Wikipedia:Begriffsklärung#BKL II. Viele Grüße, --Quartl (Diskussion) 19:30, 17. Sep. 2012 (CEST)

????? (=was willst du damit sagen)--Fritzbruno (Diskussion) 21:07, 17. Sep. 2012 (CEST)

Ich will lediglich damit sagen, dass für die Einrichtung einer BKL II (wie sie hier vorhanden ist) die Häufigkeit der Verwendung und auch die Häufigkeit der Verlinkung eines Begriffs eine Rolle spielt. Viele Grüße, --Quartl (Diskussion) 06:01, 18. Sep. 2012 (CEST)

Sehe ich das richtig, dass wir uns bisher einig sind, dass Dreieck (Symbolik) einen eigenen Artikel per Importwunsch bekommen sollte? (Die Frage nach dem Hauptartikel Dreieck, einer eventuellen umbenennung dieses Artikels in Dreieck (Mathematik) oder Dreieck (Geometrie) kann man davon ja getrennt betrachten.) --Martin Thoma 19:41, 17. Sep. 2012 (CEST)

nein, eine Beibehaltung des Abschnitts in Dreieck erachte ich nach wie vor als sinnvoller.--Fritzbruno (Diskussion) 21:07, 17. Sep. 2012 (CEST)

gudn tach!

bin heute ueber einen artikel gestolpert, der sowas wie eine erweiterte bks darstellt: Resilienz. das koennte beim dreieck imho auch sinn machen: also Dreieck als bks mit einer mehrsaetzigen, bebilderten, aber kurzen erklaerung des begriffs und anschliessend einer uebersicht der versch. artikel, die ja alles etwas damit zu tun haben. dort wuerden dann auch die links zu Dreieck (Geometrie) und Dreieck (Symbol) oder Dreieck (Symbolik) platz finden. -- seth 22:17, 17. Sep. 2012 (CEST)

Ich könnte zwar auch mit einer Auslagerung Dreieck (Symbolik) leben, fände aber eine Beibehaltung (und Ausbau!) des Abschnitt im Artikel sinnvoller. Es geht ja wie schon gesagt wurde darum, dass die geometrische Figur als Symbol verwendet wird. Außerdem zeigen die Anfragen, dass wohl viele Leser so einen Abschnitt hier erwarten. -- HilberTraum (Diskussion) 22:36, 17. Sep. 2012 (CEST)

Abgesehen von dieser Diskussion hier sehe ich genau 1 Beitrag auf hießiger Disku, der sich mit dem Dreieck als Symbol der Illuminati beschäftigt - der Rest ist Mathe. Welche "Anfragen" meinst du, und wie "viele" sind es denn? (sorry: --arilou (Diskussion) 09:57, 18. Sep. 2012 (CEST))

Äh, ich meinte die drei Links ganz am Anfang dieses Diskussionsabschnitts. Wenn schon drei Leute sich die Mühe machen deswegen auf die Disk zu schreiben ... -- HilberTraum (Diskussion) 10:51, 18. Sep. 2012 (CEST)

Zur Beibehaltung des Abschnitts „Nicht-mathematische Verwendung als Symbol“ in diesem Artikel:

Ich finde der Abschnitt wirkt hier absolut deplaziert. Zuerst kommen 12 Bildschirmlängen nur mathematische Inhalte und dann ... etwas über polnische Herrentoiletten.

Ich denke, dass die meisten Leser das geometrische Dreieck erwarten, wenn sie Dreieck eingeben. Allerdings bin ich in dieser Hinsicht als Mathematik-Student vielleicht etwas voreingenommen.

Vielleicht könnte man einen ausführlichen Artikel Dreieck (Symbolik) schreiben (gibt es Freiwillige? Fachleute?), den momentanen Artikel nach Dreieck (Mathematik) bzw. Dreieck (Geometrie) verschieben und die BKL nach Dreieck verschieben oder die BKL dort lassen und einen neuen, ausgewogenen Artikel „Dreieck“ schreiben, der auf verschiedene Symbole und kurz auf das mathematische Dreieck eingeht.

Mein Problem bei dem „Dreieck als Symbol-Thematik“ ist, dass ich nicht sehe wie daraus ein ausführlicher Artikel werden soll. Momentan sind das drei Sätze, die nur auf einen Hauptartikel verweisen. Interessant wird das Dreieck als Symbol doch erst, wenn es dazu eigene Inhalte und Literatur gibt. Dort müsste dann das „Warum?“, also „Warum wurde das Dreieck als Symbol gewählt?“ erklärt und belegt sein. Sonst ist es, wie mit der polnischen Herrentoilette, nur eine Aufzählung von Stellen, wo man halt zufällig ein Dreieck verwendet hat.

Grüße, --Martin Thoma 09:43, 18. Sep. 2012 (CEST)

+1 zu deiner Aussage, lieber Benutzer:MartinThoma.

Der Abschnitt ist hier absolut deplatziert. Das ist nunmal ein Mathe-Artikel. Da haben polnische Herrentoiletten halt nichts drin zu suchen.

Die Liste von Links, wo ein Dreieck als Symbol verwendet wird, gehört in eine BKS, die als Dreieck (Begriffsklärung) ja auch schon besteht.

Und da (wie wohl bereits geklärt) die überwiegende Hauptbedeutung von "Dreieck" das mathem.-geometr. Objekt ist, braucht's wohl auch keine Verschiebung.

Einziges Problemchen: Es wird andauernd gejammert, wenn man ein bischen mehr als nur Stichworte in eine BKS schreibt. Die Prinzipienreiter können wohl ganze Sätze in BKSn nicht ertragen.

--arilou (Diskussion) 09:53, 18. Sep. 2012 (CEST)

Bei anderen geometrischen Figuren wie Pentagramm oder bei den ganzen Artikeln zu Zahlen (Vier, Goldener Schnitt, Kreiszahl) werden ja auch die mathematischen Objekte und ihr symbolische Bedeutung in einem Artikel gemeinsam behandelt. Würdet ihr die denn auch aufteilen wollen? Dass der Abschnitt in Dreieck so deplaziert wirkt liegt doch nur daran, dass er so kurz und qualitativ bescheiden ist. Das wird aber nicht unbedingt besser, indem man ihn auslagert. -- HilberTraum (Diskussion) 12:23, 18. Sep. 2012 (CEST)

Das "deplatziert" wird (zumindest für hießigen Artikel) dann deutlich besser, weil WEG *g*

--arilou (Diskussion) 12:29, 18. Sep. 2012 (CEST)

Man könnte natürlich auch noch drei Bildschirmseiten mit Filmen, Mangas und Videospielen dranhängen, in denen irgendwas Dreieckiges vorkommt ... -- HilberTraum (Diskussion) 14:26, 20. Sep. 2012 (CEST)

Enzyklpädische Relevanz sollte hier schon die Grundlage sein.--Fritzbruno (Diskussion) 21:30, 20. Sep. 2012 (CEST)

Resümee; Dreieck als Symbol

Da mich Martin Thoma auf diese Diskussion hingewiesen hat, möchte ich die bisherigen Meinungen zusammenfassen und aus meiner Sicht kommentieren.

1. Die Einrichtung eines eigenen Artikels Dreieck (Symbol) findet überwiegende Zustimmung. Ich habe vor, demnächst damit zu beginnen. Zur Frage, ob ein kurzer Abschnitt zum Symbol im Hauptartikel Dreieck verbleiben soll, gibt es jedoch unterschiedliche Ansichten. Dafür spricht v.a., dass das Dreieckssymbol oft eine geometrische Bedeutung hat.
2. Ein neuer Artikel Dreieck (Symbol) wäre klarerweise in Dreieck (Begriffsklärung) anzuführen. Manche schlagen in diesem Zusammenhang vor, die BKL auf Dreieck zu verschieben und den vorstehenden Artikel in Dreieck (Mathematik) oder Dreieck (Geometrie) umzubenennen.
3. Gegen ersteres spricht vor allem die Anzahl der Verlinkungen, die ja zeigen, was die meisten Wikipedianer unter "Dreieck" verstehen: Auf Dreieck (math./geometrisch) wird derzeit fast 500 x verlinkt, auf den Begriff der Graphentheorie ~90x, auf Dreiecksnetz 33x, auf Pascalsches Dreieck, Sierpinski- und Semiotisches Dreieck je ~60x, auf die Sternbilder Dreieck (Sternbild) und Südliches Dreieck ~180 bzw. 120x (v.a. als Verortung von Himmelsobjekten), auf alle Magischen Dreiecke cca 30 mal. Die anderen Lemmata wie geografische und Autobahndreiecke, Goldenes Dreieck usw. habe ich nicht untersucht, weil sie wohl kaum unter "Dreieck" gesucht würden.
4. Ob man den vorstehenden Artikel in Dreieck (Mathematik) oder/und Dreieck (Geometrie) umbenennen bzw. aufsplitten soll, müsste eine eigene Disku zeigen. Ich selber halte nichts davon, weil die betreffenden Inhalte stark miteinander verquickt sind.
5. Mit anderen teile ich die Meinung, dass der derzeitige Abschnitt "Nicht-mathematische Verwendung als Symbol" nicht optimal ist, und ändere ihn vorerst auf "Dreieck als Symbol".

Ich hoffe, hiermit der Diskussion und einem gezielteren Vorgehen gedient zu haben. Geof (Diskussion) 15:23, 23. Sep. 2012 (CEST)

Sieht mir soweit

Dieser Abschnitt kann archiviert werden. arilou (Diskussion) 09:51, 5. Okt. 2012 (CEST)

aus. --arilou (Diskussion) 09:51, 5. Okt. 2012 (CEST)

Dreieck als Symbol

Besonders populär ist die in den Romanen verbreitete Annahme, die Illuminaten hätten bestimmte Symbole besessen, mit denen sie ihre Existenz für Eingeweihte und findige „Symbolologen“ erkennbar gemacht hätten. Zu diesen vermeintlichen Illuminaten-Symbolen gehören unter anderem auch das Dreieck. (nicht signierter Beitrag von 91.89.249.52 (Diskussion) 19:38, 17. Mai 2012 (CEST))

(hier:)

Dieser Abschnitt kann archiviert werden. arilou (Diskussion) 16:23, 16. Okt. 2012 (CEST)

Eckpunkt-Bezeichnungen

Die Eckpunkte im Dreieck werden gegen den Uhrzeigersinn beschriftet. Wieso nennt man die Richtung gegen den Uhrzeigersinn die positive Richtung?

Wäre mal interessant zu wissen.

Regina.

Drehrichtung#Mathematische Definitionen bezüglich Koordinatensystemen. --arilou (Diskussion) 10:14, 5. Okt. 2012 (CEST)

Dieser Abschnitt kann archiviert werden. --seth 11:36, 3. Feb. 2013 (CET)

Drei Angaben, eine Seite

Hab das mal mit den 3 Angaben geändert. Wenn ich nur die Winkel hab, kann ich die Seiten nicht eindeutig ausrechnen. Nur die Verhältnisse der drei Seiten (nicht signierter Beitrag von 81.210.135.149 (Diskussion) 2008-03-02T01:14:00)

und ich hab's noch weiter umformuliert. auch mit einer seite ist's naemlich nicht immer eindeutig. -- seth 11:37, 2. Mär. 2008 (CET)

Dieser Abschnitt kann archiviert werden. --seth 11:36, 3. Feb. 2013 (CET)

Grafik: Gleichschenkliges- bzw. Gleichseitiges Dreieck

Ich würde gerne dieses rechte Bild durch diese beiden Bilder ersetzen.

Links ein gleichschenkliges, rechts ein gleichseitiges Dreieck

• 
  Ein gleichseitiges Dreieck, da gilt: $\alpha =\beta =\gamma$ und a = b = c
• 
  Ein gleichschenkliges Dreieck, da gilt: $\alpha =\beta$ und a = b

Gibt es dazu Anmerkungen? --Martin Thoma 18:53, 10. Jul. 2012 (CEST)

Ich würde die Bezeichnungen der Seiten auf die Außenseiten schreiben :-). Ansonsten: Gefällt mir. --Digamma (Diskussion) 21:07, 10. Jul. 2012 (CEST)

Ich habs geändert. --Martin Thoma 12:03, 11. Jul. 2012 (CEST)

Ich habe keine wirkliche Präferenz, damit aber auch nichts gegen einen Austausch. Prinzipiell ist es allerdings von Vorteil, wenn erläuternde Texte nicht Teil der Grafik selbst sind, denn dadurch bleiben sie für andere WPner einfach bearbeitbar.--Kmhkmh (Diskussion) 12:15, 11. Jul. 2012 (CEST)

Das spricht ja für meine Bilder. Ich habs mal im Artikel ersetzt. --Martin Thoma 15:18, 11. Jul. 2012 (CEST)

gudn tach!

ich finde die neuen bilder auch besser (schon allein, weil sie nicht pixelig sind). aber jetzt sind im artikel auf engem raum drei bilder eines gleichseitigen dreiecks. zwei davon (die ohne kreise) sind fast identisch, sodass ich dafuer plaediere eines davon rauszuschmeissen. (welches davon, waere mir egal.) -- seth 22:52, 31. Jul. 2012 (CEST)

Ich habe mal das erste rausgeschmissen. So gut? --Digamma (Diskussion) 10:15, 1. Aug. 2012 (CEST)

Ja, sieht gut aus. Vielleicht sollte ich die Buchstaben im Verhältnis etwas größer machen (bzw. die Kantenlänge reduzieren). Außerdem könnte ich der Dreiecksfläche noch eine dezente Hintergrundfarbe verleihen. Mal schauen ... --Martin Thoma 12:36, 1. Aug. 2012 (CEST)

gudn tach!

@Digamma: ja, sehr gut! -- seth 00:37, 3. Aug. 2012 (CEST)

Es ist nun einige Monate kein Vorschlag mehr zu diesen Bildern gekommen. Ich vermute, das Thema ist erledigt.

Dieser Abschnitt kann archiviert werden. --Martin Thoma 11:11, 2. Feb. 2013 (CET)

Rechtschreibung

Ich bin selber nicht so fit, daher erst einmal eine Frage. Heisst es nicht "Dreieckberechnung" anstatt "Dreiecksberechnung"? Also ohne das "s" zwischen k und b. 93.192.230.54 21:25, 9. Jan. 2013 (CET)

Fugen-s. --Digamma (Diskussion) 22:13, 9. Jan. 2013 (CET)

iow: beides ist korrekt. -- seth 11:38, 3. Feb. 2013 (CET)

Dieser Abschnitt kann archiviert werden. --seth 11:38, 3. Feb. 2013 (CET)

Rechtwinkliges Dreieck

Aus dem Artikel: Bei Kenntnis drei der Angaben (a, b, c, p, q und h) lassen sich die fehlenden 3 anderen Werte aus den, in der Tabelle aufgeführten Formeln berechnen.

Reichen dafür nicht 2 Angaben ?

Nicht immer. Bei Kenntnis von c und h kann man vielleicht noch tricksen. Aber wie ist es bei Kenntnis von a und h? Aber vielleicht stimmt deine Ansicht ja doch, und ich muß es korrigieren. --Arbol01 00:39, 5. Okt 2004 (CEST)

Zum Beispiel: mit a und h kannst du p ausrechnen (p² + h² = a²), mit p und h kannst du q ausrechnen (p*q = h²), mit p und q kannst du c ausrechnen (p+q = c), und mit a und c kannst du b ausrechnen (a² + b² = c²).

Aber was ist, wenn nur b und p bekannt sind? Dann kann das Dreieck nicht erschlossen werden.

Doch. Die Beziehung p + q = c und der Kathetensatz b² = q c ergeben zusammen b² = (c - p) c. Aus dieser quadratischen Gleichung kann man c bestimmen und dann mit Pythagoras auch a. (Was mir nicht einfällt, ist eine Konstruktion mit Zirkel und Lineal. Hat da jemand einen Vorschlag?) --Digamma 20:15, 19. Feb. 2007 (CET)

Irgendwie hast du da nen kleinen Buchstabendreher drin. b² = q c und nicht p c

Korrigiert!--Digamma 17:46, 20. Feb. 2007 (CET)

Vorschlag: Man könnte das Dreieck nach Pythagoras mit den entsprechenden Quadraten darstellen. Dann trennt man c² mit h "senkrecht" in a² und b², und c in q und p. Nachdem trennt mann c² "waagerecht" im Abstand der Größe p von c, wodurch der eine Teil von c² in p² und h² und der andere Teil in h² und q² geteilt wird. Dadurch entsteht im c² ein exzentrisches Kreuz mit zwei Quadraten und zwei Rechtecken (h²). 79.197.139.9 19:55, 31. Mär. 2011 (CEST)

Synonym Triangel für Dreieck?

Mir ist das Synonym Triangel für Dreieck noch nicht untergekommen. Auch in diversen Synonymwörtebüchern [5] und [6] kommt es nicht vor. Für mich ist Triangel ein Musikinstrument. Die englische Übersetzung triangle halte ich in diesem Zusammenhang nich für relevant. Ich bin deshalb für wieder raus. -- Petflo2000 18:53, 10. Jun. 2007 (CEST)

Das Synonym existiert tatsächlich [[7]], wird aber in der Sprache der Gegenwart nicht mehr oft genutzt. Anders ist dies für den Begriff "triangulär" für "dreieckig", der in der Fachsprache durchaus häufig Verwendung findet. --Kaizen77 14:19, 21. Mär. 2011 (CET)

Das Substantiv Triangel (wie auch Zentrum und Zirkel) ist im 15. Jahrhundert mit anderen lateinischen Fachausdrücken der Mathematik und der Naturwissenschaften in die deutsche Sprache übernommen worden. Als Fachwort der Geometrie bezeichnete es bis ins 19. Jahrhundert hinein die geometrische Figur »Dreieck«. Dreieck, im 16. Jh. aus dem mhd. Adjektiv rückgebildet, konnte sich erst im Laufe des 18. und 19. Jahrhunderts gegenüber Triangel behaupten.

Triangel in der Bedeutung »Musikinstrument« ist seit Ende des 16. Jahrhunderts belegt. Beide Bedeutungen gehören im Französischen, im Englischen und in anderen benachbarten Sprachen zum heutigen Sprachschatz. Literatur: Matthäus Roritzer, »Geometria deutsch«, Nürnberg 1497; Deutsche Wortkunde, Sammlung Göschen, Band 929.--Piatti 16:18, 9. Nov. 2011 (CET)

Winkeldreisatz

Ein Dreieck kann anstelle mit dem Kosinus- und Sinussatz auch mit dem Winkeldreisatz berechnet werden. Der Winkeldreisatz könnte lauten: G²*α/a²*180 . Das heißt das Gesamtquadrat, G²(=a²+b²+c²), wird multipliziert dem Winkel α, dessen Ergebnis dividiert wird durch die multiplikation von A-Quadrat, a², mit 180, der Summe aller Innenwinkel eines Dreiecks. Der Vorteil bei dieser Formel ist die Anpassung oder Umstellung der Formel nach den Maßen die gegeben und gesucht sind. 79.197.146.148 19:03, 30. Mär. 2011 (CEST)

Und welche Größe des Dreiecks wird dabei bestimmt? -- Digamma 16:33, 31. Mär. 2011 (CEST)

Der Winkeldreisatz steht analog zum Prozentsatz: G*p%/W*100. Der Grundwert G ist analog zum Gesamtquadrat G², der Prozentsatz p% ist analog zum Alphawinkel α und der Prozentwert W ist analog zum A-Quadrat a², während die 100 analog zur 180, dem Gesamtinnenwinkel eines Dreiecks steht. Auf diese Weise läßt sich analog im Winkeldreisatz das selbe berechnen wie im Prozentsatz. Also z.B. G=100*W/p% analog dazu G²=180*a²/α oder z.B. W=G*p%/1oo analog dazu a²=G²*α/180 oder z.B p%=100*W/G analog dazu α=180*a²/G². Dabei ist α ein beliebiger Winkel eines Dreiecks mit dem gegenüberligenden Quadrat a². 79.197.139.9 19:38, 31. Mär. 2011 (CEST)

Es gibt keinen Satz, der "Prozentsatz" heißt. "Prozentsatz" ist die Bezeichnung für die Größe "p%".

Weiter: Die Formel der Prozentrechnung heißt z.B. $W=G*p/100$. Ohne ein Gleichheitszeichen kann man da nach nichts auflösen. (Und in der Schreibweise mit "%"-Zeichen und der "100" ist die Formel mathematisch unsinnig.)

Du hast noch immer nicht die Frage beantwortet, welche Dreiecksgröße Du mit der Formel berechnen möchtest. Einen Winkel? Eine Seitenlänge?

Davon abgesehen: Wenn Du sie analog wie deine Prozent-"Formel" benutzen möchtest, dann ist sie falsch. Das Quadrat der Seitenlänge ist nicht proportional zur Größe des gegenüberliegenden Winkels. Gib doch mal ein Beispiel an für eine Rechnung mit dem "Winkeldreisatz". -- Digamma 20:53, 31. Mär. 2011 (CEST)

Ich möchte den Winkel α berechnen. Gegeben sind a 3cm, b 4cm, c 5cm und γ 90°. Zuerst berechne ich das Gesamtquadrat G² mit a²+b²+c², also 9cm² + 16cm² + 25cm² = 50cm². Nun berechne ich den Winkel mit α = a²*180/G², also 9cm²*180 ÷ 50cm² = 32,4°. 79.197.131.40 14:32, 2. Apr. 2011 (CEST)

Hier ist der korrekte Wert aber $\alpha \approx 36,9^{\circ }$. --Daniel5Ko 14:45, 2. Apr. 2011 (CEST)

Ein Beweis das meine Rechnung stimmt:180°÷ α 32,4° ≈5,56° und G²÷a², also 50cm²÷9cm² ≈5,56cm². 79.197.132.139 12:56, 3. Apr. 2011 (CEST)

Ja, du verwendest die Formel, die du angegeben hast, richtig. Sie berechnet aber nicht $\alpha$, sondern etwas anderes. Für das echte Alpha im vorliegenden Dreieck ist $\alpha =\arcsin {\frac {3}{5}}=\arccos {\frac {4}{5}}=\arctan {\frac {3}{4}}\approx 36,9^{\circ }\neq 32,4^{\circ }$.

Lustigerweise funktioniert deine Formel für gleichseitige Dreiecke und für gleichschenklige rechtwinklige. Bei dem Dreieck $(a,b,c)=(3,4,5)$ aber schon nicht mehr. Im degenerierten Fall $a=b,c=a+b$, wo eigentlich die Winkel $0^{\circ },0^{\circ },180^{\circ }$ herauskommen müssten, liefert deine Formel $30^{\circ },30^{\circ },120^{\circ }$. Nicht gut. --Daniel5Ko 14:26, 3. Apr. 2011 (CEST)

Aber die Proportionszahl 5,5 Periode ist bei α und a² die selbe, d.h. 5,56°=5,56cm². Bei a ist sie 4cm (U÷a=b, 12cm÷3cm=4cm), also 5,56°≠4cm. Und bei a³ ist sie 9,26cm³ (G³÷a³=x, 250cm³÷ 27cm³≈9,26cm³), also 5,56°≠9,26cm³. 79.197.132.139 19:51, 3. Apr. 2011 (CEST)

Nochmal zum Mitschreiben: Der richtige Wert von Alpha ist ca. 36,9°. Dass dieser Wert nicht herauskommt, ist ein erheblicher Mangel an deinem Winkeldreisatz. --Daniel5Ko 21:00, 3. Apr. 2011 (CEST)

Sonderfall bei sSw

Hallo Fritzbruno,

ich glaube, dass du falsch liegst. Der Sonderfall tritt nicht nur dann ein, wenn das Dreieck die Winkel 60°, 30° und 90° hat, sondern immer dann, wenn der der längeren Seite gegenüberliegende Winkel 90° beträgt. Das kann auch auch ein gleichschenkliges rechtwinkliges Dreieck sein oder ein Dreieck mit den Winkeln 40°, 50°, 90°. Sind b und c die gegebenen Seiten und $\beta$ der gegebene Winkel, mit c > b, dann ist das Dreieck i. A. deshalb nicht eindeutig bestimmt, wei der Kreis um A mit Radius b die Halbgerade a in der Regel in zwei Punkten oder gar keinem Punkt schneidet. Die Konstruktion ist genau dann eindeutig, wenn der Kreis die Halbgerade nur in einem Punkt trifft, also berührt. Das ist dann der Fall, wenn der Winkel bei C ein rechter Winkel ist. Auf die Größe der andern beiden Winkel kommt es dabei nicht an. Der Winkel $\beta$ kann ein beliebiger spitzer Winkel sein. Die Bedingung für das Seitenverhältnis von b und c ist: $b:c=\sin \beta .$ Für $\beta =30^{\circ }$ ergibt sich das von dir genannte Seitenverhältnis von 1 : 2, aber das ist nur ein Spezialfall von unendlich vielen. --Digamma (Diskussion) 11:20, 3. Jun. 2012 (CEST)

akzeptiert, danke. Leider gibt der Text diese Information nicht her. Mal sehen, was sich daraus machen lässt.--Fritzbruno (Diskussion) 11:51, 3. Jun. 2012 (CEST)

Vielleicht könnte man das auch durch "intuitive" Zirkelkonstrunktionen illustrieren (2 Schnittpunkte, 2 Schnittpunkte bei 90 Grad (eindeutig, da 2 kongruente Lösungen), 1 Schnittpunkt (Berührungspunkt, eindeutig).--Kmhkmh (Diskussion) 14:54, 3. Jun. 2012 (CEST)

Das mit den 2 Schnittpunkten bei 90 Grad verstehe ich nicht. Meinst du (in meinen Bezeichnungen oben) $\beta =90^{\circ }$? Das ist der Fall SsW, der sowieso eindeutig ist. Der Schnittpunkt, der auf der andern Seite liegt, zählt nie mit, denn dann liegt das Dreieck ja auf der andern Seite von c, der gegebene Winkel $\beta$ ist dann kein Innenwinkel, sondern wird zum Außenwinkel. --Digamma (Diskussion) 18:20, 3. Jun. 2012 (CEST)

Ich hatte an die 2 Schnittpunkt mit der Geraden statt der Halbgeraden gedacht, die liefern ja immer 2 unterschiedliche Dreiecke von denen aber eines (mit dem Ergänzungswinkel) scheidet wegen des falschen Winkels ausscheidet bis eben auf den 90-Grad-Fall in dem man 2 kongruente Dreiecke erhält, aber das spielt sich natürlich alles im SsW-Fall ab und ist somit für die obige Diskussion nicht von Bedeutung. Bleibt also, dass wir den die beiden Fälle (2 Schnittpunkte, 1 Berührungspunkt) mit Konstruktionszeichnungen illustrieren sollten, das macht die Situation auch für Leser ohne jegliche Trigonometriekenntnisse leicht erfassbar.--Kmhkmh (Diskussion) 19:09, 3. Jun. 2012 (CEST)

Allgemeines Dreieck

Bei der Abbildung eines Allgemeinen Dreiecks auf der Seite, sollte Gamma deutlich sichtbar größer oder kleiner als 90 Grad sein - entweder ein stumpfwinkeliges oder spitzwinkeliges Allgemeines Dreieck. Hier ist scheinbar ein Rechtwinkliges Dreieck dargestellt, , also da sollte mal ein anderes Bild hin, bzw. die Unterschrift in Rechtwinkeliges Dreieck geändert werden. Jakob Mitzlaff 08:46, 29. Nov. 2009 (CET)

Um welches Bild (bitte Dateinamen nennen) an welcher Stelle (bitte Link auf Abschnitt setzen) geht es dir genau? Besteht deiner Meinung nach das Problem noch? --Martin Thoma 13:41, 2. Sep. 2012 (CEST)

Berechnung eines beliebigen Dreiecks

In der Darstellung der Abbildungstabelle wird der Fall WWS durch SSW ersetzt. Das ist aber nicht korrekt, da SSW ja mehrdeutig ist und die Berechnungsvorschrift von einem eindeutigen Fall auf einen theoretisch mehrdeutigen Fall führt. Das ist unlogisch. Die Mehrdeutigkeit lässt sich nur mit WSW sinnvoll auflösen! Michael -- 213.23.75.114 08:46, 6. Okt. 2011 (CEST)

Bild auskommentiert, bis was besseres vorliegt. --arilou (Diskussion) 08:44, 14. Sep. 2012 (CEST)

Die Grafik finde ich schwer verständlich. Es wird aber nicht der Fall WWS durch SSW ersetzt, sondern in beiden Fällen wird auf die gleiche weitere Rechnung mit Hilfe des Sinussatzes verwiesen, beim SSW-Fall um den 2. Winkel zu berechnen (was nicht eindeutig möglich ist, wenn der bekannte Winkel der kürzeren Seite gegenüber liegt), beim WWS-Fall um die zweite Seite zu berechnen.

Ich sehe ein anderes Problem: In dem eingezeichneten SSW-Fall liegt der Winkel der kürzeren Seite gegenüber. Er ist deshalb nicht eindeutig lösbar. Beim WWS-Fall kann für die weitere Rechnung der 2. bekannte Winkel benutzt werden. --Digamma (Diskussion) 17:03, 14. Sep. 2012 (CEST)

Die von mir eingebrachte Grafik sollte die in punkto Rechenschritte optimierte Verfahrensweise beim Berechnen eines beliebigen Dreiecks illustrieren, also: Wie berechne ich so ein Dreieck mit möglichst wenigen und, wenn dabei die Wahl zwischen verschiedenen Formeln besteht, möglichst einfachen Rechenschritten? Wobei sich dann zB. zeigt, dass man den relativ komplizierten Kosinussatz eigentlich nur in zwei Fällen wirklich braucht. Und in meiner Unterrichtspraxis funktioniert diese "Landkarte" eigentlich sehr gut - wenn dabei irgendwelche theoretischen Fallunterscheidungen unter den Tisch fallen, war das für mich erstmal sekundär. Die Grafik sollte in erster Linie "anwenderfreundlich" sein und hat ja in dieser Form bis jetzt anscheinend auch ihren Dienst getan. Wenn sie nun rausgenommen wird, hilft das den Leuten weiter? --Qniemiec (Diskussion) 10:24, 15. Sep. 2012 (CEST)

Nachtrag: Klar, beim SSW-Fall gibt es die beiden Alternativen: Bekannter Winkel gegenüber der längeren Seite, oder (wie in der gestrichenen Abbildung gezeigt) bekannter Winkel gegenüber der kürzeren Seite, wodurch im letztgenannten Fall dann zwei mögliche Dreiecke zu berechnen sind, also jeder der folgenden Schritte zweimal ausgeführt werden muss, einmal für das eine, einmal für das andere Dreieck. Und da die Leute das mit den beiden Alternativen erfahrungsgemäß schnell vergessen, zeigt die Abbildung sicherheitshalber den aufwändigeren und nicht den einfachen Fall. Wenn's also partout "idiotensicher" sein soll, könnte ich das Schema natürlich noch durch eine neunte Spalte ergänzen, die den SSW-Fall mit "bekannter Winkel gegenüber der längeren Seite" wiedergibt - wäre das dann ok? Was die Symbolik angeht, könnte man beide Fälle dann zB. durch Schreibweisen wie "sSW" und "SsW" voneinander unterscheiden. --Qniemiec (Diskussion) 12:56, 16. Sep. 2012 (CEST)

Die Grafik ist ziemlich gut, und ich hätte sie gerne wieder drin - verbessert. Es sollte in den SSW- und WWS-Fällen irgendwie deutlicher werden, dass es dazu 0, 1 oder 2 Lösungen geben kann. Denn entweder

• der Leser weis, wie man Dreiecke berechnet ("Nicht-Idiot"), dann braucht er die Grafik eigentlich gar nicht.
• Oder der Rat suchende Benutzer weis nicht genau, wie er "sein Dreieck" berechnen soll - dann sollte die Grafik doch besser idiotensicher sein...

--arilou (Diskussion) 10:02, 5. Okt. 2012 (CEST)

Danke für das Lob, und die neue Grafik zeigt nun auch beide SSW-Fälle, also sSW und SsW, separat.
Frage eines Wissbegierigen: In welchen Fällen (außer WWW) kann es denn keine Lösung geben?
Und was die Nützlichkeit für "Nicht-Idioten" angeht: Worum es mir bei der Grafik ursprünglich ging, war sozusagen eine zeitoptimierte Abfolge der Rechenschritte, weil inzwischen auch schon in der Schule auf Zeit gerechnet werden muss, man also mit einem Blick auf die Grafik sofort sieht, dass man den zeitaufwändigen Kosinussatz genaugenommen nur in zwei Situationen wirklich braucht und in allen anderen Fällen besser mit Sinussatz und Winkelsumme operiert. Na ja, hoffe also, dass diese Fassung meiner Grafik mehr Gnade bei den geschätzten Betrachtern findet ;-)). --Qniemiec (Diskussion) 23:45, 5. Okt. 2012 (CEST)

Ok, habe selbst rausgefunden, was Ihr meintet bzgl. der Nichtlösbarkeit. Wenn die Seitenlängen einem tatsächlich existierenden Dreieck entstammen, kann dieser Fall ja eigentlich nicht vorkommen, aber in manchen Lehrbüchern finden sich trotzdem Aufgaben, die auf eine solche Nichtlösbarkeit hinauslaufen. Hab das also noch der Vollständigkeit halber mit reingebaut. --Qniemiec (Diskussion) 13:11, 6. Okt. 2012 (CEST)

Es geht um das folgende Bild, oder?

Grüße, --Martin Thoma 08:47, 6. Okt. 2012 (CEST)

Genau, eine frühere Version dieser Grafik, bei der die beiden SSW-Fälle noch nicht separat dargestellt waren, hatte ich 2010 reingestellt, und die war dann im September 2012 als missverständlich auskommentiert worden. Nun aber sollten alle Mehrdeutigkeiten ausgeräumt sein (hoffe ich). --Qniemiec (Diskussion) 12:24, 6. Okt. 2012 (CEST)

Sinussatz vs. Kosinussatz

Hallo allerseits, wo wir schon unter Experten sind ;-)), noch eine Frage: In meiner Grafik habe ich angegeben, dass es im SSS- und SWS-Fall am (zeitlich) günstigsten ist, den zweiten Winkel mit Hilfe des schnelleren Sinussatzes zu bestimmen. Nun aber lese ich in der englischen Wikipedia, dass man für diesen Schritt doch besser den Kosinussatz benutzt, weil der halt eindeutiger ist (allerdings auch wesentlich mehr Rechenzeit und Präzision verlangt). Was meint ihr? --Qniemiec (Diskussion) 13:11, 6. Okt. 2012 (CEST)

Bei "ernsthaften" Anwendungen (also eher nicht in der Schule ;-) wäre es bei der Auswahl der Formeln wohl noch wichtiger auf Kondition (Mathematik) und Stabilität (Numerik) als auf den Zeitbedarf zu achten. Aber auch da dürfte der Sinussatz deutlich im Vorteil sein, weil es nicht zu Auslöschung durch Subtraktion ungefähr gleich großer Fließkommazahlen kommen kann. Man bräuchte aber dann tatsächlich noch Zusatzregeln um aus dem Sinus eindeutig auf den Winkel schließen zu können. Der schwierige Fall aus Sicht der Numerik dürfte SSS sein. Da kann es gleich am Anfang durch den Kosinussatz zur Auslöschung kommen und man müsste sich wohl vorher überlegen, welcher der drei Winkel am stabilsten zu berechnen ist. Interessant wäre auch, ob es günstig sein könnte, anstelle der Winkelsumme, bei der es ja auch zu Auslöschung kommen kann, lieber nochmal den Sinussatz zu verwenden. -- HilberTraum (Diskussion) 18:50, 8. Okt. 2012 (CEST)

Hallo allerseits, hab nochmal etwas nachgeforscht, und es in der Tat so, dass man bei Lösung der Fälle SSS und SWS das Pech haben kann, dass der im Fall SSS ermittelte bzw. im Fall SWS vorgegebene erste Winkel der kürzeren bzw. kürzesten Seite gegenüberliegt, man also bei unkritischer Anwendung des Sinussatzes im Folgeschritt in dieser Situation die alternative zweite Lösung unterschlägt. Obwohl das also etwas mehr Arbeit macht, müsste in den genannten beiden Fällen der zweite Winkel, damit's "idiotensicher" ist, ebenfalls mit Hilfe des Kosinussatzes berechnet werden. Werde die Grafik daher umgehend diesbezüglich ändern. --Qniemiec (Diskussion) 15:46, 16. Okt. 2012 (CEST)

Links bei "Dreieck als Symbol"

// verschoben von Benutzer Diskussion:Arilou#Dreieck als Symbol

Hallo Arilou, kennst du WP:Verlinken#Klartextlinks? Aus den Linktexten ist a priori nicht ersichtlich, wohin die Links führen. Außerdem muss wirklich nicht fünfmal hintereinander auf den gleichen Artikel verlinkt werden. Meiner Einschätzung nach können die vier Links im Text auch gerne ganz wegfallen. Dass es einen Hauptartikel zum Thema gibt, steht ja schon drüber. Viele Grüße, --Quartl (Diskussion) 09:15, 30. Nov. 2012 (CET)

(Ich war mal so frei, diese Diskussion, die doch sehr Artikel-spezifisch ist, hierher zu verschieben.)

Nuja, das ist eine Abwägungsfrage.

Von meinem Gefühl her würde ich als Leser erwarten: Es wird davon gesprochen, dass Dreieck auch in der Theologie, als Symbole und in der Mathematik verwendet werden; wenn ich dann darauf klick, erwarte ich, etwas über "Dreiecke in Theologie", "Dreiecke als Symbole", "Dreiecke in der Mathematik" zu lesen zu bekommen. Aber, hm, das hängt davon ab, wie lange man den Kontext "nachfühlt", und ab wann man gefühlsmäßig die Begriffe ohne nennenswerte Kontext-Nachwirkung versteht.

Dass dabei 5* nacheinander auf den gleichen Artikel verlinkt wird, ist ein Argument, das fällt, sobald selbiger so lang wird, dass jedermann froh ist, gleich zum richtigen Abschnitt verknüpft worden zu sein. Aber, zugegebenermaßen, "hätte wäre würde wenn". Derzeit ist Dreieck (Symbol) recht kurz.

Im Prinzip kann man daher auch deine Variante vertreten.

--arilou (Diskussion) 11:33, 30. Nov. 2012 (CET)

PS: Es geht um diesen Edit von Quartl und den nachfolgenden Revert meinerseits . --arilou (Diskussion) 11:36, 30. Nov. 2012 (CET)

Wenn der Linktext "Dreieck in der Theologie" o.ä. wäre, hätte ich (abgesehen von der Mehrfachverlinkung) auch kein Problem damit. Der Linktext ist allerdings nur "Theologie" und so finde ich die Verlinkung für den Leser verwirrend. Andererseits muss man Theologie von diesem Artikel auch nicht verlinken, insofern wäre die Variante ganz ohne Links wohl die beste. Viele Grüße, --Quartl (Diskussion) 12:02, 30. Nov. 2012 (CET)

Wie gesagt, wenn du auf "Linktext ohne Kontext" abhebst, dann setzt du "Kontext_Anteil = 0".

(Mal ein krasses -hm- Gegenbeispiel: "Die Farbe Rot steht häufig für 'STOPP' - für weitere Erklärung siehe hier." Wenn man bei sowas immer das Wort "hier" erklärt, statt auf einen Artikel zu verlinken, der eine Erklärung für etwas zuvor genanntes beinhaltet, ist das "Linktext-mäßig" korrekt...)

Wie gesagt, das ist Gefühlssache.

Die Variante "gar keine Links" finde ich am schlechtesten. Außerdem würde die sowieso bald irgend jemand auf die eine oder andere Art verlinken...

--arilou (Diskussion) 14:12, 30. Nov. 2012 (CET)

Diese "hier"-Links sind ganz besonders grausig, siehe Linktext#Aussagekraft und Zugänglichkeit. Viele Grüße, --Quartl (Diskussion) 14:47, 30. Nov. 2012 (CET)

Ich finde auch, dass in einem Absatz höchstens ein mal auf einen Artikel verlinkt werden sollte. Mich persönlich stören die vielen Links dort sehr. 5 Links auf die gleiche Seite in zwei Zeilen ist eindeutig zu viel. --Martin Thoma 15:21, 30. Nov. 2012 (CET)

Sonderfall: Gleichschenkliges, rechtwinkliges Dreieck

ich vermisse bei all diesen dreicken: das "gleichschenklige, rechtwinklige dreieck" mit der basis bzw. hypotenuse = ${\sqrt {2}}$ = 1,414213562… :

Quadrat mit Wurzel 2

siehe auch: [8]. ist es zu "unwichtig" oder wurde dies ganz einfach (nur) vergessen? ;-) Dontworry (Diskussion) 07:38, 3. Feb. 2013 (CET)

und dann das rechtwinklige Dreieck mit hypotenuse = ${\sqrt {3}}$, mit hypotenuse = ${\sqrt {4}}$, mit hypotenuse = ${\sqrt {5}}$, ...

spielt allenfalls beim geometrischen Wurzelziehen eine Rolle, hier nicht. --Fritzbruno (Diskussion) 07:44, 3. Feb. 2013 (CET)

bei diesen fällen fehlt aber die achsensymmetrie! Dontworry (Diskussion) 07:59, 3. Feb. 2013 (CET)

na und? --Fritzbruno (Diskussion) 08:09, 3. Feb. 2013 (CET)

das musst du die ägypter fragen, warum sie ihre pyramiden achssymmetrisch + nicht anders gebaut haben, nicht mich! ;-) Dontworry (Diskussion) 08:17, 3. Feb. 2013 (CET)

Ich frage aber dich: Warum hat dieses Dreieck im Artikel Dreieck eine besondere Hervorhebung verdient und bitte dich das mit WP:Belegen zu untermauern. Wenn es da nichts gibt, dann bleibt's draußen. --Fritzbruno (Diskussion) 08:25, 3. Feb. 2013 (CET)

gegenfrage: warum haben dann aber "quadrat" [9] + "würfel" [10] einen eigenen artikel? Dontworry (Diskussion) 08:33, 3. Feb. 2013 (CET)

Das ist keine Antwort! --Fritzbruno (Diskussion) 08:37, 3. Feb. 2013 (CET)

diese artikel sind meine belege, weil in beiden fällen dieses dreieck eine wesentliche, sozusagen "mass-" + "formgebliche" rolle spielt! Dontworry (Diskussion) 08:41, 3. Feb. 2013 (CET)

und die anderen von mir genannten Dreiecke spielen bei Rechtecken eine Rolle. Ich werde sie dennoch nicht erwähnen. Offensichtlich hast du das Gefühl, hier fehlt etwas. In einem solchen Fall recherchiere ich die Fachliteratur, ob jemand anderes dazu etwas geschrieben hat. Dann kann ich das Fehlende mit diesem Beleg einfügen. Anderenfalls riskiere ich, dass mein Beitrag als WP:POV oder irrelevant gelöscht wird.--Fritzbruno (Diskussion) 09:55, 3. Feb. 2013 (CET)

hat ja ziemlich gedauert - aber bei nächster sich bietender gelegenheit bekommst du von mir dafür den "grossen abwimmelorden mit eichenlaub & schwertern am bande"! schlage vor du bindest jetzt das quadrat in den artikel "parallelogramm" und den würfel in den artikel "hexaeder" ein, damit das ganze wieder stringent logisch, "rund" + kausal wird! die disk driftet mir zu sehr ins absurde ab, ende der durchsage! schönen sonntag noch! 84.176.173.188 10:14, 3. Feb. 2013 (CET)

Wir haben als Sonderfälle gleichschenklige Dreiecke und rechtwinklige Dreiecke. Ein Dreieck, das beides erfüllt, ist natürlich erst recht ein Sonderfall. Die Frage ist, ob es dazu etwas Nennenswertes zu schreiben gibt, was über das hinausgeht, was unter "rechtwinklige Dreiecke" und "gleichschenklige Dreiecke" schon steht. --Digamma (Diskussion) 11:47, 3. Feb. 2013 (CET)

das ist doch wenigstens mal der ansatz einer möglichen lösung! mir geht es ja nur darum, dass dieser sonder-sonderfall überhaupt in der wp ausdrücklich erwähnt + nicht (wie bisher) totgeschwiegen wird. ich würde daher vorschlagen, diesem dreieck als sonderfall einen eigenen abschnitt im artikel "gleichschenkliges dreieck" zu spendieren. oder aber den gesamten artikel neu derartig zu gliedern, dass man vom spitzwinkligen über der sonderfall rechtwinklig letztlich zum stumpfwinkligen dreieck die verschiedenen möglichen formen beschreibt. Dontworry (Diskussion) 12:29, 3. Feb. 2013 (CET)

Nach wie vor ist es egal, was deine personliche Ansicht über die Bedeutung dieses Dreiecks ist, sondern ob es belegbare Hinweise für eine Sonderstellung gibt. Ersteres ist WP:POV bzw. WP:Theoriefindung, letzteres ist das Ergebnis einer guten Recherche. --Fritzbruno (Diskussion) 22:00, 3. Feb. 2013 (CET)

Dass es sich um einen Spezialfall handelt (nämlich gleichschenklig und rechtwinklig), scheint mir offensichtlich zu sein. Die Frage ist nur, wie relevant der Sonderfall ist. --Digamma (Diskussion) 15:40, 4. Feb. 2013 (CET)

Also das POV/WP:TF-Argument bzw. ein WP:TF-Literalimus scheint mir völlig überzogen zumal es völlig unumstrittene Inhalte geht. Natürlich kann man sich streiten, welche Sonderfälle erwähnt sollen oder können, aber das ist hier mMn. mehr eine Frage des editoriellen Ermessens als von POV/WP:TF.--Kmhkmh (Diskussion) 16:05, 4. Feb. 2013 (CET)

Imo ist der Artikel noch nicht soooo lang, dass nicht ruhig noch ein paar Zeilen dazukommen dürften. Die paar Zeilen stören doch niemand. --arilou (Diskussion) 17:30, 4. Feb. 2013 (CET)

na super. Wie wär es mit ein paar Zeilen über Witze mit Dreiecken? Ist das hier noch Wikipedia? Ich dachte, hier gibt es klare Relevanzkriterien, nach denen Beiträge beurteilt werden. Zeilenfüller gehört mW nicht dazu. --Fritzbruno (Diskussion) 17:37, 4. Feb. 2013 (CET)

Die sogenannten Relevanzkriterien beziehen auf die Relevanz eines Lemmas, d.h. ob ein Artikel angelegt werden kann/sollte, und regeln nicht auf die detailierten Inhaltes eines solchen.--Kmhkmh (Diskussion) 18:41, 4. Feb. 2013 (CET)

Sie besagen schon, dass nicht nur das Lemma, sondern auch der Artikelinhalt relevant sein soll. Mehr fordere ich auch nicht. Sowie der Nachweis erbracht wurde, dass besagtes Dreieck in einer Liste spezieller Dreiecke nicht fehlen darf (weil Euklid oder sonst ein namhafter Gelehrter das ebenso machte) freue ich mich über die Ergänzung. --Fritzbruno (Diskussion) 20:06, 4. Feb. 2013 (CET)

Wir hätten auch noch Geodreieck! Spaß beseite, hier habe ich eine Erwähnung gefunden. Ist zwar nicht gerade Euklid himself, aber meiner Meinung nach könnte man solche Spezialfälle schon erwähnen, notfalls als Beispiel oder so. Im Artikel Gleichschenkliges Dreieck wird ja auch auch schon kurz erwähnt, dass rechtwinklig es sein kann. -- HilberTraum (Diskussion) 20:24, 4. Feb. 2013 (CET)

Mir persönlich ist völlig egal, ob nun dieser Sonderfall explizit erwähnt oder nicht, aber mich stört es bei solchen Fragen es editoriellen Ermessens eine POV/TF-Keule aufzufahren, die ich eben hier für völlig unangemessen halte. Natürlich muss in den Artikel im Wesentlichen das was in der Sekundärliteratur als wichtig angesehen wird und die dort wiederholt auftretenden Sonderfälle bzw. üblichen Klassifizierung. Wie und wo man diese jedoch genau darstellt und ob das expliziten eines weiteren (offensichtlich richtigen) "Sonderfall" beinhaltet ist jedoch editorielles Ermessen. Die POV/TF-Regelung spielt erst dann einer Rolle, wenn man wichtige Standardinhalte zugunsten persönlicher Interessen (oder "Trivialitäten") weglässt oder verdrängt. Wenn man "Sonderfälle" erfindet deren Sonderfalleigesnchaft für andere nicht nachvollziehbar oder gar falsch ist. Dann ist der Rahmen des zulässigen editoriellen Ermessens überschritten, dann greifen die RL und klassifizieren solche Inhalte als unzulässig, aber eben erst dann und all das ist hier nicht der Fall. Das heißt jetzt natürlich nicht, dass man sich Dontworry's Ansicht anschließen muss, man kann sie durchaus als überflüssig/unnötig ansehen, aber da muss man sich eben wie in anderen Fällen auch im Rahmen des editoriellen Ermessens einigen. Es ist jedoch kein Fall der über die RL bzw. einen vermeintlichen RL-Verstoß entschieden werden kann.--Kmhkmh (Diskussion) 00:13, 5. Feb. 2013 (CET)

Hab' den 1 Satz jetzt hinzugefügt. Um mehr geht's ja wohl auch nicht. --arilou (Diskussion) 10:07, 5. Feb. 2013 (CET)

nett. Allerdings hatte ich den Eindruck, hier war mehr geplant (siehe Abb. + Exkurs zu Ägyptern). Für das belanglose Sätzchen hätte ich mir keine Diskussionsmühe gemacht. --Fritzbruno (Diskussion) 10:13, 5. Feb. 2013 (CET)

warum diese hektik beim archivieren? (ich war leider 2 tage durch missliche admins am diskutieren gehindert.;-)) "geplant" war diesbezüglich von meiner seite eigentlich edit-mässig nichts (bin ja schliesslich nur mathematischer laie!), aber anregungen + fragen dazu hätte ich schon noch: weil ich mir die verlinkungs-artikel - für die dieser sonderfall ebenfalls von bedeutung/relevanz ist - angesehen + dabei festgestellt habe, dass sich dort auch nur eine allenfalls beiläufige [11] + [12] usw., und keine spezielle erwähnung (zu besonderheiten) befindet. so gibt es z.b. keinerlei erwähnung der "ähnlichkeit" bei teilung eines derartigen dreiecks durch die symmetrie-achse sowie weiterer spezifikation, was "kreise am dreieck" [13] oder "ausgezeichnete punkte im dreieck" [14] betrifft. ich denke mir, fachleuten wird sicherlich noch mehr dazu einfallen? Dontworry (Diskussion) 15:19, 5. Feb. 2013 (CET)

Ebenso kann ein gleichschenkliges Dreieck zwischen seinen Schenkeln rechtwinklig sein; es ist dann gleichzeitig ein rechtwinkliges Dreieck.

Das ist ein Scherz, ja? Das geht ja schon in Richtung Tautologie! Also es gibt die Aussage: "Es gibt den Sonderfall von gleichschenklig rechtwinklig." Dann würde sich sich ein Leser natürlich fragen, warum das extra erwähnt werden muss, deshalb sollte dann wenigsten ein Satz folgen, mit den tollen Eigenschaften, die die Erwähnung rechtfertigen. Meiner Meinung gibts da aber nicht wirkich etwas. Vorschlag: An Stelle der Tautologie könnte man den prominentesten Vertreter erwähnen, etwa der Art: "Ein Geodreieck ist gleichzeitig gleichschenklig und rechtwinklig etc." Das ist nämlich noch nicht erwähnt im Artikel. --χario 18:10, 5. Feb. 2013 (CET)

Du betreibst hier Totschlag-Argumentation. Mit derselben Argumentationsweise könnte man auch "Gleichschenklig" und "Gleichseitig" aus dem Artikel werfen, weil ein Mathematiker das ja als "triviale Sonderfälle des allgemeinen Dreiecks" betrachten könnte.

Ist es ein Sonderfall? Ja. Dann gehört's auch erwähnt. Ist es ein herausragender Sonderfall, der bestimmte besonders einfache Gleichungen nach sich zieht? Nein. Dann reicht 1 Satz. (Wer's besser weis, ergänze entsprechende Formeln im Artikel.)

"beinahe eine Tautologie" ~ Ich denke beim Artikel-Schreiben immer an meinen 10-jährigen Neffen. Wenn der in der 5.Klasse Dreiecke in Mathe bekommt, schaut er vielleicht hier nach. Und obigen 1 Satz wird er bestimmt verstehen.

Und ich nehme mal an, dass Wikimedias Festplatten groß genug sind, dass der 1 Satz noch Platz hat.

--arilou (Diskussion) 23:11, 5. Feb. 2013 (CET)

nein, nein, keine Totschlag-Argumentation. Rechtwinklige, gleichschenklige und gleichseitige Dreiecke bilden die Grundlage vieler Berechnungen an geometrischen Figuren. Aber das gleichschenklig rechtwinklige kenne ich aus dem Zusammenhang nicht (außer als Geodreieck - danke!). Ich warte darauf, das Dontworry (oder sonst ein Befürworter der Erwähnung) endlich die besondere Hervorhebung belegt. Das ist nicht passiert, deshalb steht nur dieser Satz im Artikel. Der besagt nicht viel mehr, als dass es dieses Dreieck gibt. Wenn das das Resultat dieser Diskussion ist - meinetwegen. Um des Neffens und des geringen Festplattenspeicherverbrauchs Willen mag der Satz stehen bleiben. Er sagt nur nichts! --Fritzbruno (Diskussion) 00:04, 6. Feb. 2013 (CET)

@Arilou: Du benutzt Scheinargumente. Wir füllen Artikel mit sinnvollen Informationen und nicht mit irgendwas, nur damit sie länger werden. Die einzelnen Sonderfälle sind belegt und unbezweifelt, nur die diese spezielle Kombination nicht. Was ist denn daran erwähnenswerter als am gleichschenkligen Dreieck mit einem einschließenden Winkel von 80°? Die Sonderstellung muss belegt sein. Hier kam noch nichts überzeugendes in dieser Hinsicht. --χario 18:54, 6. Feb. 2013 (CET)

das "rechtwinklige, gleichschenklige dreieck", ist der einzige fall - in der unendlichen reihe von gleichschenkligen dreiecken - der bei halbierung in der mittel-/symmetrieachse, 2 "ähnliche" (bezogen auf das "ausgangsdreieck" und gleichzeitig untereinander kongruente) dreiecke ergibt. dazu bedarf es keinerlei weiterer belege, sondern einzig + allein der grundschulkenntnisse der 4-6 klasse, wenn ich das noch richtig erinnere! Dontworry (Diskussion) 07:02, 7. Feb. 2013 (CET)

Bitte belege einfach mal mit einem netten Buchzitat o.ä., dass nicht nur du, deine Grundschullehrerin oder irgendwelche leider schon verstorbenen Ägypter das irgendwie relevant fanden. Wir drehen uns hier im Kreis mit deiner Aussage "ist wichtig!", meimer Frage "wieso?" und deiner Antwort "ist wichtig!". --Fritzbruno (Diskussion) 07:52, 7. Feb. 2013 (CET)

das ist aber jetzt nichtmehr nachvollziehbar! verweigerst du jetzt auch noch das logische (nach-)denken?? jetz wirds aber schon karnevalistisch (ist ja angemessen an "weiberfassnacht"!) ;-). ich hab' keine grundschulbücher mehr im besitz, nur noch grundschulwissen im kopf! ich schlage vor, wenn es dir nicht gelingt, meine obige aussage: "...das "rechtwinklige, gleichschenklige dreieck", ist der einzige fall..." durch quellen explizit zu widerlegen, ist es richtig + bleibt als "herausstellungsmerkmal" bestehen! Dontworry (Diskussion) 08:10, 7. Feb. 2013 (CET)

ps. ich erweitere mein "angebot" dahingehend: wenn es dir gelingt rechnerisch und/oder zeichnerisch den gegenbeweis anzutreten, verzichte ich auf weitere "quellen" - ist das ein wort? Dontworry (Diskussion) 08:24, 7. Feb. 2013 (CET)

Bitte belege einfach mal mit einem netten Buchzitat o.ä., dass das irgendwie relevant ist. Wir drehen uns hier im Kreis mit deiner Aussage "ist wichtig!", meimer Frage "wieso?" und deiner Antwort "ist wichtig!". Die letzten beiden Diskussionsabsätze solltest du vielleicht einfach wieder löschen, weil sie ziemlich albern wirken. --Fritzbruno (Diskussion) 08:50, 7. Feb. 2013 (CET)

Das rechtwinklige Gleichschenklige ist auch das einzige Gleichschenklige, auf das die sehr einfachen Formeln für rechtwinklige anwendbar sind.

Besonders wichtig finde ich diesen Sonderfall nicht, aber in einem Artikel von >2500 Worten können sich ruhig 17 mit diesem Fall beschäftigen, diese 0,7% sind imo wenig genug bzgl. der relativ geringen Bedeutung.

--arilou (Diskussion) 08:56, 7. Feb. 2013 (CET)

PS: bezüglich der Wichtigkeit haben wir also bisher unstrittig:

• einziges Gleichschenkliges, dass bei Halbierung in der Mittel-/Symmetrieachse zu 2 untereinander kongruenten dreiecken wird;
• die beiden sind dabei selbstähnlich zum Ausgangsdreieck;
• die Rechenregeln zum Sonderfall "rechtwinklig" können verwendet werden.

@arilou: dein punkt "...einziges Gleichschenkliges, das bei Halbierung..." gilt bei allen gleichschenkligen, die ergebnisse sind immer gegenseitig kongruent (+ rechtwinklig, weil dabei die symmetrieachse, =höhe, =winkelhalbierende, =basis-halbierende, lotrecht auf der basis steht!) - jedoch nicht mehr achssymmetrisch wie im "sonderfall"!), alles andere ist richtig. Dontworry (Diskussion) 09:08, 7. Feb. 2013 (CET)

Zitat arilou: „Das rechtwinklige Gleichschenklige ist auch das einzige Gleichschenklige, auf das die sehr einfachen Formeln für rechtwinklige anwendbar sind.“

Für mich wäre das ein Grund, dies als Spezialfall im Artikel Gleichschenkliges Dreieck zu behandeln. Aber nicht unbedingt hier in dem Übersichtsartikel über Dreiecke, wo zwar die verschiedenen Klassifizierungen von Dreiecken dargestellt werden sollen. Für die einzelnen Typen gibt es aber eigene Artikel.

Zitat Dontworry: „das "rechtwinklige, gleichschenklige dreieck", ist der einzige fall - in der unendlichen reihe von gleichschenkligen dreiecken - der bei halbierung in der mittel-/symmetrieachse, 2 "ähnliche" (bezogen auf das "ausgangsdreieck" und gleichzeitig untereinander kongruente) dreiecke ergibt.“

Klar: Wenn man ein rechtwinkliges Dreieck entlang der Höhe teilt, erhält man zwei Teildreiecke, die zum ursprünglichen Dreieck (und untereinander) ähnlich sind. Wenn man ein gleichschenkliges Dreieck entlang der Achse teilt, bekommt man zwei rechtwinklige Dreiecke, die zueinander kongruent sind. Die Kombination von beidem ergibt deine Aussage. Aber ist sie deshalb wirklich erwähnenswert?

In jedem Schulbuch würden diese Aussagen nicht im erklärenden Text, sondern in einer Übungsaufgabe behandelt.

Allgemein gesprochen: Die rechtwinkligen und gleichschenkligen Dreiecke sind innerhalb der gleichschenkligen Dreiecke ein beachtenswerter Sonderfall. Sie sind auch innerhalb der rechtwinkligen Dreiecke ein beachtenswerter Sonderfall. Innerhalb der Dreiecke bilden sie aber einfach nur die Schnittmenge der rechtwinkligen und der gleichschenkligen Dreiecke. Dass es solche gibt und dass sie deshalb sowohl die Eigenschaften der rechtwinkligen als auch die der gleichschenkligen Dreiecke besitzen mag erwähnenswert sein. Aber muss man wirklich ausbreiten, was das bedeutet?

Was ich mir jedoch gut vorstellen könnte, ist das, was HilberTraum oben vorgeschlagen hat: Das rechtwinklige und gleichschenklige Dreieck als (wichtiges) Beispiel einzubauen.--Digamma (Diskussion) 19:26, 7. Feb. 2013 (CET)

+1 für für das Geodreieck, hatte oben ja die selbe Idee, ohne das von HilberTraum gesehen zu haben. :D --χario 00:43, 8. Feb. 2013 (CET)

Dann kann man sich doch eventuell darauf einigen die Aspekte/Eigenschaften dieses Sonderfalls in gleichschenkliges Dreieck oder rechtwinkliges Dreieck zu integrieren und hier ganz wegzulassen. Denn die dortigen Artikel sind derzeit noch recht dünn, so das Ausbreiten (in Maßen) einer einfacheren Sache nicht unbedingt schadet. Auch sollte man ruhig im Hinterkopf behalten, dass diese Artikel ja gerade auch von Leuten mit geringen oder keinem Mathematikverständnis gelesen werden und aus deren Sicht mögen viele Dinge, die den Diskutierenden hier wegen Offensichtlichkeit keiner Erwähnung wert sind, eben nicht so offensichtlich sein. Solange das Erwähnen solcher Dinge keine wichtigen Inhalte verdrängt bzw. Artikel unnötig aufbläht und/oder unübersichtlich macht, kann man sie mMn. im Zweifelsfall ruhig erwähnen. --Kmhkmh (Diskussion) 03:07, 8. Feb. 2013 (CET)

d'accord, was diesen punkt betrifft. inzwischen habe ich den deutschen artikel 'mal mit anderssprachlichen verglichen: englisch [15], spanisch [16], französisch [17] + japanisch [18] und muss gestehen, dass mir alle anderen, sowohl was das layout als auch was die thematische einteilung und den einsatz geeigneter grafiken betrifft, besser als der deutsche artikel zusagen. wir sollten deshalb den artikel unter diesem gesichtspunkt (gescheiterter versuch einer "eierlegendenwollmilchsau") nochmals grundsätzlich diskutieren. nur den absatz "Dreiecke der nichteuklidischen Geometrie" halte ich in diesem vergleich für besser, weil er in den anderssprachlichen artikeln ganz fehlt. Dontworry (Diskussion) 07:48, 8. Feb. 2013 (CET)

Also ich hab jetzt erstmal einfach den Satz umformuliert, damit Geodreiecke erwähnt werden. Ich sehe bei der sonstigen Qualtität kein dringendes Problem. --χario 03:47, 13. Feb. 2013 (CET)

Grafiken mit LaTeX und TikZ

Hallo zusammen,

ich habe heute wieder eine SVG-Alternative zu einer PNG erstellt:

• 
  Old PNG
• 
  SVG created with LaTeX

Was haltet ihr davon? Was sollte ich ändern?

Folgendes wäre - falls es erwünscht ist - kein Problem:

• Beschriftung der Eckpunkte A, B, C entfernen
• Beschriftung der Seiten entfernen
• Winkel markieren (wie in diesem Bild)
• $r_{u}$ und $r_{i}$ hinzufügen
• Den Mittelpunkt markieren (und benennen - eventuell mit $M$? Was wäre üblich?)

Ich will allerdings nicht direkt "Umkreis" oder Inkreis" in das Bild schreiben. Die Beschriftung der Seiten mit $a$ finde ich auch nicht so sinnvoll, würde ich aber machen, wenn es gewünscht ist.

Grüße, --Martin Thoma 11:00, 2. Feb. 2013 (CET)

Ich würde es bei Kreislinien belassen und die Flächen nicht einfärben. Unter "Umkreis" und "Inkreis" versteht man m.E. immer die Kreislinien und nicht die Flächen. --Digamma (Diskussion) 13:19, 2. Feb. 2013 (CET)

Man beachte auch, dass so ein Kreis vollständing gefüllt ist der andere aber nicht, was in gewisser Weise inkonsinstent ist und vielleicht jemande irritiert.--Kmhkmh (Diskussion) 13:33, 2. Feb. 2013 (CET)

Ok,hab die Füllung entfernt. --Martin Thoma 13:40, 2. Feb. 2013 (CET)

Gibt es weitere Änderungswünsche? Soll ich irgendwas von den oben genannten Punkten umsetzen? --Martin Thoma 16:13, 4. Feb. 2013 (CET)

Da es keine weiteren Wünsche gibt, habe ich das alte Bild mal ersetzt. Das neue Bild ist auch mit nur 250px gut zu erkennen und passt besser ins Wiki-Layout. --Martin Thoma 09:46, 7. Feb. 2013 (CET)

Damit ich nicht dauern neue Abschnitte erstelle, habe ich diesen mal in "Grafiken mit LaTeX und TikZ" umbenannt.

Ich habe wieder eine Grafik erneuert:

• 
  Old SVG
• 
  SVG created with LaTeX

Wie immer bin ich an Verbesserungsvorschlägen interessiert. --Martin Thoma 19:54, 13. Feb. 2013 (CET)

Gefällt mir. --Digamma (Diskussion) 20:00, 13. Feb. 2013 (CET)

Schön :-) Ich hab meine neue Grafik in den Artikel eingebaut. --Martin Thoma 12:17, 16. Feb. 2013 (CET)

ungereimtheiten im artikel

• 1. die eingangs-skizze [19] ist deshalb nicht korrekt bzw. unpassend, weil sie parallel zu den dreiecksseiten jeweils zusätzliche - hier überflüssige + nur bei technischen zeichnungen übliche - sog. "bemaßungslinien" hat, die den betrachter nur verwirren können + nichts zum eigentlichen dreieck aussagen oder irgendeine sonstige sinnvolle funktion haben.
• 2. ist es ausserdem beim eingangsbild nicht notwendig oder auch sinnvoll überhaupt (am dreick) etwas zu beschriften (siehe auch: [20] oder [21]). es geht hierbei einzig um die wesentlichen merkmale: die 3 ecken [22], allenfalls eine bildunterschrift macht hier sinn.
• 3. eher verwirrend als erhellend, ist ausserdem diese grafik: [23] sowie der dazugehörige absatz: [24].
• 4. ist der deutsche artikel - im gegensatz, z.b. zum englischen [25] - amorph und wenig logisch bzw. eher "zufällig" in struktur und aufbau seiner thematischen abfolge, wie aus einem schlechten geometriebuch abgeschrieben. diese gewollt "komplizierte" [26] dreiecksgrafik (mit α=26,57° und β=63,43°) ist nur eines von mehreren schlechten beispielen! Dontworry (Diskussion) 11:23, 13. Feb. 2013 (CET)

Also, meiner Meinung nach sollten die ersten zwei Bilder vertauscht werden, dann sollten sich deine Probleme erstmal gelockert haben. Zu 3.: Wenn man eine Ahnung davon hat, ist es als Lernhilfe nützlich. So ist es aber wirklich verwirrend, man sollte es zumindest besser erläutern. Zu 4.: Das zu verbessern ist aber sehr langwierig und kann das Problem verschlechtern (Je nach Bewerter). Aber meiner Meinung nach ist der Artikel nach diesem Kriterium "akzeptabel". Derdoobi (Diskussion) 14:41, 13. Feb. 2013 (CET)

du verstehst da etwas ganz falsch: ich habe mit dem artikel keine probleme - ich benutze ihn höchstens noch als denksportübungs-hobby - sondern, mir tun die armen schüler leid, die sich davon eventuell eine hilfe zum geometrie-lehrstoff erhoffen und dann das desaster erleben müssen! ;-) und langwierig ist/wird es nur, wenn man versucht am satzbau o.ä. herumzufrickeln. da ist es schon besser den englischen artikel annähernd 1 zu 1 übersetzt zu übernehmen. Dontworry (Diskussion) 15:09, 13. Feb. 2013 (CET)

Also, wenn mein 10-jähriger Neffe die Einleitung liest (versucht zu lesen), dann klickt er WP gleich wieder weg. Was da steht mag mathematisch korrekt sein, aber als Einleitung für jemand, der kein Mathematiker ist, ist das Overkill. --arilou (Diskussion) 15:59, 13. Feb. 2013 (CET)

die Schüler (incl. der Neffe) sind, wenn sie Geometrie lernen wollen, hier einfach verkehrt. Lehrbücher stehen auf dem Schwesterprojekt Wikibooks, nicht auf der Wikipedia. Vielleicht recherchiert jemand einmal, ob dort schon ein geeignetes steht zum Verlinken in diesem Artikel. --Fritzbruno (Diskussion) 16:10, 13. Feb. 2013 (CET)

Da bin ich gegenteiliger Meinung. Eine Enzyklopädie ist für jene, die über einen Begriff nicht bescheid wissen. Bei einem recht einfachen Begriff wie "Dreieck" ist zumindest die Einleitung entsprechend sehr einfach zu halten.

Vorschlag Einleitung:

---

Ein Dreieck ist eine Fläche, die durch drei gerade Seiten begrenzt wird. Die Seiten werden meist a, b und c genannt. Die drei Eckpunkte, an denen die Kanten zusammenstoßen, werden meist A, B und C genannt. Die gleichnamigen Seiten liegen „ihren Ecken“ jeweils gegenüber. An jedem Eckpunkt gibt es einen sogenannten Innenwinkel, genannt α (alpha), β (beta) und γ (gamma) (Griechisch a, b und c). Die Innenwinkel liegen bei den gleichnamigen Eckpunkten.

Das Dreieck wird veraltet auch Triangel, lateinisch: triangulum genannt. Es ist ein Polygon und eine geometrische Figur. In der Trigonometrie, einem Teilgebiet der Mathematik, spielen Dreiecke die wesentliche Rolle. Siehe dazu insbesondere Dreiecksgeometrie.

Es handelt sich innerhalb der euklidischen Geometrie um die einfachste Figur in der Ebene, die von geraden Linien begrenzt wird. Eine Verallgemeinerung des Dreiecksbegriffes auf nichteuklidische Geometrien ist möglich.

---

--arilou (Diskussion) 16:18, 13. Feb. 2013 (CET)

Also das Dreieck als Fläche statt geometrischer Figur zu bezeichnen bzw. zu definieren halte ich für keine gute Idee, da Fläche eine Eigenschaft ist die man einem Dreieck zuordnen kann aber nicht muss. Zudem haben wir dazu ein eigenes Lemma Dreiecksfläche.

Was nun den Zweck der Enzyklopädie bzw. von WP betrifft, es ist ein Nachsclag bzw. Referenzwerk für alle, sowohl für Leute mit als auch ohne Kontextwissen. Dementsprechend sollen Artikel auch möglichst omafreundlich gestaltet sein. Der Omafreundlichkeit sind aber Grenzen gesetzt, denn zum Einen sollen WP-Artikel kein Ersatz für Lehrbücher/Lehrmaterialien sein und zum Anderen haben ein gewisser enzyklopädischer Stil und fachliche Korrektheit im Zweifelsfall Vorrang. Ein guten Anhaltspunkt erhält man, wenn man einen entsprechenden Eintrag in einem allgemeinbildenden Lexikon (z.B. Meyers, Brockhaus, etc.) nachschlägt oder auch in einem Schülerlexikon wie z.B. dem Schülerduden Mathematik. Eine größere Verständlichkeit als bei diesen kann man von einen WP-Artikel nicht erwarten. Der Schülerduden (5-10. Klasse) beginnt z.B. wie folgt: "Dreieck: eine ebene Figur, die man erhält wenn man drei Punkte A,B,C, die nicht auf einer Geraden liegen, durch Strecken miteinander verbindet."--Kmhkmh (Diskussion) 16:30, 13. Feb. 2013 (CET)

Dann denk' nochmal an den 10-Jährigen; wenn du ihm lieber erklären willst, was nun 'ne mathematische "Figur" ist, dann bitte. Eine Schachfigur kennt er bestimmt schon. --arilou (Diskussion) 16:43, 13. Feb. 2013 (CET)

Wenn seine bisherige Ausbildungen nicht schief gelaufen ist, kennt er (geometrische) Figuren sprachlich/anschaulich oft schon aus Kindergarten oder Grundschule. Und etwas formaler konkreter spätestens aus der 5-6. Klasse. Wie schon oben angesprochen ist es nicht Aufgabe von WP diesen Schulunterricht zu ersetzen, noch Artikel so abzufassen, dass sie ohnen dieses minimale Kontextwissen verständlich sein müssen. Polemischer formuliert: "(de.)WP ist kein Kinderlexikon". Kinderlexika sind eine gute Sache, aber eben ein separate Projekte. --Kmhkmh (Diskussion) 16:57, 13. Feb. 2013 (CET)

Ich habe mir gerade den Artikelanfang auf die Problematik hin durchgelesen und verstehe die Kritik danach nioch weniger. Nach der wirklich guten Maßnahme, die einfachere Abbildung an den Anfang zu setzen, sollte jedem, der dem Text nicht ganz folgen kann, doch wohl klar sein, was ein Dreieck ist, selbst irgendwelchen 10-jährigen Neffen. Allenfalls könnte in der Bildunterschrift noch eine Erklärung zu den Seitenbeschriftungen etc. sein, um den Textbezug zu verbessern ("Eckpunkte: A,B,C, Seiten: a,b,c, Innenwinkel: α,β,γ"). --Fritzbruno (Diskussion) 17:20, 13. Feb. 2013 (CET)

es ist wirklich schwer, hier eine vernünftige + fruchtbare diskussion zu führen, wenn sich jeder mit tunnelblick, fokussierend auf einzelne aspekte meiner o.a. 4 - in worten: vier - kritikpunkte stürzt + rosinenpickerei betreibt! und wenn sich plötzlich alle an den bedürfnissen des exemplarisch 10-jährigen neffen delektieren! ich hatte explizit auf den - nach meiner meinung - vorbildlich strukturierten englischen artikel zum vergleichen hingewiesen. + es ist wie es ist: das bessere ist der feind des guten. wenn also noch irgendwer wirkliches + ernsthaftes interesse an einer artikelverbesserung hat, möge er sich doch bitte auf diesen gesamtaspekt in seinen beiträgen beziehen, sonst ist das thema - zumindest für mich - gegessen (das halt ich sonst im kopf nicht aus!). Dontworry (Diskussion) 08:19, 14. Feb. 2013 (CET)

Sachliche Entgegnung hierzu: ich kann deine Punkte nicht nachvollziehen, finde den Artikel so wie er ist stringend und informativ. Beim Diskussionsstil können wir gerne uns auf mehr Sachlichkeit konzentrieren. Dann möchte ich aber auch von Beschuldigungen wie "Tunnelblick" nichts hören. --Fritzbruno (Diskussion) 18:56, 14. Feb. 2013 (CET)

mit verlaub, unter sachlich verstehe ich, dass man etwas dezidiert zur sache - hier punkt 1...4 sagt + nicht, wenn man "sachlich" nur als bezeichnung für eigenes um-den-heissen-brei-herum-reden verwendet - also wie z.b. bei der "real-lasagne" - eigenes verhalten falsch etikettiert. ich weiss jetzt immer noch nicht, was du zu dieser grafik [27] + ihrem verbleib oder nicht im artikel meinst + wie dein urteil im vergleich zum englischen artikel ist. Dontworry (Diskussion) 13:36, 15. Feb. 2013 (CET)

Da unterscheiden sich unsere Vorstellungen von Diskussionskultur mächtig: Ich würde dich nie mit Lasagne vergleichen. Zur sachlichen Diskussion zurück: meine Meinung zur Grafik und zum Vergleich mit der En-WP lassen sich aus dem Gesagten ableiten. Da ich keine Änderung empfehle sollte klar sein, dass ich die Grafik behalten möchte (ich halte sie für excellent) und eine Anpassung an den En-WP-Artikel nicht befürworte. --Fritzbruno (Diskussion) 15:45, 15. Feb. 2013 (CET)

---

Also zur Einleitung: Ich finde unsere Reihenfolge "Seiten -> Winkel -> Ecken" etwas ungewöhnlich und auch, dass das Wort "drei" erst am Ende des vierten Satzes auftaucht. Obiger Vorschlag von arilou ist aber imho nicht besser, insbesondere die Aussagen zu den Bezeichnungen ("meist A, B und C ... etc") tragen nicht wirklich zum Verständnis bei und brauchen imho nicht in die Einleitung. In dem Sinne sind die ersten beiden Sätze in en:triangle tatsächlich klarer als unserer Ansatz. --χario 16:41, 15. Feb. 2013 (CET)

@fritzbruno: da unterscheiden wir uns wiederum, und zwar in der diskussionswahrhaftigkeit bzw. in der genauigkeit bei der wortwahl + deren sinngehalt. ich habe dich garnicht mit lasagne verglichen, sondern (zitat: "...,wenn man "sachlich" nur als bezeichnung für... eigenes verhalten falsch etikettiert...") dein verhalten mit dem verhalten der lebensmittelindustrie - + hierbei dem lieferanten von real - + ihrer "falsch-etikettierung" verglichen, ein ganz wichtiger unterschied! + wenn diese grafik von dir als "excellent" geadelt wird, obwohl ich oben deren mängel präzise benannt habe, dann ist ja scheinbar (nach deiner meinung) alles in butter mit dem artikel? an welchen punkten du das genau festmachst, bleibt für den leser deiner worte allerdings nebulös - er soll sich selber ableiten, was + wie du denkst? also haben wie anscheinend das problem, dass du mit deiner einstellung + deinem editierverhalten (revertieren) eine sachlich-fachliche diskussion +/oder artikelverbesserung blockierst? Dontworry (Diskussion) 10:25, 16. Feb. 2013 (CET)

Nicht alles was du persönlich für einen Mangel hältst ist notwendigerweise auch einer und Verweis auf en.wp oder es.wp beweist so gut wie nichts. Die Zeichnung um die es geht ist in der Tat recht gut und gehört in den Artikel, allerdings ist sie nicht unbedingt die beste Wahl als einführendes Bild, da sie weiterführende Aspekte illustriert. Dementsprechend hat ja auch keiner etwas gegen die Verschiebung an eine andere Stelle im Artikel eingewandt.--Kmhkmh (Diskussion) 14:02, 16. Feb. 2013 (CET)

Tja, da unterscheiden wir uns. Ich empfinde deine Beiträge sehr beleidigend und du verstehst meine Beiträge erst gar nicht. Daher werde ich diesen sinnlosen Dialog hier nicht weiter ausufern lassen sondern warte auf konstruktivere Beiträge anderer. --Fritzbruno (Diskussion) 11:03, 16. Feb. 2013 (CET)

Einletung

Um noch einmal die Punkte aufzugreifen die bzgl. der Einleitung angesprochen wurden. ES gibt da einen Gewissren Konflikt, da die Einleitung im Zweifelsfall alle ASpekte des Lemmas ansprechen sollte und zugleich omafreundlich sein soll und es mit der Omafreundlichkeit der nicht-euklidischen Geometrie nicht allzu weit her ist.

Ich würde daher vorschlagen die Einelitung in zwei Absätze aufzuteilen. Der erste befasst sich nur mit den elementargeometrischen Aspekten bzw. Teilen des Lemmas und kann in etwa so gestaltet werden wie auf en.wp oder auch im Schülerduden (eben ohne unnötiges oder schwer verständliches Fachvokabular). Der zweite Absatz kann dann auf die nicht elementargeometrsichen Aspekte (ekludische/nichteiklidische Geometrie, sphärische Dreiecke, etc.) eingehen. Das würde aus meiner Sicht sowohl der Omafreundlichlichkeit als auch der angemessen Zusammenfassung gerecht werden, denn das Hauptproblem der aktuellen scheint mit die Vermischung dieser Aspekte zu sein, was dazu führt dass die gesamte Einleitung für Omas schwer verständlich ist. Stattdessen sollte man es eben in einen leicht verständlichen und einen schwer verständlichen Absatz aufteilen.--Kmhkmh (Diskussion) 14:20, 16. Feb. 2013 (CET)

• 1. anscheinend bin ich hier (gezwungenermassen) der "einäugige unter blinden"? wie ich bereits oben angeführt habe hat die skizze [28] definitiv 2 fehler: die eckenbezeichnung beginnt (unten links) mit "B" (statt korrekt: "A") + die parallelen linien (a, b, c = ausserhalb der eigentlichen dreiecksseiten) sind fern jeder trigonometrischen skizzenregeln. hinzu kommt, dass nur einer der 3 ankreise durch einen teilbogen angedeutet wird und sein einschluss/seine tangenten durch die seitenverlängerung nicht ausreichend deutlich gezeigt wird! was daran "excellent" oder auch nur befriedigend/brauchbar sein soll, erschliesst sich mir in keiner weise? besser brauchbare skizzen sind hier: [29] + [30] oder [31] zu finden.
• 2. du kannst es ja versuchen, es hört sich zumindest gut an. ob es dann besser ist/wird, lässt sich erst nach den änderungen beurteilen. Dontworry (Diskussion) 16:55, 16. Feb. 2013 (CET)

Du kannst dich ja gerne zum "Einäugigen unter Blinden" stilisieren, dem Sachargument jedoch hilft das nicht. Die vermeintlichen Fehler die bemängelst sind nun einmal keine, d.h. die Zeichnug ist mathematisch korrekt und verstößt auch nicht wirklich gegen irgendwelche relevanten Konventionen, dass sie nicht deinen persönlichen Vorstellung entsprechen ("A muss unten rechts sein ", "trigonometrische Skizzenregeln" (was immer das genau auch sein soll)) mag ja sein, ist das ist aber kein Problem des Artikels. Natürlich kann man die Zeichnung durch eine bessere Zeichnung ersetzen (statt sie zu löschen), dagegen hat niemand einen Einwand erhoben. Ob nun die von dir vorgeschlagenen Zeichnungen besser sind hängt, von genauen Kontext bzw. Intention ihrer Verwendung ab, je nachdem sind sie besser oder auch nicht. Letztlich hängt es von der genauen Verwendung im Text und dem editoriellen Ermessen ab. Einen zwingenden Grund, warum die Zeichnung nicht im Artikel stehen kann oder stört hast du jedenfalls nicht vorgelegt.--Kmhkmh (Diskussion) 19:05, 16. Feb. 2013 (CET)

Punkte verschieden?

Hier fehlt mir in der Definition des Dreiecks, ob die drei Punkte, die es bilden, verschieden voneienander sein müssen (oder sind mit mehreren Punkten automatisch werschiedene Punkte per definitionem gemeint?). (nicht signierter Beitrag von 79.245.186.24 (Diskussion) 22:07, 5. Jan. 2015‎ (CET))

Der erste Satz der Definition lautet: Ein Dreieck wird durch drei Punkte definiert, die nicht auf einer Geraden liegen. Das impliziert, dass die drei Punkte verschieden sind. Grüße, --Quartl (Diskussion) 22:13, 5. Jan. 2015 (CET)

Danke für die schnelle Antwort. (nicht signierter Beitrag von 79.245.186.24 (Diskussion) 11:34, 6. Jan. 2015 (CET))

Bild Right triangle abchpq.svg

Hallo zusammen,

ich habe gerade ein neues Bild gemacht:

• 
  Alt, aktuell im Artikel
• 
  Neu

und würde das gerne ersetzen, weil ich mein neues Bild schöner finde. Gibt es Einwände oder Verbesserungsvorschläge? (z.B. würde ich die Höhe eigentlich gerne $h_{c}$ nennen...).

Viele Grüße, --Martin Thoma 07:39, 10. Nov. 2015 (CET)

Vielleicht etwas Farbe ? Die Senkrecht-Symbole etwas größer ? $h_{c}$ würde ich nicht benutzen. Man schreibt ja auch nicht $p_{c},q_{c}$. Die Formeln würden durch die Indizes nur unübersichtlicher. --Ag2gaeh (Diskussion) 09:37, 10. Nov. 2015 (CET)

Also ich stehe solchen Ersetzungen eher skeptisch gegenüber. Man sollte Bildersetzungen im Zweifelsf all auf Fälle beschränken, wo entweder eine klare Verbesserungen vorliegen bzw. das Format WP-Empfehlungen angepasst wird, wie z.B. bei Zeichnungen ein png/jpg durch eine gleichwertige svg-Variante ersetzen.

Wenn man jedoch im Wesentlichen gleichwertige Bilder durcheinander ersetzt, so führt das am Ende zu Streitereien oder Editwars zwischen Leuten, die jeweils "ihr" Bild im Artikel sehen wollen. Vor allem aber werden Resourcen (Arbeitszeit und Nerven) verschwendet ohne, dass ihnen eine nennenswerte Qualitätsverbesserung gegenübersteht. Sinnvoller wäre es da, sich auf Fälle zu konzentrieren, wo Verbesserungen viel dringlicher und damit meinst auch unumstriiten sind. Also Artikel, wo Illustrationen/Zeichnungen noch fehlen, bei denen die in Illustrationen/Zeichnungen verwendeten Bezeichnungen nicht mit denen im Artikeltext übereinstimmen, mit Illustrationen/Zeichnungen in denen wichtige Details oder Aspekte fehlen, mit Illustrationen/Zeichnungen im "falschen" Format, etc. .--Kmhkmh (Diskussion) 11:51, 10. Nov. 2015 (CET)

P.S.: Während ich die Bilder im Moment als weitgehend gleichwertig ansehe und sich ein Austausch mMn. aus den oben genannten Gründen nicht lohnt, will ich noch darauf hinweisen, dass man die Bezeichnung $h_{c}$ hier sogar als Verschlechterung ansehen könnte. Zwar ist die Bezeichnung an sich genauer, aber da im gegebenen Kontext besteht keine Verwechslungsgefahr besteht, wirkt der Index unnötig kompliziert. Zudem stimmt er nicht mit den im Artikeltext verwendeten Bezeichnung überein.--Kmhkmh (Diskussion) 12:01, 10. Nov. 2015 (CET)

Mein Empfinden (Geschmack) als kleines Beispiel dafür wie unterschiedlich die "Geschmäcker", über die man bekanntlich nicht streiten soll (d. h. meine Hinweise könnten einige Leser ganz anders sehen...), sind:

- die Größe der Buchstaben ist zu dominierend

- eine volle Höhenlinie drückt die Unterteilung in zwei rechtwinklige Dreiecke eher besser aus als eine strichlierte. Siehe Beschreibung: "Die Höhe h = h_c eines rechtwinkligen Dreiecks teilt die Hypotenuse in zwei Teile p und q, sodass die beiden Teildreiecke mit den Seiten p, a, h und q, h, b wiederum rechtwinklig sind."

- das Symbol für den rechten Winkel zwischen a und b ist zu klein

- die Angabe eines rechten Winkels an der Höhenlinie ist nicht erforderlich, sie ist immer senkrecht zur Bezugsseite. Hierfür gilt auch der Hinweis zur Beschreibung.

@ Martin Thoma Ein positives Zeichen setzt dein Vorschlag schon: Du hast ihn vorgestellt und nicht einfach eingearbeitet! Viele Grüße --Petrus3743 (Diskussion) 14:45, 10. Nov. 2015 (CET)

@Kmhkmh: Ich versuche momentan viele Bilder im Bereich Dreiecksgeometrie zu verbessern (vgl. Category:Images_by_Martin_Thoma/Mathematics/Triangles). Bei den Artikeln scheinen die meisten Bilder schon ziemlich gut zu sein. Wenn mir jemand eine Skizze macht (z.B. von Hand und auf imgur.com hochladen), kann ich auch gerne neue Bilder erstellen. Dafür habe ich Benutzer Diskussion:MartinThoma/Visualisierungen. Das Angebot wurde aber noch nicht wirklich genutzt. Deshalb gehe ich halt die Bilder, die ich so finde (vgl. Benutzer:MartinThoma/Visualisierungen) durch.

Die Gefahr eines Edit-Wars sehe ich im konkreten Fall auch nicht, da Benutzer:Gunther seit 2006 nicht mehr aktiv ist.

@Ag2gaeh: Wo willst du Farbe? Soll ich die zwei Teildreiecke sehr dezent rötlich bzw. bläulich einfärben?

@Petrus3743: Ich habe deine Verbesserungsvorschläge umgesetzt. Nur die Markierung für den rechten Winkel der Höhenline habe ich gelassen. Die schadet ja nicht und ich finde es macht die Sache klarer. --Martin Thoma 16:07, 10. Nov. 2015 (CET)

@MartinThoma: Dagegen Gunthers zum Teil sehr altes und oft auch noch recht pixelige Zeichnungen die oft als jpg/png hochgeladen wurden spricht nichts. Aber das ist hier eben nicht der Fall, hier geht es um ein svg, das mit seinen Bezeichnungen genau zum Text passt und zu dem deine vorgeschlagene Alternative keine nennenswerte Verbesserung darstellt, sondern allenfalls eine rein geschmacksbasierte, wenn dickere Linien und eine größeren Font bevorzugt. Richtig ist zwar, das es mit Gunther nicht (mehr) zum Konflikt kommen wird, aber der generelle Ansatz alle Dreieckszeichnungen zu überarbeiten bzw. stylistisch einheitlich zu gestalten ist, prädestiniert früher oder später Ärger zu verursachen. Gunther ist nicht der einzige der Dreieckszeichnungen auf Commons beiträgt noch der einzige Autor im Mathematikbereich dessen stylistische Vorstellungen sich von deinen unterscheiden mögen. Was würdest du sagen, wenn in einem Jahr der nächste kommt, der eine etwas andere einhetliche Gestaltung von Dreiecken wünscht und dann deine and andere Graphiken systematisch ersetzt, durch Graphiken die sich nur marginal in Linienstil, Font oder Schattierung unterscheiden? Was ist mit Autoren denen der neue Stil in "ihren" Artikeln nicht passt? All das birgt Konfliktpotenzial und WP hat in der Vergangenheit schon viele resourcenfressende oft erbitterte Streitereien um Format und Stilfragen gehabt. Deswegen ist WP mMn. mehr gedient, wenn man von solchen Vereinheitlichungsversuchen ablässt und sich auf die oben schon genannten Fälle beschränkt, wo Verbesserungen dringender sind und auch von (fast) allen Kollegen als Verbesserung empfunden werden.--Kmhkmh (Diskussion) 16:33, 10. Nov. 2015 (CET)

Ich will auf deine Fragen mal direkt antworten

Was würdest du sagen, wenn in einem Jahr der nächste kommt, der eine etwas andere einhetliche Gestaltung von Dreiecken wünscht und dann deine and andere Graphiken systematisch ersetzt, durch Graphiken die sich nur marginal in Linienstil, Font oder Schattierung unterscheiden?

Wenn das vorher abgesprochen wird (wie ich es fast immer mache), würde ich das vermutlich begrüßen :-)

Was ist mit Autoren denen der neue Stil in "ihren" Artikeln nicht passt?

Wie du schon angedeutet hast, gehören Artikel niemanden. Wenn es Uneinigkeiten darüber gibt was besser ist, wird darüber diskutiert. Wenn es keinen Konsens / keine Mehrheit für eine Sache gibt, würde ich immer dazu tendieren es zu lassen wie es ist.

Ich finde es steigert die Qualität ziemlich, wenn unwesentliche Dinge einheitlich sind. Dann kann man sich besser aufs wesentliche konzentrieren. Außerdem sieht es professioneller aus. --Martin Thoma 17:02, 10. Nov. 2015 (CET)

Ich sehe in der neuen Zeichnung auch keine großartige Verbesserung und halte einen Austausch für nicht erforderlich. Aber vielleicht bin ich etwas voreingenommen, da ich die Zeichnung von Gunther selber erst im Oktober verändert habe, da mir die Darstellung des rechten Winkels in Punkt $C$ fehlte. Für mich als Ingenieur ist die zeichnerische Darstellung immer noch eine wichtige Ausdrucksform. Und hier fehlen bei WP IMHO noch sehr viele Zeichnungen. Vielleicht sollte Martin Thoma seine Arbeit darauf konzentrieren. -- Petflo2000 17:07, 10. Nov. 2015 (CET)

Mir gefällt das alte Bild besser, auch weil ich die TeX-Fonts schöner finde. --Digamma (Diskussion) 21:14, 10. Nov. 2015 (CET)

Ok, dann scheint eine Mehrheit dafür zu sein, dass man das alte Bild behält. Für mich wäre die Sache damit erledigt. Aber vielleicht habt ihr ja direkt Vorschläge, was ich als Bild machen sollte? (@Petflo2000: Wenn du was konkretes hast, wo du mir eine kleine Skizze machen kannst, dann wie gesagt gerne auf Benutzer Diskussion:MartinThoma/Visualisierungen :-) ) --Martin Thoma 07:49, 11. Nov. 2015 (CET)

Das allgemeine (beliebige) Dreieck

Was spricht eigentlich dagegen das im Artikel eingearbeitet Bild durch folgendes zu ersetzen?

Dreieck mit seinen Ecken, Seiten und Winkeln sowie Umkreis, Inkreis und Teil eines Ankreises in der üblichen Form beschriftet

Begründung für das neue Bild das m. E. tatsächlich "in der üblichen Form beschriftet" ist:

• Beginn der Eckenbezeichnung links unten
• Beschriftung der Dreieckseiten ohne Darstellung zusätzlicher Strecken
• längste Dreieckseite ist c

Gruß Petrus3743 (Diskussion) 16:18, 25. Mai 2016 (CEST)

Aus meiner Sicht nichts. Allerdings gehört es m.E. nicht zu den Konventionen, dass c die längste Seite ist. --Digamma (Diskussion) 17:10, 25. Mai 2016 (CEST)

Pardon Digamma, du hast selbstverständlich recht, nur im rechtwinkligen Dreieck es es erforderlich die längste Seite (sprich Hypotenuse) mit c zu bezeichnen. Petrus3743 (Diskussion) 20:34, 25. Mai 2016 (CEST)

Bild im Artikel ausgetauscht. erledigtErledigt Petrus3743 (Diskussion) 00:12, 31. Mai 2016 (CEST)

Höhenberechnung

Höhenberechnung über einer Seite c

Statt

$h_{c}={\sqrt {2(a^{2}b^{2}+b^{2}c^{2}+c^{2}a^{2})-(a^{4}+b^{4}+c^{4})}}/(2c)$ ginge die Höhenberechnung über einer Seite c auch etwas kürzer

$h={\sqrt {b^{2}-((c^{2}-a^{2}+b^{2})/2c)^{2}}}$

wegen

(1) $h^{2}=b^{2}-p^{2}$

$h^{2}=a^{2}-q^{2}$

(2) $a^{2}-q^{2}=b^{2}-p^{2}$

Es gilt aber

$c=p+q$

$q=c-p$

$q^{2}=c^{2}-2pc+p^{2}$

Also mit (2)

$a^{2}-c^{2}+2pc-p^{2}=b^{2}-p^{2}$

$a^{2}-c^{2}+2pc=b^{2}$

$p=(c^{2}-a^{2}+b^{2})/2c$

und nun mit (1)

$h^{2}=b^{2}-((c^{2}-a^{2}+b^{2})/2c)^{2}$

$h={\sqrt {b^{2}-((c^{2}-a^{2}+b^{2})/2c)^{2}}}$

(nicht signierter Beitrag von Mtade (Diskussion | Beiträge) 12:18, 17. Sep. 2018 (CEST))

---

Höhen aus den Seitenlängen

Höhe h_c

(1) $h_{c}^{2}=b^{2}-p_{c}^{2}$

$h_{c}^{2}=a^{2}-q_{c}^{2},$  daraus folgt

(2) $b^{2}-p_{c}^{2}=a^{2}-q_{c}^{2},$  für $q_{c}^{2}$ gilt auch

$q_{c}=c-p_{c}\;|^{2}$

$q_{c}^{2}=c^{2}-2p_{c}\cdot c+p_{c}^{2},$  eingesetzt in (2)

$a^{2}-c^{2}+2p_{c}\cdot c-p_{c}^{2}=b^{2}-p_{c}^{2}$

$a^{2}-c^{2}+2p_{c}\cdot c=b^{2},$  daraus $p_{c}$

$p_{c}=\left(c^{2}-a^{2}+b^{2}\right)/2c,$  eingesetzt in (1)

$h_{c}^{2}=b^{2}-\left(\left(c^{2}-a^{2}+b^{2}\right)/2c\right)^{2},$ folgt

$h_{c}={\sqrt {b^{2}-\left(\left(c^{2}-a^{2}+b^{2}\right)/2c\right)^{2}}}.$

Höhe h_a

(1) $h_{a}^{2}=b^{2}-p_{a}^{2}$

$h_{a}^{2}=c^{2}-q_{a}^{2},$  daraus folgt

(2) $b^{2}-p_{a}^{2}=c^{2}-q_{a}^{2},$  für $q_{a}^{2}$ gilt auch

$q_{a}=a-p_{a}\;|^{2}$

$q_{a}^{2}=a^{2}-2p_{a}\cdot a+p_{a}^{2},$  eingesetzt in (2)

$c^{2}-a^{2}+2p_{a}\cdot a-p_{a}^{2}=b^{2}-p_{a}^{2}$

$c^{2}-a^{2}+2p_{a}\cdot a=b^{2},$  daraus $p_{a}$

$p_{a}=\left(b^{2}-c^{2}+a^{2}\right)/2a,$  eingesetzt in (1)

$h_{a}^{2}=b^{2}-\left(\left(b^{2}-c^{2}+a^{2}\right)/2a\right)^{2},$ folgt

$h_{a}={\sqrt {b^{2}-\left(\left(b^{2}-c^{2}+a^{2}\right)/2a\right)^{2}}}.$

Höhe h_b

(1) $h_{b}^{2}=a^{2}-p_{b}^{2}$

$h_{b}^{2}=c^{2}-q_{b}^{2},$  daraus folgt

(2) $a^{2}-p_{b}^{2}=c^{2}-q_{b}^{2},$  für $q_{b}^{2}$ gilt auch

$q_{b}=b-p_{b}\;|^{2}$

$q_{b}^{2}=b^{2}-2p_{b}\cdot b+p_{b}^{2},$  eingesetzt in (2)

$c^{2}-b^{2}+2p_{b}\cdot b-p_{b}^{2}=a^{2}-p_{b}^{2}$

$c^{2}-b^{2}+2p_{b}\cdot b=a^{2},$  daraus $p_{b}$

$p_{b}=\left(a^{2}-c^{2}+b^{2}\right)/2b,$  eingesetzt in (1)

$h_{b}^{2}=a^{2}-\left(\left(a^{2}-c^{2}+b^{2}\right)/2b\right)^{2},$ folgt

$h_{b}={\sqrt {a^{2}-\left(\left(a^{2}-c^{2}+b^{2}\right)/2b\right)^{2}}}.$

• Eine Ausarbeitung nach obigem Vorschlag von Mtade.
• Was spricht dagegen, die kurzen und nachvollziehbaren Formeln in den Artikel aufzunehmen sowie die Tabellen–Einträge in Höhen aus den Seitenlängen zu ersetzen? Petrus3743 (Diskussion) 18:00, 20. Sep. 2018 (CEST)

Auf jeden Fall brauchen wir für drei analoge Fälle keine drei Herleitungen. --Digamma (Diskussion) 18:04, 20. Sep. 2018 (CEST)

@Digamma, richtig, das habe ich mir beim Entwurf auch schon gedacht, aber wie soll man es am besten für $h_{a}$ und $h_{b}$ abkürzen, dass es es auch noch gut verstanden wird (Form)? Nur das Ergebnis mit folgendem Bild ...? --Petrus3743 (Diskussion) 18:15, 20. Sep. 2018 (CEST)

Es ist doch klar, dass man aus der Formel für die eine Höhe die Formeln für die andern Höhen erhält, indem man die Größen passend ersetzt. Da ist überhaupt keine Extra-Arbeit nötig. --Digamma (Diskussion) 18:30, 20. Sep. 2018 (CEST)

Höhen aus den Seitenlängen

Höhe h_c

(1) $h_{c}^{2}=b^{2}-p_{c}^{2}$

$h_{c}^{2}=a^{2}-q_{c}^{2},$  daraus folgt

(2) $b^{2}-p_{c}^{2}=a^{2}-q_{c}^{2},$  für $q_{c}^{2}$ gilt auch

$q_{c}=c-p_{c}\;|^{2}$

$q_{c}^{2}=c^{2}-2p_{c}\cdot c+p_{c}^{2},$  eingesetzt in (2)

$a^{2}-c^{2}+2p_{c}\cdot c-p_{c}^{2}=b^{2}-p_{c}^{2}$

$a^{2}-c^{2}+2p_{c}\cdot c=b^{2},$  daraus $p_{c}$

$p_{c}=\left(c^{2}-a^{2}+b^{2}\right)/2c,$  eingesetzt in (1)

$h_{c}^{2}=b^{2}-\left(\left(c^{2}-a^{2}+b^{2}\right)/2c\right)^{2},$ folgt

$h_{c}={\sqrt {b^{2}-\left(\left(c^{2}-a^{2}+b^{2}\right)/2c\right)^{2}}}.$

Höhen h_a und h_b

Mithilfe der Formel zur Höhe $h_{c},$ erhält man durch passendes Einsetzen der Größen die Höhen $h_{a}$ bzw. $h_{b}$

$h_{a}={\sqrt {b^{2}-\left(\left(b^{2}-c^{2}+a^{2}\right)/2a\right)^{2}}}$

$h_{b}={\sqrt {a^{2}-\left(\left(a^{2}-c^{2}+b^{2}\right)/2b\right)^{2}}}.$

So würde die Kurzform ausehen...--Petrus3743 (Diskussion) 19:09, 20. Sep. 2018(CEST)

In den Artikel eingearbeitet erledigtErledigt--Petrus3743 (Diskussion) 21:57, 20. Sep. 2018 (CEST)

Wenn ich so nachdenke, man hätte den neuen Benutzer Mtade vorher ermutigen sollen, dass er seine, m. E. sehr gute Idee der verkürzten Höhenformel, selber in den Artikel einbringt. Auch damit gewinnt man wahrscheinlich neue produktive Mitstreiter in der WP. Ich hoffe es gibt noch einige die ähnlich denken ... Gruß--Petrus3743 (Diskussion) 10:50, 21. Sep. 2018 (CEST)

Archivierung dieses Abschnittes wurde gewünscht von: Petrus3743 (Diskussion) 22:49, 17. Okt. 2018 (CEST)

Überarbeiten der Einteilung

Die Einteilung bedarf einer Überarbeitung:
Im Artikel:

"Einteilung

nach Seitenlängen:

• gleichseitiges Dreieck
• gleichschenkliges Dreieck
• unregelmäßiges Dreieck

nach Winkeln:

• spitzwinkliges Dreieck
• rechtwinkliges Dreieck
• stumpfwinkliges Dreieck"

Gleichzeitig heißt es bei Dreieck#Unregelmäßige Dreiecke:

"Unregelmäßige Dreiecke

• Alle drei Seiten sind unterschiedlich lang.
• Alle drei Winkel sind unterschiedlich groß."

Das heißt bei unregelmäßigen Dreiecken sind auch die Winkel und nicht nur die Seiten von Bedeutung. Sinnvoller wäre es so:

"Einteilung

nach Seitenlängen:

• gleichseitiges Dreieck [alle drei Seiten gleich lang; lat. triangulum aequilaterum, triangulum isopleuron]
• gleichschenkliges Dreieck [genau zwei Seiten gleich lang; lat. triangulum aequicrurum, triangulum isosceles]
• ungleichseitiges Dreieck [alle drei Seiten unterschiedlich lang; lat. triangulum scalenum]

nach Winkeln:

• rechtwinkliges Dreieck [mit einem rechten Winkel und somit mit zwei spitzen; lat. triangulum rectangulum bzw. (triangulum) rectiangulum]
• schiefwinkliges Dreieck [ohne rechten Winkel; lat. triangulum obliquangulum]
  • spitzwinkliges Dreieck [mit drei spitzen Winkel; lat. triangulum acutangulum, oxygonum & oxygonium]
  • stumpfwinkliges Dreieck [mit einem stumpfen Winkel und somit mit zwei spitzen; lat. triangulum obtusangulum bzw. triangulum obtusiangulum, triangulum amblygonium (ambligonium)]

nach Seitenlängen und Winkeln:

• unregelmäßiges Dreieck"

Als Anmerkung zu rectangulum/rectiangulum und obtusangulum/obtusiangulum: Die Form mit i könnte richtiger, klassischer sein, neulateinisch scheint aber die Form ohne i üblicher zu sein und in romanischen Sprachen könnte das i auch üblicherweise fehlen (z.B. engl. obtuse-angled, franz. obtusangle, ital. ottusangolo, span. obtusángulo).
Erklärungsversuch: rectilineus (rectus, Genitiv recti, + linea) ist auch neulateinisch mit i üblich. obtusangulus (obtusus, Genitiv obtusi, + angulus) dagegen ist ohne i üblicher. Im Neulateinisch und in romanischen Sprachen könnte der Ausfall des i vom nachfolgenden Buchstaben abhängen. Bei linea ist es ein Konsonant, also bleibt das i, bei angulus ein Vokal und da fiel das i dann weg. Das wäre teils vergleichbar mit griechischstämmigen Präfixen wie pseudo-/pseud- (siehe z.B. www.duden.de/rechtschreibung/pseudo_ : "pseu­do- [..], vor Vokalen meist pseud- [..]") -80.133.109.170 10:11, 25. Aug. 2016 (CEST)

Die Bedingungen

• "Alle drei Seiten sind unterschiedlich lang."
• "Alle drei Winkel sind unterschiedlich groß."

bei unregelmäßigen Dreiecken sind nicht unabhängig voneinander, sondern äquivalent. Wenn bei einem Dreieck alle drei Seiten unterschiedlich lang sind, dann sind auch alle drei Winkel unterschiedlich groß. Es gibt also keinen davon verschiedenen Begriff "ungleichseitiges Dreieck". Es ist deshalb sinnvoll, die die unregelmäßigen Dreiecke bei der Einteilung nach Seitenlänge einzuordnen. --Digamma (Diskussion) 10:34, 25. Aug. 2016 (CEST)

• Ich habe den Artikel so verstanden, dass von der Definition her beide Bedingungen erfüllt sein müssen. Also: "unregelmäßiges Dreieck := Dreieck mit drei unterschiedlichen langen Seiten und unterschiedlich großen Winkeln". Den Begriff ungleichseitiges Dreieck gibt es (z.B. www.zeno.org/Meyers-1905/A/Dreieck+[2]) und der bezieht sich von den Worten her nur auf die Seitenlänge. Also: "ungleichseitiges Dreieck := Dreieck mit drei unterschiedlich langen Seiten". Nach diesen Definitionen, nur von den Worten her, wäre jedes unregelmelmäßge Dreieck ein ungleichseitiges Dreieck, aber nicht unbedingt jedes ungleichseitige Dreieck ein unregelmelmäßge Dreieck. Es könnte ja auch auch *ungleichwink(e)lige Dreiecke geben - keine Ahnung, ob dieser Begriff existiert, deshalb der Stern -, die nicht ungleichseitig sind. Von der Mathematik aus gesehen fallen zwar ungleichseitiges und unregelmäßiges Dreieck zusammen, von den Worten, also der Sprache, und von der Betrachtung aus gesehen aber nicht. "ungleichseitiges Dreieck" gehört nur zu "nach Seiten", da es sich nur auf die Seiten bezieht. "unregelmäßiges Dreieck" dagegen könnte man nach der zweiten Bedingung ebenso bei "nach Winkeln" einsortieren und die Wahl wäre vollkommen willkürlich. Statt es zweimal einzusortieren und statt es bei "nach Seitenlängen und Winkeln:" einzusortieren, könnte man es dann eben bei "nach Seitenlängen oder Winkeln:" einsortieren.
• Nebenbei: Mathematiker kannten auch Begriffe wie "Triangulum curvilineum" (im 17. Jahrhundert als "krummlinischer Triangel" wiedergegeben) und "Triangulum rectilineum" (im 17. Jahrhundert "rechtlinischer Triangel") (als Quelle z.B. books.google.com/books?id=U5RmAAAAcAAJ S. 16 und S. 19). Vielleicht könnte man das auch irgendwo im Artikel erwähnen, vielleicht in einem Abschnitt wie "Geschichtliches"?

-80.133.101.2 12:44, 25. Aug. 2016 (CEST)

• Zu deinem ersten Punkt: Im Grunde könnte man alle Unterscheidungen, die unter "nach Seitenlänge" einsortiert sind, auch "nach Winkeln" einsortieren, denn gleichseitige Dreiecke sind genau die, die drei gleiche Winkel haben, und gleichschenklige Dreiecke sind genau die, bei denen (mindestens) zwei Winkel übereinstimmen. Diese Einteilung ist aber - egal ob nach Seiten oder nach Winkeln - von anderer Art als die unter "nach Winkel" getroffene Einteilung in spitz-, recht- und stumpfwinklige Dreiecke.
• Zum zweiten Punkt: Krummlinige Dreiecke gibt es auch heute. Wer aber nur Dreieck sagt, meint eines, dessen Seiten gerade sind. --Digamma (Diskussion) 12:59, 25. Aug. 2016 (CEST)

---

Höhen aus den Seitenlängen

Ich weiß nicht ob dieser Abschnitt wirklich sinnvoll ist, die betreffenden Formeln stehen im Artikel schon an andere Stelle. Das explizite Umstellen bzw. Auflösen nach einer anderen Variable macht aus enzyklopädischer Sicht mMn. eigentlich nur Sinn, wenn das Umstellen aus irgendeinem Grund überraschend kompliziert ist oder die umgestellte Version eine häufig in der Literatur genannte Darstellung ist. Enzyklopädische Artikel sollen ja zusammenfassend sein und das Wichtigste prägnant darstellen, d.h. eine Formel reicht hier.--Kmhkmh (Diskussion) 16:24, 25. Mär. 2020 (CET)

Wenn man den Abschnitt Höhen aus den Seitenlängen mit Bild etc. herausnehmen würde, wo wäre dann im Artikel, bezüglich allgemeines Dreieck, der entsprechende Ersatz an anderer Stelle zu finden? Übrigens, hierzu gab es bereits eine Diskussion vor der Einarbeitung im September 2018, die derzeitige Vereinfachung (Heronsche Flächenformel) besteht seit 3. März 2019.

• Was mich irritiert, die Formeltabelle ist seit 22. März 2020 „Formatierungen geändert, kleine Korrekturen” (!) umstrukturiert, u. a. mit Änderung der Formeln für Höhe aus den Seitenlängen. Nun, das ist vielleicht eine Sache des Geschmacks, aber ist die Tabelle (mit ihrem derzeitigen Umfang) jetzt für den Leser besser? Wünschenswert wären m. E. eigentlich nur Änderungen, die den Artikels verbessern und dabei den vorherigen korrekten Stand miteinbeziehen. --Petrus3743 (Diskussion) 18:12, 25. Mär. 2020 (CET)

Also wenn ich das richtig sehe, hat sich @Digamma: in der der damaligen Diskussion eher gegen einen solchen Abschnitt ausgesprochen. Ich kann ihm jedenfalls weiterhin nur wenig abgewinnen und nicht jede Frage die auf der zugehörigen Diskussionsseite aufgeworfen wird, muss im Artikel selbst behandelt werden. Dementsprechend halte ich die Höhenformel weder in der Tabelle noch mit eigenen Abschnitt für sinnvoll. Aber in der Tabelle nicht es immerhin weniger Platz ein.--Kmhkmh (Diskussion) 11:21, 26. Mär. 2020 (CET)

Kann dein erstes Argument halbwegs nachvollziehen, beim zweiten sehe ich es etwas anders: Ich übernehme lieber eine Formel wie z. B. Formulierung des Satzes bzw. die kürzere. Fazit: Der Absatz Höhen aus den Seitenlängen wird gelöscht, in der Tabelle bleiben die kürzeren Formeln, die entsprechende Zeile enthält bereits den Hinweis (mittels Satz des Heron). Eine Frage ist noch offen, „... die betreffenden Formeln stehen im Artikel schon an andere Stelle.“, wo ist diese Stelle bezüglich allgemeines Dreieck? Mit Gruß Petrus3743 (Diskussion) 11:56, 26. Mär. 2020 (CET)

Unter Flächeninhalt stehen doch die beiden benötigten Formeln.--Kmhkmh (Diskussion) 15:47, 26. Mär. 2020 (CET)

Danke, jetzt ist alles klar, vor lauter Formeln sah ich die Formel nicht! Mit Gruß--Petrus3743 (Diskussion) 10:01, 27. Mär. 2020 (CET)

Archivierung dieses Abschnittes wurde gewünscht von: Petrus3743 (Diskussion) 11:27, 1. Apr. 2020 (CEST)

Dreiecksungleichung

„Die Gesamtlänge zweier Seiten eines Dreiecks ist immer größer als die Länge der dritten Seite“ ist nicht ganz das, was die Dreiecksungleichung fordert. Korrekt wäre „mindestens so groß wie“. --95.112.224.62 10:23, 29. Jul. 2019 (CEST)

Das ist schon ok bzw. hängt davon ab, ob man die Dreiecksungleichung mit $>$ oder $\geq$ formuliert und im Falle des Dreiecks auch entartete Fälle betrachtet bzw. als Dreieck bezeichnet.--Kmhkmh (Diskussion) 13:51, 29. Jul. 2019 (CEST)

P.S. Allerdings wäre es natürlich schon wünschenswert die Darstellung hier mit der Darstellung im verlinkten Artikel Dreiecksungleichung abzugleichen, das habe ich jetzt mal gemacht.--Kmhkmh (Diskussion) 14:00, 29. Jul. 2019 (CEST)

3 - 4 - 5 als Konstruktion für rechtwinkliges Dreieck

Ich ergänzte unter "SSS":
"Ein Rechtwinkliges SSS-Dreieck wird durch ein Pythagoreisches Tripel konstruiert, beispielsweise mit den Seitenlängen $(3,4,5)$."

Benutzer:Fritzbruno löschte dies mit der Begründung "gehört nicht zu SSS".

Statt löschen bitte verbessern: woanders einfügen, inhaltlich verbessern, oder so. Aber Information bitte erhalten! Danke, --Markus (Diskussion) 07:38, 6. Aug. 2020 (CEST)

hier handelt es sich um allgemeine Dreiecke, die sehr spezielle Konstruktion mittels der PT gilt nur für rechtwinklige Dreiecke und ist auch da ein Spezialfall. Das muss hier nun wirklich nicht stehen und bei den rechtwinkligen Dreiecken wird es mW erwähnt. --Fritzbruno (Diskussion) 11:27, 6. Aug. 2020 (CEST)

Hallo Fritzbruno, jetzt hast Du schon wieder gelöscht - statt den Text einfach sprachlich zu verbessern :-( Seit vielen hundert Jahren konstruieren die Menschen einen rechten Winkel mit einem Dreieck mit den Kantenlängen $(3,4,5)$. Viele erinnern sich daran, suche die Lösung bei Dreieck aber Du meinst, sie sollen es hier nicht finden, sondern nur alle anderen Formeln ;-) Löschen ist einfach unfein!

Habe es jetzt sprachlich noch etwas verbessert. Falls Fritzbruno wieder einfach löscht: vielleicht kann sich hier jemand der Sachen mal annehmen und seien "Editwar" beenden :-) Gruss, --Markus (Diskussion) 10:43, 17. Aug. 2020 (CEST)

Scharfes Geschütz: Editwar! Das, was du eingefügt hast, gehört einfach nicht zum Thema. Wie schon in meiner Zusammenfassung erwähnt: so konstruiert man nicht rechtwinklige Dreiecke sondern im Alltag Rechte Winkel. Das ist etwas ganz Anderes! --Fritzbruno (Diskussion) 18:02, 19. Aug. 2020 (CEST)

Hier der Text (damit man ihn nicht immer aus der Historie raussuchen muss):

---

Konstruktion durch Seitenlängen $(3,4,5)$

Konstruiert wird ein rechter Winkel durch ein rechtwinkliges Dreieck, beispielsweise nach der alten Handwerkermethode durch ein Seitenverhältnis von $(3,4,5)$ oder durch ein anderes pythagoreisches Tripel.

---

Servus Markus,

ich muss dir leider sagen, Fritzbruno hat nicht unrecht. Deine Ausdrucksweise ist so missverständlich, dass anzunehmen ist, noch weitere WP-ner würden eine solche Bearbeitung, mit Erklärung in der Zusammenfassung (ohne Diskussion), löschen. Bitte lese dir deinen letzten Eintrag nochmals mit Bedacht durch. Hinweis: u. a. Bedeutungen von „durch“ ... Mit Gruß --Petrus3743 (Diskussion) 12:33, 17. Aug. 2020 (CEST)

Der Inhalt ist wichtig, er soll dem Leser zur Verfügung stehen. Wenn das sprachliche Konstrukt besser (i.S. von verständlicher und oder unmissverständlicher) sein kann, dann einfach umformulieren. Kontinuierliche Verbesserung ist immer ein guter Plan! Danke, --Markus (Diskussion) 15:03, 17. Aug. 2020 (CEST)

Eine missverständliche Formulierung transportiert aber gegebenenfalls einen falschen Inhalt und die problematische Formulierung unverändert/verbessert einfach wieder einzusetzen ist keine akzeptable Lösung.

Hier liegt eine historische praktische Anwendung pythagoreischer Tripel oder auch spezieller rechtwinkliger Dreiecke vor. Das ist passt inhaltlich ohnehin weniger zu einem Übersichtsartikel zu Dreiecken, sondern ist besser in den Artikeln zum rechtwinkligen Dreieck oder zu pythagoräischen Tripeln aufgehoben. Dort sollte es als handwerkliches Konstruktionsv erfahren, Anwendung in der Vermessungstechnik oder Ähnlivhes beschrieben werden.--Kmhkmh (Diskussion) 16:02, 17. Aug. 2020 (CEST)

P.S.: Es gibt zu der Sache übrigens auch schon einen eigenen Artikel: Zwölfknotenschnur--Kmhkmh (Diskussion) 16:08, 17. Aug. 2020 (CEST)

Danke für Deine Erläuterung. Ja, etwas Miss- oder Unverständliches ist sicher keine "Lösung". Den Inhalt einfach zu löschen aber eich keine ;-) Hier handelt es sich um eine zwischen Wissenschaftlern und Laien typisches Konfliktmuster, das aber durch Synergie simpel lösbar ist. Der Laie (ich) erklärt, warum der Inhalt hier für den Laien wichtig ist, und der Wissenschaftler findet dafür eine korrekte und gleichzeitg laienverständliche Formulierung. Eine laienverständliche Grafik habe ich via Grafikwerkstatt ja schon beigesteuert, ebenso den vertiefenden Link zu den "Tripeln".

Ich bin immer wieder beeindruckt, wie ausführlich und genau in WP mathematische Artikel aufgebaut sind! Für mich est es ok, wenn ein Grossteil der Inhalte nur von Menschen mit mindestens Mathe-Leistungskurs letztes Schuljahr technisches Gymnasium verstanden wird, oft vermutlich sogar nicht mal von durchschnittlichen Mathe-Studenten (habe schon Mathe-Studenten sagen gehört, dass sie erst durch lesen der WP-Artikels verstanden haben, was der Prof. ihnen sagen wollte ;-) ).

Voraussetzung für einen guten Mathe-Artikel

Voraussetzung für einen guten Mathe-Artikel ist aber zwingend (!) eine laienverständliche Einleitung (Hauptschüler) und sogar die "Oma" sollte die Einleitung inhaltlich "irgendwie" erkennen können (ich weiss, dass das nicht trivial ist, und dass die wenigsten Mathematiker wissenschaftspädagogische Fähigkeiten für Laienniveau haben. Trotzdem erfordert Schreiben für Wikipedia, dass - bevor das "Formelgedöns" ;-) - beginnt, ein paar laienverständliche Absätze den dem Hauptschulabsoventen die im Artikel beschriebenen Inhalte verständlich erklären :-)

Lebenspraktische Mathematik

Und noch etwas: m.E. ist Mathematik in WP nicht gedacht als "Nachschlagewerk für angehende Mathematiker". Sondern WP soll der Allgemeinheit dienen. Kultur-, Sprach- und insbesondere Bildungs-übergreifend. Stell Dir vor, Du bist Elternteil, ohne oder mit längst vergessener mathematischer Bildung, und musst Deinem Kind eine mathematische Aufgabe erklären. Dann greifst Du zu Wikipedia. So sehe ich unseren Bildungsauftrag :-) Wenn der Artikel dann den Leser (idealerweise) neugierig macht auf mehr, dann findet er durch Links und Quellen viele Vertiefungsmöglichkeiten.

Wissen auffindbar machen

Hier bei Dreieck gibt es unter "besondere Dreiecke" ein Kapitel "rechtwinkliges Dreieck" (als Zusammenfassung für den spezifischen gleichnamigen WP-Artikel. Schon diese Zusammenfassung ist für die meisten Leser unverständlich. Vermutlich werden sehr viele bereits im Kapitel "Allgemeines Dreieck" nach etwa der Hälfte aufgeben. Wenn sie aber (via Inhaltsverzeichnis) bis zum "Rechtwinkligen" vorstossen, dann sollten sie die uralte weltweit verbreitete und auch heute noch genutzte $(3,4,5)$ Technik kennenlernen/wiederfinden. Gruss, --Markus (Diskussion) 09:15, 18. Aug. 2020 (CEST)