Dieses Diskussionsarchiv hat die empfohlene Seitengröße erreicht und gilt damit als abgeschlossen. Sein Inhalt sollte nicht mehr verändert werden (ausgenommen Kleinbearbeitungen wie Link- und Vorlagenfixe). Verwende für die Archivierung von Diskussionsbeiträgen bitte das aktuelle Archiv und benutze bitte für aktuelle Diskussionen die aktuelle Diskussionsseite.

Um einen Abschnitt dieser Seite zu verlinken, klicke im Inhaltsverzeichnis auf den Abschnitt und kopiere dann Seitenname und Abschnittsüberschrift aus der Adresszeile deines Browsers, beispielsweise

[[Diskussion:Allgemeine Relativitätstheorie/Archiv/1#Abschnittsüberschrift]]

oder als Weblink zur Verlinkung außerhalb der Wikipedia

https://de.wikipedia.org/wiki/Diskussion:Allgemeine_Relativit%C3%A4tstheorie/Archiv/1#Abschnittsüberschrift

- 2004 -

Verschiedenes

Letzter Kommentar: vor 20 Jahren2 Kommentare2 Personen sind an der Diskussion beteiligt

Die Aktivitäten von Ce und meine haben sich zeitlich ein wenig überschnitten. Zum Glück hatten wir uns thematisch verschiedenes vorgenommen. Ich habe meine 5 Kapitel einfach mal um sein Kapitel herumgruppiert und seine Einleitung etwas umformuliert. Das Äquivalenzprinzip wollte ich nicht unbedingt an den Anfang stellen, weil es mir zu wenig spektakulär ist. Letztlich geht's um eine Krümmung des Raumes, die unvorstellbar ist, als Ursache der Gravitation, während das Äquivalenzprinzip eher eine nicht allzu schwer nachvollziehbare Konsequenz ist. Auch wenn es vielleicht historisch gesehen Einstein auf den richtigen Weg gebracht hat (war das so? Keine Ahnung.). Habe einen Moment gezögert, was ich mit der Passage über die instantane Gravitation als Notwendigkeit für eine aRT machen sollte. Finde sie nicht so unbedingt auf den ersten Blick zwingend, denn vielleicht hätte man ihr einfach eine endliche Ausbreitungsgeschwindigkeit zuweisen und dann bei der sRT bleiben können. Die Elektrodynamik funktioniert ja auch mit der sRT. Dass es mit der Gravitation nicht geht (geht es nicht?), könnte nur daran liegen, dass es positive und negative Ladungen gibt, aber nur einen Massentyp. Die richtige Argumentation dazu ist mir nicht bekannt. Wäre aber mal interessant. Wusste nicht so recht wohin mit dieser Passage und habe sie dann erst mal rausgenommen, bestehe aber keineswegs drauf. Wolfgangbeyer 09:37, 26. Jan 2004 (CET)

Hallo Geof: Die Allgemeine RT ist deutlich mehr als nur eine Erweiterung auf beschleunigte Bezugssysteme. Was soll "wo z.B. die Dimensionen bewegter Körper konstant sind" heißen? der Rest ist spezielle und nicht allgemeine RT. Habe den alten Absatz wieder hergestellt. Ferner werden laut Wikipediaregeln Begriffe nur bei ihrem ersten Auftauchen verlinkt und Artikel zu Adjektiven sind verpönt. Wolfgangbeyer 16:45, 25. Feb 2004 (CET)

Im letzten Kapitel steht, dass im rotierenden Bezugssystem die Geschwindigkeit die Lichtgeschwindigkeit überschreiten kann. Das ist mMn unglücklich formuliert und kann verwirren; auch in der aRT ist die Lichtgeschwindigkeit absolutes maximum. -- Schewek 18:08, 23. Feb 2004 (CET)

Hm, schwierig. Aber wenn ich auf einem Drehschemel sitze, rotieren die Sterne nun mal so schnell. Und das Argument, das sei kein zulässiges Koordinatensystem zieht in der aRT nicht mehr. Also sind rein formal Überlichtgeschwindigkeiten möglich. So habe ich das auch mal gelesen, glaube ich. Vielleicht finde ich die Literaturstelle noch mal. Und darauf, dass sich nirgendwo Objekte mit Überlichtgeschwindigkeit begegnen können, und dass ein Transport von Materie oder Information von einem Körper zu einem anderen mit Überlichtgeschwindigkeit auch in der aRT nicht möglich ist, wird in den folgenden Sätzen ja eingegangen. Die Behauptung, die Lichtgeschwindigkeit sei auch in der aRT ein absolutes Maximum ist zumindest ebenso missverständlich und bedarf einer Erläuterung. Wolfgangbeyer 16:37, 25. Feb 2004 (CET)

Ich hab mal versucht, mich schlau zu machen: Um ein beschleunigtes Bezugssystem in ein Ruhesystem zu transformieren, muss die Transformation die Raum-Zeit derart krümmen, als ob eine entsprechende Masse verantwortlich wäre. Bei dem rotierenden Beobachter bedeutet das eine gewaltige Masse, die allen umkreisenden Objekten eine krumme Bahn aufzwingt. Als Beobachter im Zentrum, sehr sehr tief im 'Trichter', vergeht die Zeit extrem langsam, also ist die Geschwindigkeit der umkreisenden Sterne nicht mehr über der Lichtgeschwindigkeit (zumindest vermute ich, dass eine genaue Rechnung das zeigen würde). - Mit den genannten Argumenten, was hälst Du davon, den Artikeltext anzupassen? -- Schewek 17:28, 1. Mär 2004 (CET)

Der ganze Formalismus der allgemeinen Relativitätstheorie basiert doch auf Riemammscher Geometrie . Das bedeutet,daß die gekrümmte Raumzeit zwar lokal auf einen (flachen) Minkowski-Raum abgebildet werden kann, man aber nicht eine solche Abbildung finden kann,die für die gesamte Raumzeit gilt. Die Parallelverschiebung von Geschwindigkeitsvektoren ist damit keine allgemein zulässige Operation, der Geschwindigkeitsvergleich zwischen weit entfernten Objekten mithin auch nicht. Das "Drehstuhlparadoxon" basiert also auf Begrifflichkeiten,die in der Natur keine Entsprechung haben. --AllSystems 02:21, 23. Okt 2005 (CEST)

Bin mit den Änderungen an "Die Wechselwirkung zwischen Materie und der Raum-Zeit" nicht einverstanden. Es mag sein, dass historisch der Ausgangspunkt der aRT das Äquivalenzprinzip ist. Von daher war es missverständlich formuliert. Habe "Ausgangspunkt ... ist die Entdeckung ..." durch "Grundgedanke ... ist die Annahme ..." ersetzt. Aber darauf sollte dieser Abschnitt gar nicht eingehen, sondern darauf, dass die Vorstellung von einer Wechselwirkung zwischen Massen durch eine zwischen Masse und Raum-Zeit ersetzt wird. Das ist der revolutionäre Grundgedanke der aRT. Und dass wollte ich am Artikelanfang deutlich machen. Das Äquivalenzprinzip ist zwar wichtig aber überhaupt nicht spektakulär und verwässert die Schilderung dieses wichtigen Gedankens hier oben. Es genügt in dem Abschnitt weiter unten darauf einzugehen. Die Formulierung " ... einen Zusammenhang zwischen der Wechselwirkung zwischen Massen ...", mal abgesehen davon dass das auch sprachlich unsinnig ist, ist missverständlich, denn es gibt keine direkte Wechselwirkung zwischen Massen mehr, sondern sie wird über die Krümmung vermittelt. Das ist ja gerade das, was hier gesagt werden soll. Habe die alte Version daher weitgehend wieder hergestellt. Wolfgangbeyer 18:20, 25. Feb 2004 (CET)

Ich bin der Ansicht, das die Krümmung der Raum-Zeit durch die Masse werder Ausgangspunkt noch Grundgedanke ist. Historisch und von grundlegenden Prinipien her ist das verallgemeinerte Äquivalenzprinzip (eine Symmetrie) Ausgangspunkt. Die Krümmung ist eine Folgerung aus den zur Erfüllung dieser Symmetrie notwendigen Feldgleichungen. Es war eine Leistung Einsteins, die Möglichkeit einer Krümmung zu akzeptieren, aber ich finde, man sollte die Krümmung klar als Folgerung darstellen. -- Schewek 18:38, 25. Feb 2004 (CET)

Hm, so genau habe ich das nicht mehr in Erinnerung. Da könntest Du recht haben. Schon zu lange her. Man sollte aber die Krümmung nicht schon hier oben als Folge des Äquivalenzprinzips darstellen, denn diesen Schluss kann der Laie wohl kaum nachvollziehen. Aber ein Laie sollte noch verstehen können, dass da eine Krümmung ist und was sie macht. Habe noch mal umformuliert. Aber man sollte auf Deinen Gedanken im Abschnitt Äquivalenz von träger und schwerer Masse zurückkommen. Da steht diesbezüglich noch nichts. Bin allerdings inhaltlich überfordert, da ich mich nicht mehr erinnere, wie man aus dieser Symmetrie auf Feldgleichungen schließt, die die Krümmung zur Folge haben. Oder war das ein ganz simpler Gedanke? Wolfgangbeyer 21:15, 25. Feb 2004 (CET)

Der von 141.63.56.202 eingefügte Text kommt mir etwas merkwürdig vor: ..., welche dadurch entsteht, dass das Koordinatensystem so gewählt wird das die Geodäten keine Geraden sind. Das hört sich so an, als hinge es von einer willkürlichen Wahl des Koordinatensystems ab, ob Geodäten Geraden sind. Andererseits: Wie könnte man den Geraden in einem krummen Raum überhaupt anderes definieren als eben Geodäten? Weiß nicht recht, was dieser Satz sagen wollte. Wer kann das richtig stellen? Andere Scheinkräfte sind zum Beispiel die Zetrifugal und die Corioliskraft ... Scheinkräfte wurden doch weiter oben schon erwähnt. Habe diesen Satz daher gelöscht. Die Gravitationskraft unterscheidet sich von den anderen Scheinkräften insoweit als das es kein euklidisches Koordinatensystem gibt in dem sie an jedem Punkt verschwindet: Es gibt überhaupt kein globales euklidisches Koordinatensystem mehr. Gibt es ein globales nicht-euklidisches ohne Gravitation? Kenne mich da zuwenig aus, aber ich könnte mir das vorstellen. Falls es das nicht gibt, sollte man euklidisches streichen, andernfalls den ganzen Satz. Wer kennt sich da aus? --Wolfgangbeyer 20:58, 16. Apr 2004 (CEST)

Kein Kommentar? Dann entferne ich mal diese ziemlich fragwürdige Passage. --Wolfgangbeyer 20:26, 4. Jun 2004 (CEST)

Durch die Link-Diskussion darunter hatte ich diese Frage ganz übersehen.

Die Aussage war so, wie sie da stand, durchaus fragwürdig. Da im Anfangsabschnitt eine korrektere Erklärung steht, war das ersatzlose Entfernen m.E. die richtige Entscheidung.

Dafür habe ich jetzt am Anfang eine andere korrekturwürdige Stelle entdeckt: Die Raumkrümmung hängt nicht nur von der Masse, sondern vom Energie-Impuls-Tensor ab. Das heißt, nicht nur die Energie, sondern Energie und Impuls bestimmen das Gravitationsfeld (= die Raumzeitkrümmung). Ich werde den Artikel entsprechend korrigieren. --Ce 19:35, 5. Jun 2004 (CEST)

ich habe das vorangestellte Wikipedia:Wikiprojekt_Physik_in_der_Schule/Organisation Relativitätstheorie|Hinweis für das Bearbeiten dieser Seite entfernt. begründung:

der link enthält kaum konkrete hinweise zum bearbeiten der seite
selbst wenn, dann sollten solche richtlinien (wenn sie denn nötig sind) aus einem konsens entstehen und nicht durch einen einzelnen benutzer vorgegeben werden
warum soll das thema allgemeine relativitätstheorie bei wikipedia denn nur im schulischen zusammenhang / durch schüler und lehrer behandelt werden? können und sollten nicht auch experten mitwirken? (selbstverständlich sollte trotzdem jeder wp-artikel möglichst allgemeinveständlich sein.)

das soll jetzt aber keine wertung des "Wikiprojekt Physik in der Schule" darstellen. grüße , Hoch auf einem Baum 18:01, 25. Mai 2004 (CEST)Beantworten

Die Richtlinien auf Wikipedia:Wikiprojekt Physik in der Schule/Kategorien sind in der Diskussion auf Wikipedia:Wikiprojekt Physik in der Schule/Diskussion von allen Projektteilnehmern positiv beurteilt worden, und keiner hat sich negativ geäußert. Insofern kann man denke ich schon sagen, dass sie einen gewissen Konsens darstellen. Daß an der Organisationsseite bisher nur ich mitgewirkt habe, folgt aus der Tatsache, daß eben bisher niemand anders mitgemacht hat. Ein wesentlicher Grund, die Links zu setzen (ich hatte lange gezögert), war auch, um endlich auch mal eine breitere Diskussion darüber zu bekommen. Zumal die Seite im momentanen Aufbau v.a. eine (unvollständige) Beschreibung des Ist-Zustands und nur ein paar wenige Probleme (über die natürlich diskutiert werden darf und soll) auflistet.

Wo bitte steht, dass das Thema nur durch Schüler/Lehrer behandelt werden sollte? Ich bin weder Schüler, noch Lehrer. Es geht darum, insgesamt eine Struktur aufzubauen, die vor allem vermeidet, gleich beim Einstieg ein zu hohes Niveau vorauszusetzen. Wenn Du die Kategorien einmal anschaust, dann wirst Du feststellen, daß insbesondere der Kategorie "vertiefend" keinerlei Grenzen gesetzt sind – wenn z.B. jemand die mathematischen Eigenschaften der Ringsingularität der Kerr-Newman-Lösung bei Drehimpulsen und Ladungen, bei denen sich kein Horizont bildet, eines enzyklopädischen Artikels wert findet, dann kann er darüber schreiben, und sogar beliebig komplizierte mathematische Konzepte verwenden, ohne mit dem Wikiprojekt irgendwie in Konflikt zu kommen. Er sollte eben nur vermeiden, das z.B. direkt in den Artikel "Allgemeine Relativitätstheorie" zu schreiben. Wobei diese Regeln nicht nur für Schüler, sondern auch für andere Nicht-Experten vorteilhaft sind: Wer nicht gerade ein Physiker ist, der würde es z.B. nicht schätzen, wenn der Artikel "Allgemeine Relativitätstheorie" z.B. anfinge mit "Die Allgemeine Relativitätstheorie ist die Verallgemeinerung der speziellen Relativitätstheorie. Sie beschreibt die Gravitation, indem der flache Minkowski-Raum durch eine Pseudoriemannsche Mannigfaltigkeit der Signatur (3,1) ersetzt wird."

Was jetzt nicht heißt, dass diese Regeln irgendwie in Stein gemeißelt wären. Wie gesagt, es war Konsens all derer, die sich bis jetzt dafür interessiert haben, was (leider) nur eine sehr geringe Anzahl von Wikipedianern ist. Insofern kann die Seite Wikipedia:Wikiprojekt_Physik_in_der_Schule/Organisation Relativitätstheorie als eine Art Versuchsprojekt betrachtet werden. Wenn das Projekt auf keine Akzeptanz stößt oder keinerlei positive Wirkung zeitigt, dann kann es auch klang- und sanglos wieder eingestampft werden. Aber die Vergangenheit hat gezeigt, dass wenn man nicht genügend darauf aufmerksam macht, es auch niemand überhaupt zur Kenntnis nimmt. Und wenn das Projekt erfolgreich sein soll, dann muß es auch beachtet werden (und wenn es sich als für die meisten nicht akzeptabel erweisen soll, dann auch, weil wie soll jemand seine Ablehnung kundtun, wenn er es nicht einmal bemerkt?) – und da diese Beachtung nur beim Bearbeiten einen Sinn ergibt, habe ich den gewählten Text für sinnvoll gehalten.

Ich würde mich freuen, wenn dies jetzt der Anfang einer breiteren Diskussion würde. Damit das Projekt entweder abhebt, oder wenigstens definitiv zu Grabe getragen werden kann. Der bisherige Zombie-Zustand war jedenfalls kein wünschenswerter Dauerzustand. --Ce 19:14, 25. Mai 2004 (CEST)Beantworten

Eigentlich sollte diese Diskussion woanders stattfinden. Ich würde aber sagen, dass man vielleicht Hubi und Wipape, offenbar die beiden fast einzigen Mitstreiter in dieser Sache, fragen sollte, wie sie inzwischen diese Geschichte einschätzen. Vielleicht mal direkt anfragen. Offenbar lebt die Geschichte nicht richtig. Es wäre natürlich ein Traum, wenn man eine Enzyklopädie hätte, in der jeder Begriff auf den verschiedensten Schwierigkeitslevels erklärt würde, die man je nach Bedarf wechseln kann. Aber das übersteigt die Möglichkeiten der Wikipedia-Strukturen. Man müsste so was wie Begriff (Level x) einführen, aber das ist sicher nicht konsensfähig. Artikel mit gemischtem Niveau sind daher unvermeidbar und auch ok, wenn dabei darauf geachtet wird, dass das Niveau im Verlauf des Artikels von unten nach oben ansteigt. Ferner finde ich die Bezeichnung Physik in der Schule total irreführend. Kaum ein Leser dürfte der Angelegenheit soweit nachgehen, bis er verstanden hat, um was es überhaupt geht. Auch ich dachte zunächst, was kümmert mich die Schule, und habe erst relativ spät kapiert, dass es im Wesentlichen um eine Klassifizierung von Artikeln nach Schwierigkeitsgrad geht, was meiner Ansicht nach mit Schule nur wenig zu tun hat. Auch bei den anderen Themenpunkten (didaktische Standards, Schreibweisen) sehe ich kaum, wieso man sich dabei an Schulischem orientieren sollte. Didaktik und einheitliche Schreibweisen sind immer prima. Meiner Ansicht nach sollte das Zielpublikum einer Enzyklopädie immer der interessierte Laie sein. Weiter unten im Artikel oder in kurzen Zwischenbemerkungen darf auch was für den Spezialisten stehen. Ihr habt da viel Zeit reingesteckt, und ich begrüße Euer Engagement, aber ich gebe der Geschichte offen gestanden keine allzu große Chance. --Wolfgangbeyer 18:57, 10. Jun 2004 (CEST)

hallo Ce, sorry dass ich erst jetzt antworte (ich hatte deinen beitrag gelesen, aber dann kam irgend was dazwischen und ich habe das aus den augen verloren). ich war hier nur so hereingeschneit - von Gravitationslinse, wo ich einige sachliche fehler einfach nicht so stehen lassen konnte -, und war von dem Physik in der Schule doch ziemlich irritiert.

Wo bitte steht, dass das Thema nur durch Schüler/Lehrer behandelt werden sollte? - nun ja, im namen des projekts. zumindest impliziert der, dass das thema nur für schulzwecke behandlet werden sollte

genau wie wolfgangbeyer vermutet, habe ich auch nicht kapiert, dass es dabei hauptsächlich um Wikipedia:Wikiprojekt Physik in der Schule/Kategorien geht. diese schwierigkeitsstufen scheinen mir auf den ersten blick keine schlechte idee, und meinetwegen kann man auch den (lehrplan-)kenntnisstand bestimmter klassenstufen als objektive marken dafür verwenden. ihr könnt ja versuchen, die einzelnen abschnitte der artikel so zu klassifizieren.

dass jeder wp-artikel möglichst allgemeinverständlich sein sollte, und dass im artikel nicht erklärte begriffe in anderen artikeln erklärt sein sollten, ist doch hoffe ich selbstverständlich.

wenn z.B. jemand die mathematischen Eigenschaften der Ringsingularität der Kerr-Newman-Lösung bei Drehimpulsen und Ladungen, bei denen sich kein Horizont bildet, eines enzyklopädischen Artikels wert findet... - ich weiß nichts über diese fälle, aber zumindest über die gewöhnliche kerr-newman-lösung kann man doch durchaus noch einiges halbwegs allgemeinverständliches sagen, zb mit bildern (wie das in en:Rotating black hole, wobei es in dem buch von hawking-ellis ein imho erhellenderes bild gibt. - und ich behaupte nicht, dass dieser en:-artikel im moment optimal verständlich wäre). "allgemeinverständlich" würde in diesem fall heißen: ganz oder teilweise verständlich für jemanden, der keine differentialgeometrie gelernt hat, aber schon etwas mit begriffen wie Ereignishorizont anfangen kann.

viel erfolg noch jedenfalls - grüße, Hoch auf einem Baum 23:49, 23. Jun 2004 (CEST)

Geodätenproblem

Mir fällt gerade auf, dass eine Geodäte in der aRT auch die längste Strecke sein kann. Siehe Zwillingsparadoxon. Kann es überhaupt auch mal die kürzeste sein? Im Internet fand ich lediglich den Satz, dass eine Geodäte in der aRT die längste sein kann. Man würde eine evtl. existierende kürzeste wohl auch Geodäte nennen. Aber wäre das auch eine physikalisch mögliche kräftefreie Teilchenbahn? Gibt es also vielleicht einen feinen Unterschied zwischen Geodäte und Teilchenbahn? Wer weiß dazu was? Evt. müsste man " kürzeste " ganz streichen. --Wolfgangbeyer 19:11, 10. Jun 2004 (CEST)

Allgemein gibt es mit den Begriffen "längste" und "kürzeste" bei einer indefiniten Metrik einige Probleme :-) Allerdings, da wir es hier nur mit zeitartigen Geodäten zu tun haben, bezieht sich "längste" und "kürzeste" auf die Eigenzeit, und da gilt:

Es gibt einen längsten Weg. Dieser ist, da extremal, eine Geodäte.
Es gibt keinen kürzesten Weg. Man kann zu jedem Weg einen kürzeren finden (indem man sich immer näher an die Bahn eines Lichtstrahls annähert, der vom Ereignis 1 ausgeht, ein- oder mehrfach gespiegelt wird, und schließlich Ereignis 2 erreicht; da der Weg des Lichtstrahls durch die Raumzeit definitiv lichtartig ist, hat er in der Raumzeitmetrik die Länge Null).
Es kann mehr als eine Geodäte geben, wobei die anderen Geodäten nicht unbedingt global maximal sein müssen, sondern auch lokal maximal sein oder sogar einen Sattelpunkt darstellen können.

Generell kann man viele Aussagen für zeitartige Kurven zwischen zwei Punkten dadurch erhalten, daß man die entsprechende Raum-Analogie nimmt und dann "größer" und "kleiner" vertauscht (so kommt man z.B. von der Dreiecksungleichung zum Zwillingsparadoxon). Das ist unmittelbare Folge davon, daß die Zeit in die Metrik mit umgekehrtem Vorzeichen eingeht.

Den dritten Punkt kann man sehr schön anhand der Kugel verstehen: Die Geodäten der Kugel sind ja die Großkreise. Nun ist der kürzeste Weg zwischen zwei Punkten das kürzere Stück des Großkreises zwischen diesen Punkten, und natürlich auch Geodäte. Aber der Großkreis "hintenrum" ist natürlich auch geodätisch, obwohl er sicher nicht minimal ist. Es handelt sich hier um einen Sattelpunkt: Man kann einin ähnlichen, längeren Weg finden (indem man einfach an einer Stelle einen kurzen Umweg einbaut), aber auch einen ähnlichen, kürzeren (indem man die Ebene des Großkreises ein klein wenig um die Gerade um die zwei Punkte dreht; die neue Schnittlinie mit der Kugel ist etwas kürzer und keine Geodäte mehr).

Die korrekte Aussage wäre, daß Geodäten stets extremal sein müssen (auch Sattelpunkte sind extremal!), aber der Durchschnittsleser wird "extremal" bestenfalls mit "maximal oder minimal" übersetzen. --Ce 19:46, 10. Jun 2004 (CEST)

Ja ,Dein Argument mit den beiden Teilen des Großkreises hatte ich gerade vorhin auch unter Diskussion:Geodätische_Linie eingebracht. Dort stand nämlich bis vorhin nur, das Geodäten die kürzeste Verbindung seien. Deinem Punkt 2 von 3 oben ist eigentlich zu entnehmen, dass man den Weg beliebig nahe an Null nähern kann, wenn man nur schnell genug reist. Kleiner Null wäre aber raumartig und damit hier nicht relevant. "kürzeste" müsste man also eigentlich streichen. Probleme machen also nur sattelpunktartige Extrema, denn das sind ja weder Maxima noch Minima. Hm, handelt es sich dabei vielleicht um seltene Fälle? Schwierig hier korrekt zu bleiben ohne auszuufern. Vielleicht sollten wir korrekterweise einfach "extremal" schreiben auch wenn der Durchschnittsleser das wohl als "maximal oder minimal" übersetzt. --Wolfgangbeyer 20:37, 10. Jun 2004 (CEST)

Ich glaube nicht, dass das nur seltene Fälle sind. Wenn wir z.B. das Kepler-Problem nehmen, dann haben alle Umlaufbahnen mit derselben großen Halbachse dieselbe Umlaufzeit. Und es gibt dabei durchaus Bahnen unterschiedlicher Exzentrizität, die sich kreuzen. Nun ist in der ART natürlich die Bahn zu korrigieren, aber ich vermute sehr stark, dass sich auch hier unterschiedliche Bahnen finden, die in der Raumzeit wieder zusammenlaufen. Und es würde mich nicht wundern, wenn diese generell Sattelpunkte sind.

Für den Moment ist es sicher am besten, extremal zu schreiben, dann ist es zumindest schonmal korrekt. Eine bessere Formulierung kann man danach ja immer noch suchen. --Ce 12:26, 11. Jun 2004 (CEST)

Äquivalenzprinzip

Hallo, der Text auf Äquivalenzprinzip behandelt "ein älteres Prinzip zur Rechtfertigung der Erhebung von Steuern". Das verträgt sich ja kaum mit dem physikalischen Prinzip ;-) Wäre schön, wenn man eine Begriffsklärungsseite einfügt und dann den Physiktext reinstellt (oder hab ich den nur noch nicht gefunden??). Gruß von nem Neuling. --Gluon 15:10, 19. Jul 2004 (CEST)

Ok, Begriffsklärungsseite ist eingestellt; physikalischer Inhalt muss auf Vorhandensein nötiger Zeit warten :-) --Ce 15:23, 19. Jul 2004 (CEST)

- 2005 -

Abweichende Deutung

Letzter Kommentar: vor 19 Jahren1 Kommentar1 Person ist an der Diskussion beteiligt

Hallo Paul Conradi, habe ein paar Fragen zu Deinem Zusatz zur Protophysik. Kraftfeldlinien sind ja generell gekrümmt, sofern die Quelle (Massen bzw. Ladungsverteilung) nicht kugelsymmetrisch ist. Wie definierst Du denn die Geodäte eines Kraftfeldes? Ist im Rahmen dieser Deutung das Geschehen in einen euklidischen Raum eingebettet? Wie passt das mit den einsteinschen Feldgleichungen zusammen? Und sprachlich "..Relativität, also etwa die relativistische Krümmung .." hört sich so an, als sei Raumkrümmung ein Beispiel für Relativität. Was bedeutet der Plural bei "Deutungen"? Gibt es verschiedene? Wird jede einzelne vielleicht nur von einer oder einigen wenigen Personen vertreten? Ich bin absolut kein Kenner der Protophysik und des Konventionalismus. Ich möchte aber verhindern, dass wir hier vielleicht absolut exotische Einzelmeinungen ausbreiten, die sonst niemand ernst nimmt bzw. die vielleicht sogar widerlegt sind. Poincaré und Weinberg sind da natürlich eine solide Referenz. Allerdings war ersterer schon lange tot als Paul Lorenzen die Protophysik ausgearbeitet hat. --Wolfgangbeyer 21:58, 31. Jan 2005 (CET)

Hallo Wolfgangbeyer, danke für Deinen Diskussionsbeitrag. Mit Geodäte meine ich die "Gerade" auf der sich ein Lichtstrahl bewegt. Nur dass das keine geometrische Gerade ist. Lichtstrahlen werden abgelenkt, zum Beispiel vom Gravitationsfeld eines Himmelskörpers. Das ergibt sich aus der ART und das nenne ich deshalb relativistische Krümmung. Insofern ist die Geodäte auf der der Lichtstrahl "fließt" eine "Gerade" der nichteuklidischen Geometrie. Sprachlich ist mein Beitrag wohl etwas ungeschickt, oder? Was sollte ich verbessern? - Sehr zustimmen möchte ich, dass exotische Einzelmeinungen sich hier nicht ausbreiten. Deshalb nochmal zur Erklärung: Poincaré hat zeitlebens diesen Konventionalismus vertreten. Er meinte, wir können die nichteuklidische Geodäte als geometrische Gerade deuten, oder eben nur als Feldlinie. Es ist Konvention. (Entsprechend auch die konventionelle Deutung zwischen Lorentz und Einstein in der SRT) Aber bei Poincaré hast Du recht, der ist lange tot. Weinberg hat seine Deutung so vorgestellt, dass er selber sagt, dass das zur Zeit exotisch ("heterodox") wirkt. Weinberg Quelle: Gravitation and Cosmology, New York 1972 Seite 147f Nun bin ich kein Nervbolzen, wir können es auch wieder löschen. Es muss halt ausgelotet werden, wieviel Exotik gut ist und auch als Info gewünscht wird und wieviel wir abwenden müssen. - Schaun wir mal. Grüße --Paul 1:50, 1. Feb 2005 (CET)

Hm, schwierig, ein Problem sehe ich darin, dass es so aussieht, als müsse man vielleicht doch nicht von der Vorstellung eines euklidischen Raumes abrücken. Das könnte viele Leser, insbesondere die zahlreichen, die ein gewisses Misstrauen gegenüber naturwissenschaftlicher Erkenntnis mitbringen, und einen hier auf den Diskussionsseiten manchmal ziemlich auf Trab halten, auf die falsche Fährte bringen ("Wusst' ich's doch, dass das mit dem krummen Raum Käse ist"). Ich denke aber, dass Dein vorgestellter Ansatz keine Chance auf eine Renaissance des euklidischen Raumes bietet, sondern eher noch radikaler ist, insofern als er den Begriff "Raumzeit" wohl völlig infrage stellt und nicht nur die krumme, wenn ich das richtig interpretiere. Letztlich deckt sich das ja auch mit der mir bekannten Feststellung, dass die einzigen Aussagen über das Naturgeschehen in der aRT solche über Begegnungen sind. Wo und wann sie stattfinden ist relativ und nur eine Frage des Koordinatensystems. Deine Definition von Geodäte ist ja schon die übliche und mir bekannte. Aber die Formulierung "Geodäte eines Kraftfeldes" im Artikel bringe ich damit nicht so recht zur Deckung. Ich kenne mich mit diesem Thema zu wenig aus, um hinsichtlich dieser Probleme eine unmissverständliche Formulierung zu finden. Es sollte ja auch hier nicht zu viel Text erfordern, da es ja doch offenbar ein eher exotischer Aspekt zu sein scheint, wenn selbst Weinberg selbst das so sieht. Vielleicht sollten wir es besser bei einem Siehe auch: Protophysik belassen? --Wolfgangbeyer 23:29, 1. Feb 2005 (CET)

Hm. Ähm ich werde mal folgendes machen. Ich überarbeite meinen Beitrag und dann sagst Du nochmal was dazu, OK? --Paul 11:00, 2. Feb 2005 (CET)

Habe mal etwas umformuliert und formatiert. Da die potenziellen Skeptiker nun den Satz "... sondern als durch die Maxwellschen Gleichungen in relativistischer Revision bestimmtes Tensorfeld" genauso wenig verstehen, wie ich, ist zumindest dieser Teil meiner Bedenken überflüssig ;-). Damit finde ich auch den Hinweis auf die identische empirische Grundlage nicht mehr nötig. Inwieweit es inhaltlich korrekt ist, kann ich allerdings nicht beurteilen. Findest Du's so ok? --Wolfgangbeyer 21:27, 2. Feb 2005 (CET)

Danke für die Umformulierung! Ich habe einen Halbsatz am Schluss ergänzt. Ich hätte es anders geschrieben und mit weniger Angst vor potenziellen Skeptikern, aber mit dem Text wie er jetzt dasteht kann ich gut leben. Danke für die Ergänzung des genauen Titels des Weinbergbuches und den Litverweis.

--Paul 23:14, 2. Feb 2005 (CET)

Aber ist das denn mit Deiner Ergänzung inhaltlich noch korrekt? Ich hatte das Problem ja weiter oben schon angesprochen, und ich hatte bisher Dein Schweigen dazu als Zustimmung zu meinen Ausführungen (23:29, 1. Feb 2005) gedeutet. Bedeutet dieser Ansatz denn tatsächlich, dass man das Geschehen in einen euklidischen Raum einbetten kann, ohne dass dabei Konflikte mit den experimentellen Beobachtungen auftreten? Das würde mich schon sehr wundern. Und genau damit habe ich ja die erwähnten Probleme. Im übrigen ist der Begriff "klassisch" in Deinem Zusatz irritierend, denn die aRT zählt ja zur klassischen Physik. --Wolfgangbeyer 00:14, 3. Feb 2005 (CET)

Uppps, dann habe ich zuviel geschwiegen. Genau das bedeutet es. (Klassische Geometrie hier also, wie üblich, vorrelativistische protophysikalische Geometrie)--Paul 10:24, 3. Feb 2005 (CET)

Der Abschnitt zur Protophysik wirft einfach dermaßen viele Fragen auf, dass ich doch lieber auf Dein obiges Angebot zurückkommen möchte, meinen Vorschlag, es bei einem siehe auch: Protophysik bewenden zu lassen, umzusetzen. Ich glaube kaum, dass im Brockhaus oder der Encyclopedia Britannica diese Sache auch unter aRT thematisiert wird (habe mir eben die Encyclopedia Britannica auf 3 CDs gekauft und werde bei Gelegenheit nachsehen). Wenn selbst Weinberg es für exotisch hält, sollte ein Link genügen. Siehe übrigens auch Wikipedia:Wie_schreibe_ich_gute_Artikel#Inhalt. Das trifft genau den Punkt. Unter einer Enzyklopädie verstehe ich nicht unbedingt, dass man in jedem Artikel alles, was man dazu sagen könnte, auch sagt. Weniger ist oft mehr. Und hier verwirren wir die Leser einfach nur. Die konventionelle aRT ist ja für sie schon schwierig genug. Es ist so, als hätten wir gerade eben mühsam versucht, einem Menschen aus dem Mittelalter zu erklären, dass die Erde eine Kugel ist, und bevor er es überhaupt verstanden und akzeptiert hat, sagen wir zum Abschluss, dass das doch evtl. alles gar nicht stimmt (weil sie ein Ellipsoid ist, aber das sagen wir ihm nicht). Oder als würden die Buchläden jedem Stadtplan einen Zettel mit einem Warnhinweis beilegen: Vorsicht, die Erde ist eigentlich eine Kugel und ein Globus wäre evtl. der angemessenere Kauf ;-). Das heißt überhaupt nicht, dass ich für ein Verschweigen dieses Themas plädiere. In einem eigenen Artikel sollte es natürlich ausführlich dargestellt werden. Sehe gerade, dass unter Paul Lorenzen ja alles noch mal dargelegt wird. Einmal – wo auch immer – sollte eigentlich genügen. 3mal ist auf jeden Fal zuviel. Bin übrigens bis Di (8.2.) in Urlaub. --Wolfgangbeyer 01:29, 4. Feb 2005 (CET)

Es tauchen zwei Fragen auf (teilweise in Protophysikdiskussion schon erwähnt):

1. Lässt sich die aRT so deuten, dass der euklidische Raum (geometrisch) beibehalten wird, obwohl man eingesteht, dass die elekrodynamischen und Gravitations-"Metriken" nichteuklidisch sind?

2. Falls 1. ja, darf man das hier publik machen. Verwirrt es eher? Bereichert es? Oder klärt es sogar?

Du bist in Gefahr den Admin-Polizisten raushängen zu lassen, der genau weiß was richtig ist.

Ich bin in Gefahr den Exotik-Durchpeitscher raushängen zu lassen, der auch genau ...

Vielleicht solltest Du bei Frage 1 die Möglichkeit der Antwort ja nicht ausschließen. Ich sollte mehr Fachwissen liefern und das mache ich demnächst.

Bis dahin können wir ja Friedenspfeife auf Einstein rauchen :) --Paul 16:04, 4. Feb 2005 (CET)

Hm, ich hab's mir ja fast gedacht... Ich finde es bereits schlimm genug, dass sich im Artikel Protophysik ein physikalisch falscher Abschnitt zur ART befindet (das gleiche steht auch nochmal bei Paul Lorenzen), aber habe inzwischen aufgegeben den Hauptautor des Artikels davon zu ueberzeugen dass es falsch ist (siehe auch Diskussion:Protophysik) - bleibt's halt ein Artikel von Crackpots fuer Crackpots. Aber dass hier ein Verweis auf den Bloedsinn gegeben wird finde ich eindeutig zu krass. Schaut Euch doch bitte mal die Ausfuehrungen unter Protophysik an und entscheidet selbst of ein Link darauf gerechtfertigt ist. Da koennen wir auch gleich Links auf alle moeglichen "Alternativen" und "Widerlegungen" der ART aufnehmen - und davon gibts tausende. --Florian G. 19:00, 29. Apr 2005 (CEST)

Wie Du sicher gesehen hast, habe ich ziemlich viel Diskussionsenergie investiert, um eine diesbezügliche Textpassage hier abzuwenden. Bei dem gebliebenen "Siehe auch" hatte ich die ganze Zeit schon Bauchweh. Die Diskussion, die Du geführt hast, bestätigt eher meine Bedenken. Ich denke, wir können mit diesem 2:1 diesen Verweis entfernen. --Wolfgangbeyer 23:01, 1. Mai 2005 (CEST)Beantworten

Oh Menno, Wolfgang Beyer, da schaue ich mal einen Monat hier nicht rein... Wieviele Benutzer hat Wikipedia? Und Du/Sie suggerierst/en hier eine 2:1 Abstimmung. Hat das Stil? Und von FlorianG werde ich in die Rolle eines Crackpots gedrängt. Es ist halt doch keine Kollegialität mit Ihnen möglich. Bin enttäuscht. :( --Benutzer:Paul Conradi 15:46, 9. Juni 2005 (CET)

sorry, :) war nicht so gemeint PaCo 12:05, 4. Aug 2005 (CEST)

Relativitätsprinzip

Hallo 198.73.252.11, ich bitte um Begründung Deiner Sicht des Relativitätsprinzips der aRT. --Wolfgangbeyer 19:26, 24. Feb 2005 (CET)

Habe mal die Änderungen von 198.73.252.11 revertiert, nicht um irgendeine Formulierung durchzusetzen, sondern um eine Diskussion ins Leben zu rufen, gerne auch mit allen anderen natürlich, was mir bisher anders nicht gelungen ist. Da die Änderungen von 198.73.252.11 Aussagen betreffen, die fast ausnahmslos schon länger unbeanstandet da standen, nehme ich an, dass 198.73.252.11 sich nur an irgendwelchen Feinheiten der Formulierung stößt. Anstelle diese Passagen ersatzlos zu streichen, würde ich gerne nach einer weniger angreifbaren oder irreführenden Formulierung suchen. Dazu müsste ich aber die Einwände von 198.73.252.11 kennen. --Wolfgangbeyer 19:08, 26. Feb 2005 (CET)

Der zweite Absatz ("Damit gilt in der allgemeinen Relativitätstheorie ein deutlich erweitertes Relativitätsprinzip. Die Gesetze der Physik haben danach nicht nur in allen Inertialsystemen die gleiche Form wie in der speziellen Relativitätstheorie, sondern in beliebigen Koordinatensystemen.") ist irrefuehrend. Physikalische Gesetze sollten nicht von der Wahl eines Koordinatensystems abhaengen. Tatsaechlich kann man auch die SRT (oder viele andere Theorien) in einem Sinn koordinatenunabhaengig formulieren, sodass sie wie die ART in beliebigen Koordinatensystemen die gleiche Form hat. Mir ist bekannt, dass der obige Irrglaube dennoch weitverbreitet ist. Das mag zum einen daran liegen, dass die benoetigte Mathematik fuer eine koordinatenunabhaengige Darstellung einem grossen Teil der Physiker nicht bekannt/vertraut ist. Ein weiterer Grund mag eine Vermischung von passiven und aktiven (Koordinaten-)Transformationen sein. Wenn man sagt, Physik sei koordinatenunabhaengig, denkt man an passive Transformationen. Wenn man im Kontext der SRT dagegen sagt, Physik ist invariant unter Lorentztransformationen, denkt man an aktive Transformationen. Insofern sind diese beiden Aussagen (bei entsprechend praeziser Formulierung) kein Widerspruch. Ich schaetze, man (ich?) wird diesen Abschnitt deutlich ueberarbeiten muessen. --C.Appel 19:33, 1. Mär 2005 (CET)

Wenn ich dich richtig verstehe, dann ist dein Einwand, auch die sRT habe in allen Koordinatensystemen die gleiche Form.

Bei geeigneter Formulierung, ja.

Ich denke man kann selbst die newtonsche Physik in beliebigen Koordinaten formulieren, und sie hat dann natürlich für alle diese Koordiantensysteme zunächst die gleiche, wenn auch ziemlich komplizierte Form (vielleicht kann man das sogar koordiantensystemunabhängig formulieren).

Ah, vielleicht reden wir doch noch geringfuegig aneinander vorbei. Ich meinte genau eine koordinatensystemunabhaengige Formulierung (was, wie Du vermutest, auch fuer Newton moeglich ist). Diese Form wuerde ich auch nicht als kompliziert ansehen. Die Komplexitaet steckt in der Definition der verwendeten Objekte. Die Gleichungen sehen aber "einfach" aus. Und die Form dieser Gleichungen ist per constructionem nicht abhaengig von der Wahl spezieller Koordinaten. Beispiel E-Dynamik: In koordinatenfreier Form lauten die Maxwell-Gleichungen dF = 0, \delta F = J. F ist eine 2-Form, die dem Feldstaerketensor entspricht; es gilt F = dA, A ist die 1-Form, die dem Vektorpotential entspricht. J ist die 1-Form, die dem Stromdichtevektor entspricht.

Aber der Punkt ist doch, dass sich diese Form bei der Wahl von speziellen Koordinaten, nämlich den Inertialsystemen, erheblich vereinfacht (und zwar auch in einer dazu passenden koordiantensystemunabhängigen Form). Damit haben die Gesetze der newtonschen Physik nicht in allen Systemen die gleiche Form, sondern in manchen eine einfachere, derart dass sich diese

Sobald ich ein bestimmtes Koordinatensystem waehle, kann ich natuerlich meine Gleichungen in diesen Koordinaten formulieren. Und wie Du sehr richtig feststellst, gibt es (zumindest in Raeumen mit genuegend Symmetrie, also z.B. dem Minkowskiraum) Koordinatensysteme, in denen die Gleichungen dann einfacher aussehen als in anderen.

Systeme experimentell über diese Eigenschaft ermitteln und damit von den anderen x-beliebigen unterscheiden lassen. Ist das bei der von dir angesprochenen koordinatenunabhängig Formulierung der sRT anders?

Natuerlich sind die Inertialsysteme in der SRT ausgezeichnet. Die experimentelle Ueberpruefung, ob ich mich in einem Inertialsystem befinde, kann dennoch schwierig sein.

Die Unterscheidung zwischen passiven und aktive Transformationen ist mir tatsächlich nicht bekannt. Wundert mich auch, denn im Rahmen des Konzepts einer Raumzeit kann ich eigentlich keinen Unterschied dazwischen sehen. Ich weiß nicht, ob ich dich richtig verstanden habe. Du kannst gerne mal einen Vorschlag für eine alternative Formulieren machen. Vielleicht wird es dann klarer. Aber bedenke den Laien ;-). --Wolfgangbeyer 21:24, 1. Mär 2005 (CET)

Natuerlich bedenke ich den Laien. Vielleicht komme ich am Wochenende dazu, etwas zu formulieren. Um nochmals auf die inhaltlichen Punkte zurueckzukommen: Letztlich gilt auch Deine Argumentation fuer die ART, da die SRT letztlich "nur" ein Spezialfall der ART ist. Das solltest Du immer bedenken! -- C.Appel 11:29, 2. Mär 2005 (CET)

In Kürze: Bei "Letztlich gilt auch Deine Argumentation fuer die ART" verstehe ich nicht ganz, was du meinst. Aber gerade sehe ich, dass der kritisierte Satz tatsächlich missverständlich war, wenn auch nur in sprachlichem Sinne. Man konnte ihn nämlich lesen als die Behauptung, die aRT habe in allen Koordinatensystemen die gleiche Form wie die sRT. Aber das hattest du wohl nicht gemeint, oder? Habe es trotzdem mal korrigiert. --Wolfgangbeyer 01:38, 3. Mär 2005 (CET)

Nein, das hatte ich nicht gemeint. Wobei ich mich gerade selbst ueber meine Formulierung wundere... Ich versuch's mal etwas klarer auszudruecken: Die SRT ist ein Spezialfall der ART. Daraus folgen zwei Dinge: 1. Alles, was fuer die ART gilt (also z.B. die "koordinatensysteminvariante" Formulierung) gilt automatisch auch fuer die SRT. 2. Dinge, die fuer die SRT gelten (z.B. Existenz von ausgezeichneten Bezugssystemen) gelten mindestens in Spezialfaellen auch fuer die ART. Ich hoffe, das war jetzt etwas klarer! -- C.Appel 11:50, 3. Mär 2005 (CET)

Nicht so ganz: 1. Die Winkelsumme im Dreieck beträgt in der aRT i. A. nicht 180° und damit ist das automatisch auch in der sRT so ;-)? 2. Verstehe ich nicht. Klar, in Fällen besonderer Symmetrie gibt es ausgezeichnete Koordiatensysteme, in denen sich die Gleichung in eine besonders einfache Form bringen lassen. Aber es geht ja in unserer Diskussion ausschließlich um den allgemeinen Fall. Was hältst Du eigentlich von der alternativen Formulierung "Damit gilt in der allgemeinen Relativitätstheorie ein deutlich erweitertes Relativitätsprinzip. Danach haben die Gesetze der Physik in beliebigen Koordinatensystemen die gleiche Gestalt, und es gibt abgesehen von speziellen Situationen keine Klasse von Koordinatensystemen, in denen sie eine besonders einfache Gestalt annehmen, so wie es in der speziellen Relativitätstheorie bei Inertialsystemen der Fall ist." Kommt mir so vor, als würde das Deinem Einwand gerecht. --Wolfgangbeyer 00:40, 4. Mär 2005 (CET)

1.: Aber ja: _I.A._ beträgt die Winkelsumme im Dreieck nicht 180°. Sie beträgt genau in flachen Räumen immer 180°, also genau im Spezialfall der SRT. Die Aussage als solche ist schon korrekt. Zu Deinem Vorschlag: Es gilt _kein_ erweitertes Relativitätsprinzip (zumindest nicht in dem Sinn, wie Du es suggerierst). Lassen wir mal diesen Satz weg und passen die Formulierung im folgenden entsprechend an: "Die Gesetze der Physik haben in beliebigen Koordinatensystemen die gleiche Gestalt. Es gibt abgesehen von speziellen Situationen keine Klasse von Koordinatensystemen, in denen sie eine besonders einfache Gestalt annehmen. Eine spezielle Situation ist beispielsweise die spezielle Relativitätstheorie, die als Spezialfall in der ART enthalten ist. Eine Klasse von Koordinatensystemen, in denen konkrete physikalische Gesetze eine besonders einfache Gestalt annehmen, sind in der SRT die Inertialsysteme". Hm, vielleicht kann man die Forumulierung noch etwas verbessern. Perfekt elegant scheint sie mir noch nicht, aber sie sollte inhaltlich korrekt sein. -- C.Appel 18:00, 6. Mär 2005 (CET)

Nochmal zu 1.: Du sagtest "Alles, was fuer die ART gilt, gilt automatisch auch fuer die SRT. ". Angewandt auf den Satz "Die Winkelsumme im Dreieck beträgt in der aRT i. A. nicht 180° " folgt "Die Winkelsumme im Dreieck beträgt in der sRT i. A. nicht 180°" ;-). Du wolltest sicher etwas ganz anderes sagen.

Hm, ich glaube, wir haben geringfügig aneinander vorbeigeredet. Also lass uns die Aussage etwas genauer analysieren. Tatsächlich kann ich die Aussage auf zwei Arten und Weisen lesen: 1. Ich betrachte alle möglichen/denkbaren Lösungen der (Feldgleichungen der) ART. Dann ist die Aussage offensichtlich korrekt, denn es gibt Lösungen der ART, in denen die Winkelsumme im Dreieck nicht 180° beträgt. Du scheinst die Aussage etwas anders zu interpretieren: 2. Für eine beliebige Lösung der ART gilt jeweils, dass die Winkelsumme i.A. nicht 180° beträgt. Nun, diese Aussage ist aber offenbar schlicht falsch, da dies im Spezialfall der SRT eben nicht gilt.

Ich verstehe nicht. Dein Punkt 1. ist der 2. kursive Satz meines Textes darüber. Klar ist er korrekt. Es ging aber darum, dass der 1. kursive Satz meines Textes, ein Zitat Deines Textes, zum 3. kursiven Satz führt, und der ist falsch. Dass dieser 1. Satz nicht korrekt ist, lässt sich nicht wegdiskutieren. --Wolfgangbeyer 22:41, 20. Mär 2005 (CET)

Vielleicht "Alle Phänomene der sRT lassen sich auch mit der aRT beschreiben"?

Das ist zwar richtig, erscheint mir aber irreführend. Die Aussage ist nämlich trivialerweise korrekt, da die SRT eben "nur" ein Spezialfall der ART ist. Und konkreter: Was soll denn "mit der ART beschreiben" überhaupt heissen? Wo ist denn der Unterschied der "Beschreibungsweise" (gräßliches Wort) der ART zur SRT? Der Satz ist meiner Meinung nach inhaltsleer.

Klar sagt dieser Satz nur, dass die sRT ein Spezialfall der aRT ist. Den Rest Deines Kommentars verstehe ich nicht, denn der Satz war ja nur eine Vermutung meinerseits, was Du mit dem von mir kritisierten Satz oben evtl. hast sagen wollen. --Wolfgangbeyer 22:41, 20. Mär 2005 (CET)

Dein Textvorschlag ist inhaltlich korrekt (ich würde lediglich "Spezielle Situationen sind beispielsweise solche, die sich durch die spezielle Relativitätstheorie beschreiben lassen, die als Spezialfall in der ART enthalten ist." schreiben).

Gerne.

Aber wenn ich mir dann den resultierenden Gesamttext ansehe, bleiben wir dann nicht dem Leser eine Definition des Relativitätsprinzips der aRT schuldig und erklären ihm statt dessen eher das Korrespondenzprinzip zwischen sRT und aRT?

Hm, zu den _beiden_ _unterschiedlichen_ "Relativitätsprinzipien" schreibe ich unten noch mehr. Wenn wir uns irgendwann einig sind, formuliere ich auch gerne was (hoffentlich) öffentlichkeitstaugliches.

Dass die Gesetze der Physik in allen Koordinatensystemen die gleiche Gestalt haben, scheint für Dich ja nicht das Relativitätsprinzip der aRT auszumachen, da Du den Standpunkt vertrittst, das gelte auch für die newtonsche Mechanik, wenn ich Dich richtig verstanden habe.

Das habe ich so hoffentlich nicht gesagt. (Und falls doch, dann war es in der Hitze des Gefechts. Ich bitte um Entschuldigung für etwaige Verwirrung.) Die Unterschiede zu meiner Aussage sind jedenfalls subtil: Die Gesetze der Physik sollten/dürfen nicht von der Wahl eines Koordinatensystems abhängen. Das ist hoffentlich allgemein einsichtig: Was ich messe, ob ich etwas messe, das sollte nicht davon abhängen, welche Etiketten ich bestimmten Punkten der Raum-Zeit gebe.

Die moderne Mathematik stellt nun auch Methoden zur Verfügung, die eine solche Beschreibung ermöglichen (Stichwort Differentialgeometrie, Vektoren, Formen, etc.). Wenn ich nun solche Objekte zur Formulierung meiner physikalischen Gesetze verwende, sind diese trivialerweise nicht mehr von einem Koordinatensystem abhängig (die Maxwellgleichungen bspw. lauten in entsprechender Schreibweise dF = 0, \delta F = J).

Natürlich kann ich diese Gleichungen auch für die Koordinatendarstellung der verwendeten Objekte formulieren. Die Gleichungen sehen dann komplizierter aus (sie erhalten vor allem einen ganzen Haufen Indizes), sollten aber immer noch in jedem Koordinatensystem dieselbe Form haben (z.B. das Skalarprodukt zweier Vektoren lautet g_ij a^i b^j).

In Räumen mit genügend Symmetrie kann ich nun Koordinatensysteme finden, in denen sich die Metrik eine einfache Darstellung hat. Die entsprechenden Gleichungen werden dann in dieser expliziten Koordinatendarstellung entsprechend einfacher. In der SRT bspw. kann ich immer Koordinatensysteme angeben, in denen die Metrik die Form g_ik = diag(1, -1, -1, -1) hat (das sind genau die Inertialsysteme). Das oben als Beispiel angegebene Skalarprodukt zweier Vektoren vereinfacht sich dann weiter zu a_i b^i.

Wie gesagt hängt diese Vereinfachung davon ab, ob die zugrundeliegende Raumzeit genügend Symmetrie besitzt. In diesem Fall sind die "vereinfachten" Gleichungen (hm, ich weiss jetzt auswendig nicht genau, ob das immer gilt) im allgemeinen forminvariant bezüglich entsprechender Symmetrietransformationen.

Was folgt? In entsprechender Form hingeschrieben, sehen physikalische Gesetze bereits in der SRT in jedem Koordinatensystem gleich aus bzw. sind von Koordinaten überhaupt unabhängig. Andererseits kann ich in der SRT spezielle Koordinatensysteme finden (die Inertialsysteme), in denen die physikalischen Gesetze, wenn ich sie in einer expliziten koordinatenabhängigen Darstellung formuliere, eine etwas einfachere Form annehmen. Diese Form ist dann invariant bezüglich Lorentztransformationen.

Die allgemeine Verwirrung hat meines Erachtens mehrere Ursachen: Die genannten Erkenntnisse haben sich erst im Laufe der Zeit herausgebildet. In älteren Abhandlungen, aber auch in aktuellen Einführungen in die Thematik, wird oft noch die "alte" koordinatenabhängige Darstellung verwendet. Moderne Differentialgeometrie mit koordinatenfreier Darstellung (Formenkalkül, etc.) ist vielen Physikern unbekannt. Insofern ist eine Sichtweise, wie Du sie zu haben scheinst, weit verbreitet und wird leider nach wie vor in vielen Abhandlungen suggeriert.

Kann ich aus "Es gilt _kein_ erweitertes Relativitätsprinzip (zumindest nicht in dem Sinn, wie Du es suggerierst)" schließen, dass es doch ein erweitertes Relativitätsprinzip gibt nur eben nicht so, wie ich es für Dich zu suggerieren scheine?

Ich hoffe, meine obige Ausführung ist einigermassen verständlich und macht das ganze etwas klarer.

Wie würdest Du dieses dann formulieren? Ich versuche mal zu beschreiben, was ich mit "erweitert" sagen wollte. In der sRT nehmen die Gesetze der Physik in Inertialsystemen eine besonders einfach Gestalt an. Da diese Koordinatensysteme in der sRT alle gleichwertig und ununterscheidbar sind, gilt bezüglich dieser Koordinatensysteme ein Relativitätsprinzip. In der aRT sind alle beliebigen Koodinatensysteme gleichwertig und ununterscheidbar und damit gilt das Relativitätsprinzip bezüglich aller Koordinatensysteme.

In dem Sinne, wie dies in der ART gilt, gilt es in der SRT ebenfalls. Siehe meine Ausführung oben. Nochmals mit anderen Worten: Du sprichst hier von zwei unterschiedlichen Relativitätsprinzipien (daher vermutlich die Verwirrung): 1. Das "Relativitätsprinzip" der ART (das so auch für die SRT gilt), besagt in etwa, dass physikalische Gesetze nicht von der Wahl eines Koordinatensystems abhängen. Mit entsprechenden mathematischen Hilfsmitteln kann ich die entsprechenden Gleichungen auch tatsächlich so formulieren, dass sie in jedem Koordinatensystem dieselbe Form haben. 2. Das "Relativitätsprinzip" der SRT besagt, dass die Raumzeit der SRT eine besondere Symmetrie besitzt (die gekrümmte Räume i.A. nicht haben). Diese erlaubt es, besondere Koordinatensysteme zu wählen, in denen sich Gleichungen noch etwas vereinfachen gegenüber der allgemeinen Darstellung. Weiter sind die Gleichungen in der vereinfachten Form invariant unter der entsprechenden Symmetriegruppe (nämlich der Lorentzgruppe).

Da das "mehr" Systeme sind als in der sRT würde ich dieses Relativitätsprinzip als erweitert bezeichnen. Dabei ist lediglich vielleicht irritierend, dass dieses "mehr" eigentlich mit einem "weniger" an Gesetzmäßigkeit korrespondiert, also gewissermaßen einem Mangel an physikalischen Gesetzen, mit deren Hilfe man bestimmte Koordinatensysteme von anderen unterscheiden könnte. Ist es das, was Dich an der Bezeichnung "erweitert" stört? --Wolfgangbeyer 00:41, 8. Mär 2005 (CET)

Mich stört, dass zwei deutlich unterschiedliche "Relativitätsprinzipien" nicht sauber unterschieden werden. Ich hoffe, meine Ausführungen haben das einigermassen deutlich machen können. Das, was Du hier "Mangel an physikalischen Gesetzen" nennst, ist eigentlich der Mangel an Symmetrie(n). Der springende Punkt der SRT ist eben, dass sie Aussagen über die Struktur der Raumzeit macht: Sie sagt, dass die Raumzeit eine besondere Symmetrie besitzt, mit der man eben bestimmte Koordinatensysteme von anderen unterscheiden kann. Darüberhinaus gilt alles, was allgemein für die ART gilt, auch für die SRT. Die SRT ist nur etwas "einfacher", da in ihr die Raumzeit besondere Symmetrie besitzt. -- C.Appel 17:14, 8. Mär 2005 (CET)

"Die Gesetze der Physik sollten/dürfen nicht von der Wahl eines Koordinatensystems abhängen." Das klingt auf den ersten Blick plausibel, ist aber durchaus angreifbar formuliert. Das Geschehen selbst hängt trivialerweise nicht von einer Wahl des Koordinatensystems ab. Es gibt aber 2 verschiedenartige Einwände. 1. Kritik an Deinem Nachsatz "Was ich messe, ob ich etwas messe, das sollte nicht davon abhängen, welche Etiketten ich bestimmten Punkten der Raum-Zeit gebe.": Das was ich messe, kann schon vom Koordinatensystem abhängen, nämlich trivialerweise dann, wenn das Messergebnis aus Koordinatenwerten von Raum und Zeit besteht.

Das ist trivialerweise richtig. Das ist allerdings auch keine Physik. Was mich als Physiker vielmehr interessiert, ist, an Dein Beispiel angelehnt, die Frage, ob ein Teilchen einen bestimmten Punkt der Raum-Zeit passiert. Welche Etiketten ich diesem Punkt gebe, ist aber belanglos.

Und 2. ist die Frage, ob man mit den Gesetzen der Physik die Gleichungen meint, mit denen man sie formuliert. Wir hatten ja festgestellt, dass manche Gesetze in bestimmten Koordinatensystemen eine besonders einfache Gestalt annehmen. Gewöhnlich versteht man unter diesen Gesetzen der Physik dann auch diese einfachere Form.

Aeh, Beweis durch Behauptung?!? Ich sehe das nicht so. Die "Gesetze der Physik" haengen nicht von der Form ab, in denen ich sie formuliere. Bsp. Elektrodynamik: Es gibt viele Varianten, um die Maxwell-Gleichungen zu formulieren, und sie sind letztlich alle aequivalent (integrale Schreibweise, differentielle Schreibweise, Formulierung unter Verwendung von Differentialformen, ...). Eine bestimmte dieser Formen als "Gesetz der Physik" zu bezeichnen waere auch einer gewissen Beliebigkeit ausgesetzt: Wer definiert, welches die "einfachste" Form ist? Nein, das "Gesetz" ist vielmehr, dass es eine elektromagnetische Wechselwirkung gibt, die ein bestimmtes, definiertes Verhalten zeigt. In welcher Form ich dieses Verhalten beschreibe, ist dafuer irrelevant und aendert nichts am Verhalten.

Das kollidiert ein wenig mit Deinem Satz. Beispiel die newtonsche Gesetze. Sicher könnte man in F=ma die beteiligten Größen womöglich so definieren, dass diese Beziehung auch in krummlinigen Koordinaten so geschrieben Sinn gibt. Das macht aber kein Mensch, sondern jeder interpretiert sie als Abkürzung für (F_x, F_x, F_x)=m (:x, :y, :z) (lies ":" hier als Operator der 2. Ableitung nach der Zeit) für beliebige kartesische Koordinatensysteme.

??? Auch hier muss ich Dir widersprechen. Gerade (oder bereits) in der Form F=ma ist es eine Gleichung zwischen Vektoren, und somit nicht mehr abhaengig von der Wahl eines konkreten Koordinatensystems. Ich kann nun ein kartesisches Koordinatensystem waehlen und die Gleichung dann fuer die einzelnen Koordinaten explizit hinschreiben, so wie Du es gemacht hast. Das macht aber genau nicht _jeder_; das macht man vielleicht in der Schule, oder wenn kartesische Koordinaten aufgrund weiterer Randbedingungen eine konkrete Rechnung vereinfachen. Bereits im ersten Semester Physik lernt man, dass es neben den kartesischen Koordinaten auch andere gibt, und es durchaus Sinn machen kann, solche anderen zu verwenden. Hast Du in Deinem Studium nie Nabla oder den Laplace-Operator in Kugelkoordinaten ausdruecken muessen? Fuer einen (theoretischen) Physiker ist es Standard, alle moeglichen Koordinatensysteme zu verwenden; man waehlt das, was weitere Rechnungen vereinfacht. Kartesische Koordinatensysteme treten dann im Tagesgeschaeft sogar eher selten auf. Insofern wuerde ich Deine Aussage genau umgekehrt formulieren: _Jeder_ (Physiker/Mathematiker) liest F=ma als koordinatenunabhaengige Gleichung zwischen Vektoren; _kein_ (Physiker/Mathematiker) interpretiert diese Gleichung als Abkuerzung fuer nur genau (F_x, F_x, F_x)=m (:x, :y, :z).

Du tust aber immer so, als gäbe es nur Sinn, die Gesetze der sRT stets in einer Form hinzuschreiben, die auch krummlinige Koordinaten zulässt, obwohl sie sich im Falle Gültigkeit der sRT wegen g_ik = diag(1, -1, -1, -1) vereinfach ließen.

Ich habe nicht gesagt, dass nur dieses Sinn ergibt. Ich habe gesagt, dass man die SRT, genau wie die ART, koordinatenunabhaengig formulieren kann. Das man es _kann_, das ist der Knackpunkt.

Mag sein, das man das in manchen Bereichen tatsächlich macht, in einer Anfängervorlesung, sicher nicht. Und auch Einstein dürfte es vor 1916 nicht so hingeschrieben haben. Trotzdem hat er die Gesetze der sRT zu Papier gebracht.

Natuerlich. Das ist auch unabhaengig von meiner Aussage.

Beantworte doch mal bitte die Frage, ob nach Deiner Auffassung der Satz "Das Relativitätsprinzip der sRT besagt, dass die Gesetze der sRT in allen Inertialsystemen die gleiche Gestalt haben, so dass diese Inertialsysteme ununterscheidbar und gleichwertig zur Beschreibung der Vorgänge sind" einen Sinn gibt. Falls nicht, was wäre dann Deiner Ansicht nach die Aussage des Relativitätsprinzip der sRT? Vielleicht kommen wir weiter, wenn Du einfach mal einen konkreten Textvorschlag machst, und schreibst wie Du das Relativitätsprinzip der sRT und der aRT inkl. der Unterschiede definieren bzw. laiengerecht beschreiben würdest. Der Satz "Alles, was allgemein für die ART gilt, gilt auch für die SRT." kommt hoffentlich darin nicht vor ;-). --Wolfgangbeyer 22:41, 20. Mär 2005 (CET)

Ja, ich hatte mir ohnehin vorgenommen, einen Textvorschlag zu formulieren. Wie Du gerade an meiner Antwortzeit merkst, fehlt mir momentan allerdings etwas die Zeit dazu. :-(. -- C.Appel 12:24, 29. Mär 2005 (CEST)

Termin Veröffentlichung

Hallo zusammen - die Archenhold-Sternwarte in Berlin beansprucht für sich, der erste öffentliche Vortrag zur Allgemeinen Relativitätstheorie von Albert Einstein habe bei ihr stattgefunden. Da war hier im Lokalblättchen ein Bericht eines Mitarbeiters dazu veröffentlicht, dem man entnehmen kann, dass Einstein die Allgemeine Relativitätstheorie am 4. Nov. 1915 auf der Gesamtsitzung der Preußischen Akademie der Wissenschaften in Berlin vorgestellt hat (etwas ausführlicher dazu in Diskussion:Archenhold-Sternwarte) - es ist keine hochwissenschaftliche Quelle, aber es werden zumindestens überprüfbare Fakten genannt - falls es jemanden interessiert, dachte ich, ich erwähne das hier mal ;-) -- Schusch 16:40, 7. Mär 2005 (CET)

Änderung eines Wikipedia-Laien

Hallo, hier hat wohl ein Laie versucht etwas beizutragen - ich traue mir nicht zu, etwaige Informationen in den Artikel zu übernehmen, aber sinnlos war es ja keinesfalls, was er schrieb. -- Schusch 22:25, 11. Mär 2005 (CET)

Beziehung zwischen sRT und aRT und "Wäscheleine"

Die allgemeine Relativitätstheorie stellt eine Erweiterung der speziellen dar und geht für hinreichend kleine Gebiete der Raumzeit in diese über. Das halte ich als Physiker für zweifelhaft. Die ART ist eine Gravitationstheorie. In der SRT gibt es keine Gravitation. Wie kann die ART als Grenzfall in die SRT übergehen? Schweikhardt

Im Fall hinreichend kleiner Raumzeitgebiete lassen sich immer lokal Inertialsysteme definieren, in denen die sRT anwendbar ist, da die Effekte der Krümmung verschwinden. Die Gravitation äußert sich in diesen Raumzeitgebieten dann nur noch als "konstantes Kraftfeld", das durch eine entsprechende Wahl dieser Inertialsysteme verschwindet, indem man es an frei fallenden Gegenständen orientiert. Habe Deinen Satz " Mit zunehmender Geschwindigkeit wird diese Krümmung immer stärker" wieder entfernt, da er den Leser eher verwirren dürfte. Die Geschwindigkeit von der Du sprichst, ist ja v=c, mit der wir uns gewissermaßen in Richtung x₄=ct bewegen. Da sie in diesem Sinn konstant ist, sollte man nicht von "zunehmend" sprechen. Außerdem würde die Krümmung dieser Bahn in der Raumzeit ja nicht stärker, wie Du schreibst, sondern nur aus der Sicht des sich Bewegenden auffälliger. Finde, die Sätze davor beschreiben den Sachverhalt eigentlich ausreichend. Habe Deinen Diskussionsbeitrag an die übliche Stelle, das Ende der Diskussionsseite, verschoben. --Wolfgangbeyer 23:01, 23. Mär 2005 (CET)

Zum Raumkrümmungs-Bild

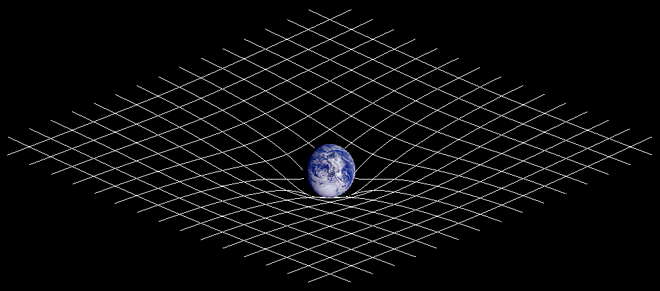
Es geht um folgendes, in den Artikel eingefügte Bild:

Bilder wie dieses werden zwar gerne in populärwissenschaftlichen Präsentationen verwendet, sind aber irreführend: Durch die auf der gekrümmten Fläche liegende Kugel wird suggeriert, daß die Fläche durch das Gewicht der Kugel in einer im Bild senkrecht wirkenden Gravitation eingedellt würde (also: man spannt ein Tuch horizontal und legt eine Kugel drauf, und weil die Kugel nach unten angezogen wird, wird das Tuch nach unten ausgebeult). Entsprechend kommt man dann leicht auf die Idee, die Anziehung beruhe darauf, dass andere Körper auf dem eingedellten Tuch nach unten rollen (was anschaulich ist, aber mit den tatsächlichen Verhältnissen in der ART nichts zu tun hat).

Um es klarzustellen: Das Problem ist nicht, dass das Bild objektiv falsch wäre (ein passend gewählter zweidimensionaler Schnitt durch den Raum bei konstanter Schwarzschild-Zeitkoordinate würde vermutlich eine ungefähr so gekrümmte Fläche ergeben). Das Problem ist, dass das Bild einen falschen Eindruck vermittelt (es ist nirgendwo gesagt, dass z.B. die Kugel die Fläche durch ihr Gewicht nach unten zieht, aber es entsteht der Eindruck).

Vielleicht wäre die einfachste Art, diesen falschen Eindruch zu vermeiden, das Bild einfach um 90° zu drehen, so dass die Fläche senkrecht steht. Da normalerweise niemand die horizontale Richtung mit der Erdanziehung in Verbindung bringt, würde das vermutlich Fehlinterpretationen vorbeugen. --Ce 20:17, 24. Mär 2005 (CET)

Das Bild hat ja eigentlich gleich 3 gravierende Probleme:

Es wird, wie erwähnt, der Eindruck erweckt, eine nach unten gerichtete "Schwerkraft" würde die Delle bewirken,
die Krümmung des Raumes ist um viele Größenordnungen überzogen, und
es wird der Eindruck erweckt, diese Raumkrümmung würde Satelliten und den Mond auf seiner Bahn halten, indem sie sich auf ihren Geodäten oder gar unter dem Einfluss der nach unten gerichtete "Schwerkraft" bewegen.

Mit einer Drehung um 90° lösen wir nur das erste Problem. Wir müssten dann aber viele Worte verlieren, um zu erklären, was denn überhaupt dargestellt ist, denn es wäre dann nicht mehr so intuitiv klar (wenn auch falsch) wie vorher. Und dabei kämen wir angesichts der beiden anderen Probleme in Schwierigkeiten. Es wird einfach ganz schön viel Korrektkeit der Verständlichkeit geopfert. Ich denke wir sollten es eher ganz entfernen. --Wolfgangbeyer 22:49, 24. Mär 2005 (CET)

Die Übertreibung der Krümmung sehe ich nicht als ein gravierendes Problem (da die reale Krümmung nicht sichtbar wäre, wäre eine nicht-überzogene Krümmung witzlos; auch in anderen Bereichen werden Effekte gerne überhöht dargestellt, um sie überhaupt sichtbar zu machen). Inwieweit die (auch so bestehende) Gefahr, daß jemand denken könnte, Objekte folgten Raumgeodäten statt Raumzeitgeodäten, durch das Bild verstärkt werden könnte, weiß ich nicht. Auf jeden Fall sollte die Tatsache, dass Körper nicht Raumgeodäten, sondern Raumzeitgeodäten folgen, aber im Text betont werden, ob nun mit oder ohne Bild. Ich versuche mal, eine entsprechende Formulierung einzubauen.

Der Punkt, dass das Bild seine Intuitivität gerade der falschen Interpretation verdankt, ist allerdings ein guter. Insofern ist es wahrscheinlich tatsächlich am besten, das Bild aus dem Artikel zu entfernen. --Ce 13:14, 26. Mär 2005 (CET)

Hallo Ce, auf die Tatsache, dass Körper nicht Raumgeodäten, sondern Raumzeitgeodäten folgen, wird ja im Abschnitt Der schiefe Wurf als Folge einer gekrümmten Raumzeit ausgiebig eingegangen. Letztlich handelt dieser ganze Abschnitt von nichts anderem. Insofern hätte ich es soweit oben nicht zusätzlich erwähnt. Insbesondere nicht direkt in der Aufzählung dieser beiden Eigenschaften. Dieser Abschnitt ist ja so aufgebaut, dass zuerst mal die beiden Eigenschaften formuliert werden und im Rest des Abschnittes nacheinander erläutert werden. Dein Satz zählt zu den Erläuterungen. Ich habe den Satz daher mal wenigstens gekürzt und auch sprachlich korrekt eingepasst. Aber eigentlich wäre ich eher dafür, ihn ganz zu entfernen. --Wolfgangbeyer 15:21, 26. Mär 2005 (CET)

Ich halte es schon für eine gute Idee, den Leser schon an dieser Stelle auf das mögliche Missverständnis hinzuweisen. Andererseits kann ich auch damit leben, wenn der Satz entfernt wird. --Ce 10:53, 30. Mär 2005 (CEST)

5. Dimension

Hallo Szs: "Es wird jedoch mit den Mitteln der allgemeinen Relativitätstheorie daran geforscht, welche Auswirkungen eine 5. raumartige Dimension hätte. Wenn auf diese Weise messbare Effekte vorhergesagt würden, könnte man experimentell oder durch Beobachtung ein solche Dimension nachweisen oder widerlegen." Sind tatsächlich solche Varianten der ART in der Diskussion, die noch nicht durch die bestehenden Daten falsifiziert sind? Und haben sie tatsächlich den Stellenwert, dass sie in diesem Artikel erwähnenswert wären? Oder soll das heißen, man kann nicht 100%ig ausschließen, dass noch jemandem eine einfällt? Wir sollten den Leser nicht unnötig mit exotischen Ausflügen, die er nicht einschätzen kann, verwirren. Er hat's bei diesem Thema ja schon so schwer genug ;-). --Wolfgangbeyer 23:00, 1. Jun 2005 (CEST)

Hi Wolfgang: Ich werde nochmal den Kollegen fragen, wer da genau wie intensiv dran forscht, und ob das noch aktruell ist, danach können wir weiter sehen. Danke für den Hinweis! --Szs 15:23, 3. Jun 2005 (CEST)

Hallo nochmal: also ich habe mich schlau gemacht und das mit der 5.Dimension ist sehr aktuell; ein bedeutender Forscher auf dem Gebiet ist Cavaglia. Interessant und bald dem Experiment zugänglich sind weitere Dimensionen, weil sie einen Einfluss auf die Planck-Einheiten haben. Z.B. Wird die Planckenergie bei zehn Raumdimensionen, wie sie die Stringth. annimmt erst auf ca. 1 TeV herabgsetzt und dadurch für neue Teilchenbeschleuniger zugänglich. D.h. vorhergesagte quantengravitative Effekte werden nur sichtbar, wenn es extra-Dimensionen gibt. Die Frage bleibt trotzdem, ob man das erwähnen sollte. Meinungen? Extra-Artikel Extra-Dimensionen? --Szs 20:54, 11. Jun 2005 (CEST)

Ich bin etwas verwundert über die explizite Nennung der 5. Dimension. Das erscheint mir irreführend. 1. ist das dann nicht mehr Allgemeine Relativitätstheorie. Auch Deine weiteren Kommentare (Stichwort Planckenergie, Quantengravitation) ist eben nicht mehr Allgemeine Relativitätstheorie. 2. sind "Extra"-Dimensionen nichts besonderes (für theoretische Physiker). Im Rahmen der Super-Stringtheorie bspw. hat die Raum-Zeit 10 Dimensionen, wie Du auch oben erwähnst. Mit Extra-Dimensionen, wie sie in SF-Filmen oder -Büchern erwähnt werden, hat das aber nicht viel zu tun (so nach dem Motto "... wir reisen in eine andere Dimension ..."). Insofern dürfte ein Artikel Extra-Dimensionen nur zur Verwirrung beitragen, weil er diesem Begriff eine Bedeutung gibt, die er meiner Meinung nach aus Physiker-Sicht nicht hat. Interessierte könnte man auf (Super-)Stringtheorie verweisen. Zu Cavaglia: Eine kurze Recherche zeigt, dass Cavaglia im Bereich Stringtheorie unterwegs ist. Zu sagen, er forscht nach einer 5. Dimension, erscheint mir irreführend. C.Appel 11:38, 14. Jun 2005 (CEST)

@c.Appel: Hi! Danke für die Kritik.

ad 1: Die ART ist eine geometrische Theorie über Riemann-Mannigfaltigkeiten und nicht an die Zahl der Dimensionen gebunden. Normalerweise wird mit 4 Dim. gerechnet, die Mathe kann aber auch in anderesdimensionierten Räumen angewendet werden und zu Erkenntnis führen.

Ja, klar. Dann sollte man das aber auch so formulieren. Wobei dann noch die Frage bleibt, ob das tatsächlich ein aktuelles Forschungsgebiet ist. Bei Cavaglia habe ich da, wie schon gesagt, nichts gefunden (zum Thema ART in mehr als 3+1 Dimensionen). (Super-)Stringtheorie oder sonstige Versuche einer Quantengravitationstheorie mögen zwar mit mehr Dimensionen hantieren, sind aber eben nicht mehr ART.

ad 2: Wenn es nichts besonderes ist, warum wundert Dich dann die Nennung ;-) Aber im Ernst: Ich bin (auch?) Physiker und rede nicht von Science Fiction. Dass die Nennung der Forschung an Extra-Dimensionen Verwirrung stiftet, kann ich nicht nachvollziehen, und es wird dem Begriff "Dimension" auch keine unphysikalische Bedeutung gegeben. Der Verweis auf Stringtheorie ist natürlich gerechtfertigt, wenn dann da über ebendiese Forschung berichtet wird.

Mich wundert die explizite Nennung der _5._ Dimension. Was ist an der 5 so speziell? Mir erscheint einfach diese Hervorhebung der 5 in diesem Zusammenhang ein wenig irreführend. Und ja, ich bin auch Physiker.

ad Cavaglia: "nach einer 5.Dim. forschen" hat ja auch keiner gesagt...

? Dann reden wir unterschiedliche Sprachen. Ich zitiere: "... das mit der 5.Dimension ist sehr aktuell; ein bedeutender Forscher auf dem Gebiet ist Cavaglia".

Er nimmt für seine Berechnungen Extradimensionen an und sagt Effekte voraus. Das ist ein Unterschied. Er ist zwar im Bereich Stringtheorie unterwegs, aber ebenso in der ART. Ein Blick auf seine Publikationen zeigt, dass er und seine Kollegen sich in letzter Zeit immer wieder auf SL beziehen und das ist ja eindeutig ART... Die suchen halt TeV-Löcher in den neuen Beschleunigerm und nicht nach supermassereichen im Universum.

Ich habe gerade einmal in eines dieser Paper reingeschaut: Er redet explizit von Quantum Gravity. Es geht bei seiner Forschung also eben nicht um reine ART.

Fazit: Ich denke, eine Nennung, dass es diese Forschung gibt, ist hier nicht fehl am Platz. Gerade um Missverständnissen vorzubeugen.

Wenn es momentan in diesem Bereich ernstzunehmende Forschung gibt. C.Appel 12:27, 15. Jun 2005 (CEST)

MMhhh... Du hast recht mit Es geht bei seiner Forschung also eben nicht um reine ART. Berührungspunkte sind zwar da, aber reine ART ist das nicht. Ich werde meinen Zusatz im Artikel also erstmal vorläufig auskommentieren, bis ich nochmal unseren ART-Spezi befragt habe. Vielleicht läuft das auf einen Artikel Extra-Dimensionen hinaus oder ein neues Unterkapitel in den Artikel ART oder Quanten-Gravitation... Mal seh'n... --Szs 11:34, 16. Jun 2005 (CEST)

ART protophysik

(von meiner Diskussionsseite hierherkopiert, --Florian G. 21:18, 8. Jun 2005 (CEST))

Hallo Floriang, hast Du vor dem Löschen meines Beitrags gelesen, was ich geschrieben habe? Ich habe nichts geschrieben, dem du bisher widersprochen hättest. Hast Du nicht nur schubladenmäßig gelöscht?? --Paul 15:52, 8. Jun 2005 (CEST)

Hallo Paul. Nein, ich habe nicht schubladenmäßig geloescht. Die "Interpretation" der ART durch die Protophysik ist mathematisch und physikalisch unklar und ein Produkt der unsäglichen "Deutschen Physik". Es ist meiner Meinung nach schlimm genug, dass in dem Artikel Protophysik so wirres Zeug zur ART steht, aber in Allgemeine Relativitätstheorie gehört es sicherlich nicht rein. Dazu gab es doch auch schonmal eine Diskussion hier. Ausserdem ist der Inhalt Deines Absatzes physikalisch falsch, ich habe Dir bereits auf Diskussion:Protophysik zu erklaeren versucht, dass ART und Elektrodynamik erstmal nichts miteinander zu tun haben. Glaub mir, ich will Dich bestimmt nicht persönlich ärgern, es geht einfach darum diese philopsophische "Deutung" im Hauptartikel zur ART meiner Meinung nach (und ich glaube kaum dass ich da eine Außenseiterposition vertrete) nichts zu suchen hat. Grüße, --Florian G. 21:18, 8. Jun 2005 (CEST)

Hallo Floriang, zwei Antworten: 1. Ich bin nicht nur "gegen" die Deutsche Physik, sondern ich bin auch sehr erfreut darüber, dass es allgemein eine starke Sensibilität dafür gibt, Tendenzen entgegenzuwirken, dass an die Nazis angeknüpft wird. Dies ist mir übrigens viel wichtiger als alles andere (und auch als mein Engagement für die Protophysik).

2. Licht ist ein elektromagnetisches Phänomen, oder? Lichtstrahlen werden (bei der Überprüfung der ART ist das ja so berühmt geworden) von Gravitationsfeldern abgelenkt. Wer (keiner außer der Deutschen Physik vor 80 Jahren) das bestreitet, wird ignoriert. - Nun zu Deinem Beitrag: Wieso sagst Du die ART hat nichts mit Elektrodynamik zu tun?--Paul 21:43, 8. Jun 2005 (CEST)

zu 1.: Prima, da sind wir uns einig.

zu 2.: Setz den Energie-Impuls-Tensor null (Vakuum) und such nach Loesungen. Diese existieren, also ist die Theorie konsistent ohne Materie. --Florian G. 21:54, 8. Jun 2005 (CEST)

zu 1. Ja!

zu 2. Das ist zu philosophisch. Wir haben kein Vakuum. - Ich fasse die gekrümmten Mannigfaltigkeiten physikalisch auf und das ist eben keine philosophische Raumzeit, sondern "nur" mathematisch-physikalisches Beschreibungsmittel.--Paul 22:06, 8. Jun 2005 (CEST)

Hm, verstehe ich nicht. Das hat nichts mit Philosophie zu tun. Da geht es nur um die pragmatische Suche nach Loesungen der Feldgleichungen. Vielleicht definierst Du mal ein bisschen genauer (mathematisch) was Du mit Deiner "physikalischen Auffassung" meinst. Gute Nacht, --Florian G. 22:21, 8. Jun 2005 (CEST)

Oben (Zum Raumkrümmumgsbild) ist ja ein recht anschauliches Bild mit einem Gitternetz, das bei einem Himmelskörper halt typisch "relativistisch gekrümmt" ist. Ich fasse dieses Gitternetz als ein Hilfsmittel auf, zu beschreiben, auf welchen Bahnen Licht (und andere e-dynamische Phänomene), also Photonen sich bewegen. Das ist Physik a posteriori. Ob die "Raumzeit" damit etwas zu tun hat ist philosophisch umstritten. Ich sage nein. Du sagst: Ja, ohne Frage. Ob wir mal einander akzeptieren können, weiß ich nicht, hoffe es aber. Grüße Paul 15:29, 9. Jun 2005 (CEST)

Bilder

Tach auch, dieser Artikel ist wohl einer der umfangreichsten ohne Bild. Ich wollte mal eine Diskussion anregen, ob und wie man das ändern könnte. Eine Idee wäre als Mindestens einen oder mehrere Links auf die AG "Visualisierungen der ART" von Prof. Ruder in Tübingen zu setzen. (Ist keine Eigenwerbung, ich habe mit jener AG nichts zu tun, mein ART Wissen begrenzt sich auf meine Nebenfachkenntnisse.) AlterVista 18:22, 17. Jun 2005 (CEST)

GPS inkl. Rechenbeispiel

Die Abschnitte zum GPS inkl. Rechenbeispiel sind eine totale Themaverfehlung, bei der ein winziges Teilphänomen der ART in einer völlig unangemessenen Detailtreue dargestellt wird. Die Textpassage, in der das GPS-Problem kurz erwähnt wird, ist völlig ausreichend. Zusätzlich ist die Darstellung nicht korrekt, siehe dazu Global_Positioning_System#Genauigkeit_der_Positionsbestimmung sowie die vorausgegangene Diskussion, die sich unter Diskussion:Relativitätstheorie#Uhren_im_Gravitationsfeld befindet. Habe diese Abschnitte daher wieder entfernt. --Wolfgangbeyer 22:07, 8. Aug 2005 (CEST)

Hallo Wolfgangbeyer,
ob das völlig ausreichend ist, werden Physiker und interessierte Laien völlig unterschiedlich beurteilen.
Ich wurde schon oft gefragt, wie man die gravitative Zeitdilatation berechnet, oder was das überhaupt in der Praxis bedeutet.
In der Zwischenzeit findet man diese Erkärungen hier:
Diskussion:Relativitätstheorie#Praxisnahes Rechenbeispiel
Mit freundlichen Grüssen,
Karl Bednarik 10:57, 10. Aug 2005 (CEST).

Versionsbereinigung

Durch das Löschen der Versionen, die eine URV beinhalteten (am 28. Juni eingestellt, der kopierte Text wurde aber erst durch Benutzer:Wolfgangbeyer am 8. August gelöscht) sind diese Änderungen in der Versionshistorie nicht mehr zu sehen:

(Aktuell) (Vorherige)  17:40, 7. Aug 2005 Karl-Henner K (+ th)
(Aktuell) (Vorherige) 13:43, 4. Aug 2005 Floriang K (→Populärwissenschaftlich - korr.)
(Aktuell) (Vorherige) 13:43, 4. Aug 2005 Floriang (→Literatur - ergaenzt)
(Aktuell) (Vorherige) 12:04, 3. Aug 2005 134.76.61.111 (→Weitere Überprüfungen)
(Aktuell) (Vorherige) 12:02, 3. Aug 2005 134.76.61.111 (→Weitere Überprüfungen)
(Aktuell) (Vorherige) 12:00, 3. Aug 2005 134.76.61.111 (→Weitere Überprüfungen)
(Aktuell) (Vorherige) 11:30, 3. Aug 2005 134.76.61.95 (→Weitere Überprüfungen)
(Aktuell) (Vorherige) 11:24, 3. Aug 2005 134.76.61.95 (→Weitere Überprüfungen)
(Aktuell) (Vorherige) 20:05, 2. Aug 2005 134.76.60.102 (→Weitere Überprüfungen)
(Aktuell) (Vorherige) 14:45, 31. Jul 2005 213.54.139.203
(Aktuell) (Vorherige) 14:44, 31. Jul 2005 213.54.139.203
(Aktuell) (Vorherige) 09:10, 31. Jul 2005 Karl Bednarik (plus Schwarzes Loch)
(Aktuell) (Vorherige) 15:04, 30. Jul 2005 Karl Bednarik (plus Ende des möglichen Verstoßes)
(Aktuell) (Vorherige) 14:10, 30. Jul 2005 Karl Bednarik (plus Wurzel)
(Aktuell) (Vorherige) 13:51, 30. Jul 2005 Karl Bednarik (korr. Wikilink)
(Aktuell) (Vorherige) 13:47, 30. Jul 2005 Karl Bednarik (plus Praxisnahes Rechenbeispiel)
(Aktuell) (Vorherige) 14:15, 28. Jul 2005 80.130.219.191 (URV)
(Aktuell) (Vorherige) 14:10, 28. Jul 2005 AlterVista K (→Autor: Harry Lotric - Autoren werden bei
Wikipedia prinzipiell nicht im Artikel genannt)

--Lyzzy 11:10, 13. Aug 2005 (CEST)

Völlig inakzeptabler Text

Dieser Wiki-Eintrag zur Allg. R-Theorie ist so nicht hinnehmbar. Die ganze Einleitung ist für einen Laien vollkommen unverständlich, verquast und schreckt eher ab, als dass sie zum Weiterlesen ermutigt - und dies bei einem Thema, das ohnehin als schwierig gilt. Ich jedenfalls habe nach der EINLEITUNG nicht mehr weiterlesen und mich weiterärgern wollen...

Kann sich ein Fachkundiger vielleicht die Mühe machen und uns eine neue Einleitung schreiben?

Shoshone

Ich denke, dass es kaum einfacher geht. Solange R_μνρσ nicht schon ein der Einleitung auftaucht... AlterVista 01:31, 22. Okt 2005 (CEST)

Energieerhaltungssatz verletzt?

Gilt der Energieerhaltungssatz wirklich nicht mehr streng in der ART? So steht dies nämlich im Artikel Energieerhaltungssatz... --Dark-Immortal 12:57, 7. Nov 2005 (CET)

Der Energie-Impuls-Tensor beschreibt eine lokal erhaltene Größe, die Energie alleine ist, da nicht invariant unter Transformationen, auch nicht Erhaltungsgröße. Siehe im englischen Artikel, Kapitel "Conservation of energy-momentum". -- Schewek 14:35, 7. Nov 2005 (CET)

gekrümmter Raum

Da ich im schwerelosen Fall durchaus auch einer Gravitation unterliegen kann, in Wahrheit also beschleunigt werde, also ich mein Inertialsystem ändere, ist daher die Geodäte etwas anderes?

Liegt der Unterschied im Weg des Lichtes gegenüber dem Weg eines schwereren Körpers? Oder ist die Geodäte sogar noch "gerader" als selbst das (ziemlich leichte) Licht.

11.11.2005 ra-raisch

Es geht nicht um Geodäten im krummen Raum sondern in der krummen Raumzeit. Lies noch mal den Abschnitt Allgemeine_Relativitätstheorie#Der_schiefe_Wurf_als_Folge_einer_gekrümmten_Raumzeit. Licht und Materie können zwar im Raum im Prinzip den selben Weg zurücklegen, aber in der Raumzeit geht das nicht, denn die Materie müsste sich dann auch mit Lichtgeschwindigkeit bewegen. --Wolfgangbeyer 15:04, 11 November 2005 (CET)

- 2006 -

Verständnisprobleme

Letzter Kommentar: vor 18 Jahren2 Kommentare2 Personen sind an der Diskussion beteiligt

kann man dass auch ohne fach-chinesisch irgendwie erklären? also ohne sich dauernd auf irgendwelche prinzipien von dem und dem und da und dort zu berufen? kennt sich ja niemand mehr aus :) ..... ich werde nur noch mehr und mehr verwirrt :P .... so ein kleiner text am rande der zeile ders einfach erklärt wäre sehr nett. ... für den einfachen arbeiter sozusagen =) --62.178.135.149 01:55, 25. Apr 2006 (CEST)

Eine Frage zur Lichtgeschwindigkeit: wieso ist sie eine absolute Größe? Oder besser: in Relation wozu wird sie gemessen? Findet diese Messung auf verschiedenen Ebenen statt? Als vergleich z.B. eine Messung auf chemischer und eine auf subatomarer Ebene? Müßte die Geschwindigkeit die zu Materie führt [also Rekursion] nicht schneller als c sein?

Die Sache ist ganz einfach, alles was schneller ist als Licht, ist Dunkel. Nun das ist natütlich erst einmal eine simple Erklärung aber für alle die sich mit der Lichtgeschwindigkeit an beschäftigen ausreichend. Die formulieungen sind sehr wichtig und so gesehen muß der Begriff Zeit grundsätzlich formuliert werden. Was ist Zeit? Bewegung, wäre die einfache Antwort. Nun ganz so einfach ist es nicht aber erst in einer weiteren Überlegung muß man eine Tatsache formulieren, die zu gänzlich anderen Ansichten führt. Die Linearlichtgeschwindigkeit ist nun mal eine Grenze, die nicht überschritten werden kann. In der Elektrotechnik könnte man das folgendermaßen beschreiben; Bei überscheiten der Torzeit ist eine Signalmessung nicht mehr möglich. Ein einfaches Beispiel ist wenn wir einen Rennwagen hätten der Lichtgeschwindigkeit fährt, startet und einen Kreis rund abfährt, würde ein Beobachter feststellen das sich der Wagen zurückbewegt hat und zwar genau um eine Wagenlänge. Achtung das ist nur ein plastisches Beispiel! --Behfra 09:43, 21. Jun 2006 (CEST)

"Zur Krümmung trägt dabei nicht nur die Masse, die über die Beziehung E=mc2 einer Energie entspricht, und ihren Impuls bei, sondern alle Energieformen."

Meine Frage: Ist Krümmung nicht = Masse = Energie, so daß sie nicht dazu beiträgt, sondern eine andere Darstellungsweise ist...

134.2.240.186 22:00, 14. Apr 2006 (CEST)

Die Lichtgeschwindigkeit wird in Meter/Sekunde gemessen, also in Relation zu Meter und Sekunde. Man stellt dabei empirisch fest, dass sie konstant ist, d.h. es hat noch nie jemand mit ausreichend kleinem Fehler eine andere Lichtgeschwindigkeit gemessen. Die Lichtgeschwindigkeit wird, soweit ich weiß, hauptsächlich interferometrisch bestimmt, als auf makroskopischer Skala. Eine Messung der Lichtgeschwindigkeit ist nur auf Skalen deutlich oberhalb der Wellenlänge überhaupt möglich.

Müßte die Geschwindigkeit die zu Materie führt [also Rekursion] nicht schneller als c sein?

Verstehe ich nicht.

Ich denke nicht, dass man behaupten kann, das Krümmung = Energie ist. Zum Thema Masse = Energie empfehle ich den Artikel Relativistische Masse. Die Krümmung wird durch den Energie-Impuls-Tensor verursacht. Dessen Informationsgehalt ist viel größer, (10 mal so groß aufgrund seiner 10 Komponenten, wenn man so will) als eine simple Energie. --80.136.14.105 03:14, 23. Apr 2006 (CEST)

Habe den ersten Teil des Artikels gelesen - von wegen Energie und Inpuls und Masse - und der taugt nichts. Die ART ist relativ simpel: Kein Unterschied zwischen Beschleunigung und Gravitation <=> träge = schwere Masse <=> Raumkrümmung.(Vorstehender nicht signierter Beitrag stammt von 85.0.71.197 (Diskussion • Beiträge) 21:54, 7. Aug. 2006)

Die Folgerungen <= sind beide falsch, das rechte => auch, denn sonst hätten ja schon Galilei und Newton auf die Raum(zeit)krümmung kommen müssen. Das erste => dagegen ist eine Trivialität. Das besagt nämlich nur, dass das schwache Äquivalenzprinzip aus dem starken folgt. So einfach scheints dann doch nicht zu sein... -- 217.232.49.205 22:25, 27. Okt. 2006 (CEST)Beantworten

Zur Konstanz der Lichtgeschwindigkeit und Experimenten

Die Lichtgeschwindigkeit wird heutztage im SI System einfach festgelegt. Insofern bedarf es keiner Messungen der Lichtgeschwindigkeit mehr (man bedient sich der Postulate der Speziellen Relativitätstheorie) und daraus (mit der Definition der Sekunde) ergibt sich automatisch der Wert für einen Meter.

Zu Experimenten Heutzutage ist die Richtungsunabhängigkeit der Lichtgeschwindigkeit zu 1:10^15 nachgewiesen (Peters et. al, Tobar et al, Schiller et al) und die Geschwindigkeitsunabhängigkeit (vom Laborsystem) zu 1:10^11 (ebenda). Solche Tests werden im Rahmen von Vorschlägen zu Quantentheorien der Gravitation durchgeführt. Mögliche Effekte einer (noch bei weitem unvollständigen und daher nicht als Theorie zu bezeichnenden) Quantengravitationstheorie können die Verletzung der Richtungsunabhängigkeit und der Geschwindigkeitsunabhängigkeit (des Laborsystems) der Vakuumlichtgeschwindigkeit sein (auch als Verletzung der Lorentz-Invarianz bekannt) und sogar die Verletzung des schwachen Äquivalenzprinzips. Insofern müsste zu den Experimenten zum Äquivalenzprinzip - um einen möglichst vollständigen Überblick zu erhalten - das Satelittenprojekt MICROSCOPE (CNES/ONERA (Frankreich) im Verbund mit Partnern (u.a. das ZARM in Bremen) ) erwähnt werden, welches eine Genauigkeit von 1:10^15 anstrebt. --134.102.236.219 11:38, 13. Dez. 2006 (CET)Beantworten

Archiviert

Was soll denn das komische Hin und Her mit archivieren und entarchivieren? Ich habe es jetzt noch einmal richtig archiviert (mit "Verschieben"). --Pjacobi 15:11, 3. Jan 2006 (CET)

Sternschnuppe hat einen Schweif deshalb wird sie Masse verlieren

Und warum soll dann kein Photon eine Masse velieren

E= Masse* Lichtgeschw.im Quadrat

E=m1* c2 - m2*c2

E= c2(m1-m2)

m2 Masseverlust m1 Ausgangsmasse c2 Lichteschwindigkeit im Quadrat

Lieber anonymer User,

Ich schlage vor, Sie lesen mal den Artikel über die Relativistische Masse. Das sollte Ihre Frage klären. Selbstverständlich kann ein Photon keine (Ruhe-)Masse verlieren, da es keine (Ruhe-)Masse hat. --80.136.14.105 02:57, 23. Apr 2006 (CEST)

Rechtschreibung und Formulierung

Letzter Kommentar: vor 18 Jahren3 Kommentare3 Personen sind an der Diskussion beteiligt

Hier ist das was ich gefunden habe. Steht alles im ersten Absatz nach dem Inhaltsverzeichnis. Es wäre schön, wenn es geändert würde:

Genauer betrachtet handelt es sich um eine so genannte Geodäte, das heißt eine Linie

hier wäre Geodäte der Raumzeit sehr viel verständlicher, da die hier erwähnte Geodäte sofort zu einer Raumgeodäte kontrastiert wird.

Zur Krümmung trägt dabei nicht nur die Masse, die über die Beziehung E=mc2 einer Energie
entspricht, und ihren Impuls bei, sondern alle Energieformen.

Rechtschreibung/Grammatik

In welcher Weise er die Raumzeit krümmt, wird durch die einsteinschen Feldgleichungen
festgelegt (siehe unten).

Es müsste, soweit ich weiß, Einstein'schen geschrieben werden. Aber da bin ich mir nicht ganz sicher.

geht beides RS, Maiende 6

Vielen Dank für die schnelle Entsperrung übrigens :) --80.136.23.199 20:29, 12. Apr 2006 (CEST)

Und direkt noch was im Kapitel "Experimentelle Überprüfung der allgemeinen Relativitätstheorie"

Die Periheldrehung von Planetenbahnen als auch die Ablenkung und die Rotverschiebung
von Licht im Gravitationsfeld sind Voraussagen der allgemeinen Relativitätstheorie, auf denen die
drei so genannten klassischen Tests der ART beruhen.

Hier sollte der Satz mit einem Sowohl beginnen. --80.136.23.199 20:33, 12. Apr 2006 (CEST)

Geändert ("einsteinsch" ist korrekt).--Gunther 17:52, 12. Mai 2006 (CEST)Beantworten

Danke! Hier ist noch was: Die klassischen Tests und deren moderne Varianten, Absatz 3:

In den 1960ern wurde die Position von Quasaren vermessen,

Positionen wäre schöner.

Weitere Überprüfungen, Absatz 2:

Direkte Test der Gleichheit von schwerer und träger Masse wurden bereits von Eötvös ab
1890 vor der Entwicklung der Relativitätstheorie durchgeführt.

Direkte Tests

ebenda, 3. Absatz:

Zwar wurde 1969 behauptet, Signale aus dem Zentrum der Milchstraße empfangen zu haben,
was aber nicht bestätigt werden konnte.

es seien Signale aus dem Zentrum der Milchstraße empfangen worden oder man habe Signale aus dem Zentrum der Milchstraße empfangen wäre schöner.

ebenda, 6. Absatz:

Messungen der Bewegungen von Objekten wie Sternen oder Galaxien, die unter dem Einfluss eines
Gravitationsfeldes von galaktischen und intergalaktischen Dimensionen stehen, zeigen jedoch
generell eine Abweichung von der Bewegung, welche allein durch ein von der sichtbaren Materie
gemäß der ART berechnetem Gravitationsfeld erwartet wird.

Schlechter Stil. Schöner wäre: Messungen der Bewegungen von Objekten wie Sternen oder Galaxien, die unter dem Einfluss eines Gravitationsfeldes von galaktischen und intergalaktischen Dimensionen stehen, zeigen jedoch generell eine Abweichung von der Bewegung, welche nach einem gemäß der ART berechneten Gravitationsfeld zu erwarten ist, wenn man nur von der sichtbaren Materie ausgeht.

Und:

Auch wurden bei Raumsonden wie etwa Pioneer 10 und 11, welche sich in den äußeren Bereichen
des Sonnensystems bewegen, kleine, aber bisher unerklärliche Abweichungen der Bahnen entdeckt.

Hinweis auf Pioneer-Anomalie wäre toll.

Letzter Absatz:

Abweichungen von den Vorhersagen der ART könnten auch ein neuer Anstoß zur Entwicklung einer
schlüssigen und experimentell überprüfbaren Quantentheorie der Raumzeit führen.

sein wäre hier sinnvoller.

Und noch:

Um beide Theorien zu vereinen, wird schon seit einiger Zeit an einer Quantentheorie der
Gravition gearbeitet (siehe auch TOE).

Gravitation :)

Es wäre schön, wenn man bei den Experimentellen Überprüfungen noch Zwischenüberschriften einbringen könnte. Das liest sich momentan echt zäh. --80.136.32.202 18:50, 12. Mai 2006 (CEST)Beantworten

Die Überschrift

==Die allgemeine Relativitätstheorie und das Machsche Prinzip==

enthält einen Wiki-Link. Außerdem sollte es "das machsche Prinzip heißen, oder? --80.136.0.254 15:55, 14. Mai 2006 (CEST)Beantworten

Masse

Letzter Kommentar: vor 18 Jahren1 Kommentar1 Person ist an der Diskussion beteiligt

Es sollte ein Verweis auf die ADM-Masse in den Artikel. Am besten in den Abschnitt über das Äquivalenzprinzip. Es wird mit dem Massenbegriff der Relativitätstheorie viel Schindluder getrieben. Vielleicht sollte hier geklärt werden, dass die Masse in einer gekrümmten Raumzeit "keine gute Größe" ist, wie man so schön(?) sagt. --80.136.14.105 19:45, 22. Apr 2006 (CEST)

Ja, aber es sollte gleichzeitig der Artikel über die ADM-Masse verbessert werden, u.a. wegen der nicht erklärten Verwendung der "Komma für Ableitung"-Schreibweise, der Schreibweise des Flächenelementes und fehlender physikalischen Erklärung (Masse-Metrik-Zusammenhang). Mit Bezug auf deine zweite Bemerkung könnte man in diesem Zusammmenhang das Schoen-Yau-Theorem erwähnen, falls es nicht zu weit führt. RS Mai 6

Da ich durch die Wikipedia zum ersten Mal von der ADM-Masse gehört habe und das Schoen-Yau-Theorem nicht kenne, würde ich diese Arbeiten gerne dir antragen. --80.136.11.114 20:16, 24. Mai 2006 (CEST)Beantworten

Struktur

Letzter Kommentar: vor 18 Jahren4 Kommentare4 Personen sind an der Diskussion beteiligt

Momentan ist die Struktur:

Inhaltsverzeichnis
1 Die Wechselwirkung zwischen Materie und der Raumzeit 
2 Der schiefe Wurf als Folge einer gekrümmten Raumzeit 
3 Gravitative Rotverschiebung und Raumzeitkrümmung 
4 Äquivalenz von träger und schwerer Masse 
5 Krümmung der Raumzeit ohne eine 5. Dimension 
6 Die mathematische Beschreibung der Gravitation 
7 Das Relativitätsprinzip in der allgemeinen Relativitätstheorie 
8 Die allgemeine Relativitätstheorie und das Machsche Prinzip 
9 Experimentelle Überprüfung der allgemeinen Relativitätstheorie 
9.1 Die klassischen Tests und deren moderne Varianten 
9.2 Weitere Überprüfungen

Ich würde eine Umstrukturierung Vorschlagen:

Inhaltsverzeichnis
1 Wechselwirkung zwischen Materie und Raumzeit 
2 Mathematische Beschreibung der Gravitation 
2.1 Krümmung der Raumzeit ohne 5. Dimension 
3 Physikalische Auswirkungen
3.1 Gravitative Rotverschiebung und Raumzeitkrümmung 
3.2 Relativitätsprinzip in der ART
3.3 Äquivalenz von träger und schwerer Masse  
3.4 ART und machsches Prinzip 
4 Experimentelle Überprüfung der ART
4.1 Die klassischen Tests und deren moderne Varianten 
4.1.1 ...
4.1.2 ...
...
4.2 Weitere Überprüfungen
4.2.1
4.2.2
... 
5 Anschauliche Erläuterung: Der schiefe Wurf als Folge einer gekrümmten Raumzeit

Eventuell kann 5 auch vor 2. Ich denke, dass sich mit weniger Hauptthemen und mehr Unterthemen allgemein die Struktur besser nachvollziehen lässt. --80.136.32.202 19:00, 12. Mai 2006 (CEST)Beantworten

-edit --80.136.0.254 15:54, 14. Mai 2006 (CEST)Beantworten

Das Kapitel "5. Dimension" fand ich immer schon unverhältnismäßig hervortretend, vielleicht sollten wir gar keine Überschrift dafür spendieren? --Pjacobi 21:41, 20. Mai 2006 (CEST)Beantworten

Also meinetwegen kann die Überschrift auch raus. Das ist, glaub ich, auch das kürzeste Kapitel. --80.136.27.155 00:06, 21. Mai 2006 (CEST)Beantworten

Hinzugefügtes

Letzter Kommentar: vor 18 Jahren6 Kommentare4 Personen sind an der Diskussion beteiligt

Ich habe einige kleinere Umformulierungen zum Zwecke der Strukturierung gemacht und im Kapitel Äquivalenzprinzip hinzugefügt, von deren Richtigkeit ich nur zu 99% überzeugt bin. Kann die mal jemand mit Sachverstand testlesen? Hier sind sie:

Eine Schwierigkeit bei der Formulierung des Äqivalenzprinzips in der allgemeinen
Relativitätstheorie ist, dass sich die schwere Masse nicht mehr wie in der klassischen
Mechanik definieren lässt, da im Gravitationsgesetz nun der Energie-Impuls-Tensor steht um die
Eigenschaften der Materie auszudrücken und nicht mehr die Masse. Man kann für asymptotisch
flache Raumzeiten die sogenannte ADM-Masse definieren aber dennoch formuliert man das
Äquivalenzprinzip in der ART nicht mehr über die Masse.

und

In der ART folgt das Äquivalenzprinzip direkt aus der Beschreibung der Bewegung von Körpern.
Da sich alle Körper entlang Geodäten der Raumzeit bewegen, kann ein Beobachter, der sich
entlang einer Geodäte bewegt, nur dann eine Krümmung der Raumzeit feststellen, die er als
Kraft interpretiert, wenn das von ihm beobachtbare Raumzeitstück maßgeblich gekrümmt ist.
Beispielsweise ist direkt an der Erdoberfläche die Raumzeit stark gekrümmt, da dort eine
Gegenkraft den Beobachter daran hindert, durch den Boden zu fallen. Ein Mensch ist so groß,
dass allein sein Körper als Raumzeitgebiet ausreicht, um diese Kraft zu beobachten, doch auf
der Größenskala eines Moleküls lässt sich diese Kraft nicht beobachten, das Molekül kann also
nicht entscheiden, ob sich in Schwerelosigkeit befindet oder von zwei entgegengesetzten
Kräften in der Schwebe gehalten wird.

Außerdem habe ich die oben vorgeschlagene Umstrukturierung vergenommen. Ich hoffe, dass ich nicht der einzige bin, der findet, dass man sich jetzt anhand der TOC einen besseren Überblick verschaffen kann und so besser gezielt Teile des Artikels lesen kann. (Bei einem so langen Artikel nimmt sich leider fast niemand die Zeit, ihn ganz zu lesen...) Vielleicht können einige Zwischenüberschriften weg und ein paar Sachen könnte noch sinnvoller geordnet werden.

Ich habe mich entschlossen, das "Wäscheleinengleichnis" schon recht früh als zweites Kapitel einzusetzen, da es sehr schön allgemeinverständlich ist und hier gelegentlich Bitten um eine "einfache Erklärung für einen einfachen Menschen" geäußert wurden. Im ganzen Artikel vermischt sich Fachsprache mit anschaulischen Erklärungen, ich weiß nicht, ob man das vielleicht ein bisschen trennen sollte. Andererseits quillt der Artikel meiner Meinung nach nicht vor Fachsprache über und eine gewisse Schwierigkeit des Themas ist implizit. --80.136.31.253 13:07, 21. Mai 2006 (CEST)Beantworten

Der erste Abschnitt ist m.E. im Wesentlichen Ok. Nur "um die Eigenschaften der Materie auszudrücken" ist falsch: Viele Eigenschaften der Materie werden weder von der Masse, noch vom Energie-Impuls-Tensor ausgedrückt, und die Trägheit wird auch in der ART noch mit der Masse beschrieben. Anders als bei Newton ist allerdings nicht die Masse, sondern der Energie-Impuls-Tensor die Quelle der Gravitation.

Der zweite Abschnitt ist jedoch falsch. Die Raumzeitkrümmung an der Erdoberfläche ist nicht wesentlich verschieden von der Raumzeitkrümmung in 300 km Höhe. Was Du als Kraft wahrnimmst, ist die Abweichung vom freien Fall (= Bewegung entlang einer Geodäten). Hierbei ist es irrelevant, ob der Raum gekrümmt ist (die vom Boden einer mit 1g beschleunigten Rakete im leeren Raum verursachte Abweichung von der geodätischen Bewegung führt zur selben Kraftwahrnehmung wie die vom Erdboden verursachte Abweichung). Die Raumkrümmung sorgt lediglich dafür, dass die geodätische Bewegung in der Raumzeit keine geradlinige Bewegung im Raum ist. Beispielsweise führt die Raumkrümmung dafür, dass der Mond um die Erde kreist, statt einfach geradlinig davonzufliegen. Raumkrümmung lässt sich allerdings auch anhand der Gezeitenkräfte nachweisen: Zwei frei fallende, zueinander ruhende Objekte werden im gekrümmten Raum generell nicht in diesem Zustand verbleiben, sondern sich relativ zueinander bewegen (anschaulich: weil sie an unterschiedlichen Orten sind, wirkt auf sie auch eine unterschiedliche Gravitationskraft). Für einen ausgedehnten Körper ergibt das Verformungskräfte (wenn Du im freien Fall senkrecht auf die Erde zufällst, dann wirst Du ganz leicht in die Länge gezogen; aber nur sehr wenig, weil die Krümmung ziemlich gering ist).

Die Umstrukturierung habe ich mir noch nicht angeschaut, kann also jetzt nichts dazu sagen. --Ce 18:36, 21. Mai 2006 (CEST)Beantworten

In einem früheren Kapitel steht, dass auch andere Energien die Raumzeit krümmen. Die Energie in den Van-der-Waals-Kräften, die verhindern, dass ich durch den Boden falle, müssten also die Raumzeit krümmen, so dass ich eben unbegrenzt lange auf dem Boden liegen kann, ohne eine Kraft zu spüren, wenn ich so klein bin wie ein Molekül. Wo liegt mein Fehler? Habe ich das falsch verstanden, dass alle Energieformen zum Energie-Impuls-Tensor beitragen? --80.136.50.118 10:25, 22. Mai 2006 (CEST)Beantworten

Daß alle Energieformen zum Energie-Impuls-Tensor und damit auch zur Raumkrümmung beitragen, ist schon richtig. Falsch ist einerseits die Annahme, dass die Krümmung sich auf den Bereich der Materie beschränkt. Die Materie modifiziert zwar die Krümmung, aber auch der Vakuum-Raum kann gekrümmt sein. Beispielsweise sind Gravitationswellen Krümmungswellen der Raumzeit, die durchaus auch durchs Vakuum laufen. Aber auch der leere Raum um eine Masse (bzw. eine Energie/Impulsverteilung) herum ist gekrümmt, obwohl dort ja nichts außer dem Raum selbst ist (der Energie-Impuls-Tensor verschwindet dort). In diesem Fall ist das (aus anderen Gründen eher ungünstige) Gummituchbeispiel instruktiv: Das Gummituch ist nicht nur dort gekrümmt, wo die Kugel aufliegt, sondern auch in der Umgebung der Kugel, wo nichts draufliegt. Falsch ist außerdem die Annahme, dass die wahrgenommene Kraft eine Folge der Krümmung sei. Folge der Krümmung ist schlicht, dass Geodäten der Raumzeit zu nicht-geradliniger Bewegung im Raum führen. Abgesehen von Gezeitenkräften wirst Du im freien Fall weder bei verschwindender, noch bei extremer Krümmung irgendeine Kraft spüren, und umgekehrt wirst Du bei Abweichungen von der Geodäte immer eine Kraft spüren, egal ob diese Abweichung darauf beruht, dass Du in einer flachen Raumzeit beschleunigst, oder in einer gekrümmten Raumzeit z.B. einen festen Abstand zum Gravitationszentrum beibehältst. Genau in dieser Tatsache besteht ja das Äquivalenzprinzip.

Außerdem scheinst Du das Mißverständnis zu haben, dass Du alle Kräfte als Raumzeitkrümmung interpretierst. Das ist zumindest im Rahmen der ART nicht der Fall. Die Van-der-Waals-Wechselwirkung ist eine elektromagnetische Kraft und daher auch in der ART nicht durch Raumkrümmung, sondern durch die Wechselwirkung des elektromagnetischen Feldes mit elektrischen Ladungen zu erklären. Es gibt zwar Erweiterungen der ART, die auch die anderen Kräfte durch Raumzeitkrümmungen zu erklären versuchen (die Kaluza-Klein-Theorien, die unter anderem auch in der Stringtheorie verwendet werden), aber die gehen definitiv über die ART hinaus (beispielsweise benötigen sie zusätzliche Raumdimensionen). Im Rahmen der ART wird ausschließlich die Gravitation durch Raumkrümmung beschrieben.

Oder um es anders auszudrücken: Wann immer Du in der ART eine Kraft spürst, ist auch eine (nicht durch Raumkrümmung zu beschreibende) Kraft im Spiel (auch die Gezeitenkraft kannst Du nur deshalb spüren, weil die elektromagnetische Wechselwirkung zusammen mit dem quantenmechanischen Pauli-Prinzip für eine Kraft sorgt, die sich Formänderungen entgegenstellt). --Ce 12:37, 22. Mai 2006 (CEST)Beantworten

Hab heute drüber nachgedacht und bin zu demselben Ergebnis gekommen. Ich werde den falschen Absatz jetzt entfernen und den anderen korrigieren. Danke fürs Testlesen. Mein Denkfehler war tatsächlich, dass ich alle Kräfte als Krümmung der Raumzeit interpretiert habe, wobei mich dazu ermuntert hat, dass ja auch em-Felder den Energie-Impuls-Tensor beeinflussen. Aber die em-Wechselwirkung beruht nicht hauptsächlich, wie von mir angenommen, auf diesem Beitrag. Die Ladungswechselwirkung ist davon unabhängig, wie du sagst.

(Ich hab auch gleich an Kaluza-Klein gedacht, als mir mein Irrtum klar wurde.) --80.136.50.118 16:35, 22. Mai 2006 (CEST)Beantworten

Ich habe die Mathematische Beschreibung etwas aufgemotzt. (Ich denke, wenn der Abschnitt so heißt, muss den nicht jeder Laie verstehen, obwohl ich mir Mühe gegeben habe, die Verbindung zum Verständlichen herzustellen.) Außerdem fehlt die Bewegungsgleichung der ART hier noch. Ich fühle mich allerdings nicht so sicher in dem Thema und finde leider momentan nichts in meinen Mitschriften, darum muss das erstmal warten. Wer was drüber weiß, kann gerne loslegen. --80.136.11.114 17:34, 24. Mai 2006 (CEST)Beantworten

Jetzt habe ich endlich was zu den Bewegungsgleichungen geschrieben. Wenn mal jemand vorbeischneit, wäre ich dankbar, wenn es korrekturgelesen würde. -- 84.61.177.232 18:18, 2. Jul 2006 (CEST)

Lücken

Letzter Kommentar: vor 18 Jahren1 Kommentar1 Person ist an der Diskussion beteiligt

Bewegungsgleichungen: Kovariante Ableitungen Erledigt -- 84.61.177.232 18:18, 2. Jul 2006 (CEST)
Geschichte
SRT als Grenzfall für kleine Massen- und Energiedichte, kann denke ich in den "Physik"-Teil

Zur Geschichte muss noch etwas hier hin. Und zur Änderung der Bewegungsgleichungen sollte noch ein bisschen was gesagt werden. Das ist erstmal so das, was mich so am meisten anspringt. --80.136.31.181 14:04, 25. Mai 2006 (CEST)Beantworten

Mich stört da noch etwas. Ich zitiere mal: "...Die Feldgleichung beinhaltet keine Information über die Bewegung von Teilchen in der gekrümmten Raumzeit. Sie gibt lediglich an, wie der Materie- und Energieinhalt sich auf die Krümmung der Raumzeit auswirkt. Für die andere Richtung der Wechselwirkung, also die Auswirkung der Raumzeitkrümmung auf die Dynamik der Teilchen, muss man die Bewegungsgleichungen betrachten." Ich bin mir nicht sicher wie das gemeint ist, aber das wunderschöne an der ART ist ja gerade (im Gegensatz zur Maxwell-Theorie zum Beispiel) das die Bewegungsgleichungen eine Folge der Feldgleichungen sind.

Vielleicht klärt sich diese Frage durch das neue Kapitel. Man muss schon noch die Geodätengleichung lösen, um die Bahnkurve des Teilchens zu erhalten. Zur Lösung der Geodätengleichung muss man jedoch die Feldgleichung schon gelöst haben, weil man die Metrik kennen muss. -- 84.61.177.232 18:18, 2. Jul 2006 (CEST)

Lösen muss man natürlich alles, aber man muss die Bewegungsgleichung nicht zusätzlich fordern. (die MW-Gleichungen sind auch für zwei Elektronen erfüllt, die sich nicht bewegen; die Bewegungsgleichung muss zusätzlich gefordert werden) In der ART sind sie eine direkte Folge der Integrabilitätsbedingungen. siehe dazu auch Stephani "Allgemeine Relativätstheorie" Kapitel 9.3. Aber aus deiner Antwort sehe ich schon, dass die Aussage des Artikels nicht in diese Richtung gehen sollte. Vielleicht wäre es eine gute Idee diese nette Eigenschaft der Theorie noch zu erwähnen?

Stimmt, diese Aussage ist durchaus relevant. Es wäre toll, wenn du dich bemühen würdest, das möglichst laienverständlich in das entsprechende Kapitel zu bringen. Ach ja, unterschreib doch mit -- ~~~~ damit man die Diskussionsbeiträge beim Lesen einfacher zuordnen kann ;) -- 84.61.164.179 15:34, 29. Jul 2006 (CEST)

Gravitationswellen

Wie sollen sogenannte Gravitationswellen entstehen, wenn die Gravitation eine punktuelle Kraft der Masse und einer beschleunigten Materie um die Masse darstellt oder eines geladenen Körpers eine entgegengesetzte geladene beschleunigte Masse formuliert oder eine Beschleunigung als Gravitationskonstante festgelegt ist.

Gravitationswellen gibt es nicht und wird es nicht geben, vermutlich hat Einstein selbst dieses grundsätzlich schon gewusst, denn bedingt durch die Raumzeitkonstante wird die Gravitation als ein fester Bestandteil der Beschleunigung dargelegt.

Gravitationswellen sind einfach nicht darzustellen und entbehren jeder theoretischen Grundlage oder wenn sie denn doch darstellbar wären, einen grundsätzlichen Konflikt mit der Relativitätstheorie verursachen würden.

Die einfache Erklärung ist, das eine Gravitation immer von einem Punkt ausgeht und sich zu diesem Punkt auswirkt. Gravitationswellen könnten so nur entstehen, wenn eine wechselwirkende Masse auftreten würde und diese müßte zunächst, wenn auch nur theortisch erklärbar sein. Wäre das aber zu erklären, wäre das Energieerhaltungsgesetz in Frage gestellt. Energie würde sich dann im Raum auflösen oder auf unerklärbare weise verschwinden und so etwas kann man nicht ernsthaft annehmen.

Die Raumkrümmung ist keine Auswirkung deren Grundlage auf irgendeine Form der Gravitation zurückzuführen wäre, denn in diesem Fall hätte der "Äther" eine für uns darzustellende Physikalische Eigenschaft und das kann nicht möglich sein, auch das wurde von Einstein selbst in letzter Konsequenz aller Überlegungen in Gottes Hände gelegt. Was soll den eigendlich eine Raumzeitkrümmung sein? Zeit ist ein konstanter Begriff von Bewegung und Raum steht relativ dazu. Dieser Raum müßte also formuliert werden und der Raum außerhalb des Äther stehen, damit innerhalb unserer Physik, folglich wäre die sogenannte Raumzeitkrümmung durch die Physik zu beweisen. Ist das so?--Behfra 09:43, 21. Jun 2006 (CEST)

Die Erklärung ist eben, dass Gravitation nicht eine "punktuelle Kraft der Masse" (ich nehme an, dass Du damit das Newtonsche Gravitationskonzept meinst) ist. Und die Gravitationswellen entbehren keineswegs einer theoretischen Grundlage, sondern folgen direkt aus der Allgemeinen Relativitätstheorie, in der die Gravitation nicht auf einer Newtonschen Massen-Fernwirkung, sondern auf einer lokalen Raumzeitkrümmung beruht. Und die koppelt auch nicht an die Masse, sondern an Energie und Impuls. --Ce 14:10, 2. Jun 2006 (CEST)

Lieber Benutzer Behfra, bitte versuche auch du die "Vorschau"-Funktion zu benutzen, um nicht für jeden edit 5 Versionen zu produzieren, die die Versionsgeschichte und damit den Speicher des Servers zumüllen. Vielen Dank. -- 217.232.67.176 19:52, 25. Jun 2006 (CEST)

Experimentelle Überprüfung der ART

Es erscheint fraglich, ob die ART als experimentell bewiesen angesehen werden kann. Die als "klassische Tests" angeführten Beobachtungen der Lichtkrümmung und Rotverschiebung können ohne ein neues Äquivalenzprinzip oder eine neue Theorie aus dem Gravitationsgesetz, der Äquivalenz schwerer und träger Masse sowie der speziellen Relativitätstheorie präzise erklärt werden.

Die spezielle Relativitätstheorie wurde zunächst an der Wechselwirkung von Photonen mit Materie dem Photoeffekt überprüft. Der Photoeffekt sowie der Comptoneffekt zeigen, dass elektromagnetische Wellen ebenso wie Materieteilchen mit Masse, Energie und Impuls betrachtet werden können. Ihre Masse ist proportional der Frequenz ist (E = hf).

Durch diese Erscheinungen wird zwar zunächst nur belegt, dass Licht eine träge Masse hat. Das Äquivalenzprinzip von träger und schwerer Masse wurde jedoch nie ernsthaft in Zweifel gezogen und ist experimentell mit höchster Genauigkeit bestätigt. Die durch die spezielle Relativitätstheorie postulierte Äquivalenz von Masse und Energie (E = mc²) gilt für schwere und träge Masse. Die freiwerdene Energie in Kernreaktionen kann über dieses Prinzip berechnet werden. Die Art der Massenbestimmung spielt dabei keine Rolle. Die Masse kann über die schwere Masse mittels einer gewöhnlichen Waage oder mittels der Bestimmung der Trägheit in einem Massenseparator gemessen werden.

Daher ist vernünftiger Weise nicht daran zu zweifeln, dass elektromagnetische Wellen durch die Schwerkraft abgelenkt werden oder ihre Masse, gleichbedeutend mit ihrer Energie oder Frequenz, sich im Gravitationsfeld verändert. Die Bahn des Photons kann als Grenzfall der Bahn eines Teilchen, etwa eines Elektrons, betrachtet werden, dessen Geschwindigkeit sich immer stärker der Lichtgeschwindigkeit annähert. Es wäre dagegen geradezu widersinnig anzunehmen, die schwere Masse eines Himmelskörpers, wie etwa der Sonne, würde sich durch Wechselwirkung im Innern von Materie mit Photonen beim Photoeffekt, dem Comptoneffekt, der Paarbildung oder der Annihilation verändern. Die Wirkung der Schwerkraft auf Photonen ist experimentell durch die Lichtkrümmung und die gravitative Rotverschiebung bestätigt. Diese Experimente können auch quantitativ exakt "klassisch", ohne die ART, erklärt werden.

Dass 1916 Einstein keine neue Theorie vorgelegt hat, die im Widerspruch zu seiner eigenen speziellen Relativitätstheorie oder anderen etablierten Erkenntnissen der Naturwissenschaft stand, ist kaum besonders bemerkenswert. Es gibt aber bis heute keine durch die ART erklärbare Beobachtung, die sich nicht bereits mit der klassischen Physik inklusive der speziellen Relativitätstheorie verstehen lässt. (oder schwarze Löcher ???).

Eine physikalische Theorie kann niemals bewiesen werden.
Das Äquivalenzprinzip bezieht sich auf Ruhemassen, ist also nicht auf Licht anwendbar.
Wie schon merhfach erwähnt ist die nach der speziellen Relativitätstheorie berechnete Lichtablenkung um den Faktor 2 zu klein.
Die ART steht nicht im Widerspruch zur speziellen Relativitätstheorie, sie enthält diese sogar als Spezialfall kleiner Raumzeitkrümmung
Die ART steht nicht im Widerspruch zu irgendwelchen "Erkenntnissen" (also Messergebnissen), sonst wäre sie widerlegt und damit weg vom Fenster. Wenn du was weißt: Immer raus damit!
Wie mehrfach erwähnt (was du aber immer wieder geflissentlich ignorierst) kann in jedem Fachbuch nachgelesen werden, dass weder Lichtablenkung, Periheldrehung, schwarze Löcher, Gravitationsabhängigkeit der Zeit noch Umlaufbahnenverfall durch Gravitationswellen klassisch richtig berechnet werden können.

Bitte versuche erstmal diese Theorie zu verstehen (ich weiß, sie ist kompliziert), anstatt hier alle nur zu stören. -- 84.61.157.57 23:50, 29. Sep 2006 (CEST)

Wenn eine physikalische Theorie niemals bewiesen werden kann, ist insbesondere die ART nicht zu beweisen.
Wenn Licht keine schwere Masse hätte, würde es auch nicht von der Sonne oder anderen schweren Körpern abgelenkt. Es gibt keinen vernünftigen Grund anzunehem Licht habe keine schwere Masse. Hätte das Licht keine schwere Masse wäre zwar die Energie und träge Masse eine Erhaltungsgröße nicht jedoch die schwere Masse (siehe Paarbildung).
Sogar rein klassisch (ohne RT oder ART) kann die Bahn eines Teichen, das mit Lichtgeschwindigkeit die Sonne passiert berechnet werden. Der Wert stimmt im Rahmen der Meßgenauigkeit mit der beobachteten Ablenkung überein.
Wenn das einzige echte Ergebnis der ART ist, dass die SRT (lokal) gilt, kann auf diese Theorie gut verzichtet werden.
Die Le-Sage-Gravitation ist wohl auch nicht wirklich widerlegt.
Die von Einstein angegebene, vermeintlich aus der ART abgeleitete, Formel für die Periheldrehung ist offenbar falsch, da sie für Venus und Erde eine viel zu große Periheldrehung vorhersagt. Die Formel ist durch das Experiment damit eindeutig widerlegt. Sollte diese falsche Formel tatsächlich eine direkte Folge der ART sein (kann ich nicht nachvollziehen), ist damit auch die ART widerlegt. Die Massenabnahme kann nach der SRT auch als Energieabnahme oder Rotverschiebung interpretiert werden. Eine Rotverschiebung ist nichts anderes als eine Zeitdilatation. Dass ein Photon durch die Schwerkraft bei seiner "Flucht" aus dem Schwerfeld Energie verliert, kann nicht nur qualitativ klassisch verstanden werden, sondern durch Anwendung des Kraftgesetzes von Isaac Newton auch quantitativ korrekt berechnet werden. Die Existenz von schwarzen Löchern und Gravitationswellen, ist nach meinem Kenntnisstand nicht nachgewiesen. 84.169.231.26 15:22, 1. Okt 2006 (CEST)

Periheldrehung

Die Geschichte mit der Periheldrehung ist kurios. Für Kreisbahnen sollte es in Folge der ART keinerlei Änderungen geben, da die Masse bei Kreisbahnen auch nach der ART konstant ist. Die schwach exzentrische also annähernd kreisförmige Bahn der Venus sollte weit weniger durch die ART beeinflußt werden als Merkur. Dies ist laut Wikipedia auch tatsächlich der Fall. In den Orginalarbeiten von Einstein von 1916 wird jedoch eine Formel für die Periheldrehung angegeben, die sich aus der ART ergeben soll, die auch für nahezu kreisförmige Bahnen eine praktisch identische Periheldrehung vorhersagt. Die Venus sollte daher eine nur im Verhältnis der Halbachsen geringere Periheldrehung im Vergleich zum Merkur aufweisen.

In der vermeintlichen Orginalarbeit von Einstein wird als Formel 75 auf Seite 337 für die Periheldrehung pro Umlauf die folgende Formel angegeben

\epsilon =24\pi ^{3}{\frac {a^{2}}{T^{2}c^{2}(1-e^{2})}}

Dabei sind a die große Halbachse, T die Umlaufperiode und c die Lichtgeschwindigkeit. Das dritte Kepplersche Gesetz besagt, dass ${\frac {a^{3}}{T^{2}}}$ für die verschiedenen Planeten eine konstante Größe ist. Ferner ist $1-e^{2}$ für alle Planeten deutlich größer als 0,9 und daher zu vernachlässigen, so dass die Periheldrehung der ART nach dieser Formel für die verschiedenen Planeten nur von der großen Halbachse a abhängt und proportional 1/a ist.

Damit ergeben sich auch für die Venus und die Erde noch beträchtliche Periheldrehungen durch die ART. Laut dem Artikel zur Periheldrehung ist diese jedoch für diese Planeten wesentlich geringer als nach der Einsteinschen Formel zu erwarten.

Klassische Berechnung der Lichtkrümmung

Die Lichtkrümmung kann bereits rein klassisch (ohne jede Relativitätstheorie) als Hyperbelbahn eines Teilchens berechnet werden, das die Sonne mit Lichtgeschwindigkeit passiert. Dies Berechnung ist völlig analog der Ablenkung eines Asteroiden durch den Jupiter und zur Rutherford-Streuung, wobei allerdings keine Mitbewegung der Sonne oder des Jupiter erfolgt. Im Fall des Photons ist die Annäherungsgeschwindigkeit gleich der Lichtgeschwindigkeit. Die Masse oder Frequenz des Photon kürzt sich heraus und spielt daher keine Rolle.

Als Ergebnis der klassischen Berechung ist der halbe Winkel im Bogenmaß gerade durch das Verhältnis des Radius der Sonne zu ihrem Gravitationsradius gegeben. Damit errechnet sich die Lichtkrümmung in Bogensekunden zu

2*3600*{\frac {180}{\pi }}*{\frac {2,95}{696.000}}=1,75

Da die Photonenmasse sich herauskürzt, ist dies sogar eine rein klassische Rechnung. Lediglich die Geschwindigkeit des vorbeifliegenden Teilchen wird gleich der Lichtgeschwindigkeit gesetzt. Es gibt nur einen minimalen Unterschied (hier vernachlässigt), weil die relativitische Massenzunahme (Blauverschiebung) bei Annäherung an die Sonne und die Rotverschiebung bei Entfernung in einer exakten Rechnung zu berücksichtigen sind. Dieser Unterschied liegt jedoch unterhalb der Messgenauigkeit.

Mit anderen Worten, die beobachte Ablenkung des Licht weicht innerhalb der Messgenauigkeit nicht von der ohne Berücksichtigung jeder Relativitätstheorie berechneten Bahn eines Teilchen mit Lichtgeschwindigkeit ab. Dies kann nicht als Beweis für die ART betrachtet werden. Bereits Newton hätte diese Berechnung durchführen können, sofern er die Lichtgeschwindigkeit, den Abstand der Sonne und ihre Masse gekannt hätte.

Äquivalenzprinzip der allgemeinen Relativitätstheorie

Das Äquivalenzprinzip der speziellen Relativitätstheorie ist plausibel. Wenn wir uns z.B. im Zug mit hoher aber konstanter Geschwindigkeit bewegen, verspüren wir von dieser Bewegung nichts. Auch die Bahngeschwindigkeit der Erde um die Sonne bemerken wir kaum, da sie fast konstant ist. Eine beschleunigten Bewegung, die zu einer Richtungsänderung oder einer Zu- oder Abnahme der Geschwindigkeit führt, ist jedoch immer durch eine Scheinkraft wie die Zentrifugalkraft erkennbar.

Entgegen dem postulierten Äquivalenzprinzip der ART, ist es sehr wohl möglich zwischen Scheinkräften, die durch eine beschleunigte Bewegung hervorgehoben werden und der Schwerkraft zu unterscheiden. Wir können unterscheiden, ob eine Kraft durch eine Drehbewegung hervorgerufen wird oder etwa durch die Anziehung der Erde. Falls die Kraft durch eine Drehbewegung bewirkt wird, merken wir dies sobald wir uns bewegen durch die Corioliskraft. Eine annähernd homogene Kraft könnte durch eine Drehbewegung um ein weit entferntes Zentrum hervorgerufen sein. Wenn wir uns um die Erde bewegen erkennen wir jedoch, dass sich die Richtung der wirkenden Schwerkraft ändert und immer auf den Mittelpunkt der Erde gerichtet ist. Die Schwerkraft der Erde wird hauptsächlich durch die Masse der Erde verursacht. Kleinere Abweichung entstehen in erster Linie durch die Rotation der Erde und die Gezeiten von Mond und Sonne. Die Schwerkraft der Erde und die kleineren Abweichungen durch die Schwerkraft der Sonne und es Mondes sowie die Bewegung der Erde kann keineswegs allein durch eine beschleunigte Bewegung der Erde erklärt werden.

ToDo-Liste

Hier steht, dass die ART 1915 fertig war, aber erst 1916 offiziell in den Annalen der Physik veröffentlicht wurde. Der Link zu Einsteins Erben war... schwach. Anscheinend Privatseite mit wenig Gehalt. Ich hab den mal wieder rausgenommen. -- 84.61.161.253 15:32, 2. Jul 2006 (CEST)

Ich habe ein paar ungelöste Fragen. Wenn jemand eine Lösungsidee hat, möge er sie hier veröffentlichen.

Aberration: Hier steht:
Auch in der ART können sich Veränderungen im G-Feld maximal mit c ausbreiten. Dass in der ART trotz der endlichen Geschwindigkeit keine Aberrationseffekte auftreten, hat nach Steve Carlip den Grund im Vorhandensein von geschwindigkeitsbedingten Effekten, welche der Aberration entgegenwirken und somit aufheben.
Der Autor scheint sich auch nicht ganz sicher darüber zu sein. Weiterhin steht hier:
Bewegt sich z.b. die Sonne, verändert sich auch das Gravitationsfeld - diese Veränderung erreicht die Erde bei einer angenommenen Grav-Geschwindigkeit von c jedoch erst nach 8 Minuten - zu diesem Zeitpunkt befindet sich die Sonne jedoch bereits auf einer anderen Position. Diese Diskrepanz zwischen aktueller und scheinbarer Position der Sonne führt zu einer zusätzlichen Beschleunigung der Erde, welcher (im Gegensatz zum Bremseffekt) zu einer kontinuierlichen Vergrößerung der Umlaufbahn führt.
Warum führt das zu einer zusätzlichen Beschleunigung? Wodurch wird sie, falls sie auftritt, kompensiert? Falls das irgendwas erwähnenswertes ist, sollte es in den Artikel.
Selbstfokussierender Lichtstrahl: Ich meine, ich hätte in einer Vorlesung mal gehört, dass sich ein Lichtstrahl aufgrund der Gravitationswirkung des Lichts auf ausreichend langen Strecken selbst fokussiert. Stimmt das? Wenn ja, kann jemand die Hintergründe rauskramen und es in den Artikel bringen?
Gravitationswellen, Schwarze Löcher, etc: Ich werde das mal unter "Weitere Effekte" packen und die Artikel verlinken.

-- 217.232.36.142 11:34, 17. Jul 2006 (CEST)

Zur Aberration: Ein ausführliche Darstellung der Problematik findet sich hier: Aberration and the Speed of Gravity bzw. vollständige pdf-Datei hier. Es handelt sich um eine Arbeit von Prof. Carlip, einem ausgewiesenen ART-Experten. Diese antwortet dort auf die Kritik Van Flanderns, welcher meinte, dass Gravitation sich mit mindestens 2*10^10 * c ausbreiten müsse um Aberrationseffekte zu vermeiden. Carlip führt in seinem Artikel aus, warum dieser Effekt in der ART ausgeglichen wird - Er schreibt in der Einleitung: The observed absence of gravitational aberration requires that Newtonian gravity propagate at a speed c g > 2 * 10^10 c. By evaluating the gravitational effect of an accelerating mass, I show that aberration in general relativity is almost exactly canceled by velocity-dependent interactions, permitting c g = c. This cancellation is dictated by conservation laws and the quadrupole nature of gravitational radiation. --D.H 20:44, 23. Jul 2006 (CEST)

Alles klar, Danke! Ich glaube, das ist sogar genug Stoff für einen eigenen Artikel Aberration (Gravitation). Ich muss mir das mal in 'ner ruhigen Minute zu Gemüte führen, dann schreib ich was hier in den Artikel. -- 217.232.9.231 17:29, 24. Jul 2006 (CEST)

Also ich habe die Aberration reingebracht und was zur Wirkung geschrieben. Das ist wohl nur für Physiker und Mathematik wirklich durchschaubar, aber ich denke das geht nicht wirklich verständlicher und es muss halt rein. Außerdem wurde Hilbert vorher nicht einmal erwähnt, obwohl er auf der mathematischen (differentialgeometrischen) Seite sehr viel für die Theorie geleistet hat. Es gibt noch ein paar Dinge, die ich gerne reinbringen würde:

Selbstfokussierender Lichtstrahl: Ich meine, ich hätte in einer Vorlesung mal gehört, dass sich ein Lichtstrahl aufgrund der Gravitationswirkung des Lichts auf ausreichend langen Strecken selbst fokussiert. Stimmt das? Wenn ja, kann jemand die Hintergründe rauskramen und es in den Artikel bringen? (Oben schonmal erwähnt)
Lineare Näherung der Metrik: Falls sich jemand dafür interessiert, wie man damit konkret rechnet, wäre es vielleicht sinnvoll, die lineare Näherung als Rechengrundlage zu erwähnen. Andererseits könnte man das als einen zu technischen Aspekt für einen Enzyklopädie-Artikel sehen. Bitte um Meinungen.
Geschichte: Kann da jemand mal genau die Einstein, Hilbert, etc Zuordnung vornehmen? Sonst durchforste ich mal selbst den Daten-Dschungel und suche was dazu.

Soweit erstmal. -- 217.232.23.174 23:52, 7. Aug 2006 (CEST)

@ Lineare Näherung der Metrik: Da solltest erstmal die Metrik selbst erklären, und zwar ab besten im Abschnitt "Krümmung der Raumzeit ohne eine 5. Dimension".--timo 23:34, 27. Sep 2006 (CEST)

Das Problem ist Folgendes: Wenn man anfängt, differentialgeometrische Begriffe hier im Artikel zu klären, bläht der sich sehr schnell sehr weit auf. Sehr gut zu beobachten ist das bei vielen anderen Wikipedias (z.B. fr). Deshalb habe ich (und auch die anderen Autoren) bisher die Politik vertreten, die Mathematik hier weitgehend draußen zu halten. Dafür gibt es ja schon diverse Mathe-Artikel. Ich sehe folgende mögliche Wege für den Artikel:

Zentrale mathematische Begriffe fett schreiben und am Anfang des Mathe-Kapitels darauf hinweisen, so dass interessierte Leser sich durchklicken können.
Verwendete mathematische Begriffe kurz umreißen und auf die Hauptartikel verweisen.
Verwendete mathematische Begriffe vollständig erklären.

Ich würde zu 2. tendieren. Sinnvoll? -- 217.232.7.52 23:47, 27. Sep 2006 (CEST)

Bild-Vorschläge

Letzter Kommentar: vor 18 Jahren9 Kommentare5 Personen sind an der Diskussion beteiligt

Ich werde hier einige Bilder vorschlagen. Da ich mich 0,0 mit Copyright auskenne, bitte ich um Hinweise, welche davon ich nicht verwenden kann. Außerdem wären Bewertungen zu den Bildern gut. Zusätzliche Vorschläge sind auch immer gern gesehen.

Ein Bild aus fr, zur Veranschaulichung von Geodäten:

Geodäten in einem zweidimensionalen gekrümmten Raum

Ein Bild aus Apsidendrehung:

Die Periheldrehung der Bahn eines Planeten (roter Punkt). Die Exzentrizität der Bahn und der Betrag der Drehung sind schematisch übertrieben.

Ein Bild aus Gravitationslinse:

Ein Bild aus pl:

Gravitationswellen, die von zwei sich umkreisenden Neutronensternen ausgesandt werden.

Ein Bild aus it:

Ein Bild aus Schwarzes Loch das sich auch für Gravitationslinse/Lichtkrümmung verwenden lässt:

Das ist erstmal alles, was ich für verwertbar halte. Ein schönes Titelbild ist mE nicht dabei. Viele andere Sprachen verwenden das hier:

Welches jedoch eine falsche Vorstellung nährt. Gerade solche Bilder werden oft angegriffen, mit der Feststellung, dass diese Krümmung in 2D ja nur zustande kommt, wenn transversal zur Fläche eine anziehende Kraft auf die Erde wirkt, so dass diese nach "unten" sinkt und die Krümmung verursacht.

Ich halte diese Darstellungsart dennoch für hilfreich, sie bedarf ja so oder so der Erläuterung. Was mir dabei aber als vermeidbar falsch erscheint, ist die Kugelform des Körpers – er müsste als Scheibe dargestellt werden, wenn ich mich nicht irre. Rainer Z ... 14:38, 12. Okt. 2006 (CEST)Beantworten

-- 217.232.46.134 12:38, 12. Okt. 2006 (CEST)Beantworten

Urheberrechte: Alle Bilder stammen m.E. aus dem gemeinsamen Medienserver der Wikipedien, http://commons.wikimedia.org/, und dürfen deshalb in allen Wikipedien benutzt werden. --Pjacobi 12:48, 12. Okt. 2006 (CEST)Beantworten

Zum Copyright kann ich nichts sagen.

Gefallen tun mir alle Bilder, bis auf die Peripheldrehung. Dieses sieht zum Einen etwas lieblos aus, zum Andern müsste die Bahn geschlossen sein, keine 3 Einzelelipsen.

Das letzte Bild halte ich als Titelbild für ganz gut geeignet, weil es die Raumverzerrung visualisiert. Ohne eine Dimension wegzulassen, kann man halt kein Bild hinbekommen. Ein kleiner Hinweis, dass es eine 2dimensionale Analogie ist, sollte reichen. Und dass die Erde kugelformig (und blau) ist, finde ich auch o.k., weiße Koordinaten gibt es ja schließlich auch nicht. Abgesehen davon: wenn man es ganz genau nimmt, ist das Loch dann nicht tatsächlich mulden- oder kegelförmig (nicht flach), weil die Schwerkraft von der Erdoberfläche zum -mittelpunkt stetig abnimmt. -- Zoelomat 15:30, 12. Okt. 2006 (CEST)Beantworten

Nee, also das "Erde-in-der-Hängematte-Bild" bitte nicht. Die anderen sind O.K. (das Periheldrehungsbild könnte man neumalen). --Pjacobi 15:41, 12. Okt. 2006 (CEST)Beantworten

Das Geodätenbild ginge dann wohl auch nicht. Aber mich würde eine genauere Begründung schon interessieren. Mir ist klar, dass solche Darstellungen nicht „korrekt“ sind, aber wesentlich „korrektere“ sind mir nicht bekannt. Rainer Z ... 15:49, 12. Okt. 2006 (CEST)Beantworten

Das "Erde-Hängematte-Bild" hat schon einmal den Fehler, daß die Erde hier auf der Raumzeit liegt, statt sich darinnen zu befinden (da hier ein zweidimensionaler Raum gezeigt wird, wäre die Erde dann ein kreisförmiger Abschnitt dieses Raumes). Auch das "nach unten ziehen" liefert eine falsche Vorstellung (es ist eine Sache, wenn man ein ohne Erklärung unverständliches Bild hat; aber ein Bild, das ohne Erklärung eine falsche Vorstellung vermittelt, ist eine ganz andere Sache und sollte m.E. auf jeden Fall vermieden werden).

Das Geodätenbild ist deshalb wesentlich besser, weil es diese Kugel nicht hat (und außerdem ist es in dem, was es darstellen soll − Geodäten in einem nicht näher spezifizierten gekrümmten Raum – sogar völlig korrekt).

Was man auch noch machen könnte, ist die "Matte" statt nach unten nach oben "auszubeulen", das wäre dann aus geometrischer Sicht äquivalent, würde aber nicht den Eindruck einer nach unten wirkenden Gravitation hervorrufen. --Ce 17:26, 12. Okt. 2006 (CEST)Beantworten

Den Hinweis auf die Scheibe hatte ich etwas weiter oben auch schon gegeben – das ist ein ganz offensichtlicher Fehler, der seltsamerweise immer bei derartigen Darstellungen gemacht wird. Was die „falsche“ Erdanziehungskraft unter der Hängematte angeht: Man kann das als eine Hilfskonstruktion betrachten, um überhaupt eine intuitive Vorstellung der Angelegenheit zu ermöglichen. Es ist ein bisschen wie mit Atommodellen. Die stimmen auch nicht, können aber Teilaspekte visuell zugänglich machen. Ich möchte übrigens gar nicht die konkrete Grafik verteidigen, die ist nicht sehr überzeugend, sondern nur das Grundkonzept. Es sei denn, jemand hat eine überzeugende Idee für eine korrekte und anschauliche Darstellung. Rainer Z ... 17:57, 12. Okt. 2006 (CEST)Beantworten

Hier ist ein Bild zur Perihelpräzession aus in en, dass ich hier nicht eingebunden kriege. Ist das Copyright ok und kann das jemand bitte hier hinbringen, zur Diskussion? Es hat den Vorteil, dass die Bahn geschlossen ist. Allerdings ist die Präzession extrem übertrieben. -- 217.232.46.134 19:28, 12. Okt. 2006 (CEST)Beantworten

Schwache statische Gravitationsfelder

Letzter Kommentar: vor 18 Jahren4 Kommentare2 Personen sind an der Diskussion beteiligt

Ich habe ein schlechtes Gewissen eine Erweiterung vorzuschlagen, wo ich doch sonst immer für kurze Darstellungen bin, aber:

Vielleicht sollte man den Fall schwacher statischer Gravitationsfelder noch explizit ansprechen. D.h. $g^{ik}={\begin{pmatrix}1-2\phi &0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix}}$ Und dass ${1 \over {\sqrt {g^{00}}}}\approx 1+\phi$ wie ein Brechungsindex wirkt und damit sowohl die "Verlangsamung" als die Ablenkung des Sternenlichts am Sonnenrand erklärt.

Pjacobi 16:33, 26. Okt. 2006 (CEST)Beantworten

Ich könnte mir das als letztes Kapitel im Mathe-Teil als "Beispiel" vorstellen. Wäre das der richtige Ort? Ich fang mal an was zu tüfteln und stelle es dann hier aus. -- 217.232.49.205 15:42, 27. Okt. 2006 (CEST)Beantworten

Vorschlag 0.02

Für schwache, zeitunabhängige Gravitationsfelder erhält man als Näherung für die Metrik

g={\begin{pmatrix}1+2\phi (x)&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix}}

Mit dieser Näherung lässt sich anschaulich die Lichtablenkung durch Gravitation als Brechungseffekt interpretieren. Dazu muss man sich überlegen, was die reale Zeit an einem Raumzeitpunkt ist. Wir definieren für ein winziges Zeitintervall $d\tau$ :

d\tau ={\frac {\sqrt {g_{00}(x)}}{c}}dx^{0}

als die von einem Beobachter am Raumzeitpunkt x gemessene reale Zeit oder Eigenzeit. Betrachten wir jetzt einen Lichtstrahl, der sich in $x^{1}$ -Richtung bewegt, so ist seine reale Geschwindigkeit ${\frac {dx^{1}}{d\tau }}=c$ die Vakuumlichtgeschwindigkeit und seine gemessene Geschwindigkeit ist $c{\frac {dx^{1}}{dx^{0}}}$ . Sie stehen nach der obigen Definition der Eigenzeit in folgendem Zusammenhang

c{\frac {dx^{1}}{dx^{0}}}={\sqrt {g_{00}(x)}}{\frac {dx^{1}}{d\tau }}\approx {\frac {c}{1-\phi (x)}}

Wenn man beachtet, dass $\phi$ ein anziehendes Gravitationspotential, also negativ ist, erkennt man, dass die gemessene Geschwindigkeit des Lichtstrahls kleiner ist, als die Vakuumlichtgeschwindigkeit. Man kann also das Gravitationsfeld in dieser Betrachtung als Medium mit dem ortsabhängigen Brechungsindex $n(x)\approx 1-\phi (x)$ interpretieren.

Am Sonnenrand ist $\phi =10^{-6}$ woraus sich als Brechungsindex $n=0,999.999$ ergibt. Der Effekt ist also im Vergleich zur gewöhnlichen optischen Brechung sehr klein. Dementsprechend klein ist also der Winkel der Lichtablenkung im Gravitationsfeld.

Ist leider sehr formellastig geraten... -- 217.232.49.205 16:39, 27. Okt. 2006 (CEST)Beantworten

Also mir ist es recht. Vielleicht zur Anschauung noch den "Brechungsindex" am Sonnenrand numerisch angeben. Als Zweitnutzung könnte man glatt noch einen Artikel Shapiro-Verzögerung schreiben. --Pjacobi 15:42, 30. Okt. 2006 (CET)Beantworten

Review von 07.10.2006 bis 30.10.2006

Letzter Kommentar: vor 18 Jahren23 Kommentare15 Personen sind an der Diskussion beteiligt

Ich habe in den letzten Monaten ein wenig an dem Artikel herumgeschrieben und ihn um einige Punkte erweitert (unter verschiedenen IPs). Den Vergleich des Themenspektrums mit Artikeln anderer Sprache braucht er meiner Meinung nach nicht mehr zu scheuen. Mittelfristig möchte ich gern, dass der Artikel wie sein Bruder Spezielle Relativitätstheorie lesenswert wird. Darum wärs schön, wenn sich Fachkundige aber auch nicht-Fachkundige den Artikel mal ansehen und was zur Verständlichkeit, Formulierung und zum Inhalt sagen würden. Noch zwei Punkte im Voraus:

Der Artikel hat keine Bilder. Erstens ist es schwer, gute Bilder zu finden; zweitens ist es noch schwerer Bilder zu finden, die eine sinnvolle Anschauung ermöglichen.
Ich habe versucht, möglichts wenig Differentialgeometrie in den Artikel reinzuziehen, sondern da meist auf andere Artikel verwiesen, damit der Artikel nicht zu sehr in Formeln versinkt.

-- 217.232.42.25 15:08, 7. Okt 2006 (CEST)

Vielleicht kann bei zu den Abschnitten Gravitationslinse und Gravitationswelle je ein Bild zur Auflockerung einbauen. Für ein "Intro"-Bild ganz oben habe ich aber auch keine gute Idee. --Pjacobi 16:48, 7. Okt 2006 (CEST)

Sollen dann auch Texte zu den beiden Themen geschrieben werden? Bisher sind nur die beiden Hauptartikel verlinkt. -- 217.232.42.25 20:24, 7. Okt 2006 (CEST)

Finde ich nicht, beide Themen werden doch kurz angesprochen. --Pjacobi 22:55, 7. Okt 2006 (CEST)

So mal ein paar mehr Kommentare. Ich finde den jetzigen Artikelstand eigentlich sehr gut, der Artikel erklärt viel, ohne den Leser mit vielen Formeln zu verschrecken. Er ist aber auch nicht Formel-frei, wie hier manchmal wegen des unsäglichgen "Oma-Test" gefordert wird. Die verbleibende Kritikpunkte sind oftmals Geschmacks- und Stilfragen:

Im ganzen hat der Artikel einen eher (Anfänger-)lehrbuchartigen Stil, etwas enzyklopädische Knappheit würde ich vorziehen. Die Frage ist, ob sich dies ohne einen Verlust an Verständlichkeit erreichen lässt
Die Wäscheleine würde ich aus dem motivierenden Beispiel herauslassen
5. Dimension: ob es dem Leser wirklich hilft (und einen Unterschied macht), dass man sich den gekrümmten 3+1-Raum in nun in einen höherdimensionalen Raum eingebettet vorstellt oder nicht? Ist das alles Whitney, oder? Und wenn, bräuchte man doch 8, nicht 5 Dimensionen...
Einige Wikilinks sollten noch ergänzt werden, da hast Du beim Schreiben wohl gar nicht drauf geachtet, oder angenommen, dass wonaders im Artikel schon verlinkt ist. Ich fang am besten mal an, das geht schneller als es hier aufzuzählen.

Pjacobi 22:55, 7. Okt 2006 (CEST)

Ich sehe mal, ob sich der Text irgendwie straffen lässt. Ich werde mal versuchen einige Physik-Komilitonen, die von ART nicht viel Ahnung haben, einzuspannen, um Tips zu kriegen, was sich straffen lässt.

Einbettungssatz von Whitney sagt, dass man einen maximal 2n-dimensionalen Raum braucht. Also sollte das wohl wirklich umgestrickt werden auf "mehr als 4" anstelle von "5".

Die Wikilinks sind vermutlich ein bisschen chaotisch, weil ich den Text ein paar mal umstrukturiert habe. Ich geh das mal durch und versuche, soviel wie möglich zu glätten.

Danke für die Hilfe. -- 217.232.52.137 02:27, 8. Okt 2006 (CEST)

Whitney tut wenig zur Sache, man braucht ein Analogon von Nash für pseudoriemannsche Mf., wie auch immer das aussehen mag.--Gunther 03:26, 8. Okt 2006 (CEST)

Semiriemannsche Mf sind doch insbesondere differenzierbare Mf und daher sollte Whitney doch reichen, oder macht die zusätzliche Struktur es schwieriger, die Kritierien für eine Einbettung zu erfüllen? Das Kapitel ist auch nicht gerade mein Steckenpferd, man könnte das auch auf zwei oder drei Sätze, in denen die fetten Links stehen, zusammenstreichen. -- 217.232.49.151 03:39, 8. Okt 2006 (CEST)

P.S.: Gehts bei einer Semiriemannschen Mf dann um isometrische Einbettungen? -- 217.232.49.151 03:42, 8. Okt 2006 (CEST)

Ja. Der höherdimensionale Raum soll ja dafür da sein, dass die "krumme" Einbettung genau der Krümmung der Mf. entspricht. Bei Nash heißt das, dass die Metrik durch die Metrik des umgebenden Raums R^N induziert wird. Bei pseudoriemannschen Mf. ist mir nicht klar, welcher umgebende Raum in Frage kommt, der diese Metrik induzieren sollte. Whitney kümmert das nicht, und wenn Du nicht irgendwelche globalen Phänomene haben willst (also z.B. dass man in eine Richtung immer weiterfliegt, dass man irgendwann wieder zurückkommt), genügt dafür schon Dimension 4.--Gunther 21:50, 8. Okt 2006 (CEST)

Ok, soll ich dann die entsprechende Formulierung wegnehmen, oder schreiben "Man würde naiv erwarten ..."? Hier das Messer anzusetzen würde wohl (wie vorgeschlagen) den "Anfängerlehrbuchcharakter etwas rausnehmen, oder? Ich machs mal weg. -- 217.232.3.40 12:21, 9. Okt. 2006 (CEST)Beantworten

Ich weiß nicht, ob es eine sinnvolle Präzisierung dieser Vorstellung gibt, kann es aber auch nicht ausschließen. Das kann man halt nicht hinschreiben: "Man wúrde naiv erwarten ... vielleicht ist die Erwartung auch richtig ... wissen wir aber auch nicht so genau." Man kann vielleicht hinschreiben, dass Krümmung klassischerweise von einer "krummen" Einbettung herkommt, sich aber intrinsisch in der Metrik niederschlägt (evtl. Hinweis, dass nicht alles, was anschaulich krumm ist, die Metrik beeinflusst bzw. an der Metrik abzulesen ist, Beispiel Kurven oder Zylinder).--Gunther 21:43, 9. Okt. 2006 (CEST)Beantworten

Ich befürchte, dann könnte es sich etwas zu weit von der ART entfernen. Ich habe einfach den ersten Absatz rausgenommen, so dass das Thema Einbettung gar nicht mehr vorkommt. Andererseits ist diese Schwierigkeit, eine Einbettung in einen höherdimensionalen Raum zu beschreiben, ein allgemeiner Kontrapunkt gegen Bilder zum Artikel, oder? -- 217.232.17.171 11:45, 10. Okt. 2006 (CEST)Beantworten

Bilder sind immer teils falsch, teils richtig. Wenn man sich dessen bewusst ist, was im jeweiligen Bild falsch ist, können die richtigen Aspekte dennoch hilfreich sein.--Gunther 18:16, 11. Okt. 2006 (CEST)Beantworten

Was die ART angeht, bin ich absoluter Laie. (i) Verständnisprobleme habe ich mit dem metrischen Tensor. Bei der Bewegungsgleichung heißt es, der metrische Tensor folgt aus der Feldgleichung. Später erhält man den Eindruck, dass der metrische Tensor beliebig gewählt werden kann. Am Ende erscheint es gar als herausragende Leistung, die richtige Metrik zu finden. Vielleicht könnte man das etwas klarer herausarbeiten. (Auch den Zusammenhang Metrik <-> metrischer Tensor.) (ii) Die Gleichungen wären leichter zu erfassen, wenn zuerst beschrieben würde, wie man mit ihnen umzugehen hat, also z.B. für die Feldgleichung: Energie-Impuls-Tensor ist gegeben, metrischer Tensor muss man geschickt wählen (?) dann kann die Gleichung gelöst werden und man erhält den Krümmungstensor. Mit dem kann dann die Bewegungsgleichung gelöst werden... Das war's erstmal. --Aegon 15:34, 9. Okt. 2006 (CEST)Beantworten

Metrik = Kurzform für "metrischer Tensor". Werde ich in den Artikel schreiben.
Der metrische Tensor folgt aus der Feldgleichung. Diese ist eine nichtlineare partielle Differentialgleichung (wenn ich die Definitionen richtig im Kopf habe) und daher meist nur näherungsweise lösbar. Daher ist es eine große Leistung, eine exakte Lösung der Feldgleichung zu finden. Werde mal sehen, wie ich das in den Text bringe.
Der Krümmungstensor besteht aus 1. und 2. Ableitungen der Metrik, wie in Kapitel 2.1 gesagt wird. Daher hat man mit der Feldgleichung eine nichtlineare Differentialgleichung für die Metrik. Dass man bei der Feldgleichung den Energie-Impuls-Tensor gegeben hat und die Metrik bestimmen will schreibe ich mal rein.

Danke für deine Fragen. Es ist toll, wenn ein ART-Laie mitmacht, dann sieht man besser, wo beim Verständnis der Schuh drückt. -- 217.232.35.210 18:40, 9. Okt. 2006 (CEST)Beantworten

Das ist jetzt viel besser. Mir ist noch eine Frage eingefallen. Einstein hat doch mal gesagt, dass die kosmische Konstante seine größte Narretei gewesen wäre. (oder hab ich das falsch im Kopf?) Ist es möglich innerhalb diese Artikels darauf einzugehen? Ich glaube, das Zitat kennen viele, aber kaum jemand weiß, was es bedeuten soll. --Aegon 21:21, 9. Okt. 2006 (CEST)Beantworten

Das steht schon im Text, und zwar hier:

Allgemein wurde entdeckt, dass die Feldgleichungen kein kosmologisches Modell eines statischen Universums ermöglichen. Da Einstein jedoch eine solche Lösung ermöglichen wollte, führte er die kosmologische Konstante ein. Als jedoch Edwin Hubble mit der Rotverschiebung einen Beleg für die Expansion des Universums fand, verwarf Einstein die kosmologische Konstante und bezeichnete sie als seine "größte Eselei".

-- 217.232.7.159 23:11, 9. Okt. 2006 (CEST)Beantworten

Oh je. Diesen Abschnitt habe ich wohl nur überflogen. Trotzdem, wenn Einstein die kosmologische Konstante verworfen hat, wieso steht sie dann noch in der Gleichung? --Aegon 15:35, 10. Okt. 2006 (CEST)Beantworten

Habe ein bisschen was ergänzt. Das Kapitel über gravitative Rotverschiebung habe ich mal umgeschrieben und an den Literatur-Mainstream angeglichen. Die vorherige Formulierung erscheint mir im Nachhinein etwas zweifelhaft... @Pjacobi: Wie siehts mit Bildern aus? Kannst du ein paar im Artikel oder auf der Diskussionsseite vorschlagen? Bzw wie kann ich selber welche (im Wiki) suchen und worauf muss ich achten? -- 217.232.17.171 19:31, 10. Okt. 2006 (CEST)Beantworten

Systematisch? Wüsste ich auch nicht. In den verlinkten Unterartikeln und deren englsichen Pendants stöbern. Benutzer:CorvinZahn fragen (per e-Mail), der kann u.U. einzelne Bilder von http://www.tempolimit-lichtgeschwindigkeit.de/ freibekommen. --Pjacobi 20:25, 10. Okt. 2006 (CEST)Beantworten

Ich habe hier eine Bilder-Sammlung zusammengetragen. Ich wäre dankbar für Kommentare und natürlich auch für zusätzliche Vorschläge. Ich habe bewusst eher schematische Darstellungen als Teleskop-Aufnahmen verwendet, da ich persönlich Teleskop-Aufnahmen immer schwer zu interpretieren finde. Sie sind einfach nicht so "perfekt". Wenn jemand aber ein tolles Teleskop-Bild hat dass er gern einbringen möchte: Immer her damit! -- 217.232.46.134 12:44, 12. Okt. 2006 (CEST)Beantworten

Stilistisch würde ich "wir" durch "man" ersetzen. Der Satz "Das ist offenbar sinnvoll." wirkt unfreiwillig komisch. Evtl. könnte noch rein, dass man sich den Unterschied zwischen ko- und kontravarianten Vektoren eines gekrümmten Koordinatensystems als einmal auf den Koordinatenflächen senkrecht stehenden und einmal zu den Koordinatenlinien parallelen Vektoren vorstellen kann. Dann hätte der Leser etewas "greifbares" und könnte sich unter dem Unterschied oben und unten stehender Indizes etwas vorstellen. Sonst bleibt das mystisch. - AlterVista 13:23, 12. Okt. 2006 (CEST)Beantworten

Danke für den Kommentar. Das erste "wir" finde ich ok, das zweite habe ich mal weggemacht. Der komische Satz gefiel mir auch nicht wirklich. Ist die neue Formulierung besser? (Schreib ruhig eine bessere Formulierung rein, wenn dir eine einfällt!) Deine vorgeschlagene Anschauung zu ko- und kontravariant funktioniert nur bei Tensoren 1. Stufe (also Vektoren). Daher weiß ich nicht, ob die wirklich viel helfen würde. Was meint ihr anderen? -- 217.232.46.134 19:44, 12. Okt. 2006 (CEST)Beantworten

Ich finde die Einleitung ein wenig schlecht gelungen. Es ist richtig, dass die Kernaussage der ART die Behandlung der Gravitation ist, aber nur gegenüber der speziellen Relativitätstheorie. Es sollte also entweder auf Bezugssysteme und die Lichtgeschwindigkeit als absoluten Wert eingegangen werden, oder klargestellt werden, dass zuerst der Artikel über SRT gelesen werden sollte (in dem hoffentlich alles drin steht, ich habe nicht reingeschaut). Dies sind für mich nicht physikalische Auswirkungen, sondern Grundlagen der Theorie. Außerdem denke ich, man kann noch erwähnen, dass Unvereinbarkeiten mit anderen wichtigen Theorien vorliegen. Der Satz "Inzwischen gibt es für die allgemeine Relativitätstheorie eine ausreichende Zahl von experimentellen Bestätigungen, so dass sie als Gravitationstheorie allgemein anerkannt ist," erweckt sonst vielleicht den Eindruck, dass sie der Weisheit letzter Schluss ist, statt nur das Beste, was verfügbar ist. Etwas unklar finde ich den Hinweis, dass partielle Ableitungen durch kovariante ersetzt werden (unter Bewegungsgleichugnen der ART). Wenn ich das richtig verstehe, bedeutet das einfach nur, dass Ableitungen unter Lorentztransformationen auch transformiert werden? Die Ausführlichkeit des Artikels ist für mich wegen der Komplexität des Themas in Ordnung. Dies muss nur durch eine gute Einleitung ausgeglichen werden, die das Wichtigste in "enzyklopädischer Knappheit" zusammenfasst.(Vorstehender nicht signierter Beitrag stammt von 80.136.28.36 (Diskussion • Beiträge) 23:13, 12. Okt. 2006)

Es steht in der Einleitung, dass die allgemeine eine Erweiterung der speziellen Relativitätstheorie ist und in kleinen Raumzeitbereichen in diese übergeht. Damit folgt sofort, dass lokal die Lichtgeschwindigkeit nicht überschritten werden kann. Ich verstehe leider nicht genau dein Problem mit der Einleitung. Wie würdest du dir die Einleitung genau vorstellen?
Die Überschrift "Physikalische Auswirkungen" ist tatsächlich unglücklich, da in dem Kapitel sowohl Auswirkungen als auch Grundlagen der ART stehen. Sollte man das Kapitel zweiteilen und die Grundlagen (Relativitätsprinzip und Äquivalenzprinzip) vor das Mathekapitel setzen und den Rest dahinter belassen, oder einfach nur das Kapitel in "Physikalische Aspekte" oder so umbenennen?
Es stimmt, dass "allgemein anerkannt" und "experimentelle Belege" immer etwas anrüchig sind, weil sie suggerieren, die Theorie sei "bewiesen", was bei physikalischen Theorien allgemein unmöglich ist. Ich sehe mal, wie sich das besser formulieren lässt.
Kovariante Ableitungen haben den selben Sinn wie bei eichkovarianten Ableitungen, nämlich die Form der Bewegungsgleichung unter Koordinatentransformationen (dort: Eichtransformationen) invariant zu halten. Die Christoffelsymbole transformieren genau so, dass sie die Veränderungen der Felder unter Transformationen genau "auffressen".

Danke für die Teilnahme. -- 217.232.46.134 01:21, 13. Okt. 2006 (CEST)Beantworten

Auf die Gefahr hin, dass jetzt zu zerreden: "Physikalische Aspekte" klingt noch deutlich unglücklicher als "Physikalische Auswirkungen" -- es hat auch gleich jemand revertiert. Vielleicht hilft ein größerer Umbau, nämlich "Physikalische Auswirkungen" und "Experimentelle Überprüfung der ART" zusammenzulegen. Die Überprüfungen sind doch jeweils beobachtete Auswirkungen. Zur Zeit ist es doch etwas unpassend das Gravitationswellen (fast) nur bei (ausstehenden) "Überprüfungen" vorkommt, nicht aber bei den "Auswirkungen". --Pjacobi 08:59, 13. Okt. 2006 (CEST)Beantworten

Es fehlt für mich in der Einleitung der genaue Bezug zur SRT. Den Hinweis momentanen Version finde ich gut, aber ergänzenswert. Es stimmt, dass jemand, der etwas über die SRT weiß, damit auf die entsprechenden Konsequenzen hingewiesen wird. Die Einleitung ist aber gerade für Leute wichtig, die noch gar nichts über das Thema wissen (und nicht den ganzen Artikel lesen möchten). Ich vermute, die Formulierung kann den Eindruck erwecken, dass die SRT eine "ältere Version" der ART ist und sich auch mit Gravitation beschäftigt. Das kann dazu verleiten, nicht in den anderen Artikel zu schauen.
Den Vorschlag, den Abschnitt zu teilen und die Grundlagen vor das Mathekapitel zu setzen, halte ich für sinnvoll. Das sollte dann zusammen mit der Krümmung des Raums und einem Satz, der die aus der SRT "geerbten" Sachen aufzählt einen Abschnitt bilden.
Bei der kovarianten Ableitung würde ich einen Link auf eine Erklärung (falls es schon eine gibt) vorschlagen.

80.136.31.5 10:06, 13. Okt. 2006 (CEST)Beantworten

Ich werde mal einen größeren Umbau machen und dabei auch testweise die Physikalischen Auswirkungen mit der experimentellen Überprüfung zusammenführen.

Du hast recht, dass ein detaillierterer Bezug zur SRT vielleicht sinnvoll ist, für Leute, die sich gar nicht auskennen. Ich werde mir da was überlegen, aber das kommt nach dem Umbau. -- 217.232.16.235 13:22, 13. Okt. 2006 (CEST)Beantworten

Ok, ich habe den Artikel umstrukturiert. Ist die neue Form besser? Einige Kapitel sind jetzt recht lang, aber wenn Theorie und Experiment zusammen in einem Abschnitt stehen, lässt sich das wohl kaum vermeiden.

Ich habe eine getarnte Überschrift für einen Abschnitt zur SRT in das Kapitel "Grundlegende Konzepte" gesetzt. (Eventuell muss in dem besagten Kapitel auch die ein oder andere Referenz auf die Feldgleichung umgestaltet werden.)

P.S.: Ich habe bei der Bildersammlung ein Bild aus en verlinkt, dass ich irgendwie nicht implementiert kriege. Ist das nicht für de zugelassen oder so? Könnte das einer von euch, der sich etwas mit Bildern auskennt, klären?

Danke. -- 217.232.16.235 13:49, 13. Okt. 2006 (CEST)Beantworten

Ich finde die neue Form besser.
Der letzte Satz unter dem Abschnitt Lichtkrümmung ist doppelt gemoppelt.
Sollte unter Geschichte nicht noch etwas dazu stehen, auf welchen Arbeiten Einstein aufbaute? Und vielleicht die Experimente und Beobachtungen, die die Entwicklung einer neuen Theorie motivierten.
Die Überschrift "Mathematische Beschreibung der Gravitation" würde ich schlicht auf "Mathematische Beschreibung" kürzen.

80.136.12.147 16:30, 13. Okt. 2006 (CEST)Beantworten

Dopplung entfernt.
Auf welche Arbeiten Einstein sich bezog: Das ist recht schwer alles akurat aufzulisten. Einstein nennt: Gauss, Riemann, Christoffel, Ricci, Levi-Civita, aufbereitet durch Marcel Großmann (er hat sie also nicht im Original gelesen); Mach (bei der erkenntnistheoretischen Motivation). Er nennt nicht explizit (baut aber darauf auf) das Raumzeit-Konzept von Poincaré und Minkowski (das er zunächst abgelehnt hatte). Fehlt da noch was Wichtiges?
Überschrift kommt auf die Liste für meinen nächsten größeren Edit.

-- 84.61.170.131 00:35, 14. Okt. 2006 (CEST)Beantworten

Ich habe jetzt etwas zu SRT geschrieben, bin aber nicht zufrieden damit. Ich bin nicht ganz sicher, was ich genau darüber schreiben sollte. Sollen die wichtigsten Aussagen der SRT kurz erklärt werden? Was ist dabei hervorzuheben? Soll in dem Kapitel erklärt werden, warum die allgemeine Relativitätstheorie notwendig war? Oder soll das Kapitel doch wieder raus, weil der Artikel Relativitätstheorie sowieso vorausgesetzt wird und da die Grundzüge der SRT schon erläutert werden? -- 84.61.139.244 03:05, 15. Okt. 2006 (CEST)Beantworten

Was fehlt noch, was ist zu viel, was muss besser?

Weiß jemand ein gutes "Titelbild"?

Mal ehrlich: Hat der Artikel noch einen langen Weg vor sich, bis zur Lesenswert-Kandidatur?

-- 217.232.2.110 00:07, 19. Okt. 2006 (CEST)Beantworten

Kommentare zur Lesenswert-Kandidatur

Letzter Kommentar: vor 18 Jahren7 Kommentare3 Personen sind an der Diskussion beteiligt

Ich denke du hast viel Arbeit in den Artikel investiert und das was ich beim so-mal-mitlesen mitbekommen habe scheint mir auch zumindest fachlich ok. Daher schreib ich mal meine Kommentare zum "lesenswert" hier hin, da ich bei der Abstimmung wohl eher ein Kontra geben würde: Ganz pauschal gesagt: Der Artikel wirkt auf mich wie eine Ausformulierung von Stichpunkten die man sich mal eben vor einer Prüfung als Gedächtnisstütze hinskizziert hat. Ich kann meine Probleme mit dem Artikel leider nicht wirklich artikulieren; ich versuchs mal so: Die meisten Aussagen im Artikel verstehe ich nur dann wenn ich sie in mein Bild der ART übersetze, dort nachvollziehe und dann auf die Originalformulierung zurückkonvertiere. Das kann ja nicht Sinn der Sache sein, dass ich ART kennen muss um den Artikel über ART zu verstehen.

Insbesondere die ersten beiden Kaptitel finde ich ziemlich mau. Der "abstract" liest sich für mich wie "scheisse, den Teil gibts ja auch noch, na dann rotz ich halt mal drei, vier passende Sätze hin" (drei zusammenhangslose Abschnitte mit jeweils 1 oder 2 Sätzen). Das Kapitel "Einleitung" finde ich auch von eher zweifelhafter Qualität, sowohl von der Lesbarkeit her als auch ausnahmsweise inhaltlich; die Wurfparabel halte ich dann für völlig unnütz und tatsächlich kann ich da selbst mit etwas Vorwissen nur noch erahnen was mir das sagen soll. Beim folgenden Kapitel "grundlegende Konzepte" kommt das oben angesprochene "Ausformulierung von Prüfungsnotizen" ziemlich deutlich zum tragen. Ein Alibisatz zur Einleitung und dann die vier Stichpunkte mit ihrer Erklärung - und obs wirklich so viel Text braucht um zu sagen "SRT: Gilt in allen Inertialsystemen -> ART: Jetzt passts für alle Koordinatensysteme" (Relativitätsprinzip) weiss ich auch nicht.

Soweit erstmal zu meiner Negativkritik an dem Artikel (ich hab mich mal bewusst nicht zurückgehalten, ich find ihn nicht so schlecht wie das jetzt wahrscheinlich klingt). Leider habe ich selbst keine guten Verbesserungsvorschläge zur Hand (ich werd mich wohl mal wenigstens am "abstract" probieren), daher bin ich im Endeffekt wahrscheinlich keine grosse Hilfe: Das Problem ist einfach mal, dass bei dem Thema eine ziemlich grosse Kluft zwischen eigentlich notwendigen Vorkentnissen (Abiturwissen reicht wahrscheinlich nicht um ART auch nur ansatzweise zu verstehen; die Komplexität siedelt sich wohl eher im Bereich Vordiplom Mathe/Physik an) und dem tatsächlich zu erwartenden Vorwissen potentieller Leser (mal grob gesagt: Jeder der grade bei Star Trek was über Wurmlöcher gehört hat) klafft. Lass mich noch als als Positivkritik anmerken, dass ich den Teil "Mathematische Beschreibung" überraschend gut gelungen finde; alles was ich da zu kritisieren hätte kann man getrost unter "Haarspaltereien" abhaken.

--timo 05:15, 31. Okt. 2006 (CET)Beantworten

Mensch, das ist ja noch schwerer als ich dachte. Hier mal ein Draft für die Kurzzusammenfassung:

Die allgemeine Relativitätstheorie (kurz: ART) ist die derzeit bestakzeptierte physikalische Theorie zur Beschreibung der gravitativen Wechselwirkung. Sie wurde von Albert Einstein zunächst aus rein theoretischen Gründen entwickelt und 1916 veröffentlicht - die zuvor akzeptierte Newtonsche Gravitationstheorie war mathematisch nicht kompatibel zur speziellen Relativitätstheorie (nicht kovariant). Inzwischen wurden allerdings auch Experimente durchgeführt, die Vorhersagen der allgemeinen Relativitätstheorie bestätigen und sie gegen die Newtonsche Gravitationstheorie abgrenzen.

Im Gegensatz zur Newtonschen Gravitationstheorie, in der gravitative Wechselwirkungen durch ein Kraft- oder Potentialfeld vor einem statischen Gerüst von Raum und Zeit erklärt werden, postuliert die ART eine Wechselwirkung zwischen physikalischen Objekten und einer dynamischen Raumzeit. Die wahrgenommene gegenseitige gravitative Beeinflussung zweier physikalischer Objekte wird auf ihre Wechselwirkung mit der dynamischen Raumzeit zurückgeführt.

Newtonsche Gravitation gibts übrigens nicht; ich wollte nichts rotes verlinken; macht sich glaub schlecht bei "lesenswert" :]. --timo 09:23, 31. Okt. 2006 (CET)Beantworten

Danke für deine Kritik. Es ist im Review schon mal kritisiert worden, dass der Artikel sich z.T. wie ein Anfängerlehrbuch liest. Zu deinen einzelnen Punkten:

Die jetzige Einleitung enthält die Hälfte des Korrespondenzprinzips, nämlich die SRT-Seite, dein Draft enthält die andere Hälfte. Beides sollte zusammen in den Abstract. Ich überlege mal, wie ich das mache.

Haus rein, auch wenn ich grad nicht sehe was fehlen sollte.

Der jetzige Text sagt, dass die Einstein-Formulierung sich durchgesetzt hat (z.B. gegen Brans-Dicke). Dein Draft bezeichnet sie als "derzeit bestakzeptierte physikalische Theorie zur Beschreibung der gravitativen Wechselwirkung". Ich bin nicht sicher, was besser ist, aber ich denke, die jetzige Einleitung gruppiert die Aussagen recht sinnvoll.

Mir ging es hauptsächlich darum die Aussage nach vorne zu stellen. Mit der Formulierung "derzeit bestakzeptiert" bin ich selbst nicht völlig glücklich.

Ich finde den momentanen Aufbau sinnvoll: 1. Was ist die ART (Kernaussage)? 2. Worauf baut sie auf, was ersetzt sie ("Prolog")? 3. Wie erfolgreich war/ist die Theorie ("Epilog")?

Das Kapitel Einleitung soll im Prinzip die Kapitel "3.2 Einsteinsche Feldgleichungen" und "3.3 Bewegungsgleichungen", die ein Laie kaum lesen wird, für eben diesen Laien mit Worten erklären. Es wäre gut, wenn du versuchen könntest, deine Kritik zu präzisieren, da ich (aufgrund meiner Beschäftigung mit dem Thema) dieses Kapitel für absolut trivial halte. ;)

Spontan:

Die Wechselwirkung von Raumzeit und Teilchenfeldern ist imho nicht ein Ergebnis der ART, sondern eher die zentrale Aussage.
Beim Term "krümmen" gehen bei mir immer ein bisschen die Alarmglocken hoch, insbesondere wenn der Term nicht erklärt wird. Es wirkt auf mich immer so als ob man Informationen suggerieren will. Der Leser denkt etwas verstanden zu haben weil er ja das Wort "Krümmung" kennt, aber die transportierte Information ist praktisch Null. Schreib statt dessen "Beeinflussen" und du hast genausowenig Information transportiert aber warst dabei wenigstens Ehrlich und bringst niemand auf die falsche Idee etwas verstanden zu haben.

Ich habe mal eingefügt, dass man sich die Krümmung der 4-dimensionalen Raumzeit eher nicht vorstellen kann und der Begriff der Krümmung eher als abstrakter Fachterminus zu verstehen ist.

Kräfte haben meines Erachtens nichts in einem ART Artikel zu suchen, ausser falls man explizit vorrechnen will inwieweit Gravitation eine Scheinkraft ist. EDIT: Ist weiter unten halbwegs ordentlich erklärt (da wo dann steht das nichtgravitative Kräfte gemeint sind), muss aber meiner Meinung nach oben schon hin. Die Leser werden sonst auf die falsche Spur geführt. Dir mag es als trivialität vorkommen das ART keine Kraftfelder kennt, für jemanden der nur Newton kennt ist es das nicht. Und es ist ein sehr wichtiger Punkt.
Was ist eine Wechselwirkung im nicht-Wortsinn ?
E=mc² ist auch so ein Ding wo ich mich frage ob das denn sein muss. Kann man das nicht ein für alle mal ausrotten und E²=m²+p² schreiben? Der Mehraufwand für den zweiten Summanden wiegt den Aufwand jedem zweiten erklären zu müssen, dass E=mc² nur ein Sonderfall ist locker auf (ich kann aber auch damit leben es so drin zu lassen, ich stolper nur alle Nase lang über E=mc²-verseuchte Leute).
Zu erwähnen das auch EM-Felder beitragen ist fein und mag vielleicht auch für Laien hilfreich ist. Die Wahrheit ist aber noch ein Stück einfacher als beschrieben: Es tragen schlicht und einfach alle Teilchenfelder bei.

Man braucht nicht den Input zu machen, dass sich elektromagnetische Felder als "Teilchenfelder" interpretieren lassen. Ich finde so gehts auch. Sonst entsteht wieder diese Vorstellung von träger Masse eines Photons...

Ich halte es für ein populärwissenschaftliches Gerücht das Raumkrümmung die Ursache von Gravitationskraft ist. Nimm ne flache Raumzeit, stell dich in nen Aufzug der hochfährt -> Beschleunigung -> Scheinkraft (Gravitation), und das alles in einer flachen Raumzeit (Krümmungstensor ist eine Invariante unter Transformationen und daher Null). Es wird zwar nicht explizit so gesagt, aber doch ziemlich heftig suggeriert.

Du hast recht, im homogenen Gravitationsfeld ist in riemannschen Normalkoordinaten (freier Fall) keine Krümmung vorhanden. Was aus dem Krümmungstensor kommt, sind die Gezeitenkräfte. Allerdings gehen reale Gravitationsfelder immer mit Krümmung der Raumzeit einher, sonst könnte es ein System geben, in dem alle Geodäten gerade Linien sind (d.h. die Raumzeit wäre global flach). Daher braucht man eben doch eine Krümmung der Raumzeit, damit ein reales Gravitationsfeld da ist, das sich nicht einfach durch eine Koordinatentransformation wegkriegen lässt. Darum finde ich, dass dort das "richtige" suggeriert wird.

Sowas für trivial halten ist vielleicht die falsche Einstellung. Immerhin musst du idealerweise genau das was im Matheteil steht in einer "Fremdsprache" (halt ohne die Mathematik) korrekt und verständlich rüberbringen. Ich halte das für wesentlich anspruchsvoller als das Abtippen von ein paar Formeln aus dem Lieblingsbuch - unterschätze das mal lieber nicht. Insbesondere da es der Abschnitt ist, den die meisten lesen sollte er auch solide sein.

Ich merke, dass ich den Kontakt zur Realität manchmal verliere. ;)

Das Kapitel "Wurfparabel" ist soweit ich weiß noch von Wolfgangbeyer. Ich vermute dass es den Sinn hat, dem Laien zu erklären, wie man die Raumzeitkrümmung sehen kann, ohne eine Raumkrümmung zu beobachten (ich glaube dass sogar eine falsche Assoziation erzeugt wird). Aber ich muss zugeben, dass ich zu derlei Pop-Science Texten auch ein eher gespaltenes Verhältnis habe, daher kann das meinetwegen auch ruhig raus.

Löblicher Versuch, ich wills grad nicht nochmal lesen darum sag ich inhaltlich mal nichts dazu. Mindestens die Überschrift könnte besser gewählt sein.

Bei den grundlegenden Konzepten wird ganz kurz die SRT aufbereitet, falls irgendein Hornochse diesen Artikel liest, ohne vorher Relativitätstheorie zu lesen. Die drei folgenden Konzepte sind genau in dieser Reihenfolge von Einstein in einem Artikel von 1918(?) als seine Motivation angegeben. Ich weiß dass die Texte etwas lang sind und ich arbeite gerade an einem Bild mit Fahrstühlen (oh Gott!) zum Äquivalenzprinzip. Ich denke, den ersten Absatz beim Relativitätsprinzip kann man in das erste Mathe-Kapitel verschieben. Das Drehschemel-Beispiel finde ich recht illustrativ und an dieser Stelle auch am passendsten. Das Problem ist, dass die Feldgleichungen erst später kommen. Das ist ein Problem mit all diesen "Prinzipen": Sie werden dargestellt und es wird darauf eingegangen, ob die ART sie letztendlich auch erfüllt. Ersteres muss logisch vor das Mathe-Kapitel, letzteres dahinter. Hast du eine Idee, wie sich das machen ließe?

Ich frag mich grad ob es nicht möglich währe, die Einleitung und die grundlegenden Konzepte, die ja schliesslich auch nur verbalisiert werden, zu einem für Laien halbwegs verständlichen Text zusammenzubasteln, das dann im Wesentlichen als den Artikel anzusehen und die mathematische Umsetzung dann im Sinne von "und so sieht das ganze aus wenn mans richtig macht" hintendranzuschieben. Wesentliche Aussage hier: Ich denke grade bei den Voraussetzungen kann man schon noch denken, dass das jemand versteht (von Dingen wie Forderungen nach hinreichend häufiger Differenzierbarkeit als Voraussetzung für Differentialgeometrie mal abgesehen). Da müsste sich doch was basteln lassen was halbwegs verständlich ist und trotzdem noch Information transportiert.

Ich möchte das Mathe-Kapitel lieber da haben, wo es jetzt ist, denn ich denke gerade in der ART kommt man ohne Mathe nicht zu ernsthaftem Verständnis. Die physikalischen Phänomene möchte ich gern hinter dem Mathe-Teil belassen, weil sie daraus folgen.

-- 217.232.42.152 11:13, 31. Okt. 2006 (CET)Beantworten

Meine Kommentare sind direkt in den Text von 217.xxx hineineditiert; die Auflistung der einzelnen Punkte hat sich so angeboten --timo 15:04, 31. Okt. 2006 (CET)Beantworten

Auch ich habe meine Kommentare eineditiert. -- 217.232.42.152 16:06, 31. Okt. 2006 (CET)Beantworten

Ich hatte gar nicht gemeint das Physikkapitel zu verschieben, ich meinte obs nicht sinnvoll ist die ersten beiden Kaptitel zu vermatschen. Tatsächlich könnte Vertauschen von Einleitung und grundlegenden Konzepten schon eine grosse Hilfe sein, da man sich dann wenigstens in der verbalisierten Beschreibung auf irgendwas stützen kann und Halbwahrheiten wie "in der ART gibts keine Kräfte" mit "man kann immer ein Koordinatensystem wählen in dem sie verschwinden, siehe <welches Prinzip da auch immer passen mag>" ersetzen kann.

Die Krümmung werde ich dir wohl nicht mehr ausreden können, wenn dich schon ein konkretes Gegenbeispiel nicht überzeugt - na gut noch einen Versuch: Es steht geschrieben die Krümmung sei die Ursache für die beobachteten Bahnkurven. In der Bewegungsgleichung stehen aber nur die Metrik unde ein paar ihrer ersten Ableitungen. Ist die Metrik Folge ihrer zweiten Ableitungen (Krümmung) oder isses nicht doch eher andersrum? Ach nee, noch einen: Wir sind uns wohl einig das ich die beobachteten Kräfte immer wegtransformieren kann. Wir sind uns hoffentlich auch einig, dass die Krümmung (sei es der Tensor oder der Skalar) entweder immer oder nie Null sind. Fändest du es nicht etwas verwirrend, dass eine nichtverschwindende Ursache keine Wirkung hat (oder in meinem früheren Beispiel halt andersrum). Ok, das war denn mal mein letzter Versuch dir die Krümmung auszureden, wenn dus drinlässt kann ich da auch mit leben - mir ist es letztenendes egal und man trifft die Ansicht auch oft genug woanders.

Eiun wichtiger Punkt noch: Was ist ein Gravitationsfeld? --timo 22:17, 1. Nov. 2006 (CET)Beantworten

Setzen wird mal einen nicht verschwindenden Krümmungstensor voraus. Richtig ist, dass man immer in ein Koordinatensystem gehen kann, in dem die Christoffelsymbole in einem Punkt verschwinden (Riemannsche Normalkoordinaten). Sobald man jedoch eine Umgebung des Punktes betrachtet, werden die Christoffelsymbole in der Umgebung mit zunehmender Entfernung zum Punkt immer mehr beitragen. Was ich daraus folgere ist: Ich kann für einen Raumzeitpunkt alle Kräfte durch eine Koordinatentransformation zum Verschwinden bringen. Aber da man nur nichtverschwindende Raumzeitvolumina beobachten kann, sind immer die Gezeitenkräfte beobachtbar, wenn ich genau genug messe.

Die Bahnkurven sind also (natürlich) nicht nur vom Krümmungstensor abhängig, sondern in erster Linie von der Wahl der Koordinaten. Aber das ist eine Binsenweisheit, die schon in der Galilei-Mechanik gilt. Wenn ich aber in einem nichtverschwindenden Raumzeitvolumen kein Koordinatensystem finden kann, so dass im ganzen Volumen alle Kräfte verschwinden, habe ich eine Raumzeitkrümmung, und kann damit ohne Zweifel auf ein "echtes" Gravitationsfeld schließen. Was ich daher eher als "populärwissenschaftliches Gerücht" bezeichnen würde, ist die Behauptung Gravitationsfelder seien in der ART nicht von Beschleunigungen unterscheidbar. Das gilt nur für den unphysikalischen Fall eines homogenen Gravitationsfeldes, ansonsten gilt es nur näherungsweise.

Die Überlegung, Einleitung und Prinzipien zu tauschen, wäre für den logischen Aufbau vermutlich nicht schlecht. Andererseits soll die Einleitung kurz die wichtigsten Aussagen zusammenfassen, so dass es vielleicht für Laien, die sich nicht die ganzen 57kB reinziehen wollen, da ganz gut steht. Die von dir angesprochene Formulierung ist tatsächlich etwas schwach. Ich werde mal über was Besseres nachdenken. -- 217.232.1.122 00:18, 2. Nov. 2006 (CET)Beantworten

Krümelpieken re "Ausbreitung_der_Gravitation_und_Gravitationswellen"

Letzter Kommentar: vor 18 Jahren5 Kommentare2 Personen sind an der Diskussion beteiligt

Ich glaube dort hat sich eine fehlerhafte Argumentation eingeschlichen, die auch den Hauptartikel Aberration (Gravitation) (und viele populärwissenschaftliche Darstellungen) plagt: Die Ausbreitungsgeschwindigkeit geht gar nicht in die Umlaufnahnen ein, wenn man im Bezugssystem mit ruhender Sonne arbeitet, ist es egal um wieviel das Potential retardiert wird, da die Quelle stationär ist. Wie nicht anders zu erwarten ist die Situation gleich der elektromagnetischen, was ja auch kein Wunder ist, wegen der Analogie zwischen lineariserter ART und EM. --Pjacobi 13:33, 1. Nov. 2006 (CET)Beantworten

Hmm... Das Ruhesystem der Sonne ist ja nicht fix, weil auch die Planeten die Sonne anziehen, insofern ist die geschwindigkeitsabhängige Feldkomponente imho nicht egal. Die transformation auf das bewegte System der Sonne muss natürlich denselben Effekt haben, wie das Einbeziehen ihrer Geschwindigkeit im Schwerpunktsystem, dürfte aber, wegen der beschleunigten Koordinaten schwerer zu rechnen sein (Mutmaßung!). In jedem Fall halte ich es für "richtig", dass eine bewegte Masse ein anderes Feld erzeugt als eine ruhende und darum das Aberrationsphänomen nicht auftritt. Zumindest ist das ziemlich genau die Argumentation von Carlip. -- 217.232.1.122 18:24, 1. Nov. 2006 (CET)Beantworten

Es ist das gleiche wie im EM-Fall. Nimm zur Einfachheit zwei Massepunkte (Punktladungen) A, B relativ zueinander geradlinig gleichförmig bewegt.

Betrachtung im Ruhesystem von A: B wird durch das stationäre Newtonsche Gravitationsfeld (elektrostatische Feld) von A angezogen.
Betrachtung im Ruhesystem von B: B wird durch das Newtonsche Gravitationsfeld (elektrostatische Feld) von A plus einem gravitomagnetischem Effekt (Magnetfeld) angezogen.

Vielleicht bekomme auch ich etwas durcheinander, aber so erscheint es mir schlüssig.

Pjacobi 19:16, 1. Nov. 2006 (CET)Beantworten

Ich verstehe, was du meinst. Was ich meine ist:

Betrachtung im Ruhesystem von A: A wird durch das Newtonsche Gravitationsfeld (elektrostatische Feld) von B plus einem gravitomagnetischem Effekt (Magnetfeld) angezogen. B wird durch das stationäre Newtonsche Gravitationsfeld (elektrostatische Feld) von A angezogen. Das Bezugsystem ist beschleunigt.
Betrachtung im Ruhesystem von B: A wird durch das stationäre Newtonsche Gravitationsfeld (elektrostatische Feld) von B angezogen. B wird durch das Newtonsche Gravitationsfeld (elektrostatische Feld) von A plus einem gravitomagnetischem Effekt (Magnetfeld) angezogen. Das Bezugsystem ist beschleunigt.
Betrachtung im Schwerpunktsystem: A wird durch das Newtonsche Gravitationsfeld (elektrostatische Feld) von B plus einem gravitomagnetischem Effekt (Magnetfeld) angezogen. B wird durch das Newtonsche Gravitationsfeld (elektrostatische Feld) von A plus einem gravitomagnetischem Effekt (Magnetfeld) angezogen. Das Bezugsystem bewegt sich gleichförmig.

Darum fahre ich auf das letztere Bezugsystem ab. (Denke ich zu speziell-relativistisch?) -- 217.232.1.122 19:30, 1. Nov. 2006 (CET)Beantworten

Ich grübel noch... --Pjacobi 12:32, 4. Nov. 2006 (CET)Beantworten

Vorschlag zur Kosmologie

Letzter Kommentar: vor 18 Jahren3 Kommentare3 Personen sind an der Diskussion beteiligt

Die Kosmologie ist ein Teilgebiet der Astrophysik, das sich mit dem Ursprung und der Entwicklung des Universums befasst. Da die Entwicklung des Universums maßgeblich durch die Gravitation bestimmt ist, ist die Kosmologie eines der Hauptanwendungsgebiete der ART. In der Kosmologie wird das Universum auf großen Skalen als homogen und isotrop angenommen. Mit Hilfe dieser Symmetrien vereinfachen sich die Feldgleichungen der ART zu den Friedmann-Gleichungen. Die Lösung dieser Gleichungen für ein Universum mit Materie implizieren stets eine Expansion des Universums. Dabei ist das Vorzeichen der Skalarkrümmung auf kosmischer Skala entscheidend für die Entwicklung eines expandierenden Universums.

Bei einer positiven Skalarkrümmung wird das Universum zunächst expandieren und sich dann wieder zusammenziehen, bei verschwindender Skalarkrümmung wird die Expansionsgeschwindigkeit einen festen Wert annehmen und bei negativer Skalarkrümmung wird das Universum beschleunigt expandieren

Einstein fügte 1917 die kosmologische Konstante in die Feldgleichungen ein, um ein Modell eines statischen Kosmos zu ermöglichen. Die kosmologische Konstante kann je nach Wahl die kosmische Expansion verstärken oder kompensieren.

Messungen der Expansion des Universums haben innerhalb der Fehlergrenzen eine verschwindende Skalarkrümmung ergeben. Allerdings geht man aufgrund von Beobachtungen der kosmischen Expansion und der Hintergrundstrahlung davon aus, dass das Universum beschleunigt expandiert, was mit einer kleinen positiven kosmologischen Konstante erklärt wird.

-Ende Vorschlag-

Und direkt noch eine Frage: In der Feldgleichung steht (Kosmologische Konstante - Skalarkrümmung/2) zusammen. Kann man überhaupt beide getrennt messen oder misst man immer nur die Differenz? Dann ließe sich nämlich eine positive kosmologische Konstante auch als negative Skalarkrümmung erklären und umgekehrt. Es erschien mir ein erstaunlicher Zufall zu sein, als ich gelesen habe, die kosmologische Konstante sei klein und positiv und die Skalarkrümmung klein und negativ...

-- 217.232.56.187 11:24, 2. Nov. 2006 (CET)Beantworten

Zur Zeit ist das Universum flach. Nimmt man an.

-0.010_{-0.012}^{+0.014}

. Siehe auch en:Lambda-CDM model. --Pjacobi 09:40, 3. Nov. 2006 (CET)Beantworten

Danke, habs nach den englischen Artikeln angepasst. Ist es jetzt ok? -- 217.232.64.173 10:29, 3. Nov. 2006 (CET)Beantworten

Lesenswert-Kandidatur: Allgemeine Relativitätstheorie (Archivierung Abstimmung 30. Oktober bis 6. November 2006)

Letzter Kommentar: vor 18 Jahren18 Kommentare11 Personen sind an der Diskussion beteiligt

Die allgemeine Relativitätstheorie (kurz: ART) beschreibt die Wechselwirkung zwischen Raum und Zeit einerseits und Materie (inklusive Feldern) andererseits. In ihrer Kernaussage führt sie die Gravitation auf ein geometrisches Phänomen in einer gekrümmten 4-dimensionalen Raumzeit zurück. Sie wurde von Albert Einstein entwickelt und 1916 veröffentlicht.

Der Artikel kommt gerade aus dem Review, wo er in einigen Punkten überarbeitet wurde und Bilder erhalten hat. Falls ihr (auch Pro-Stimmende) Verbesserungsvorschläge habt, bitte nennt sie und ich sehe, was ich tun kann. Da ich in den letzten Monaten viel am Artikel gearbeitet habe: Neutral -- 217.232.14.67 19:12, 30. Okt. 2006 (CET)Beantworten

Pro Für Leser mit Physikkenntnissen aber ohne Vorkenntnisse der ART ist dieser Artikel eine hervorragende Einführung in das schwere Thema. Die mathematische Formulierung ist bei Vorkenntnissen sehr hilfreich und sollte keinesfalls gekürzt werden. Ein Verbesserungsvorschlag: Im Abschnitt Lichtkrümmung sollte für schwache, zeitunabhängige Gravitationsfelder ein Beispiel gegeben werden (z.B. für Sterne der größe x-Sonnenmassen, nicht mehr gültig für y-Sonnenmassen, oder ähnlich) sowie das Potential erklärt werden. --Aegon 16:50, 31. Okt. 2006 (CET)Beantworten

Mir fällt auf:

Die Summenkonvention ist falsch zitiert. Man summiert über doppelt vorkommende Inizes, nicht nur wenn einer kovariant und der andere kontravariant ist.
Das Kapitel "Physikalische Auswirkungen" schwankt inhaltlich zwischen der Erklärung von diversen Effekten und deren konkretem Nachweis. Dies sollte getrennt werden, mindestens aber über alle Unterabschnitte hinweg einheitlich gehalten werden.
Im Abschnitt "Lichtkrümmung" fehlt die zentrale Aussage, dass sich Licht entlang von Geodäten bewegt. Außerdem ist dieser Effekt bekannter unter der Bezeichnung "Lichtablenkung".
Der Abschnitt über "Gravitationswellen" enthält viele Unschärfen und sollte gründlich überarbeitet werden. Die Existenz von Gravitationswellen folgt direkt aus der Lichtgeschwindigkeit als oberer Grenzgeschwindigkeit, also der SRT. Die ART wird dazu nicht benötigt. Statt dieser positiven Folgerung argumentieren die ersten beiden Absätze des Gravitationswellen-Absatzes vage mit der Existenz von Widersprüchen und "lässt sich auffassen als". Einen Absatz weiter wird implizit die Energieerhaltung vorausgesetzt. Im Rahmen der ART gilt jedoch keine Energieerhaltung. Zu den Gravitationswellendetektoren fehlen Aussagen, über die Form (Transversalwellen, Streckung und Stauchung der Raumzeit), den Charakter (Quadrupolwellen), die Quellen (Colliding Binaries, Supernoa-Explosion, Sonne) und die erwarteten Amplituden ( $10^{-21}$ bis $10^{-23}$ ). Die wenigen Aussagen zu Gravitationswellendetektoren hängen schief. Zum Beispiel lässt die Aussage zu mechanische Resonatoren vermuten, dass sie die großen Michelson-Interferometern dierkt ersetzten könnten, was nicht der Fall ist. Beim Interferometer von GEO600 ist 600 Meter die Armlänge, nicht die Ausdehnung. Es fehlt die Aussage, dass die diversen erdgebundenen Detektoren nur genmeinsam eine Chance haben, eine G-Welle sicher zu detektieren.
Der Abschnitt zu schwarzen Löchern sagt nur, dass deren Existenz als gesichert gilt, schweigt sich aber darüber aus, was sie sind und welche Hinweise es konkret gibt.
Der Abschnitt Lense-Thirring-Effekt ist ähnlich unbefriedigend. In dem Fall fehlt sogar die Aussage, dass der Effekt nachgewiesen wurde.
Der Abschnitt "Noch ausstehende Probleme" ist viel zu kurz. Insbesondere verdient die Inkompatibilität von Quantenmechanik und ART eine ausführlichere Erklärung. Dies wird immerhin als eine der größten Ungereimtheiten des aktuellen physikalischen Weltbilds angesehen. Es fehlen Verweise auf Versuche die ART mit der QED zu vereinigen.
Das große Parade-Thema der ART, die Kosmologie, wird nur als Unterpunkt der Geschichte erwähnt. Insbesondere fehlen die verschiedenen Möglichkeiten offenes, geschlossenes, oder flaches Universum, die die ART bei verschiedenen Energiedichten vorhersagt.
An vielen Stellen fehlen Wikilinks (Einstein-Mannigfaltigkeit, LISA, VIRGO, GEO600, Geodätengleichung, VLBI, Einstein-Hilbert-Funktional, TEPEE/GREAT, STEP, ...)

Fazit: Der Artikel hat ohne Zweifel Potential. Für einen lesenswert-Orden patzt er im Mopment noch an zu vielen Stellen. Außerdem sollte die innere Struktur des Artikels sauberer gehalten werden und Unterabschnitte sich aauf das Thema des Kapitels beschränken. Daher von mir ein Kontra---<(kmk)>- 03:13, 1. Nov. 2006 (CET)Beantworten

Ad Vorredner und ad Autor:
- Die Summenkonvention ist mir mit Summation über ko- und kontravariant bekannt (aus dem Physikstudium).
- Dass sich Licht entlang von Geodäten bewegt ist in der Tat zentral, das sollte herausgestellt werden
- Die SRT befasst sich nicht mit Gravitation, wie soll diese dann Gravitationswellen vorhersagen (Interessiert mich, bin leider kein Experte dafür)?
- Schwarze Löcher (Vorhersage von Herr Schwarzschild - der mit dem gleichnamigen Radius auf Grund der ART, Überlegung Hawkins zu Schwarze Löcher und Urknall) und Kosmologie (s. vorhin) sollten ausführlicher werden.
- Verlinkung erweitern: Ja, bin ich auch für. Auch "allgemeine" Links z.B. auf Differentialgeometrie wären für den weniger vorgebildeten Leser gut.
- Ein tieferes Eingehen auf die Problematik ART versus Quantenmechanik wäre gegen Ende des Artikels angebracht. Stringtheorie und Schleifenquantengravitation sollten eingelinkt werden.
- Ergo: Die Liste meines Vorredners (Summenkonvention noch mal nachschauen, bin mir aber ziemlich sicher, dass über ko- und kontravariant summiert wird) und ggf. die Geschichte mit den SRT-Gravitationswellen (wäre zu zeigen, kann ich mir so nicht vorstellen) wäre vor Exellenzkandidatur auf jeden Fall vollständig abzuarbeiten. Ich habe die Sachen, die mir besonders wichtig erscheinen einmal fett gemacht, wenn das gemacht ist uneingeschränktes Pro, die kursiven Sachen wären mir vor einer Exellenzkandidatur essententiell. Cup of Coffee 10:48, 1. Nov. 2006 (CET)Beantworten

Offensichtlich wird die Summenkonvention unterschiedlich gelehrt. Meine Dozenten (Uni-Hannover) haben die lockere Form bevorzugt, bei der Indizes nur doppelt vorkommen müssen. Der WP-Artikel zum Thema erklärt beide Formen für richtig :-)

Das hängt halt auch mal davon ab was es für Indizes sind. Bei ko- und kontravarianten Indizes sollte man sich schon besser 2x überlegen ob man da wirklich summieren oder nicht besser mal seine Gleichung nach Fehlern durchsuchen sollte. Bei anderen Indizes wie z.B. die Nummer eines Objekts isses oft egal ob der Index oben oder unten steht und wird dann normalerweise auch nicht beachtet. --timo 14:54, 1. Nov. 2006 (CET)Beantworten

Da laut SRT c die allgemeine obere Grenzgeschwindigkeit für die Ausbreitung von Wirkungen ist, dann kann auch die Verschiebung von Massen sich nicht schneller auf die Umgebung auswirken. Im Grunde war es das schon. Aber man kann es auch noch am Beispiel verdeutlichen. Wenn sich nun eine Masse von A nach B bewegt, dann kann ein Beobachter an der Stelle C dies auch in der Wirkung der Gravitation nur mit einer gewissen Verzögerung wahrnehmen. Erst zieht es ihn in Richtung A und dann in Richtung B. Je weiter der Beobachter entfernt ist, desto länger dauert die Verzögerung. Diese entfernungsabhängige Verzögerung ist gleichbedeutend mit einer sich mit c ausbreitenden Welle. Dieses Beispiel kommt so konkret im realen Leben nicht vor, denn eine Masse bewegt sich nicht spontan von A nach B. Aber zwei Massen können sich umkreisen, Zum Beispiel in Form von Doppelsternen. Für die Umgebung macht es bereits nah Newton einen gravitativen Unterschied, ob die Sterne gerade in einer Flucht ausgerichtet sind, oder nebeneinander stehen. Diesen Unterschied kann man zu messen versuchen. Wenn diese Veränderung synchron mit einer optischen Beobachtung abläuft, hat sich die Gravitation mit c ausgebreitet. Es stimmt schon, die genaue Form der G-Wellen und die tatsache, dass sie sich genau mit c ausbreiten folgt aus der ART. Aber die Existenz der G-Wellen lässt sich schon aus der SRT ableiten.

Insgesamt meine ich nicht, dass der Artikel schlecht wäre. Aber als lesenswert in dem Sinn, dass ich einen Laien ohne Einschränkungen dorthin schicken würde, finde ich ihn noch nicht. Ein exzellenter Artikel würde dann das Thema noch besser im Zusammenhang darstellen und die Unterpunkte einsichtiger gestalten.---<(kmk)>- 13:13, 1. Nov. 2006 (CET)Beantworten

Kommentar zu -<(kmk)>-: Der Artikel ist nur der Überblicksartikel zum ganzen Feld, dass deshalb z.B. bei Gravitationswellen vieles nicht erwähnt wird, scheint mir in Ordnung. Falsches sollte aber natürlich nicht da stehen. Du hast anscheinend leider den Rebiew verpasst, aber vielleicht können Deine Bedenken ja jetzt noch rechtzeitig einfließen. --Pjacobi 11:40, 1. Nov. 2006 (CET)Beantworten

Hallo Pjakobi. Mir ist schon klar, dass es sich um einen Überblicksartikel handelt. Wir sind uns vermutlich einig, dass in einem Überblicksartikel zu jedem Unterthema nur die zentralen Aspekte erwähnt werden sollten. Dabei liegt die Betonung sowohl auf "nur" als auch auf "zentral". Bei den G-Wellen halte ich die Kleinheit des erwarteten Ausschlags für wichtiger für den Überblick als eine Aufzählung der aktuellen Detektoren inklusive des noch in der Zukunft liegenden LISA und einer Anekdote über einen Messfehler in 1969. Bei den Schwarzen Löchern und Lense-Thirring sollte auch ein Überblicksartikel in zwei, drei Sätzen sagen, worum es geht. Im Moment wird das komplett auf den jeweiligen Hauptartikel abgeschoben. Die ganze Review-Geschichte ist offensichtlich bisher unter meinem Radar geblieben. Werde sie in meine Beobachtungsliste aufnehmen. Danke für den Hinweis.---<(kmk)>- 13:13, 1. Nov. 2006 (CET)Beantworten

Die SRT sagt also nur aus, dass falls es Gravitationswellen gibt, sich diese maximal mit c ausbreiten, aber nicht, dass es sie gibt (lediglich, dass das Gravitationsfeld sich ändert). Cup of Coffee 15:57, 1. Nov. 2006 (CET)Beantworten

Nicht ganz. Die SRT sagt aus, dass es G-Wellen geben muss. Wenn es sie nicht gibt, ist die SRT falsch. Das G-Feld müsste man sich bei SRT ohne ART wie ein elektrisches Feld, aber eben auf die Masse wirkend vorstellen. Seine Änderung breitet sich laut SRT maximal mit c aus. Das ist gleichbedeutend mit G-Wellen.---<(kmk)>- 21:43, 1. Nov. 2006 (CET)Beantworten

@Kai: Ich meine, dass Du einem Irrtum oder einer ungewöhnlichen Definition von "Gravitationswelle" aufsitzt. Hast Du eine konkrete Literaturstelle, die Deine Ansicht stützt? (Followup an einem Ort Deiner Wahl, hier eher peripher) --Pjacobi 22:49, 1. Nov. 2006 (CET)Beantworten

@Pjakobi: Habe einen entsprechenden Abschnitt in der Diskussion Gravitationswellen angelegt.---<(kmk)>- 02:50, 2. Nov. 2006 (CET)Beantworten

Danke für die vielen Hinweise! Ich habe einige Veränderungen vorgenommen. Ich hoffe, dass der Abschnitt über Gravitationswellen richtiger und besser geworden ist. Zu schwarzen Löchern und Lense-Thirring-Effekt habe ich eine Ultrakurzerklärung geschrieben. Zu kosmologischen Modellen sollte tatsächlich noch was gemacht werden, aber das kriege ich jetzt nicht so ad hoc hin. Jeder von euch ist eingeladen, Korrekturen und Ergänzungen auch selbst einzutragen. Wenn ihr nicht direkt reinschreiben wollt, könnt ihr ja Formulierungsideen auf die Disku-Seite posten. Ein paar Kommentare:

Ich kenne die Summenkonvention auch nur ko-kontra, also so wie es im Text steht.
Viele der Wiki-Links, die du angibst wären rot... aber gerade bei Wiki-Links weiß ich, dass ich schlampig/vergesslich bin, daher wäre ich dankbar, wenn ihr jeden der euch auffällt einfach macht. ;)
Über Quantengravitation will ich in diesem Artikel nicht zu viel schreiben. Dafür gibt es den Artikel Quantengravitation. Der Artikel ist schon ~57kB groß und mit den kosmologischen Modellen geht der bestimmt auf die 65kB zu. Auch Masse schreckt vom Lesen ab!
Bei den "physikalischen Effekten" soll idealerweise immer zuerst kurz der Effekt erklärt werden und dann der Experiment-Status angegeben werden.
Dass die Kapitel zu den "physikalischen Effekten" unterschiedlich umfangreich sind, ist vermutlich subjektiv begründet. Ich zumindest halte die umfangreicheren Kapitel auch für die ergiebigeren Themen (abgesehen von schwarzen Löchern, die aber einen sehr guten und umfangreichen Hauptartikel haben).

-- 217.232.1.122 19:11, 1. Nov. 2006 (CET)Beantworten

Hallo 217.232.1.122. Schön, dass meine Anregungen auf fruchtbaren Boden fallen. Ich denke, die Sache mit der Summenkonvention ist Geschmacksache und geklärt. Es sollte auf keinen Fall zu einzelnen Unterthemen ein halber Artikel geschrieben werden --- Auch nicht zur Role der ART in der Kosmologie. Drei bis fünf prägnante Sätze müssen reichen. Dass es nicht leicht ist, diese Sätze zu finden, ist klar. IMHO behindern rote Links auf relevante Lemmata nicht die Einstufung als lesenswert. Sie weisen lediglich darauf hin, dass es auf diesem Gebiet noch einige Artikel zu schreiben gibt. Gerade bei lesenswerten Artikeln kommen viele Leser vorbei, von denen vielleicht doch der eine oder andere die roten Links als Aufforderung zur Autorenschaft versteht.---<(kmk)>- 21:43, 1. Nov. 2006 (CET)Beantworten

Aaalso hier ist ein Vorschlag für das Kapitel zur Kosmologie. Ich habe auch gleich noch eine Frage dazu geschrieben. Wäre toll, wenn ihr das mal korrekturlesen und Verbesserungsvorschläge (dort) machen könntet. -- 217.232.56.187 11:27, 2. Nov. 2006 (CET)Beantworten

Der Artikel ist sehr informativ und auch für Anfänger gut verständlich, deswegen gibt es von mir ein Pro (Vorstehender nicht signierter Beitrag stammt von 84.63.103.49 (Diskussion • Beiträge) 12:01, 3. Nov. 2006)

Bitte in Zukunft mit vier Tilden unterschreiben. Etwa so: -- ~~~~. -- 217.232.64.173 12:07, 3. Nov. 2006 (CET)Beantworten

Auch ich finde, dass der Artikel sowohl für einen Laien als auch für einen Physikstudenten lesenswert ist, da er sowohl viele anschauliche Erklärungen als auch Stoff, den ein bereits Eingelesener nutzen kann, sich näher damit zu beschäftigen, enthält. Pro --87.78.224.204 22:34, 3. Nov. 2006 (CET)Beantworten

Pro interessanter und informativer Artikel--Stephan 06:23, 6. Nov. 2006 (CET)Beantworten

Nette Worte

Letzter Kommentar: vor 18 Jahren2 Kommentare2 Personen sind an der Diskussion beteiligt

UND NU ISSER DURCH

Na dann will ich dir (217.xxx) mal als wohl praktisch Hauptautor persönlich dazu gratulieren, dass der Artikel in den Kreis der Lesenswerten aufgenommen wurde. Es freut mich zu sehen, dass der doch wahrscheinlich ziemlich grosse Aufwand den du in der Artikel gesteckt hast sich gelohnt hat. Ich hätte ja gerne etwas konstruktiver beigetragen, aber wir scheinen an ein paar Punkten doch sehr verschiedene Meinungen vom Thema zu haben (das ist auch der Grund warum ich dann einfach nichts mehr gesagt habe; es hätte nichts gebracht nur unnötig deine Zeit an nutzlosen Diskussionen zu verschwenden). Besonders freut mich, dass sich mit Benutzer:FredericII auch noch ein scheinbarer Nichtphysiker gefunden hat, der den Artikel informativ fand - da hatte ich so meine Bedenken. --timo 16:06, 6. Nov. 2006 (CET)Beantworten

Danke! Ich bin aber eher Strukturierer als Hauptautor. Ich bin erst seit der Entsperrung im Mai Hauptautor, vorher wurde der Artikel vor allem von WolfgangBeyer, Ce und Epo geschrieben.

Es tut mir leid, dass ich zuweilen vielleicht etwas dogmatisch wirke. Ich halte es für sehr schwer, in der Einleitung genau auf den Zusammenhang zwischen Krümmung und Gravitation einzugehen. Ich werde mich mal bemühen, das zumindest konsequent zu formulieren. Ich habe in mittlerer Zukunft vor, den Abschnitt über das ÄP um zwei Bilder aufzupeppen, die unsere beiden Sichtweisen wiedergeben, nämlich erstens die Äquivalenz von Schwerelosigkeit und freiem Fall im homogenen Gravitationsfeld und zweitens die Erkennbarkeit des "echten" Gravitationsfeldes an Gezeitenkräften in endlichen Volumina bei endlichen Zeitintervallen.

Perfekt lässt sich das Ganze in riemannschen Normalkoordinaten mit der Taylorreihe der Metrik darstellen. Wenn daran Interesse besteht, könnte ich den Artikel über die Koordinaten schreiben und hier im Kapitel übers ÄP verlinken. (Würde ich aber erstmal auf die lange Bank schieben.)

Ich bemühe mich, dass der Artikel den Aufkleber auch verdient (und sei es nachträglich...). Daher wäre ich dir dankbar, wenn du auch in Zukunft gelegentlich mal deine Meinung hier abwirfst. ;) -- 217.232.62.106 17:00, 6. Nov. 2006 (CET)Beantworten

Frage zur Krümmung

Letzter Kommentar: vor 18 Jahren1 Kommentar1 Person ist an der Diskussion beteiligt

Mir kommen einige Aussagen fragwürdig vor, kann aber auch auf Missverständnissen beruhen, z.B.:

"Es können immer lokale Koordinaten gewählt werden, in denen alle ersten Ableitungen des metrischen Tensors verschwinden und der Krümmungstensor daher nur durch zweite Ableitungen des metrischen Tensor bestimmt ist."

Wenn die ersten Ableitungen in einem Gebiet verschwinden (nur auf einem Gebiet ist Differenzierbarkeit definiert), dann natürlich auf die zweiten und der Krümmungstensor ist identisch null. Welche Bedeutung hat die Aussage (Quelle?)? --RS, , Nov 06

Richtiger müsste es heißen:

"Es können für jeden Punkt lokale Koordinaten gewählt werden, in denen alle ersten Ableitungen des metrischen Tensors in diesem Punkt verschwinden und der Krümmungstensor daher nur durch zweite Ableitungen des metrischen Tensor bestimmt ist."

Dann verschwinden die zweiten Ableitungen nicht und alles wird gut. Ich versuche das mal im Text richtig zu formulieren. -- 217.232.33.118 15:47, 7. Nov. 2006 (CET)Beantworten

Ich frag mich ...

Letzter Kommentar: vor 18 Jahren7 Kommentare4 Personen sind an der Diskussion beteiligt

Kann man mit der ART eigentlich wirklich etwas ausrechnen ?

Ok, die Bahn im freien Fall verläuft im Schwerefeld der Erde entlang einer Geodäte, die im dreidimensionalen Raum gekrümmt ist. Diese Erkenntnis nützt aber wenig, wenn nicht bekannt ist wie diese Geodäte, im dreidimensionalen Raum, in Abhängigkeit von der Zeit, verläuft. Wie berechne ich also diese Geodäte ? (Vorstehender nicht signierter Beitrag stammt von 84.169.206.61 (Diskussion • Beiträge) 18:02, 23. Nov. 2006)

Die Geodäte berechnet sich nach der im Artikel angegebenen Geodätengleichung. Das geht in beliebigen Koordinaten, man muss nur die Christoffelsymbole kennen. Die erhält man, indem man die Metrik ableitet, die man wiederum aus der Feldgleichung erhält. Am einfachsten ist es, in Riemannschen Normalkoordinaten zu rechnen, weil da alle Christoffelsymbole in einem Raumzeitpunkt verschwinden, so dass die Geodäten durch den Punkt alle Geraden sind.

Im Fall eines kleinen Feldes, wie hier auf der Erde braucht man die ART zur Beschreibung einer Bahnkurve nicht, weil die Abweichungen von der newtonschen Beschreibung winzig sind. Aber fürs GPS werden ART-Korrekturen beim Uhrengang berücksichtigt.

-- 217.232.10.108 19:36, 23. Nov. 2006 (CET)Beantworten

Ich hab den Begriff Bewegungsgleichung mal minimalinvasiv verlinkt. Gibt es den Begriff "Geodätengleichung der gekrümmten Raumzeit" eigentlich wirklich? Klingt spontan irgendwie nach "Hohlrohrvolumen" --timo 21:30, 23. Nov. 2006 (CET)Beantworten

Es gibt den Begriff "Geodätengleichung" wirklich. Ich habe einfach angenommen, dass der Zusatz "der gekrümmten Raumzeit" klarer macht, worum es geht (evtl. sollte das nicht kursiv sein). Btw: Du hast Bewegungs(g)leichungen geschrieben, daher hat die [[Bewegungsgleichung]]en-Verlinkung nicht geklappt. ;)

-- 217.232.0.83 08:43, 24. Nov. 2006 (CET)Beantworten

Langsame Bahnen sind länger! In der t-Richtung. Deshalb nicht stärker gekrümmt. --Pjacobi 10:52, 24. Nov. 2006 (CET)Beantworten

Sorry, ich habe noch immer keinen Plan wie die Wurfparabel mit der ART berechnet werden kann. Was mich dabei verwirrt ist, dass die Form der Parabelbahn von der Anfangsgeschwindigkeit abhängt. Je langsamer der Körper ist, um so stärker ist die Parabelbahn gekrümmt. Die Bahn des Lichts ist nahezu eine Gerade. Dies gilt jedoch nicht für den Apfel der vom Baum fällt, falls er etwa durch den Wind eine horizontale Geschwindigkeitskomponente hat. Wie berechne ich nun die Bahn des fallenden Apfels mit der ART ?

Du musst, um deine Geodäte eindeutig zu definieren, den Raumzeitpunkt und den Geschwindigkeitsvektor zu einem beliebigen Punkt der Bahnkurve (in Abhängigkeit der Parametrisierung) kennen. Dann kannst du den 4-Vektor der Beschleunigung ausrechnen und damit die Bahn in 4 Dimensionen. Wenn du dann die 0-Komponente deiner Kurve (also die Zeit in deinem Koordinatensystem) als Parametrisierung der Kurve benutzt, ist die 0-Komponente konstant und die anderen Komponenten geben dir die Bahnkurve in 3 Dimensionen. Aber ich weise nochmal drauf hin, dass du es dir damit unnötig kompliziert machst, weil für den Apfel die newtonsche Mechanik ein gutes Ergebnis liefert. -- 217.232.0.83 12:29, 24. Nov. 2006 (CET)Beantworten

Sorry, meine Frage war nicht wie die Wurfparabel in der klassischen Mechanik berechnet wird, sondern ob und gegenenfalls wie diese Berechnung in der ART erfolgen kann. Die Antwort, die Berechnung erfolgt nach Newton, weil die Geschwindigkeiten klein sind, ist keine. Aufgrund der Erklärungen hier, komme ich zu dem Schluss, dass die Berechnung mit der ART gar nicht möglich ist. Nach Newton lässt sich die Position des Apfels zu jedem Zeitpunkt (während des freien Falles) berechnen, falls Ort und Impuls zu einem Anfangszeitpunkt bekannt sind. Die Zeit und die drei Koordinaten (x,y,z) kann also zu jedem Zeitpunkt t in einem Vierervektor (t,x,y,z) angegeben werden. Die Zeit (0-Komponente) ist dabei allerdings nicht konstant. Die Beschreibung in orthogonalen Koordinaten mit einer Achse (z-Ache) entgegen der Richtung der Schwerkraft ist dabei üblich und zweckmäßig. Die Bahn kann jedoch in beliebige andere Koordianten transformiert werden und ein bestimmtes Einheitensystem ist dabei auch nicht erforderlich.

In der klassischen Mechanik löst du die Bewegungsgleichung

{\ddot {x}}=g(x)

, wofür du das Gravitationsfeld g, v(0) und x(0) kennen musst. In der ART löst du die Bewegungsgleichung

{\ddot {x}}=-\Gamma (x){\dot {x}}{\dot {x}}

, wofür du das Gravitationsfeld Gamma, v(0) und x(0) kennen musst. Vom Prinzip her ist es genau das gleiche: Wenn du das Gravitationsfeld und die Randbedingungen (v(0),x(0)) kennst existiert eine eindeutige Lösung der Bewegungsgleichungen. Die einfachste (im Sinne von "muss man am wenigsten denken") Möglichkeit an diese Lösung zu kommen, ist es, die Bewegungsgleichung einfach in den Rechner zu stecken und die Lösung numerisch abzuschätzen. Für die meisten realistischen Probleme muss man das sowieso machen - sowohl klassisch als auch relativistisch. --timo 12:32, 25. Nov. 2006 (CET)Beantworten

Hast recht, es muss heißen: ...ist die 0-Komponente linear... ansonsten stimmts. -- 217.232.0.83 16:52, 24. Nov. 2006 (CET)Beantworten

Link-Vorschläge

Letzter Kommentar: vor 18 Jahren1 Kommentar1 Person ist an der Diskussion beteiligt

Ich würde gerne diesen Link in der Liste unter dem Artikel sehen:

http://www.kornelius.de/arth/

Die Seite erklärt die ART wirklich einfach, sogar besser als einstein-online, und hat mir selbst sehr geholfen. Würde jemand den Link eventuell hinzufügen?

Obwohl ich die Aufmachung der Seite nicht mag, erscheint sie mir recht solide. Ich konnte beim Rumstöbern keinen fachlichen Fehler finden. Meinetwegen könnte der Link also rein, auch wenn er sich wohl eher an den jung(geblieben)en Leser wendet. -- 88.76.234.57 23:22, 25. Nov. 2006 (CET)Beantworten

Oma fragt sich..

Letzter Kommentar: vor 17 Jahren59 Kommentare20 Personen sind an der Diskussion beteiligt

#Einleitung

Ein Gegenstand, auf den keine nichtgravitative Kraft ausgeübt wird .. das ist "keine nicht-schlechte" formulierung, könntest Du das auch nicht-undeutsch sagen, später kommt dann noch bezieht sich … die Kräftefreiheit … auf die Abwesenheit von nicht-gravitativen Kräften: es gibt in der ART keine Gravitation, und freiheit ist die abwesenheit dessen was nicht das ist, was es nicht gibt. uff..
Da ein Beobachter in jedem Moment… (beispiel sternhaufen) - irgendwie ist das ziemlich unklar:
- wieso sollte der Beobachter nicht auf gravitation schliessen, wenn er mit seinem stern mitfliegt (newton hat auch auf gravitation geschlossen, obwohl er mit seiner erde mitflog)
- insbesondere erläutert das beispiel aber die oberbei genannte Weltlinie nicht (es nennt sie garnicht), noch wird klar, wieso das (was eigentlich?, der vorhergehende satz ist so lang) aus der Krümmung der raumzeit folgt
- ausserdem war weder klar, wo das beispiel anfängt (hab ich Dir gemacht). noch wo es zuende ist
- und insgesamt ist das beispiel zwar nett, aber was erläutert es jetzt eigentlich genau?

#Die Wurfparabel

der abschnitt ist mir ziemlich unverständlich.
- die wurfparabel des balles entsteht dadurch, dass der ball 300.000 km geodätisch-geradlinig zurücklegt, und daher nach einem meter wieder in der anderen hand landet. diese wurfparabel ist dann eine winzige Krümmung der Raumzeit in einem Gebiet von astronomischem Ausmaß???
- der jongleur hingegen bewegt sich krummlinig, weil die elektrostatische Gegenkraft die Gravitationskraft (die es, wie wir oben gelernt haben, nicht gibt) kompensiert, obwohl das Argument, dass sich hier zwei Kräfte kompensieren würden, haltlos ist.
- hier auch wieder: was erklärt uns dieses beispiel eigentlich? und was willst Du uns eigentlich erklären??

bitte versuch gar nicht mir in einer antwort zu erklären, was Du meinst. im artikel muss es stehen.

ich nehme an dass die beispiele irgenwelche "FAQ"s beantworten, von denen ich aber nicht weiss, was sie sind (Jeopardy). ich glaube, Du müsstest das sauber nach Frage-Antwort-Erläuterung der Antwort anhand eines Beispiels aufbauen. zum zweiten abschnitt, denk ich, ist die frage "wieso gibt es eine Wurfparabel, wenn es keine Gravitation gibt?", aber die antwort "Weil sie eine scheinkraft ist" gehört zur Frage des ersten abschnitts "wieso gibt es keine Gravitation", und die frage nach der wurfparabel ist die frage zur antwort des ersten abschnitts "weil ein körper auf seiner weltlinie kräftefrei ist". .. aber das ist meine interpretation des textes - und was beantwortet dann die antwort die zugrundeliegende Ursache ist vor allem die Wahl des Koordinatensystems. die was zugrundeliegende ursache wofür?
und wer zum teufel ist der "ruhende beobachter"? in Relativitätstheorie haben wir doch gelernt, dass es keinen ruhenden beobachter gibt ausser dem, den wir dazu erklären. jetzt aber erklärt diese von uns definierte willkürliche auswahl die allgemeine nichtexistenz von gravitation als scheinkraft. das will mir so, wie's dargelegt ist, nicht einleuchten. wieso ist plötzlich der ball gegenüber dem jongleur ausgezeichnet?

hallo 88.76.246.231, ich hoffe diese meine vorsätzlich "saudummen" interpretationen helfen Dir , den text präziser zu formulieren. dann les ich weiter. gruß -- W!B: 22:04, 19. Nov. 2006 (CET)Beantworten

Ich habe hier eine Sandbox erstellt, worin ich den Text bearbeite, bevor ich ihn hier einsetze (um nicht so viele Versionen zu produzieren). Ich habe beim Kugelsternhaufen drangeschrieben, dass das veranschaulichen soll, dass die Weltlinie im Raum gekrümmt erscheinen kann. Außerdem habe ich diese Anspielung auf lokal Näherungsweise flache Koordniatensysteme rausgenommen.

Ich hatte lange Bauchschmerzen mit der Wurfparabel, die ja auch im Review schon gekürzt wurde, und habe sie jetzt ganz entfernt. Das Kapitel hat fälschlich suggeriert, dass die Wurfparabel durch die Raumzeitkrümmung zustande kommt, obwohl das auch in einem Aufzug prächtig funktioniert. Auch die Anspielung auf riemannsche Normalkoordinaten war nicht so berauschend. Ist das OK, wenn ich das einfach weglasse?

Danke für deine Hilfe! -- 217.232.36.253 12:30, 20. Nov. 2006 (CET)Beantworten

freut micht, dass Du es als hilfe empfindest und dich nicht verulkt fühlst, mein kritik-stil wird manchmal falsch verstanden.. :-)

nochmal als zusammenfassung, seh ich das richtig, was die zwei abschnitte sagen wollten:

die klassische Mechanik sagt: ein körper bewegt sich - im kräftefreien zustande - entlang einer geraden linie (geodäte des 3-dimensional Raumes)
die ART sagt: ein körper bewegt sich - im kräftefreien zustande - entlang einer im 4-dimensionalen geradlinigen geodäte. deren Projektion kann bei dir im R3 dann durchaus gekrümmt erscheinen
die klassische Mechanik sagt: zur erklärung dieser krümmung muß eine Kraft herangezogen werden
die ART sagt: von mir aus gesehen ist die 4-dimensionale raumzeit nicht krumm, sie sieht nur für dich so aus. daher braucht's keine Kraft als erklärung. solang der körper auf der geodäte bleibt, ist er kräftefrei.
die klassische Mechanik sagt: wo kommt dann die gravitation her?
die ART sagt: von mir aus gesehen ist das genauso eine scheinkraft, wie für dich die zentrifugalkreft eines um einem punkt kreisenden beobachters. die braucht auch nur dieser als erklärung. für dich erklärt sie sich, weil er sich nicht geradlinig bewegt, sondern im kreis
die klassische Mechanik sagt: wo kommt dann die wurfparabel im schwerefeld her?
die ART sagt: von mir aus ist der geworfene körper kräftefrei, also ist sein weg eine geodäte und geradlinig, von dir aus schaut das dann krumm aus. ist ja umgekehrt genauso: wenn er bei dir wirklich auf einer Gerade fliegt, schaut er von mir aus krumm aus: er verlässt die geodäte und braucht dazu eine kraft. du sagts "das schwerefeld überwinden" dazu, ich sag "krumme bahn in der raumzeit" dazu. ich brauch also weder die schwerkraft noch ein schwerefeld dazu, ich muß nur verstehen, wie der 4D dort aussieht, also, wie die geodäten verlaufen
die klassische Mechanik sagt: du meinst also, du siehst mich etwa so von "oben", wie ich den beobachter auf der kreisbahn "von oben" sehen kann, und seh, wie sein "raum" dort ausschaut.
die ART sagt: jupp, und du kannst meinen raum genausowenig überblicken, wie dieser den deinen. er kann nur drauf schliessen, wie's bei dir ausschaut, indem er beobachtet, wie du dich - relativ zu ihm auf einer krummen bahn - bewegst. dir gehts mit mir genauso. (ist aber kein grund für minderwertigkeitskomplexe)

stimmt das so? und versteht oma das dann? -- W!B: 00:20, 21. Nov. 2006 (CET)Beantworten

Ja ich denke so ist das alles gemeint. Ich bin nur nicht ganz zufrieden mit dem Begriff "krumme Bahn" bei der Wurfparabel, weil die ja eben auch ohne Raumzeitkrümmung auftritt. Man kann sich das eher analog zur schiefen Ebene vorstellen, wo ein Beobachter von oben auch eine Parabel sieht. (Nur leider hat diese Analogie den Nachteil, dass die Parabel dann eben doch auf eine "Kraft" zurückgeht, so dass wieder der falsche Eindruck entstehen könnte, in der Raumzeit müssen eine Kraft "nach unten" wirken, die die Körper auf Geodäten hält.)

Meinst du, man könnte das vielleicht in Form einer Tabelle am Ende der Einleitung gegenüber stellen? Oder soll ich versuchen dazu ein bisschen Text zu schreiben? Oder beides? Also erst Text, dann noch mal ne Tabelle als Übersicht? -- 217.232.31.85 09:45, 21. Nov. 2006 (CET)Beantworten

nennen wir die zwei mal KLM und ART. wie Du sieht, war mein dialog schlecht formuliert, OMA versteht ihn vielleicht, Du aber nicht ;-) :

bleibt der körper auf der 4D-geodäte, nennt KLM die Bahn "krumm" (parabel), ART die bahn "gerade" (geodätisch)
verlässt der körper die 4D-geodäte, nennt ART die Bahn "krumm", und KLM auch "krumm" (ausser, sie ist zufällig in 3D exakt eine gerade - da liesse dann auf abwesenheit eines schwerefelds schliessen, der "idealfall")

stimmt das so? -- W!B: 11:20, 21. Nov. 2006 (CET)Beantworten

PS ich seh schon, zuerst gehört nochmal der sprachgebrauch geklärt (siehe Geodäte)

KLM sagt: die Gerade ist definiert als kürzeste verbindung zwischen zwei punkten. sie ist die Geodäte des R3
ATR sagt: die Geodäte ist definiert als kürzeste verbindung zwischen zwei punkten. sie ist die „Gerade“ in 4D
KLM, ART (chorus) zu OMA: „gerade“ ist synonym zu geodätisch, und nicht-geodätisch nennen wir „krumm“

-- W!B: 11:48, 21. Nov. 2006 (CET)Beantworten

Hmhmm, mein Problem ist genau die letzte Aussage. Aber da das erste Kapitel für Laien gedacht ist, ist das wohl eine zulässige Vereinfachung. Ich tüftel mal an einem Text, der die Sichtweisen von ART und Kl.Mech. gegenüberstellt. Ein Dialog ist wohl leider zu "formlos". Ich werde diesmal wohl mindestens 24 Stunden brauchen (viel zu tun...). Danke, dass du dir so viel Mühe machst. -- 217.232.31.85 15:56, 21. Nov. 2006 (CET)Beantworten

ganz klar, Du schreibst den artikel, ich sag versuch nur einen gedankenanbfolge reinzukriegen, die in sich schlüssig ist, in dem sie nicht von einem vorhandenen wissenstand ausgeht (wie Du ihn wohl hast), sondern diesen aufbaut (wies ein Enzyklopädie-rtikel machen muß) .. und es macht mir spass ;-) -- W!B: 04:26, 23. Nov. 2006 (CET)Beantworten

ich aber hab jetzt problem mit der verwendung des worts „Raumzeitkrümmung“. ich fände, der dialog ginge so weiter:

KLM: du meinst also, dass das, was ich als gravitationsfeld beschreibe, für dich ein effekt der Raumzeitkrümmung ist?
ART: Nein. eine geodäte ist für mich so wenig krumm wie eine gerade für dich. nehmen wir als beispiel einen menschen auf einer Kugeloberfläche. er geht immer gerade(aus). aber du sieht ihn eine krumme bahn in deinem raum beschreiben. so gehts mir mit deinen geraden. aber mein Raum ist für mich genausowenig krumm wie deiner für dich oder dem auf der Kugel seiner für ihn. Raumzeitkrümmung sagt du zu meinem raum, weil er es für dich ist (beziehungsweise du ihn dir nur so vorstellen kannst, also nur die projektion meines raumes).
KLM: wieso spricht man dann bei euch von „Gekrümmte Raumzeit“?

tja, wieso? die krümmung einer krummen linie wie f(x)=x² zu berechnen ist klar, aber wie berechnet man die krümmung einer geodäte? ich dachte, die ist definiert als linie der krümmung 0 (sie geht den kürzesten weg = sie macht keine umwege). wo ist da mein denkfehler? -- W!B: 04:26, 23. Nov. 2006 (CET)Beantworten

Aaalso das ist genau das Problem, in das wir jetzt reinlaufen: Für Kurven gibt es die Geodätische Krümmung, die für Geodäten verschwindet. Aber das ist ein Begriff aus der klassischen Differentialgeometrie, die nicht einfach auf die riemannsche Geometrie (und auf Mannigfaltigkeiten) übertragbar ist. Die Krümmung der Raumzeit wird aber durch den Krümmungstensor beschrieben, der aus der riemannschen Geometrie kommt. Der kann anschaulich glaub ich als "Nichtkommutativität des Parallelentransports" beschrieben werden. Das würde dann sowas heißen wie: Wenn zwei in einem Punkt parallele Geodäten an einem anderen Ort nicht parallel sind (z.B. sich treffen) ist der Raum gekrümmt. Auf ner Kugel treffen sich zwei parallel am Äquator loslaufende Geodäten am Pol. -- 131.220.55.161 13:13, 23. Nov. 2006 (CET)Beantworten

"Krümmung" ist ohnehin in diesem Kontext eine unglückliche Bezeichnung. Aus Riemanns Sicht ist ein zusammengerolltes Blatt Papier nicht gekrümmt, weil man das intrinsisch nicht feststellen kann. Zumindest für die Anschauung sollte man vielleicht besser von "Verzerrung" o.ä. sprechen, auch wenn das dann wieder das Problem des fehlenden Bezugsrahmens aufwirft.--Gunther 13:19, 23. Nov. 2006 (CET)Beantworten

Es ist glaube ich für einen Laien alles am einfachsten begreiflich, wenn man riemannsche Normalkoordinaten verwendet. Wie wärs mit folgendem:

Wie oben erklärt ist die Gravitation lokal eine Scheinkraft. Man kann also ein Bezugsystem lokal so wählen, dass die Kraft nicht auftritt. Dieses Bezugsystem ist natürlich das frei fallende System. Wenn man die Gravitation als Scheinkraft ansieht ist dieses System ein lokales Inertialsystem, also verwendet man es in der Physik meist als ausgezeichnetes System. Da sieht man dann direkt, dass der Ball sich gerade bewegt und der Jongleur beschleunigt wird. Andererseits können sich zwei parallel frei fallende Beobachter an einem Punkt ihrer Bahn (z.B. im Erdkern) treffen, so dass also die Raumzeit verzerrt (gekrümmt) ist. Also nur lokal ausgezeichnetes System, weil auf großer Skala verzerrt, Blah Blah Blah Yada Yada Yada...

Ist zwar auch eine etwas krude Formulierung (man verwendet durchaus meist keine Normalkoordinaten, sie sind eigentlich nur für die Anschauung gut...) aber da es in der Einführung gerade um Anschauung geht, kann man da doch drauf abheben, oder? -- 131.220.55.161 14:04, 23. Nov. 2006 (CET)Beantworten

jedenfalls, was die geodätische Krümmung angeht, sind dann also „geodätisch“ und „gerade“ synonym - Riemannsche Normalkoordinaten, wo find ich da was? das mit dem fallenden koordinatensystem gefällt mir aber schon ganz gut. es ist ja kein klassisches Inertialsystem, weils beschleunigt ist. das zeigt uns den unterschied der betrachtungsweisen wohl viel effektiver als der geodäten-ansatz, der immer ein frage dessen ist, ob der beobachter die ART von „innen“ oder von „aussen“ betrachtet, aber wir wollen ja darlegen, dass es für die physik kein „von aussen“ auf die ART gibt, vulgo, dass sie gültig ist. weniger gut gefällt mir das mit „lokal ausgezeichnetes System“, ich dachte, aus sicht der ART ist der euklidische Raum ein lokal brauchbares modell (heisst, aus ARTs sicht ist es lokal als "gerade" brauchbar, global aber (geodätisch) krumm: seine geodäten fangen an, die ART-geodäten zu verlassen) -- W!B: 16:19, 23. Nov. 2006 (CET)Beantworten

freut mich dass näher am punkt des misverständnisses sind. guther hat oben auf des problem der inneren und äusseren krümmung hingewiesen. welcher natur ist die „Gekrümmte Raumzeit“. es wird ja in der einleitung daraufhingewiesen, dieser artikel „baut auf den Ausführungen des Artikels Relativitätstheorie auf“. dort wird aber in #Gravitation und die Krümmung des Raumes das beispiel mit den scheinbaren anziehungskraft richtung nordpol gebracht, das mir so auch partout nicht einleuchten will. irgendwie gibt es da in den bildern einen kuddelmuddel, der imho aus der erweiterung den dimensionsbegriffs auf die zeit kommt: daher lassen geometrische bilder, die von räumlichen einbettungen in höhere dimensionen ausgehen, immer so ein diffuses gefühl, da würde böse getrickst (was soweit führt, die ART immer noch zu bezweifeln). ist es nicht so, dass eine ART auch auf einem R2+Zeitdimension gültig sein müsste? die üblichen bilder über „Raumzeitkrümmung“ (wie der trichter im artikel) versuchen aber immer, rein geometrisch herunterzurechnen. in Krümmung steht Für eine riemannsche Mannigfaltigkeit kann eine Krümmung definiert werden, die ohne Rückgriff auf einen umgebenden Raum auskommt. Sie misst, inwieweit die lokale Geometrie der Mannigfaltigkeit von den Gesetzen der euklidischen Geometrie abweicht. - heisst das, dass in umgebung einer masse die euklidische geometrie nicht gültig ist? wär sie im o.e. fallenden inertialsystem gültig? -- W!B: 16:19, 23. Nov. 2006 (CET)Beantworten

Ein "ruhendes" System nahe einer Masse ist nach der ART durchweg beschleunigt. Daher muss man das System als nach oben beschleunigt auffassen, damit die "richtigen" Bahnkurven herauskommen. Im frei fallenden System ist die euklidische Geometrie dagegen bei nicht zu großen Abständen und Zeitintervallen ohne diese Scheinkraft anwendbar (auf großen Skalen gibts Gezeitenkräfte). Das wird im Kapitel "Äquivalenzprinzip" angeschnitten.

Das heißt das System, dass man nahe einer Masse klassisch als "Inertialsystem" ansieht, ist nach der ART beschleunigt und das frei fallende system, dass man klassisch als beschleunigt sehen würde ist in der ART zumindest lokal ein Inertialsystem.

Riemannsche Normalkoordinaten = frei fallendes Bezugsystem = alle Geodäten durch einen Raumzeitpunkt sind Geraden, in einer Umgebung.

Ja man kann die ART in auch in 2+1 oder 1+1 Dimensionen darstellen. Solche Theorien sind dann zwar mathematisch und physikalisch einfacher (in d<=3 wird die Krümmung ganz durch den Ricci-Tensor beschrieben), aber man hat dann wenigstens eine Dimension als Zeitdimension. Dann kann man z.B. auf sowas wie raum- licht- und zeitartige Geodäten abheben... Der Trichter soll noch gar nichts mit ART zu tun haben (ein Disclaimer, dass 2D-Vergleiche nicht so richtig sind, steht ja direkt im Text daneben) sondern nur Geodäten anschaulich machen.

Es sollten in der Einleitung also vielleicht vor allem folgende Punkte geklärt werden:

Inertialsysteme nach der ART sind z.T. verschieden von Inertialsystemen der KLM, weil in der ART die Gravitation eine Scheinkraft ist.
In der KLM entsteht die Wurfparabel durch ein Kraft, in der ART, weil man sich nicht in einem Inertialsystem befindet.
Wenn man in ein lokales Inertialsystem nach der ART geht, werden sich auf großen Skalen manche parallele Geodäten (also "gerade" Linien) treffen, was auf eine "Verzerrung" (Krümmung) der Raumzeit hinweist. Daran kann man erkennen, dass man ein "echtes" Gravitationsfeld hat und sich nicht einfach in einem linear beschleunigten System befindet.

Da ist dann schon ein Teil des Äquivalenzprinzips drin, aber das ist ja auch gewissermaßen der Kern der ART. Wäre das so OK? -- 217.232.10.108 19:22, 23. Nov. 2006 (CET)Beantworten

Ich habe jetzt einen neuen Text zur Wurfparabel geschrieben. Wäre dankbar für Kritik. (Außerdem habe ich hier etwas umgebaut, damit dieser Diskussionspunkt nicht in Vergessenheit gerät.) -- 88.76.242.50 00:33, 26. Nov. 2006 (CET)Beantworten

doch ja, ich denke das erfasst den sachverhalt deutlicher, nur sprachlich ists noch recht krud, ich bin nicht sicher ob ich den text nur drum versteh, weil ich weiß was Du sagen willst.. und über die krümmung will noch geredet sein.. -- W!B: 00:10, 27. Nov. 2006 (CET)Beantworten

Raum und Zeit vs Raumzeit

was mich jetzt nocht stört, ist dass nicht unnunterbrochen im text klargestellt wird, dass der raum, den die ART beschreibt, nicht irgendein "krass-würmlöchriger-hyperraum" ist, in den unser universum eingebettet ist, sondern dass sie eine andere beschreibung unseres raumes ist. genau aus dem missverständnis denken die kiddies ja immer an raumschiff enterprise, wenn sie ART hören, und die reaktionäre halten sie für quatsch. der raum der ART ist der raum der klassischen mechanik, das sollte mindestens jeden absatz durchschimmern. ich finde ja noch immer, dass das geodäten-bild zu geodäte gehört, und nicht in den artikel hier: er suggeriert, dass die raumzeit irgend ein mysteriöses gebilde ist. vorstellen könnt ich mir aber vielleicht ein bild dazu, das die abgelenkten lichtstrahlen um eine masse zeigt, sodass man sieht, dass die kurven in der klassischen und der relativistischen mechanik exakt dieselben sind, nur die begründung dafür einen andere.. -- W!B: 00:10, 27. Nov. 2006 (CET)Beantworten

Naja, der Punkt ist: Die ART "erlaubt" solche Räume, nur unserer ist (allen Beobachtungen zufolge) nicht so. Ich habe mal versucht, das in der Einleitung einzustreuen. Ich habe einige kleine Änderungen vorgenommen, die du am besten mit dem Versionsvergleich findest. Leider sind meine Formulierungskünste sehr beschränkt, daher wärs toll, wenn du ein paar konkrete Vorschläge machen, oder einfach selber in der Sandbox schreiben könntest. Das Geodätenbild finde ich hilfreich um zu illustrieren, was eine Geodäte ist, da dieser Begriff nunmal recht zentral ist. Es steht im Text direkt daneben, dass zweidimensionale Bilder eine schlechte Illustration sind, insofern kommt hoffentlich keiner auf die Idee, daraus auf exotische Eigenschaften des Raumes zu schließen. Ein Lichtstrahl-Bild ist im Kapitel Lichtablenkung. -- 217.232.23.213 11:29, 27. Nov. 2006 (CET)Beantworten

na hab mich mal getraut, ich hatte nicht gedacht, mal über die ART zu schreiben.. jedenfalls sollten wir dem leser nicht unter die nase reiben, dass er doof wäre, daher hab ich die "nicht anschaulich vorstellbar" und "der naiven Anschauung unzugängliche" rausgetan: sinn des artikels ist ja, es der anschauung zugänglich zu machen, sonst bräuchten wir den artikel nicht.. wird jetzt klarer, dass ART keine hexerei ist, sondern nur eine umformulierung eines problems? -- W!B: 00:55, 29. Nov. 2006 (CET)Beantworten

ich hab für das bild mit der geodäte eher so eine vorstellung: (http://upload.wikimedia.org/wikipedia/de/archive/a/a9/20061225142501%21Geodesiques-var.png). da ist dann halbwegs zu erkennen, dass die zwei beschreibung ein und derselben angelegenheit sind: der anblick von "oben" ist die normale Keplerbahn, die Raumkrümmung das Schwerefeld. -- W!B: 01:03, 29. Nov. 2006 (CET)Beantworten

Hmmm...

Deine sprachlichen Vereinfachungen finde ich gut, aber du hast viele Sachen in Klammern geschrieben. Ich persönlich finde das schlechten Stil. Entweder etwas ist wichtig, dann sollte es ohne Klammer stehen, oder es ist unwichtig, dann kann es ganz weg.
Die Änderungen an der Einleitung finde ich nicht ganz so gelungen. Da werde ich nochmal durchgehen und den ein oder anderen Satz ändern.
Dein neues Bild erzeugt wieder den Eindruck, dass der (3D-)Raum gekrümmt ist, was ich nicht so günstig finde. Das alte Bild sollte nur an einem einfachen Beispiel zeigen, was eine Geodäte ist, dieses dagegen hat eine falsche physikalische Implikation. Zuallermindest sollte die gelbe Kugel weg, sonst krümmt da wieder ein 3D-Objekt eine 2D-Ebene, weil es von einer "Kraft" nach "unten" gezogen wird... die schlimmste Sünde bei ART-Illustrationen.
Das Problem ist, dass in der Einleitung (wie üblich) zuerst die Raumzeitkrümmung und dann die Gravitation beschrieben wird. Ich grüble mal, wie man die von dir monierten Bemerkungen in der Einleitung hinkriegen kann.

-- 217.232.51.117 11:11, 29. Nov. 2006 (CET)Beantworten

passt, recht hast Du, war ja nur „sandbox“ ;-) - ich hab das bild jetzt zu Geodäte getan, dort gehörts auch hin. wer nicht weiss, was eine g. ist, sieht es dort, und wer es weiß, brauchts nicht. das sollte ja meine skizze aussagen, das die zeitdimension weglassen immer problematisch ist, wenn schon herunterrechen, dann indem eine raumdimension weggelassen wird. ich find das trichterbild auch nicht so passend, allein schon, wenn der trichter nach oben zeigen würd, würde es suggerieren, das die gravitation "höher" ist, also das gelbe ding (stimmt, sollte eine scheibe bleiben, wie rechts) die ebene „an/verzieht“, und nicht umgekehrt. besser aber wohl kein bild als ein irreführendes. -- W!B: 03:44, 30. Nov. 2006 (CET)Beantworten

Ich möchte gern vermeiden, dass das erste Kapitel zu groß wird. Das soll ja eher ein "das Wichtigste in Kürze und anschaulich" sein. Ich bin atm nicht so ganz zufrieden mit dem Abschnitt "Raumzeitkrümmung". Der Umfang ist im Moment mE akzeptabel aber viel größer sollte es nicht grade werden. Vielleicht kann der Abschnitt "Raumzeitkrümmung" ganz raus, die Korkenzieherbahn ist gewissermaßen redundant, die Bemerkungen zum "Star-Trek-Raum" sind wohl auch nicht so wichtig und die Ausführungen über Impuls und Energie des e.m.-Feldes sind ja auch schon weiterführend. Man könnte dann einfach vorher mal kurz auf den Energie-Impuls-Tensor und die Feldgleichung verweisen. Was meinst du? -- 131.220.55.146 14:49, 29. Nov. 2006 (CET)Beantworten

who is Du? ich finds jetzt ganz gut geschrieben, aber auch unnötig. oder aber, wir bauen noch aus und lagern das ganze nach Raumzeitkrümmung aus, dort wird dann nur dieses phänomen erläutert, und hier nur ein verweis auf den artikel, dann ist mehr raum für das folgende -- W!B: 03:44, 30. Nov. 2006 (CET)Beantworten

Also hier ist mein Kürzungsvorschlag. Die IP 131.220.X.X war übrigens auch ich. (Das sind die IPs unserer Unirechner.) Jemand hat mir empfohlen überschüssige Ausführungen an die Wiki-Books weiterzugeben. Mal sehen. :) -- 217.232.14.213 12:33, 30. Nov. 2006 (CET)Beantworten

das, freund aus bonn, ist imho sowieso der "richtigere" weg in solch komplexen angelegenheiten: gleichzeitig auf wikibooks ein gutes buch schreiben, das das ganze themenum klärt, und hier bei uns nur eine zusammenfassung, mit konzentration auf präzise didaktische struktur und saubere verlinkung auf andere artikel, die einzelne unterbereiche näher erläutern. perfekterweise ist das wikibook dann eine harmonisch innernandergearbeitete ganzheit aus einem duzend hiesiger artikel. die wikipedia zwingt einen dazu weder zu schwafeln, noch zu schwurbeln, was auch dem book zugute kommt, aber zu näheren erläuterungen kann man dann immer auf das book verweisen.. gruß -- W!B: 19:45, 30. Nov. 2006 (CET)Beantworten

Kann das Einleitungskapitel jetzt so bleiben? Wie siehts dann mit dem weiteren Zeug aus? Soll ich die neue Einleitung reinschreiben und den Artikel ins Review stellen? -- 217.232.33.115 15:59, 1. Dez. 2006 (CET)Beantworten

meinst Du das ernst? ich hab erst bis seite 4 gelesen.. -- W!B: 00:08, 4. Dez. 2006 (CET)Beantworten

Ich finde, dass die "gekrümmte Raumzeit" jetzt recht gut dargestellt ist. Gerade bei der laienverständlichen Darstellung dieses Punktes können auch große Geister straucheln, und z.B. im Vergleich zu dem was Brian Greene in "The fabric of the cosmos" zum Thema bringt, ist unser Kapitelchen Gold wert. --Pjacobi 19:11, 4. Dez. 2006 (CET)Beantworten

schön zu hören (hab Dich raufgeschoben wegen überschrift, wenns gefällig ist) -- W!B: 14:04, 5. Dez. 2006 (CET)Beantworten

Grundlegende Konzepte

Spezielle Relativitätstheorie:
- 2.abs „Die Gesetze der Physik haben danach …“ wonach?
- 4. „Im allgemeinen Fall wie beispielsweise eines Kugelsternhaufens aus Neutronensternen und Schwarzen Löchern“ - wieso ist eine singularität der allgemeine fall? bei mir heisst sowas spezielfall..
- „so dass die Raumzeit hochgradig gekrümmt und zudem dynamisch ist“ - ha! - zuerst den Reisser, aber im nebensatz dann die wirklich dramatische aussage dem leser unterschieben: die raumzeit ist dynamisch! wow, was heisst das?
Äquivalenzprinzip
- „…durch überhaupt kein Experiment feststellen kann, ob er sich in der Schwerelosigkeit befindet oder im freien Fall“ - hm, wieder, der artikel muß sich entscheiden, ob er ARTs standpunkt einnimmt oder OMAs: ich dachte, es gibt keine gravitation..
- „Das bedeutet insbesondere, dass auch ein Lichtstrahl für einen Beobachter im freien Fall nicht gekrümmt erscheint, oder anders ausgedrückt, dass ein Beobachter, der im Gravitationsfeld ruht einen Lichtstrahl gekrümmt wahrnehmen muss, da er in Wirklichkeit die ganze Zeit gegen den freien Fall nach oben beschleunigt wird.“ den satz versteh ich nicht mehr. erstens derselbe kuddelmuddel: welches gravitationsfeld, welche krümmung, und wieso wird er gegen den freien fall beschleunigt? oben stand er auf einer masse, und da gabs eine gegenkraft. und das jetzt? ich dachte im freien fall ist er kräftefrei, also gibts keine bescheunigung

.. viel spaß derweil gruß -- W!B: 00:08, 4. Dez. 2006 (CET)Beantworten

Ich habe ein bisschen was umgeschrieben. Zum ÄP und dem "gekrümmten" Lichtstrahl arbeite ich im Moment an einem Bild, das das hoffentlich illustriert. Ich häng mich mal rein und versuche das in den nächsten Tagen fertig zu kriegen. -- 217.232.28.104 17:45, 4. Dez. 2006 (CET)Beantworten

- „so dass die Raumzeit hochgradig gekrümmt und diese Krümmung zeitlich veränderlich ist“, das meint ich nicht, dass danymisch das heisst war mir klar, aber: in der ART ist, wie wir gelernt haben, die Zeit eine Koordinate wie die räumlichen ist, und gleichwertig zu behandeln. „die krümmung der zeit ändert sich mit der zeit“ wir sind doch in der ART, da gibt es keine explizite zeit an sich, sondern nur weltlinien, oder? .. wo ist da der wurm?

Jein. Die Raumzeitkrümmung ist abhängig vom Raumzeitpunkt, das heißt von allen 4 Raumzeit-Koordinaten. Je nach Koordinatensystem ist sie zeitlich veränderlich oder auch nicht. Dabei ist immer die x⁰-Komponente die "Zeit" des entsprechenden Koordinatensystems. In einem Koordinatensystem, in dem die Erde ruht, ist die durch sie verursachte Raumzeitkrümmung zu jedem Zeitpunkt gleich, also statisch. Wenn man ein Mehrkörpersystem hat, ist in jedem Koordinatensystem mindestens einer der Körper bewegt, so dass man in jedem Koordinatensystem eine dynamische Krümmung hat. Es sollte genauer heißen: "In diesem Fall gibt es kein Koordinatensystem, in dem die Krümmung zeitlich konstant ist." Ich hab das etwas umgeschrieben. Oder muss ich da eher weiter ausholen? -- 217.232.9.68 15:26, 5. Dez. 2006 (CET)Beantworten

Zusatz: Der Krümmungstensor ist ein Tensor 4. Stufe. Man gibt 3 Vektoren (genauer gesagt Vektorfelder) hinein und bekommt einen heraus. Das macht man so, dass man einen Vektor entlang des Parallelogramms der beiden anderen Vektoren parallel verschiebt. Das Ergebnis ist der Vektor, den man nach der Parallelverschiebung hat. Wenn dieser immer mit dem Anfangsvektor übereinstimmt, hat man keine Krümmung, der Tensor ist 0. Der Tensor ist ein Ausdruck für eine Art infinitesimale Differenz von Anfangs- und Endvektor eines infinitesimalen Parallelogrammtransports in jedem Punkt. (Ja diese Erklärung ist "Handwaving", es geht nur um das grundsätzliche Prinzip.) -- 217.232.9.68 02:21, 6. Dez. 2006 (CET)Beantworten

ah nein, nicht weiter ausholen, guter trick, das wieder am früheren beispiel aufzuhängen

„dass ein Beobachter in einem geschlossenen Raum ohne Information von außen durch überhaupt kein Experiment feststellen kann, ob er sich in der Schwerelosigkeit fernab von Massen befindet oder im freien Fall nahe einer Masse.“ - also, in ARTs worten, er kann die Raumzeitkümmung nicht messen, bzw mit dem späteren zusatz: er kann sie nur in vergleich zu einem nahen objekt messen, indem er seine und dessen geodäten vergleichen kann, eigentlich eh eine relativ triviale aussage, so gesehen ;-) - und super, jetzt verstehen wir auch, warum es gerade die experimente sind, die die ART bestätigen oder widerlegen können.

und das mit gravitation versteh ich auch: jeder abschnitt fängt wieder mit der klassischen sichtweise an. drum sollte die ART erst wieder erwähnt werden, wenn aus ihrer sichtweise gesprochen wird .. ich les mal weiter, bin schon gespannt auf dasbild -- W!B: 09:02, 6. Dez. 2006 (CET)Beantworten

Hier ist mal der erste Entwurf zum Bild. (Hab meinen Aktenordner-Account benutzt, um es hochzuladen.) Natürlich muss im Artikel ein vernünftiger Erklärtext in die Bildunterschrift. Es sieht außerdem noch etwas "brachial" aus. Halt wie ein typische Schemaskizze in einem Physikbuch. Hast du Verbesserungsvorschläge? -- 217.232.12.184 13:34, 6. Dez. 2006 (CET)Beantworten

(verzeihung, hab mich ein paar tage woanders verzettelt..) super, unglaublich, wie das ganze sich in intuitiv einleuchtende und garnicht "abwegige" sachverhalte auflöst. was noch ginge, wär, a aussen, und g gegenüber innen anzusetzen, dann würde der "Scheinkraft"-ansatz gleich miterläutert. -- W!B: 07:36, 12. Dez. 2006 (CET)Beantworten

Machsches Prinzip: da wird mir irgendwie überhaupt nicht klar, in welchen zusammenhang das MP mit der ART steht. dass es es schwierig ist, glauben wir ja, aber inwiefern ist es "grundlegend" (wir sind ja im abschnitt "grundlegende Konzepte") - ist es eine mögliche option, ein ungeklärtes rätsel, eine unnötige annahme, eine nötige aber unbewiesene voraussetzung, ein philosophisches "feature" der ART, und was wird derzeit favorisiert? wie erfahren im abschnitt zwar etwas über zwei "abstruse" spezialfälle, aber nichts über die welt in der wir leben (über die reden wir ja), und auch nicht, ob moderne auf der ART aufbauende konzepte wie die stringtheorien es verwenden. das gehörte irgendwie eingebunden.. -- W!B: 08:02, 12. Dez. 2006 (CET)Beantworten

Machsches Prinzip: Einstein gibt Mach als eine seiner wichtigsten Quellen für philosophische Fragestellungen an. Insofern hat ihn vermutlich das machsche Prinzip dazu inspiriert, in der ART Trägheit und Schwere auf dasselbe Phänomen zurückzuführen. Anders als Mach führt er jedoch Schwere auf Trägheit zurück und nicht andersherum. Außerdem besteht durch die kosmologische Konstante die Möglichkeit, das machsche Prinzip zu verletzen. Ob das Prinzip für dieses Universum gilt, ist unklar- Laut mancher Quellen gibt es Modelle, die es erfüllen und andere die es nicht erfüllen. Es gibt andere Aussagen, dass die ART als Ganzes das machsche Prinzip nicht erfüllt. Ich suche mal nach, wo ich das alles aufgeschnappt habe und versuche das dann unterzubringen.

Meinst du beim Bild mit "innen" im Raum oder in der Mitte zwischen den Einzelbildern? -- 217.232.46.225 11:57, 12. Dez. 2006 (CET)Beantworten

Also:

Hier wird recht drastisch dargestellt, wie wenig wohldefiniert "das machsche Prinzip" ist. Auch der Artikel Machsches Prinzip sagt, dass das Prinzip nicht gerade eindeutig definiert ist.
Hier wird Einsteins mutmaßliche Interpretation des Prinzips genannt.
Hier wird gesagt, dass Einstein den Lense-Thirring-Effekt als Bestätigung für seine Version des machschen Prinzips sah.
Hier steht, dass gar nicht klar ist, ob das Gödel-Universum dem machschen Prinzip widerspricht, weil es eine nicht-verschwindende kosmologische Konstante braucht und außerdem nur manchen Formulierungen des Prinzips widerspricht.

Fazit: Ich werde mal versuchen, das irgendwie klarer zu formulieren. -- 217.232.46.225 17:47, 12. Dez. 2006 (CET)Beantworten

 *---------*
 |         |
 |    | g  |
 |    V    |
 *---------*
      ^
      | a

hihi, grafik wie zu DOS-zeiten.. -- W!B: 22:29, 12. Dez. 2006 (CET) PS nochmal kompliment zu den sympatischen strichmännchen.. o}−<Beantworten

Datei:Geodesiques-var.png

ich hab jetzt einen #Raumzeitkrümmung und Dimensionen angelegt, um die sätze dazu zusammenzufassen. das dazugehörige Bild wäre dann so etwa.. -- W!B: 15:29, 25. Dez. 2006 (CET)Beantworten

die einleitung des kapitels erklärt jetzt nicht mehr, sondern führt begriffe ein, und die einzelnen folgenden abschnitte erläutern das und kehren am ende zu diesen "einfachen" sätzen der einleitung zurück. so schliessen sich gedankliche kreise, ohne zu verwirren. schau bitte nochmal drüber, ob ich keine fachlichen fehler eingebaut hab.. -- W!B: 16:03, 25. Dez. 2006 (CET)Beantworten

Ich bin mal drüber gegangen und habe den Gegensatz Gekrümmtes Blatt <-> Verzerrte Raumzeit noch etwas ausgeführt und den Satz über 3-dimensionale ART weg gelassen. Ich finde das nicht so wichtig. Da sollte der Artikel mehr bei der Kernaussage bleiben. Notiz: Wenn wir fertig sind mit Durcharbeiten, sollten wir uns die Wiki-Links mal vornehmen... -- 88.76.245.14 17:02, 26. Dez. 2006 (CET)Beantworten

ich hab die flachländer wieder rausgetan, die verwirren hier nur: sie legen wieder eine höherdimensione einbettung nahe, aber die raumdimensionen sind genauso 3 wie in der klassischen mechanik, unten wird geklärt, dass der flachländer anhand von gezeitenkräften sehrwohl feststellen kann, dass der raum gekrümmt ist, und insgesamt ist der raum eben nicht gekrümmt, sonder die ihn beschreibenden koordinatensysteme. krumm ist also eigentlich die Metrik, nicht die Raumzeit, wenn ich die bisherigen gespräche richtig verstanden hab. insoferne ist der begriff geradezu irreführend. aber all diese details können ja ausführlichst in dem artikel Raumzeitkrümmung erläutert werden, offenbar gibt es da weitaus genug zu sagen, das einen eigenen artikel rechtfertigen würde.

wikilinks find ich persönlich unnötig, wir arbeiten ja an diesem artikel, obwohl die disks hier genug material auch für andere artikel abgeben. und sonst schau ich eh bei jedem link nach, ob dort zumindest nicht das gegenteil von dem hier steht.. -- W!B: 02:47, 28. Dez. 2006 (CET)Beantworten

Mathematische Beschreibung

Einleitung: hab ich dahingehend überarbeitet, dass es nicht so klingt, als hätte die ART die Tensoren erfunden.
- Es können für jeden Punkt lokale Koordinaten gewählt werden, so dass alle ersten Ableitungen des metrischen Tensors in diesem Punkt verschwinden und der Krümmungstensor dort nur durch zweite Ableitungen des metrischen Tensor bestimmt ist. - anlaß und tragweite dieser aussage ist nicht klar: ist es eine typische eigenschaft des Riemanntensors, oder der Lorentzmannigkaltigkeit, oder nötige voraussetzung der ART, oder was. ist die bemerkung überhaupt notwendig? -- W!B: 08:46, 12. Dez. 2006 (CET)Beantworten
Einsteinsche Feldgleichungen: ob es da nicht sinnvoller wäre, statt den einzelnen symbolen (das wird eh im fachartikel geklärt) nur die allgemeine struktur und bedeutung der summanden zu erläutern: $-{\frac {R}{2}}\,g_{\mu \nu }$ .. was beschreibt uns das, oder $\Lambda \,g_{\mu \nu }$ - es könnte auch beim fachartikel stehen, aber dann sind auch die folgenden sätze hier zuviel..

Die Aussage über den Krümmungstensor versuche ich sinnvoller zu gestalten. (Das jetzt ist ein "Insiderhinweis" auf riemannsche Normalkoordinaten, der hier unsinnig ist.) Bei der Feldgleichung finde ich die Benennung der einzelnen Symbole wichtig für jemand der in Vertiefungsartikeln weiterlesen will. Die Bedeutung der Terme wird ja darunter erklärt. --217.232.46.225 11:57, 12. Dez. 2006 (CET)Beantworten

Bewegungsgleichungen: na gut, dann auch bei der nächsten gleichung saubere beschriftung. was mir hier nicht gefällt, ist, dass nicht explizit erklärt wird, dass die geodätengleichung den simplen sachverhalt ${\vec {a}}=0$ darstellt. dann ist die zweite gleichung redundant, weil sie $m\cdot a=K$ nach den komponenten ${\mu }$ darstellt. der folgende abschnitt "Dabei berechnen sich..." bleibt aber wirr: was heisst da jetzt genau was? dem hinweis auf Christoffelsymbol entnehme ich, dass hier wieder die sachverhalte der ART im Koordinatensystem der klassischen physik dargestellt wurden, die schreibeweise mit den Christoffelsymbol dann die wäre, die die ART auf sich selbst anwendet. stimmt das? -- W!B: 07:35, 14. Dez. 2006 (CET)Beantworten

Wirkung: „Die mathematische Definition einer Einstein-Mannigfaltigkeit fordert nur, dass die Variation des Einstein-Hilbert-Funktionals für jede Variation der Metrik verschwindet.“ - auch der satz wirkt irgendwie drangekleistert. ist das ein sonderfall, und was ist das Einstein-Hilbert-Funktional? Volumenfunktional gehörte wahrscheinlich einfach in Volumenform eingetragen.. -- W!B: 08:04, 14. Dez. 2006 (CET)Beantworten

Hmm...

Die $x^{\mu }$ sind die Komponenten der Geodäte (so wie sie in der klassischen Mechanik Komponenten der Bahnkurve wären).
${\vec {a}}=0$ gilt nach der Geodätengleichung ja allgemein erstmal nicht, sondern nur in geigneten Koordinaten, in denen die $\Gamma$ verschwinden. Die Gleichung ist also so etwas wie ein "verallgemeinertes Analogon zu ${\vec {a}}=0$ " und das volle Kraftgesetz ist ein "verallgemeinertes Analogon zu $m\cdot a=K$ ". Sollte eher zuerst das volle Kraftgesetz und dann als Spezialfall die Geodätengleichung hingeschrieben werden?
Der Absatz "Dabei berechnen sich..." bezieht sich auf nicht-gravitative Kräfte, also e.m.-, schwache und starke Kraft. Zum Beispiel muss man bei den Maxwell-Gleichungen jetzt kovariante Ableitungen verwenden. Außerdem muss man beim Hoch- und Runterziehen von Indizes jetzt die Metrik g(x) verwenden.
Die Christoffelsymbole sind koordinatenabhängig, Tensoren auch. (Die Christoffelsymbole sind aber keine Tensoren, weil sie anders koordinatenabhängig sind als Tensoren.) Die Formen der Formeln im Mathe-Kapitel sind alle koordinatenunabhängig ("kovariant").
Ähm... jaja, ich setze wieder zuviel voraus. Die Wikung ist ein Funktional, daher wird in der Literatur meist E-H-Wirkung, E-H-Wirkungsfunktional und E-H-Funktional äquivalent verwendet. Ich werde mich mal auf E-H-Wirkung festlegen. Der Satz soll auf diesen Begriff (aus der Mathematik) verweisen, falls irgendein Schlaumeier den mal gehört hat und nicht genau weiß, was das ist. Könnte prinzipiell auch raus, ist aber mE kein schlechter Aufhänger für den Link.
Volumenfunktional: Najaaa... ist ja im Gegensatz zur Volumenform etwas nicht-infinitesimales... ;)

Ich versuchs mal zu verbessern... -- 217.232.8.243 17:51, 14. Dez. 2006 (CET)Beantworten

PS: Ich sehe gerade, dass en:Einstein manifold mir widerspricht. Habe daher die Aussage zur Einstein-Mannigfaltigkeit erstmal rausgenommen. -- 217.232.8.243 18:19, 14. Dez. 2006 (CET)Beantworten

ad 2) jupp

ad 6) mißverständnis, klar ists was _anderes_ als Volumenform, aber, ist es genug für einen eigenen artikel? wenn nein, kann es dort miterklärt werden (es kann auch dort reifen, bis es ein eigener artikel wird, wenn Dich der rotlink stört..)

ad 5) siehe Wikipedia:Assoziative Verweise ("siehe auch"), wenns keine passende stelle im text hat..

ad 4) eben, oben haben wir gelernt, das es in der ART kein ausgezeichnetes koordinatensystem gibt, in welchem koordinatensystem erhalten wir also x^µ, wenns die komponenten sind? komponenten von was? ortsvektoren zu einer punktemenge wohl? und wo setzt der an?

-- W!B: 19:07, 14. Dez. 2006 (CET)Beantworten

ad 6) Ist mir egal. Kann auch als Rotlink bleiben. Vielleicht motiviert das jemanden (evtl. sogar mich eines Tages...).

ad 4) Naja, man muss um am Ende Physik (und nicht "nur" Mathematik) rauszukriegen immer in Koordinaten rechnen. Die Feldgleichung ist ja auch schon Koordinatenabhängig (nur ihre Form nicht). Üblicherweise definiert man den Energie-Impuls-Tensor in einem bestimmten Koordinatensystem und rechnet dann die Metrik in diesem Koordinatensystem aus. Wenn man die Geodätengleichung dann in anderen Koordinaten lösen will, muss man zunächst die Metrik in diese Koordinaten bringen. Wie man jetzt Koordinaten festlegt ist rein technisch oft ein kniffliges Problem. Rede ich noch immer an deinem Problem vorbei?

-- 217.232.8.243 19:31, 14. Dez. 2006 (CET)Beantworten

ganz im gegenteil, das war jetzt genau die Antwort ..einfaches deutsch: „kniffliges Problem“, genau das hat mich interessiert. wie geht man damit um kein ausgezeichnetes Referenzsystem zu haben - ich hab ja den verdacht, das die newtonsche Mechanik reine Faulheit war.. ;-) -- W!B: 20:44, 14. Dez. 2006 (CET)Beantworten

Hier das geänderte Bild. (ich finde das andere schöner...)

Außerdem habe ich das Kapitel "Bewegungsgleichungen" jetzt umgeschrieben. Ich weiß nicht, ob das so wirklich besser ist. Hier zum Gucken und Verbessern. Ich bin noch nicht so ganz zufrieden damit. -- 217.232.66.50 19:28, 18. Dez. 2006 (CET)Beantworten

hallo, hatte die letzten tage keinen kopf für ART. der neue abschnitt ist aber in sich gedanklich gut aufgebaut. bezüglich bild kann ih mich eigentlich auch nicht entscheiden.. -- W!B: 14:47, 25. Dez. 2006 (CET)Beantworten

Ok, ich kann mich auch langsam ein bisschen damit anfreunden. Wenn du nicht allgemein nicht mehr so die Zeit hast, kann ich auch das bisherige Ergebnis in den Artikel einstellen und ein Review starten. -- 88.76.245.14 17:02, 26. Dez. 2006 (CET)Beantworten

wenn Du's nicht unbedingt vor neujahr durchbringen willst.. (ich hab erst nacher wieder zeit) - tatsächlich arbeit ich aber noch dran: ich hab mich jetzt mal durch die gesamte diskussion bisher durchgelesen (immerhin auch schon einige duzend a4-seiten), um draufzukommen, welche fragen noch offen sind, ich hab unten noch einen Todo-abschnitt eingefügt -- W!B: 02:52, 28. Dez. 2006 (CET)Beantworten

Online Links zur Referenzierung

Letzter Kommentar: vor 17 Jahren2 Kommentare2 Personen sind an der Diskussion beteiligt

So, ich hab mal die Links zu den Arbeiten von Robertson, Nordström und Reissner eingefügt. Mal sehen, ob zu den restlichen Referenzen auch noch Links aufzufinden sind... --D.H 19:48, 23. Dez. 2006 (CET)Beantworten

Hey toll! Danke für die Arbeit! (BTW: Wenn du Zeit und Lust hast, wärs toll, wenn du mir mit der Überarbeitung des Artikels in der Sandbox helfen würdest. (S. obigen Diskussionspunkt mit Unterpunkten) ;) -- 88.76.236.61 00:50, 25. Dez. 2006 (CET)Beantworten

ToDos

Letzter Kommentar: vor 17 Jahren8 Kommentare4 Personen sind an der Diskussion beteiligt

"Schwaches Äquivalenzprinzip", "starkes ÄP" (27. Okt) .. sind das die hier "klassisches" und "einsteinsches" genannten? (könnte aber auch in Äquivalenzprinzip (Physik) geklärt werden
ADM-Masse siehe oben #Masse
im Mai gab es etwa noch den abschnitt #Krümmung der Raumzeit ohne eine 5. Dimension ([1]), der unserem jetzigen #Raumzeitkrümmung und Dimensionen entspricht. sollen wir das wieder "zurückholen"?
wir hatte da auch mal Umlaufbahnenverfall als test für die ART (84.61.157.57 23:50, 29. Sep 2006 (CEST) #Experimentelle Überprüfung der ART) und Aberration (Gravitation), entspricht das dem 2. Absatz von #Ausbreitung der Gravitation und Gravitationswellen?
unter # Ich frag mich ... stand dafür als "physikalische anwendung" eine hübsche umformulierung der Wurfparabel in die bewegungsgleichnung, die mir eigentlich ganz gut gefällt, sie zu erleutern. könnte aber auch im artikel Bewegungsgleichung# Bewegungsgleichung der Allgemeinen Relativitätstheorie gemacht werden

da gibts zwar noch einiges zu "holen" in den bisherigen diskussionen, das passt aber meist zu den spezialartikeln besser

übrigens gehören vor den einspielen die änderungen am derzeitigen artikel eingepflegt. ob die versionsgeschichte der "sandbox" erhaltenswert ist? ich kaprizier mich nicht darauf, meine bearbeitung sind mir nicht so sonderlich "wertvoll", der großteil ist ehe von Dir - anderenfalls müssten wir einen admin bitten, die zwei versionsgeschichten zu vereinen (etwa, indem die letzten änderungen hier in einem sammeledit vereint werden)
ach ja, und die typo der LIT und REF gehört WP:LIT angepasst, das mach ich aber gern, wenn ich zeit find..

-- W!B: 03:40, 28. Dez. 2006 (CET)Beantworten

ÄP: Ja, steht in dem entsprechenden Artikel. Ich werde das in die Sandbox übertragen.
ADM-Masse: Ich weiß nicht, wo das hinsoll. Ich finde es passt nicht so recht in das Kapitel zum ÄP.
Der damalige Abschnitt war nicht so doll. Ich finde das heutige enthält mehr sinnvolles und weniger unsinniges.
Die Aberration ist tatsächlich das im Kapitel über Gravitationsgeschwindigkeit und -wellen. Ist hier eher kurz abgehandelt, weil es ja den Hauptartikel gibt.
Das Rechenbeispiel sollte lieber unter Bewegungsgleichung# Bewegungsgleichung der Allgemeinen Relativitätstheorie weil der Artikel hier sonst zu groß wird. Hier könnte man dann darauf verweisen.
Versionsgeschichte: Ich frag mal den frisch wieder aufgebackenen Admin Pjacobi.
LIT/REF: Danke! Ich krieg das mit den Standards nie auf die Reihe. :/
Ich habe es nicht unglaublich eilig. Ich hab am 08.01.07 meine letzte Diplomprüfung insofern hab ich auch grad nur recht knapp Zeit.

-- 217.232.33.19 13:41, 29. Dez. 2006 (CET)Beantworten

wie ists gelaufen? wär schön, wenn ich Dich jetzt Dipl.IP nennen dürfte. LIT hab ich mal überarbeitet, verzeih die rotlinks, aber das sind werke und publikationen, die wir einfach unbedingt noch als artikel brauchen, und wenn nicht hier dem fachkundigen unter die nase reiben, wo dann.. gruß -- W!B: 07:53, 16. Jan. 2007 (CET)Beantworten

ich hab ganz übersehen, dass Du schon "eingepflegt" hast und der review am laufen ist.. insgesamt aber fühl ich mich in bezug auf "Oma fragt sich.." aber "verbraucht", ich ab mich zu sehr eingearbeitet, um noch beurteilen zu können was der laie versteht oder nicht.. - das machen jetzt hoffentlich eh andere

ein großes problem hab ich aber noch: in finde, dass der ganze abschnitt "Physikalische Auswirkungen" auf ein einziges kapitel zusammengekürzt gehört.

ich persönlich würde einen artikel nie als ausgezeichnet beurteilen, der jedes kapitel mit "Hauptartikel" beginnt, aber dann ausführlich drüber schreibt. imho gehört hier nur:

Überblick über die "klassischen Tests der ART" (dieser begriff versumpert in einem hintersten absatz von # Gravitative Zeitdilatation und Rotverschiebung, obwohl er die eigentliche überschrift wäre)
#Lichtablenkung ? Lichtablenkung
#Periheldrehung ? komplett nach Periheldrehung
#Gravitative Zeitdilatation und Rotverschiebung ? zu Zeitdilatation und Rotverschiebung#Relativistische Herleitung der kosmologischen Rotverschiebung, sofern nicht gravitative Rotverschiebung etwas anderes ist oder einen eigenen artikel bekommen soll
1. Ausbreitung der Gravitation und Gravitationswellen zu Gravitation und Gravitationswelle
2. Lense-Thirring-Effekt gibts auch

insgesamt ist es richtig unangenehm, wenn hier in den hinteren kapiteln mehr zu einem gewissen sachverhalt steht als im eigentlichen artikel. wie gesagt, der aufbau des jetzigen artikels wäre für Wikibooks akzeptabel, für die Wikipedia ist es aber - imho - ein bisschen närrisch (wie, wenn man unter Newtonsche Mechanik ihre gesamte anwendung vom Hebelgesetz bis zu den Keplerbahnen erläutern wollte). Es sollte auf keinen Fall zu einzelnen Unterthemen ein halber Artikel geschrieben werden --- Auch nicht zur Role der ART in der Kosmologie. Drei bis fünf prägnante Sätze müssen reichen. Dass es nicht leicht ist, diese Sätze zu finden, ist klar schrieb schon <(kmk)>- 21:43, 1. Nov. 2006 (CET) in der lesenswert-kandidatur.

nun ist mir aber durchaus klar, dass für die exzellenz sowohl eine unmässige epische länge (vulgo "vollständigkeit") als auch ein gewisses bildibunti-design erwartet werden, und wenn die kapitel wegfallen, schauts da nicht mehr so gut aus mit bildern. da ich aber finde, dass, wenn Du es anstrebst, die mühe auch belohnt sein soll, solls wohl so bleiben. vielleicht werde ich in ein paar wochen mal die ganze info in den fachartikeln einbetten, und niemand wird sich trauen, deswegen die exzellenz wieder zu entfernen..

viel wichtiger fände ich es, platz zu schaffen für die wirklich zentrale frage, die in dem artikel nicht behandelt wird: warum brauchen wir die ART, ich meine, was war eigentlich die veranlassung, sie überhaupt aufzustellen, warum wurde sie beibehalten? auch bricht die #Geschichte irgendwie so um 1935 herum ab. was ist dann nachher passiert? wieso stehen die #Noch ausstehende Probleme vorher. und insbesondere: ist der abschnitt ernst gemeint? da haben wir eine theorie, die zwar fast hundert jahre alt ist, und als die aktuelle physikalische theorie schlechthin gehandelt wird, deren unzulänglichkeiten aber bekannt sind und an deren ersatz schon fleissig gearbeitet wird (hat nicht einstein selbst damit angefangen?), aber anderseits noch immer gegen zweifler verteidigt werden muss, und dann gibt es über ihre noch ausstehenden probleme nicht mehr zu sagen, als die paar worte? ein bisschen wirkt das wie (wer war das? Helmholtz ?, der ende des 19. jhd gesagt hat:), „die physik sei fertig und der rest nurmehr feinarbeit“. tatsächlich würde ich mir für die entwicklung der ART von 1935 bis heute sowie ihre zukunft wohl genau die zusätzlichen seiten erwarten, die jetzt unnötigerweise mit zeug belegt sind, das unter anderen Lemmata einsortiert gehört. was ich eigentlich den ganzen artikel über nicht kapiert hab: ist die ART jetzt eine veraltete theorie, die Einstein in den 40er-jahren wieder verworfen hat, oder wird sie noch verwendet? sind die anderen "varianten" auch der ART an sich zuzurechenen, oder eigene theorien? am anfang von #Grundlegende Konzepte wird gesagt, sie sei nur eine mögliche lösung. was sind die anderen? in der einleitung steht noch groß: "Insbesondere hat sie sich bisher in der von Einstein formulierten Form gegen alle später vorgeschlagenen Alternativen durchsetzen können.", aber dieser aspekt wird nurmehr in andeutungen zu spezialfällen und einelphänomenen erwähnt. alles fragen, die hier geklärt gehörten. und falls das jetzt noch nicht gemacht wird, sollte zumindest "Luft" sein, es später noch dazuzuschreiben..

ein anderes projekt würde mich auch noch interessieren: statt da irgendwelche alten hüte anzuführen, um die ART zu "beweisen", wär es imho viel aufschlussreicher, beispielhaft unsere Jongleur-Ball situation auf die ART umzurechen und zu zeigen, wie die zusammenhänge da laufen. da hätten wir dann ein 2D+1-System, das sich in grafiken sauber darstellen lässt (sogar als 3D-Weltliniendiagramm). dann können wir auch den 2. Ball hinzunehmen und dessen situation exemplarisch durchrechnen. so hätten wir auf 2,3 DINA4-Seiten die ART so nachvollzogen, das keiner sie für "Hexerei" hält, und das ewige gesemsel darüber, ob sie auch "wahr" sei, können wir uns sparen..

weil ich aber weden "Deinen" [sic] review noch die hoffentlich folgende exzellenz torpedieren will, und wir das alles auch später machen können, wenn Du spaß und Zeit hast, schreib ichs hierher (ich hätts gern Dir persönlich geschrieben, aber mit Deinen wechselnden IPs weiß ich nicht, wo Dich erreichen) nochmal Gruß, die arbeit hat mir Spaß gemacht -- W!B: 10:12, 16. Jan. 2007 (CET)Beantworten

Danke noch mal für die viele Arbeit die du dir gemacht hast. Die Prüfung habe ich geschafft, jetzt muss ich noch die Arbeit schreiben. ;)

Die ART gilt bis heute als "das beste was es in dem Gebiet gibt". Das steht in der Einleitung. Es gibt keine einzige Beobachtung, die die ART sicher widerlegt. Die Bestrebungen bezüglich der Quantengravitation speisen sich aus theoretischen Überlegungen, dass ART und Quantenmechanik bei der Planck-Länge zu widersprüchen führen.
Alternativ gibt es Brans-Dicke, MoND, die van-Flandern-Theorie und viele andere wenig bekannte Modelle. Viele davon sind schlicht widerlegt. Brans-Dicke bringt zusätzliche Parameter ein, ohne zusätzliche Antworten zu geben und ist daher auch kein Gewinn. Für die Alternativtheorien hatte ich mal einen Artikel wie en:Alternatives to general relativity angedacht.
Die Frage "Wofür braucht man die ART" wird im Kapitel über Gravitationswellen angeschnitten.
Die Geschichte der ART wird später immer mehr zu einer Geschichte der Kosmologie und der Näherungslösungen. Die bekannten exakten Lösungen sind alle schon recht alt.
Ich möchte die Effekte gern drinbehalten, weil es nunmal das ist, was auch jeder Laie schonmal gehört hat und daher hier suchen wird.

--217.232.18.195 11:47, 16. Jan. 2007 (CET)Beantworten

passt passt. eben genau das "angeschnitten" wars, und die effekte bräuchten nur verlinkt sein, so wie die wirklich zentralen folgerungen über Zeitsysteme usw. auch nur verlinkt sind. aber wie gesagt, hat zeit.. gratuliere, und über was schreibst Du? gehört die arbeit hier dazu? Hast Du über meine Idee über ein "Einführung in die ART" auf Wikibooks schon nachgedacht, falls uns langweilig wird.. gruß -- W!B: 12:54, 16. Jan. 2007 (CET)Beantworten

Evtl wird das Kapitel "Spezielle Relativitätstheorie" auf "Korrespondenzprinzip" umgemünzt, dann würde ich da schon die Unvereinbarkeit von newtonscher Gravitation und SRT ansprechen. Würde das auch in deine Richtung gehen?

Ich schreibe über axiomatische Quantenfeldtheorie auf gekrümmten Raumzeiten. Ich werde vermutlich eine Art "Toy Model" zur Entwicklung von Quantenfeldern auf Raumzeiten ähnlich dem Universum in der Inflationsphase untersuchen. Es geht darum, ob verschiedene materiegefüllte Zustände nach der Inflation auf ähnliche Zustände vor der Inflation zurückgehen, d.h. um die Auswirkung der Inflation auf wechselwirkende Quantenfeldtheorien. So grob. (Hab grad erst angefangen, mich einzuarbeiten...)

Es würde mir schon Spaß machen, das Wikibook zu schreiben. Aber ich möchte auch die Artikel Quantenfeldtheorie und Axiomatische Quantenfeldtheorie fertig schreiben. D.h. ich möchte dafür sorgen, dass sie wenigstens die Grundlagen kurz anreißen. --217.232.22.148 09:54, 18. Jan. 2007 (CET)Beantworten

oh, heisses thema. erstaunlich, dass Du da bereit bist, in den primitivsten grundlagen herumzubasteln. nichts geht über eine solide ausbildung.. ;) aber Du hast recht, das es da noch einiges zu schreiben gibt. der vorteil der WP ist ja, das sie einen zu einem extrem strukturierten und auch sehr knappen stil zwingt, und jegliche literarischer schwurbelei (essayismus) verbietet - das kommt jeder arbeit zugute, ausformulieren lässt sich nachher immer noch..

und der vorschlag mit Korrespondenz gefällt mir sehr gut

und eigentlich sind ein paar der sachen, die ich oben noch eingefordert hätte, eh im allgemeinen relativitäts-artikel halbwegs erklärt (den hab ich bisher gernicht gelesen, damit ich diesen artikel besser beurteilen kann), obwohl zur geschichte brichts auch dort in den 30er-jahren ab.. -- W!B: 13:18, 18. Jan. 2007 (CET)Beantworten

Diskussion:Allgemeine Relativitätstheorie/Archiv/1

- 2004 -

Verschiedenes

Geodätenproblem

Äquivalenzprinzip

- 2005 -

Abweichende Deutung

Relativitätsprinzip

Termin Veröffentlichung

Änderung eines Wikipedia-Laien

Beziehung zwischen sRT und aRT und "Wäscheleine"

Zum Raumkrümmungs-Bild

5. Dimension

ART protophysik

Bilder

GPS inkl. Rechenbeispiel

Versionsbereinigung

Völlig inakzeptabler Text

Energieerhaltungssatz verletzt?

gekrümmter Raum

- 2006 -

Verständnisprobleme

Zur Konstanz der Lichtgeschwindigkeit und Experimenten

Archiviert

Sternschnuppe hat einen Schweif deshalb wird sie Masse verlieren

Rechtschreibung und Formulierung

Masse

Struktur

Hinzugefügtes

Lücken

Gravitationswellen

Experimentelle Überprüfung der ART

Periheldrehung

Klassische Berechnung der Lichtkrümmung

Äquivalenzprinzip der allgemeinen Relativitätstheorie

ToDo-Liste

Bild-Vorschläge

Schwache statische Gravitationsfelder

Vorschlag 0.02

Review von 07.10.2006 bis 30.10.2006

Kommentare zur Lesenswert-Kandidatur

Krümelpieken re "Ausbreitung_der_Gravitation_und_Gravitationswellen"

Vorschlag zur Kosmologie

Lesenswert-Kandidatur: Allgemeine Relativitätstheorie (Archivierung Abstimmung 30. Oktober bis 6. November 2006)

Nette Worte

Frage zur Krümmung

Ich frag mich ...

Link-Vorschläge

Oma fragt sich..

Raum und Zeit vs Raumzeit

Grundlegende Konzepte

Mathematische Beschreibung

Online Links zur Referenzierung

ToDos

Navigationsmenü

Suche