Diskussion:Skalarprodukt/Archiv/001
reihenfolge; gescheite definition vs. oma-kompatibilitaet
Ich verstehe nicht wieso der wichtigste Teil, nämlich die Definition des Skalarproduktes weichen musste. Was momentan an erster Stelle steht ist lediglich das euklidische Standard-Skalarprodukt. Ein Skalarprodukt im allgemeinen definiert sich durch seine Bilinearität, Symmetrie, und positive Definitheit. (nicht signierter Beitrag von 80.133.126.162 (Diskussion) 18:27, 19. Jul. 2004 (CEST))
- Die Verzahnung der Artikel Skalarprodukt und Innenproduktraum ist noch nicht optimal; die Idee hinter dieser Aufteilung ist aber klar: der Artikel Skalarprodukt soll auf dem Niveau der Schulmathematik zugänglich sein und, in auch historisch korrekter Weise, das Skalarprodukt aus der Geometrie heraus begründen; nur wer das verinnerlicht hat, ist zu einem produktiven Umgang mit dem abstrakt definierten Skalarprodukt in einem beliebigen Innenproduktraum in der Lage. -- Weialawaga 10:07, 20. Jul 2004 (CEST)
- ich möchte nicht als unwissender in dem artikel rumschreiben, aber mir fehlt bei einer einfachen zusammenschau des skalarproduktes das wort "projektion"; ich denke das sollte erwähnt werden (siehe englischer artikel ziemlich am anfang!). (nicht signierter Beitrag von 85.181.111.58 (Diskussion) 14:41, 29. Dez. 2005 (CET))
- Da muss ich leider zustimmen. Ich finde, dass die geometrische Bedeutung des Skalarprodukts im R^n und der Zusammenhang von Skalarprodukt und Projektion, sowie die Darstellung des Skalarproduktes als Flächeninhalt eines Rechtecks mit der Länge des "ersten" Vektors als Länge und der senkrechten Projektion des "zweiten" Vektors auf den ersten als Breite im Artikel fehlen. Diese Interpretation ist aus den folgenden Gründen wichtig´:
- Die geometrische Darstellung kann Schülern helfen die Bedeutung der Hessischen Normalform zu erfassen. Insbesondere bei der Abstandsberechnung zwischen Ebene und Punkt im R^3 (was in diesem Artikel als Anwendung angegeben werden könnte) führt meiner Meinung nach kein Weg an dieser Interpretation vorbei, falls man sie verstehen will.
- Auch für die Fortgeschrittenen ist diese geometrische Interpretation bei der Einführung von Halbräumen, Hyperebenen, Satz von Hahn-Banach im R^n und wahrscheinlich bei zahlreichen anderen Themen von entscheidender Bedeutung für das Verständnis. Beispielsweise werden gewöhnlich Halbräume im R^n über das Skalarprodukt der Vektoren aus R^n mit dem Normalenvektor der entsprechenden Hyperebene dargestellt(Bsp. x aus R^3 (x-x_0)*n>0, wobei x_0 in der Ebene liegt und n der Normalenvektor der Ebene ist). Dies kann man sich leicht als Projektion vorstellen und somit die Definition eines Halbraums leicht nachvollziehen.
- Kann mir jemand sagen, wer diesen Artikel geschrieben hat? Muss ich ihn/sie erst fragen, bevor ich etwas ändere? Oder ist jemand vielleicht anderer Meinung über die Bedeutung der geometrischen Interpretation des Skalarprodukts? (Der vorstehende, nicht signierte Beitrag stammt von 80.219.2.128 (Diskussion • Beiträge) 2007-09-23T19:49:11)
Darstellung von Vektoren im Artikel
moin, warum werden im artikel die Vektoren dickgedruckt dargestellt, also A und nicht als ? im artikel Spatprodukt zum beispiel wird weder auf die darstellung mittels pfeil noch mit disckschrift zurückgegriffen. ich denke sowas sollte mal angeglichen werden. - cu AssetBurned 23:53, 30. Nov 2004 (CET)
- Stimmt. Das hat mich auch geärgert, als ich die verwendeten Symbole vor einigen Wochen umgearbeitet habe. Ich bin der Meinung, dass eine große Nähe zu einführenden Werken (aus der Schule, aber auch der FachHochschule) vorhanden sein muss. In diesem Sinne habe ich die Symbolik umgesetzt und bin auch gerne bereit, den gesamten Artikel noch einmal anzupassen. - Hhoffmann (nicht signierter Beitrag von Hhoffmann (Diskussion | Beiträge) 08:32, 1. Dez. 2004 (CET))
gudn tach! waere es sinnvoll, den kompletten artikel mit dem jetzigen teil "notation" (in leicht geaenderter form) beginnen zu lassen? dass im artikel selbst dann verschiedene notationen verwendet werden, halte ich fuer _sinnvoll_, da somit der richtige gebrauch der verschiedenen notationen verdeutlicht wird. --seth 22:19, 18. Aug 2005 (CEST)
- Klingt sinnvoll.--Gunther 13:56, 20. Aug 2005 (CEST)
der rest dieser diskussion wurde in den artikel eingearbeitet. -- seth 02:04, 16. Sep. 2007 (CEST)
Pfeile
Hm ... irgendwie ist das im Artikel mit den tollen Pfeilen über den Vektoren nicht so einheitlich, man sollte sich irgendwie einigen --AB, Martini 20:01, 25. Aug 2006 (CEST)
- Also ich war dann mal mutig und habe es vereinheitlicht. Keine Pfeile. -- AB, Martini 12:47, 27. Sep 2006 (CEST)
- Ich hab's wieder rückgängig gemacht. Das Skalaprodukt ist Thema in der Schule. Dort wurden zumindest zu meiner Zeit immer Vektorpfeile zur Unterscheidung von Vektoren und Skalaren (Variablen) verwendet. Deshalb sollten sie auch im Artikel verwendet werden. Bei Themen oder Teilabschnitten, bei denen man Wissen in Linearer Algebra voraussetzt kann man natürlich gut auf diese Pfeilchen verzichten. --Squizzz 14:12, 27. Sep 2006 (CEST)
- Da hast Du natürlich recht. Das hatte ich nicht recht bedacht. In meinen Schulbücher war es allerdings auch nicht einheitlich (Pfeile oder Fraktur). Wer den Abschnitt "Berechnung des Skalarprodukts mit Hilfe seiner Komponenten" braucht IMHO auch keine Pfeile, von daher schlage ich mal vor die Pfeile in der Einleitung und im Abschnitt "Skalarprodukt und Winkel" zu lassen und ansonsten zu streichen (oder überall zu setzen). Toll wäre auch, wenn die Vektoren einheitlich oder hießen. -- AB, Martini 14:20, 27. Sep 2006 (CEST)
- Ich bin dafür, die Vektoren mit zu benennen, dann bleiben neben für Skalare. Bei den Komponenten ist wieder die Schulmathematik zu beachten. Der Vektor ist mit den Komponenten . --Squizzz 14:49, 27. Sep 2006 (CEST)
- Jetzt sind's überall und , ich hoffe, das mit den Pfeilen habe ich diesmal richtig gemacht. -- AB, Martini 18:21, 27. Sep 2006 (CEST)
- Ich habe es in der Einleitung und im ersten Teil (euklidischer Raum) einheitlich auf a und b mit Pfeilen geändert. Grund: a und b (mit Pfeil) sind in der Schule eher üblich. -- Digamma 19:37, 13. Aug. 2010 (CEST)
- Jetzt sind's überall und , ich hoffe, das mit den Pfeilen habe ich diesmal richtig gemacht. -- AB, Martini 18:21, 27. Sep 2006 (CEST)
- Ich bin dafür, die Vektoren mit zu benennen, dann bleiben neben für Skalare. Bei den Komponenten ist wieder die Schulmathematik zu beachten. Der Vektor ist mit den Komponenten . --Squizzz 14:49, 27. Sep 2006 (CEST)
benennung
Sehr unglücklich die Vektoren x und y zu nennen, da bin ich beim inneren Produkt als fast Dipl Info gerade 5 sekunden drübergestolpert. (Der vorstehende, nicht signierte Beitrag stammt von 88.66.19.144 (Diskussion • Beiträge) 2007-09-15T19:37:55)
Definition ueber Eigenschaften: positiv definit, sesquilinear, hermitesch.
Das Skalarprodukt sollte erst wirklich über die drei Eigenschaften definiert werden, dann im Sinne der Schulmathematik erklärt werden und am Ende kann man auf andere Skalarprodukte verweisen. Ich finde man kann der Artikel zum Skalarprodukt nicht ohne die drei Eigenschaften schreiben. (nicht signierter Beitrag von 217.228.28.32 (Diskussion) 21:44, 11. Jan. 2005 (CET))
sehe ich auch so, das skalarprodukt sollte als symmetrische bilinearform eingefuehrt werden und nicht also standardskalarprodukt auf dem R^n (nicht signierter Beitrag von 212.117.94.157 (Diskussion) 20:08, 3. Feb. 2005 (CET))
- Warum? ---NeoUrfahraner 11:36, 4. Feb 2005 (CET)
- Hoffentlich ist mein Beitrag noch nicht zu spät. Ich kann der Meinung nur anschließen. Erst die korrekte (was heißt hier abstrakt? In einem mathematischen Lemma auf Abstraktheit hinzuweisen ist doch Quatsch) Definition. Und das sind bei mir nur vier Punkte:
- falls . Falls ist
- Der zweite Punkt im Artikel ist zur Definition nicht nötig. Er lässt sich aus der hier gegebenen Definition folgern. Außerdem ist die Unterteilung in reelle und komplexe Zahlen nicht nötig. Wer eine reelle Zahl komplex konjugieren möchte, kann das gerne tun. An der Zahl wird das nix ändern. Elasto 14:54, 27. Mai 2005 (CEST)
- Die Verwendung des Attributes "abstrakt" ist durchaus üblich, ob sie an dieser Stelle berechtigt ist, kann man diskutieren. ("Abstrakter" Vektorraum vs. oder "abstrakte" Mannigfaltigkeit vs. eingebettete Untermannigfaltigkeit des .)
- Die Definition erklärt jeweils die Begriffe, die da stehen. Und für Bilinearität (ohne Symmetrie) ist die zweite Bedingung nicht überflüssig.
- Symmetrisch ist ein eigenständiger Begriff und nicht etwa ein Spezialfall von "hermitesch". Für die Definition eines reellen Skalarproduktes muss ich nichts über komplexe Zahlen wissen, auch nicht, dass die Konjugation reelle Zahlen invariant lässt.
- Welchen Vorteil soll eine kürzere Definition haben?--Gunther 15:11, 27. Mai 2005 (CEST)
- Eine kürzere Definition hat auf jeden Fall den Vorteil, dass ich, wenn ich wissen will, ob eine Abbildung ein Skalarprodukt ist, weniger überprüfen muss. Ein sehr praktischer Nutzen. Elasto 20:33, 27. Mai 2005 (CEST)
- An diese Arbeitsersparnis glaube ich nicht, die wirklichen Schwierigkeiten liegen woanders. Dagegen helfen Bezüge zu anderen Begriffen, den neuen Begriff zu analysieren. Beispielsweise kann man jede Bilinearform auf einem endlichdimensionalen Vektorraum durch eine Matrix darstellen, und die Bilinearform ist genau dann symmetrisch, wenn die Matrix symmetrisch ist. Führt man Skalarprodukte über eine minimale Definition ein, muss man Bilinearformen als ganz neuen Begriff lernen.--Gunther 20:57, 27. Mai 2005 (CEST)
- Eine kürzere Definition hat auf jeden Fall den Vorteil, dass ich, wenn ich wissen will, ob eine Abbildung ein Skalarprodukt ist, weniger überprüfen muss. Ein sehr praktischer Nutzen. Elasto 20:33, 27. Mai 2005 (CEST)
- Hoffentlich ist mein Beitrag noch nicht zu spät. Ich kann der Meinung nur anschließen. Erst die korrekte (was heißt hier abstrakt? In einem mathematischen Lemma auf Abstraktheit hinzuweisen ist doch Quatsch) Definition. Und das sind bei mir nur vier Punkte:
- An Elasto: die Frage, warum zuerst die allgemeine Definition kommen soll, hast Du nicht beantwortet. Meiner Meinung nach ist das lediglich eine Geschmacksfrage; der eine geht lieber vom Konkreten () zum Abstrakten; der andere vom Abstrakten zum Konkreten. Wieder andere definieren lieber über den Kosinus (z.B. die englische Version en:Dot_product). Man kann es natürlich ändern, aber dann kommt vielleicht der nächste und sagt, der Artikel ist zu formal und unverständlich, und das Spiel geht von vorne los. Was das Wort "Abstrakte Definition" betrifft: gefällt Dir "Allgemeine Definition" in diesem Zusammenhang besser? --NeoUrfahraner 21:35, 27. Mai 2005 (CEST)
- Hab ich glatt übersehen, hole ich aber gerne nach. Meine Meinung zur Stelle, an der die Allgemeine (das klingt gut!) Definition stehen sollte ist: Das ist gut so. Zuerst das, was jeder versteht, dann das Spezielle. Zu den Bilinearformen: Ich hab die Bilinearformen (und allgemein Multilinearformen) vor dem Skalarprodukt gelernt, also getrennt und das fand ich nicht schlecht.
- Meinst du wirklich, dass es dann zu formal wird? Ab dem Punkt "Allgemeine Definition" kann der Artikel meiner Meining nach ruhig etwas formaler werden. Nicht-Mathematiker werden ab dort sowieso zu lesen aufhören. Und als Mathematiker fänd ich eine kurze knackige Definition ganz gut.Elasto 23:46, 27. Mai 2005 (CEST)
- An Elasto: die Frage, warum zuerst die allgemeine Definition kommen soll, hast Du nicht beantwortet. Meiner Meinung nach ist das lediglich eine Geschmacksfrage; der eine geht lieber vom Konkreten () zum Abstrakten; der andere vom Abstrakten zum Konkreten. Wieder andere definieren lieber über den Kosinus (z.B. die englische Version en:Dot_product). Man kann es natürlich ändern, aber dann kommt vielleicht der nächste und sagt, der Artikel ist zu formal und unverständlich, und das Spiel geht von vorne los. Was das Wort "Abstrakte Definition" betrifft: gefällt Dir "Allgemeine Definition" in diesem Zusammenhang besser? --NeoUrfahraner 21:35, 27. Mai 2005 (CEST)
- Ich habe es jetzt auf "Allgemeine Definition" geändert. --NeoUrfahraner 00:00, 28. Mai 2005 (CEST)
- Ich denke, man kann ja damit leben, dass das Standard-SKP als erstes kommt. Allerdings sollte im Intro gleich stehen, dass damit eben nicht das SKP, sondern der Spezialfall des Standard-SKP, der im endl. dim. die häufigste Wahl darstellt, erklärt wird. -- JFKCom 22:50, 12. Jul 2005 (CEST)
- Wäre es nicht sinnvoller, mit der allgemeinen DEfinition anzufangen, und zwar mit zwei Abschnitten, je einen für das reelle und das komplexe Skalarprodukt und dann zu den konkreten BEispielen überzugehen? Dann könnte man z.B. auch auf Euklidisches_Skalarprodukt verweisen und dort hin das einfache Rechenbeispiel verschieben. Im übrigen ist das Skalarprodukt nicht in einem euklidischen Raum definiert, sondern ein reeller Vektorraum wird erst durch die Konstruktion eines skalaren Produktes zu einem euklidischen Raum. DEs weiteren weiß ich nicht, wie sinnvoll es ist weitere Beispiele anzugeben, z.B. ein Integral-Skalarprodukt auf einem Funktionenraum? --KapitanSpaltnagel 00:48, 30. Jul 2005 (CEST)
allgemeine definition
gudn tach! die aktuellen letzten aenderungen gefallen mir teilweise gar nicht. in so ziemlich jedem mathebuch (welches ich kenne), in dem vom skalarprodukt die rede ist, wird es so und nicht so eingefuehrt/benutzt. dass es gelegentlich auch anders verwendet wird, stand ja schon im artikel. aber jetzt sieht es fuer mich so aus, als waere die ausnahme zur regel gemacht worden. da ich aber keinen edit-war ausloesen moechte, bitte ich um weitere meldungen dazu. --seth 16:00, 29. Sep 2005 (CEST)
- Ich hatte das damals so gewählt, weil ich mich dunkel erinnere, dass für und die Standardnotation ist, und wenn man nun ein Skalarprodukt benutzt, um und zu identifizieren, dann sollte wenigstens ein Teil gleich bleiben. Keine Ahnung, was der Standard ist, wenn man direkt mit Skalarprodukten anfängt.--Gunther 16:06, 29. Sep 2005 (CEST)
Also ich denke, dass die Definition, in der die erste Komponente halbliniear ist, ist für eine Enzyklopädie die geschicktere, da sie in der durchgängig in der Physik benutzt wird (zumindest seitdem sich vor ein paar Jahrzehnten die Dirac'sche Bra-Ket-Definition in der Quantenmechanik durchgesetzt hat). Wenn man diesen Artikel nur für Mathematiker haben will, könnte man sich ja streiten, welche Version Prozentual höher vertreten ist, aber mit einem Blick auf die Physik halte ich die Version mit erste Komponente halbliniear sinnvoller --Dark-Immortal 17:00, 29. Sep 2005 (CEST)
- Ja, mit V = Kets ist es die Notation natürlich genau umgekehrt. Da es den Mathematikern eigentlich egal sein müsste, sollte man sich den Physikern anpassen (und dankbar sein, dass sie einmal keine Koordinaten verwenden *fg*).--Gunther 17:08, 29. Sep 2005 (CEST)
- Hab mal kurz meine Bücher durchschaut, und danach steht es unentschieden: Bosch - Lineare Algebra - von Springer verwendet die wo die erste Komponente linear ist und Artin - Algebra - Birkhäuser verwendet die andere... :) (natürlich nur die Mathematik-Bücher, würde ich meine Quantenmechanik-Bücher mit dazunehmen sähe es anders aus ;) ) --Dark-Immortal 17:15, 29. Sep 2005 (CEST)
- ok, ok, wenn es bei den mathematikern gar nicht so genau festgelegt ist, wie ich dachte, dann hat Gunther (mit seinem letzten satz) mal wieder recht.--seth 21:27, 29. Sep 2005 (CEST)
Inzwischen steht es ja wieder "falsch" herum (im Physiker-Sinne) drin. Das passt dann aber nicht mehr mit dem Abschnitt zu den abweichenden Definitionen ("Im komplexen Fall ließe sich das Skalarprodukt alternativ als semilinear im zweiten und linear im ersten Argument definieren. In der Physik wird jedoch die obige Variante durchgängig benutzt"), da es ja bereits so da steht. -- 85.181.238.214 12:38, 29. Jul. 2008 (CEST)
Eindrücke
Wenigstens für mich hinterlässt der Artikel einen reichlich verworrenen Eindruck mit Hinblick auf die schon früher diskutierte Definition des Skalarprodukts. Es standen in der Hauptsache zwei Alternativen zur Verfügung, und zwar erstens die Definition mit Verwendung des Winkels und zweitens die in der linearen Algebra übliche Definition des komponentenweisen Multiplizierens mit nachfolgender Addition. Für den Spezialfall des Euklidischen Raumes sind beide Definitionen äquivalent. Da nur zwei Vektoren beteiligt sind, kann man sich mit Hinblick auf den Euklidischen Raum ohne Einschränkung der Allgemeinheit auf eine Ebene beschränken.
Der in der Mathematik übliche Standpunkt sieht so aus, dass man bei äquivalenten Definitionen frei wählen kann, welcher Alternative der Vorzug gegeben wird. Sofern erforderlich zeigt man dann die Äquivalenz mit anderen Definitionen. Da es an dieser Stelle um einen Artikel geht, der für Laien verständlich sein soll, beginnt man mit derjenigen Definition, mit der am bequemsten umgegangen werden kann. Unter diesem Gesichtspunkt sehe ich aus der früheren Debatte den folgenden Vorschlag an:
- Das Skalarprodukt ist die Länge des einen (ersten) Vektors multipliziert mit der senkrechten Projektion des anderen (zweiten) auf den einen (ersten) Vektors; bzw. die Länge des "anderen" (zweiten) Vektors multipliziert mit der senkrechten Projektion des "einen" (ersten) Vektors auf den "anderen"(zweiten).
Nicht dass es mir an mathematischer Vorbildung fehlen würde (Das Gegenteil ist der Fall.), aber eine solche Definition finde ich schauerlich. Sollte es dies sein, was im Mathematikunterricht an der Schule verbreitet wird, dann bin ich froh, diesem Unterricht entwachsen zu sein. Die Definition ist noch dazu schlecht formuliert. Gemeint ist offenbar:
- Das Skalarprodukt zweier Vektoren ist das Produkt der Länge des ersten Vektors und der Länge der senkrechten Projektion des zweiten Vektors auf die als lineare Mannigfaltigkeit des ersten Vektors definierte Gerade.
Vom Standpunkt der Mathematik ist einzuwenden, dass es Probleme gibt, wenn einer der beiden Vektoren der Nullvektor ist. Aus der Definition ergibt sich dann kein eindeutiger Sinn. Ein "normaler" dagegen Leser wird kaum einen anderen Eindruck gewinnen, als dass Mathematik nun einmal unverständlich und nach ihrem Wesen eine Spielwiese für Masochisten ist. Es ist zu bezweifeln, dass er mit dieser Definition eine zweckdienliche Vorstellung verbinden kann.
Die einfachste Definition wird diejenige der komponentenweisen Multiplikation zweier Vektoren in der Euklidischen Ebene sein. Warum also nicht damit beginnen? Die Vektoren werden mit ihrer Komponentendarstellung als Zahlenpaare identifiziert. Eine Definition des Skalarprodukts schreibt man dann mit einer einfachen Formel hin. Als nächstes wird erwähnt, dass das Skalarprodukt auch anders definiert werden kann. Hierfür bietet sich die bisher als erste Definition vorgelegte Formel mit dem Winkel an. Die Äquivalenz der beiden Definitionen muss man dann explizit zeigen, Das wird in Kapitel 4 schon jetzt getan, so dass dieser Beweis keinen zusätzlichen Platz in Anspruch nimmt.
- Aus meiner Sicht spricht folgendes dagegen: Die Euklidische Ebene "kommt" nicht mit Koordinaten daher. Man muss also erst Koordinaten darin einführen. Und dann muss man streng genommen nachweisen, dass die Definition nicht von der Wahl des Koordinatensystems abhängt. --Digamma 21:31, 1. Mär. 2009 (CET)
Um zu der Definition des Skalarprodukts in abstrakten Räumen zu gelangen, leitet man zuerst für den Fall der Euklidischen Ebene die üblichen Rechenregeln ab, was keinerlei Mühe macht. Diese Regeln werden dann als Axiome formuliert. Nachdem dies erledigt ist, muss man natürlich Beispiele für abstrakte Vektorräume geben. Dafür fallen mir viele lehrreiche Beispiele ein, darunter die sogenannte "Obertonreihe" in der Musik.
Generell möchte ich daran erinnern, dass "weniger" manchmal "mehr" sein kann. Ich würde also raten, den Artikel zu enschlacken, indem man sich auf besonders wichtige Teilaspekte des Skalarprodukts beschränkt. In einem Artikel über die Grundrechenarten kommt niemand auf die Idee, sämtliche Anwendungsmöglichkeiten aufzuschreiben. Dies braucht man dann auch für das Skalarprodukt nicht zu tun.85.22.23.42 12:18, 31. Dez. 2008 (CET)
Summenprodukt?
Die Liste besonderer Zahlen verlinkt auf Summenprodukt, das ein Redirekt hier her ist. Im gesamten Artikel taucht dieser Begriff aber gar nicht auf. Was hat es damit nun auf sich? --RokerHRO 14:58, 2. Dez. 2008 (CET)
- Summenprodukt sagt man auch normalerweise nicht - ich habe den Link nunmehr korrigiert. Das Standardskalarprodukt im ist die Summe des Produkts der einander entsprechenden Einträge, d.h., , wie auch recht weit oben im Artikel steht. --Tolentino 15:36, 2. Dez. 2008 (CET)
- In Liste besonderer Zahlen steht aber immernoch "Summenprodukt" und im verlinkten Artikel Skalarprodukt steht das Wort nirgends. Damit ist meine ursprüngliche Kritik immernoch nicht beseitigt. ;-( --RokerHRO 15:58, 2. Dez. 2008 (CET)
- Der Link geht aber auf Skalarprodukt, nicht auf Summenprodukt. Ich finde Summenprodukt aber auch in Ordnung, weil zum einen eine Skalarproduktstruktur zum Verständnis völlig unnötig ist, außerdem ist es eine unendliche Reihe. Man könnte allenfalls darüber diskutieren, den Link auf Skalarprodukt komplett zu entfernen, das solltest du aber auf der dortigen Diskussionsseite anregen. --Tolentino 10:20, 3. Dez. 2008 (CET)
- Wenn Summenprodukt hier her verweist, würde ich diesen Begriff eben schon gerne hier im Artikel erwähnt und erklärt haben. --RokerHRO 22:34, 3. Dez. 2008 (CET)
- Diskutiere bitte erst einmal dort, ob man nicht den Begriff Summenprodukt komplett rausschmeißt bei der besonderen Zahl. Dann brauchen wir hier keine Scheindebatte zu führen. Im Übrigen sehe ich keinerlei Änderungsbedarf, da das Standardskalarprodukt hier schon längst drinsteht. --Tolentino 08:26, 4. Dez. 2008 (CET)
- es geht RokerHRO afaics um OMA. wenn "summenprodukt" verlinkt ist auf skalarprodukt, sucht OMA dort vielleicht nach "summenprodukt" und wird nicht fuendig. also glaubt OMA, dass der link falsch gesetzt wurde oder dass summenprodukt=skalarprodukt gilt. da der begriff "summenprodukt" recht gelaeufig zu sein scheint, sollte der begriff auch mal im hiesigen artikel fallen und sei es nur in der form "Standardskalarprodukt (selten auch Summenprodukt)". -- seth 11:10, 4. Dez. 2008 (CET)
- Eben. Ich war anscheinend die Oma, die den Begriff "Summenprodukt" bisher nicht kannte und neugierig dem Link gefolgt bin und dann hier landete und ... die Neugier nicht befriedigt wurde durch den Artikel in der jetzigen Form. --RokerHRO 11:17, 4. Dez. 2008 (CET)
- Das Skalarprodukt passt nicht ordentlich in den Kontext der Zahl in Liste besonderer Zahlen, weil dort eine unendliche Reihe ist, während das Standardskalarprodukt nicht die unendliche Reihe ist. Außerdem hat die Zahl nichts, aber auch gar nichts mit irgendeiner Skalarproduktstruktur zu tun. Daher sollte man den Begriff in Liste besonderer Zahlen entfernen, der meiner Meinung nach dort völlig unsinnig ist. Wenn dieser Begriff dort nicht vorkommt, kann OMA auch nicht auf diese Seite gelangen. Die Diskussion wird hier an der falschen Stelle geführt. --Tolentino 11:55, 4. Dez. 2008 (CET)
- wir haben imho zwei sachen zu klaeren:
- 1. was soll mit dem link im listen-artikel passieren? (dazu habe ich keine meinung und mir ist auch egal, ob das hier oder dort auf der DS geklaert wird.)
- 2. unabhaengig davon ist summenprodukt eine weiterleitung auf diesen artikel. also sollte der begriff auch hier erlaeutert werden oder der redir wird zu einem eigenstaendigen artikel/stub, der OMA-kompatibler ist, umfunktioniert. (und das sollte hier geklaert werden.) -- seth 13:49, 4. Dez. 2008 (CET)
1. Da ich anzweifle, dass ein Link im Listen-Artikel auf Skalarprodukt in irgendeiner Form sinnvoll ist, sollte man das dort ansprechen. 2. Das ist sehr wohl etwas, worüber man reden kann. Skalarprodukte sind selbstverständlich natürlich im Allgemeinen nicht die Summe von Produkten, also ist dies auch kein Synonym. Der Begriff Summenprodukt könnte sich nur auf das Standardskalarprodukt beziehen und gehört daher auch nur in Abschnitt 1 hinein. Dort steht: "als die Summe der Produkte der Komponenten der Vektoren definiert"... Hier könnte man gerne einfügen, dass man aus diesem Grunde gelegentlich "Summenprodukt" für Standardskalarprodukt sagt (obgleich mir das so noch nicht untergekommen ist, schon gar nicht als terminus technicus). --Tolentino 14:21, 4. Dez. 2008 (CET)
- 2. hab den begriff auch noch nicht in mathematischen buechern gesehen. aber google liefert >20k treffer (darunter viel ms-excel-kram). als existenzbeweis des begriffs sollte das genuegen, hihi, nur spass. 20k treffer sollten in diesem fall aber auch ein hinreichendes indiz dafuer sein, dass der begriff haeufig genug gebrauch wird, um den redir und damit die begriffsnennung zu rechtfertigen.
- du magst das, was du schriebst, doch bestimmt noch im artikel irgendwie einbauen, gell? :-) -- seth 14:34, 4. Dez. 2008 (CET)
- Hm, wenn man alle Beiträge abzieht, die sich auf die Funktion "SUMMENPRODUKT" aus MS-Excel beziehen, habe ich nichts mehr gefunden, was hierzu passt. Danach muss man alle Beiträge abziehen, die "Summe, Produkt" oder ähnliche Hintereinanderaufführung dieses Begriffs beschreiben und bei "Summenprodukt" in Google erscheinen. Nur weil MS eine Funktion so nennt, sehe ich noch nicht ein, dass das in einen mathematischen Artikel eingebaut werden sollte. Die 20k sind sicher real ganz erheblich weniger, oder irre ich mich da? --Tolentino 14:51, 4. Dez. 2008 (CET)
- ok, bei einer suche nach '"summenprodukt"+-excel' gibt's nur noch ca. 2,8k treffer. und auch dort ist noch viel excel-kram dabei. aber der begriff wird so oder so haeufig verwendet; waere auch nicht das erste mal, dass miscrosoft einen begriff hypet. -- seth 17:36, 4. Dez. 2008 (CET)
- Wenn man nach "Summenprodukt" -excel sucht, gibt Google übrigens nur 137 Treffer aus (wenn man auf die letzte Seite geht). Auch bei diesen Treffern gibt es in vielen Fällen einen Zusammenhang zu Excel o.ä. Daher sollte bei einer Erwähnung, in welchem Artikel auch immer, dies klar gestellt werden. Wobei ich nach dieser Google-Sucher eher gegen eine Erwähnung bin. --Sabata (D|WZ) 17:44, 4. Dez. 2008 (CET)
- hmm, wenn man auf die letzte seite geht... das zaehlt nicht. fueg halt den parameter &filter=0 hinzu. ;-p.
- wenn man "summenprodukt" durch "skalarprodukt" ersetzt ist bei ca. 600 auch irgendwann sense. google ist komisch. -- seth 18:02, 4. Dez. 2008 (CET)
- Ich stell gleich mal einen LA auf Skalarprodukt ;-). Aber die Nähe zu Excel bleibt trotzdem und sollte mMn erwähnt werden. --Sabata (D|WZ) 18:16, 4. Dez. 2008 (CET)
- mach mal 'n vorschlag. wir duerfen ja nicht (nur aufgrund eines mini-google-vergleichs) behaupten, dass der begriff vor allem in/wegen excel bekannt ist/verwendung findet, oder?
- hmm, *ueberleg*, die neutrale version waere wohl, wenn wir einfach auf die existenz dieses begriffs im umgangssprachlichen und in tabellenkalkulationssoftware/excel-aehnlicher software hinweisen.
- puh, und wenn wir das erledigt haben, trinken wir 'n bier und pruefen mal, ob ein LA fuer skalarprodukt aufgrund von zu wenigen google-hits durchkaeme. ;-) -- seth 18:54, 4. Dez. 2008 (CET)
- Winziger Nachtrag: Punkt 1 habe ich jetzt erledigt und in der Liste umformuliert. Ich denke auch, dass der unendliche Summationsprozess hier eine größere Bedeutung besitzt als die Feststellung, dass es - wenn es endlich viele Summanden gewesen wären - dann ausgesehen hätte, als wenn es ein Standardskalarprodukt wäre.
- Zu 2.: Wenn man mir ein einziges Mathematik-Buch gäbe, in dem das stände, wäre die Sache mit dem Summenprodukt ja in Ordnung. Aber ich kenne nun mal kein einziges derartiges... --Tolentino 08:32, 5. Dez. 2008 (CET)
- 2. ein buch ueber wirtschaftsmathe (scnr) ;-)
- hihi, nee, ich habe sogar ein buch gefunden, das den begriff "summenprodukt" andersherum benutzt: [1]
- aber wie gesagt duerfen wir nicht nur ueber das schreiben, was wir mathematiker definieren, sondern wenn halt nun mal ein genuegeng grosser haufen nicht-mathematiker vom "summenprodukt" spricht, duerfen wir das nicht ignorieren. die frage war ja bloss, ob der haufen gross genug ist. falls nicht, sollte auch die weiterleitung von summenprodukt geloescht werden, siehe mein erstes und zweites posting zum thema. -- seth 11:49, 5. Dez. 2008 (CET)
- mir faellt gerade ein, wir koennten aus summenprodukt eigentlich wirklich einen stub oder eine BKS (summe des produktes vs. produkt der summe) machen. was meint ihr? -- seth 11:55, 5. Dez. 2008 (CET)
- Naja, das Excel-Buch wollen wir mal rausschmeißen: Klar, alle Bücher über Excel werden schon die Behelfe von Excel enthalten... :-)
- Ich finde die Verbindung von Excel zu Skalarprodukt trotzdem insofern problematisch, als es dem Excel wohl kaum um Skalarproduktstruktur geht, sprich: Excel möchte daraus ja beispielsweise keine Orthogonalität folgern, falls sein Summenprodukt als Ergebnis null hat. Und das andere Buch, welches ja nun die erste saubere Referenz zu Summenprodukt abzüglich des Excel-Befehls ist, verwendet den Begriff ja auch völlig anders.
- Daher bin ich gegen einen Einbau des Befehls ins Skalarprodukt, schließe mich dem Vorschlag von seth an, würde den Redirect streichen und eher einen Stub anlegen oder eine BKS machen. --Tolentino 12:33, 5. Dez. 2008 (CET)
Punktprodukt?
Ich habe den Begriff 'Punktprodukt' noch niemals in mathematischer Literatur gefunden. Ich vermute stark, dass es sich hierbei nur um eine (mittlerweile weit verbreitete) Unsitte handelt, den englischen Begriff 'dot product' direkt zu übersetzen. Sogar im Netz findet man nur vergleichsweise wenige Hits zu dem Begriff. Ich schlage vor, den Begriff nicht kommentarlos als korrekte Alternative zu 'Skalarprodukt' stehen zu lassen, sondern zumindest zu erwähnen, dass er zweifelhaft ist. (nicht signierter Beitrag von 213.23.239.100 (Diskussion) 14:47, 4. Dez. 2008 (CET))
- Ich habe nach der Änderung http://de.wikipedia.org/w/index.php?title=Skalarprodukt&diff=73079590&oldid=72953042 kurz gegoogelt. "Fälschlicherweise" trifft es nicht (wer entscheidet über richtig und falsch), daher habe ich es als vermutlichen Anglizismus bezeichnet. --NeoUrfahraner 16:08, 13. Apr. 2010 (CEST)
- Naja, über richtig bzw. falsch entscheiden in diesem Fall diejenigen Mathematiker, die diese Begriffe für die jeweiligen Definitionen gewählt haben. Ich habe hier ein Mathematisches Wörterbuch (zweibändiger A4-Wälzer mit 2000 Seiten) und in dem kommt sowohl das Skalarprodukt als auch das innere Produkt vor. Aber mit keinem Wort wird ein 'Punktprodukt' erwähnt. Auch in meinem Mathestudium habe ich das Wort niemals gehört. Bei meiner Suche im Netz kam keine vertrauenswürdige Quelle raus, nach der ich das Wort in dem Zusammenhang als korrekt ansehen würde. Ich bleibe daher dabei, dass es schlichtweg falsch ist. Aber sei's drum...-- 217.95.187.148 20:34, 13. Apr. 2010 (CEST)
- Ja eh, es entscheiden die Mathematiker. Ich habe ein wenig gegoogelt und das Wort (leider) unter anderem bei Google-Books "Vektor- und Tensorpraxis" (Dieter Schroeder) gefunden. Mit "manchmal" und "Anglizismus" steht es wenigstens nicht mehr "kommentarlos als korrekte Alternative". Damit sollten wohl alle leben können. Inhaltlich geht es allerdings auch mir so, dass ich die Verwendung des Wortes "Punktprodukt" ablehne. --NeoUrfahraner 14:53, 14. Apr. 2010 (CEST)
- vermutungen muessen belegt werden. deswegen loesche ich die sie erst mal. -- seth 17:21, 18. Apr. 2010 (CEST)
Problem: "komponentenweise"
Komponentenweise ist ein (ungebräuchliches) Adverb und kann deshalb nicht in der Form "Komponentenweise Berechnung" verwendet werden. Bitte einen in korrektem Deutsch gehaltenen Ersatz finden! Danke. -- Carbidfischer 19:47, 23. Jan 2005 (CET)
- Nicht dass mich die Formulierung "mit Hilfe seiner Komponenten" stören würde - aber was soll an "komponentenweise" ungewöhnlich sein? Google findet das Wort ungefähr 9.580 Mal. ---NeoUrfahraner 14:45, 4. Feb 2005 (CET)
- Mit ist der Ausdruck auch geläufig. Aber kann ja auch elementweise sagen. --Philipendula 14:43, 5. Feb 2005 (CET)
- Inzwischen steht dort "mit Hilfe seiner Komponenten", und ich sehe keine Grund, das nochmals zu ändern. Ich finde es lediglich schade, wenn Energie verschwendet wird, um Scheinverbesserungen durchzuführen, die letztlich eine reine Geschmackssache sind. Es gibt in der Wikipedia genügend Möglichkeiten, echte Verbesserungen anzubringen. --NeoUrfahraner 16:09, 5. Feb 2005 (CET)
- Das Problem ist, dass Wörter auf -weise Adverbien sind und die Verwendung als Adjektiv wie in "komponentenweise Berechnung" schlicht falsch ist. "...wird komponentenweise berechnet..." wäre o.k.--Gunther 13:55, 20. Aug 2005 (CEST)
- neuerdings wird der kram mit "produkt der komponenten" bezeichnet, was imho kaese ist, weil unterm dem produkt der komponenten normalerweise sowas verstanden wird wie .
- die attributive verwendung von adverbien ist in der deutschen sprache nix neues und gar nicht so falsch. der duden sagt bspw. zu "paarweise":
- paar|wei|se <Adv.>: in Paaren: sich p. aufstellen; <mit Verbalsubstantiven auch attr.:> -s Zusammengehen. (duden)
- ich bin fuer den in der mathematik ueblichen begriff "komponentenweise" in der ueblichen attributen verwendung. man kann ja notfalls "produkt" durch "multiplizieren" (als substantiviertes verb) ersetzen. -- seth 17:38, 16. Jul 2006 (CEST)
- da sich niemand mehr gemeldet hat, gehe ich nun davon aus, dass ich das entsprechend aendern darf. -- seth 11:18, 29. Jul 2006 (CEST)
- Das Problem ist, dass Wörter auf -weise Adverbien sind und die Verwendung als Adjektiv wie in "komponentenweise Berechnung" schlicht falsch ist. "...wird komponentenweise berechnet..." wäre o.k.--Gunther 13:55, 20. Aug 2005 (CEST)
- Inzwischen steht dort "mit Hilfe seiner Komponenten", und ich sehe keine Grund, das nochmals zu ändern. Ich finde es lediglich schade, wenn Energie verschwendet wird, um Scheinverbesserungen durchzuführen, die letztlich eine reine Geschmackssache sind. Es gibt in der Wikipedia genügend Möglichkeiten, echte Verbesserungen anzubringen. --NeoUrfahraner 16:09, 5. Feb 2005 (CET)
- Mit ist der Ausdruck auch geläufig. Aber kann ja auch elementweise sagen. --Philipendula 14:43, 5. Feb 2005 (CET)
positive definitheit
Mal zu nem andern Punkt: Anstatt euch hier über Quantenpyhsik zu unterhalten, hättet ihr euch mal lieber an eure Mathe-Grundvorlesungen erinnert und gemerkt, dass das Skalarprodukt auf einem komplexen Vektorraum natürlich gar nicht positiv definit sein kann, und dies in der Definition fehl am Platz ist. Zur Erinnerung: C ist nicht angeordnet. (nicht signierter Beitrag von 84.56.223.11 (Diskussion) 00:28, 9. Feb. 2006 (CET))
- Woher nimmst Du nur dieses Selbstbewusstsein? Das sollte Deinen Irrtum aufklären.--Gunther 00:40, 9. Feb 2006 (CET)
- Hallo Gunther! Strenggenommen ist <x,x> ja immer noch ein Element aus C. Und daher ist <x,x> >= 0 formal nicht erklärt. Mit dem Zusatz gebe ich mich zufrieden. Allerdings muss ich zu meiner Verteidigung sagen, dass ich eine Definition ohne den dritten Punkt kannte und nicht gesehen habe, dass es per Definition tatsächlich in R liegt. --84.56.223.11 00:51, 9. Feb 2006 (CET)
- Es dürfte nicht viele Bücher geben, die hermitesche Sesquilinearformen behandeln, ohne auf Definitheit einzugehen. Zum "Strenggenommen": Es ist absolut üblich, als Teilmenge von aufzufassen, genau wie usw.; man kann auch so konstruieren, dass es sich um eine "richtige" Inklusion handelt.--Gunther 01:17, 9. Feb 2006 (CET)
- Hallo Gunther! Strenggenommen ist <x,x> ja immer noch ein Element aus C. Und daher ist <x,x> >= 0 formal nicht erklärt. Mit dem Zusatz gebe ich mich zufrieden. Allerdings muss ich zu meiner Verteidigung sagen, dass ich eine Definition ohne den dritten Punkt kannte und nicht gesehen habe, dass es per Definition tatsächlich in R liegt. --84.56.223.11 00:51, 9. Feb 2006 (CET)
Wie kann es denn positiv definit sein, wenn da ≤ steht?
Das ist doch dann semidefinit.
Ist vielleicht das ≤ falsch?
84.58.181.180 19:34, 22. Okt. 2007 (CEST)
- du irrst. vielleicht wird es dir durch die folgende aequivalenz klar
- noch fragen? -- 141.3.74.36 13:17, 23. Okt. 2007 (CEST)
Neue Einleitung
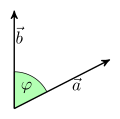
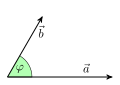
Wieso ist die neue Einleitung "verständlicher" und "genauer"? "Das Skalarprodukt zweier Vektoren a und b erechnet sich aus dem Produkt der Beträge der beiden Vektoren multipliziert mit dem Kosinus des von den Vektoren eingeschlossenen Winkels" sowie "Mit Hilfe des Skalarproduktes ist es möglich die Länge eines Vektors und den Winkel zwischen zwei Vektoren zu berechnen." Wie berechne ich mit Hilfe des Skalarprodukts die Länge und den Winkel? Ich brauche doch die Länge und den Winkel schon vorher, damit ich laut dieser Definition das Skalarprodukt überhaupt berechnen kann! Wie ist denn überhaupt der Winkel zwischen zwei Vektoren definiert? --NeoUrfahraner 06:56, 12. Aug 2006 (CEST)
- Das sagt die Einleitung (leider?) nicht, was man zumindest diskutieren kann. Im Artikel ist es dann vorhanden. Man könnte vielleicht in Klammern Hinweise anbringen, etwa Länge (Quadratwurzel des Skalarprodukts) und Winkel (Auflösung der Formel nach cos(Phi)). --Hubi 08:04, 12. Aug 2006 (CEST)
- Das ändert nichts am prinzipiellen Problem. Die Definition ist zirkulär. Das Skalarprodukt ist mit dem Winkel defniert, der Winkel mit dem Skalarprodukt. --NeoUrfahraner 09:06, 12. Aug 2006 (CEST)
- Wäre es möglich in der ersten Zeile neben dem "was", auch ein "wozu" hinzuzufügen? Bei anderen mathematischen Verknüpfungen wird dies dort ebenfalls erwähnt. "Das Skalarprodukt (auch inneres Produkt) ist eine mathematische Verknüpfung und dient u.a. zur einfachen Bestimmung der Orthogonalität zweier Vektoren." --Ebon 20:48, 03. Dez 2007 (CEST)
- Jetzt hab ich mal den Artikel so geändert, dass das Wesentliche für Praktiker am Anfang ist. In der Einleitung ist es tatsächlich so, dass man meinen könnte, alles wäre zirkulär. Das stimmt jedoch nicht, weil es eine alternative Methode zur Berechnung gibt, nämlich zeilenweise Multiplikation und Aufsummieren. Vektoren werden normalerweise durch die Koordinaten des Endpunkts definiert, wenn der Anfangspunkt im Ursprung ist. Dann wendet man die Alternativmethode - die man auch als Definition sehen kann -- an und bekommt eine bequeme Berechnung des Winkels mit Hilfe der Formel in der Einleitung. --Hubi 20:33, 12. Aug 2006 (CEST)
- Irgendwie ist der Artikel falsch aufgebaut, so dass er wohl erst ab Grundstudium-Niveau verständlich ist. Dabei kommt das Skalarprodukt ja schon im Mathematik-/Physikunterricht vor. Das liegt mE in einer Überfrachtung von vermeintlicher Exaktheit und falschem Aufbau. Es sollte zunächst - also noch vor der Notation - ein Abschnitt mit dem SP im euklidischen Raum inkl. (wenigen) Beispielen zur Berechnung des SK zu Fuss (wie bereits im Artikel), der Länge und des Winkels ohne den folgenden mathematischen Ballast, eingefügt werden. --Hubi 08:32, 12. Aug 2006 (CEST)
@Neourfahraner Da ist nichts zirkulär definiert. Es steht da, dass der Winkel sich mittels des Skalarproduktes berechnen läßt, nicht dass er darüber definiert ist. Wie ein Winkel definiert ist steht im Artikel "Winkel". Auch dort erfolgt die Def. nicht mit Hilfe des Skalarproduktes. Gruss --Stefanwege 18:01, 15. Aug 2006 (CEST)
- Und wie berechnest Du den Winkel mit dem Skalarprodukt, wenn Du den Winkel brauchst, um das Skalarprodukt zu berechnen? --NeoUrfahraner 20:30, 15. Aug 2006 (CEST)
- Hubi hat das eigentlich schon schön erklärt. Aber du hast recht für jemanden, der von der Sache keine Ahnung hat wirkt, dass vieleicht etwas verwirrend. Wie wärs statt dessen mit dem Satz Es gibt eine weitere einfache Methode das Skalarprodukt zu berechnen, und zwar durch komponentenweises Multiplizieren der Vektoren und anschließendes Aufsummieren. Diese Berechnungsmethode für das Skalarprodukt wird oft verwendet um Winkel zwischen Vektoren und die Länge von Vektoren zu bestimmen --Stefanwege 21:01, 15. Aug 2006 (CEST)
- OK, einverstanden. --NeoUrfahraner 08:00, 16. Aug 2006 (CEST)
einfache methode?
was heißt den das?
Es gibt eine weitr höhere Dimensionedas Skalarprodukt zu berechnen, und zwar durch komponentenweises Multiplizieren der Koordinaten der Vektoren und anschließendes Aufsummieren. Diese Berechnungsmethode für das Skalarprodukt wird oft verwendet um Winkel zwischen zwei Vektoren und die Länge von Vektoren zu bestimmen.
es erscheint mir unwahrscheinlich das eine multiplikation und summe von (angenommen) ganzen zahlen ein ähnlich "schönes" ergebnis liefert wie die erste formel in der wurzel und division vorkommt.
gehts da um einheitsvektoren??? -- Qopep 21:01, 6. Mär. 2007 (CET)
Öh, Deine so genannte erste Formel ist das Skalarprodukt von x mit x. Daher die Summe der Quadrate. Die Wurzel ist dann die Länge des Vektors und hat mit dem Skalarprodukt unmittelbar nix mehr zu tun. --Philipendula 21:16, 6. Mär. 2007 (CET)
langsam kapier' ichs echt nicht mehr... also das skalarprodukt ist wirklich nur die summe der einzelnen produkte. warum dann die unnötig komplizierte rechnung mit ? weil das eine allgemeine/andere/??? möglichkeit ist, über die sich aber dann der winkel zwischen den vektoren herleiten lässt? -- Qopep 23:39, 6. Mär. 2007 (CET)
- Was man verwendet hängt davon ab, welche Angaben gegeben sind. Hat man die Vektoren als Tupel gegeben, dann berechnt man das Skalarprodukt nach der Formel. Daraus kann man dann, wenn man möchte, mit der Formel den Winkel zwischen den beiden Vektoren und ausrechnen. Hat man aber umgekehrt die Längen der Vektoren und den Winkel zwischen beiden gegeben, dann kann man mit der letzteren Formel das Skalarprodukt ausrechnen. --Digamma 12:40, 11. Mär. 2007 (CET)
Der Rest sind nur weitere Anwendungen des Skalarprodukts. Dat Ding heißt so, weil das Produkt eines Zeilen- mit einem Spaltenvektor ein Skalar, also eine Zahl ergibt. --Philipendula 23:43, 6. Mär. 2007 (CET)
Malpunkt
Im Artikel steht:
- Wie bei der normalen Multiplikation wird das Multiplikationszeichen auch ganz weggelassen: .
Ich bin ja i.A. auch immer dafür, Malpunkte woimmer es geht, wegzulassen. Aber beim Skalarprodukt ist das meines Wissens nicht üblich. Im Gegenteil, manche Bücher verwenden speziell fette Punkte.
Weiter unten wird im Artikel die Schreibweise mit spitzen Klammern verwendet, ohne dass dies erklärt wird. --Digamma 23:32, 10. Nov. 2007 (CET)
- ich kenne profs, die das so handhaben, also den malpunkt weglassen, und es kommt mir auch nicht unueblich vor. (allerdings verwenden die alle keine pfeile. die pfeile werden afaik eher bei physikern und ing. verwendet.) -- seth 12:40, 11. Nov. 2007 (CET)
- Das mit den Punkten weiß ich nicht. Aber die eckigen Klammer werden in der Einleitung erklärt und sind in der Linearen Algebra gebräuchlicher (siehe zum Beispiel im Fischer).Gruß Azrael. 02:32, 12. Nov. 2007 (CET)
Ich habe mir heute von einem Professor der Elektrotechnik sagen lassen, dass die Schreibweise mit dem Malpunkt falsch sei. Man müsse dann einen Vektor mit einem T für translatiert versehen. Er begründet dies mit der MAtrixmultiplikation, die nur dann einen Sinn ergibt. Ansonsten soll diese Schreibweise mißverständlich sein. Die Schreibweise mit den eckigen Klammern kenne ich auch aus Vorlesungen über Höhere Mathematik und bin der Meinung, dass diese geeignet sind < , >.
Produkt-Punkt oder Skalarprodukt-Kringel?
Hey, ich bin grad recht zufällig auf den Artikel gestoßen und muss erst mal Protestieren. Warum steht denn überall für das Skalarprodukt der normale Punkt und nich der Kringel ? Ich hätte da von jedem Mathelehrer in der Schule Punktabzug dafür bekommen. --Slian 16:18, 1. Mär. 2009 (CET)
- Den Kringel kenn ich gar nicht als Verknüpfungszeichen für das Skalarprodukt, auch nicht aus der Schule. Höchstens einen fetten Punkt. Kannst Du eine Quelle (z.B. ein Schulbuch) für den Kringel angeben? --Digamma 21:27, 1. Mär. 2009 (CET)
- z.B. in "Anschauliche analytische Geometrie", 1997 Oldenbourg-Verlag (Barth, Krumbacher, Barth) und in der bayerischen Formelsammlung "Mathematische Formeln und Definitionen", BSV (Barth, Mühlbauer, Nikol, Wörle) --Slian 19:40, 8. Mär. 2009 (CET)
- Hallo. Es gibt die unterschiedlichsten Notation für das Skalarprodukt. Einige verwenden zur besonderen Kennzeichnung dicke Punkte, Kringel oder eben eindeutigerweise die Notationen . Wenn dir dein Leher dafür wirklich Punkte abzieht, würde ich mich erstens beschweren und zur Not einen anderen Lehrer konsultieren, das hat nicht einmal mehr was mit Penibilität zu tun, außer er hat euch vorher eindeutig auf eine zu verwendende Notation hingewiesen. Iammrvip 23:53, 1. Jun. 2009 (CEST)
weitere Notation
Ich würde gerne noch eine weitere Notation des Skalarprodukts anmerken. So schreibt man in der Analysis das Skalarprodukt auch oft in der Form (vgl. dazu u.a. Heuser):
Vielleicht könnte man dazu noch einen kleinen Satz verlieren à la "Auch die Notation ... ist gebräuchlich." Iammrvip 23:49, 1. Jun. 2009 (CEST)
Die allgemeine Definition des Skalarprodukts ist ja mal ziemlich chaotisch.
Erstens muss ein Skalarprodukt nicht symmetrisch sein,
zweitens ist das komplex konjugierte Lambda falsch verwandt worden! (nicht signierter Beitrag von 79.212.12.112 (Diskussion | Beiträge) 01:25, 6. Aug. 2009 (CEST))
Verwendung des Malpunktes zwischen zwei skalaren Größen?
Leider wird im gesamten Artikel die Multiplikation zweier Skalare sehr inkonsequent mal mit, mal ohne Malpunkt geschrieben. Los geht es bereits bei der ersten Formel:
- ,
rechts stehen nur Skalare, trotzdem wird einmal der Malpunkt verwendet, einmal nicht. Das Problem zieht sich durch den ganzen Artikel. Wie wäre es mit folgender Regelung: Skalarprodukt grundsätzlich mit Malpunkt, Multiplikation zweier Skalare grundsätzlich ohne Malpunkt? --KMic 17:26, 3. Sep. 2010 (CEST)
- Hier wurde der Malpunkt erst heute von einer IP eingefügt. Ich habe es soeben rückgängig gemacht. Ansonsten bin ich zur Zeit daran, den Artikel zu überarbeiten. Soweit ich bisher gekommen bin, habe ich es genau so gehandhabt, wie Du es vorschlägst. In konkreten Zahlenbeispielen lässt sich der Malpunkt jedoch nicht vermeiden. -- Digamma 21:04, 3. Sep. 2010 (CEST)
- Habe es im restlichen Artikel auch geändert. Nur im Abschnitt "Winkeldefinition im abstrakten Fall" war ich nicht sicher, ob es nicht verständlicher ist, dort den Malpunkt stehen zu lassen, und im letzten Abschnitt "Anwendung" war ich im letzten Term nicht sicher, ob da nun Skalare stehen oder nicht. Wahrscheinlich eher schon, ist aber nicht so recht erklärt.--KMic 10:52, 4. Sep. 2010 (CEST)
- Das sind auf jeden Fall genau die Fälle, wo ich auch den Malpunkt entfernt hätte bzw. gelassen. Im abstrakten Fall, wo das Skalarprodukt mit spitzen Klammern geschrieben wird, ist es weniger verwirrend, wenn der Malpunkt stehen bleibt. Ich hätte ihn hier auch gelassen.
- Bei der Anwendung sind und auch Skalare. -- Digamma 21:19, 4. Sep. 2010 (CEST)
- Habe es im restlichen Artikel auch geändert. Nur im Abschnitt "Winkeldefinition im abstrakten Fall" war ich nicht sicher, ob es nicht verständlicher ist, dort den Malpunkt stehen zu lassen, und im letzten Abschnitt "Anwendung" war ich im letzten Term nicht sicher, ob da nun Skalare stehen oder nicht. Wahrscheinlich eher schon, ist aber nicht so recht erklärt.--KMic 10:52, 4. Sep. 2010 (CEST)
Linearität
Im Artikel geht es ja völlig durcheinander, in welchen Argument man Linearität hat. Definition: vorne linear, als Alternative (!) wird vorne linear angeboten, die Beispiele sind dann meist wieder hinten linear. --91.13.253.35 19:20, 11. Mär. 2008 (CET)
- Ich versteh nicht ganz was du meinst. Kannst du die Stelle genauer beschreiben? Auf jedenfall steht in der Allgemeinen Definition, dass das reelle Skalarprodukt bilinear ist, womit es "vorne" und "hinten" linear ist. Gruß Azrael. 00:12, 12. Mär. 2008 (CET)
- Bei komplexen Vektorräumen unter "Allgemeine Definition" wird "sesquilinear" als vorne linear definiert. Der zweite Punkt unter "abweichende Definitionen" passt nicht dazu und das Beispiel unter "Skalarprodukt als Matrizenprodukt" ist hinten linear. --91.13.201.164 09:51, 12. Mär. 2008 (CET)
- Ah jetzt versteh ich was du meinst. Ja du hast recht das ist nicht gerade einheitlich, deshalb hab ich mal die allg. Definition geändert. Ich hoffe es passt jetzt alles... Ich bin zwar eher der Meinung dass, die Definiton mit rechts semiliniear verbreiteter ist, aber das wurde ja weiter oben schon ausdiskutiert... Danke für den Hinweis. Gruß Azrael. 15:22, 12. Mär. 2008 (CET)
- Danke! Ich habe übrigens mal in anderen Artikeln nachgeschaut: Z.B. in euklidisches Skalarprodukt und Prähilbertraum ist es vorne linear, in Sesquilinearform und Hilbertraum ist es hinten linear. Auch wenn es eigentlich egal ist, wie man es definiert, ist das schon ziemlich verwirrend.--91.13.247.137 18:37, 12. Mär. 2008 (CET)
- innerhalb eines artikels sollte es einheitlich sein. in der gesamten wikipedia ist eine einheitlichkeit jedoch nicht durchzufuehren, weil immer leute existieren werden, die's links und andere, die es rechts besser finden. und das ist auch ok, weil's in der literatur ja auch mal so und mal so gemacht wird. imho sollten wir es da einfach so halten wie in vergleichbaren faellen auch, d.h., egal, wie es in einem artikel verwendet wird: leute, die was ergaenzen, muessen sich an die im jeweiligen artikel verwendete schreibweise anpassen. das macht am wenigsten stress. -- seth 22:42, 12. Mär. 2008 (CET)
- Danke! Ich habe übrigens mal in anderen Artikeln nachgeschaut: Z.B. in euklidisches Skalarprodukt und Prähilbertraum ist es vorne linear, in Sesquilinearform und Hilbertraum ist es hinten linear. Auch wenn es eigentlich egal ist, wie man es definiert, ist das schon ziemlich verwirrend.--91.13.247.137 18:37, 12. Mär. 2008 (CET)
- Ah jetzt versteh ich was du meinst. Ja du hast recht das ist nicht gerade einheitlich, deshalb hab ich mal die allg. Definition geändert. Ich hoffe es passt jetzt alles... Ich bin zwar eher der Meinung dass, die Definiton mit rechts semiliniear verbreiteter ist, aber das wurde ja weiter oben schon ausdiskutiert... Danke für den Hinweis. Gruß Azrael. 15:22, 12. Mär. 2008 (CET)
- Bei komplexen Vektorräumen unter "Allgemeine Definition" wird "sesquilinear" als vorne linear definiert. Der zweite Punkt unter "abweichende Definitionen" passt nicht dazu und das Beispiel unter "Skalarprodukt als Matrizenprodukt" ist hinten linear. --91.13.201.164 09:51, 12. Mär. 2008 (CET)
Was mir also fehlt
Um einmal von der Wissenschaft wegzukommen: Ich habe den Artikel gelesen und er hat mir gar nichts gebracht. Ich wollte wissen, was ein Skalarprodukt eigentlich ist, klar und konkret und so, dass man es auch als Nichtmathematiker verstehen kann. Das kann der Artikel leider in keinster Weise leisten.
Was mir also fehlt, ist eine konkrete und verständliche Erklärung, was genau ein Skalarprodukt ist, warum man es braucht und wieso es berechnet wird - nicht in Fachchinesisch und vielleicht an einem kleinen einfachen Beispiel
Wäre super, wenn das mal jemand leisten könnte - für alle die nach mir kommen. (Der vorstehende, nicht signierte Beitrag stammt von 79.220.26.156 (Diskussion • Beiträge) NeoUrfahraner 14:32, 26. Mär. 2008 (CET))
- Also als jemand der gerade sein Abitur gemacht hat mit Matheleistungskurs und jetzt Mathe studieren möchte, kann ich dir leider nur erklären inwiefern man das Skalarprodukt in der Oberstufe definiert und verwendet. (Von diesem aufgeblähten Artikel hier versteht ja kein Mensch was).
- Ganz wichtig ist mal die wortwörtliche Definition, die hier komischerweise fehlt!
- "Das Skalarprodukt ist die Länge des einen(ersten) Vektors multipliziert mit der senkrechten Projektion des anderen(zweiten) auf den einen(ersten) Vektors; bzw. die Länge des "anderen"(zweiten) Vektors multipliziert mit der senkrechten Projektion des "einen"(ersten) Vektors auf den "anderen"(zweiten)"
- Also stell dir vor du hast zwei Vektoren a und b die einen gewissen Winkel Phi einschließen(Vektoren können überall im raum sein, deswegen sage ich nicht "die dem gleichen Punkt entspringen"). Am besten dreht man das ganze(zur Unterstützung der Vorstellungskraft) so, dass einer der beiden in der horizontalen steht(erster) und der andere(zweiter) darüber ragt. Jetzt stellt man sich vor, dass senkrecht von oben (also senkrecht zum horizontalen) Lichtstrahlen dafür sorgen, dass der Rüberragende einen Schatten auf den anderen wirft (Die senkrechte Projektion).
- Ok laut der Definition ist das Skalarprodukt jetzt die Länge des vertikalen Vektors, mal die Länge des Schattens der auf ihn vom anderen Vektor geworfen wurde, das gilt auch im umgekehrten Fall, also wenn ein senkrecht projizierter Schatten vom vertikalen auf den anderen fiele.
- Sorry, bin etwas zu müde um das noch ausführlicher zu machen, wenn man das mal zeichnet, erhält man 2 rechtwinklige Dreiecke, aus den Hypotenusen usw. kann man sich dann die Sache mit dem Cos(Phi) herleiten... und über den Kosinussatz auch die Sache mit dem multiplizieren+aufaddieren der Koordinaten.
MfG Diddmaster (nicht signierter Beitrag von 82.83.156.41 (Diskussion) 06:44, 20. Jul. 2008 (CEST))
geometrische deutung
Mir fehlt die geometrische Deutung, bzw. die zugehörige Graphik die einem sofort ins Auge sticht und die Bedeutung des Skalarprodukts visuell verständlich macht. Ich habe den höchsten Respekt vor den mathematischen Artikeln auf diesem Wiki, aber denke auch, dass Begriffe aus der Schulmathematik AUCH an geeigneter Stelle in etwas knapperer Form mit einfacherer Sprache erklärt werden sollten. (so dass es für einen ehemals sehr guten Schüler auch später wieder schnell verständlich wird...) (nicht signierter Beitrag von 85.178.194.65 (Diskussion) 14:45, 16. Apr. 2006 (CEST))
- Ich weiß, was du meinst, schon Merkwürdig, dass sie nirgendwo wörtlich auftaucht, als hätten die ganzen Autoren die ursprüngliche Natur des Skalarproduktes nicht verstanden, ich habe hier ganz unten in der Diskussion was dazu geschrieben, hier nochmal der wichtigste Satz:
- "Das Skalarprodukt ist die Länge des einen(ersten) Vektors multipliziert mit der senkrechten Projektion des anderen(zweiten) auf den einen(ersten) Vektors; bzw. die Länge des "anderen"(zweiten) Vektors multipliziert mit der senkrechten Projektion des "einen"(ersten) Vektors auf den "anderen"(zweiten)"
- (Wenn man das einmal visualisiert, dann ist auch sofort klar, warum bei Orthogonalität das Skalarprodukt 0 ist... und man braucht nicht mit "weil cos(90°) = 0" argumentieren... Ich finde es so jedenfalls viel eleganter)
- MfG Diddmaster (nicht signierter Beitrag von 82.83.156.41 (Diskussion) 06:51, 20. Jul. 2008 (CEST))
Ich finde auch hier Fehlt die Visuelle erklärung, was man mit dem Skalarprodukt eigentlich berechnet. Generell habe ich in diesem Artikel keine Beschreibung gefunden was man mit dem Skalarprodukt berechnet. Das finde ich Merkwürdig. Ich muss zwar zugeben das ich mir nicht alles durchgelesen habe, da für mich sowas ganz oben mit rein gehört. (nicht signierter Beitrag von 212.201.18.24 (Diskussion) 07:35, 25. Nov. 2010 (CET))
- Könntest Du bitte konkreter werden? Was genau fehlt dir oben? Deine Ergänzung ist jedenfalls völlig unverständlich. -- Digamma 17:30, 25. Nov. 2010 (CET)
Inneres Produkt oder Skalarprodukt?
Was soll der Unterschied zwischen innerem Produkt und Skalarprodukt sein? Die Unterscheidung, dass das eine im endlichdimensionalen und das andere allgemein sei, habe ich weder auf der englischen Wikipediaseite noch in der Literatur gefunden. Rudin: Functional Analysis; Friedman: Modern Analysis, Collatz: Funktionalanalysis kennen diese Unterscheidung nicht. Ich habe daher die Formulierung gändert -NeoUrfahraner 17.1.2005 (nicht nach ISO formatiert signierter Beitrag von NeoUrfahraner (Diskussion | Beiträge) 21:46, 17. Jan. 2005 (CET))
- gudn tach!
- ja, wird normalerweise synonym gebraucht. ist mir auch noch nie in unterschiedlichen bedeutungen untergekommen. -- seth 21:48, 11. Jan. 2011 (CET)
Gram Matrix
Vieleicht sollte man noch irgendwo einfügen, dass sich jedes Skalarprodukt durch eine Gram Matrix A darstellen lässt. Mit und , wobei A nur beim Standardskalarprodukt die Einheitsmatrix ist.... Wenn ich mal Zeit hab, werd ich mich mal dran probieren... Bis dann.--Gruß Azrael. 00:30, 16. Okt. 2006 (CEST)
- Gehört mMn nach Bilinearform. Hier könnte man dann noch schreiben, dass jede Matrix der Form symmetrisch und positiv definit ist und auf die Hauptachsentransformation verweisen.--Gunther 00:56, 16. Okt. 2006 (CEST)
- Ich finde die Matrixdarstellung hier wichtig und habe deswegen einen Abschnitt dazu geschrieben. -- Digamma 18:33, 13. Jan. 2011 (CET)
Überarbeitung
Ich habe mal angefangen, den Artikel zu überarbeiten. Insbesondere ist mir wichtig:
- Den konkreten Anschauungsraum der euklidischen Geometrie und den abstrakten Koordinaten-Raum auseinander zu halten.
- So zu schreiben, dass Oberstufenschüler möglichst viel Gewinn daraus ziehen können.
Daraus ergibt sich, dass der erste Teil den geometrischen Vektoren im euklidischen Raum gewidmet ist (hier sind noch die Anwendungen zu ergänzen, die bisher noch weiter unten stehen), danach das Standardskalarprodukt im und im folgt und erst danach die abstrakte Definition eines beliebigen Skalarprodukts. -- Digamma 22:53, 4. Aug. 2010 (CEST)
- Ich habe den Artikel jetzt im Wesentlich so wie angekündigt überarbeitet. Womit ich noch nicht so ganz zufrieden bin:
- Dadurch, dass erst das geometrische Skalarprodukt eingeführt wird, dann das Standardskalarprodukt und zuletzt die allgemeine Definition, werden die charakteristischen Eigenschaften eines Skalarprodukts mehrfach aufgelistet: erstens als Eigenschaften des geom. SP und des Standard-SP, dann als Axiome. Ähnlich ist es bei der Definition (bzw. Berechnungsformel) von Norm und Winkel. Hat jemand eine Idee, wie man das straffen könnte?
- Das Standardskalarprodukt wird im komplexen wie im reellen Fall mit einem Malpunkt geschrieben. Das verträgt sich aber sehr schlecht mit der Semilinearität, da man dann das Produkt immer klammern muss. Ist die Schreibweise mit Malpunkt im komplexen Fall überhaupt gebräuchlich? Eine Möglichkeit, die ich mir vorstelle könnte, ist, im zweiten Abschnitt "Standardskalarprodukt" nur das reelle zu nennen, und das komplexe unten im Allgemeinen Fall als Beispiel aufzuführen (neben einer Erwähnung des reellen Standardskalarprodukts).
- -- Digamma 15:51, 15. Jan. 2011 (CET)
- In diesem Sinne nochmal überarbeitet. Über Kommentare würde ich mich freuen. -- Digamma 23:59, 15. Jan. 2011 (CET)
Struktur des 1. Abschnitts "euklidischer Raum"
@Joachim Mohr: Ich bin mit Deinen Umstellungen und Ergänzungen nicht ganz glücklich. Auch wenn ich im geometrischen Fall die Beschreibung mit dem Kosinus des Winkels als eigentliche Definition betrachte, so möchte ich die Darstellung in Koordinaten doch eher als alternative Definition statt als Folgerung verstanden wissen. Das bedeutet, dass der Abschnitt nicht zu weit von der Definition weggeschoben werden sollte. Ich habe zwar die Beispiele nach oben geschoben, aber nur deshalb, weil sie direkt die Berechnung von Skalarprodukten mit Hilfe der geometrischen Definition illustrieren. Beispiele, die darüber hinausgehen, wie die physikalische Anwendung, würde ich lieber weiter nach unten schieben.
Im Abschnitt "kartesische Koordinaten" würde ich die Herleitung und die Basisvektoren lieber weg lassen. Wie gesagt, ich sehe das eher als eine alternative Definition. Die Herleitung an dieser Stelle ist aber auch deshalb problematisch, weil die benötigten Eigenschaften des Skalarprodukts (Linearität) erst weiter unten formuliert werden. -- Digamma 22:13, 11. Jan. 2011 (CET)
Ergänzung: Ich vermute mal, dass du die Beispiele nach oben gezogen hast, um den Leser schon früh auf die vielfältigen Anwendungen hinzuweisen. Das könnte man vielleicht durch ein paar ergänzende Sätze in der Einleitung tun. -- Digamma 07:24, 12. Jan. 2011 (CET)
- Genau das war der Grund. Weiter oben hier in der Diskussion wird ja deutlich, dass manche Leser wissen wolle, wozu das Skalarprodukt gut ist. Deshalb schon früh ein Ausflug in die Physik (Den zu überspringen - ohne den Faden zu verlieren - dem Leser offensichtlich ist) und deshalb auch den Ausflug zu den mathematischen Anwendungen (Kosinussatz). Ich überlasse besser Dir, den verweis und die Verschiebung vorzunehemn.
- Die Sache mit den Einheitsvektoren brachte ich deshalb ins Spiel, weil hier geradlinig der Zusammenhang zwischen Geometrischer Definition und Definition über Koordinaten gezeigt wird - unter Vorwegnahme der Bilienarität des Skalarproduktes (das aber als Rechenregeln z.B. den Gymnasiasten geläufig ist). Klar: Das schwierigste bei der geometrischen Definition des Skalarproduktes ist die Herleitung des Distributivgesetztes. (Bei Definition über Koordinaten ist geradlinig.) Hier im Artikel wird darauf verzichtet, sondern nur darauf bei den "Eigenschaften des Skalarproduktes" verwiesen. Nun: Darauf kann man ja bei den Einheitsvektoren noch hinweisen (was ich hiermit getan habe). --Joachim Mohr 10:02, 12. Jan. 2011 (CET)
Hallo Digamma! Ich konnte einfach der Versuchung nicht widerstehen, ein kleines Rechenbeispiel für das Rechnen mit Vektoren einzufügen. Bei "Orthogonalität und orthogonale Projektion" fügt sich die kleine Herleitung so passend ein. Gruß --Joachim Mohr 10:13, 16. Jan. 2011 (CET)
- So glücklich bin ich nicht damit. Auf jeden Fall geht <small> überhaupt nicht. -- Digamma 19:35, 16. Jan. 2011 (CET)
Definition des Skalarproduktes mit komplexen Skalaren
Tut mir leid, wenn ich den normalen Rahmen dieser Diskussionsseite sprenge, aber das stimmt doch mal garnicht! Die Allgemeine Definition des komplexen Skalarprodukts ist einfach falsch! Bitte schnellstmöglichst bearbeiten! (nicht signierter Beitrag von 88.65.235.160 (Diskussion) 12:58, 12. Jan. 2011 (CET))
Rechenfehler in Anwendungen/In der Physik
Im Bereich Anwendungen/Physik wird bei der Berechnung der Arbeit auf der schiefen Ebene 5N * 3m * cos63 = 3,8J angegeben.
Tatsächlich errechnen sich da rund 6,81 J. (nicht signierter Beitrag von 88.75.70.152 (Diskussion) 20:01, 7. Feb. 2011 (CET))
- Hab's mal ausgebessert. Der Abschnitt ist aber noch viel weiter verbesserbar, weil zum Beispiel der Text gar keine Verbindung zur Abbildung herstellt. --Daniel5Ko 23:25, 7. Feb. 2011 (CET)
Doppeltes entfernt
Der Kosinussatz kommt schon weiter oben. Der folgende Teil wurde deshalb entfernt.
Winkelberechnung im euklidischen Raum
Das Skalarprodukt ist ursprünglich im Rahmen der analytischen Geometrie im euklidischen Raum eingeführt worden. So ist es mit Hilfe des Skalarproduktes beispielsweise möglich, den Winkel zwischen zwei Vektoren zu berechnen: Das Skalarprodukt ergibt sich nämlich auch aus den Beträgen der beiden Vektoren und dem Kosinus des von diesen eingeschlossenen Winkels gemäß der Formel
Um dies zu zeigen, mögen drei Vektoren, des euklidischen Raumes betrachtet werden.
Wegen des Kosinussatzes ist die Länge des dem Winkel gegenüberliegenden Vektors
Da sich als ergibt, erhält man
Berechnet man nun die Länge über das Skalarprodukt, so erhält man
Aus den Rechenregeln für das Skalarprodukt ergibt sich dann
und daraus die gewünschte Beziehung
--Joachim Mohr 17:41, 10. Jan. 2011 (CET)
Hallo Joachim,
Das, was Du entfernt hast, war noch eine "Altlast" aus der Zeit vor der Überarbeitung, die ich angefangen haben, dann aber mangels Zeit nicht zu Ende gebracht habe. Überarbeitet habe ich damals die ersten zwei Abschnitte
- Im euklidischen Raum
- Das Standardskalarprodukt
- im
- im
Der 3. Abschnitt "Allgemeine Definition" harrt noch einer Überarbeitung (außer der Definition selbst vielleicht). Ich hatte mir die Gliederung wie folgt vorgestellt.
- Allgemein
- Definition
- reell
- komplex
- Norm, Winkel, Abstände
- Weitere Beispiele (z. B. Polynomräume, Funktionenräume, weitere Skalarprodukte auf dem (bzw. ), die durch eine positiv definite symmetrische (bzw. hermitesche) Matrix gegeben werden.
- Darstellung in Koordinaten (Darstellung eines beliebigen Skalarprodukts (im endlich-dimensionalen Fall) bzgl. einer Basis durch eine Matrix; Spezialfall ONB)
- Definition
Das von Dir hinzugefügte Anwendungsbeispiele würde ich lieber im ersten Teil (Euklidischer Raum) sehen. Vielleicht unter einer Überschrift "Skalarprodukt in der Physik" (?). -- Digamma 21:10, 10. Jan. 2011 (CET)
- Programm im Wesentlichen abgearbeitet. Es fehlen noch Beispiele für allgemeine Skalarprodukte. Was sollte da rein? Vorschläge: Das L^2-Skalarprodukt, Riemannsche Metriken (?), ... Letzteres könnte auch unter einem neuen Abschnitt "Verallgemeinerungen" stehen. Dort könnte auch auf "Norm" verwiesen werden und auf "semi-inneres Produkt". Wie man die anderen Punkte der "Siehe auch"-Liste (Kreuzprodukt, Quaternionen, Skalare Multiplikation) einarbeiten könnte, sehe ich nicht. -- Digamma 22:05, 11. Jan. 2011 (CET)
Anwendungen in der Geometrie
Das Skalarprodukt wird über den Kosinussatz bewiesen, bzw hergeleitet. Von daher ist die Behauptung man kann mit dem Skalarprodukt den Kosinussatz beweisen, ein Biss in den eigenen Schwanz. Statt dessen sollte man diese Herleitung irgendwo in den Artikel einbauen. --193.110.129.66 06:18, 13. Aug. 2011 (CEST)
- Die geometrische Formel für das Skalarprodukt wird zwar häufig mit Hilfe des Kosinussatzes hergeleitet, dies ist jedoch nicht zwingend und eigentlich mit Kanonen auf Spatzen geschossen. Sie ergibt sich vielmehr schon (wie im Text genannt) aus den "natürlichen Forderungen, dass das Skalarprodukt eine Vektors mit sich selbst das Quadrat seiner Länge ist, und dass das Skalarprodukt die obigen Eigenschaften 1–3 erfüllt". Mit den Eigenschaften 1-3 ist gemeint, dass sich das Skalaprodukt algebraisch wie ein Produkt verhält: Es ist bilinear und symmetrisch. Das einzige, was man benötigt, ist der Satz des Pythagoras. -- Digamma 09:46, 13. Aug. 2011 (CEST)
- Den Satz des Pythagoras kann man ja nur in rechtwinkeligen Dreiecken anwenden. Von daher muss man entweder über eine Projektion arbeiten, die wiederum auf der geometrischen Formel des Skalarproduktes beruht. Oder man verwendet den Kosinussatz, bzw müsste man ansonsten den Beweis des Kosinussatzes gleich mit einbauen, was wieder aufs selbe rausläuft.--Haegar666 23:33, 31. Aug. 2011 (CEST)
- Die Projektion braucht die geometirsche Formel nicht, sondern nur die Tatsache, dass das Skalarprodukt von orthogonalen Vektoren null ist. Dies folgt aus dem Satz des Pythagoras zusammen mit den binomischen Formeln. Man kann dann, wie im Abschnitt über die orthogonale Projektion beschrieben, den Vektor in einen Vektor in Richtung von und einen dazu orthogonalen Vektor zerlegen: mit , also . Die Pfeile von , und bilden die Hypothenuse und die Katheten eines rechtwinkligen Dreiecks. Nach Definiton der trigonometrischen Funktionen gilt . Da dieselbe Richtung wie hat, ist . Da und parallel sind, gilt für ihr Skalarprodukt: . Zusammen ergibt sich die Formel . (Das gilt so, wenn der eingeschlossene Winkel spitz ist. Ist er stumpf, so gilt die analoge Argumentation mit einem Minuszeichen an den notwendigen Stellen.)
- Ok danke, alles klar so rum funktionierts auch. Wäre wohl einen Eintrag im Wikibooks: Beweisarchiv: Geometrie – Lern- und LehrmaterialienWert ;).--193.110.129.66 05:00, 8. Okt. 2011 (CEST)
- Ok danke, alles klar so rum funktionierts auch. Wäre wohl einen Eintrag im
Fehler in "Aus der Darstellung des Skalarprodukts mittels Winkel"
\langle x, y\rangle = |x||y| \cdot \cos\measuredangle (x,y)
folgt geometrisch, dass das Skalarprodukt invariant gegenüber längen- und winkeltreuen Abbildungen sein muss. Dies lässt sich auch analytisch nachrechnen. Längen- und winkeltreue Abbildungen werden durch unitäre Matrizen U dargestellt, das sind Matrizen mit der Eigenschaft UUH = I oder
\sum_k u_{ik}\overline{u_{jk}}=\delta_{ij},
wobei δij das Kronecker-Delta darstellt. Für die i-te Komponente von Ux und Uy gilt
{\left(Ux\right)}_i=\sum_j u_{ij}a_j
und
{\left(Uy\right)}_i=\sum_k u_{ik}b_k.
Muss da nicht:
{\left(Ux\right)}_i=\sum_j u_{ij}x_j
und
{\left(Uy\right)}_i=\sum_k u_{ik}y_k
stehen? (Der vorstehende, nicht signierte Beitrag – siehe dazu Hilfe:Signatur – stammt von 129.13.186.1 (Diskussion • Beiträge) 25. Nov. 2008, 14:16)
- erl. --Sabata (D|WZ) 14:26, 25. Nov. 2008 (CET)
Bildbeschreibung fehlt bei [[Bild:SkalarproduktSkizze.jpg]]
Der Artikel enthält ein Bild, dem eine Bildbeschreibung fehlt, überprüfe bitte, ob es sinnvoll ist, diese zu ergänzen. Gerade für blinde Benutzer ist diese Information sehr wichtig. Wenn du dich auskennst, dann statte bitte das Bild mit einer aussagekräftigen Bildbeschreibung aus. Suche dazu nach der Textstelle [[Bild:SkalarproduktSkizze.jpg]] und ergänze sie.
- Wenn du eine fehlende Bildbeschreibung ergänzen willst, kannst du im Zuge der Bearbeitung folgende Punkte prüfen:
- Namensraum Datei: Bilder sollte im Namensraum Datei liegen. Bitte ändere die alten Bezeichnungen
Bild:undImage:inDatei:. - Skalierung: Außerhalb von Infoboxen sollten keine festen Bildbreiten (zum Beispiel 100px) verwendet werden. Für den Fließtext im Artikelnamensraum gibt es Thumbnails in Verbindung mit der automatischen Skalierung. Um ein Bild/eine Grafik in besonderen Fällen dennoch größer oder kleiner darzustellen, kann der „upright“-Parameter verwendet werden. Damit erfolgt eine prozentuale Skalierung, die sich an den Benutzereinstellungen orientiert. --SpBot 10:20, 2. Mär. 2009 (CET)
- Namensraum Datei: Bilder sollte im Namensraum Datei liegen. Bitte ändere die alten Bezeichnungen
Ich glaube, das erübrigt sich. --Slian
Fehler in allg. Definition
Hi, in der allgemeinen definition im komplexen wird zwar korrekt von semilinear gesprochen aber nach der Definition gibt es keinen unterschied zwischen semilinear und linear. AFAIK fehlt da ein * oder ein Dagger, da ich mir gerade nicht ganz sicher war habe ich es erstmal so gelassen aber bitte mal drüber gucken! -- 141.99.254.253 17:11, 18. Okt. 2011 (CEST)
- Da steht doch ein Strich über dem Lambda, der die komplexe Konjugation bezeichnet (in der Mathematik das übliche Zeichen). --Digamma (Diskussion) 22:48, 10. Mai 2012 (CEST)
Länge oder Betrag?
Ich habe vorhin den Begriff "Länge" durch "Betrag" ersetzt. Diese Änderung wurde rückgängig gemacht. "Länge" sei ebenfalls gebräuchlich. Es kann zwar sein, dass das in der Mathematik so gehandhabt wird. Das kann ich nicht beurteilen, ich bin kein Mathematiker. In der Physik wäre der Begriff "Länge" aber definitiv falsch, denn die Länge hat die Einheit "Meter", während der Betrag eines Vektors je nach Typ der Größe jede beliebige Einheit haben kann. Z. B. käme nie jemand auf die Idee, den Betrag der elektrischen Feldstärke (Einheit: V/m) als "Länge" der Feldstärke zu bezeichnen. Ich plädiere daher dafür, dass der Begriff tatsächlich in "Betrag" geändert wird! (Ich versuch's jetzt nochmal selbst, in der Hoffnung, dass es nicht gleich wieder rückgängig gemacht wird). -- Pyrrhocorax 01:05, 24. Dez. 2011 (CET)
- Hallo, wir hatten die Diskussion schon einmal ausführlich im Artikel Vektor. Dort mit umgekehrtem Vorzeichen: Ein Mathematiker hat die Bezeichnung "Betrag" beanstandet. In der Geometrie ist Länge definitiv richtig (und zunächst sind Vektoren geometrische Objekte). Mathematiker reservieren den Begriff "Betrag" für Zahlen (bzw. für Körperelemente). Ich habe den Begriff "Länge" in Klammern wieder ergänzt. --Digamma 10:18, 24. Dez. 2011 (CET)
- Hallo Digamma. Du schreibst "(...) zunächst sind Vektoren geometrische Objekte". Das wurde mir grundsätzlich anders beigebracht. Es wurde von den Mathematik-Dozenten viel Wert auf die Feststellung gelegt, dass ein Vektor ein Element eines Vektorraums sei (siehe zum Beispiel Kowalski Lineare Algebra). Jede andere Antwort hätte zu Abzügen in der Vordiplomsprüfung geführt. Hast Du Belege für Deine Ansicht?---<)kmk(>- 02:11, 25. Dez. 2011 (CET)
- Konkret ist in dem Zusammenhang, in der die Bezeichnung "Länge" moniert wurde, von Vektoren im Anschauungsraum die Rede. Nur dort macht die Einführung über den Winkel überhaupt Sinn. Über abstrakte Vektorräume spricht der Artikel später. --Digamma 20:27, 30. Dez. 2011 (CET)
- Hallo Digamma. Du schreibst "(...) zunächst sind Vektoren geometrische Objekte". Das wurde mir grundsätzlich anders beigebracht. Es wurde von den Mathematik-Dozenten viel Wert auf die Feststellung gelegt, dass ein Vektor ein Element eines Vektorraums sei (siehe zum Beispiel Kowalski Lineare Algebra). Jede andere Antwort hätte zu Abzügen in der Vordiplomsprüfung geführt. Hast Du Belege für Deine Ansicht?---<)kmk(>- 02:11, 25. Dez. 2011 (CET)
- Konkret moniere ich die Einstellung, dass Vektoren "zunächst (...) geometrische Objekte" seien. Nein, das sind sie nicht. Es ist didaktisch für die Fachbereiche, die Vektoren anwenden (Physik, Elektrotechnik, Maschinenbau, ...) wenig hilfreich, wenn das so dargestellt wird. Ein Winkel benötigt im übrigen mitnichten einen Anschauungsraum, um sinnvoll definiert zu sein.---<)kmk(>- 21:23, 30. Dez. 2011 (CET)
- Vektoren sind auf jeden Fall historisch zunächst geometrische Objekte. Dasselbe gilt für den Schulunterricht. Im Physikunterricht ist von "Vektorgrößen", die durch Pfeile dargestellt werden, die Rede (so in Dorn Bader). Was dir deine Professoren beigebracht haben, das ist eine Verallgemeinerung des ursprünglichen Vektorbegriffs. So wie "Zahlen" zunächst natürliche Zahlen sind, und allgemeiner Elemente eines Zahlbereichs. --Digamma 22:52, 30. Dez. 2011 (CET)
- Konkret moniere ich die Einstellung, dass Vektoren "zunächst (...) geometrische Objekte" seien. Nein, das sind sie nicht. Es ist didaktisch für die Fachbereiche, die Vektoren anwenden (Physik, Elektrotechnik, Maschinenbau, ...) wenig hilfreich, wenn das so dargestellt wird. Ein Winkel benötigt im übrigen mitnichten einen Anschauungsraum, um sinnvoll definiert zu sein.---<)kmk(>- 21:23, 30. Dez. 2011 (CET)
- Wie sich ein Begriff historisch entwicklt hat, ist für die Darstellung hier in Wikipedia nur für die Geschichtsabschnitte relevant. Ähnliches gilt für vereinfachte Teilkonzepte, mit denen man Schülern den Einstieg in das Thema erleichtert. Auch das kann und sollte in einem entsprechenden Abschnitt, oder in einem eigenen Artikel dargestellt werden -- aber nicht als Hauptbedeutung des Lemmas "Vektor". Kindermärchen sind kein tragfähiges enzyklopädisches Konzept. Die Hauptaussage eines Artikels sollte selbstverständlich auf der Bedeutung liegen, die dem Lemma heute zugeschrieben wird. In dem Beispiel Natürliche Zahl kommt auch niemand auf die Idee, den Artikel auf die Zahlen von 1 bis 10 zu beschränken, weil das der Zahlenraum ist, der in der Grundschule zunächst ausschließlich gelehrt wird.---<)kmk(>- 01:54, 31. Dez. 2011 (CET)
- Wir sollten uns hier auf die Diskussion zu diesem Artikel und an dieser Stelle auf die von Pyrrhocorax aufgeworfene Frage beschränken und keine Grundsatzdiskussion zum Thema Vektor führen. Das ist an anderer Stelle schon geschehen und kann von mir aus dort wieder aufgenommen werden. --Digamma 09:36, 31. Dez. 2011 (CET)
- Wie sich ein Begriff historisch entwicklt hat, ist für die Darstellung hier in Wikipedia nur für die Geschichtsabschnitte relevant. Ähnliches gilt für vereinfachte Teilkonzepte, mit denen man Schülern den Einstieg in das Thema erleichtert. Auch das kann und sollte in einem entsprechenden Abschnitt, oder in einem eigenen Artikel dargestellt werden -- aber nicht als Hauptbedeutung des Lemmas "Vektor". Kindermärchen sind kein tragfähiges enzyklopädisches Konzept. Die Hauptaussage eines Artikels sollte selbstverständlich auf der Bedeutung liegen, die dem Lemma heute zugeschrieben wird. In dem Beispiel Natürliche Zahl kommt auch niemand auf die Idee, den Artikel auf die Zahlen von 1 bis 10 zu beschränken, weil das der Zahlenraum ist, der in der Grundschule zunächst ausschließlich gelehrt wird.---<)kmk(>- 01:54, 31. Dez. 2011 (CET)
- gudn tach!
- oops, hab diese diskussion erst jetzt gesehen, sorry. (und naechstes mal bitte im summary auf etwaige diskussionen verweisen.)
- habe eben auf talk:Betrag (Vektor) ebenfalls eine diskussion dazu begonnen. "definitiv falsch" ist es in der physik sicher nicht, was sich anhand mehrerer physikbuecher, die sich via google-books finden lassen, zeigt. beide begriffe sind in physik, mathe und ing.-wissenschaften ueblich (und mir auch schon gesprochen von jeweiligen vertretern untergekommen). -- seth 18:13, 24. Dez. 2011 (CET)
- Im Ernst? Es gibt Lehrbücher, die von der "Länge einer Geschwindigkeit" oder von der "Länge eines Impulses" schreiben? Bitte Butter bei die Fische. Das kann ich mir wegen der von Pyrrhocorax angedeuteten Einheiten-Problematik kaum vorstellen.---<)kmk(>- 02:03, 25. Dez. 2011 (CET)
Ich bin gegen die bezeichnung "Länge" und für die bezeichnung "Betrag" aus systematischen Gründen - auch für Vektoren aus dem Anschaungsraum.
Zum Beispiel sagt die Aussage "Die Länge des Vektors ist 5" noch gar nicht über seine Länge aus. Zum Mindestens müßte man dann noch etwas über die Längeneinheit sagen.
Eine Erwähnung, dass man mit dem betrag die Länge berechnen kann, wäre allerdings nützlich. --Joachim Mohr (ohne Datum signierter Beitrag von Joachim Mohr (Diskussion | Beiträge) 19:41, 25. Dez. 2011 (CET))
- gudn tach!
- da ich von -<)kmk(>- nach belegen gefragt wurde, habe ich jetzt also die besagte google-book-recherche noch mal durchgefuehrt. ich nehme absichtlich nicht nur (hochtrabende) fachbuecher, sondern auch populaerwissenschaftliche/massenkompatible buecher wie "... for dummies", da auch jene zur sprache bzw. zum sprachgebrauch beitragen. und ich habe auch ein sehr altes buch hinzugenommen, um zu zeigen, dass die synonymie nicht nur in der aktuellen sprache vorhanden ist.
- Mathematische Formelsammlung: Für Ingenieure und Naturwissenschaftler, S. 49: "Betrag (Länge) eines Vektors"
- Handbuch maschinenbau (Böge), S. A-43: "Der Betrag [...] eines Vektors ist die Länge eines Vektors"
- Physik für Ingenieure für Dummies, S. 33: "Hier lernen Sie, wie Sie die Länge (den Betrag, den Wert) eines Vektors bestimmen."
- Physik für Dummies, S. 60: "[...] besitzt genau wie ein Vektor einen Betrag (die Länge) [...]"
- Experimentalphysik 1: Mechanik und Wärme, S. 441: "Ihre Länge heißt Betrag des Vektors. [...] Zwei Vektoren [sind] auch dann gleich, wenn sie [...] gleiche Länge haben."
- Rechenmethoden für Studierende der Physik im ersten Jahr, S. 2: "Dabei ist r die Länge (oder Betrag) des Vektors"
- Rechenmethoden der Physik, S. 3: "Er wird durch eine Richtung und eine Länge (einen Betrag) charakterisiert."
- Physik: Bachelor-Edition, S. 32: "Betrag (Länge)"
- Lehrbuch der Physik: Bd. l : Mechanik, Akustik, Wärmelehre, S. 399: "Einen Vektor von der Länge 1 bezeichnet man als Einheitsvektor"
- Clark University, 1889-1899: decennial celebration: "Die so bestimmte Länge ist die Geschwindigkeit"
- Physik, Alonso/Finn, S. 172: "Die Geschwindigkeit [wird] durch einen rotierenden Vektor der Länge [...] dargestellt"
- Physik: Mechanik, Wellen, Wärme, S. 29: "Indem wir den Tangenten-Einheitsvektor [...] als den Vektor definieren, dessen Länge gleich der Längeneinheit ist [...]"
- Moderne Methoden in der Spektroskopie, S. 187: "Die Länge des Vektors, der den Bahndrehimpuls eines einzelnen Elektrons repräsentiert [...]"
- Grundkurs Theoretische Physik 1: Klassische Mechanik: Band 1, S. 53: "Jeder Vektor [...] hat eine Länge, einen Betrag [...] und eine Richtung [...]"
- Feynman Vorlesungen über Physik. 1. Mechanik, Strahlung, Wärme, S. 255: "Somit sehen wir, daß das Quadrat der Länge dieses Vektors, der Vierervektorimpuls [...]"
- dass begriffe doppelt belegt sind, heisst nicht, dass sie nicht trotzdem verwendet werden. aus dem kontext geht meist hervor, welche bedeutung gemeint ist. falls nicht, praezisiert man oder verwendet andere begriffe. wenn's in einem absatz um die sog. physikalische laenge und die laenge eines vektors geht, dann kann man selbstverstaendlich beim vektor statt "laenge" z.b. "vektorlaenge", "(vektor)betrag", "vektorgroesse" oder sowas schreiben; und auch fuer die physikalische laenge gibt es kontextabhaengige synonyme (wie z.b. "ausdehnung", "breite", "hoehe", "weg", ...). -- seth 22:34, 28. Dez. 2011 (CET)
- In all Deinen Beispielen ist von der "Länge eines Vektors", also eines mathematischen Objekts die Rede. In keinem Beispiel ist es die Länge einer Geschwindigkeit, eines Impulses, Drehimpulses, Spins oder allgemein einer physikalischen Größe. Das war es, nach was ich gefragt hatte.---<)kmk(>- 01:12, 29. Dez. 2011 (CET)
- In diesem Artikel ist auch nur von der Länge eines Vektors die Rede und nicht von der "Länge" von vektoriellen physikalischen Größen. --Digamma 20:30, 30. Dez. 2011 (CET)
- In all Deinen Beispielen ist von der "Länge eines Vektors", also eines mathematischen Objekts die Rede. In keinem Beispiel ist es die Länge einer Geschwindigkeit, eines Impulses, Drehimpulses, Spins oder allgemein einer physikalischen Größe. Das war es, nach was ich gefragt hatte.---<)kmk(>- 01:12, 29. Dez. 2011 (CET)
- Auf seths Wunsch hin diskutieren wir hier nicht nur den Inhalt des Artikels Skalarprodukt, sondern auch den des Artikels Betrag (Vektor).---<)kmk(>- 21:29, 30. Dez. 2011 (CET)
- gudn tach!
- "Die Länge des Vektors, der den Bahndrehimpuls eines einzelnen Elektrons repräsentiert [...]", "Die Geschwindigkeit [wird] durch einen rotierenden Vektor der Länge [...] dargestellt". siehe oben.
- selbstverstaendlich wird sich in der physik immer auch auf die mathematischen konstrukte bezogen. ein vektor ist nun mal ein mathematisches konstrukt, dass u.a. in den natur- und ing.wissenschaften anwendung findet. je nach anschauung kann man die mathematik ja auch durchaus historisch als hilfswissenschaft betrachten (auch wenn ich persoenlich die anschauung, die in dem pov-artikel Strukturwissenschaft vermittelt wird, bevorzuge). -- seth 03:11, 29. Dez. 2011 (CET)
- Auch diese beiden Beispiele beziehen die Eigenschaft "Länge" ausdrücklich auf das mathematische Objekt und nicht auf den Bahndrehimpuls bzw. die Geschwindigkeit selbst. Sie erklären mit den Verben "repräsentieren" und "darstellen" sogar die Beziehung zwischen den beiden Begriffen. Du stößt gerade darauf, dass Physiker in der Sprache ein Unterschied zwischen den Eigenschaften des mathematischen Objekts und Eigenschaften der physikalischen Größe machen, die durch das mathematische Objekt repräsentiert werden. Ich warte weiter auf Beispiele, in denen von der Länge einer Geschwindigkeit, Drehimpuls, Impuls, etc. die Rede ist.---<)kmk(>- 07:30, 30. Dez. 2011 (CET)
Hier die von mir weiter oben erwähnte Diskussion beim Artikel Vektor. --Digamma 20:34, 30. Dez. 2011 (CET)
- Hinweis auf Bündelung der Diskussion: Portal:Mathematik/Qualitätssicherung#Länge/Norm/Betrag eines Vektors. --Quartl 12:05, 5. Jan. 2012 (CET)
- ah, danke fuer die buendelung.
- dennoch moechte ich, um die hauptdiskussion, die sich ums wesentliche dreht, nicht unnoetig aufzublaehen, hier noch auf nebenaspekte eingehen.
- @-<)kmk(>-: wenn du aber so streng trennst, dann muesste man doch konsequenterweise sagen, dass z.b. der bahndrehimpuls gar kein vektor ist, sondern nur durch das mathematische vektor-konstrukt symbolisiert wird, oder? -- seth 14:44, 8. Jan. 2012 (CET)
Die erwähnte Diskussion ist inzwischen im Archiv: Portal:Mathematik/Qualitätssicherung/Archiv/2012/Januar#L.C3.A4nge.2FNorm.2FBetrag_eines_Vektors. Gibt es hier noch Diskussionsbedarf, oder kann das auch archiviert werden? --MartinThoma (Diskussion) 06:57, 11. Mai 2012 (CEST)
- Ist zwar noch nicht wirklich erledigt (siehe Portal:Mathematik/Qualitätssicherung#Betrag (Vektor)), aber an dieser Stelle muss man, denke ich, nicht weiterdiskutieren. Viele Grüße, --Quartl (Diskussion) 09:37, 11. Mai 2012 (CEST)
Standardskalarprodukt
Verschoben aus Portal:Mathematik/Qualitätssicherung:
Etwas off-topic: bei der Gelegenheit könnte man auch über einen eigenen Artikel Standardskalarprodukt nachdenken, um den Artikel Skalarprodukt (immerhin einer der meistaufgerufenen Mathe-Artikel) etwas zu entlasten. Als wohl äquivalenten Begriff dazu gäbe es Euklidisches Skalarprodukt. Viele Grüße, --Quartl (Diskussion) 08:44, 9. Mai 2012 (CEST)
- Gehört eigentlich nicht hierher, trotzdem:
- Bei dem Lemma "Euklidisches Skalarprodukt" hätte ich große Bauchschmerzen. Schließlich ist jeder endlichdimensionale reelle Vektorraum mit Skalarprodukt ein euklidischer Vektorraum. Was soll am Standardskalarprodukt besonders "euklidisch" sein? Jedenfalls nicht die euklidische Struktur des so entstehenden Raums, denn diese ist allen euklidischen Vektor- und Punkträumen gemeinsam. Was soll denn in diesem Artikel genau stehen? Und was würdest du aus dem Skalarprodukt herausnehmen? --Digamma (Diskussion) 10:03, 9. Mai 2012 (CEST)
- Inhaltlich würde ich die Abschnitte Skalarprodukt#Das Standardskalarprodukt im Rn und Skalarprodukt#Das Standardskalarprodukt im Cn nach Standardskalarprodukt (nicht Euklidisches Skalarprodukt) auslagern. Der Artikel hätte immerhin knapp 40 interne Links. Viele Grüße, --Quartl (Diskussion) 11:39, 9. Mai 2012 (CEST)
- Auslagern heißt natürlich hier mit Verweis auf den Hauptartikel kurz zusammenzufassen. Viele Grüße, --Quartl (Diskussion) 11:41, 9. Mai 2012 (CEST)
- Auch der Abschnitt Skalarprodukt#Matrixdarstellung könnte da mit rein. Viele Grüße, --Quartl (Diskussion) 11:47, 9. Mai 2012 (CEST)
Also als neue Struktur:
- Im euklidischen Raum
- Geometrische Definition und Notation
- ...
- Allgemeine Definition
- Beispiele
- Standardskalarprodukt im Rn und Cn
- Gewichtete Skalarprodukte im Rn und Cn
- Hilbert-Schmidt-Skalarprodukt auf Matrizen
- L2-Skalarprodukt auf Funktionen
- Eigenschaften
- Norm, Winkel und Orthogonalität
Viele Grüße, --Quartl (Diskussion) 11:56, 9. Mai 2012 (CEST)
- Ich sehe eine schrittweise Abstraktion vom geometrisch definierten Skalarprodukt im euklidischen Raum über das Standardskalarprodut zur allgemeinen Definition eines Skalarprodukts. Das spricht für mich gegen eine Auslagerung. Man kann die in der allgemeinen Definition geforderten Eigenschaften aber natürlich auch aus dem geometrisch definierten motivieren. Ich sehe aber einerseits eine enge Klammer zwischen dem euklidischen Skalarprodukt und dem Standardskalarprodukt, weil man ja doch in der Regel in kartesischen Koordinaten rechnet. Andererseits aber auch zwischen dem Standardskalarprodukt und dem allgemeinen.
- Eine sinnvolle Aufteilung wäre für mich eher zwischen dem geometrischen Skalaprodukt einerseits und dem abstrakten andererseits. Der erstere Artikel müsste aber natürlich die Koordinatendarstellung enthalten und damit das Standardskalarprodukt zumindest im . Und der letztere natürlich das Standardskalarprodukt im als Beispiel. Bei dieser Aufteilung sehe ich aber beim allgmeinen Fall eine starke Redundanz zu Prähilbertraum.
- Bei der von dir vorgeschlagenen Aufteilung: Der Abschnitt "Das Standardkskalarprodukt im " ist relativ kurz. Wie würdest du ihn weiter ausbauen? Der neue Artikel müsste auf jeden Fall die Eigenschaften enthalten, außerdem die Definition von Orthogonalität, Norm und Winkel. Die Matrixdarstellung gehört eigentlich zum allgemeinen Fall.
- Beim nochmaligen Nachdenken: Für jemanden, der keine ausführliche Ausarbeitung zum Thema lesen möchte, sondern vor allem eine Definition des Standardskalarprodukts, wäre ein Artikel Standardskalarprodukt wohl tatsächlich sinnvoll.
- Was das Argument mit der Zahl der Links betrifft: Der Artikel Skalarprodukt selbst hat ca. 300 interne Links. --Digamma (Diskussion) 13:22, 9. Mai 2012 (CEST)
- So wie ich es sehe sind in diesem Artikel mehrere Themenbereiche für den Leser vereint:
- das geometrische Skalarprodukt im R3
- das Standardskalarprodukt im Rn und Cn
- das gewichtete Skalarprodukt im Rn und Cn
- das allgemeine Skalarprodukt auf reellen oder komplexen Vektorräumen
- Da die Bereiche in natürlicher Weise aufeinander aufbauen und immer stärker abstrahieren, kann man sie gut in einem Artikel vereinen und ich hatte jetzt auch a priori nicht vor, den Artikel komplett zu zerschlagen. Insgesamt weist der Artikel aber eine Menge interner Redundanz (Eigenschaften, Norm/Winkel/Orthogonalität, Standardskalarprodukt) auf, die man evtl. abschwächen kann.
- An eine Auftrennung zwischen dem Skalarprodukt auf dem R3 und dem abstrakten Skalarprodukt hatte ich auch schon gedacht, das löst aber das "Problem" mit dem Linkziel Standardskalarprodukt nicht. Außerdem sehe ich die Begriffe in etwa als gleichwertig an und man bräuchte ein neues Lemma und mindestens eine etwas unschöne BKL II der Art
- Vielleicht sollten wir aber den Ansatz trotzdem nicht aus den Augen verlieren. Die Redundanz mit dem Artikel Prähilbertraum könnte man verringern, wenn man die Definition und Eigenschaften des Skalarprodukts rauszieht, so wie wir das bei Normierter Raum und Norm (Mathematik) auch gemacht haben.
- Zurück zum Thema. Für die Abstraktion vom geometrischen (R3) zum allgemeinen Skalarprodukt braucht man jedenfalls den Zwischenschritt über den Rn nicht unbedingt. Die Klammer liefert ja bereits der (erste) Abschnitt Skalarprodukt#Eigenschaften. Die Matrixdarstellung am Ende hängt auch, denn hier geht es wieder um einen Spezialfall (endlichdimensionaler Vektorraum) des allgemeinen Falls. Im Artikel Standardskalarprodukt könnte sie sich aber mit der Message "Jedes Skalarprodukt im Kn lässt sich durch geeignete Basiswahl als Standardskalarprodukt darstellen" gut machen. Oder man schreibt einen eigenen Artikel zum gewichteten Skalarprodukt.
- Die Links hatte ich nur angeführt um zu zeigen, dass der Begriff „Standardskalarprodukt“ ein sinnvolles Lemma wäre. Da in diesem Artikel der reelle und komplexe Fall separat aufgeführt werden, ist das Linkziel von Standardskalarprodukt ja auch nicht immer so ganz klar und eine BKL zwischen dem reellen und dem komplexen Fall wäre auch doof. Viele Grüße, --Quartl (Diskussion) 14:35, 9. Mai 2012 (CEST)
- Gut, einverstanden. Aber die Matrixdarstellung sollte wirklich hier drin bleiben. Das ist zwar ein Spezialfall, nämlich dass der Vektorraum endlichdimensional ist, aber für diese Klasse ist es ganz allgemeine Aussage. Für mich ist das wichtig im Zusammenhang mit Riemannschen Metriken. Diese werden ja in der Regel dadurch angegeben, dass man bezüglich einer Basis die Gramsche Matrix angibt. --Digamma (Diskussion) 16:08, 9. Mai 2012 (CEST)
- Ok, wird aber etwas dauern. Viele Grüße, --Quartl (Diskussion) 16:34, 9. Mai 2012 (CEST)
- So, der Artikel Standardskalarprodukt ist jetzt da und ich habe diesen Artikel entsprechend etwas gekürzt. Den neuen Artikel kann man sicher noch weiter ausbauen, ich muss aber erstmal nachdenken, welche Eigenschaften das Standardskalarprodukt hat, die ein allgemeines Skalarprodukt nicht hat. Viele Grüße, --Quartl (Diskussion) 15:02, 10. Mai 2012 (CEST)
- Also wenn ich geschrieben hätte, "das wird aber etwas dauern", dann würden Tage oder Wochen vergehen und nicht nur wenige Stunden. Ist super geworden. Ein paar Anmerkungen habe ich noch zu Standardskalarprodukt, die werde ich dort auf der Diskussionsseite anbringen. --Digamma (Diskussion) 19:54, 10. Mai 2012 (CEST)
- Danke für das Lob. Ich wusste vorher nicht, ob und wieviel Zeit ich finden würde. Es ging aber dann doch schneller als erwartet. Viele Grüße, --Quartl (Diskussion) 21:39, 10. Mai 2012 (CEST)
Grafiken
Hallo Quartl, um auf dein Angebot in Diskussion:Orthogonalprojektion zurückzukommen: Ich fände es schön, wenn du die Grafiken hier durch schönere (bunt, schönere Pfeile, schönere Schrift) ersetzen könntest. Im Prinzip können sie einfach genauso sein wie die bisherigen von Benutzer:Joachim Mohr. Bei den Beispielen kann die Rechnung auch gerne aus den Bildern ausgelagert werden. Viele Grüße, --Digamma (Diskussion) 21:15, 5. Jul. 2012 (CEST)
- Ok, ich schaue mal was sich machen lässt. Ein paar der Grafiken würden sich auch sicher in verwandten Artikeln gut machen. Viele Grüße, --Quartl (Diskussion) 09:03, 6. Jul. 2012 (CEST)
- Hallo Digamma, ich habe gerade die erste mal besser gemacht. Was hältst du davon: http://www.martin-thoma.de/wikipedia/ ?
- Ich habe es mit tikz gemacht, kann also leicht änderungen hinzufügen. Soll ich die SVG oder die Gif hochladen? Eigentlich finde ich die GIF-Datei schöner. --Martin Thoma 14:29, 6. Jul. 2012 (CEST)
- Das SVG wäre in jedem Fall vorzuziehen, aber es gibt scheinbar Probleme bei der Darstellung der Pfeile. Viele Grüße, --Quartl (Diskussion) 17:48, 6. Jul. 2012 (CEST)
- Bei den Pfeilen sehe ich bei mir kein Problem. Ich finde das alpha nicht so schön wie in der GIF-Version. Also soll ich mal alle Bilder mit tikz machen? --Martin Thoma 18:20, 6. Jul. 2012 (CEST)
- Sowohl FF als auch IE zeigt bei mir die Pfeile falsch an. Kannst du nicht evtl. einen anderen Font einstellen? Von mir aus kannst du gerne alle Bilder nachzeichnen, wenn du willst. Viele Grüße, --Quartl (Diskussion) 18:29, 6. Jul. 2012 (CEST)
- Das ist interessant. Bei mir zeigen sowohl FF als auch Chrome die Pfeile richtig an. Mal schauen wie es aussieht, wenn ich es hochlade. --Martin Thoma 18:32, 6. Jul. 2012 (CEST)
- Sieht bei mit gut aus. Viele Grüße, --Quartl (Diskussion) 18:55, 6. Jul. 2012 (CEST)
- Das ist interessant. Bei mir zeigen sowohl FF als auch Chrome die Pfeile richtig an. Mal schauen wie es aussieht, wenn ich es hochlade. --Martin Thoma 18:32, 6. Jul. 2012 (CEST)
- Sowohl FF als auch IE zeigt bei mir die Pfeile falsch an. Kannst du nicht evtl. einen anderen Font einstellen? Von mir aus kannst du gerne alle Bilder nachzeichnen, wenn du willst. Viele Grüße, --Quartl (Diskussion) 18:29, 6. Jul. 2012 (CEST)
- Bei den Pfeilen sehe ich bei mir kein Problem. Ich finde das alpha nicht so schön wie in der GIF-Version. Also soll ich mal alle Bilder mit tikz machen? --Martin Thoma 18:20, 6. Jul. 2012 (CEST)
- Das SVG wäre in jedem Fall vorzuziehen, aber es gibt scheinbar Probleme bei der Darstellung der Pfeile. Viele Grüße, --Quartl (Diskussion) 17:48, 6. Jul. 2012 (CEST)
Wow, also ich frage mich, warum ich jemals etwas anderes als Tikz verwendet habe. Das ist ein Unterschied wie Tag und Nacht:
Den Rest mache ich morgen, wenn ich die Zeit finde. --Martin Thoma 19:36, 6. Jul. 2012 (CEST)
- Sieht wirklich klasse aus. Ein paar Kleinigkeiten zum zweiten Bild:
- Der rechte Winkel ist bei mir keiner. Wird das Bild irgendwie verzerrt?
- Es wäre schön, wenn du den rechten Winkel markieren könntest.
- Ich fände es besser, wenn die Farbe von näher bei der Farbe von (blau) als bei (rot) wäre, z.B. ein deutlich bläuliches Violett.
- --Digamma (Diskussion) 19:43, 6. Jul. 2012 (CEST)
- Damit sich die Leser nicht wegen des rechten Winkels beschweren habe ich die von Digamma vorgeschlagenen Verbesserungen (mit Inkscape) vorgenommen und eine neue Version drübergeladen. Bei Nichtgefallen einfach revertieren. Viele Grüße, --Quartl (Diskussion) 20:24, 6. Jul. 2012 (CEST)
- Wow, das ging ja fix. Wenn das so schnell und einfach geht, schieb ich noch ein paar Wünsche nach:
- Es wäre schön, wenn die beiden Vektoren deutlich unterschiedlich lang wären (z.B. länger).
- Kann man den Radius des Winkelbogens etwas kleiner machen? Das grüne Feld ist sehr dominant.
- --Digamma (Diskussion) 20:30, 6. Jul. 2012 (CEST)
- Ihr Wunsch sei mir Befehl :-). Viele Grüße, --Quartl (Diskussion) 20:42, 6. Jul. 2012 (CEST)
- Das wollte ich auch gerade schreiben^^ - naja, ich hab es direkt im LaTeX-Code geändert, so ist es schöner. Der rechte Winkel sollte nun auch wirklich 90° haben :-) Grüße, --Martin Thoma 20:44, 6. Jul. 2012 (CEST)
- Vektor a wurde gestreckt. --Martin Thoma 20:47, 6. Jul. 2012 (CEST)
- Wow, das ging ja fix. Wenn das so schnell und einfach geht, schieb ich noch ein paar Wünsche nach:
- Damit sich die Leser nicht wegen des rechten Winkels beschweren habe ich die von Digamma vorgeschlagenen Verbesserungen (mit Inkscape) vorgenommen und eine neue Version drübergeladen. Bei Nichtgefallen einfach revertieren. Viele Grüße, --Quartl (Diskussion) 20:24, 6. Jul. 2012 (CEST)
Ich bin gerade dabei, File:Skalarprodukt3.gif zu TeX-en. Was soll "a=5 b=3" bedeuten? Soll das die Länge der Vektoren a und b sein? Müsste das nicht im Betrag stehen und, um eine einheitliche Notation zu verwenden, a und b Vektor-Pfeile bekommen? --Martin Thoma 20:58, 6. Jul. 2012 (CEST)
- Es ist denke ich nicht so günstig, längere Formeln im Bild zu haben, siehe den ersten Beitrag von Digamma. Viele Grüße, --Quartl (Diskussion) 21:01, 6. Jul. 2012 (CEST)
- Das ist mein aktueller Stand: http://www.martin-thoma.de/wikipedia/dot-product-3.svg für das erste Bild aus File:Skalarprodukt3.gif - was sollte ich anders machen? --Martin Thoma 21:15, 6. Jul. 2012 (CEST)
- Erst mal vielen Dank. Ich habe mir gerade Inkscape installiert, vielleicht kann ich dann ja zukünftig selber Grafiken erstellen oder editieren.
- Zu Bild 3: Die Beträge der Vektoren werden in diesem Teil des Artikels wie in der Physik und teilweise der Schulmathematik alternativ zu den Betragsstrichen auch einfach durch die lateinischen Buchstaben ohne Vektorpfeil bezeichnet: .
- Den Text kann man weglassen. Den kann man in die Bildunterschrift schreiben, oder man ordnet das ganze in einer Tabelle an und schreibt den Text neben, unter oder über die Bilder. --Digamma (Diskussion) 21:36, 6. Jul. 2012 (CEST)
- Gern geschehen. Zu Inkscape: Ich habe alle Bilder komplett mit LaTeX erstellt. Inkscape benutze ich nur automatisiert über die Kommandozeile, um die PDFs in SVGs zu konvertieren. Hier sind noch ein paar Bilder, um dich von TikZ zu überzeugen: Complex LaTeX visualizations --Martin Thoma 22:44, 6. Jul. 2012 (CEST)
- Ich denke drüber nach. Mein TeX ist ziemlich eingerostet. Aber apropos TeX: Die Beschriftung ist mit TeX gemacht, oder? Ein paar Anmerkungen zum Formelsatz: Einheitenzeichen schreibt man aufrecht (z. B.
5\, \mathrm{m}ergibt ), entsprechendes gilt für den Cosinus (\cosstattcos).- Oh, vielen Dank, das vergesse ich immer wieder. Ich hab es für File:Dot-product-4.svg nachgetragen. --Martin Thoma 08:57, 7. Jul. 2012 (CEST)
- Ich denke drüber nach. Mein TeX ist ziemlich eingerostet. Aber apropos TeX: Die Beschriftung ist mit TeX gemacht, oder? Ein paar Anmerkungen zum Formelsatz: Einheitenzeichen schreibt man aufrecht (z. B.
- Gern geschehen. Zu Inkscape: Ich habe alle Bilder komplett mit LaTeX erstellt. Inkscape benutze ich nur automatisiert über die Kommandozeile, um die PDFs in SVGs zu konvertieren. Hier sind noch ein paar Bilder, um dich von TikZ zu überzeugen: Complex LaTeX visualizations --Martin Thoma 22:44, 6. Jul. 2012 (CEST)
- Das ist mein aktueller Stand: http://www.martin-thoma.de/wikipedia/dot-product-3.svg für das erste Bild aus File:Skalarprodukt3.gif - was sollte ich anders machen? --Martin Thoma 21:15, 6. Jul. 2012 (CEST)
Hallo Martin, noch eine Bitte. Wir haben damals beim Überarbeiten des Artikels den Winkel zwischen und nur deshalb genannt, weil er in den von Joachim Mohr gelieferten Grafiken so hieß. Davor hieß er , was mir besser gefällt. Dies ist auch die übliche Bezeichnung in der Physik (deshalb fiel mir das gerade bei Grafik Nr. 4 auf), und weiter unten im Artikel, bei der Winkeldefinition in allgemeinen Vektorräumen mit Skalarprodukt heißt er auch noch . Wäre es möglich, das zu ändern? Ich ändere das dann im Text. Viele Grüße, --Digamma (Diskussion) 09:52, 7. Jul. 2012 (CEST)
- Hi Digamma, kein Problem, ich habe nun durch in File:Dot-product-4.svg ersetzt. --Martin Thoma 11:24, 7. Jul. 2012 (CEST)
- Danke. Ich dachte allerdings auch an die andern Grafiken, also auch Nr. 1 und 2. Eine Anmerkung noch zum letzten Bild (Nr. 6): Hier wäre es schön, wenn das Koordinatensystem mit eingezeichnet wäre. Gemeint ist ja nicht einfach eine Orthonarmalbasis, sondern die Standardbasis bezüglich eines gegebenen kartesischen Koordinatensystems. --Digamma (Diskussion) 12:28, 7. Jul. 2012 (CEST)
- So in etwa? Viele Grüße, --Quartl (Diskussion) 13:25, 7. Jul. 2012 (CEST)
- Danke. Ich dachte allerdings auch an die andern Grafiken, also auch Nr. 1 und 2. Eine Anmerkung noch zum letzten Bild (Nr. 6): Hier wäre es schön, wenn das Koordinatensystem mit eingezeichnet wäre. Gemeint ist ja nicht einfach eine Orthonarmalbasis, sondern die Standardbasis bezüglich eines gegebenen kartesischen Koordinatensystems. --Digamma (Diskussion) 12:28, 7. Jul. 2012 (CEST)
- Da Quartl schneller war, lass ich Bild 6 mal so wie es ist. Bild 1 und Bild 2 hat nun auch ein anstelle des . --Martin Thoma 14:33, 7. Jul. 2012 (CEST)
- Fein, ich habe den Text entsprechend angepasst. Ich habe bei mir eben den Computer Modern Font von LaTeX für Inkscape installiert, um den Font an den Text anzugleichen. Das klappt im SVG ganz gut, aber der Thumbnailer von Commons kennt den Font offenbar nicht und ersetzt ihn durch einen hässlicheren. Bei deinen Grafiken sind die Labels schön, aber sie sind nicht als Schrift, sondern als Grafik eingebunden, was die Nachnutzung erschwert (man kann nicht einfach alpha durch phi tauschen). Ich weiß auch nicht was hier eine gute Lösung ist, vielleicht ist das eine Frage für FzW. Viele Grüße, --Quartl (Diskussion) 15:49, 7. Jul. 2012 (CEST)
- Ich denke, es wäre für die Nachnutzung am besten, wenn man den LaTeX-Code bereitstellen würde, z.B. so: File:Homomorphismen-venn-diagramm.png. Ich habe für jedes LaTeX-Dokument ein Makefile, mit dem ich die PDF, SVG bzw. (animierte) GIF automatisch erstelle. Hier ist ein Blog-Artikel, in dem ich meine Vorlagen zur Verfügung stelle. --Martin Thoma 17:25, 7. Jul. 2012 (CEST)
- Fein, ich habe den Text entsprechend angepasst. Ich habe bei mir eben den Computer Modern Font von LaTeX für Inkscape installiert, um den Font an den Text anzugleichen. Das klappt im SVG ganz gut, aber der Thumbnailer von Commons kennt den Font offenbar nicht und ersetzt ihn durch einen hässlicheren. Bei deinen Grafiken sind die Labels schön, aber sie sind nicht als Schrift, sondern als Grafik eingebunden, was die Nachnutzung erschwert (man kann nicht einfach alpha durch phi tauschen). Ich weiß auch nicht was hier eine gute Lösung ist, vielleicht ist das eine Frage für FzW. Viele Grüße, --Quartl (Diskussion) 15:49, 7. Jul. 2012 (CEST)
- Da Quartl schneller war, lass ich Bild 6 mal so wie es ist. Bild 1 und Bild 2 hat nun auch ein anstelle des . --Martin Thoma 14:33, 7. Jul. 2012 (CEST)
Gerade habe ich das letzte pixel-Bild als valides SVG mit Tikz erstellt:
Ich wäre froh, wenn jemand anderes die einbinden könnte. Anmerkungen sind wie immer willkommen (z.B.: Gibt es nicht ein "Symbol" für Parallelität? Durch beide Vektoren zwei kurze, parallele Striche oder etwas in der Art?). Grüße, --Martin Thoma 19:32, 9. Jul. 2012 (CEST)
- Sehr schön. Ich habe es mal mit einer Gallerie versucht, so sind nur die Formeln etwas klein. Könntest du die drei Bilder evtl. auf die gleiche Leinwandgröße (oder zumindest das gleiche Seitenverhältnis) bringen, damit die Längen übereinstimmen? Vielleicht wäre es dabei günstiger, den Parallelfall statt vertikal horizontal zu zeichen? Viele Grüße, --Quartl (Diskussion) 19:52, 9. Jul. 2012 (CEST)
- Hallo Quartl,
- ich habe das erste Bild nun gekippt und das Seitenverhältnis auf 1:1 gebracht. Leider habe ich noch nicht herausgefunden, wie man die Leinwandgröße in LaTeX festsetzt, ohne dass das Bild verzerrt wird. Grüße, --Martin Thoma 21:22, 9. Jul. 2012 (CEST)
- Man kann die Leinwandgrößen in den SVGs auch noch nachträglich angleichen, soll ich? Vorteilhaft wäre, wenn der Vektor a immer in die gleiche Richtung zeigt, dann muss man nicht rumrechnen ;-). Die Alternative wäre, alle drei Bilder in eines zu packen. Viele Grüße, --Quartl (Diskussion) 21:32, 9. Jul. 2012 (CEST)
- PS: Eine WP-Seite neu rendern geht auch ohne Dummy-Edits: [2]. Viele Grüße, --Quartl (Diskussion) 21:34, 9. Jul. 2012 (CEST)
- Ich habe nun herausgefunden, wie es mit LaTeX geht. Ist das wirklich so gewünscht? Falls ja, änder ich morgen noch das dritte Bild.
- Soll ich die beiden Vektoren in File:Dot-product-3.1.svg "hinlegen" (a unten)? --Martin Thoma 21:57, 9. Jul. 2012 (CEST)
- Ja, fände ich besser. Ideal wäre, wenn alle drei Bilder die gleiche Leinwandgröße hätten (also die von Nr. 2 in der alten Version), wobei der Vektor a immer die gleiche Position im Bild besitzt, sodass nur b variiert. Viele Grüße, --Quartl (Diskussion) 22:02, 9. Jul. 2012 (CEST)
- PS: als Verdeutlichung: mit "gleiches Seitenverhältnis" meinte ich die Bilder untereinander, nicht ein quadratisches Format. Also beispielsweise alle drei Bilder auf 1,41:1 (122 × 86 px). Ich kann das aber auch nachträglich noch anpassen. Viele Grüße, --Quartl (Diskussion) 22:24, 9. Jul. 2012 (CEST)
- Gedreht ist es schonmal, das Seitenverhältnis passt noch nicht ganz. --Martin Thoma 07:47, 10. Jul. 2012 (CEST)
- Sieht gut aus. Ich habe die Seitenverhältnisse noch ganz leicht aneinander angepasst. Viele Grüße, --Quartl (Diskussion) 09:40, 10. Jul. 2012 (CEST)
- Ich habe bei mir MathJax eingeschaltet. Da sind die Formeln länger als die GIFs, weil MathJax das \scritpstyle am Anfang ignoriert (zu Recht). Die Folge: Die Formeln unter den Bildern passen nicht in die Zeile, sie werden hinten abgeschnitten. Kann man die Bilder breiter machen, oder die Breite variabel? --Digamma (Diskussion) 20:37, 10. Jul. 2012 (CEST)
- Hm, vielleicht wäre ein anderes Layout doch besser: die drei Rechenbeispiele als Liste und die Bilder nebendran oder drunter? Viele Grüße, --Quartl (Diskussion) 06:14, 11. Jul. 2012 (CEST)
- Ich habe die Größe mal geändert. Passt das nun? --Martin Thoma 06:57, 11. Jul. 2012 (CEST)
- Ok, so geht es auch. Viele Grüße, --Quartl (Diskussion) 07:06, 11. Jul. 2012 (CEST)
- Ich habe bei mir MathJax eingeschaltet. Da sind die Formeln länger als die GIFs, weil MathJax das \scritpstyle am Anfang ignoriert (zu Recht). Die Folge: Die Formeln unter den Bildern passen nicht in die Zeile, sie werden hinten abgeschnitten. Kann man die Bilder breiter machen, oder die Breite variabel? --Digamma (Diskussion) 20:37, 10. Jul. 2012 (CEST)
- Sieht gut aus. Ich habe die Seitenverhältnisse noch ganz leicht aneinander angepasst. Viele Grüße, --Quartl (Diskussion) 09:40, 10. Jul. 2012 (CEST)
- Gedreht ist es schonmal, das Seitenverhältnis passt noch nicht ganz. --Martin Thoma 07:47, 10. Jul. 2012 (CEST)
Redundanz in der Axiomatik
Die Linearität im zweiten Argument folgt aus der Linearität/Semilinearität im ersten Argument und der Symmetrie/Hermitizität. Bei vielen Autoren wird sie daher in der Definition weggelassen (wie beispielsweise im Rudin, der als Literatur angegeben wird). Wenn wir im Artikel wirklich eine axiomatische Charakterisierung wollen, sollten wir sie auch weglassen und in den Anmerkungen darauf hinweisen. Viele Grüße, --Quartl (Diskussion) 20:09, 7. Jul. 2013 (CEST)
- Ich finde, man sollte sie nicht weglassen. Für mich ist ein Skalarprodukt eine Bilinearform/Sesquilinearform, die zusätzlich noch symmetrisch bzw. hermitesch ist. Ich würde deshalb eher umgekehrt in den Anmerkungen darauf hinweisen, dass die Semilinearität im ersten Argument aus der Linearität im zweiten und der Hermitizität folgt. (Auf gar keinen Fall würde ich die Linearität im zweiten Argument aus der Semilinearität im ersten folgern.)
- Es gibt zahlreiche Beispiele für Axiomatisierung mit Redundanz. Z.B. werden die Axiome für eine Boolesche Algebra in der Regel redundant formuliert um die Symmetrie zwischen den zwei Verknüpfungen deutlich zu machen. Auch bei den Gruppenaxiomen wird in der Regel gefordert, dass das neutrale Element linksneutral und rechtsneutral ist und die inversen Elemente linksinvers und rechtinvers, obwohl linksneutral und linksinvers genügt. --Digamma (Diskussion) 00:20, 8. Jul. 2013 (CEST)
- Ok, wie wäre es mit folgenden Anmerkungspunkt:
- Die beiden angegebenen Axiomensysteme sind redundant. Im reellen Fall folgt aufgrund der Symmetrie die Linearität im ersten Argument aus der Linearität im zweiten Argument (und umgekehrt). Analog dazu folgt im komplexen Fall aufgrund der Hermizität die Semilinearität im ersten Argument aus der Linearität im zweiten Argument (und umgekehrt).
- Viele Grüße, --Quartl (Diskussion) 06:23, 8. Jul. 2013 (CEST)
- Ok, wie wäre es mit folgenden Anmerkungspunkt:
- Ja, den Vorschlag finde ich gut. --Digamma (Diskussion) 08:11, 8. Jul. 2013 (CEST)
Eigenschaften
Angeblich sollen die Distributivgesetze der Additivität entsprechen, das stimmt aber nicht:
Das Skalarprodukt müsste, um additiv sein zu können, eine einstellige Funktion sein mit
Additiv sind aber nur die Translationen und denn:
Das Skalarprodukt ist folglich nicht additiv. --RPI (Diskussion) 12:51, 30. Aug. 2013 (CEST)
Das gleiche gilt für die angebliche Homogenität, denn es müsste gelten:
Tatsächlich sind aber wieder nur die Translationen homogen:
und nicht das Skalarprodukt. --RPI (Diskussion) 13:25, 30. Aug. 2013 (CEST)
- Man spricht von "additiv im ersten Argument" bzw. "additiv im zweiten Argument" und von "linear im ersten bzw. zweiten Argument". Zusammenfassend von "linear in jedem Argument". Das meint genau das, dass die Abbildungen, die man erhält, wenn man in das rechte (bzw. linke) Argument einen Vektor fest einsetzt, also das was du als "Translation" bezeichnest, linear sind. --Digamma (Diskussion) 12:14, 2. Sep. 2013 (CEST)
Der Name "inneres Produkt"
Wieso heißt das Skalarprodukt eigentlich "inneres Produkt", während das Kreuzprodukt als "äußeres Produkt" bezeichnet wird? Man könnte - was man hier sicherlich nicht tut - die Bezeichungen darauf beziehen, ob die Verknüpfung eine innere ist oder nicht; täte man dies aber, so wäre keines der beiden Produkte wirklich ein inneres, weil das "innere" Produkt nicht wieder einen Vektor, sondern einen Skalar ergibt und das äußere einen Tensor; und im Spezialfall <\math>\R^3</math> müsste man sogar die Begrifflichkeiten umtauschen, denn da ist das äußere Produkt immerhin ein Pseudovektor.
Also, so stammen diese Bezeichnungen her?--Slow Phil (Diskussion) 19:24, 31. Okt. 2013 (CET)
- Schau mal: Hier gibt's gleich zwei Erklärungen, such dir eine aus :) -- HilberTraum (Diskussion) 19:46, 31. Okt. 2013 (CET)
Darstellung
Weiß irgendjemand warum das Scalarprudukt mit einem * gekennzeichnet wird? Ich finde das sehr verwirrend.
wieso wird nicht <a,b> verwendet, statt a*b
ich fände das deutlich übersichtlicher. (nicht signierter Beitrag von 93.200.70.63 (Diskussion) 00:02, 22. Jan. 2014 (CET))
- finde ich persönlich auch besser. Dies wird ja im Abschnitt allgemeine Vektorräume auch so benutzt. --V4len (Diskussion) 07:46, 22. Jan. 2014 (CET)
- Wir müssen und schon an den jeweiligen Konventionen orientieren. In der Geometrie wird eben sehr häufig die Darstellung verwendet und davon handelt der erste Teil des Artikels. Erst in der linearen Algebra und der Funktionalanalysis nimmt man dann meist die Notation oder . Ich finde die Darstellung so wie sie derzeit ist gut.
- Das einzige, woran man evtl. denken könnte, wäre eine Aufteilung des Artikels in den Teil Skalarprodukt im euklidischen Raum (2D/3D) mit ersterer Notation und einen Teil Skalarprodukt in der linearen Algebra mit letzterer. Was dafür sprechen würde wären direktere Linkziele, denn wenn man auf Skalarprodukt verlinkt ist nicht klar, ob die geometrische oder algebraische Variante gemeint ist. Dagegen spricht, dass es ohne übermäßige Begriffsbildung kein geeignetes Lemma für die Auslagerung gibt und dass inhaltlich Zusammengehöriges normalerweise in einem Artikel abgehandelt wird. Aber ein ähnliches Problem haben wir auch schon bei den den Vektoren (Vektor vs. Vektorraum). Viele Grüße, --Quartl (Diskussion) 08:13, 22. Jan. 2014 (CET)
Und wieso existiert in der Geometrie eine andere Notation? ich kenn das nur aus der linearen Algebra. Letztendlich bleibt das Standardskalarprodukt doch eben das Standardskalarprodukt, egal ob man es mittels Winkel und längen oder mit Vektorrechnung berechnet.
Vor allem bei "Orthogonalität und orthogonale Projektion" finde ich es sehr verwirrend, da man nicht auf den ersten blick sieht wann von einem Scalarprodukt die Rede ist und wann z.B. 2 Skalare oder ein Skalar mit einem Vektor mulitpliziert wird/werden.
Klar kann man logisch schlussfolgern und gucken was ein Vektor und was ein Skalar ist, das widerspricht aber der Übersichtlichkeit.
da die Rechenregeln für Multiplikation nicht für das Skalarprodukt gelten:
Beispiel:
a=(1,0)T
b=(0,1)T
<a,b> * <a,b> = 0 * 0 = 0 (richtig)
<a,b> * <a,b> = a*b * a*b = a*a * b*b = <a,a> * < b,b > = 1 * 1 = 1 (falsch)
Finde ich diese Notation generell Unsinnig, hat diese Notation in der Geometrie irgendwelche Vorteile?
Grüße Siggi (nicht signierter Beitrag von 93.200.68.14 (Diskussion) 19:50, 23. Jan. 2014 (CET))
- Mit der Argumentation dürfte man Matrizenmultiplikationen nicht als Multiplikation bezeichnen. Nicht jede Multiplikation ist kommutativ. In der Geometrie wird das Skalarprodukt nuneinmal als Multiplikation geschrieben. --V4len (Diskussion) 21:43, 23. Jan. 2014 (CET)
- Die Schreibweise mit Multiplikationspunkt ist im Übrigen nicht nur in der Geometrie üblich, sondern auch in der Physik beim Skalarprodukt von vektoriellen Größen (nicht in der Quantenmechanik, wo es ja auch nicht um geometrische Vektoren geht). Zum Beispiel gilt für die von der (konstanten) Kraft längs des Wegs verrichtete Arbeit . --Digamma (Diskussion) 22:13, 23. Jan. 2014 (CET)
stimmt beides, unübersichtlich finde ich es dennoch, genauso wie ich diese Flut an Vektorpfeilen über den Buchstaben teilweise unnötig/überladen finde, aber das finden andere vlt. übersichtlicher, hat wohl alles Vor- und Nachteile. (nicht signierter Beitrag von 93.200.68.14 (Diskussion) 01:22, 24. Jan. 2014 (CET))
"durchgängig"
- Im Artikel: "während in der Physik durchgängig die obige Version benutzt wird"
- In Heisenbergsche Unschärferelation: "Hier und im Weiteren wird der Darstellung von John von Neumann und den Gepflogenheiten der Analysis gefolgt, wonach das Skalarprodukt in der ersten Komponente linear und in der zweiten Komponente antilinear ist. In der Physik findet man oft die entgegengesetzte Praxis."
Also "durchgängig" (= immer, ausnahmslos) oder nur "oft"?
Zum Widerlegen der Aussage würde ein Physik-Text mit normaler Notation ausreichen, während ein Beweisen der Aussage unmöglich sein sollte.
Nebenbei: Nutzen Physiker nicht auch eher die Form "<*|*>" statt "<*,*>", sodaß man im Artikel eher die normale, gängige Variante des Skalarprodukts erwähnen sollte (d.i. linear im 1. und semi-/antilinear im 2. Argument)?
Nebenbei 2: Sollte erwähnt werden, daß es auch die Schreibweise mit runden statt spitzen Klammern gibt?
-93.196.229.31 04:58, 17. Nov. 2013 (CET)
- Zum ersten Punkt: Ich habe nichts gegen eine schwächere Formulierung, wie z.B. "überwiegend". Ich selbst habe dazu keine Recherche beschrieben, es war aber der Tenor mehrerer Diskussionen hier und in anderen Artikeln, wie z.B. Prähilbertraum, Sesquilinearform. Vielleicht sollte man bei der Physik-Redaktion anfragen.
- Zum zweiten Punkt: Die in der Physik verwendete "Bra-Ket-Notation" unterscheidet sich von der hier verwendeten nicht nur dadurch, dass statt des Kommas ein senkrechter Strich verwendet wird. Bei der Bra-Ket-Notation sind die spitzen Klammern und der senkrechte Strich Bestandteile der beteiligten Vektoren.
- Zum dritten Punkt (Schreibweise mit runden Klammern): sehr gern, sei mutig. --Digamma (Diskussion) 10:08, 17. Nov. 2013 (CET)
- Ich habe "durchgängig" in "überwiegend" geändert und die alternativen Schreibweisen ergänzt. OK so? --Digamma (Diskussion) 19:00, 17. Nov. 2013 (CET)
- Die Bra-Ket-Notation ist - streng genommen - nicht mal ein Skalarprodukt, denn die Bra-Vektoren stammen aus dem Dualraum (sind also Funktionale) und die Ket-Vektoren sind normale Vektoren. Ein Bra-Ket ist also irgendwas zwischen einem Skalarprodukt und einer Dualen Paarung --PatrickC (Diskussion) 13:23, 22. Jul. 2014 (CEST)
Warum nur? :)
Ich mache Variationsprobleme und iterative LGS-Löser. Ich frage mich, ob es nicht auch sinnvolle Geometrien geben kann, die kein symmetrisches Skalarprodukt haben. Wieso also definiert man Skalarproduke als symmetrisch? Ich denke, ein Grund dafür sollte auch im Artikel ergänzt werden, sofern es ihn gibt. (nicht signierter Beitrag von 88.78.116.253 (Diskussion) 23:01, 19. Aug. 2014 (CEST))
- Ohne die Symmetrie hat man lediglich eine Bilinearform, die, wenn man auch noch auf die positive Definitheit verzichten möchte, auch indefinit sein kann. Die Symmetrie braucht man zum Beispiel für den Beweis der Cauchy-Schwarz-Ungleichung, aus der wiederum die Dreiecksungleichung der von dem Skalarprodukt abgeleiteten Norm folgt. Mit der Norm hat man dann auch eine Metrik und damit auch eine Topologie. Durch die Symmetrie (und die anderen Axiome) erhält man also einen ganzen Rattenschwanz von weiteren grundlegenden Eigenschaften. Wenn man statt der Symmetrie die Cauchy-Schwarz-Ungleichung als Axiom nimmt, erhält man ein semi-inneres Produkt mit ähnlichen Eigenschaften. Grüße, --Quartl (Diskussion) 07:36, 20. Aug. 2014 (CEST)
Definition des Skalarproduktes
Hallo 79.219.87.103,
Den im 1. Abschnitt von dir eingefügten Satz:
"Die obige Beziehung des Skalarprodukts kann elementargeometrisch mit Hilfe des Kosinussatzes hergeleitet werden."
habe ich wieder entfernt.
Er ist unverständlich, da noch gar keine Definition des Skalarprodukte erwähnt wird. Er könnte folgendermaßen lauten:
"Definiert man das Skarprodukt über die Koordinaten der Vektoren (siehe untere Beziehung), dann kann die obige Beziehung des Skalarprodukts elementargeometrisch mit Hilfe des Kosinussatzes hergeleitet werden."
Aber auch diesen Satz finde ich unpassen, da die "obige Beziehung" ja auch schon als Definition des Skalarproduktes im R^2 bzw, R^3 gewählt werden. --Joachim Mohr 08:06, 30. Jan. 2011 (CET)
positive definitheit
Unser Mathe-Prof hat bei der Definition von positiver Definitheit > 0 und nicht >= 0 verwendet, wer liegt denn nun richtig? -- 178.202.83.137 11:55, 15. Jan. 2012 (CET)
- in welcher definition genau? wie lautet die exakte definition deines profs? -- seth 22:02, 16. Jan. 2012 (CET)
- Für ist immer , das folgt aus der Bilinearität. Deshalb ist die richtige Bedingung:
- für .
- Das kann man aber auch so formulieren, wie es im Artikel steht:
- und
- genau dann, wenn .
- Ich weiß nicht, ob eine der beiden Formulierungen zu bevorzugen ist. --Digamma 22:02, 21. Jan. 2012 (CET)
OK, dann war es mein Fehler, scheint ja beides das selbe zu bedeuten. Schönen Dank :) -- 141.99.252.129 12:27, 30. Jan. 2012 (CET)
- Archivierung dieses Abschnittes wurde gewünscht von: --MartinThoma (Diskussion) 20:44, 10. Mai 2012 (CEST)
Andere Skalarprodukte
Unser Mathelehrer hat behauptet, jede Verknüpfung zwischen zwei Vektoren eines beliebigen Vektorraums, die die Eigenschaften des "gewöhnlichen" Skalarprodukts hat, sei ein Skalarprodukt. Beispiele hat er keine genannt, aber möglich sind solche Definition. Irgendwie fehlt so ein Hinweis darauf komplett im Artikel. Wenn nicht, dann gebt mir bitte einen Hinweis.
Und andere Frage: Warum sollen immer nur die reellen Zahlen und die komplexen Zahlen Grundlagen eines Vektorraums sein? Man kann doch fast beliebige Körper definieren, solange sie die geforderten Eigenschaften es eines Körpers erfüllen. Auf solchen Körpern können ebenfalls Vektorräume aufgebaut werden. Im Artikel ist immer Fallunterscheidung zwischen R und C gemacht, ohne Allgemeingültigkeit. --GelberBaron (Diskussion) 19:08, 21. Okt. 2014 (CEST)
- Sorry, ich war wohl etwas voreilig. Den ersten Teil nehme ich wieder zurück, es wird der Hinweis an einigen Stellen gegeben. Der zweite Teil bleibt dennoch: Warum ist der Artikel auf R und C beschränkt? --GelberBaron (Diskussion) 19:12, 21. Okt. 2014 (CEST)
- Vektorräume gibt es über beliebigen Körpern. Aber für Skalarprodukte muss die Bedingung für erfüllt sein. Das ergibt nur Sinn, wenn der Körper eine Anordnung besitzt, oder, wie im Fall komplexer Skalarprodukte immer in einer Teilmenge liegt, die so eine Anordnung besitzt. Endliche Körper und solche mit endlicher Charakteristik fallen damit schon mal weg. Man könnte nehmen, aber man könnte dann keine Länge (Norm) definieren, weil man in vielen Fällen in auch aus positiven Zahlen nicht die Wurzel ziehen kann (z.B. nicht aus 2). --Digamma (Diskussion) 20:05, 21. Okt. 2014 (CEST)
- Für einen Vektorraum über müsste man selbstverständlich ein anderes Skalarprodukt definieren. Für jeden Vektorraum, der sich von wesentlich unterscheidet (also keinen eineindeutige Zuordnung möglich ist, beispielsweise), müsste man ein anderes Skalarprodukt definieren. Das ist aber dennoch ein Skalarprodukt. Aber ich sehe, das wird haarspalterisch.
Unser Mathelehrer hat immer als Abbildung für einen Vektorraum über den Körper angegeben. Das könnte man im Artikel genauso machen, dann wäre es allgemein. Die Sache mit der Ordnung (wegen für ) kann man ja dazuschreiben.--GelberBaron (Diskussion) 12:41, 22. Okt. 2014 (CEST)
- Für einen Vektorraum über müsste man selbstverständlich ein anderes Skalarprodukt definieren. Für jeden Vektorraum, der sich von wesentlich unterscheidet (also keinen eineindeutige Zuordnung möglich ist, beispielsweise), müsste man ein anderes Skalarprodukt definieren. Das ist aber dennoch ein Skalarprodukt. Aber ich sehe, das wird haarspalterisch.
- Vektorräume gibt es über beliebigen Körpern. Aber für Skalarprodukte muss die Bedingung für erfüllt sein. Das ergibt nur Sinn, wenn der Körper eine Anordnung besitzt, oder, wie im Fall komplexer Skalarprodukte immer in einer Teilmenge liegt, die so eine Anordnung besitzt. Endliche Körper und solche mit endlicher Charakteristik fallen damit schon mal weg. Man könnte nehmen, aber man könnte dann keine Länge (Norm) definieren, weil man in vielen Fällen in auch aus positiven Zahlen nicht die Wurzel ziehen kann (z.B. nicht aus 2). --Digamma (Diskussion) 20:05, 21. Okt. 2014 (CEST)
- Kurze Antwort: In der Literatur werden Skalarprodukte nur über den Körpern und definiert. Deshalb können wir gar nicht anders, als dies so darzustellen. Was sonst noch denkbar wäre, ist eine andere Sache.
- Symmetrische Bilinearformen kann man über beliebigen Körpern definieren. Manche Autoren nennen dies dann "Skalarprodukt". In diesem Fall gibt es also wirklich über jedem Körper ein Skalarprodukt. Aber die überwiegende Mehrheit spricht nur dann von einen Skalarprodukt, wenn es positiv definit ist. Und diese Eigenschaft gibt es eben nur, wenn es auf dem Körper eine Anordnung gibt.
- Bist du sicher, dass dein Mathelehrer hier wirklich beliebige Körper zulassen wollte? Oft will man offenlassen, ob es um oder geht und schreibt dann "". --Digamma (Diskussion) 14:58, 22. Okt. 2014 (CEST)
- Gut, dann ist die Artikelveränderung nicht nötig. Ich gebe auch zu, die allermeisten Vektorräume, die angewendet werden, sind auf oder definiert.
Mit dem positiv definit stimme ich völlig überein. Mein Lehrer hat das Skalarprodukt auch als positiv definit definiert. Aber wenn man jetzt tatsächlich einen Vektorraum über definiert - es muss ja nicht ein Vektorraum sein, sondern kann auch etwas völlig anderes sein - dann gibt es doch dafür auch ein oder mehrere positiv definite(s) Skalarprodukt(e)? Die Definition des Skalarprodukts muss ja keine Wurzel oder Quadrate enthalten, das ist ja erstmal völlig offen.
Kurze Frage am Rande: Warum widerspricht ein endlicher Körper dem positiv definit? --GelberBaron (Diskussion) 11:24, 23. Okt. 2014 (CEST)- Endliche Körper können nicht angeordnet werden, siehe geordneter Körper. Grüße - HilberTraum (d, m) 20:49, 23. Okt. 2014 (CEST)
- Ups! Danke für den Hinweis, jetzt hab ich das Problem verstanden.
Und auf der Körperseite sind auch keine weiteren unendlichen Körper (also solche, die positiv definit sein können) aufgelistet außer , und . Da nicht wirklich eine Rolle spielt, ist die Artikeländerung hinfällig, und die Diskussion auch. Ich möchte an dieser Stelle den geduldigen Antworten noch einmal herzlich danken.
(Natürlich ist das Problem nur hinfällig, wenn alle anderen das Problem auch als erledigt ansehen.) --GelberBaron (Diskussion) 23:49, 23. Okt. 2014 (CEST)
- Ups! Danke für den Hinweis, jetzt hab ich das Problem verstanden.
- Endliche Körper können nicht angeordnet werden, siehe geordneter Körper. Grüße - HilberTraum (d, m) 20:49, 23. Okt. 2014 (CEST)
- Gut, dann ist die Artikelveränderung nicht nötig. Ich gebe auch zu, die allermeisten Vektorräume, die angewendet werden, sind auf oder definiert.
Einsteinsche Summenkonvention?
Ich bin mir nicht sicher, ob und wenn dann wo, man ggf die Einsteinsche Summenkonvention hier noch mit reinbringen könnte / sollte? Entweder am Ende vom Abschnitt "in kartesischen Koordinaten" oder unter "Eigenschaften" oder aber weiter hinten unter "Anwendungen" / "in der Physik"? Dort wird es nämlich teilweise verwendet um Operatoren in kurzer Schreibweise darzustellen. Ein Operator zum Quadrat wird dann einfach schnell mal zur Komponente zum Quadrat... --Dunstkreis (Diskussion) 21:49, 19. Jul. 2015 (CEST)
- Warum hier? --Digamma (Diskussion) 06:23, 20. Jul. 2015 (CEST)
Kontravariante, Kovariante Vektoren
Warum werden diese mit keinem Wort in dem Artikel erwähnt? Ein allgemeines Skalarprodukt formt man mit einem Kovarianten und Kontravarianten Vektor mit Hilfe der Metrik wodurch immer ein Skalar entsteht.--Neoleviathan (Diskussion) 00:23, 13. Feb. 2016 (CET)
- könnte man machen, nur ist die Welt nicht immer kartesisch :)) WIr lagen vor Madagaskar (Diskussion) 00:30, 13. Feb. 2016 (CET)
- @Neoleviathan: Du vermischt zwei Dinge:
- Einen kovarianten und einen kontravarianten Vektor kann man ohne Metrik multiplizieren, denn der Raum der kovarianten Vektoren ist der Dualraum des Raums der kontravarianten Vektoren. Man spricht hier auch von einer dualen Paarung.
- Eine Metrik (in einem Vektorraum - nicht auf einer Mannigfaltigkeit) ist nichts anderes als ein Skalarprodukt. Wenn man eine Metrik hat, dann kann man deshalb mit ihrer Hilfe zwei kontravariante Vektoren multiplizieren. Mit der durch sie auf dem Dualraum induzierten Metrik kann man zwei kovariante Vektoren (Kovektoren) multiplizieren. --Digamma (Diskussion) 00:52, 13. Feb. 2016 (CET)
- Typisch Mathematiker, na dann auf schreibts in den Artikel ;) Mir ging es eher um die Skalarbildung (mit ko- und kontra), und nicht in welchem Raum man jetzt welche Vektorformen multiplizieren kann. --Neoleviathan (Diskussion) 00:55, 13. Feb. 2016 (CET)
"Einfaches" Produkt zweier komplexer Vektoren
Bei der Analyse der homogenen Wellengleich kommt es unter dem Ansatz von harmonischen Wellen in kartesischen Koordinaten zu folgendem Problem: Bei der Auswertung tritt der Ausdruck auf, wobei die Summanden aus dem Vektor stammen. Man könnte also einfach mal behaupten, der Ausdruck sei das Skalarprodukt von mit sich selbst, also . Leider sind die Komponenten aber nicht immer reell, schon bei der Totalreflexion treten imaginäre Bestandteile auf.
Bisher verwenden wir in der Vorlesung den Begriff Skalarprodukt, wie ich aber sehe, stehen wir damit nicht im Einklang mit den hier dargestellten Eigenschaften. Wir definieren:
Betrag von : , also das Standardskalarprodukt in physikalischer Schreibweise
und
Norm aus : , also das "einfache" Skalarprodukt, das ja in diesem Fall nicht unbedingt positiv definit ist.
Speziell der Begriff Norm ist nicht schön, da er ja die Abbildung auf einen Skalar bedeutet und eher wie der Betrag vorbelegt ist. Es wäre nun schön, wenn es für diese einfache Abbildung eines Vektors auf einen Skalar (also eine spezielle Norm) einen Ausdruck gäbe, der nicht mit den oben definierten Eigenschaften des Skalarprodukts für Vektoren aus dem im Widerspruch steht. Hat jemand einen Vorschlag, oder können wir es so lassen?
--JueM (Diskussion) 10:33, 16. Apr. 2017 (CEST)
- Kannst du das Problem (ich meine die mathematisch-physikalische Seite) ein bisschen genauer erklären? Wie kommt man zu imaginären Wellenvektoren? --Digamma (Diskussion) 12:24, 17. Apr. 2017 (CEST)
- Wenn ichs richtig verstehe, dann ist das, was oben als "Norm" definiert ist, keine Abbildung in die nichtnegativen reellen Zahlen, somit keine Norm (Mathematik). Was aber immer geht, ist die Wurzel aus dem oben definierten "Betrag" zu nehmen, das ist die induzierte Norm, auch im . Ist das Problem damit geloest? -- Iwesb (Diskussion) 13:44, 17. Apr. 2017 (CEST)
- Habe gerade gefunden, dass das Problem im Abschnitt Ebene Welle#Inhomogene ebene Welle schon ein bisschen angesprochen wird. Grüße -- HilberTraum (d, m) 20:37, 19. Apr. 2017 (CEST)
Falsche Formulierung in Bezug auf Skalarprodukt und Länge eines Vektors
Im Artikel findet sich folgender Satz:
"Mit Hilfe des Skalarproduktes ist es möglich, aus der Koordinatendarstellung die Länge (den Betrag) eines Vektors zu berechnen"
Ich habe bisher angenommen, dass man die Länge eines Vektors direkt aus seiner Koordinatendarstellung berechnen kann: sqrt(a1^2 + a2^2). Vielmehr ist es doch so, dass über das Skalarprodukt der Winkel zwischen zwei Vektoren ermittelt werden kann, so wie es auch im Artikel vorgeführt wird. Und genau dieser Absatz hat den einleitenden, oben zitierten Satz. Ich würde hier als einleitenden Satz vorschlagen: Mit Hilfe des Skalarproduktes ist es möglich, aus der Koordinatendarstellung zweier Vektoren den von ihnen eingeschlossenen Winkel zu berechnen.
Schöne Grüße! Tobias (nicht signierter Beitrag von Tobias74 (Diskussion | Beiträge) 13:21, 26. Jul. 2017 (CEST))
- [Einschub nach Bearbeitungskonflikt:] Hallo Tobias!
- Gegen Deinen Vorschlag gibt es (1) einen inhaltlichen und (2) einen formalen Einwand:
- Wie aus dem fraglichen Abschnitt erkenntlich, handelt es sich bei der von Dir erwähnten „Koordinatendarstellung“ nur um einen Spezialfall der allgemeineren (koordinatenfreien) vektoriellen (geometrischen) Darstellung des Betrags eines Vektors für den Fall, daß eine Orthogonalbasis (= ein rechtwinkeliges Koordinatensystem) vorgegeben ist. Erst bezüglich einer solchen Basis hat ein Vektor überhaupt Koordinaten und diese ändern sich bei einem Wechsel des Koordinatensystems. Es gilt also allgemein und für den Spezialfall eines rechtwinkeligen Koordinatensystems, in dem ist, außerdem , sodaß auch in diesem Fall der Betrag eigentlich mit Hilfe des Skalarprodukts berechnet wird.
- Darüber hinaus würde Dein Vorschlag den Sinnzusammenhang des ganzen Abschnitts zerstören, weil es unmittelbar nach dem von Dir vorgeschlagenen Einleitungssatz „… den eingeschlossenen Winkel zweier Vektoren zu berechnen:“ nicht um die Berechnung des Winkels, sondern um die Berechnung des Betrags geht. Um den Winkel geht es dann erst im (mit dem Satz „Indem man die geometrische Definition mit der Koordinatendarstellung kombiniert, …“ eingeleiteten) zweiten Teil des Abschnitts. Dieser Mangel bliebe selbst dann bestehen, wenn man meine oben unter Punkt (1) vorgebrachten inhaltlichen Bedenken gegen Deinen Vorschlag beiseite schöbe.
- Insgesamt bin ich daher dafür, an dieser Stelle vorerst alles beim Alten zu lassen. Falls man die (wie Dein Einwand zeigt, evtl. doch vorhandenen) Unklarheiten im Text beseitigen möchte, dann müßte das jedenfalls in einer ganz anderen Form geschehen, die meine obigen Bedenken berücksichtigten. Dritte Meinungen zu der Frage sind natürlich gern gesehen!
- Liebe Grüße, Franz 14:58, 26. Jul. 2017 (CEST) (P. S.: Bitte lies Dir kurz unsere Hilfeseite zum Signieren von Diskussionsbeiträgen durch.)
- Der Satz soll nur den ersten Teil des Abschnitts einleiten, wo es darum geht, wie man die Länge eines Vektors durch das Skalarprodukt ausdrückten kann. Dass dies auf die übliche Formel, die sich aus dem Satz des Pythagoras ergibt, führt, steht zwei Sätze später in dem Absatz.
- Dass man mit Hilfe des Skalarprodukts den Winkel berechnen kann, steht im zweiten Teil des Abschnitts.
- Kurz: Ich sehe keinen Handlungsbedarf. --Digamma (Diskussion) 14:50, 26. Jul. 2017 (CEST)
- Ahh ok, jetzt verstehe ich die zwei getrennten Abschnitte: Der erste Absatz erläutert den Zusammenhang zwischen Skalarprodukt eines Vektors mit sich selbst (=Quadrat des Betrags) und der zweite Absatz errechnet dann den Winkel zwischen zwei Vektoren. Danke für die Aufklärung :-) Wir können nun diesen Diskussionspunkt wieder löschen von meiner Seite aus. Soll ich einfach den ganzen Absatz hier auf der Diskussionsseite löschen? (nicht signierter Beitrag von Tobias74 (Diskussion | Beiträge) 16:18, 26. Jul. 2017 (CEST))
- Nein, lass das lieber stehen. Es schadet nicht, wenn andere das noch später nachlesen können. Und nach einiger Zeit wird es archiviert (siehe Baustein ganz oben).
- Möglicherweise missverstehen noch andere Leser den Abschnitt. Vielleicht hat dich eine ganz bestimmte Formulierung dazu geführt, den Abschnitt falsch zu verstehen? In diesem Fall wäre es vielleicht möglich, durch eine Änderung der Formulierung den Abschnitt zu verbessern und die Gefahr eines Missverständnisses zu verringern. --Digamma (Diskussion) 16:28, 26. Jul. 2017 (CEST)
- [Nach Bearbeitungskonflikt:] Nein, Diskussionsbeiträge werden im Allgemeinen nicht gelöscht. Dieser Abschnitt wird stattdessen nach einiger Zeit automatisch archiviert werden. Näheres zum Archiv findest Du weiter oben vor dem ersten Abschnitt. Franz 16:34, 26. Jul. 2017 (CEST) (P. S.: Ich erinnere an meinen Hinweis auf unsere Hilfeseite zum Signieren von Diskussionsbeiträgen, bitte bei Gelegenheit einmal durchlesen.)
"euklidische Anschauungsraum"
Diese Einschränkung ist mir unverständlich. Unter welchen Umständen ist das das Skalarprodukt etwas anderes? TiHa (Diskussion) 12:51, 9. Aug. 2017 (CEST)
- Ein Winkel ist zunächst nur im euklidischen Anschauungsraum überhaupt definiert. Nur hier kann man das Skalarprodukt mit Hilf des Winkels definieren. In anderen Räumen wird der Winkel erst mit Hilfe des Skalarprodukts definiert. --Digamma (Diskussion) 13:36, 9. Aug. 2017 (CEST)
- Das Problem liegt hierbei vor allem darin, dass begrifflich nicht sauber zwischen dem Skalarprodukt und dem Standardskalarprodukt unterschieden wird. Das Skalarprodukt wird für beliebige Vektorräume denen ein beliebiger Körper zugrunde liegt definiert. Das Standardskalarprodukt ist nur im euklidischen Raum definiert, also ein hoch spezifisches Skalarprodukt. --WehSchnittchen (Diskussion) 14:45, 26. Jun. 2020 (CEST)
Wohldefiniertheit
Auf der einen Seite werden Koorditnaten miteinander mutlipliziert und auf der anderen Seite wird der Winkel zwischen den Vektoren verwendet. Dieser Zusammenhang wird zwar anschaulich erklährt, aber es gibt keinen Beweis dafür. Es fehlt ein Beweis oder eine Verlinkung zum Beweis, der besagt, dass dieser Zusammenhang wohldefiniert ist. (nicht signierter Beitrag von Uhennig (Diskussion | Beiträge) 07:47, 3. Mai 2020 (CEST))
- Der Zusammenhang ist "Folklore". Sind e1, e2, e3 die Einheitsvektoren, die senkrecht aufeinender stehen, so folgt ei*ej=0 für i<>j und ei*ei=1, jetzt brauchst Du nur noch ausmultiplizieren: (a1e1+a2e2+a3e3)(b1e1+b2e2+b3e3)=a1b1+a2b2+a3b3. --Joachim Mohr (Diskussion) 18:01, 3. Mai 2020 (CEST)
- Nur am Rande: Dazu muss man aber erstmal nachweisen, dass die Bilinearität gilt. --Digamma (Diskussion) 18:19, 3. Mai 2020 (CEST)
- Wikipedia ist kein Lehrbuch und kein Fachbuch. Mathematische Aussagen müssen hier nicht bewiesen, sondern nur erläutert werden. --Digamma (Diskussion) 18:18, 3. Mai 2020 (CEST)
Titel: Standardskalarprodukt/ euklidisches Skalarprodukt
Hier wird das Standardskalarprodukt (auch euklidische Skalarprodukt) beschrieben, das in der Physik und den Ingenieurswissenschaften von hoher Bedeutung ist. Dies ist ein spezifisches von unendlich vielen Skalarprodukten. Die Eigenschaften des Standardskalarprodukts als die aller Skalarprodukte darzustellen, so wie es in diesem Artikel der Fall ist, ist faktisch falsch. Man könnte den gesamten Artikel unter dem Titel "euklidisches Skalarprodukt" oder "Standardskalarprodukt" veröffentlichen um dies richtig zu stellen. Die kurzen Anmerkungen, zu anderen Skalarprodukten schaffen nur Verwirrung.
Ein Artikel über das Skalarprodukt sollte zumindest seine Definition enthalten. In der Mathematik ist ein Skalarprodukt eine Abbildung, die zwei Vektoren eine Zahl zuordnet und 3 Eigenschaften aufweisen muss. Das Skalarprodukt ist wie folgt definiert:
Sei V ein Vektorraum über einem Körper K. Jedem Paar zweier beliebiger Vektoren x und y aus dem Vektorraum V sei eine Zahl aus K zugeordnet, wobei für alle Vektoren x,y,z aus V und alle Zahlen r,s aus K gilt:
1) (x,y) = (y,x) (im Komplexen wird die rechte Seite konjugiert, das kann ich in dem Editor hier nicht)
2) (x,x) >= 0
3) (rx + sy, z) = r(x,z) +s(y,z)
Als ein Beispiel für ein anderes Skalarprodukt könnte man das bestimmte Integral über das Produkt zweier Polynome aufführen. Dies ist auf dem Vektorraum der Polynome definiert und erfüllt alle Eigenschaften eines Skalarprodukts. Aussagen über Winkel und andere Spezifitäten des euklidischen Skalarprodukts treffen hier jedoch nicht zu.
--WehSchnittchen (Diskussion) 15:24, 26. Jun. 2020 (CEST)
- Hast du den Artikel ganz gelesen oder nur den Anfang? Alles, was du schreibst, wird im Artikel genannt. Die Aussage, dass man nur beim euklidischen Skalarprodukt Winkel definieren könne, ist allerdings falsch. --Digamma (Diskussion) 15:31, 26. Jun. 2020 (CEST)
- Genauer: Der Artikel ist in zwei große Abschnitte gegliedert. Der erste heißt "Im euklidischen Raum", der zweite "In allgemeinen reellen und komplexen Vektorräumen". In diesem zweiten Abschnitt steht genau das, was du vermisst. --Digamma (Diskussion) 18:32, 26. Jun. 2020 (CEST)
IP-Anmerkung
- übertragen von IP-Disk, betrifft: [3], -- Toni 19:39, 11. Dez. 2021 (CET)
Achtung!
Die Definition für das innere Produkt ist falsch. Ein inneres Produkt muss nicht positiv definit sein. Diese Bedingung in der Definition ist falsch und nicht nötig. Es kann genauso auch negativ definite (und anders definite) innere Produkte geben. Siehe dafür z.B. auch "Manifolds, Tensors and Forms" von Paul Renteln auf Seiten 14 und 15.
Ich bin kein Meister im Bearbeiten von solchen Seiten und hoffe, dass jemand diesen Fehler entsprechend auf der ganzen Seite ausbessern kann. Für den Moment lasse ich auf der Seite einfach eine kleine Warnung an den Leser/die Leserin da, dass dieser Punkt in der Definition nicht gebraucht wird.
Vielen Dank! (nicht signierter Beitrag von 2001:67C:10EC:5746:8000:0:0:166 (Diskussion) 11:44, 5. Aug. 2021 (CEST))
- Verschiedene Autoren bzw. verschiedene Autoren verwenden unterschiedliche Definitionen. Anscheinend verwendet Paul Renteln eine andere Definition als die hier im Artikel. Das bedeutet noch lange nicht, dass die hier verwendete falsch ist. --Digamma (Diskussion) 10:20, 23. Okt. 2022 (CEST)
Bitte den Begriff inneres Produkt beschreiben...
z.B. kleinstmöglicher Winkel zwischen zwei Vektoren??? --2A02:810A:1840:1ED4:F961:6E7C:1537:7818 08:20, 23. Okt. 2022 (CEST)
- Der Begriff "inneres Produkt" ist ein Synonym zu "Skalarprodukt". Man kann damit den genannten Winkel berechnen. Wie das geht, steht im Artikel. Das innere Produkt selbst gibt aber nicht diesen Winkel an. --Digamma (Diskussion) 10:17, 23. Okt. 2022 (CEST)
- Inneres Produkt = Skalarprodukt. Was im Artikel steht ist vollkommen richtig. Vgl Skript von Gert-Martin Greuel "Eine positiv definite symmetrische Bilinearform auf R bzw. eine positiv definite hermitesche Sesquilinearform auf C nennt man auch ein Skalarprodukt oder ein inneres Produkt auf V." --Joachim Mohr (Diskussion) 12:06, 23. Okt. 2022 (CEST)
- Die Frage zielte evtl. nich darauf ab, was wie genannt wird, sondern was es ist. Das Skalarprodukt ist ein mathematischen Objekt, das in unterschiedlichen Kontexten unterschiedlichen Nutzen bietet. Es beschreibt zunächst erstmal nur eine Rechenvorschrift. Eine Anwendung ist, dass es ein Maß für die Ähnlichkeit der Richtung von Vektoren ist. Das Skalarprodukt von z.B. Einheitsvektoren (Vektoren der Länge 1) ist ein direktes Maß für den Winkel, da es direkt der Cosinus des Winkels ist. Die "Ähnlichkeit" ist 1 wenn beide Richtungen gleich sind. Bei Vektoren, deren Länge nicht Eins ist, ist das nicht mehr ganz so einfach. Eine Andere Anwendung ist die physikalische Arbeit, die sich aus dem Kraftvektor und dem Weg-Vektor ergibt. Ihr Wert hängt einerseits von der Ähnlichkeit der Winkel der Vektoren ab und ist am größten, wenn die "Ähnlichkeit", also der Cosinus 1 ist. Er hängt andererseits von der Länge der Vektoren ab und ist um so größer, je länger sie sind. Das ist übrigens empirisch so begründet, nicht mathematisch. Usw. Es gibt darüber hinaus jede Menge andere Anwendungen. So ist z.B.in der Statistik der Zusammenhang von Datenreihen, den man Korrelation nennt, letztlich das Skalarprodukt von "Datenvektoren". Im übertragenen Sinne zeigen die Daten in eine ähnlichere Richtung, je näher der Wert an 1 rankommt. Das Skalarprodukt ist hier "nur" genau so ein nützliches Vihekel, wie ein Durchschnitt. TiHa (Diskussion) (ohne (gültigen) Zeitstempel signierter Beitrag von TiHa (Diskussion | Beiträge) 20:45, 23. Okt. 2022 (CEST))
- Das ist alles richtig. Ich kann aber nicht erkennen, was dem Fragesteller am Artikel fehlt. Joachim Mohr hat möglicherweise auf den falschen Beitrag geantwortet. Sein Beitrag wirkt eher wie eine Antwort auf den Beitrag darüber im Abschnitt "IP-Anmerkung". --Digamma (Diskussion) 06:55, 24. Okt. 2022 (CEST)
- Die Frage zielte evtl. nich darauf ab, was wie genannt wird, sondern was es ist. Das Skalarprodukt ist ein mathematischen Objekt, das in unterschiedlichen Kontexten unterschiedlichen Nutzen bietet. Es beschreibt zunächst erstmal nur eine Rechenvorschrift. Eine Anwendung ist, dass es ein Maß für die Ähnlichkeit der Richtung von Vektoren ist. Das Skalarprodukt von z.B. Einheitsvektoren (Vektoren der Länge 1) ist ein direktes Maß für den Winkel, da es direkt der Cosinus des Winkels ist. Die "Ähnlichkeit" ist 1 wenn beide Richtungen gleich sind. Bei Vektoren, deren Länge nicht Eins ist, ist das nicht mehr ganz so einfach. Eine Andere Anwendung ist die physikalische Arbeit, die sich aus dem Kraftvektor und dem Weg-Vektor ergibt. Ihr Wert hängt einerseits von der Ähnlichkeit der Winkel der Vektoren ab und ist am größten, wenn die "Ähnlichkeit", also der Cosinus 1 ist. Er hängt andererseits von der Länge der Vektoren ab und ist um so größer, je länger sie sind. Das ist übrigens empirisch so begründet, nicht mathematisch. Usw. Es gibt darüber hinaus jede Menge andere Anwendungen. So ist z.B.in der Statistik der Zusammenhang von Datenreihen, den man Korrelation nennt, letztlich das Skalarprodukt von "Datenvektoren". Im übertragenen Sinne zeigen die Daten in eine ähnlichere Richtung, je näher der Wert an 1 rankommt. Das Skalarprodukt ist hier "nur" genau so ein nützliches Vihekel, wie ein Durchschnitt. TiHa (Diskussion) (ohne (gültigen) Zeitstempel signierter Beitrag von TiHa (Diskussion | Beiträge) 20:45, 23. Okt. 2022 (CEST))
Abstand zwischen den Faktoren eines Produkts
Es ist mir schon bei anderen Artikeln aufgefallen, und ganz speziell auch bei diesem: Der Abstand zwischen den Faktoren eines Produkts, also anstatt . Habe ich da eine neue Entwicklung verpasst? Woher kommt das, woher ist das gut? Ist das ein neuer Standard oder einer, der im Begriffe ist, sich durchzusetzen? Für mich sieht das so aus, als ob da verschiedene Symbole unverbunden nebeneinanderstehen, eine Kollektion von Symbolen. Das mag aber auch daran liegen, dass mein Auge an die "alte" Schreibweise gewöhnt ist. So oder so wäre ich dankbar, wenn mich jemand aufklärt, was es damit auf sich hat. --Mathze (Diskussion) 22:22, 9. Jan. 2023 (CET)
- Wahrscheinlich bin ich dafür verantwortlich. Ich finde das einfach übersichtlicher. --Digamma (Diskussion) 17:04, 10. Jan. 2023 (CET)
- PS: Wenn es dich stört, kannst du die
\,auch gerne entfernen. --Digamma (Diskussion) 17:16, 10. Jan. 2023 (CET)- PPS: Ich kenne diese Schreibweise mit kleinem Abstand aus Schulbüchern. --Digamma (Diskussion) 18:07, 10. Jan. 2023 (CET)